Оценка несущей способности оснований щелевых фундаментов на основе анализа напряженного состояния грунтового массива и экспериментальных данных

На правах рукописи

ИВАНОВ АНТОН АНДРЕЕВИЧ

ОЦЕНКА НЕСУЩЕЙ СПОСОБНОСТИ ОСНОВАНИЙ ЩЕЛЕВЫХ ФУНДАМЕНТОВ НА ОСНОВЕ АНАЛИЗА НАПРЯЖЕННОГО СОСТОЯНИЯ ГРУНТОВОГО МАССИВА И ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ

Специальность: 05.23.02 - «Основания и фундаменты, подземные сооружения»

АВТОРЕФЕРАТ

диссертации на соискание ученой степени

кандидата технических наук

Волгоград 2013

Работа выполнена в федеральном государственном бюджетном образовательном учреждении высшего профессионального образования Волгоградском государственном архитектурно-строительном университете.

Научный руководитель:	кандидат технических наук, доцент Богомолова Оксана Александровна
Официальные оппоненты:	Доктор технических наук, профессор Дыба Владимир Петрович, ФГБОУ ВПО Южно-Российский государственный политехнический университет (НПИ) имени М.И.Платова, профессор кафедры «Промышленное, гражданское строительство, геотехника и фундаментостроение»
	кандидат технических наук, доцент Ермаков Олег Владимирович, ФГБОУ ВПО Волгоградский государственный архитектурно-строительный университет, доцент кафедры «Строительство»
Ведущая организация:	Государственное унитарное научное предприятие Научно-исследовательский, проектно-конструкторский и производственный институт строительного комплекса Республики Башкортостан (БашНИИстрой) г. Уфа

Защита состоится «19» декабря 2013 года в 13-00 часов на заседании диссертационного совета Д 212.026.04 в ФГБОУ ВПО Волгоградском государственном архитектурно-строительном университете по адресу:

400074, г. Волгоград, ул. Академическая,1, ауд. Б-203.

С диссертацией можно ознакомиться в библиотеке ФГБОУ ВПО «Волгоградский государственный архитектурно-строительный университет»

Автореферат разослан « » ноября 2013 г.

Ученый секретарь

диссертационного совета Акчурин

Талгать Кадимович

В В Е Д Е Н И Е

Актуальность темы диссертации. Несущая способность основания щелевого фундамента складывается из несущей способности по его подошве и по его боковой поверхности. Кроме сил сопротивления, обусловленных внутренним трением и сцеплением грунта, по боковой поверхности и по подошве фундамента действуют дополнительные силы сопротивления, возникающие за счет: проникновения водно-коллоидного цементного раствора вглубь грунта и последующего его твердения с образованием тонкого грунтово-цементного слоя с кристаллическими связями; расширения бетона, содержащего расширяющийся портландцемент, при твердении. Необходимость учета этих сил, делает задачу о совершенствовании методов расчета несущей способности оснований щелевых фундаментов актуальной.

Цель диссертационного исследования сформулирована следующим образом:

Разработать инженерный метод расчета несущей способности щелевого фундамента, основанный на анализе напряженного состояния грунтового массива методами теории функций комплексного переменного и конечных элементов и экспериментального определения суммарных сил трения и сцепления между боковой поверхностью фундамента и вмещающим массивом грунта непосредственно на строительной площадке в реальных инженерно-геологических условиях.

Для достижения поставленной цели необходимо решить следующие задачи:

1. Провести анализ существующих методов расчета несущей способности основания щелевых фундаментов и технической литературы, на основе которого определить интервалы изменения переменных расчетных параметров для проведения численного эксперимента.
2. Разработать механико-математическую модель и определить численные значения коэффициентов отображающей функции, обеспечивающие конформное отображение полуплоскости с вырезом при заранее заданных величинах отношения ширины его основания к глубине (2b/h).
3. Провести компьютерное моделирование процесса образования и развития областей пластических деформаций под подошвой щелевого фундамента, по результатам которого получить графические зависимости и их аналитические аппроксимации, позволяющие определять величину расчетного сопротивления и предельно допустимую нагрузку при условии учета только подошвы фундамента. Разработать компьютерную программу-калькулятор для автоматизации этого процесса.
4. Разработать и получить охранный документ на полезную модель устройства для определения в полевых условиях суммарных сил трения и сцепления, действующих по контакту «боковая поверхность щелевого фундамента - грунтовый массив».
5. Разработать механико-математическую модель и провести компьютерное моделирование процесса трансформации напряженного состояния и образования и развития областей пластических деформаций в основании двух щелевого фундамента методом конечных элементов. Получить графические и аналитические зависимости размеров ОПД от физико-механических свойств грунта, размеров фундамента и интенсивности внешнего воздействия. Предложить инженерный метод расчета несущей способности двух щелевого фундамента, формализовав его в компьютерную программу – калькулятор.
6. Провести экспериментальные исследования процесса образования и развития областей пластических деформаций под подошвой щелевого фундамента, а полученные результаты сопоставить с результатами аналитических исследований.
7. Осуществить внедрение результатов диссертационного исследования в строительную практику.

Достоверность результатов диссертационного исследования, его выводов и рекомендаций обоснованы:

1. Рабочими гипотезами, опирающимися на фундаментальные положения линейной теории упругости (методы теории функций комплексного переменного и конечных элементов), теории пластичности, инженерной геологии, грунтоведения и механики грунтов;
2. Использованием в качестве инструментария при теоретических исследованиях верифицированных компьютерных программ, зарегистрированных в государственном реестре программного обеспечения;
3. Удовлетворительной сходимостью результатов экспериментов по определению критических нагрузок для моделей оснований щелевых фундаментов, выполненных из эквивалентных материалов, с результатами сопоставительных расчетов реальных грунтовых массивов при адекватных значениях коэффициента бокового давления грунта с поведением этих объектов в природе.
4. Патентом РФ на полезную модель.
5. Результатами внедрения выводов и рекомендаций диссертационной работы в строительную практику.

Научная новизна диссертационной работы состоит в том, что

- установлены и изучены закономерности трансформирования полей напряжений и протекания процесса зарождения и развития областей пластических деформаций под подошвой и по контакту «боковая поверхность щелевого фундамента – грунт» в процессе нагружения фундамента вплоть до достижения критических нагрузок;

- построены графические зависимости размеров (глубины развития под подошву и вверх по контакту «фундамент – грунт») областей пластических деформаций от величины интенсивности внешнего воздействия для всех рассмотренных в диссертации численных значениях переменных расчетных параметров для двухщелевого фундамента; аналитические аппроксимации этих зависимостей составили базу данных компьютерной программы-калькулятора для расчета несущей способности двухщелевого фундамента;

- для определения несущей способности по подошве щелевого фундамента использованы методы теории функций комплексного переменного, позволившие полностью исключить из рассмотрения боковую поверхность щелевого фундамента;

- для определения несущей способности боковой поверхности щелевого фундамента разработана и запатентована полезная модель устройства для определения суммарных сил трения и сцепления, возникающих по контакту «боковая поверхность щелевого фундамента – грунт» при бетонировании враспор без опалубки;

- разработан инженерный метод расчета несущей способности основания щелевого фундамента, основанный на использовании запатентованного устройства и компьютерной программы-калькулятора для расчета несущей способности по подошве щелевого фундамента;

Практическая значимость работы. Диссертационная работа является частью научных исследований, проводимых на кафедрах «Прикладная математика и вычислительная техника» и «Гидротехнические и земляные сооружения» ВолгГАСУ в 2010-2013 г.г.

Полученные при работе над диссертацией результаты могут быть использованы для:

• расчета величины несущей способности основания щелевого фундамента при широком диапазоне изменения численных значений переменных расчетных параметров, включающих геометрические размеры фундамента и физико-механические характеристики грунтов основания;
• экспериментального определения непосредственно на строительной площадке суммарных сил трения и сцепления, возникающих по его боковой поверхности при бетонировании тела фундамента враспор без опалубки;
• расчета несущей способности основания двухщелевого фундамента при различных значениях его геометрических размеров и физико-механических характеристиках вмещающего грунтового массива;
• предварительной оценке несущей способности оснований щелевых фундаментов на стадии предварительного проектирования;
• оценки возможной погрешности расчетов несущей способности по боковой поверхности щелевого фундамента известными методами при помощи запатентованного автором устройства.

Апробация работы. Основные результаты выполненных автором диссертационной работы исследований доложены, обсуждены и опубликованы в материалах: ежегодных научно-технических конференций преподавателей, аспирантов и студентов Волгоградского государственного архитектурно-строительного университета (Волгоград, ВолгГАСУ, 2010-2013 г.г.), Всероссийской научно-технической конференции «Механика грунтов в геотехнике и фундаментостроении» (Новочеркасск, ЮРГТУ-НПИ, 2012 г.); III Международной научно-технической конференции «Инженерные проблемы строительного материаловедения, геотехнического и дорожного строительства» (Волгоград, ВолгГАСУ, 2012 г.); Всеукраинского научно-практического семинара с участием иностранных специалистов «Современные проблемы геотехники» (Украина, Полтава, ПНТУ им. Ю.Кондратюка, 2012 г.); на научных семинарах кафедр «Прикладная математика и вычислительная техника» и «Гидротехнические и земляные сооружения» ВолгГАСУ (Волгоград, ВолгГАСУ, 2010-2013 г.г.).

Личный вклад автора заключается в:

• разработке и составлении механико-математических моделей и расчетных схем методов теории функций комплексного переменного и МКЭ исследуемых объектов (коэффициенты отображающей функции, граничные условия, размеры, вид, степень дискретизации);
• проведении, компьютерного моделирования процессов образования и развития областей пластических деформаций в основаниях щелевого и двухщелевого фундаментов, обработке, анализе и систематизации полученных результатов, построении графических зависимостей и их аналитическом описании;
• проведении патентного поиска, анализе его результатов, разработке полезной модели и ее патентовании;
• разработке инженерных методов расчета несущей способности щелевого и двухщелевого фундаментов;
• формировании баз данных и разработке компьютерных программ-калькуляторов, предназначенных для оценки несущей способности щелевых фундаментов;
• внедрении результатов диссертационной работы в строительную практику на стадии проектирования.

На защиту выносятся:

1. Механико-математические модели и расчетные схемы методов теории функций комплексного переменного и метода конечных элементов исследуемых объектов.
2. Установленные закономерности протекания процесса образования и развития областей пластических деформаций под подошвами и по боковой поверхности щелевых фундаментов.
3. Прием исключения из рассмотрения боковой поверхности щелевого фундамента на основе использования методов теории функций комплексного переменного.
4. Полезная модель устройства для определения суммарных сил трения и сцепления, возникающих по контакту «боковая поверхность щелевого фундамента – грунт» при бетонировании враспор без опалубки;
5. Инженерный метод расчета несущей способности щелевого фундамента и компьютерная программа-калькулятор для определения несущей способности по его боковой поверхности.
6. Инженерный метод расчета несущей способности двухщелевого фундамента и формализующая его компьютерная программа-кулькулятор.
7. Результаты внедрения результатов диссертационной работы в практику строительства.

Результаты научных исследований внедрены:

- при определении несущей способности основания монолитных фундаментов, выполненных враспор грунта на объекте: «Здание столовой по ул. Баррикадной, дом 11, в р.п. Красные Баррикады Икрянинского района Астраханской области» в ООО НПФ Инженерный центр «ЮГСТРОЙ».

- при разработке проектов и строительстве подземной части зданий и сооружений, возводимых по технологии «стена в грунте», в частности: при проектировании административного комплекса «Бизнес-парк» в городе Перми, ограждения береговой зоны искусственного острова в акватории р. Камы (Пермский край).

- в учебном процессе на кафедре «Гидротехнические и земляные сооружения» Волгоградского государственного архитектурно-строительного университета.

Публикации. Основные положения диссертации опубликованы в 8 научных статьях, их них две в ведущих рецензируемых научных изданиях и 1 патент РФ на полезную модель.

Структура и объем работы. Диссертационная работа состоит из введения, четырех глав, общих выводов, списка используемой литературы из 113 наименований и приложений. Общий объем работы - 164 страницы машинописного текста, в том числе 114 страниц основного текста, содержащего 145 иллюстрации и 14 таблиц.

Автор выражает искреннюю благодарность сотрудникам кафедр «Прикладная математика и вычислительная техника» и «Гидротехнические и земляные сооружения» Волгоградского государственного архитектурно-строительного университета за помощь и поддержку при работе над диссертацией.

Особую благодарность автор выражает научному руководителю, кандидату технических наук, доценту Богомоловой О.А. за ценные советы и постоянную помощь во время написания диссертации.

Общая характеристика работы

Во введении отмечается значительный вклад отечественных и зарубежных ученых в изучение вопросов, посвященных вопросам изучения, расчета и проектирования щелевых фундаментов. Это Далматов Б. И., Зубков В. М., Павлов В. В., Горбунов-Пасадов М. И., Березанцев В. Г., Банников Н. Д., Гинзбург Л. К., Ухов С. Б., Семенов В. В., Знаменский В. В., Лушников В.В., Тер-Мартиросян З. Г., Чернышев С. Н., Платонова С. В., Иванов В. Е., Криворотов А. П., Смородинов М. И., Федоров Б. С., Ильичев В. А., Крутов В. И., Сорочан Е. М., Трофименков Ю. Г., Швецов Г. И., Пилягин А.В., Носков И. В., Слободян А. Г., Госьков Г.С., Богомолов А. Н., Богомолова О. А., Брандтль Х., Глушков В. Е., Мамаев Н. Г., Мирошин А. Н., Глушков И. В., Петров В. П. и многие другие.

Обоснована актуальность темы диссертационного исследования, определены цель работы, основные задачи, которые необходимо решить, и методы решения, указаны научная новизна, степень апробации, практическая значимость, выносимые на защиту положения, а также представлены данные о внедрении результатов диссертационной работы в строительную практику.

В первой главе диссертационной работы рассмотрены особенности расчета несущей способности основания щелевых фундаментов, определены диапазоны изменения численных значений переменных расчетных параметров, сформулирована цель работы и определены задачи, требующие решения для ее достижения.

Суммарные затраты (материалы, стоимость рабочей силы, время, энергопотребление и т.д.) на устройство фундаментов в современном строительстве составляют 10–15% от общей стоимости строительно-монтажных работ, а в сложных инженерно-геологических условиях (слабые грунты, высокий уровень грунтовых вод, тесная городская застройка и т.д.) может подниматься до 30% и более.

В грунтах естественного сложения, особенно маловлажных связных грунтах, весьма перспективным является применение монолитных щелевых фундаментов с развитой боковой рабочей поверхностью. Особенно высокую эффективность применения показывают щелевые фундаменты, представляющие собой одну или систему параллельных узких щелей в грунте, заполненных в распор бетоном, которые объединены ростверком в общий фундамент для восприятия нагрузки от надземной части здания.

Внешняя нагрузка передается на грунтовое основание по боковой поверхности щелевого фундамента, по подошве и по подошве плиты ростверка, если таковая имеется.

В случае объединения в единый фундамент двух или более щелевых, в работу включается и заключенный между стенами массив грунта, за счет чего нагрузка предается в плоскости на уровне нижних торцов стенок. Несущая способность такого фундамента существенно зависит от расстояния между стенками. При этом заключенный между стенками грунт, сами стенки и ростверк в совокупности могут быть рассмотрены как бетонно-грунтовый фундамент на естественном основании, высота которого равна высоте стенок.

Известно, что щелевые фундаменты по несущей способности грунтов основания следует рассчитывать, опираясь на выражение

, (1)

где: с; cr; ct – коэффициенты условий работы грунта; R – расчетное сопротивление грунта под подошвой фундамента; A и U – ее площадь и периметр; fi; hi – расчетное сопротивление и толщина i-го слоя грунта по боковой поверхности ЩФ.

Аналогичные формулы приведены в документах, разработанных НИИОСП им. Н.М.Герсеванова.

Формула (1) выглядит убедительно, ее использование вполне логично.

Из нее видно, что полезная нагрузка, передаваемая щелевым фундаментом на основание, делится на две части: первая часть передается через подошву фундамента, а вторая – через его боковую поверхность.

В специальной и нормативной литературе приводятся данные о долевом распределении несущей способности щелевых фундаментов по их подошве и боковой поверхности, говорящие о том, что участие боковой поверхности в общей несущей способности щелевых фундаментов в среднем составляет 10% - на глубине 1м, 25% - на глубине 2м, 41% - на глубине 4м и 55% - на глубине 6м. Причем, всегда участие боковой поверхности в общей несущей способности определяются в зависимости от показателя текучести IL, которая в данном случае как бы интегрально опосредует в себе прочностные свойства грунта (удельное сцепление С и угол внутреннего трения ).

Однако кроме сил сопротивления, обусловленных этими показателями, по боковой поверхности и по подошве фундамента действуют дополнительные силы сцепления, возникающие за счет: проникновения водно-коллоидного цементного раствора вглубь грунта и последующего его твердения с образованием тонкого грунтово-цементного слоя с кристаллическими связями; расширения бетона при твердении во влажных условиях (именно это происходит при твердении бетона в конструкциях, вмещаемых массивами, сложенными глинистыми грунтами), а так же от нагревания теплотой, выделяющейся при взаимодействии цемента с водой. Эти изменения объема фиксируется после завершения процесса твердения, применяющихся при производстве работ по устройству щелевых фундаментов бетонов, в состав которых входит расширяющийся портландцемент.

Учет этих дополнительных сил при расчете несущей способности щелевых фундаментов может существенным образом увеличить расчетное значение несущей способности и долю в ней боковой поверхности ЩФ. Поэтому определять эти силы необходимо для инженерно-геологических условий каждой конкретной площадки экспериментальным методом.

Для проведения компьютерного моделирования напряженного состояния грунтового массива, вмещающего щелевой фундамент, и процесса образования и развития областей пластических деформаций во вмещающем грунте, необходимо определить интервалы изменения численных значений переменных параметров, которые определяют ход этих процессов.

К таким переменным расчетным параметрам относятся:

1. Геометрические размеры фундамента – длина (L), ширина (2b), глубина заложения (h);

2. Физико-механические свойства грунтов – удельный вес (), удельное сцепление (С), угол внутреннего трения (), коэффициент бокового давления (о), модуль деформации (Eо) и обобщенный прочностной показатель – приведенное давление связности ;

3. Свойства бетона и арматуры: класс, пределы прочности при растяжении и сжатии, модули деформации (упругости), коэффициент Пуассона.

Анализ данных, приведенных более чем в 60 литературных источниках и нормативных документах, позволил установить:

1. При различной протяженности (длине) щелевых фундаментов, которая ограничивается лишь проектным решением, величина отношения их ширины к глубине заложения 2b/h[0,01-0,4,] при этом, что сама глубина заложения щелевого фундамента h[1,5-43]м.

2. Нормативные значения угла внутреннего трения и удельного сцепления глинистых грунтов согласно СНиП изменяются в пределах [7о-30о] и C[9-81]кПа, а среднее значение удельного веса может быть принято равным =20кН/м3. Одним из переменных расчетных параметров при проведении компьютерного моделирования является приведенное давление связности. Его экстремальные значения определяются при помощи выражений

(2)

Выполняя соответствующие вычисления, используя при этом приведенные выше данные, определим, что св[0,02-22].

Известно, что величина коэффициента Пуассона для глинистых грунтов заключена в интервале . Учитывая, что величина µ связана с величиной коэффициента бокового давления грунта о соотношением , имеем, что . Известно так же, что модуль деформации глинистых грунтов изменяется в интервале .

Монолитные щелевые фундаменты следует проектировать из тяжелого бетона, имеющего класс прочности на сжатие не ниже В12.5 или В15 в зависимости от коэффициента вариации; максимальный допускаемый класс бетона - В40.

Учитывая это, ниже приведена таблица, в которую помещены численные значения переменных расчетных параметров, необходимые при проведении компьютерного моделирования. Отметим, что в случае необходимости численные значения величин, эквивалентных и С для бетона, можно определить по известным формулам акад. А.Н.Динника

; (3)

, (4)

где: р и с – пределы прочности бетона при растяжении и сжатии.

Таблица № 1.

Интервалы изменения расчетных параметров

Параметр					(MПа)	о	(кН/м3)
Грунт	0,02	22	7	30	5/75	0,75	20
Железобетон	479		38,6		25000	0,25	25

Возвращаясь к вопросу о несущей способности основания щелевого фундамента следует сказать, что несущая способность по его боковой поверхности зависит от большого количества факторов, определяемых физико-механическими свойствами вмещающего массива грунта, инженерно-геологическими условиями строительной площадки, геометрическими размерами фундамента, физико-химическими свойствами бетона, степенью проникновения коллоидного водоцементного раствора в поверхностные слои грунта откосов траншеи, технологией сооружения фундамента и т. д.

Несущая способность основания щелевого фундамента по его подошве определяется только ее геометрическими размерами и физико-механическими свойствами грунта основания.

Выделить и определить отдельно несущую способность ЩФ только по его подошве, изучая процесс зарождения и развития областей пластических деформаций под ней, позволяет аналитическое решение первой основной граничной задачи теории упругости для односвязной изотропной области, полученное проф. А.Н.Богомоловым при помощи методов теории функций комплексного переменного.

Достоверно определить суммарные силы трения и сцепления, возникающие по контакту «боковая поверхность щелевого фундамента - грунт», учтя все перечисленные в настоящем параграфе факторы их определяющие, можно путем экспериментальных исследований, выполняемых непосредственно на строительной площадке.

При рассмотрении вопроса о несущей способности двухщелевого фундамента целесообразно использовать метод конечных элементов, который позволяет исследовать напряженное состояние неоднородных грунтовых массивов, учитывая при этом все разнообразие физико-механических свойств грунта, материала фундамента и его геометрических размеров.

Исходя из выше сказанного, цель настоящего диссертационного исследования сформулирована следующим образом:

Разработать инженерный метод расчета несущей способности щелевого фундамента, основанный на анализе напряженного состояния грунтового массива методами теории функций комплексного переменного и конечных элементов и экспериментального определения суммарных сил трения и сцепления между боковой поверхностью фундамента и вмещающим массивом грунта непосредственно на строительной площадке в реальных инженерно-геологических условия.

Во второй главе описаны этапы разработки инженерного метода расчета несущей способности основания щелевого фундамента.

Для того чтобы использовать методы теории функций комплексного переменного для анализа напряженного состояния грунтового массива, расположенного под подошвой щелевого фундамента необходимо определить такие значения коэффициентов отображающей функции (5),

(5)

где: – действительные или комплексные числа.

чтобы она совершала конформное отображение нижней полуплоскости ImZ<0 на полуплоскость с вырезом, форма которого позволяла бы рассматривать основание щелевого фундамента. Покажем, что отображающая функция (5) может быть использована для решения задач об определении напряженного состояния основания подошвы щелевого фундамента.

Наиболее часто употребляемой формой границы полуплоскости при решении геотехнических задач является полуплоскость с трапециевидным вырезом (см. рис. 1).

	Если 2b, то любую (правую или левую) часть области можно рассматривать как изолированный откос. Если основания выреза 2b и h имеют конечные размеры, а , то можно рассматривать траншею с различными углами наклона ее сторон и различными
Рис. 1. Геометрические параметры криволинейной границы односвязной области

величинами отношениями ее основания к высоте (2b/h).

Если , то можно рассматривать основание заглубленного фундамента при разных значениях отношения его ширины к глубине заложения, а при – щелевой фундамент и т.д.

В таблице № 1 приведены численные значения коэффициентов отображающей функции (5), позволяющие получать вырезы с различными значениями величин отношения ширины основания выреза к его высоте, т.е. использовать ее для анализа напряженного состояния грунтового массива

Таблица № 1.

Значения коэффициентов для отображения полуплоскости с криволинейным трапециевидным вырезом при заданных отношениях и

2b/h	С1	С3	С5		С7	С9	,°
0.01	2.043	-13.950	-57.925		-104.930	-82.944	90
0.02	2.035	-13.900	-57.850		-104.620	-82.206	90
0.05	2.013	-13.750	-57.625		-103.750	-80.100	90
0.1	1.975	-13.500	-57.250		-102.500	-76.950	87.25
0.2	1.900	-13.000	-56.500		-100.750	-72.000	86.5
0.4	1.750	-12.000	-55.000		-100.250	-67.500	80.75
а)				б)
в)				г)
Рис. 2. Графические зависимости вида (а); (б); при (в) и при (г)

под подошвой щелевого фундамента при разных отношениях величин 2b/h, а на рис. 2 – графики для их определения.

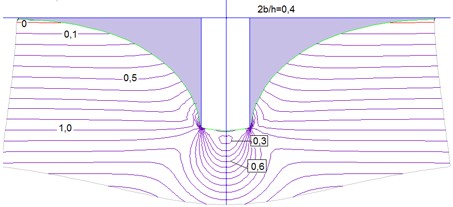
На рис. 3 в качестве примера приведены изображения фрагментов односвязных областей, которые могут быть использованы для анализа напряженного состояния основания щелевого фундамента, и картины изолиний безразмерных компонент напряжения z; x и zx.

а)	б)	в)
г)	д)	е)
Рис. 3. Фрагменты односвязных областей, которые могут быть использованы для анализа напряженного состояния основания подошвы щелевого фундамента и картины изолиний безразмерных (в долях h) напряжений z; x и zx при 2b/h=0,1 (а-б) и при 2b/h=0,4 (г-е) соответственно и о=0,75

Для полного учета влияния сил гравитации используем прием «догрузки» криволинейного контура, обеспечиваемого функцией (5), до соответствующего прямолинейного контура, заключающийся в назначении граничных условий на участке границы АВС (в нашем случае угол =90о, соответствующие области на рис. 3 отмечены фиолетовой заливкой).

«Достройка» данного конкретного контура до прямолинейного контура на участке его границы АВС осуществляется путем приложения в каждой его точке вертикальных z и горизонтальных x напряжений, возникающих в соответствующих точках ненарушенного массива с заданным очертанием внешней границы.

На основании результатов проведенных вычислений установлено, что «догружающие» напряжения для щелевых фундаментов с величиной отношения 2b/h=0,01;0,03;0,14;0,27;0,4 изменяются по закону, который со степенью достоверности R0,985 описываются экспоненциальной зависимостью вида (см. рис. 4)

, (6)

где: m и n – безразмерные коэффициенты, x – горизонтальная координата, отсчитываемая от обреза фундамента.

Коэффициенты m и n являются линейными функциями отношения 2b/h и с достоверностью Rm 0,9645 и Rn 0,9787 определяются по формулам

, (7)

. (8)

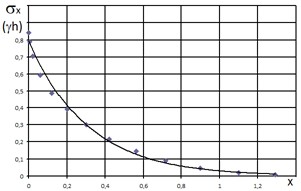а)	б)
Рис. 4. Графические зависимости вида x=f(2b/h) (а) и , (б)

Вернувшись к рис. 3, видим, что предлагаемый прием дает адекватные результаты: изолинии нормальных z и x напряжений на некотором удалении от выреза практически параллельны дневной поверхности; отношение их численных значений в соответствующих точках приблизительно равно величине о; изолинии касательных напряжений имеют классическую форму «бабочки», их значения на оси симметрии zx=0.

Расчеты по определению величины расчетного сопротивления основания щелевого фундамента выполнены при помощи компьютерных программ ASV32 и «Устойчивость. (Напряженно-деформированное состояние)», разработанных в ВолгГАСУ, для всех возможных сочетаний численных значений переменных расчетных параметров 2b/h, и , которые определены в главе I.

На рис. 5 в качестве примера приведены области пластических деформаций в основании щелевого фундамента при их зарождении, развитии и в момент достижения предельно допустимой нагрузки (смыкание ОПД).

На рис. 6 приведены, как наиболее наглядные, графические зависимости вида Z=f(q) при величине приведенного давления связности, где величины Z и q измеряются соответственно в долях h и h. Для всех остальных значений переменных расчетных параметров также построены соответствующие кривые, которые выглядят аналогичным образом. Ввиду ограниченности объема диссертационной работы некоторая их часть приведена в приложении.

а)	в)
б)
Рис. 5. Области пластических деформаций в основании щелевого фундамента при зарождении (а), развитии (б) и в момент достижения предельно допустимой нагрузки (смыкание ОПД) (в)

а)	б)	в)	г)
Рис. 6. Графические зависимости вида при b/h=0,03; 0,14; 0,27; 0,4 (а, б, в, г – соответственно

На этих графиках минимальные значения qmin, соответствуют моменту времени, когда под краями щелевого фундамента визуально наблюдается появление точек, в которых наступило предельное состояние, а максимальное qmax – моменту смыкания ОПД. То есть, величины qmin и qmax можно рассматривать как первую критическую и предельно допустимую нагрузки.

Анализируя кривые, приведенные на рис. 6, можно видеть, что они практически со 100% степенью точности аппроксимируются кусочно-линейной функцией на интервалах , и от до глубины, соответствующей смыканию областей пластических деформаций.

На каждом из этих интервалов уравнение прямой Z=f(q) может быть записано в следующем виде

, (9)

где: безразмерные коэффициенты; q – величина безразмерной (в долях h) интенсивности равномерной равномерно распределенной нагрузки и Z – глубина (в долях h) развития областей пластических деформаций.

Ниже на рис. 7 приведена часть кривых, позволяющих с погрешностью от 0 до 3,7% определить численные значения коэффициентов A и B для всех возможных сочетаний переменных расчетных параметров, рассмотренных в настоящей работе (полностью эти кривые приведены в диссертационной работе и ее приложениях). Там же приведены аналитические выражения, по которым искомые коэффициенты А и B могут быть легко вычислены с погрешностью, не превышающей указанной выше.

Рис. 7. Графические зависимости вида A,B=f(св) при и b/h=0,03

Таким образом, получены графические зависимости и формулы, позволяющие для всех возможных сочетаний переменных расчетных параметров определить глубину развития областей пластических деформаций в основании щелевого фундамента. Для этого необходимо задаться численными значениями угла внутреннего трения, приведенного давления связности и отношения геометрических параметров фундамента b/h. Затем выбрать график, который им соответствует, и определить по нему коэффициенты A и B. Подставив значения коэффициентов и величины внешней нагрузки в уравнение (9), отыщем глубину развития областей пластических деформаций Z.

Проделав те же операции и подставив вместо Z величину 2b/4, можно определить значение расчетного сопротивления R.

Еще раз отметим, что в формулу (9) величина внешней нагрузки входит уменьшенной на суммарную величину сил трения и сцепления, действующих по боковой поверхности фундамента.

Результаты проведенных вычислений составили базу данных разработанной нами компьютерной программы-калькулятора, при помощи которой можно определить величину расчетного сопротивления и предельно допустимой нагрузки на щелевой фундамент без учета работы его боковой поверхности.

Большое разнообразие грунтовых условий, случайный характер образования тонкой прослойки сцементированного грунта по боковой поверхности монолитного фундамента и другие причины обуславливают необходимость определения суммарной силы трения и сцепления только по боковой поверхности фундамента для конкретных грунтовых условий строительной площадки. Для определения суммарной силы трения и сцепления по боковой поверхности подземной части монолитного щелевого фундамента разработано устройство (см. рис.8), на которое получен патент Российской Федерации. Подробное описание устройства и копия патента приведены в диссертационной работе. Так как, силы трения и сцепления по боковой поверхности монолитного фундамента, устраиваемого в грунте без опалубки, не зависят от

Рис. 8. Схема устройства для определения суммарных сил трения и сцепления, действующих по боковой поверхности монолитного фундамента, сооружаемого враспор грунта без опалубки

формы его поперечного сечения, то испытания можно проводить на образце любого сечения, и использовать полученные результаты испытаний так же для монолитных фундаментов любого поперечного сечения: сваи, «стена в грунте», коробчатые фундаменты и т.п.

Удельная сила трения и сцепления определяется выражением:

(10)

где: R – предельная суммарная сила трения и сцепления, действующая по боковой поверхности образца и определяемая динамометром в момент «срыва»; r и H – соответственно радиус и высота образца.

Умножая величину полученной удельной силы на площадь полной боковой поверхности подземной части монолитного щелевого фундамента, можно определить долю его несущей способности по боковой поверхности для инженерно-геологических условий конкретной строительной площадки.

Затем, используя приведенные в настоящей главе графики и формулы, данные инженерно-геологических изысканий, результаты определения физико-механических свойств грунтов и геометрические параметры фундамента или разработанную компьютерную программу-калькулятор, определяют долю несущей способности по его подошве.

Складывая обе эти величины, определяют общую несущую способность щелевого фундамента по грунту.

В третьей главе диссертационной работы приведены результаты компьютерного моделирования процесса образования и развития областей пластических деформаций в основании двухщелевого фундамента и разработанный на их основе инженерный метод.

В качестве основных инструментов при проведении численного эксперимента по моделированию процесса образования и развития областей пластических деформаций в основании двух щелевого фундамента используется разработанная в ВолгГАСУ компьютерная программа «Устойчивость. Напряженно-деформированное состояние».

Эта программа, кроме всего прочего, позволяет проводить моделирование процесса распределения напряжений в приоткосной области при различных численных значениях переменных расчетных параметров и проводить графические построения картин изолиний напряжений и областей пластических деформаций в основании фундамента.

На рис. 9 изображена половина расчетной конечно-элементной схемы двухщелевого фундамента и приведены ее геометрические размеры.

Граничные условия заданы следующим образом: вдоль вертикальных границ расчетной модели запрещены перемещения узлов расчетной схемы в горизонтальном направлении; вдоль нижней горизонтальной границы расчетной схемы запрещены вертикальные перемещения узлов; на перемещения других узлов расчетной схемы МКЭ ограничения не наложены. На рис. 10 представлены картины изолиний безразмерных (в долях h) трех компонент напряжения z; x и zx в однородном основании

а)	б)
Рис. 9. Расчетная схема МКЭ (а) и ее основные размеры (б)

Расчетная схема состоит из 115200 треугольных конечных элементов, сопряженных в 58362 узлах, а ширина матрицы жесткости составляет 246. Ее линейные размеры 8b6b, где b – полуширина фундамента.

а)	б)	в)
г)	д)	е)
ж)	з)	и)
Рис. 10. Картины изолиний безразмерных (в долях h) напряжений z; x и zx в однородном основании двухщелевого фундамента при 2b=h (а-в);2b=0,4h (г-д) и 2b=0,2h (ж-з) соответственно

двухщелевых фундаментов различной ширины, но одинаковой глубины заложения, в момент смыкания областей пластических деформаций (при 2b=0,2h двухщелевой фундамент вырождается в однощелевой). Из рисунков видно, что касательные напряжения zx равномерно распределяются по боковой поверхности фундамента; в верхней зоне основания до глубины примерно 0,3-0,4h наблюдается концентрация нормальных горизонтальных напряжений x; на некотором удалении от фундамента справа и слева наблюдаются области растягивающих напряжений x; под подошвами фундамента наблюдаются значительные концентрации вертикальных нормальных напряжений z; грунт, расположенный между вертикальными несущими элементами фундамента практически не напряжен внешней нагрузкой; так, например, вертикальные нормальные напряжения z в нижней части защемленного массива в 3-8 раз меньше, чем непосредственно под подошвами фундамента.

На рис. 11 в качестве примера приведены изображения увеличивающихся, вплоть до смыкания, по мере увеличения интенсивности внешней нагрузки областей пластических деформаций в однородном основании двухщелевого фундамента. Анализ рисунков показывает, что увеличение интенсивности внешней нагрузки вызывает интенсивное развитие ОПД вверх по боковым поверхностям фундамента. Дальнейшее

а)	б)	в)
Рис. 11. Области пластических деформаций в однородном основании двухщелевого фундамента при q=5h (а); q=12h (б); q=18,6h (в) и =18кН/м3; =25о; C=20КПа; о=0,75; св=2,383 и 2b=1м

увеличение нагрузки приводит к выходу областей пластических деформаций на поверхность грунта и их смыканию под подошвами фундамента.

а)	б)	в)
Рис. 12. Области пластических деформаций в основании двухщелевого фундамента в момент их смыкания под его подошвой (в момент исчерпания несущей способности по подошве) при 2b/h=1 (а); 2b/h=0,4 (б); 2b/h=0,2 (в)

а)	б)	в)
Рис. 13. Области пластических деформаций в основании фундамента в момент исчерпания несущей способности по грунту при различных численных значениях отношения h/2b=1,0 (а) ; h/2b=0,8 (б); h/2b=0,4 (б); h/2b=0,2 (в)

На рис. 12 и 13 изображены ОПД в момент их смыкания под подошвой фундамента при различных значениях величины отношения 2b/h и h/b, а на рис. 14 – графические зависимости вида qсм=f(2b/h) и qсм=f(h/b).

а)	б)
Рис. 14. График зависимости вида qсм=f(2b/h) для условий, соответствующих рис. 12 и график зависимости вида qсм=f(h/b) для условий, соответствующих рис. 13

Анализ этих зависимостей показывает, что несущая способность двухщелевого фундамента по грунту снижается при увеличении расстояния между щелями и возрастает при увеличении значения относительной глубины заложения (h/b).

На рис. 15 приведена небольшая часть графических зависимостей вида Z=f(q) и Zв=f(q), иллюстрирующих процесс зарождения и развития областей пластических деформаций под подошвами фундамента и вдоль его боковой поверхности, построенные по результатам компьютерного моделирования.

Оказалось, что все кривые, приведенные на рис. 15, практически со 100% степенью точности можно аппроксимировать полиномом второго порядка; аппроксимирующее выражение и степень достоверности аппроксимации приведена непосредственно для каждой кривой на соответствующем рисунке.

Для отыскания аппроксимирующих коэффициентов для всех возможных сочетаний численных значений переменных расчетных параметров построены графики и составлены таблицы, часть которых приведена в диссертационной работе и приложениях к ней; они составили

а)	б)
в)	г)
д)	е)
ж)	з)
Рис. 15. Графические зависимости вида при: b/hз=1, св=7 (а); b/hз=1, св=15 (б); b/hз=0,625, св=7 (в); b/hз=0,625, св=15 (г) и графические зависимости вида Zв=f(q) при: b/hз=1, св=7 (д); b/hз=1, св=15 (е); b/hз=0,625, св=7 (ж); b/hз=0,625, св=15 (з)

базу данных разработанной нами компьютерной программы для определения величины несущей способности основания двухщелевого фундамента.

В четвертой главе диссертации описаны эксперименты по определению величины интенсивности равномерно распределенной нагрузки, соответствующей моменту зарождения областей предельного состояния на моделях из эквивалентного материала, в качестве которого использован желатино-гель XC (игдантин).

Для изготовления моделей применялись растворы с тремя значениями весовой концентрации желатина – 15%; 30% и 45%.

Испытания специальным образом изготовленных образцов проведено на сдвиговом приборе ВСВ-25 по схеме быстрого среза.

На рис. 16 приведены графики зависимостей объемного веса, удельного сцепления C и угла внутреннего трения игдантина от процентной концентрации желатина в образцах, испытанных на сдвиг, а в таблицу № 1 помещены их численные значения.

а)	б)
Рис. 16. Дубление желатиновой модели в растворе формальдегида (а); графики зависимости угла внутреннего трения (1), удельного сцепления C (2) и объемного веса (3) от процентной концентрации желатина (б);

Таблица 2.

Физико-механические свойства желатино-геля XC (игдантина)

n (%)	(т/м3)	С(кПа)	(град)
15	1,078	34,8	13,5
30	1,150	72,0	25,5
45	1,240	183,0	42

Эксперименты по определению величины интенсивности внешнего воздействия соответствующей моменту зарождения областей предельного состояния грунта под подошвой модели щелевого фундамента, проведены в сборно-разборной форме на установке, фотография которой приведена на рис. 17.

Внешние размеры формы 3030 см, а ее ширина 3,4см. Внутренние размеры соответственно 2828 см и 2см.

Форма выполнена из оргстекла толщиной 7мм, а ее элементы скреплены между собой 13 металлическими болтами. Вставки-штампы из органического стекла, представляющие собой модели щелевых фундаментов, изготовлены шириной 1,2см и толщиной 2см, т.е. последний размер равен толщине желатиногелеевой модели основания ЩФ. Модели формировались с переменной глубиной выреза, чтобы можно было имитировать щелевой фундамент с величиной отношения его ширины к глубине заложения 2b/hз=0,1; 0,15; 0,2; 0,25 и 0,3.

Рис. 17. Общий вид установки во время проведения эксперимента

Часть вставки-штампа, расположенная выше поверхности модели, служит для опирания динамометра ДОСМ-3-1, измеряющего величину передаваемого на модель основания усилия, создаваемого винтом.

Вставка-штамп перед проведением опыта тщательно смазывалась техническим вазелином для исключения сил трения.

а)	б)	в)	г)
Рис. 18. Момент образования областей пластических деформаций в основании моделей щелевого фундамента при величинах отношения его ширины к глубине заложения 2b/hз=0,1 (а); 0,15 (б); 0,2 (в); 0,3 (г)

Суть эксперимента заключалась в следующем.

Из желатино-геля ХС с весовой концентрацией желатина равной 15%, 30% и 45% последовательно изготавливались пять партий по пять моделей оснований щелевого фундамента (рис. 16а), с величиной отношения ширины 2b/hз=0,1; 0,15; 0,2; 0,25 и 0,3.

Затем эти модели нагружались через вставку-штамп вертикальной равномерно распределенной нагрузкой до того момента, пока у нижних краев вставки-штампа не начинали отчетливо проглядываться крошечные трещинки – признак начала разрушения (рис. 18). Соответствующие значения нагрузки фиксировалась, и принимались за величину первой критической нагрузки.

Среднее арифметическое из пяти (для каждой партии из пяти моделей с одинаковым значением 2b/hз) значение qз принималось в качестве результата эксперимента и помещалось в таблицу № 3. На основании полученных данных построены графические зависимости вида qз=f(2b/hз), приведенные на рис. 20.

Концентрация желатина (%) 2b/hз 0,1 0,15 0,2 0,3 15 qз(рас) 9,25 7,00 5,35 5,30 qз(экс) 9,50 6,75 5,00 5,60 30 qз(рас) 15,50 11,50 8,50 8,41 qз(экс) 15,00 10,76 7,60 9,00 45 qз(рас) 27,00 20,00 18,80 14,77 qз(экс) 28,00 17,00 15,00 12,12	В той же таблице приведены значения соответствующих нагрузок, полученные на основании расчета, выполненного при помощи компьютерной программы «Устойчивость. Напряженно-деформированное состояние», разработанной в ВолгГАСУ. Отметим, что все расчеты проведены при величине коэффициента бокового давления грунта о=0,75, что является средним значением для глинистых грунтов. Графическая интерпретация экспериментальных и теоретических данных в виде зависимостей вида qз=f(2b/hз), приведены на рис. 20. Как видно из таблицы № 3, экспериментальные и теоретические данные отличаются друг от друга не более чем на 26%, причем, отличия тем меньше, чем меньше величина отношения 2b/hз, и чем меньше процентная концентрация желатина в эквивалентном материале. На рис. 21 представлены очертания
Рис. 19.Таблица № 3. Экспериментальные и расчетные значения первой критической нагрузки qз
Рис. 20. Графические зависимости вида qз=f(2b/hз), построенные по экспериментальным и расчетным данным (помечены квадратным символом) для моделей оснований ЩФ при разной концентрации желатина в моделеобразующем материале.

а)	б)
Рис. 21. Расчетная схема МТФКП (а) и области пластических деформаций в основании модели ЩФ, построенные по напряжениям, вычисленным при помощи МТФКП (б)

ОПД, построенных для условий эксперимента при 2b/h=0,1 при помощи компьютерной программы «Устойчивость. Напряженное состояние», в которой формализованы решения, полученные на основе использования методов теории функций комплексного переменного. Сравнивая их с экспериментальными областями, констатируем их практическую идентичность.

ОСНОВНЫЕ ВЫВОДЫ

1. Несущая способность щелевого фундамента по грунту определяется суммой несущей способности по боковой поверхности и его подошве. Первое слагаемое определяется физико-механическими свойствами вмещающего массива грунта, гидро-геологическими условиями строительной площадки, геометрическими размерами фундамента, физико-химическими свойствами бетона, степенью проникновения коллоидного водоцементного раствора в поверхностные слои грунта откосов котлована (траншеи), технологией сооружения фундамента и так далее. Второе слагаемое зависит от формы и размера подошвы и ФМСГ. Поэтому определять несущую способность по подошве фундамента можно на основе анализа НДС грунтового массива при помощи МКЭ и МТФКП, а несущую способность по боковой поверхности – путем экспериментальных исследований непосредственно на строительной площадке.
2. На основе методов теории функций комплексного переменного получены графические зависимости и соответствующие аналитические аппроксимации, позволяющие определять несущую способность по подошве щелевого фундамента для всех возможных сочетаний численных значений переменных расчетных параметров, использованных в диссертационной работе. Эти результаты составили базу данных компьютерной программы-калькулятора, позволяющей автоматизировать процесс вычисления части несущей способности, приходящейся на подошву фундамента.
3. Разработано и запатентовано устройство, позволяющее в реальных инженерно-геологических условиях конкретной строительной площадки определять максимальные значения удельных сил трения и сцепления, действующих по боковой поверхности монолитных фундаментов, изготавливаемых без опалубки враспор грунта.
4. Предложен инженерный метод расчета несущей способности основания щелевого фундамента, составными частями которого являются разработанная компьютерная программа и запатентованное устройство.
5. Методом конечных элементов выполнен анализ процессов трансформации полей напряжений и образования и развития областей пластических деформаций в однородном основании двухщелевого фундамента, позволивший установить их новые закономерности: области пластических деформаций начинают зарождаться в нижней части щелевых опор с их внешних сторон; затем, по мере увеличения интенсивности внешней нагрузки, происходит интенсивное развитие ОПД вверх по боковым поверхностям фундамента, их выход на поверхность грунта и чуть позже – смыкание под подошвами фундамента. Таким образом, установлено, что в первую очередь реализуется та часть несущей способности двухщелевого фундамента по грунту, которая приходится на его боковую поверхность, причем, включение боковой поверхности щелевого фундамента в работу происходит снизу вверх. Только после этого в работу включается часть основания, которая находится непосредственно под подошвами фундамента. Показано, чем меньше расстояние между щелями, тем больше несущая способность основания и тем большая ее часть приходится на боковую поверхность. Несущая способность двухщелевого фундамента по грунту прямо пропорциональна высоте щелей. Часть несущей способности, реализуемая по боковой поверхности фундамента, может достигать 60% и более.
6. Предложен инженерный метод расчета несущей способности основания двухщелевого фундамента, включающий простые для употребления формулы и графики. Метод формализован в компьютерную программу-калькулятор. Поверочные расчеты говорят о высокой степени точности аппроксимации результатов численного эксперимента.
7. В результате экспериментальных исследований, проведенных на моделях из эквивалентных материалов, установлено, что численные значения первой критической нагрузки для основания щелевого фундамента, найденные при помощи расчета и экспериментально, отличаются друг от друга не более чем на 26%. Причем, отличия тем меньше, чем меньше величина отношения 2b/h, и чем меньше процентная концентрация желатина в моделеобразующем материале. Это дает основание полагать, что разработанный инженерный метод расчета несущей способности щелевого фундамента может быть рекомендован для практического использования.

Авторм всего опубликовано статей по теме диссертационной работы – 8, из них две в рецензируемых научных журналах и изданиях и 1 патент РФ на полезную модель.

Работы по тематике диссертации, опубликованные в рецензируемых журналах и изданиях:

1. Экспериментальное исследование процесса образования областей предельного состояния в основании щелевого фундамента на моделях из эквивалентного материала / А. А. Иванов [и др.] // Интернет-вестн. ВолгГАСУ. Сер.: Политемат. – Волгоград : Изд-во ВолгГАСУ, 2013. – Вып. 2 (27). - Режим доступа: www.vestnik.vgasu.ru
2. Богомолов, А. Н. Инженерный метод расчета несущей способности однородного основания щелевого фундамента / А. Н. Богомолов, О. А. Богомолова, А. А. Иванов // Вестн. Волгогр. гос. архитектур.-строит. ун-та. Сер.: Стр-во и архитектура. – Волгоград : Изд-во ВолгГАСУ, 2013. – Вып. 33 (52). – С. 23-28.

Публикации по тематике диссертации в других изданиях, материалах конференций:

3. Пат. 126332 Российская Федерация, МПК E 02 D 1/00. Устройство для определения суммарной силы трения и сцепления по боковой поверхности подземной части монолитного фундамента / Богомолов А. Н., Богомолова О. А., Иванов А. А. - № 2012133424/03 ; заявл. 03.08.2012 ; опубл. 27.03.2013, Бюл. № 9.
4. Определение коэффициентов отображающей функции для решения прикладных задач геомеханики на основе использования методов теории функций комплексного переменного / О. А. Богомолова [и др.] // Механика грунтов в геотехнике и фундаментостроении : материалы Всерос. науч.-техн. конф., 7-8 июня 2012 г., Новочеркасск. – Новочеркасск : Изд-во ЮРГТУ (НПИ), 2012. - С. 169-174.
5. Моделирование процесса образования и развития областей пластических деформаций в основании щелевого фундамента / О. А. Богомолова [и др.] // Инженерные проблемы строительного материаловедения, геотехнического и дорожного строительства : материалы III Междунар. науч.-техн. конф., 10-12 апреля 2012 г., Волгоград. - Волгоград : Изд-во ВолгГАСУ, 2012. – С. 109-121.
6. Моделирование процесса образования и развития областей пластических деформаций в основании двухщелевого фундамента / О. А. Богомолова [и др.] // Збiрник наукових праць. Сер.: Галузеве машинобудування, будiвництво. - Полтава : Изд-во ПолтНТУ, 2012. – Вып. 4 (34), т. 2. – С. 10-17.
7. Инженерный метод и компьютерная программа для расчета несущей способности основания щелевого фундамента : информ. л. № 34-081-13 / А. Н. Богомолов [и др.]. – Волгоград : ЦНТИ, 2013. – 3 с.
8. Компьютерная программа для расчета несущей способности основания двухщелевого фундамента «Fundament 2CH» : информ. л. № 34-082-13 / А. Н. Богомолов [и др.]. – Волгоград : ЦНТИ, 2013. – 3 с.

ИВАНОВ АНТОН АНДРЕЕВИЧ

ОЦЕНКА НЕСУЩЕЙ СПОСОБНОСТИ ОСНОВАНИЙ ЩЕЛЕВЫХ ФУНДАМЕНТОВ НА ОСНОВЕ АНАЛИЗА НАПРЯЖЕННОГО СОСТОЯНИЯ ГРУНТОВОГО МАССИВА И ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ

Специальность 05.23.02 – Основания и фундаменты,

подземные сооружения

Автореферат

диссертации на соискание учёной степени

кандидата технических наук

Подписано в печать 11.11.2013. Формат 60х84/16.

Бумага офсетная. Печать трафаретная. Гарнитура Times New Roman.

Усл. печ. л. 1,4. Уч.-изд. л. 1,2. Тираж 110 экз. Заказ № 166.

Государственное образовательное учреждение высшего профессионального образования

«Волгоградский государственный архитектурно-строительный университет»

Отпечатано в отделе оперативной полиграфии

400074, г. Волгоград, ул. Академическая, 1