Применение смешанной формы мкэ к расчетам стержневых систем
На правах рукописи
Габова Виктория Викторовна
Применение СМЕШАННОЙ ФОРМЫ МКЭ
К РАСЧЕТАМ СТЕРЖНЕВЫХ СИСТЕМ
Специальность 05.23.17 – Строительная механика
А в т о р е ф е р а т
диссертации на соискание ученой
степени кандидата технических наук
Волгоград – 2011
Работа выполнена в Государственном образовательном учреждении высшего профессионального образования
«Волгоградский государственный архитектурно-строительный университет»
Научный руководитель: кандидат технических наук,
доцент, Игнатьев Александр Владимирович
Официальные оппоненты: доктор технических наук,
профессор Клочков Юрий Васильевич
ФГОУ ВПО «Волгоградская государственная сельскохозяйственная академия», г. Волгоград
кандидат технических наук,
доцент Макаров Александр Владимирович
ГОУ ВПО «Волгоградский государственный архитектурно-строительный университет»,
г. Волгоград
Ведущая организация: ГОУ ВПО «Саратовский государственный
технический университет», г. Саратов
Защита состоится 07 июня 2011г. в 10 часов на заседании диссертационного совета Д 212.026.01 при ГОУ ВПО «Волгоградский государственный архитектурно-строительный университет» по адресу: 400074, г. Волгоград, ул. Академическая, д.1, ауд. Б-203.
С диссертацией можно ознакомиться в библиотеке ГОУ ВПО Волгоградского государственного архитектурно-строительного университета.
Автореферат разослан 04 мая 2011г.
| Ученый секретарь диссертационного совета |  | Пшеничкина В.А. |
Общая характеристика работы
Актуальность темы. Проектирование и строительство надежных, высокоэффективных конструкций и сооружений в большой степени зависят от возможности прогнозирования их поведения при возможных полях воздействий на них (силовых, температурных, кинематических и т.д.). Точность прогнозирования зависит в свою очередь от наличия соответствующих по точности методов расчета, возможностей проведения численных экспериментов и проверки достоверности результатов расчета. Именно это предопределяет основное направление развития строительной механики – разработку новых и совершенствование известных методов расчета.
Общепризнано, что самым распространенным и универсальным численным методом решения краевых задач является сегодня метод конечных элементов (МКЭ) в форме метода перемещений. Особенно широко он применяется в задачах механики деформируемого твердого тела и строительной механики. Теории и реализации МКЭ посвящена обширная литература. Популярность этого метода обусловлена его непосредственной связью с классическими методами строительной механики и вытекающей из них простотой и наглядностью, а также возможностью расчета тел любой геометрической формы. МКЭ, соединяя в себе универсальность, высокую степень формализации и алгоритмизации предоставил возможность полной автоматизации вычислительного процесса. Наличие многочисленных программных комплексов, реализующих МКЭ, расширило многократно возможности детального исследования напряженно-деформированного состояния конструкций.
Анализ литературы, посвященной МКЭ, позволяет сделать вывод о том, что большинство работ посвящено классическому варианту МКЭ в форме метода перемещений. Однако эта форма наряду с достоинствами обладаем и недостатками: более низкая по сравнению с перемещениями точность определения напряжений, учет смещения КЭ как жесткого целого и др.
Появление работ, целью которых является исследование и развитие других более эффективных по сравнению с МКЭ в форме метода перемещений, вариантов МКЭ – в форме метода сил, в смешанной форме, различные гибридные варианты, подтверждает актуальность выбранного направления исследований.
Целью диссертационной работы является:
- дальнейшее развитие и применение смешанной формы МКЭ в задачах расчета стержневых систем;
- разработка методики решения задач статики, динамики и устойчивости стержневых систем;
- разработка алгоритмов и численное исследование предлагаемой методики для решения следующих задач.
Научная новизна диссертационной работы заключается в следующем:
- реализован единый подход к получению матриц откликов стержневых КЭ для расчета стержневых систем по МКЭ в смешанной форме;
- получены матрицы откликов КЭ – стержня для задач статики, динамики и устойчивости;
- на основе единого подхода разработаны алгоритмы решения задач статики, динамики и устойчивости стержневых систем.
Практическая значимость диссертационной работы:
- изложенный в работе алгоритмы решения задач статики, динамики и устойчивости стержневых систем позволяют формализовать и автоматизировать расчет по МКЭ в смешанной форме в той же степени, что и по МКЭ в форме метода перемещений;
- результаты работы могут быть применены при разработке комплекса программ реализующих алгоритм расчета по МКЭ в смешанной форме;
- результаты работы могут быть использованы в учебных пособиях и учебнике по курсу строительной механики.
Основные научные положения, выносимые на защиту:
- алгоритм формирования матрицы откликов стержневого КЭ для задач статики, динамики и устойчивости стержневых систем;
- алгоритмы формирования разрешающих уравнений для задач статики, динамики и устойчивости стержневых систем по МКЭ в смешанной форме;
- общий алгоритм расчета стержневых систем по МКЭ в смешанной форме.
Достоверность научных положений и результатов диссертационной работы обеспечивается корректностью постановки задач в рамках классических методов строительной механики с использованием тех же гипотез и допущений, а также сравнением полученных результатов решения тестовых задач с результатами, полученными как на основе классических методов, так и по МКЭ в форме метода перемещений.
Апробация работы. Материалы диссертационной работы обсуждались на следующих конференциях: X региональная конференция молодых исследователей Волгоградской области, Волгоград, 2005; III Всероссийская научно-техническая конференция «Социально-экономические проблемы развития строительного комплекса региона. Наука. Практика. Образование», г. Волгоград – г. Михайловка, 2009; Международная научно-практическая конференция «Проблемы, состояние комплексных мелиораций и их роль в обеспечении продовольственной безопасности России», Волгоград, 2009; Научно - техническая интернет - конференция «Энерго - и ресурсосбережение в строительной индустрии. Организационно – экономические и социальные проблемы хозяйствования в строительстве», г. Михайловка Волгоградской области, 2010;
Работа выполнялась по тематическому плану Министерства образования и науки РФ (НИР № 1.2.11 – «Применение смешанной формы МКЭ к расчетам стержневых и пластинчатых конструкций»).
Основные результаты работы отражены в девяти публикациях. Из них
две в журналах, входящих в список ВАК РФ.
Структура и объем диссертационной работы. Текст диссертации изложен на 184 страницах, состоит из введения, четырех глав, заключения, списка литературы из 132 наименований и содержит 84 рисунка, 14 таблиц.
Содержание работы
Во введении обосновывается актуальность темы, сформулированы цели и задачи исследования, основные научные положения, выносимые на защиту, практическая ценность работы.
В первой главе проведен краткий обзор работ по теме диссертации и проанализированы результаты исследований, связанных с использованием смешанного метода в строительной механике.
Зарождение метода конечных элементов относится к сороковым годам прошлого века и связано с появлением ЭВМ.
На первом этапе развитие МКЭ во многом определялось именно идеей сведения задач механики континуальных систем к задачам строительной механики стержневых систем, т.е. к дискретным расчетным схемам.
Значительный вклад в развитие МКЭ на начальном этапе внесли М. Дж. Тернер, Дж.Х. Аргирис, О.К. Зенкевич и Ю.К. Ченг, С.У. Мак-Кормик, Л.А. Розин, А.М. Масленников, В.А. Постнов и др. Термин «конечный элемент» впервые был введен в статье Р.В. Клафа. Он сразу вошел в научную и затем в учебную литературу и теперь является общепринятым.
К настоящему времени имеется настолько большое число публикаций, посвященных как теоретическим основам МКЭ, так и его приложениям, что проанализировать их все не представляется возможным.
МКЭ в его современной форме является синтезом методов строительной механики стержневых систем и методов теории упругости, механики деформированного твердого тела. Родство этих методов, выявленное в ходе развития МКЭ, позволило их усовершенствовать, систематизировать и взаимно обогатить.
В зависимости от того, какие неизвестные (силовые, кинематические
или смешанные) принимаются за основные, МКЭ реализуется в форме метода перемещений, метода сил или смешанного метода.
В зависимости от вида узловых неизвестных (силовые, кинематические или смешанные) соотношения между ними и вызываемыми ими усилиями и перемещениями называются матрицей жесткости, матрицей податливости или матрицей откликов КЭ. Получение этих соотношений выполняется как на основе наиболее общего принципа возможных перемещений [Масленников А.М., Постнов В.А., Игнатьев В.А. и др.], так и на основе энергетических принципов. Основными их них являются – принцип минимума потенциальной энергии, называемый принципом Лагранжа, и принцип минимума дополнительной энергии или принцип Кастилиано. Как принцип Лагранжа, так и принцип Кастилиано, являются различными формами принципа возможных перемещений. За последние десятилетия на их основе разработано несколько гибридных и смешанных вариационных принципов (Рейсснера, Ху-Васидзу, Херрмана и др.).
Все эти методы являются альтернативой МКЭ в перемещениях, использующим единственное аппроксимирующее поле.
В гибридных методах одно поле перемещений и (или) напряжений задается внутри КЭ, другое поле перемещений или напряжений принимается независимо на границах элемента. Соответствующее энергетическое выражение для КЭ записывается через параметры введенных аппроксимирующих полей.
В смешанных функционалах, например, в известном функционале Рейсснера, используются два поля внутри элемента для описания перемещений и сил (напряжений) соответственно. Вариация этого функционала по перемещениям и силам (напряжениям) дает смешанную матрицу связи между силами (напряжениями) и перемещениями. Такую смешанную модель МКЭ первым применил Л. Херрман.
В задачах строительной механики применению МКЭ в смешанной форме посвящено сравнительно небольшое количество работ. Среди них лишь работы А.М. Масленникова, В.А. Игнатьева, А.В. Игнатьева можно отнести к МКЭ в классической смешанной форме. В работах А.А. Покровского и Р.А. Хечумова смешанный метод используется в развернутой форме.
При применении ЭВМ наибольший интерес представляют общие подходы к решению задач, позволяющие формализовать расчет и создать эффективный алгоритм реализации метода расчета. Таким общим подходом является смешанный метод.
Поэтому актуально дальнейшее развитие МКЭ в смешанной форме для решения задач статики, динамики и устойчивости стержневых систем.
Для широкого практического применения МКЭ в смешанной форме необходимы его дальнейшее развитие и разработка алгоритмов расчета и реализующих их программ.
Во второй главе изложены основные теоретические положения МКЭ в смешанной форме. Приведен вывод уравнений смешанного метода на основе смешанного вариационного принципа. Рассмотрены два подхода к получению матрицы - откликов для КЭ-стержня: классический на основе классических метода сил и метода перемещений и на основе смешанного вариационного принципа, в форме предложенной в работах В.А. Игнатьева и А.В. Игнатьева для стержневых систем. Рассмотрено формирование вектора внешних воздействий на КЭ.
За базовый КЭ принимается прямолинейный стержень, жестко закрепленный по концам (рис. 1,а). Основная система смешанного метода для него приведена на рис. 1,б.
а б
Рис. 1
Для данного КЭ введем следующие обозначения неизвестных в основной системе: 
– перемещения по направлению соответствующих связей и реакций в них, 
– неизвестные усилия в удаленных связях основной системы.
При использовании классического подхода к получению матрицы откликов. Расчет основной системы, как на единичные, кинематические и силовые воздействия, так и на заданные нагрузки и перемещения выполняется обычным методом статики сооружений и основывается на физическом смысле задачи, т.е., исходя из условий неразрывности деформаций, статических и кинематических условий.
Для максимальной наглядности на рис. 2 показаны единичные перемещения связей основной системы рассматриваемого КЭ и приведены значения соответствующих коэффициентов матрицы откликов.
Рис. 2
Структура матрицы откликов КЭ имеет следующий вид:
, (1)
Здесь 
, (
,
) - подматрица реакций во введенных кинематических связях основной системы смешанного метода от единичных смещений этих связей (подматрица жесткости);
, (
,
) - подматрица реакций во введенных связях основной системы смешанного метода от единичных силовых неизвестных в той же основной системе;
- подматрица перемещений по направлению силовых неизвестных от единичных смещений введенных кинематических связей;
, (
,
) - подматрица перемещений по направлению силовых неизвестных при единичных значениях этих неизвестных (подматрица податливости);
- вектор внешних воздействий на основную систему;
- подвектор реакций во введенных связях от нагрузки в основной системе;
- подвектор перемещений по направлению силовых неизвестных от нагрузки в основной системе.
Блоки матрицы откликов имеют следующую структуру:
. (2)
В смешанной форме метода конечных элементов при вычислении элементов блоков r и за возможные принимаются действительные состояния, соответствующие основной системе. Элементы этих блоков могут быть получены по формуле Максвелла-Мора.
Окончательно получаем блок 
следующего вида:
. (3)
Для данного рассматриваемого КЭ блок 
– квадратная нулевая матрица шестого порядка.
На рис. 3 представлен более общий случай КЭ с упруго-податливыми связями по концам. Такой КЭ позволяет моделировать стержневые конструкции с податливыми узловыми соединениями стержней в узлах.
В этом случае матрица 
является ненулевой, ее коэффициенты складываются из двух составляющих: реакций во введенных связях от единичного смещения этих связей самого стержня и реакций в упругоподатливой опоре от того же единичного смещения:
, 
, здесь все значения нулевые, кроме: 
, 
, 
, 
.
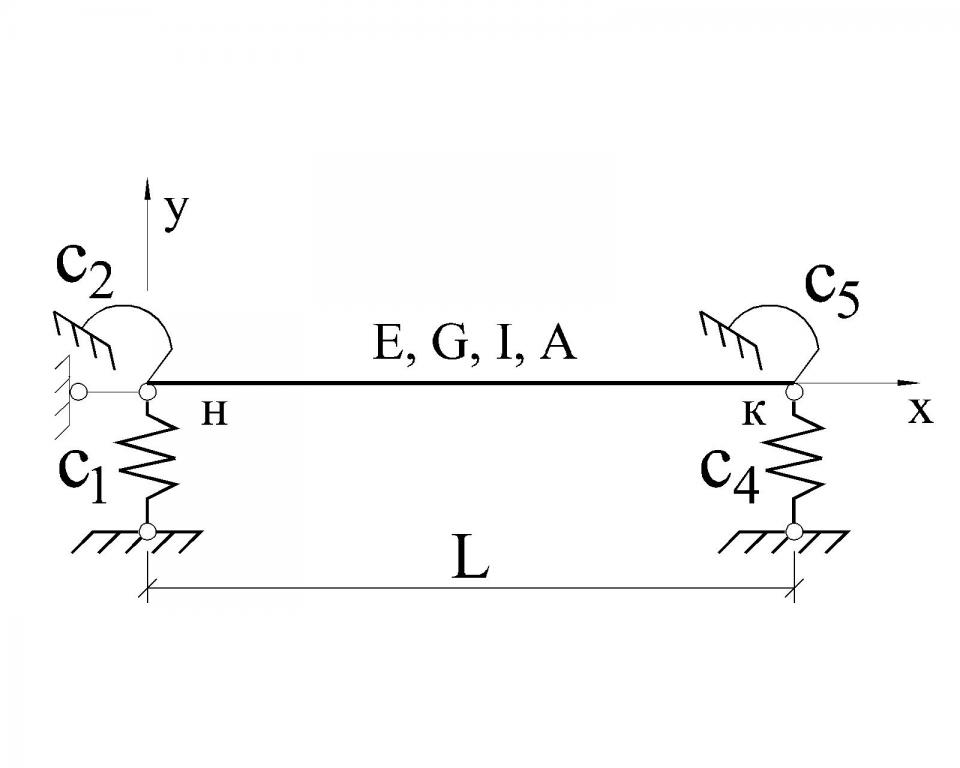
Рис. 3
Формирование вектора воздействий, аналогично формированию локальной матрицы откликов КЭ в локальной системе координат.
В этом векторе подвектор реакций формируется путем вычисления реакций от нагрузок в основной системе смешанной формы МКЭ, которая является статически определимой.
Формирование подвектора перемещений также не представляет сложности. Каждый из элементов данного подвектора может быть получен по формуле Мора.
Так, например, для варианта загружения КЭ, показанного на рис. 4,а, компоненты подвекторов перемещений и реакций определяются выражениями:
; 
;
; 
; 
;
; 
; 
; 
.
а б
Рис. 4
Использование смешанного вариационного принципа для нахождения элементов матрицы откликов приводит к тем же выражениям.
В работе получены также матрицы откликов пространственно ориентированного КЭ-стержня, используемого при расчете пространственных стержневых систем, для КЭ-криволинейного плоского стержня и для КЭ в виде двухслойной балки (рис. 5,а).
В зависимости от принимаемой расчетной схемы КЭ выбирается и основная система. Самой простой является дискретная расчетная схема, изображенная на рис. 5,б, в которой все силы взаимодействия слоев (конечных элементов первого уровня) сосредоточены в расчетных точках А, В, С основной системы (рис. 5,в).
а
Рис. 5
б
в
Рис. 5
Для построения матрицы откликов используются условия совместности деформаций конечного элемента – 1 и конечного элемента – 2 (слоев объединенного конечного элемента).
1. 
, 2. 
, 3. 
, 4. 
,
5. 
, 6. 
. (4)
Всего в основной системе смешанного метода для рассматриваемого двухслойного конечного элемента имеем 20 неизвестных: 
, 
, 
, 
, 
, 
,
, 
, 
, 
, 
, 
, 
, 
,
, 
, 
, 
, 
, 
.
Рассмотрен также уточненный вариант расчетной схемы, в которой сдвигающие усилия Т между слоями КЭ распределены по линейному закону.
Основная система для такой расчетной схемы приведена на рис. 6, на которой показаны только отличающиеся от предыдущего варианта распределенные сдвиговые обобщенные неизвестные 
, 
, 
, 
, создающие распределенный изгибающий момент и распределенную продольную нагрузку на конечный элемент первого уровня.
Рис. 6
Алгоритм формирования глобальной матрицы откликов основан на поблочном формировании глобальной матрицы откликов. При нем достаточно сформировать только матрицы 
и 
, т.к. матрица 
– квадратная нулевая матрица, с числом столбцов и строк, равному количеству связей основной системы, а 
.
Эффективной при этом оказывается возможность формирования глобальной матрицы откликов без матричных перемножений, путем прямого построения блоков глобальной матрицы откликов. В этом случае элементы матрицы откликов КЭ размещаются непосредственно в соответствующем блоке глобальной матрицы откликов. Для выполнения этой процедуры используются индексные матрицы, аналогичные индексной матрице, в алгоритме формирования матрицы жесткости в МКЭ в перемещениях.
Матрицы индексов позволяют установить связь элементов друг с другом.
Предложенный алгоритм реализован в среде Scilab и позволяет эффективно формировать глобальные матрицы откликов плоских стержневых систем.
Выполненное для некоторых типов стержневых КЭ формирование матриц откликов показало простоту и эффективность этих алгоритмов.
На основе этих алгоритмов могут быть получены матрицы откликов для любых типов стержневых КЭ.
Алгоритмы формирования глобальной матрицы откликов конструкции и составление разрешающей системы алгебраических уравнений аналогичны соответствующим алгоритмам МКЭ в перемещениях.
В третьей главе рассмотрено применение разработанных во второй главе алгоритмов в задачах статики стержневых систем.
Для иллюстрации практических возможностей и применения смешанной формы МКЭ приведены примеры статических расчетов стержневых конструкций. Эти тестовые примеры позволяют выявить особенности алгоритмов расчета в каждом конкретном случае, сравнить результаты расчетов с расчетами по другим методам, дать соответствующие рекомендации.
Как уже отмечено во введении, одним из основных недостатков в МКЭ в перемещениях является учет смещения КЭ как жесткого целого. При таких смещениях не происходит деформирование КЭ и энергия его деформации равна нулю. Однако эти смещения входят в общую величину узловых перемещений разрешающей системы уравнений, и их доля может быть очень большой в сравнении с перемещениями, вызывающими деформации КЭ. Особенно заметно это проявляется при наличии в конструкции элементов повышенной жесткости.
Для преодоления этой проблемы используются различные приемы: подбор специальных аппроксимирующих функций для смещений конечного элемента, предобуславливание разрешающей системы уравнений, многосеточные методы и т.д.
При расчете стержневых систем по методу конечных элементов в смешанной форме эта проблема не возникает.
Для иллюстрации рассмотрим расчет простейшей системы, состоящей из двух балок с различной изгибной жесткостью (рис. 7,а), т.е. 
или 
, где 
.
Примем для неё следующие исходные данные:
размеры прямоугольного сечения балки -
Основная система смешанного метода представлена на рис. 7,б.
а
б
Рис. 7
Матрица коэффициентов разрешающей системы уравнений для рассматриваемого случая хорошо обусловлена. Поэтому решение этой
системы уравнений при любых значениях 
, 
является устойчивым.
| k1,2 |  |  |  |  |  |  |
 | -0,08428 | -0,08428 | -0,08428 | -0,08428 | -0,08428 | -0,08428 |
 | -5,2253 | -0,48461 | -0,01053 | 0,04209 | 0,04213 | 0,04214 |
 | -20,9857 | -2,02272 | -0,12642 | 0,08407 | 0,08426 | 0,08427 |
 | -13,1266 | -1,27473 | -0,08955 | 0,04201 | 0,04213 | 0,04213 |
* результаты приведены в (мм).
При расчете с использованием ПК Лира при значении 
>106 из-за плохой обусловленности разрешающей системы уравнений возникает сбой и счет прекращается.
Выполненные расчеты простейших конструкций показали возможности и преимущества МКЭ в смешанной форме в задачах, связанных с учетом смещения конструкции или ее элементов как жесткого целого.
Сравнение результатов расчета с применением ПК Лира, основанном на МКЭ в перемещениях, с результатами расчета по смешанной форме метода конечных элементов показывает:
1. По смешанной форме МКЭ, принимая за конечный элемент стержень между узлами, получаем точное решение как по прогибам, так и по изгибающим моментам.
2. Измельчение сетки не требуется, так как оно не улучшает результат.
3. При расчете по МКЭ в перемещениях точный результат достигается лишь при измельчении сетки.
С использованием разработанной программы, реализующей алгоритм расчета по МКЭ в смешанной форме, выполнены примеры расчета различных конструкций: плоской фермы с шарнирным и жестким соединением стержней в узлах, рамы, системы балок, структурной плиты, двухслойной балки.
В частности, выполнен пример расчета двухслойной шарнирно опертой по концам балки, изображенной на рис. 5 на действие сосредоточенной нагрузки 
в середине пролета.
Рассмотрены два варианта расчетных схем, приведенных в главе 2.
На основании сравнения полученных результатов можно сделать вывод о том, что второй вариант расчетной схемы обеспечивает лучшую сходимость к точному решению, так как точнее отражает реальные свойства двухслойных балок.
Исследована возможность применения смешанной формы МКЭ к расчету геометрически нелинейных стержневых систем. Для этого рассмотрена известная по работам других исследователей задача об изгибе идеально упругой консольной балки, загруженной на конце сосредоточенным моментом (рис. 8,а).
а
б
Рис. 8
Выполнен анализ геометрически нелинейного поведения консольной балки (рис. 8) при значениях момента на конце соответствующих центральным углам (
): 
, 
, 
.
По результатам расчета деформированная схема консольной балки, при разных значениях момента, представлена на рис. 8,б.
Предложенный алгоритм позволяет отследить геометрически нелинейное поведение балки при линейном поведении каждого из конечных элементов. По результатам расчета, полученным по ПК Лира, такое геометрически нелинейное поведение балки отследить не удается.
Выполненные тестовые примеры расчета показали полное совпадение результатов расчета с расчетами, выполненными с использованием классических методов. Это подтверждает правильность алгоритмов построения матриц откликов и формирования разрешающих систем уравнений.
В четвертой главе излагается алгоритм построения динамической матрицы откликов КЭ-стержня и алгоритм расчета на свободные и вынужденные колебания.
При решении задач динамики на определение частот свободных колебаний по МКЭ в смешанной форме все массы должны быть приведены к узлам сетки КЭ, рассматриваемой конструкции и в некоторых случаях к дополнительным узлам в поле КЭ, т.е. к местам введения дополнительных связей в основной системе и к местам удаленных связей. В диссертации рассмотрено несколько вариантов динамической матрицы откликов стержневого КЭ, соответствующих различным вариантам приведения масс.
Ниже для наглядности приведена структура матрицы откликов (5) для КЭ с сосредоточенными массами по концам и между узлами (рис. 9). Принятый в ней порядок расположения неизвестных наиболее удобен при стыковке КЭ.
Рис. 9
(5)
Сопоставительный анализ расчетов с использованием различных вариантов динамических матриц откликов показал, что использование «согласованной» матрицы откликов (с полностью заполненной матрицей масс) не дает преимуществ по точности определения собственных частот по сравнению с динамической матрицей откликов, имеющей в своем составе диагональную матрицу масс.
При одинаковой сетке конечных элементов применение смешанной формы МКЭ обеспечивает лучшую сходимость к точному решению по сравнению с МКЭ в перемещениях.
Матрицы динамических откликов КЭ типа (5) и соответственно глобальные матрицы откликов содержат три разных типа строк элементов: строки с элементами, содержащими величины 
, с элементами 
и без них.
В диссертации разработан алгоритм преобразования частотного уравнения на основе динамической матрицы откликов (5) к стандартному виду алгебраической проблемы собственных векторов и собственных значений 
.
Выполненные на основе разработанного алгоритма примеры расчета частот свободных колебаний одномерных и двумерных систем (балок, ферм, рам, систем перекрестных балок) показали полное совпадение с точными аналитическими и численными полученными другими авторами с использованием классических методов и МКЭ в перемещениях.
Полученная в диссертации динамическая матрица откликов продольно сжатого КЭ-стержня позволяет выполнить расчет стержневой системы на совместное воздействие динамической возмущающей нагрузки и продольного сжатия. Приведены примеры таких расчетов, в частности рассмотрена классическая задача о динамической устойчивости фермы Мизеса.
Основные результаты и выводы:
1. Смешанная форма МКЭ является более общей по отношению к МКЭ в форме метода сил и перемещений.
2. Смешанная форма МКЭ может быть формализована и автоматизирована в той же степени, что и МКЭ в перемещениях.
3. Алгоритмы формирования глобальной матрицы откликов конструкции и составление разрешающей системы алгебраических уравнений также аналогичны соответствующим алгоритмам МКЭ в перемещениях.
4. Разработанный алгоритм построения матрицы динамических откликов КЭ-стержня позволяет учесть различные особенности расчетных схем и эффективно решать задачи расчета конструкций на свободные и вынужденные колебания, общую устойчивость стержневых конструкций.
5. Выполненные тестовые примеры расчета показали полное совпадение результатов расчета с различными, выполненными с использованием классических методов.
6. Преимущества смешанной формы МКЭ заключается в нахождении усилий и перемещений в результате непосредственного решения системы разрешающих уравнений и частичного, а для стержневых систем – полного, снятия проблемы учета смещения как жесткого целого и устранения связанной с ней накопления ошибок машинного счета.
7. Достоверность расчетов по МКЭ в смешанной форме и их обязательное совпадение с расчетами по классическим методам предопределяется использованием тех же допущений и положений, принятых в строительной механике стержневых систем.
8. МКЭ в смешанной форме может быть распространен на расчет стержневых систем в геометрически нелинейной постановке. При этом учет изменения геометрии системы на каждом шаге последовательных нагружений выполняется не сложнее, чем в традиционном МКЭ.
По теме диссертационной работы имеются следующие публикации:
Статьи по теме диссертации в изданиях, рекомендованных ВАК РФ:
- Габова В. В., Игнатьев А. В. Алгоритм формирования глобальной матрицы откликов плоской стержневой системы // Вестн. ВолгГАСУ. Сер.: Стр-во и архитектура. 2009. Вып. 14 (33). С. 71-74.
- Габова В. В., Игнатьев А. В. Получение матрицы откликов стержневого конечного элемента плоской стержневой системы на основе смешанного вариационного принципа // Вестн. ВолгГАСУ. Сер.: Стр-во и архитектура. 2009. Вып. 14 (33). С. 75-79.
Публикации по теме диссертации в других изданиях:
- Габова В. В., Игнатьев А. В. Алгоритм статического расчета плоских стержневых систем по методу конечных элементов в смешанной форме // Вестн. ВолгГАСУ. Сер.: Естеств. науки. 2007. Вып. 6 (23). С. 72-77.
- Габова В. В. Влияния нумерации узлов и элементов основной системы на структуру глобальной матрицы откликов и результаты расчета при численной реализации алгоритма статического расчета плоских стержневых систем по МКЭ в смешанной форме [Электронный ресурс] // Интернет-вестник ВолгГАСУ. Сер.: Строительная информатика. 2008. Вып. 3 (6). URL: http://vestnik.vgasu.ru/attachments/si-3(6)_2(1)_gabova-6-08.pdf
(дата обращения: 19.05.2008).
- Габова В. В., Игнатьев В. А. Расчет стержневой системы на динамические воздействия с применением метода конечных элементов // X Региональная конференция молодых исследователей Волгоградской области, Волгоград, 8-11 нояб. 2005 г. Направление № 16 "Архитектура, градостроительство, стр-во и эколог. проблемы" : тез. докл. - Волгоград : Изд-во ВолгГАСУ, 2006. - С. 11.
- Габова В. В. Применение алгоритма расчета плоских стержневых систем по методу конечных элементов в смешанной форме к расчету плоских рам // Материалы ежегодной научно-практической конференции профессорско-преподавательского состава и студентов ВолгГАСУ, 24-27 апреля 2007 г. : в 3 ч. Ч. 1 : Архитектура, градостроительство. Строительство. - Волгоград : Изд-во ВолгГАСУ, 2008. - С. 237-240.
- Габова В. В., Игнатьев А. В. Формирование матрицы эквивалентных узловых масс стержневого конечного элемента с распределенной по длине собственной массой при решении задач динамики по смешанной форме метода конечных элементов // Социально-экономические и технологические проблемы развития строительного комплекса региона. Наука. Практика. Образование : материалы III Всерос. науч.-техн. конф., г. Волгоград - г. Михайловка, 22-23 окт. 2009 г. - Волгоград : Изд-во ВолгГАСУ, 2009. - С. 121-123.
- Габова В. В. Построение матрицы откликов для стержневого КЭ с учетом инерционных составляющих от точечных масс // Энерго- и ресурсосбержение в строительной индустрии. Организационно-экономические и социальные проблемы хозяйствования в строительстве : материалы науч.-техн. интернет-конф. СФ ВолгГАСУ, 1 июня 2010 г., г. Михайловка Волгогр. обл. - Волгоград : Изд-во ВолгГАСУ, 2010. - С. 56-62.
- Габова В. В. Алгоритм формирования глобальной матрицы откликов плоской стерневой системы с применением индексных матриц // Проблемы, состояние комплексных мелиораций и их роль в обеспечении продовольственной безопасности России : материалы Междунар. науч.-практ. конф., посвящ. 45-летию образования эколого-мелиоратив. фак. ВГСХА, 9-11 нояб. 2009 г., г. Волгоград. - Волгоград : ИПК "Нива" ВГСХА, 2010. - С. 290-293.
Габова Виктория Викторовна
Применение СМЕШАННОЙ ФОРМЫ МКЭ
К РАСЧЕТАМ СТЕРЖНЕВЫХ СИСТЕМ
Автореферат
на соискание ученой степени кандидата технических наук
Подписано в печать 28.04.2001г. Формат 
.
Гарнитура «Times New Roman». Бумага офсетная. Печать трафаретная.
Усл. Печ. Л. 1,0. Тираж 100 экз. Заказ № 106.
Волгоградский государственный архитектурно-строительный университет
Центр оперативной полиграфии ЦИТ,
400074, г. Волгоград, ул. Академическая, д. 1
