Сопротивление растяжению арматуры со случайными свойствами при многостержневом армировании желе ­ зобетонных конструкций

На правах рукописи

МУХИН СЕРГЕЙ ВАЛЕНТИНОВИЧ

СОПРОТИВЛЕНИЕ РАСТЯЖЕНИЮ АРМАТУРЫ СО СЛУЧАЙНЫМИ СВОЙСТВАМИ ПРИ МНОГОСТЕРЖНЕВОМ АРМИРОВАНИИ

ЖЕЛЕ­ЗОБЕТОННЫХ КОНСТРУКЦИЙ

Специальность 05.23.01 – Строительные конструкции, здания и сооружения

АВТОРЕФЕРАТ

диссертации на соискание ученой степени

кандидата технических наук

Москва 2009

Работа выполнена в Государственном образовательном учреждении высшего профессионального образования «Московский государственный университет путей сообщения (МИИТ)».

Научный руководитель: доктор технических наук, профессор

Чирков Владилен Павлович

Официальные оппоненты: доктор технических наук, профессор

Король Елена Анатольевна

кандидат технических наук

Зенин Сергей Алексеевич

Ведущая организация: ОАО «ЦНИИПромзданий»

Защита состоится «_24_» __июня_____2009г. в _15-30_ час. на заседании диссертационного совета ДМ 218.005.05 в Московском государственном универ­ситете путей сообщения (МИИТ) по адресу: 127994, г. Москва, ул. Образцова, д. 9, стр.9 в аудитории № _7501_.

С диссертацией можно ознакомиться в библиотеке университета.

Автореферат разослан “_20_” _мая______2009г.

Ученый секретарь

диссертационного совета

кандидат технических наук, доцент М.В. Шавыкина

Актуальность: В железобетонных конструкциях применяется много­стержневое армирование, при котором прочность стержней в конструкции раз­лична и выше нор­мированных значений. Однако эти резервы в кон­струкции не используются. Полное использование прочностных свойств арма­туры при многостержневом армировании один из путей снижения расхода стали. В связи с этим исследова­ние механизма поведения арматурных стержней в железобетонных конструк­циях при воздейст­вии нагрузок и выявление резер­вов несущей способности, учет реальных свойств стали является актуаль­ной задачей.

С увеличение числа стержней со случайными свойствами в железобетон­ных несущих конструкциях, приводит к повышению расчетных сопротивлений арматуры, по сравнению с принятыми в технических условиях и определенных по так называемому правилу трех стандартов. В результате коллективной ра­боты стержней увеличивается общее усилие в арматуре в предельном состоя­нии конструкции, повышается их надежность работы под нагрузками и снижа­ется вероятность отказа и обрушения зданий с опасными последствиями. Осо­бенно остро стоит проблема предотвращения прогрессирующего разрушения при локальном повреждении и выходе из строя одного или нескольких несущих элементов несущего остова здания при аварийных воздействиях техногенного или природного происхождения.

Целью исследования является выявление резервов несущей способности и надежности арматуры со случайными свойствами при многостержневом ар­ми­ровании, с этой целью необходимо решить следующие задачи:

- Разработать методику определения расчетного сопротивления многоэле­ментной арматуры со случайными свойствами с применением вероятностных методов;

- Разработать методику расчета надежности железобетонных конструкций с многоэлементной арматурой при воздействии запредельных нагрузок;

- Разработать вероятностную модель механизма разрушения многоэле­мент­ной арматуры со случайными свойствами;

- Проанализировать механизмы разру­шения железобетонных конструкций с многоэлементной арматурой со случай­ными свойствами;

- Обобщить статистическую информацию о прочностных и де­форматив­ных свойствах арматуры с целью её использования в расчетах проч­ности и на­деж­ности многоэлементной арматуры;

- Составить рекомендации по применению многоэлементной арматуры в же­лезобетонных конструкциях.

Автор защищает: методику определения расчетных сопротивлений арма­туры со случайными свойствами при многостержневом армировании в различ­ных железобетонных конструк­циях, расчета надежности при действии запре­дельных нагрузках.

Объект исследования: является многоэлементная арматура со случай­ными свойствами, расположенная в железобетонных конструкциях.

Научную новизну диссертации составляет:

- Уточнение методики определения расчетного сопротивления многоэле­ментной арматуры со случайными свойствами;

- Предложен способ определения надежности неповрежденных железобетонных конструкций, после выхода из строя одного из элементов конструкции здания, при лавинообразном обрушении;

- Повышение надежности железобетонной конструкцией с многоэлементной арматурой в результате совместной работы всех арматурных стержней;

Отличие научных результатов представленных в работе от результа­тов, полученных другими авторами:

- Проанализированы и выявлены схемы разрушения плит перекрытий железобетон­ных конструкций, в том, числе и при лавинообразном обрушении;

- Построены зависимости необходимой площади многоэлементной арма­туры в зависимости от количества и диаметра стержней;

- Предложен расчет вероятности безопасной работы железобетонной кон­струкции плиты перекрытия при запредельных нагрузках;

- Определены вероятностные характеристики распределения равномерного относительного удлинения для многоэлементной арматуры, в зависимости от числа стержней в опасном сечении.

Достоверность результатов выполненной работы обосновывается приме­нением апробированных методов теории вероятности и теории надежности, обеспечивается результатами расчетов с использованием экспериментальных данных о прочностных и деформативных свойствах арматуры, которые были представлены в различ­ных ранее опубликованных научных изданиях.

Практические значения работы и реализация результатов работы:

- Прогнозирование несущей способности в железобетонных конструк­циях при различном числе элементов (проволок или стержней);

- Выявление резерва несущей способности железобетонных конструкций при их работе в предельном состоянии;

- Повышение расчетных сопротивлений арматуры на 5-10%, что по­зволяет снизить ее расход.

Внедрение результатов работы: Результаты, исследований проведенных в диссертаци­онной работе были использованы при расчете плит перекрытий, выпускаемых УПТК ОАО“Центротрансстрой”.

На защиту выносится:

- Вероятностная модель механизма разрушения многоэлементной арма­туры со случайными свойствами;

- Методика определения расчетного сопротивления многоэлементной ар­матуры со случай­ными свойствами;

- Методика расчета показателей безопасной работы конструкции при за­предельных воздействиях;

- Анализ механизмов разрушения различных видов железобетонной кон­ст­рукции с многоэлементной арматурой со случайными свойствами;

- Анализ статистической информации о прочностных и деформативных свойствах арматуры с целью её использования в расчетах прочности и надеж­ности железобетонных конструкций с многоэлементной арматуры.

Апробация работы: Основные положения работы докладывались на на­учно-технических конференциях, проходивших в Московском государственном университете пу­тей сообщения в 2004-2007г.:

1. Пятая научно-технической конференции ”Безопасность движения по­ездов”(МИИТ) г.Москва 2004г.; 2. Неделя науки (МИИТ) г.Москва 2005г.; 3. Шестая научно-практической конференции ”Безо­пасность движе­ния поездов”. (МИИТ) г.Москва 2005г.; 4. Неделя науки (МИИТ) г.Москва 2006г.; 5. Неделя науки (МИИТ) г.Москва 2007г.

Публикации: По теме диссертации опубликовано 9 работ.

Структура и объем диссертации:

Работа состоит из введения, пяти глав, выводов, приложения и списка ли­тературы из 158 наименования. Диссертация изложена на 211 страницах маши­нописного текста и содержит 58 рисунков и 46 таблиц.

СОДЕРЖАНИЕ ДИССЕРТАЦИИ

Во введении обоснована актуальность поставленной задачи, определена цель работы, ее научная новизна, изложено практическое содержание работы и ее практическая ценность.

В первой главе дается обзор исследований по вероятно­стным методам рас­чета для несущих железобетонных конструкций, применяемых многостерж­не­вое армирование. Изложены основные положения вероятностного расчета. Описаны различные методы расчета несущей способности в железобетонных конструкциях и проведен их анализ. Общие принципиальные вопросы приме­нения вероятностных методов к анализу надежности сооружений получили развитие в фундаментальных исследованиях Болотина В.В., Ржаницына А.Р. Стрелецкого Н.С. Глубокие исследования по развитию теории расчета железобетонных конструкций и нормирования конструктивной безопасности были выполнены: В.О. Алмазовым, Е.А. Антроповой, В.М. Бондаренко, А.А. Гвоздевым, Г.А. Гениевым, А.С. Залесовым, С.А. Зениным, Н.И. Карпенко, В.И. Колчуновым, А.П. Кудзисом, О.В. Лужиным, А.С. Лычевым, Л.Р. Маиляном, М.В. Мозго­ловым, В.Д. Райзером, Б.С. Расторгуевым, В.И. Римшиным, С.М. Скоробогатовым, В.И. Травушем, В.П. Чирковым, Е.А. Чистяковым и многими другими учеными. Обширные исследования в области изучения физико-механических свойств арматуры был проведен: Е.А. Гузеевым, Ю.П. Гуща, В.В. Дегтяревым, С.А. Мадатяном, К.В. Михайловым, Н.М. Мулиным, И.Н. Тихоновым и многими другими.

Сформулированы основные цели и задачи исследований.

Во второй главе изложены методы определения рас­четных со­противлений арматуры со случайными свойст­вами при многостержневом ар­мировании желе­зобетонных конструкций. Приводятся основные уравнения расчета многоэле­ментной арматуры со случайными свойствами, с помощью ко­торых решаются основные задачи работы: определение расчетного сопротивле­ния в каждом стержне; вычисление случайных величин значений расчетного сопротивления в зависимости от числа стержней со случайными свойствами; нахождение с за­данной вероятностью значение расчетного сопротивления мно­гоэлементной арматуры со случайными свойствами растяжению, при действии на конструк­цию нагрузок (в том числе запроектных).

Рис.1.Диаграмма арматурной сталидля каждого отдельного стержня много­эле­ментной арматуры (а) и плотность распределения предела те­кучести (б).

В предельном состоянии напряжения в арматуре достигают предела теку­чести. В связи со статистическим разбросом прочностных и деформативных свойств ар­матурной стали диаграммы для каждого отдельного стержня многоэле­ментной арматуры будут отличаться друг от друга.

Как видно из рис.1, усилия в отдельных стержнях многоэлементной ар­ма­туры в предельном состоянии (стадия текучести) неодинаковы и зависят от ста­тистического раз­броса проч­ностных и деформативных свойств арматуры. Ос­новой для статистиче­ского ана­лиза прочности многоэлементной арматуры слу­жит не строго зафик­сированное расчетное сопротивление , принятое в техни­ческих условиях, а полное уси­лие в арматуре в момент отказа. С этой це­лью при назначении рас­четных со­противлений необходимо рассматривать не в отдельной точке соот­ветствую­щей трем стандартам, а в области возможных значений прочности ар­матуры с последующим суммированием напряжений в каждом арматурном элементе для получения суммарного усилия .

Суммарные усилия в арматуре:

- фактически

- по ТУ (1)

Несущую способность многоэлементной арматуры можно определить как сумму предельных случайных усилий в каждом элементе:

(2)

где - несущая способность многоэлементной арматуры – случайная ве­личина; n - число арматурных элементов стержней; - проч­ность i-того арма­турного элемента - случайная величина.

Вероятностные характеристики распределения :

математическое ожидание (3)

среднее квадратичное отклонение (4)

где и - математическое ожидание и стандарт распределения проч­но­сти i-го элемента.

Случайное значение прочности многоэлементной арматуры можно по­лу­чить разделив обе части равенства на площадь арматуры :

(5)

Вероятностные характеристики распределения прочности многоэле­мент­ной арматуры:

математическое ожидание (6)

среднее квадратичное отклонение 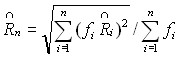(7)

При равных площадях арматурных элементов и одинаковых веро­ятно­стных характеристик распределений арматурных элементов полученные формулы приобретают следующий вид: (8)

Рис.2. Кривые плотности распределения прочности арматуры при различном числе арматурных элементов: 1 - при n =1; 2 - при n = 2; 3 - при n = 10

Плотности распределения прочности многоэлементной арматуры (рис.2) свидетельствуют о том, что с увеличением числа арматурных элементов кри­вые становятся более компактные, статистический разброс прочности снижа­ется. При прочность арматуры определяется однозначно:

Коэффициент вариации распределения прочности многоэлементной ар­ма­туры (рис.3): (9)

где , уменьшается с увеличением числа арматурных элементов.

Арматура попадает в железобетонную конструкцию, как правило, из одной партии металла, поставленной на завод железобетонных изделий или строи­тельную площадку. Поэтому в расчетах, связанных с определением проч­ности многоэлементной арматуры, следует применять партионный коэффици­ент ва­риации полученный для внутриплавочного рассеивания прочности арма­туры. Этот коэффициент вариации в 1,5-2,0 раза меньше коэффициента ва­риации прочности арматуры в генеральной совокупности.

Рис.3. Зависимость коэффициента вариации прочности арматуры от числа арматурных элементов: 1 - при = 0,02; 2 - при =0,04; 3 - при =0,06

Расчетные сопротивления арматуры установлены с обеспеченностью рабо­тоспособности Р = 0,99865, и для многоэлементной арматуры их можно опре­делить так: (10)

Нормативное сопротивление для многоэлементной арматуры можно также определить по формуле: (11)

Увеличение числа элементов стержней приводит к повышению расчет­ных сопротивлений арматуры, так как работа системы приближается к работе сис­темы с параллельным соединением элементов. При параллельном соедине­нии звеньев надежность системы повышается по сравнению с надежностью од­ного звена.

Анализ статистических данных механических свойств арматуры предос­тавленные сертификатах заводами: арматура класса А400 (А-III) (Челябин­ский металлургиче­ский комбинат) и арматура класса А500С (Белорус­ский металлур­гический завод). На основе выше приведенных данных была сформирована табл.1 для соответствующего класса арматуры и определен коэффициент вариации в партии:

- среднеквадратическое отклонение в партии-плавке; - минималь­ное среднее значение в партии-плавке.

Для обеспечения коллективной работы многоэлементной арматуры необ­ходимо, чтобы арматурные стержни обладали достаточным равномерным отно­сительным удлинением. В табл.2. приведены статистические зависимости де­форматив­ных свойств относительного удлинения арматуры , и опреде­лено отношение коэффи­циентов вариации этих случайных величин.

Рис.4. График отношения относительного удлинения в арматуре (,) при­ве­денных в различных источниках. (Испытано более 150 образцов диам.10-36мм).

Из рис.4 видно, что для различных изготовителей колеблется в интер­вале от 12,4715,7 % для арматуры А400(A-III) и от 7,0311,54 % для арматуры А500С. Партионный коэффициент вариации () и в генеральной совокуп­но­сти () с увеличением количества стержней как для арма­туры класса А400 (А-III) так и для арматуры А500С, уменьшается и нахо­дится ниже норми­руемого представ­ленного в ГОСТе и СТО АСТМ 7-93 и EN0080.

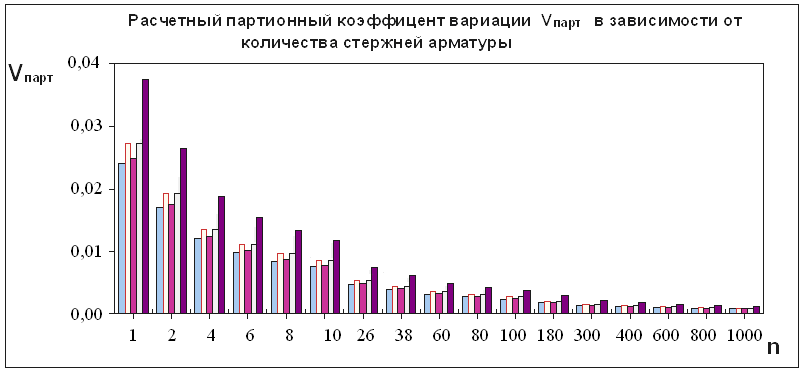
Рис.5. Диаграмма зависимости вариации от количества стержней арма­туры (n): для арматуры класса А400 (А-III).

Рассмотренная методика расчета железобетонных конструкций с использо­ванием коэффициента вариа­ции позволяет рассчитывать железобетонные эле­менты на прочность с учетом их совместного разброса случайных параметров.

Формулы (10) и (11) соответственно можно преобразовать к следую­щему виду: ; (12)

где , - расчетное и нормативное сопротивление арматуры при n=1;

,- функции, учитывающие повышение расчетных и норматив­ных сопро­тивлений арматуры: ; (13)

Значение расчетных сопротивлений не должно превышать браковочных минимумов, установленных для арматурных сталей.

В третьей главе производится анализ механизмов разрушения железо­бе­тонных конструкций. В последнее время, в связи с обрушением конструкций, стал актуальным вопрос о живучести, в этой главе также рассмотрены некото­рые аспекты при прогрессирующем обрушении железо­бетонных конструкций с арматурой со случайными свойствами при многостержневом ар­мировании.

Физические модели разрушений, которые являются основой для расчетов прочности, определяют характер армирования железобетонных элементов. В опасных сечениях может быть размещено различное число растянутых арма­турных стержней в зависимости от класса арматуры, диаметра, геометрических характеристик бетонного сечения. Если для балочных конструкций при дейст­вии изгибающего момента разрушение происходит в середине пролета в одной плоскости, перпендикулярной продольной оси элемента, то для других элемен­тов, например, плит опертых по контуру поверхность разрушения образуется несколькими плоскостями и для обоснованного учета свойств многоэлементной арматуры следует определять какое количество стержней расположено в сече­ниях поверхности разрушения железобетонной конструкции.

Рассмотрены механизмы разрушения в железобетонных конструкциях, ко­торые установлены на основе многочисленных экспериментов и приводятся в технической литературе.

На основе представленных механизмов разрушений можно выявить ре­зервы несущей способности железобетонных конструкций при их работе. При расчете на воздействие запредельных нагрузок этот дополнительный резерв прочности способствует повышению надежности и живучести желе­зобетонной конструк­ции.

Представлены модели предельного состояния плит железобетонных кон­ст­рукций (балочные плиты, плиты, опертые по контуру, панели КЖС, узлы ферм). На основании их анализа, устанавливается, что расчетная несущая спо­собность зависит от количества стержней, перпендикулярных поверхности раз­рушения.

В четвертой главе рассматривается применение разработанной мето­дики определение расчетного сопротивления много­элементной арматуры в раз­лич­ных железобетонных конструкций. Произведен сравнительный анализ по­лу­ченных результатов расчета требуемой площади рабочей арматуры с результа­тами, полученными по действующим нормам СНиП. Построены зависимости необходимой площади арматуры при много­стержневом армировании в зависи­мости от диаметра стержней.

Предлагаемая методика позволяет повысить расчетную несущую способ­ность, на основе учета совместной работы стержней в составе многоэлементной арматуры. С увеличением количе­ства стержней изменчивость прочности мно­гостержневой арматуры стремиться к нулю, что приводит к уменьшению рас­хода арматуры, в среднем 5-10%, и по­вышает надежность системы. Такой под­ход позволяет выявить резервы несущей способности железо­бетонных конст­рукций при их работе за пределами упругости, т.е. использовать вязкость арма­турных сталей и способность поглощать кинетическую энергию стержнями многоэлементной рабочей арматуры при внезапных запредельных воздейст­виях.

В пятой главе рассматривается вероятности отказов железобетонных кон­струкций с арматурой при многостержневом армировании при действии за­про­ектной нагрузки. Проанализированы схемы разрушения плит перекрытий желе­зобетонных конструкций, в том, числе и при лавинообразном обрушении с уче­том влияния количества арматурных элементов в конструкции. Предложен рас­чет вероятности безопасной работы железобетонной конструкции, плиты пере­крытия при запредельных нагрузках.

В настоящее время четко обо­значена проблема обеспе­чения конструктив­ной безопасности как одного из важнейших направлений общей безопасности строитель­ных систем, то есть безопасность железобетон­ных конструкций, как в системе здания, так и его отдельные элементы, выпол­нять заданные функции в течение всего срока службы.

Как показали результаты испытаний, равномерная относительная дефор­мация являются случайной величи­ной. Вероятностные характеристики ( и ) определяют на основе стандартных испытаний одиночных стержней. При отказе железобетонных конструкций с многоэлементной арматурой сна­чала происходит разрыв арматурного стержня обладающего наименьшей рас­тяжимостью (рис.6).

В этот момент растяжимость других стержней еще не исчерпана, и относи­тельные деформации остальных стержней будут меньше их значений, полу­ченных при испытаниях одиночных стержней арма­туры. При разрыве одного стержня происходит возрастание напряжений в дру­гих стержнях, что, как пра­вило, сопровождается разрушением железобетонной конструкции. В связи с тем деформации в остальных стержнях не достигли своих предельных значе­ний, плотность распределения для многоэлемент­ной арматуры, по­строенная с учетом деформаций арматурных элементов при отказе, сдвигается влево по отношению к кривой - плотно­сти распре­деления относитель­ных равномерных деформаций одиночных стержней арматуры.

Определение вероятностных характеристик равномерной относи­тельной деформации арматуры для арматуры со случайными свойст­вами при много­стержневом армировании.

Рис.6. Диаграммы для арматуры класса А500С: а)“”; б) плотность распределения ; в) плотность распределения равномерного удлинения .

В настоящее время отсутствуют экспериментальные данные вероятност­ных характеристик распределения для многоэлементной арматуры. В то же время имея вероятностные характеристики относительных равномерных де­формаций для одиночных стержней арматуры, можно перейти к вероятностным характеристикам этих деформаций многоэлементной арматуры на основе при­менения положений теории вероятностей – теоремы о распределении миниму­мов нескольких случайных величин.

Для равно­мерных относительных удлинений многоэлементной арматуры они имеют сле­дующий вид: (14)

(15)

где и - математическое ожидание и среднеквадратическое отклоне­ние равномерного относительного удлинения одиночных стержней ар­матуры.

Выявить резервы прочности конструкции с многоэлементной арматурой воз­можно на основе применения методов теории вероятности.

При чрезвычайных ситуациях, возможно, допустить значительные де­фор­мации железобетонных перекрытий в стадии работы их арматуры как ван­товой системы, деформирующийся в пластической стадии. Стадия деформиро­вания арматуры как вантовой системы начинается после того, когда углы рас­крыты в опорных сечениях, ригелей достигают предельных значений, сжатые зоны ри­гелей раздроблены, однако аварийное обрушение конструкций каркаса отсутст­вует и обеспечивается эвакуация людей. Расчетная схема с разрушен­ным бето­ном в сжатых зонах представляется в виде гибкой пологой нити, де­формирую­щейся в пластической стадии. Площадь поперечного сечения ванта равна пол­ной площади арматуры, расположенной в растянутой и сжатой зонах элемен­тов.

Нагрузки и несущая способность железобетонного перекрытия как ван­то­вой системы, после разрушения ниже расположенной колонны, носят слу­чай­ный характер (рис.7). Для оценки безопасной работы арматуры можно приме­нить методику с использованием характеристики безопасности .

(16)

где и - математическое ожидание и дисперсия предельной на­грузки, выдерживаемой вантами (арматурой в составе элементов перекрытия); и - математическое ожидание и дисперсия приведенной нагрузки на ри­гели и плиту перекрытия; - характеристика безотказности, соответствующая нормативному значе­нию надежности, при =0,99865 величина =3.

Рис.7. Кривые распределения усилий от нагрузки и несущей способности как вантовой системы.

Вероятность отказа Q, т. е. риск разрушения несущей конструкции, ра­бо­тающей по вантовой схеме определяется так: Q=1-P (17)

где P – вероятность надежной работы конструкции от разрушения, рабо­тающей по вантовой схеме.

Несущая способность вантовой системы с многоэлементной арматурой за­висит от предельного растягивающего усилия всех стержней арматуры (ри­геля и плиты), , которое определяется на основе анализа вероятностных свойств многоэлементной арматуры. Изложенный подход позволяет вскрыть резервы несущей способности перекрытий при чрезвычайных ситуациях. Это стало возможным благодаря учету развития пластических деформаций в много­эле­ментной арматуре после полного разрушения бетона и переходу работы пе­ре­крытия как вантовой системы.

Условие отсутствия разрыва арматуры, работающей по вантовой схеме:

(18)

Величины и определяются при средних значениях переменных.

Применив методику с использованием характеристики безопасности , вы­числяемая по формуле (17) получим:

, следовательно, при =0,99865.

Значение соответствует определенное значение вероятности P.

Вероятность Р надежной работы конструкции, с учетом совместной работы стержней в составе многоэлементной арматуры равно:

где - интеграл вероятностей.

Вероятность отказа Q, т. е. риск разрушения несущей конструкции, рабо­тающей по вантовой схеме с учетом совместной работы стержней равна:

Q=1 - 0,9997505 = 0,0002495

Вероятность Р надежной работы конструкции, без учета совместной ра­боты стержней:

Вероятность отказа Q, т. е. риск разрушения несущей конструкции, рабо­тающей по вантовой схеме, без учета совместной работы стержней увеличива­ется: Q=1 - 0,999522 = 0,000478

Расчетная вероятность отказов железобетонных конструкций с мно­гоэле­ментной арматурой при чрезвычайных ситуациях снижается в 2 раза.

Проектирование железобетонных конструкций должно осуществляться та­ким, образом, чтобы при локальном разрушении какого-либо элемента сис­темы остальные неповрежденные конструктивные элементы могли сохранить цело­стность объекта и не допустить его лавинообразного разрушения.

При сверхпредельных воздействиях допускается значительное развитие пластических деформаций в арматуре и разрушение бетона в сжатой зоне изги­баемых элементов. Ригель и плита переходят в предельное состояние 1в, при котором арматура этих элементов работает как вантовая система.

Из условия (16) математическое ожидание несущей способности не­по­вре­жденных элементов должно быть:

(19)

В расчетах целесообразно пользоваться относительными величинами веро­ятностных характеристик, входящих в формулу. Если разде­лить числитель и знаменатель левой части формулы (19), то получается квадратное уравнение относительно К и решение которого имеет вид:

(20)

где и - коэффициенты вариации несущей способности многоэле­мент­ной арматуры как вантовой системы.

Величина К, равная отношению математических ожиданий несущей спо­собности и нагрузки, представляет собой коэффициент запаса.

Как правило, значение изменчивости нагрузок и несущей способности ос­таются постоянными, что является удобным при выполнении расчетов по фор­муле (19). После определения величины К согласно (20) не представ­ляют труда найти математическое ожидание несущей способности многоэле­ментной арма­туры как вантовой системы: (21)

ОБЩИЕ ВЫВОДЫ:

1. Разработана методика определения расчетных сопротивлений много­стержневой арматуры со случайными свойствами.

2. Основой для определения расчетных сопротивлений многоэлементной арматуры со случайными свойствами является анализ фактического напряжен­ного состояния стержней в стадии текучести с учетом статических данных о прочностных и деформативных свойствах арматуры.

3. В стадии текучести, соответствующей наступлению предельного состоя­ния арматуры, напряжения в стержнях многоэлементной арматуры различны и при совместной работе по восприятию усилий от нагрузки их среднее значение превышает минимальный предел текучести, установленный в нормативных до­кументах.

4. Установлено, что для учета фактических условий работы стержней в же­лезобетонной конструкции в качестве исходной статической информации для определения расчетных сопротивлений следует применять партионное распре­деление предела текучести арматуры как случайной величины.

5. Получены расчетные зависимости для определения расчетных сопротив­лений многоэлементной арматуры при различном числе стержней (проволок) и коэффициентах вариации партионного распределения предела текучести. Зна­чение расчетных сопротивлений не должно превышать браковочных миниму­мом, установленных для арматурных сталей.

6. Установлено, что с увеличением числа стержней или проволок коэффи­ци­ент вариации предела текучести уменьшается, а расчетное сопротивление мно­гоэлементной арматуры с ярко выраженными пластическими свойствами уве­личивается, приближаясь к среднему значению предела текучести в партии.

7. Разработаны рекомендации по назначению расчетных сопротивлений многоэлементной арматуры со случайными свойствами для А240, А300, А400, А500С с обеспеченностью .

8. Учет изменчивости прочностных характеристик арматуры при много­стержневом армировании конструкции приводит к увеличению расчетной не­сущей способности, как отдельного элемента, так и конструкции в целом в слу­чае лавинообразного разрушения.

9. Разработанная методика определения расчетных сопротивлений много­элементной арматуры апробирована в расчетах необходимой площади рабочей арматуры различных железобетонных конструкций: плита перекрытия жилого дома, плиты, опертые по контуру, плита нижней ступени фундамента, балки монолитных перекрытий, ребристая плита, криволинейная плита оболочки КЖС, многопролетная второстепенная балка.

10. В связи с учетом эффекта коллективной (совместной) работы стержней в составе многоэлементной арматуры расчетное сопротивление увеличивается на 5-10%, что приводит к снижению расхода арматуры в железобетонных кон­ст­рукциях.

11. Наибольший эффект совместной работы стержней в стадии текучести проявляется тогда, когда применяется арматура относительно небольшого диа­метра, так как в этом случае число стержней в конструкции необходимой пло­щади армирования увеличивается.

12. Разработана методика расчета надежности железобетонного перекры­тия с многоэлементной арматурой при воздействии запредельных нагрузок с при­менением характеристики безопасности.

13. Обосновано, что случайными факторами, определяющими несущую спо­собность железобетонного перекрытия в чрезвычайных ситуациях после пол­ного разрушения бетона в сжатых зонах, является нагрузка, прочностные и де­формативные свойства растянутой многоэлементной арматурой, работающей как гибкая нить с допущением значительных пластических деформаций.

14. На основе теоремы теории вероятностей о распределении минимальных значений случайной величины и использования результатов обширных экспе­риментальных исследований физико-механических свойств стальной арматуры определены вероятностные характеристики (математическое ожидание и сред­неквадратическое отклонение) относительного равномерного удлинения много­элементной арматуры, которые зависят от количества стержней в железобетон­ной конструкции.

15. Получена зависимость для определения несущей способности железо­бе­тонного перекрытия при разрушении нижерасположенной колонны в стадии работы конструкции как вантовой системы, исключая неизбежность разруше­ния всего здания, с учетом вероятностных свойств нагрузок и многоэлементной арматуры.

16. Расчеты вероятности безопасной работы перекрытия при полном раз­ру­шении сжатых зон бетона и допущении значительных пластических дефор­ма­ций в арматуре показали, что учет совместной работы стержней в составе мно­гоэлементной арматуры повышает надежность конструкции при воздейст­вии нагрузок в чрезвычайных ситуациях и снижает вероятность риска отказа в 2 раза.

ОСНОВНЫЕ ПОЛОЖЕНИЯ ДИССЕРТАЦИИ ОПУБЛИКОВАНЫ В СЛЕДУЮЩИХ РАБОТАХ:

1. Чирков В.П., Мухин С.В. Сопротивление многоэлементной арматуры со случайными свойствами. //Труды пятой научно-технической конференции ”Безопасность движения поездов” (МИИТ) г.Москва 2004г., с.VII-20 -VII-21.

2. Чирков В.П., Мухин С.В. Расчетные сопротивления многоэлементной ар­ма­туры инженерных сооружений. //Труды третьей Международной научно-практической конференции ”Развитие современных городов и реформа жи­лищно-комунального хозяйства” (МИКХиС), г.Москва 2005г., с.410-413.

3. Чирков В.П., Мухин С.В. Структурная модель надежности многоэлемент­ной арматуры. //Труды общего собрания РААСН ”Непрерывное архитектурно-строительное образование как фактор обеспечения качества среды жизнедея­тельности”. (РААСН) г.Москва-г.Воронеж 2005г., с.230-235.

4. Чирков В.П., Мухин С.В. Прочностные свойства арматуры со случай­ными свойствами. Труды шестой научно-практической конференции ”Безо­пасность движения поездов”. (МИИТ) г.Москва 2005г., том 2, с.VIII-22 -VIII-23.

5. Чирков В.П., Мухин С.В. Живучесть плитных конструкций при запре­дель­ных нагрузках. // Труды общего собрания РААСН ”Проект и реализа­ция – га­ранты безопасности жизнедеятельности”. (РААСН) г.Москва-г.Санкт-Петер­бург 2006г., том 2, с.84-89.

6. Чирков В.П., Шавыкина М.В., Мухин С.В. Определение вероятности от­каза многоэлементной арматуры. //Труды пятой Международной научно-практи­ческой конференции ”Развитие современных городов и реформа жилищно-ко­мунального хозяйства” (МИКХиС), г.Москва 2006г., том 2 с.168-171.

7. Чирков В.П., Мухин С.В. Надежность конструкций с многоэлементной арматурой. //Материалы XII научно-технической конференции ”Надежность строительных объектов”. Самарский государственный архитектурно-строительный университет, г.Самара, 2007г., с.6-8.

8. Чирков В.П., Мухин С.В. Надежность железобетонных конструкций при многостержневом армировании.//Транспортное строительство, 2007г., №8, с.36.

9. Чирков В.П., Шавыкина М.В., Мухин С.В. Многоэлементная арматура – резерв расчетной надежности железобетонных конструкций. //Про­мышленное и гражданское строительство, 2007г., №9, с.61-62.

МУХИН СЕРГЕЙ ВАЛЕНТИНОВИЧ

Сопротивление растяжению арматуры

со случайными свойствами при многостержневом

армировании железобетонных конструкций

Специальность 05.23.01 – Строительные конструкции, здания и сооружения

Автореферат диссертации на соискание ученой

степени кандидата технических наук

Подписано в печать – Формат 60х84/16 Объем 1,5 п.л. Заказ № Тираж – 80 экз.

Типография МИИТ, 127994, г. Москва, ул. Образцова, д. 9, стр.9