Процессы деформации листовых сталей при формовании (модели и экспериментальная верификация)
Федеральное агентство по образованию
ФГОУ ВПО «Государственный технологический университет
«Московский институт стали и сплавов»
На правах рукописи
Назаров Роман Александрович
ПРОЦЕССЫ деформации листовых сталей при формовании
(модели и экспериментальная верификация)
Специальность 05.16.01 – Металловедение и термическая обработка металлов
Автореферат
диссертации на соискание учёной степени
кандидата технических наук
Москва, 2008
Работа выполнена на кафедре Металловедения и Физики Прочности (МиФП) Государственного Технологического Университета «Московский институт стали и сплавов (МИСиС)» и в лаборатории Инженерии Поверхности (LSGS) Национального Политехнического Института Лотарингии (INPL), г. Нанси, Франция.
Научные руководители
доктор технических наук, профессор НИКУЛИН С.А.,
доктор наук, профессор АЙАДИ З.
Официальные оппоненты
д.т.н., Родионова И.Г. (ЦНИИ Чермет им. И.П.Бардина)
д.т.н., член-корр. РАН, Карпов М.И. (ИФТТ РАН)
Ведущая организация
ИМЕТ им. А.А. Байкова РАН
Защита диссертации состоится «18» декабря 2008 г. в 15 час. 00 мин.
на заседании Диссертационного Совета Д 212.132.08
при Московском Государственном Институте Стали и Сплавов
по адресу: 119049, Москва, ГСП-1, Ленинский проспект, д.4 в ауд. Б 436.
С диссертацией можно ознакомиться в библиотеке МИСиС.
Автореферат разослан «____» 2008 г.
Учёный секретарь Совета
д. ф.-м. н., профессор Мухин С.И.
Общая характеристика работы
Актуальность темы.
В настоящее время из-за бурного роста вычислительных мощностей моделирование сложнейших технологических процессов вытесняет использующийся ранее метод проб и ошибок. Аналитическое моделирование процесса формования в отличие от метода конечных элементов (МКЭ) позволяет глубже понять физику явления, показать изменение результатов при изменении условий.
Основным затруднением для аналитических расчетов формования металлов является правильный учет поведения материала. До недавнего времени аналитические модели формования основывались на недостаточно обоснованных упрощающих гипотезах (как, например, абсолютно пластичный материал, малые деформации). Однако в связи с сильным развитием феноменологического описания поведения материала появилась надежда правильно учесть в аналитических моделях нелинейный закон упрочнения, анизотропию пластических свойств, проявление эффекта Баушингера и эффекта поперечного упрочнения.
В этой связи актуально исследование влияния перечисленных свойств на характер нагружения материала в различных процессах формования и получаемую геометрию изделия. Решение этой задачи позволит оптимизировать технологию получения изделий с заданными свойствами.
Цель диссертационной работы: выявить влияние механических свойств сталей на различные типы процессов формования материала – процессы с упругим возвратом, стационарные процессы деформирования и процессы с возможной потерей устойчивости пластического течения. Для этого необходимо получить наиболее общее математическое моделирование этих процессов, включающее феноменологическое описание поведения материала. Полученные модели необходимо сравнить с экспериментальными результатами тестов характерных для каждого из рассмотренных типов процессов – формование профиля «омега», протяжка через простой захват, штамповка стакана.
Основные задачи, которые решались для поставленной цели:
- Критический обзор и анализ существующих моделей и методов описания механического поведения материала.
- Обобщенное математическое моделирование процессов с упругим возвратом, стационарных процессов и процессов с возможной потерей стабильности пластического течения.
- Внедрение наиболее общего описания поведения материала (в том числе описание эффекта Баушингера, эффекта поперечного упрочнения) в полученные выше модели.
- Алгоритмическая и программная реализация разработанных методов в применении к конкретным тестам формования: формование профиля «омега», протяжка через простой захват, штамповка стакана.
- Обоснование работоспособности и достоверности модели по согласию расчетов с экспериментальными тестовыми испытаниями.
- Выявление влияния параметров поведения материала и технологии на результаты формования.
Научная новизна диссертационной работы заключается в следующем:
- выведены и обоснованы новые обобщенные математические модели, позволяющие описывать процессы формования материала в стационарных процессах, процессах с упругим возвратом и с возможностью потери устойчивости пластического течения;
- предложены схемы расчета полей напряжений и деформаций в изделии из металла, описываемого наиболее общими феноменологическими моделями;
- разработаны 3 пакета программ уникального алгоритмического и программного обеспечения, реализующие предложенные методы математического моделирования для конкретных процессов формования;
- экспериментальным исследованием процессов формования установлены границы применимости предложенных математических моделей на основе экспериментальных данных;
- проведено экспериментальное исследование потери устойчивости пластического течения листовых образцов (разной толщины) с разными концентраторами напряжений из различных по химическому и фазовому составам сталей;
Практическую ценность результатов работы представляют практические рекомендации по применению разработанных моделей и созданные компьютерные программные средства.
Достоверность результатов работы подтверждается корректным использованием теоретических и экспериментальных методов обоснования полученных результатов, выводов и рекомендаций, а также основывается на согласованности данных эксперимента и теоретических выводов полученных на широком спектре исследуемых сталей.
Апробация результатов работы.
Основные результаты докладывались и обсуждались на следующих международных конференциях:
- XII международный симпозиум по проблемам пластичности, Канада, г. Халифакс, 2006 г.
- IV Европейская научная конференция «Европейская школа материаловедения и инженерии», Испания, г. Барселона, 2007 г.;
- XVIII Конгресс механики франкоговорящих стран, Франция, г. Гренобль, 2007 г.;
- III Франко-русский конгресс «Новые достижения в материаловедении», Франция, г. Метц, 2007 г.;
- IV Евразийская научная конференция «Прочность неоднородных структур ПРОСТ 2008», Россия, г. Москва, 2008 г.;
- Симпозиум франкоговорящих стран по пластичности, Франция, г. Нанси, 2008 г.;
- XI Международный конгресс по формованию материалов (ESAFORM), Франция, г. Лион, 2008 г.
Публикации.
По теме диссертации опубликовано 8 работ, в том числе в изданиях рекомендованных ВАК.
Объем работы.
Диссертационная работа состоит из введения, четырех глав, заключения и списка использованных источников.
Работа содержит 160 страниц текста, 78 рисунков, 5 таблиц и 189 наименование библиографии.
Основное содержание работы
Во введении обоснована актуальность темы диссертации. Изложены цели и задачи диссертационной работы.
Первая глава содержит литературный обзор о математическом описании пластичности материала, моделировании анизотропии листового материала, его нелинейного упрочнения под нагрузкой, эффектам Баушингера и поперечного упрочнения. Кроме того, рассмотрены существующие модели поведения материала в процессах формования с упругим возвратом, в стационарных двумерных процессах и в процессах с возможной потерей стабильности пластического течения. В конце главы содержится обоснование поставленных в диссертации целей.
Во второй главе предложена теоретическая модель, описывающая поведение листового материала в процессах формования с последующим упругим возвратом.
Геометрия автолиста (толщиной h) определяется при помощи двух параметров – кривизны (k) и деформации срединной линии (10). Эти два параметра позволяют полностью определить деформационное состояние материала, а при упругой деформации и напряжение. В пространстве параметров деформации (10,hk) граница упругой области представляет собой ромб с диагоналями, совпадающими с осями координат (рис.1).
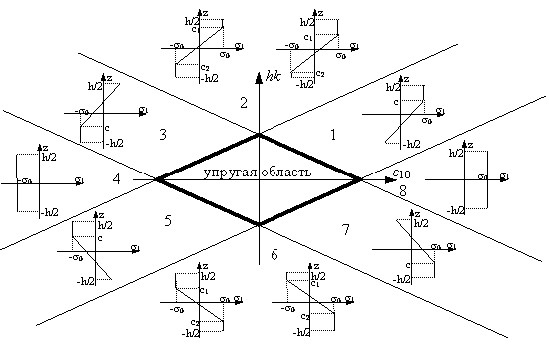  |
| Рисунок 1. Области разного деформирования в пространстве (10,hk) и распределение напряжений 1 по толщине в случае упругого-абсолютно пластичного материала |
Аналогичную область можно построить и в пространстве усилий (hN,M), где N определяет нормальное растягивающее усилие листа, а M – изгибающий момент. В первоначальном состоянии она также имеет форму ромба с диагоналями на осях координат.
При деформации листа точка, описывающая состояние деформаций движется в пространстве (10,hk), описывая определенную кривую. Аналогичный процесс происходит и в пространстве усилий. Если деформация любой точки автолиста в выбранном сечении упругая, то кривая пространства деформаций, полностью лежащая в упругой области, является линейным прообразом кривой пространства усилий. В этом случае любое приращение деформации связано с приращением усилий по формулам:
![]() (1а)
(1а)
![]() (1б)
(1б)
где =E/(1-2), а E – модуль Юнга, – коэффициент Пуассона.
В работе показана трансформация упругой области при пластификации в областях 1, 2, 8 (рис.1), а также даны уравнения, описывающие ее границу. Пластификация в остальных областях аналогична. Показано также, что материал с эффектом поперечного упрочнения (описываемого изотропным упрочнением) в какой-то мере расширяет упругую область, а материал с эффектом Баушингера (описываемого трансляционным упрочнением) – ее сужает. Для упругого-абсолютно пластичного материала происходит трансляция упругой области.
При пластификации материала уже не существует линейной связи между приращениями деформаций и приращениями усилий. В зависимости от области (рис.1), в которую попадает точка состояния деформаций при пластификации, зависимости между приращениями деформаций и приращениями усилий будут различными. Так для области 1 эта связь определяется следующими уравнениями:
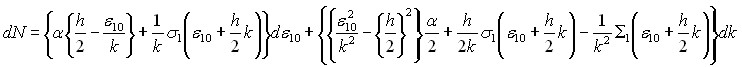 (2а)
(2а)
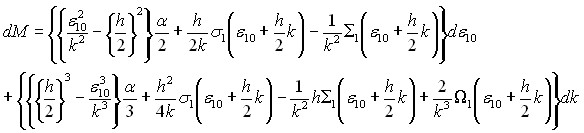 (2б)
(2б)
где
![]() (3а)
(3а)
![]() (3б)
(3б)
являются соответственно первым и вторым интегралами закона упрочнения 1(1). В уравнениях (2а,б) и далее круглые скобки используются только для показания зависимости от параметра, а в фигурные скобки заключены выражения.
Для области 2 связь между приращениями деформаций и приращениями усилий выглядит следующим образом:
![]() (4а)
(4а)
 (4б)
(4б)
где символы
![]() (5а)
(5а)
![]() (5б)
(5б)
в качестве функции f может выступать либо закон упрочнения, либо его интегралы.
И для области 8 связь между приращениями деформаций и приращениями усилий:
![]() (6а)
(6а)
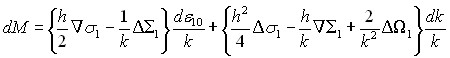 (6б)
(6б)
Зная конечную деформацию автолиста, финальные значения усилий при этом состоянии получаются при интегрировании формул (2), (4), (6).
При разгрузке происходит возврат точки состояния усилий в начальное положение (hN=0,M=0). Если все деформации при релаксации напряжений были упругими, то финальное деформационное состояние определяется при применении линейной связи между приращениями усилий и приращениями деформаций (1а,б), что в свою очередь задает геометрию автолиста после упругого возврата.
Представленная аналитическая модель является наиболее общим аналитическим подходом для вычисления упругого возврата автолистов. Опубликованные ранее теории могут быть выведены из нее как частные случаи. В качестве примера показан вывод широко известной формулы Гардинера для упругого возврата листа из упругого-абсолютно пластичного материала при чистом изгибе.
Для апробации предложенной в этой главе модели, а также моделей, описанных в других главах, использовались эталонные операции по формованию четырех сталей:
- однофазная ферритная, легированная титаном, сталь с низким содержанием углерода (сталь 06Т) с размером зерна около 15 мкм;
- ферритная сталь с небольшим количеством перлита (Сталь 10) с размером зерна 8 мкм;
- двухфазная феррито-бейнитная сталь (сталь 20ХГ);
- аустенитно-мартенситная сталь с интенсивным мартенситным превращением и возможной реализацией ПНП-эффекта (сталь 08Х14АН4МДБ).
Химический состав исследуемых сталей приведен в табл. 1.
Таблица 1.
Химический состав исследуемых материалов, масс. %
| Обозначение | Марка | Si | Mn | Cr | Ni | Ti | Cu | V | Mo | [O] | [N] | [C] | [S] |
| A | 06Т | 0,04 | 0,07 | 0 | 0,01 | 0,23 | 0,08 | 0 | 0 | 0,0088 | 0,0038 | 0,067 | 0 |
| Б | Сталь 10 | 0,04 | 0,14 | 0,02 | 0,03 | 0 | 0,08 | 0 | 0 | 0,0092 | 0,0047 | 0,099 | 0 |
| В | 20ХГ | 0,35 | 1,13 | 0,68 | 0,06 | 0 | 0,09 | 0 | 0 | 0,0068 | 0,0044 | 0,23 | 0 |
| Г | 08Х14АН4МДБ | 0,22 | 1,05 | 14,6 | 4,68 | 0 | 0,41 | 0 | 1,89 | 0 | 0,091 | 0,117 | 0,007 |
Во всех случаях речь идет о холоднокатанном листовом материале. Механические свойства сталей представлены в табл. 2.
Параметры степенного закона упрочнения =Kn для истинных деформаций =ln(lкон/l0) определены в диапазоне =8-20% для 06Т, =2-14% для Стали 10, =4-16% для 20ХГ, =2-22% для 08Х14АН4МДБ.
Коэффициент Ланкфорда r=ln(b/b0)/ln(h/h0) определен из измерений ширины и толщины образца при =10% на образцах шириной b=20мм.
Таблица 2.
Механические характеристики исследованных материалов.
| Сталь | Толщина листа h0, мм | Механические свойства | Параметры закона = Kn | Коэффициент Ланкфорда r | |||
| 02, МПа | В, МПа | , % | K, МПа | n | |||
| А | 0,739 | 128 | 290 | 24 | 540 | 0,256 | 2,64 |
| Б | 1,010 | 390 | 449 | 16 | 715 | 0,163 | 1,14 |
| В | 0,997 | 351 | 671 | 16 | 1100 | 0,178 | 1,11 |
| Г | 0,997 | 546 | 832 | 22,5 | 1412,6 | 0,207 | 1,31 |
Предложенная модель применена к описанию упругого возврата в тесте «омега» для трех различных сталей (Сталь 10, сталь 20ХГ, сталь 08Х14АН).
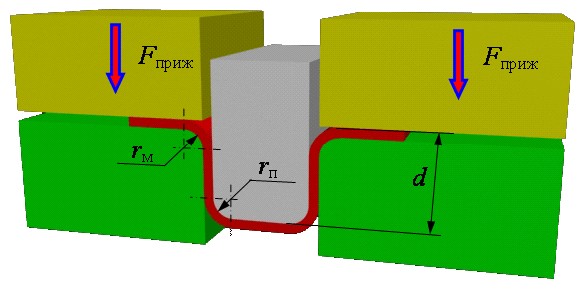  |
| Рисунок 2. Штамповка прямоугольного U-образного профиля |
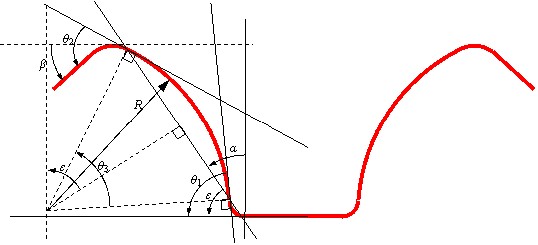  |
| Рисунок 3. Геометрические характеристики профиля «омега» |
На первом этапе этого теста происходит штамповка прямоугольного U-образного профиля (рис. 2). После выдавливания вынутый из инструмента образец деформируется из-за упругого возврата, в результате чего профиль становится похожим на перевернутую букву (рис.3).
Изучено влияние различных технологических параметров (радиуса закругления матрицы, прижимной силы, зазора между пуансоном и матрицей) на величину упругого возврата образцов (определяемое при помощи трех углов 1, 2, 3 на рис.3). В качестве примера на рис. 4 представлено влияние радиуса закругления матрицы.
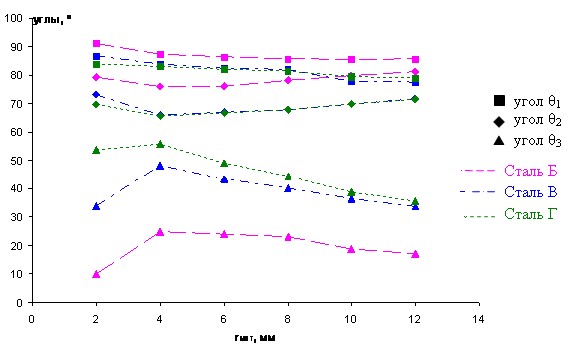  |
| Рисунок 4. Зависимость параметров упругого возврата от радиуса закругления матрицы |
Согласно теоретической модели углы 1, 3 должны расти при уменьшении радиуса закругления матрицы, а угол 2 - падать. При радиусе закругления равном 3,7мм (для стали 20ХГ) происходит смена зоны пластификации (из зоны 1 происходит переход в зону 2 (рис.1)), поэтому характер изменения углов при меньших радиусах закругления матрицы меняется. К тому же при разгрузке имеется повторная пластификация сечения листа, что объясняет несовпадение результатов модели и эксперимента (рис.5).
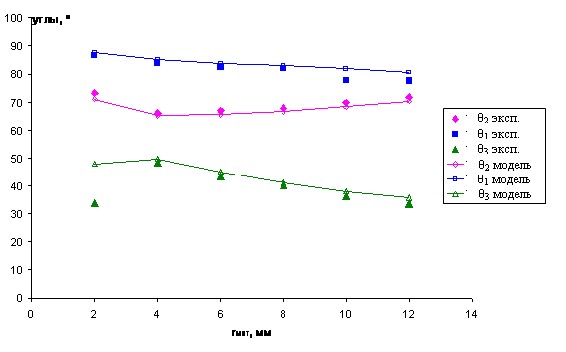  |
| Рисунок 5. Зависимость параметров упругого возврата от радиуса закругления матрицы для 20ХГ |
В третьей главе предложена обобщенная модель стационарных процессов формования. В этих процессах лист протягивается через формовочный инструмент. Каждая часть листа имеет одинаковую деформационную историю.
Состояние деформаций и напряжений исследуемого сечения, отстоящего от предыдущего на расстояние ds (в наших расчетах ds=1мм), рассчитывается исходя из предыдущего состояния деформаций и напряжений и усилий (N,M) в данном сечении. При этом каждый раз решается система двух интегральных уравнений:
 (7а)
(7а)
 (7б)
(7б)
для определения деформационных параметров (10,k).
Состояние усилий определяется из уравнения равновесия и усилий, действующих на сечение предыдущего элемента. Вся геометрия автолиста в инструменте может быть разделена на три типа областей отличающихся уравнениями равновесия – это свободные участки, зоны точечного и зоны распределенного контакта.
Лист, протягиваемый через инструмент, является системой с несколькими степенями свободы, их количество:
![]() (8)
(8)
где q0=1 степень свободы, связанная с неопределенностью первого контакта, qр=2 количество степеней свободы, связанных с распределенным контактом, а nр – количество распределенных контактов. Минимум равняется q=1 – это неопределенность положения первого контакта.
Геометрию листа в инструменте определяет минимум энергии деформации листа (W) по этим степеням свободы в области возможных значений параметров:
 (9)
(9)
где ![]() и
и ![]() - эффективные напряжение и деформация заданной точки листа, а s – общая длина листа в инструменте. Для каждого из наборов значений степеней свободы определялась энергия деформации (9), а затем выбиралось ее наименьшее значение и соответствующие оптимальные значения степеней свободы.
- эффективные напряжение и деформация заданной точки листа, а s – общая длина листа в инструменте. Для каждого из наборов значений степеней свободы определялась энергия деформации (9), а затем выбиралось ее наименьшее значение и соответствующие оптимальные значения степеней свободы.
Найдены параметры, минимизирующие энергию деформации, при описании протяжки через простой захват (рис.6).
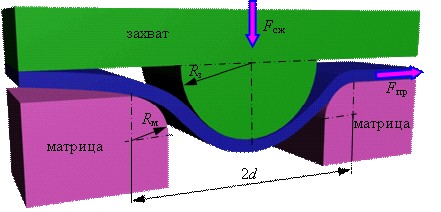  |
| Рисунок 6. Схема протяжки через простой захват |
Параметры экспериментов представлены в таблице 3.
Таблица 3
Параметры эксперимента по протяжке через простой захват
| Радиус матрицы Rм, мм | Радиус захвата, Rз, мм | Расстояние между матрицами 2d, мм | Скорость протяжки v, м/с | Ширина полос b, мм | Длина полос, мм |
| 3 | 6 | 14,9 | 5*10-3 | 20 | 310 |
Исследован диапазон перемещений 50-290мм от момента нажатия (когда произошел выход на стационарный режим). Для экспериментов использовались три стали: Сталь 10, 20ХГ и 08Х14АН4МДБ. В качестве смазочного вещества для Стали 10 использовалось масло QUAKER 6130, а для остальных сталей – масло FUCHS V14.
На рис.7 представлена зависимость силы протяжки Fпрот от силы сжатия инструмента Fсж для этих трех сталей. Все три кривые имеют s-образный вид, имеющий линейную асимптоту при больших значениях силы сжатия. Наклон этой асимптоты равен коэффициенту трения между автолистом и инструментом. Так как для сталей 20ХГ и 08Х14АН4МДБ и Стали 10 использовались разные смазочные материалы, то наклон у них разный. При малых силах сжатия сила протяжки максимальна для более мягкой Стали 10, так как лист больше облегает инструмент. При больших силах сжатия наибольшую силу протяжки имеет наиболее твердая сталь с ПНП-эффектом, так как работа по ее деформированию является максимальная. Таким образом, при протяжке листа из материала с большим коэффициентом K в степенном законе упрочнения требуется большая сила протяжки.
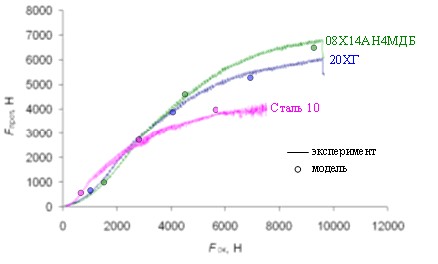  |
| Рисунок 7. Зависимость силы протяжки через простой захват от сжимающей силы |
Результаты численного моделирования сходятся с экспериментальными данными на рис.7.
В четвертой главе рассматривается влияние механических свойств материала на потерю устойчивости пластического течения. В качестве критерия этого свойства рассматривается один глобальный параметр процесса – предельный коэффициент вытяжки (ПКВ) и одна характеристика материала – предельная кривая формования (ПКФ).
Предельный коэффициент вытяжки
  |
| Рисунок 8. Процесс штамповки стакана |
Для определения ПКВ необходимо получить модель, описывающую эталонный тест – штамповку стакана (рис.8). Процесс получения стакана проходит в два этапа. Во время первого круговая листовая заготовка прижимается к матрице при помощи верхней плиты с определенной силой Fсж. На втором этапе пуансон выдавливает автолист в матрицу до получения цилиндрического стакана.
Успех этой операции зависит от материала автолиста, геометрии инструмента, условий трения, прижимной силы. Существует предельное значение соотношения начального диаметра круговой заготовки к диаметру пуансона «предельный коэффициент вытяжки (ПКВ)», выше которого формование стакана без разрушения невозможно.
Построена математическая модель, позволяющая определять поля напряжений и деформаций в каждой точке автолиста и в каждый момент времени. Для этого мгновенная геометрия образца разбивалась на 5 зон (фланец, 1ое закругление, фартук, 2ое закругление и низ стакана), в каждой из которых существовали свои уравнения равновесия и граничные условия. Поля напряжений и деформаций во всех зонах определялись из решения нелинейного уравнения относительно одной из компонент тензора напряжений:
![]() (10)
(10)
где R – параметр упрочнения материала, задаваемый законом упрочнения, а ![]() - эффективное напряжение, определяемое критерием пластичности. Отсутствие решения уравнения (10) рассматривалось как потеря устойчивости пластического течения в данной точке стакана. Остальные компоненты напряжений и деформаций определялись из текущей геометрии листа, а также при помощи закона текучести:
- эффективное напряжение, определяемое критерием пластичности. Отсутствие решения уравнения (10) рассматривалось как потеря устойчивости пластического течения в данной точке стакана. Остальные компоненты напряжений и деформаций определялись из текущей геометрии листа, а также при помощи закона текучести:
![]() (11)
(11)
Эти состояния определялись в сечениях, отстоящих друг от друга на расстояние ds (в данной работе первоначальное разбиение задавалось ds0=1мм). На выходе модели получаются поля напряжений и деформаций в каждой точке листа в каждый момент времени, а также изменение силы пуансона от времени.
Выдаваемые моделью зависимости силы от перемещения пуансона сравнены с экспериментальными данными для трех сталей: Сталь 10 толщиной 1,5 мм, сталь 20ХГ толщиной 2 мм и сталь 08Х14АН4МДБ толщиной 1,5 мм. Параметры эксперимента по штамповке стакана приведены в таблице 4.
Таблица 4.
Параметры эксперимента по штамповке стакана
| Параметр | Значение | Параметр | Значение |
| Диаметр пуансона, 2Rп | 75 мм | Начальный диаметр заготовки, 2Rвнеш0 | 142,5 мм |
| Радиус закругления пуансона, rп | 7 мм | Максимальная скорость перемещения пуансона, v | 2000 мм/с |
| Радиус закругления матрицы, rм | 7 мм | Коэффициент трения, | 0,12 |
На рис.9 представлены зависимости силы пуансона от его перемещения для разных типов сталей.
  |
| Рисунок 9. Сила пуансона в зависимости от его перемещения |
Обычно для получения наибольшего ПКВ, используется наименьшая из прижимных сил, не допускающих волнистости фланца. Ее значения: для Стали 10 – 180 кН, для стали 20ХГ – 30 кН, а для стали 08Х14АН4МДБ - 480 кН.
Все три кривые имеют s-образный вид с максимумом. Ниже остальных находится кривая для самой мягкой однофазной ферритной стали.
На рис.10 представлена сила в зависимости от перемещения пуансона для разных начальных диаметров.
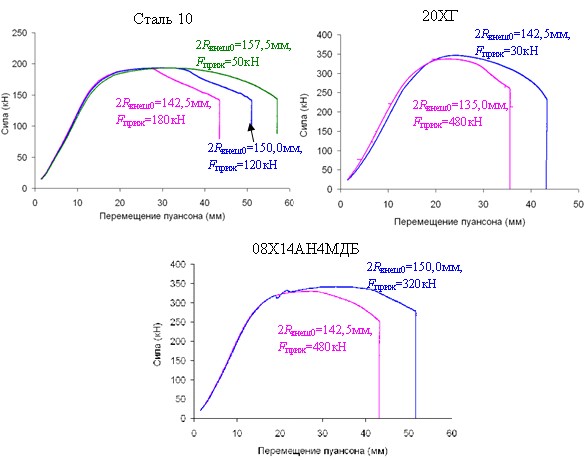  |
| Рисунок 10. Сила пуансона для разных начальных диаметров круговой заготовки |
При большем начальном диаметре заготовки необходимо и большее перемещение пуансона для окончательного формования стакана. Вне зависимости от начального диаметра заготовки все кривые для одной стали практически совпадают, до значений, близких к максимальным.
Теоретические зависимости адекватны эксперименту по значениям максимальной силы пуансона. Также теоретическим методом было получены ПКВ для всех трех сталей. Для этого проводилось увеличение начального диаметра заготовки до момента, когда в одном из сечений отсутствовало решение уравнения (10), то есть имело место разрушение образца. Для Стали 10 найденное значение ПКВ равнялось 2,35, для 20ХГ – ПКВ равнялось 2,47, а для 08Х14АН4МДБ – 2,51.
Предельные кривые формования
Предельные кривые формования представляют собой границу в пространстве деформаций (1,2) за которой происходит разрыв вследствие потери устойчивости пластического течения и образования шейки.
В четвертой главе исследовано влияния закона упрочнения, а также пластической анизотропии, на предельную кривую формования как в пространстве деформаций, так и в пространстве напряжений. Для этого вначале проводилось аналитическое построение ПКФ плоского листа из анизотропного материала. Обобщение влияния механических свойств материала (степенного коэффициента в законе упрочнения (n) и коэффициента нормальной анизотропии – коэффициента Ланкфорда (r)) приведено на рис.11.
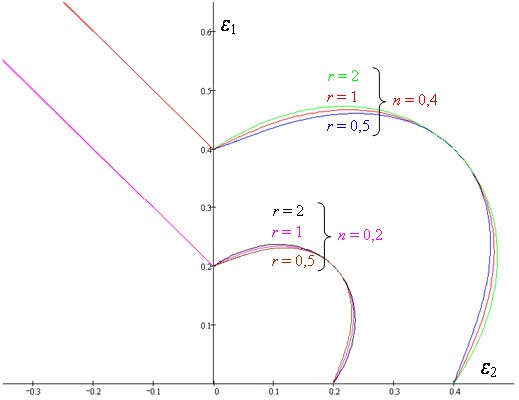  |
| Рисунок 11. Влияние материала на ПКФ |
При увеличении степенного коэффициента в законе упрочнения поднимается соответствующая ПКФ. Левая часть ПКФ испытывает при этом обычное трансляционное перемещение, в то время как правая – всестороннее расширение относительно начала координат. При изменении коэффициента нормальной анизотропии, левая часть ПКФ не изменяется (так как она не зависит от формы упругой поверхности материала), а правая часть – немного меняется. При этом правая часть ПКФ для большего значения коэффициента нормальной анизотропии лежит выше, чем кривая для меньшего значения этого же коэффициента.
Для объяснения различия экспериментальных ПКФ, построенных разными способами исследовано влияние кривизны листа (k1, k2 – компоненты кривизны листа) и возникающих при искривлении напряжений по толщине на ПКФ. Построенная модель, учитывала нелинейный закон упрочнения материала и возможную анизотропию механических свойств.
На лист заданной кривизны, действуют растягивающие силы. В точке потери устойчивости пластического течения приращение нормальной силы равно нулю. И из этого условия, меняя коэффициент пропорциональности между растягивающими деформациями, определяли предельную кривую формования в пространстве деформаций.
На рис.12 представлены ПКФ для листов с различной кривизной (h0 – начальная толщина листа).
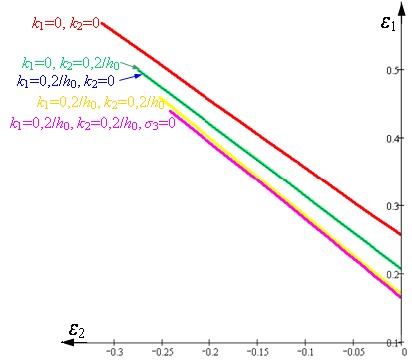  |
| Рисунок 12. ПКФ автолистов различной кривизны для Стали 10 |
ПКФ для искривленного листа находится намного ниже ПКФ плоского листа. При этом, чем больше искривление, тем больше наклон имеет левая часть ПКФ в пространстве (2,1). Не важно как искривлен лист – вдоль или поперек растягивающих усилий – в обоих случаях ПКФ будет одинаковая. Влияние на ПКФ оказывает не какая либо составляющая кривизны, а они вместе.
Расчет ПКФ, предположив отсутствие напряжений по толщине (3), даст заниженное положение ПКФ рис.12. Сжатие по толщине сильно влияет на ПКФ, повышая ее. Но неравномерное распределение деформаций и напряжений по толщине, которые понижают ПКФ, имеют на нее большее влияние, чем сжимающие напряжения по толщине – в итоге ПКФ понижается.
На рис.13 представлено влияние параметров материала на ПКФ изогнутого листа.
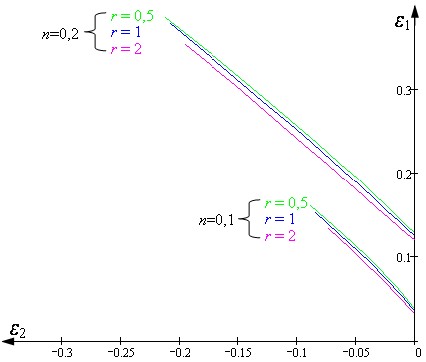  |
| Рисунок 13. Влияние материала на ПКФ изогнутого листа |
Как и в случае с плоским листом, ПКФ изогнутого листа снижается при уменьшении степенного коэффициента в законе упрочнения. Однако, в остальном существуют существенные различия. Во-первых, на этом графике лучше заметно, что левая часть ПКФ не является прямой, как это было с прямой, построенной по критерию потери устойчивости пластического течения Хилла. Затем также в отличие от левой части ПКФ, построенной по критерию Хилла, в случае изогнутого листа имеется зависимость от поверхности пластичности, а в частности – от коэффициента нормальной анизотропии. Чем больше этот коэффициент, тем ниже расположена левая часть ПКФ. Причем влияние коэффициента нормальной анизотропии более выражено для большего степенного коэффициента в законе упрочнения.
Построение профиля шейки
В четвертой главе также описываются эксперименты по определению профиля шейки, а также по влиянию различного рода концентраторов напряжений на разрушение образца.
Использовались три стали, имеющие сильно отличающиеся механические свойства (см. Табл.2): 06Т, Сталь 10 и 20ХГ. В качестве образцов использовались листовые образцы с разными концентраторами напряжения (с вырезами (тип 1), с большим центральным отверстием (тип 2), образец с малым центральным отверстием (тип 3), и стандартный листовой образец на растяжение (тип 4)) и разными толщинами (1 и 2мм) – рис.14.
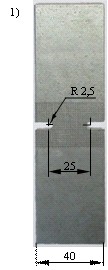  |   |   |   |
| Рисунок 14. Типы образцов и их размеры | |||
Перед проведением эксперимента на образцы наносился точечный рисунок из латексной эмульсии с флуоресцентной керамикой «Luminova». Размер точек составлял около 0,3-0,5 мм, расстояние между ними примерно 1-2 мм. Количество точек зависело от образца, но в среднем составляло 100 – 150 штук.
Образцы растягивались на машине Instron 8500+ со скоростью 5 мм/мин. Образец при этом освещался ультрафиолетовой лампой B100AP мощностью 450 Вт.
Велась видеосъемка камерой с разрешением 1024*1024 пикселей. Изображение передавалось на компьютер, на котором сразу же обрабатывалось программой Videostrain фирмы Appollor. Программа считывала положение центра точек и записывала его в файл со средней частотой 16 кадров/секунду.
По окончанию эксперимента программа создавала два типа файлов: один с координатами точек в определенные моменты времени, а второй – с силой растяжения в эти же моменты времени.
После разрыва, проводилась фрактография излома образцов на сканирующем электронном микроскопе Philips XL30 при ускоряющем напряжении 5 кВ.
Для построения профиля шейки была предложена методика определения толщины образца по перемещениям некоторых маркированных его частей. Вначале создавались интерполяционные карты перемещений (при помощи двумерных сплайновых функций) точек образца, а затем проводилось дифференцирование этих карт для получения карт деформаций. Деформация по толщине определялась через две остальные основные компоненты тензора деформаций, используя гипотезу о пластической несжимаемости материала. Толщина образца определялась через эту компоненту тензора деформаций.
На рис.12 представлена эволюция толщины образца из стали 06Т с малым отверстием в центре в области, непосредственно прилегающей к концентратору напряжений.
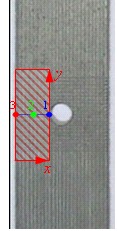 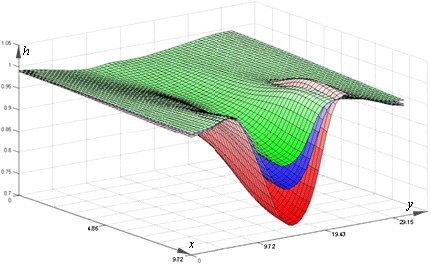  |
| Рисунок 12. Эволюция толщины автолиста из стали 06Т из заштрихованной области (представлена толщина непосредственно перед разрушением) (все размеры даны в мм) |
Можно отметить, что ширина шейки в течение эксперимента практически не менялась, происходило только ее углубление, и в образце перед разрушением толщина в самом тонком месте составляла примерно 0,73 мм.
На рис. 13 представлены пути деформации в точке наибольшей концентрации напряжений образцов из Стали 10 с разными концентраторами напряжений. На этом же графике показана теоретическая ПКФ.
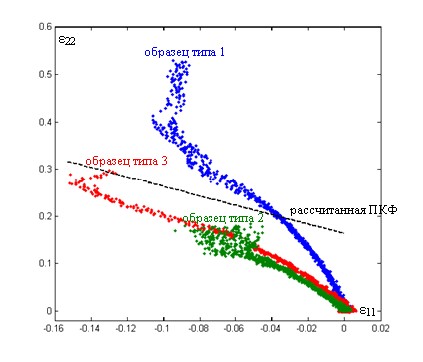  |
| Рисунок 13. Пути деформации разных образцов |
Образец с самым острым концентратором деформируется до наиболее больших значений 2, затем идет образец Б3 и образец с самым тупым концентратором разрушается при наиболее малых значениях 2. При этом теоретическая ПКФ дает заниженные значения 2 для образца Б1 и завышенные – для образцов Б2 и Б3. Объяснение этому (помимо непропорциональности деформации) может служить то обстоятельство, что в образце с самым острым концентратором и самой глубокой шейкой возникают самые сильные напряжений по толщине в области шейки. Они пытаются выровнять лист (сделать его одинаковой толщины) и поэтому увеличивают предел, до которого этот лист может деформироваться без разрушения. Ранее уже было показано, что сильные напряжения по толщине увеличивают деформируемость листа. В образцах с более тупыми концентраторами эти напряжения меньше и, поэтому, деформируемость листа меньше.
На рис.14 представлены толщины образцов в области прилегающей к зоне наибольшей концентрации напряжений непосредственно перед разрушением.
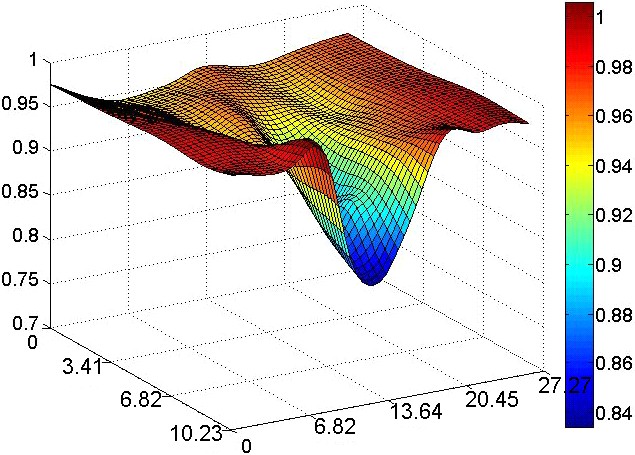  | 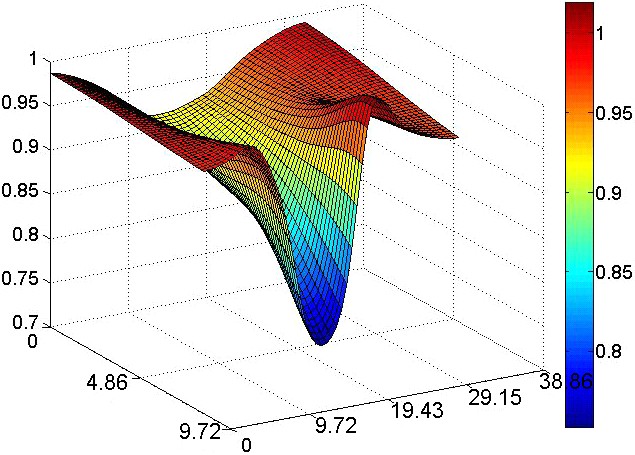  | 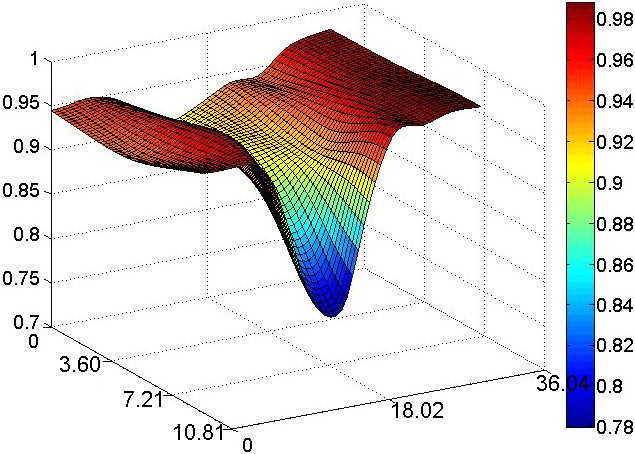  |
| Рисунок 14. Толщины образцов из разных сталей с концентратором 3-го типа а) Сталь 10 б) сталь 06Т в) сталь 20ХГ (все размеры – в мм) | ||
Наибольшее сужение наблюдается у наиболее мягкой стали 06Т. Толщина самой тонкой части образца из Стали 10 составляет 0,82 мм, образца из стали 20ХГ – 0,78 мм, и из стали 06Т – 0,75 мм. Ширина шейки для Стали 10 равняется приблизительно 10 мм, для стали 20ХГ – 16 мм, для стали 06Т – 15 мм.
На рис.15 представлены пути деформации точек из зоны наибольшей концентрации напряжений образцов из трех типов сталей. На этом же графике показаны и их теоретические ПКФ.
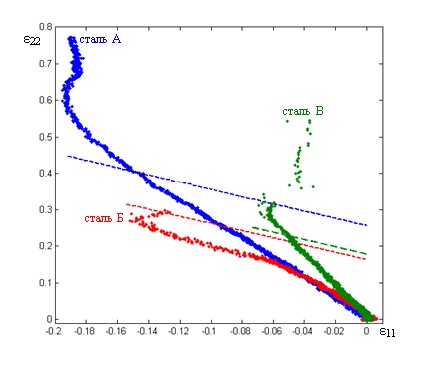  |
| Рисунок 15. Пути деформации образцов 3-го типа из разных сталей в точке максимальной концентрации напряжений и теоретические ПКФ для этих же сталей (пунктиром) |
Кривые практически совпадают для всех трех сталей до деформации 2=0,1. После этого значения начинается расхождение кривых, связанное с разными упрочнениями материалов. Причем степенной коэффициент в законе упрочнения не является причиной этого расхождения. Кривые для Стали 10 и 20ХГ с близкими степенными коэффициентами упрочнения находятся по разные стороны от кривой для стали 06Т с более высоким значением этого коэффициента. Из закона течения следует, что деформация сталей будет различной при различающихся поверхностях пластичности. Таким образом, можно заключить, что поверхности пластичности для всех трех сталей сильно различаются.
Разрушение для Стали 10 начинается при 2=0,25, для стали 20ХГ – при 2=0,3, а для стали 06Т – при более высокой деформации 2=0,55. При этом теоретическая ПКФ дает немного завышенные значения деформации разрушения для Стали 10 и немного заниженные – для сталей 06Т и 20ХГ.
Фрактографии разломов в местах наибольшей концентрации напряжений для трех сталей представлены на рис.16.
    |
| Рисунок 16. Фрактографии в местах наибольшей концентрации напряжений образца 3го типа для разных сталей |
Для всех трех сталей характерен вязкий тип разрушения. При этом поры наибольшей глубины встречаются на образцах из стали 06Т, а также они крайне неоднородны по размеру. На фрактографиях Стали 10 и стали 20ХГ видна полосчатость структуры вдоль плоскости листа.
Из экспериментов с образцами разной толщины можно сделать вывод о том, что толстый образец больше утоняется перед разрушением, чем тонкий.
выводы
- Предложена модель расчета упругого возврата деформируемого листа в зависимости от механических свойств материала. Установлены границы применимости новой модели.
- На различных по химическому и фазовому составу сталях (однофазная ферритная с низким содержанием углерода 06Т, ферритная Сталь 10, двухфазная феррито-бейнитная сталь 20ХГ, аустенитно-мартенситная с возможностью ПНП-эффекта сталь 08Х14АН4МДБ) подтверждено согласие модели упругого возврата с экспериментальными результатами теста одномерного формования профиля «омега».
- Получена наиболее общая модель двумерного стационарного процесса формования при инструменте любой формы, в том числе учитывающая эффект Баушингера и эффект поперечного упрочнения. Изучено влияние механических свойств сталей на зависимость усилия протяжки от силы прижатия при описании стационарной протяжки через простой захват. В экспериментах показано хорошее согласие модели.
- Предложен расчет интегрального параметра потери устойчивости пластического течения – предельного коэффициента вытяжки. Результаты хорошо согласуются с экспериментами по штамповке стакана из сталей разных типов.
- Изучены зависимости усилия штамповки стакана от перемещения пуансона и начального диаметра заготовки. Начальные диаграммы совпадают, но максимальная сила выше для более прочных сталей.
- Получена математическая модель предельной кривой формования листа в зависимости от его анизотропии. Описано влияние кривизны листа. Понижение предельной кривой формования зависит от обоих компонент кривизны. Влияние возникающих при искривлении напряжений по толщине листа намного ниже. С повышением показателя упрочнения материала диаграмма формования сдвигается в область больших значений деформаций.
- Предложен метод измерения полей больших перемещений и исследована эволюция профиля шейки в образцах с концентраторами напряжений. У концентратора меньшего диаметра шейка более глубокая. Поэтому образец большей толщины удлиняется и утоняется при разрушении больше, чем тонкий.
Содержание диссертации изложено в следующих публикациях:
- Назаров Р.А., Никулин С.А., Айади З., Нивуа М. Моделирование деформаций и условий разрушения материала при штамповке стакана // Деформация и Разрушение Материалов. – 2007. - № 11. – с. 31 – 36.
- R.A. Nazarov, Z. Ayadi, S.A. Nikulin, M. Nivoit. Analytical model for strip drawing // XIth ESAFORM2008 conference on material forming, 23-25 april (2008), Lyon, France.
- Никулин С.А., Назаров Р.А., Айади З., Нивуа М. Построение предельных кривых формования для анизотропного листового материала // Сб. тезисов IVой Евразийской Научно-Практической Конференции «Прочность Неоднородных Структур ПРОСТ 2008», 8-10 апреля (2008), Москва, Россия.
- Назаров Р.А., Айади З., Никулин С.А., Нивуа М.. Аналитическое построение предельных кривых формования для изогнутых автолистов // Сб. тезисов Симпозиума Франкоговорящих Стран по Пластичности 2008, 10-12 марта (2008), Нанси, Франция.
- Назаров Р.А., Айади З., Никулин С.А., Нивуа М. Аналитическая модель для процесса глубокой вытяжки // Сб. тезисов III-его Французско-Русского Семинара «Новые Достижения в Материаловедении и Инженерии NAMES-2007», 7-9 ноября (2007), Метц, Франция, с.15-18.
- Назаров Р.А., Айади З., Нивуа М., Никулин С.А., Веттембург Ж.-П. Улучшенная модель эталонного теста по штамповке стакана // Сб. тезисов XVIII-ого Конгресса Франкоговорящих Стран по Механике, 27-31 августа (2007), Гренобль, Франция, с.85.
- Z. Ayadi, R. Nazarov, M. Nivoit and S. Nikulin. Analytical Modelling of Characteristic Stamping Tests and Springback Prediction // IVth Research Conference “European School of Materials Science and Engineering” June 7-8 (2007), Barcelona, Spain, p.59.
- Z. Ayadi, R. Nazarov, M. Nivoit and J. P. Betembourg, Analytical model and experimental validation of springback prediction in U-shape stamping test // XIIth International Symposium on Plasticity, 17-22 july (2006), Hallifax, Canada, p.67-69.

