Расчет многослойных плит на грунтовом основании с учетом их упругих и упругоползучих свойств
УДК 624.131:539.215 На правах рукописи
УРАЛОВ БАИДУЛЛА КИДИРБАЕВИЧ
Расчет многослойных плит на грунтовом основании
с учетом их упругих и упругоползучих свойств
01.02.04 – Механика деформируемого твердого тела
Автореферат
диссертации на соискание ученой степени
кандидата технических наук
Республика Казахстан
Шымкент, 2010
Работа выполнена в Южно-Казахстанском государственном университете имени М.Ауезова.
Научные руководители: доктор технических наук, академик
АН РУз, профессор
| Ширинкулов Т.Ш. |
доктор технических наук, профессор
Дасибеков А.Д.
Официальные оппоненты: доктор технических наук, профессор
Баймахан Р.Б.
кандидат технических наук, доцент Тагаев Н.С.
Ведущая организация: Кыргызский государственный
университет строительства, транспорта и
архитектуры им. Н. Исанова
Защита состоится «12» февраля 2010г. в 1600 часов на заседании диссертационного Совета Д.14.23.01 при Южно-Казахстанском государственном университете им. М.Ауезова по адресу: 160012, г.Шымкент, пр. Тауке хана, 5, ауд. 342 главного корпуса.
С диссертацией можно ознакомиться в библиотеке ЮКГУ им. М.О. Ауезова по адресу: 160012, г. Шымкент, пр. Тауке хана, 5, главный корпус, ауд.215.
Автореферат разослан «___» января 2010г.
Ученый секретарь
диссертационного совета Д. 14.23.01
доктор технических наук, профессор Волненко А.А.
Введение
Общая характеристика работы. При строительстве гидротехнических, гражданских, транспортных и мелиоративных сооружений инженерно-технические работники непосредственно сталкиваются с решениями контактных задач механики деформируемого твердого тела, а именно, с расчетами элементов инженерных конструкций, взаимодействующих с грунтовым основанием. Безусловно, успех прогнозирования этих процессов во многом зависит от того, с какой степенью точности и полноты будут учтены их физико-механические свойства.
Актуальность проблемы. Правильный расчет элементов инженерных конструкций типа балочных и круглых плит, лежащих на деформируемом грунтовом основании, возможен лишь при учете таких свойств грунтов и конструкций, которые существенно влияют на устойчивость сооружения. К основным таким свойствам грунтовых оснований относятся учет свойств ползучести и неоднородности уплотняемого массива. К материалам элементов конструкций следует отнести их свойства ползучести и многослойности. Следовательно, одновременный учет этих факторов, безусловно, дает реальную картину, происходящую в уплотняемом грунтовом массиве и в самом элементе конструкции, взаимодействующей с основанием. Изучение этого вопроса по сей день остается одной из актуальных задач механики деформируемого твердого тела.
Работа выполнялась в соответствии с госбюджетной темой Б-ТН-06-05-06/7 «Нелинейная ползучесть и консолидация неоднородных грунтовых оснований», включенной в тематический план НИР ЮКГУ им. М.Ауезова на 2004–2010 годы.
Целью работы являются решения контактных задач теории упругости и ползучести, связанных с изгибами упругих и упругоползучих плит, взаимодействующих с неоднородным упругим и упругоползучим грунтовым основанием и на основе полученных решений разработана методики расчета системы «сооружение-основание».
Для достижения этой цели были поставлены и решены следующие научные задачи:
– установление математической модели для решения задач взаимодействия плит с однородным и неоднородным грунтовым основанием;
– теоретическое исследование контактной задачи об изгибе двухслойных балочных и круглых плит, расположенных на неоднородном грунтовом основании с учетом их свойства ползучести;
– изучение напряженно-деформированного состояния изгиба балочных плит с упругоподатливыми связями сдвига, взаимодействующих с линейно-деформируемым основанием;
– изучение изгиба упругих двухслойных плит, соединенных упругими связями и расположенных на упругом однородном основании;
– решение полученной системы разрешающих уравнений для различных контактных задач теории упругости и ползучести;
– на основе полученных решений разработать методику расчета системы «сооружение-основание».
Объект и предмет. Объектом исследования данной работы были выбраны упругие, упругоползучие многослойные плиты, лежащие на упругом, упругоползучем однородном и неоднородном грунтовых основаниях.
Предметом исследования является напряженно-деформированное состояние системы «сооружение-основание». Здесь одновременно могут быть учтены многослойность элементов конструкций, неоднородность грунтового основания и их свойства ползучести.
Научная новизна диссертационной работы заключается в следующем:
– разработана математическая модель, описывающая упругое и упруго- ползучее состояние системы «сооружение-основание», которая позволяет находить прогиб элементов конструкций, взаимодействующей с деформируемым неоднородным грунтовым основанием;
– получены решения контактных задач теории упругости и ползучести, связанных с расчетами двухслойных балочных и круглых плит, лежащих на неоднородном основании;
– установлено влияние неоднородности уплотняемого грунтового основания на напряженно-деформированное состояние системы «сооружение-основание»;
– выявлено влияние ползучести грунта на напряженно-деформированное состояние элементов конструкций, взаимодействующих с уплотняемым основанием;
– оценены напряженно-деформированные состояния системы «сооружение - основание» при многослойности элементов конструкций, взаимодействующих с грунтовым основанием, обладающим различными реологическими свойствами.
Научные положения, выносимые на защиту:
–математическая модель для решения контактных задач теории упругости и ползучести в виде системы «сооружение-основание», а именно теоретическое исследование состояния упругоползучих двухслойных балочных и круглых плит, взаимодействующих с упругоползучим неоднородным грунтовым основанием;
– результаты исследования задачи об изгибе упругоползучих двухслойных плит с заполнителями, лежащих на упругоползучем неоднородном основании;
–расчет многослойных балочных плит с упругоподатливыми поперечными и сдвиговыми связями, взаимодействующих с линейно-деформируемым основанием;
–решения задач об изгибе двухслойных балочных плит с заполнителями, взаимодействующих с деформируемым однородным основанием;
–новые расчетные формулы, соответственно отражающие изменения прогиба элементов конструкций, взаимодействующих с уплотняемым однородным и неоднородным упругим или упругоползучим основанием, изгибающих моментов, перерезывающих сил, реактивных давлений и осадок грунтового основания.
Практическая ценность работы. Разработана методика расчета упругих и упругоползучих слоистых балочных и круглых плит, лежащих на упругих и упругоползучих однородных и неоднородных грунтовых основаниях.
Апробация практических результатов. Результаты диссертационной работы внедрены в ТОО ПИ «Южказпроект» с общим экономическим эффектом в сумме 2,7 млн. тенге в год и применяются при проектировании оснований 4-х и 10-ти этажных домов, а также используются в учебном процессе в ЮКГУ им. М.Ауезова.
Апробация работы. Основные результаты работы доложены и обсуждены на международных, республиканских и региональных научных и научно-практических конференциях: «Республиканская научно-практическая конференция, посвященная 70-летию доктора технических наук, профессора Т.Б.Байтелиева (Туркистан, 2008); «Химия в строительных материалах и материаловедение в ХХI веке» (Шымкент, 2008); «Актуальные проблемы образования, науки и производства-2008» (Шымкент, 2008); «Актуальные проблемы механики и машиностроения» (Алматы, 2009); «Актуальные проблемы подготовки высоко квалифицированных специалистов-2009» (Шымкент, 2009).
Основная часть
Во введении дана краткая оценка современного состояния решаемой научной проблемы, основание и исходные данные для разработки темы, обоснование необходимости проведения научно-исследовательской работы, сведения о планируемом научно-техническом уровне разработки, о метрологическом обеспечении диссертации. Кроме того, содержатся актуальность рассматриваемой проблемы, цели и задачи диссертационной работы, научная новизна, обоснованность и достоверность полученных результатов, апробация практических результатов и практическая ценность работы, положения, выносимые на защиту.
В первом разделе дан обзор существующих теорий и изложено современное состояние исследуемого вопроса. Приведены различные существующие практические методы расчета конструкций, взаимодействующих со сплошным основанием. В этих методах основание считается как упругое изотропное полупространство, ограниченное плоскостью. Такая модель, применяемая к грунтовым основаниям и самой конструкций, не учитывает их деформирования во времени. Между тем, многочисленные опыты показывают, что для создания наиболее экономичных и в то же время достаточно надежных конструкций необходимо учесть такие свойства строительных материалов, как ползучесть и неоднородность. К таким материалам относятся бетон, полимерные материалы и многие разновидности грунтов.
Следовательно, если грунты-основания и материалы конструкций, кроме упругих свойств, обладают ползучестью, то напряженно-деформированное состояние инженерных сооружений в процессе эксплуатации будет меняться. В итоге оно может существенно повлиять на долговечность всего сооружения и возникает необходимость разработки методов расчета упругоползучих балочных и круглых плит, лежащих на упругоползучем неоднородном основании.
Для расчета сооружений на неоднородном основании, где модуль деформации грунта изменяется по степенному закону, Г.П.Клейн применил способ Б.Н.Жемочкина. В отличие от них, Т.Ш.Ширинкулов предлагает другой способ расчета. Он для аппроксимации реактивных давлений применяет специальные полиномы Гегенбауэра. Этим он добился высокой степени сходимости процесса приближения решения задачи и показал, что в большинстве случаев достаточно ограничиваться лишь двумя-тремя членами разложения ряда.
В целом анализ существующих работ по контактным задачам теории упругости и ползучести показывает, что при расчете плит на сплошном деформируемом основании одновременно не учитываются такие факторы, как слоистость плит, свойства ползучести материалов и неоднородность уплотняющего грунтового основания.
В связи с этим в настоящем разделе, в отличие от вышеуказанных работ, предлагается метод расчета бесконечной упругоползучей двухслойной балочной плиты постоянной ширины, лежащей на неоднородном основании. Модуль деформации и мера ползучести грунта с глубиной изменяется в виде:
, 
. (1)
Нагрузка, приложенная к плите, распределена равномерно по любой линии вдоль плиты и по произвольному закону 
поперек плиты. При таких условиях расчет плиты сводится к расчету балки-полоски длиной 
, шириной, равной единице (рисунок 1).
Рисунок 1 – Схема для расчета плиты, лежащей на деформируемом основании
Свойства ползучести материала изгибающей плиты и грунтового основания описаны теорией упругоползучего тела Г.Н.Маслова-Н.Х.Арутюняна. Коэффициент упругой поперечной деформации считается постоянным во времени. При этих предположениях между деформациями и напряжениями имеет место следующее соотношение:
, (2)
где 
;
.
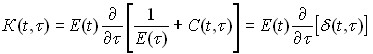Математическая постановка данной задачи сводится к решению системы трех уравнений:
Первое представляет собой интегро-дифференциальное уравнение изгиба двухслойных упругоползучих плит. Оно при (1),(2) имеет вид:
, (3)
где 
, 
, 
.
Второе уравнение выражает осадку неоднородного основания, которое с учетом ползучести имеет вид:
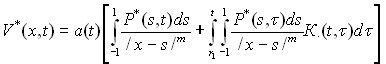, (4)
где 
, 
.
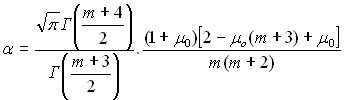Третье уравнение - это условие контакта поверхности плиты с основанием, которое выражается тождеством:
. (5)
Кроме вышеприведенных уравнений (3)–(5), должны выполняться условия равновесия плиты и граничные условия исследуемой задачи.
Решение рассматриваемой задачи сводится к определению закона распределения реактивных давлений 
. Эту функцию, 
удовлетворяющую уравнению (3), ищем в виде ряда из полиномов Гегенбауэра с переменными во времени 
коэффициентами:
. (6)
Подставляем выражение (6) в уравнение (3), затем полученное равенство четырехкратно проинтегрируем по независимой переменной 
. Тогда, для общего случая загружения балочных плит, их прогиб находится из следующей формулы:
. (7)
Функции 
, входящие в (7) являются частными интегралами дифференциальных уравнений:
. (8)
Из соотношения (4), после подстановки в него значения реактивного давления 
для осадки неоднородного основания получим:
. (9)
Здесь 
.
Таким образом, для общего случая при помощи выражений (3)-(9) можно определить прогиб плиты, который дает возможность определить в ней внутренние усилия и осадку основания.
В данном разделе рассмотрены различные случаи нагружения плит внешней нагрузкой, а именно равномерно распределенной, сосредоточенной и прерывно – симметричной нагрузками, т.е. когда имеются несколько участков интегрирования.
Если нагрузка симметричная, то в разложении (6) участвуют четные полиномы, а при несимметричной нагрузки только нечетные. Пусть заданная нагрузка равномерно распределена по балке и не изменяется во времени, то прогиб плиты, изгибающий момент и перерезывающие силы соответственно находятся из следующих расчетных формул:
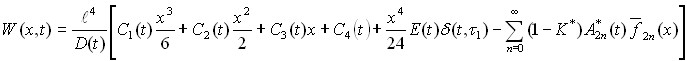; (10)
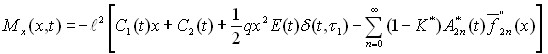; (11)
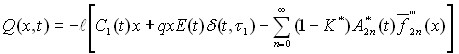, (12)
где произвольные постоянные интегрирования 
, входящие в (10)-(12), определены из граничных условий задач.
Используя формулы (11) и (12), на рисунке 2 при 
=0,5 приведены графики изменения функций 
и 
, где пунктирными линиями приводится решение упруго-мгновенной, а сплошными упругоползучей задачи.
Рисунок 2 – Эпюры 
при коэффициенте неоднородности 
На основании анализа этих графиков и полученных результатов, в работе сделан вывод, что для случая нагружения балки симметричной равномерно распределенной нагрузкой учет ползучести как материала плиты, так и грунтов основания, значительно влияет на распределение усилия в сечениях балки. Так, для случая, когда 
, максимальный изгибающий момент уменьшается на 20% (при 
=180 суток) и на 29% (при 
= 360 суток) по сравнению с решениями упруго-мгновенной задачи. Реактивное давление грунта (хотя на концах остается бесконечным) внутри интервала 
значительно выравнивается. Однако в середине полосы оно больше, чем для однородного основания. С возрастанием показателя неоднородности грунта 
при симметричных нагрузках реактивное давление в середине увеличивается, а изгибающие моменты уменьшаются по сравнению с однородным основанием.
Для инженерных расчетов определенный интерес представляет решение задачи об изгибе слоистых упругоползучих балочных плит, лежащих на упругоползучем неоднородном основании, когда учитываются переменность модуля упругости и старение материалов плиты и основания. При этом приходится решать систему интегральных уравнений при ядрах достаточно общего вида. В этом случае не удается получить точного решения исходной системы. Однако с помощью известного метода Н.М.Крылова и Н.А.Боголюбова в данном разделе найдены приближенные решения задач, позволяющие определить искомые величины с любой степенью точности.
В разделе также приводится расчет упругоползучих двухслойных плит с заполнителями, лежащих на упругоползучем неоднородном основании.
Многие конструкции, такие как фундаменты доменных печей и фабричных труб, днища резервуаров и газгольдеров и др., рассчитываются по схеме круглых плит на деформируемом основании. Эти конструкции работают под действием симметричной относительно центра нагрузки и поэтому во всех точках, равноудаленных от центра плиты, прогибы будут одинаковы. Это обстоятельство дает то, что при расчете плит под действием осесимметричных нагрузок можно ограничиться рассмотрением их лишь в одном единственном диаметральном сечении, проходящем через ось симметрии.
Учитывая это, во втором разделе диссертации, в отличие от существующих работ, излагаются методы расчета двухслойных круглых плит на неоднородном полупространстве с учетом ползучести материала плиты и грунтового основания.
Предлагаемый метод основан на использовании полиномов Гегенбауэра для представления реакции основания. Он является дальнейшим развитием метода Т.Ш.Ширинкулова, разработанного для расчета упругоползучих круглых плит на упругоползучем однородном основании. Здесь исследованы круглые упругоползучие двухслойные плиты радиусами 
и с постоянными толщинами 
, свободно (без трения) лежащие на упругоползучем неоднородном основании, модуль упругости и мера ползучести которого с глубиной изменяется по (1). Плиты находятся под действием нормальных и осесимметричных нагрузок интенсивностью 
.
Задача сводится к установлению закона распределения реактивного давления. При этом должны быть соблюдены условия равновесия плит в целом, т.е.:
, (13)
и тождественно удовлетворено контактное условие
. (14)
Прогиб плиты определяется решением интегро-дифференциального уравнения изогнутой поверхности, т.е. оно имеет вид:
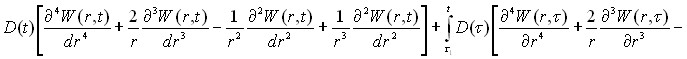
, (15)
где 
.
Осадку основания можно определить как решение интегрального уравнения, связывающего реактивное давление с перемещением поверхностных точек основания. Согласно Т.Ш.Ширинкулову, эту величину можно представить так:
, (16)
где 
; 
.
Реактивное давление 
представлено рядом из четных полиномов Гегенбауэра 
, т.е.:
. (17)
Тогда для осадки грунта имеем:
. (18)
Решая систему уравнений (13)-(18), для прогиба плит получим:
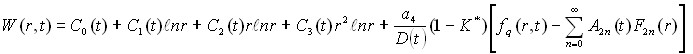. (19)
Здесь функции 
и частный интеграл 
в общем виде можно определить из формул:
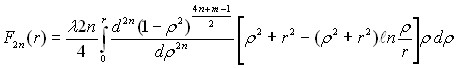; (20)
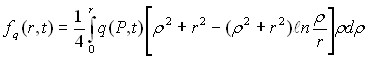. (21)
Значения этих функций для различных параметров 
в диссертации даны в таблице, а постоянные интегрирования 
определены из граничных условий рассматриваемой задачи. Коэффициенты разложения 
вычисляются на основании уравнений (13) и (14).
Для иллюстрации изложенного метода в данном разделе рассмотрены различные случаи нагружения. Один из них показан на рисунке 3.
Рисунок 3 – Эпюры
и 
при 
Анализ расчетов показывает, что учет ползучести материалов плиты и основания приводит к уменьшению радиальных и кольцевых изгибающих моментов по сравнению с моментами, полученными при решении задачи, когда не учитывается ползучесть материалов как плиты, так и грунтов основания (пунктирная линия).
Для общего случая, т.е. когда учитывается переменность модуля упруго-мгновенных деформаций и старение материалов плиты и основания, приближенное решение задачи получено методом Крылова-Боголюбова.
В третьем разделе приводится расчет многослойных балочных плит с упругоподатливыми поперечными и сдвиговыми связями (заполнителями), взаимодействующих с линейно-деформируемым основанием.
Во всех работах, посвященных расчету составных балок, учет податливости связей в поперечном направлении принимается по гипотезе Винклера, согласно которой заполнители рассматриваются как система отдельных, не связанных между собой пружин и конструкций. Это в ряде случаев приводит к результатам, резко расходящимся с действительностью. В связи с этим перед современной теорией расчета составных балочных плит, взаимодействующих с деформируемым основанием, стоит ряд серьезных проблем. Учитывая это, в данном разделе предлагается методика расчета составных балок, взаимодействующих с деформируемым основанием. При этом для описания деформативных свойств заполнителей, находящихся между балочными плитами применяется двухпараметровая модель В.З. Власова.
Получить точное решение поставленной задачи очень трудно. Ее решение можно упростить, если сделать некоторые допущения. Например, при действии на составную плиту только нормальных нагрузок 
можно пренебречь касательными напряжениями 
в заполнителях и контактным касательным усилием основания 
или, наоборот, при действии только сдвигающих нагрузок можно пренебречь нормальными реакциями поперечных связей и нормальными контактными усилиями.
В разделе исследована задача об изгибе многослойных балочных плит с упругоподатливыми связями сдвига и абсолютно жесткими поперечными связями, взаимодействующих с линейно-деформируемым основанием при отсутствии трения. Решение задачи получено в полиномах Чебышева.
В четвертом разделе диссертации, основываясь на полученные теоретические результаты третьего раздела, исследован изгиб упругих двухслойных плит, соединенных упругими связями, лежащих на упругом однородном основании. Упругая связь (заполнитель) такова, что она не передает касательные усилия. Заданная внешняя нагрузка распределена равномерно по любой линии вдоль плиты и по произвольному закону 
поперек нее. При таких условиях расчет плиты сводится к расчету балочных плит длиной 
, толщиной соответственно 
и шириной, равной единице.
В качестве примеров рассмотрены случаи нагружения плиты с нагрузкой, равномерно распределенной симметрично относительно середины плиты; вертикальной сосредоточенной силой, расположенной в середине плиты.
Анализ полученных численных результатов показывает, что учет жесткостных характеристик заполнителя приводит к перераспределению внутренних усилий. При этом с увеличением жесткости заполнителя изгибающие моменты в верхней плите увеличиваются, а в нижнем уменьшаются.
Следовательно, путем подбора физических и геометрических характеристик заполнителя можно регулировать распределение внутренних усилий в плитах. Это дает возможность рационально расходовать строительные материалы, обеспечив прочность и устойчивость конструкций, и экономить строительные материалы.
В этом разделе также исследована контактная задача для двухслойных балочных плит, нагруженных обратно прерывно-симметричной нагрузкой.
По результатам исследования данной работы разработана инженерная методика расчета упругоползучих балочных и круглых плит, лежащих на упругоползучем основании.
Эти результаты работы внедрены в ТОО ПИ «Южказпроект» при проектировании оснований 4-х и 10-ти этажных домов с общим экономическим эффектом соответственно 1,3 и 1,41 млн. тенге в год.
Заключение
Краткие выводы по результатам диссертационного исследования
1. Установлена математическая модель, описывающая упругое и упруго- ползучее состояние системы «сооружение-основание», которая позволяет находить прогиб элементов конструкций, взаимодействующих с деформируемым однородным и неоднородным грунтовым основанием.
2. Получены расчетные формулы, позволяющие вычислить усилия в произвольном сечении балки, значения прогибов балок, осадок основания и его реакции в упругоползучих двухслойных балочных и круглых плитах, лежащих на упругоползучем неоднородном основании при нагружении их симметричной, обратно-симметричной, сосредоточенной, прерывно-симметричной и другими еще частными случаями нагрузок.
3. Показано, что при нагружении балок внешней нагрузкой учет свойства ползучести как материалов плиты, так и грунтов основания, значительно влияет на распределение усилия в сечениях балки.
4. Выявлено, что с возрастанием показателя неоднородности грунта 
при симметричных нагрузках реактивное давление в середине увеличивается и внутри нагружаемого интервала оно выравнивается, изгибающие моменты уменьшаются по сравнению с однородным основанием.
5. Влияние свойства ползучести, оказываемое на напряженно-деформированное состояние изгибающих плит, уменьшается с уменьшением показателя неоднородности. Например, при коэффициенте 
максимальный изгибающий момент в середине плиты уменьшается на 12% (при 
= 180 суток) и на 16% (при 
=360 суток) по сравнению с решением упруго-мгновенной задачи.
6. Изучен изгиб балочных плит с упругоподатливыми поперечными и сдвиговыми связями, взаимодействующих с линейно-деформируемым основанием.
7.Дан метод решения задачи об изгибе многослойных упругих балочных плит, с упругоподатливыми и сдвиговыми связями, лежащих на линейно-деформируемом основании.
8. Предложена методика расчета изгиба упругих двухслойных плит на упругом однородном основании, когда между плитами находятся заполнители. Анализ полученных результатов показывает, что учет жесткостных характеристик заполнителя 
приводит к перераспределению внутренних усилий. Причем с увеличением жесткости заполнителя, изгибающие моменты верхней плиты увеличиваются, а нижней уменьшаются. Это дает возможность путем подбора физических и геометрических характеристик заполнителя регулировать распределение внутренних усилий в плитах и рационально расходовать строительные материалы, обеспечив прочность и устойчивость конструкций, и экономить строительные материалы.
Оценка полноты решений поставленных задач. Новые результаты, полученные в работе, позволяют определить осадки упругоползучих неоднородных грунтовых оснований и усилия в упругих и упругоползучих слоистых плитах в зависимости от времени и позволяют заранее предугадать их реальное состояние в эксплуатации. Цель и задачи, поставленные перед работой, решены полностью. Результаты исследования, их оценка, апробация и внедрение в производство подтверждают обоснованность и полноту решений поставленных задач.
Разработка рекомендаций и исходных данных по конкретному использованию результатов. Разработанный способ расчета, результаты и выводы работы рекомендуются для использования в научно–исследовательских и проектных организациях при разработке и проектировании фундаментов и оснований с учетом упругих и упругоползучих свойств как материала изгибающих плит, так и грунтов. Они могут быть использованы также в проведении лекционных, практических занятий по механике деформируемого твердого тела и научно–исследовательских работах студентов, магистрантов и докторантов.
Исходными данными для использования результатов являются существующие конструктивные решения по данной проблеме, физико-механические характеристики изгибающих слоистых балочных и круглых плит, грунтовых оснований, их размеры и нагрузки, приложенные к ним.
Оценка технико-экономической эффективности внедрения подтверждается предварительными расчетами и актами внедрения результатов исследований в ТОО ПИ «Южказпроект» при проектировании оснований 4-х и 10-тиэтажных домов. Общий экономический эффект от внедрения результатов работы на них составил 2,7 млн. тенге в год.
Оценка научного уровня выполненной работы в сравнении с лучшими достижениями в данной области. В работе получены точные и приближенные решения задачи об изгибе балочных и круглых плит, находящихся на упругом, упругоползучем однородном и неоднородном деформируемом основании. При этом учитываются слоистость, упругое и упругоползучее свойства элементов конструкции. Предложенная методика определения реактивного давления грунта, представленного в виде суммы полиномов Гегенбауэра или Чебышева, могут иметь большое значение при решении подобных задач механики деформируемого твердого тела. На основании полученных новых расчетных формул, отражающих реальное напряженно-деформированное состояние плит, лежащих на грунтовом основании, должны быть разработаны технические рекомендации и инструкции.
Результаты работы значительно дополняют ранее известные данные об изгибе балочных и круглых плит, взаимодействующих с грунтовым основанием.
Условные обозначения: 
– соответственно мера ползучести и модуль деформации, МПа; 
– показатель неоднородности; 
– полная относительная деформация; 
– единичный тензор; 
– время приложения нагрузки, сутки; 
– коэффициент упругой поперечной деформации; 
,
– тензоры деформаций и напряжений, МПа; 
,
– интегральные операторы; 
– резольвента ядра 
; 
– прогиб плиты, м; 
– соответственно интенсивность нормальной реакции основания и внешней распределенной нагрузки, МПа; 
– коэффициенты, подлежащие определению; 
– цилиндрическая жесткость 
–ой плиты; 
– безразмерная координата, равная отношению абсолютной координаты к полудлине балки; 
– толщина плиты, м; 
– коэффициент Пуассона материала оснований; 
– гамма-функция; 
– полином Гегенбауэра; 
,
– соответственно равнодействующие внешних сил и их момент относительно середины балки-полосы, Н, Н·м; 
– корни характеристического уравнения; 
– жесткостных характеристик заполнителя, Н/м3; 
– приведенный модуль деформации.
Список опубликованных работ по теме диссертации
1 Дасибеков А.Д., Уралов Б.К., Ширинкулов К.Т. Контактная задача теории ползучести для составных балочных плит на деформируемом основании //Механика и моделирование процессов технологии. -2004.-№1.-С.3-6.
2 Ширинкулов Т.Ш., Ширинкулов К.Т., Дасибеков А.Д., Уралов Б.К. Изгиб составных упруго-вязким линейно-деформируемым основанием // Механика и моделирование процессов технологии. -2004. -№1.-С.17-21.
3 Ширинкулов Т.Ш., Уралов Б.К., Дасибеков А.Д. Расчет на изгиб упругоползучих тонких трехслойных плит на деформируемом основании //Наука и образование Южного Казахстана. -2008.-№ 1 (66).-С.161-167.
4 Ширинкулов Т.Ш., Дасибеков А.Д., Уралов Б.К., Ширинкулов К.Т. Решение задачи о контактном взаимодействии упругоползучих балочных плит с упругоползучим деформируемым основанием с учетом силы трения //Наука и образование Южного Казахстана. -2008. -№2(67)-С.129-135.
5 Ширинкулов Т.Ш., Дасибеков А.Д., Уралов Б.К., Асибеков А.Ж., Камбарова О.Б. О контактов взаимодействии составных плит с деформируемым основанием //Тр.Республиканской научно-практической конференции, посвященной 70-летию видного ученого геомеханика, доктора технических наук, профессора Т.Б.Байтелиева. МКТУ.-Туркистан. -2008.-С.54-57.
6 Ширинкулов Т.Ш., Дасибеков А.Д., Уралов Б.К., Юнусов А.А., Асибеков А.Ж. Изгиб трехслойных плит, лежащих на деформируемом основании //Сб. трудов Международной научно-методической конференции «Актуальные проблемы образования, науки и производства-2008». Том 1. Казахстанский университет дружбы народов. -Шымкент, 2008.-С.163-167.
7 Уралов Б.К. Расчет упругоползучих трехслойных балочных плит с абсолютно жесткими поперечными и упругоподатливыми сдвиговыми связями, лежащих на деформируемом неоднородном основании //Механика и моделирование процессов технологии. -2008.-№1.-С.33-38.
8 Ширинкулов Т.Ш., Дасибеков А.Д., Уралов Б.К., Камбарова О.Б., Юнусов А.А. Расчет многослойных пластин, лежащих на упруговязком основании //Тр. Международной научно-практической конференции «Химия в строительных материалах и материаловедение в ХХI веке».-Шымкент, 2008.-№2.-С.160-163.
9 Ширинкулов Т.Ш., Дасибеков А., Юнусов А.А., Асибеков А.Ж., Уралов Б.К., Абильмаженов Т.Ж. Об исследованиях методов расчета конструкций, взаимодействующих со сплошным основанием // Сб. трудов Международной научно-практической конференции «Актуальные проблемы подготовки высоко- квалифицированных специалистов-2009».-Шымкент,21-22 апреля 2009.-С.284-288.
10 Ширинкулов Т.Ш., Дасибеков А., Юнусов А.А., Уралов Б.К., Кабылбеков К.А., Абильмаженов Т.Ж. Расчет трехслойных балочных плит на неоднородном основании с учетом их упруговязких свойств//Материалы III Международной научной конференции «Актуальные проблемы механики и машиностроения». -Алматы, 17-19 июня 2009. I том. -С.299-304.
11 Ширинкулов Т.Ш., Дасибеков А., Юнусов А.А., Уралов Б.К., Кабылбеков К.А., Абильмаженов Т.Ж. Изгиб балочной плиты, нагруженной обратно-симметричной нагрузкой //Материалы III Международной научной конференции «Актуальные проблемы механики и машиностроения».- Алматы, 17-19 июня 2009. I том.-С.304-308.
12 Дасибеков А.Д., Ширинкулов Т.Ш., Уралов Б.К., Абдыхаимов М.А. Расчет упругополозучих круглых плит, расположенных на упругоползучем неоднородном основании //Наука и образование Южного Казахстана.-2009.-№4 (77).-С.94-98.
13 Уралов Б.К. Об упругоползучих круглых плитах, взаимодействующих с упругоползучим неоднородным основанием //Наука и образование Южного Казахстана. -2009.-№4(77).-С.108-111.
Оралов Байдулла ыдырбайлы
«Серпімді жне серпімдіжылжымалы асиеттері ескерілген кездегі топыра негізімен байланыстаы кпабатты плитаны есептеу»
01.02.04 – Деформацияланатын атты дене механикасы мамандыы
бойынша техника ылымдарыны кандидаты ылыми дрежесін алуа
арналан диссертацияа
ТЖЫРЫМ
Зерттеу нысаны. Бл жмысты зерттеу нысанына серпімді, серпімдіжылжымалы кпабатты плиталар мен біртекті жне біртекті емес серпімді, серпімдіжылжымалы топыра негіздері жатады.
Жмысты масаты. Серпімді, серпімдіжылжымалы кпабатты плиталар біртекті жне біртекті емес серпімді, серпімдіжылжымалы топыра негіздеріні бетінде жатан кездегі есептерін шешу. Аныталан шешімдер бойынша «имарат-негіз» жйесіні есептелу дістемесін жетілдіру.
Жмысты жргізу тсілдері мен дістері. Жмыста серпімді, серпімдіжылжымалы кпабатты плиталар біртекті жне біртекті емес серпімді, серпімдіжылжымалы топыра негіздеріні бетінде жатан кездегі байланыс есептеріні есептелу дістемесі жетілдірілген. Мнда серпімді жне жылжымалы теорияларды байланыс есептеріні шешімдері Гегенбауэр немесе Чебышев полиномдары арылы рнектелген. Бл жердегі атарлар рамына енетін белгісіз коэффициенттер плита мен топыра негізіні рбір нктедегі тыыз байланысан шарттарынан табылады.
Жмысты нтижелері. Серпімді жне жылжымалы теорияларыны байланыс есептері, берілген шарттар шін шешілген; біртекті емес топыра негізіні «имарат-негіз» жйесіні кернелену-деформациялану кйіне крсеткен ыпалы аныталан; топыраты жылжу асиетіні, онымен байланыста болан рылыс блшектеріне тигізетін сері крсетілген; ртрлі реологиялы асиеттерге ие болан, топыра негізімен беттесетін «имарат-негіз» жйесіні рамына енетін кпабатты рылыс блшектеріні кернелену-деформациялану кйі зерттелген; иіуші момент, июшы кш, реактивті ысым жне серпімді немесе серпімдіжылжымалы рылыс блшектеріні біртекті жне біртекті емес серпімді немесе серпімдіжылжымалы топыра негізіне орналасан кездегі иілуін жне негізді аншалыты отыруын айындайтын есептеу рнектері табылан.
Негізгі конструкциялы, технологиялы шешімдерді жне техниканы пайдалану сипаттары.
Жмыста деформацияланатын топыра негізіне орналасан екі жне шабатты плиталарды кернелену-деформациялану кйі зерттелген. Плита мен негіз серпімді немесе серпімдіжылжымалы асиеттерге ие болуы ммкін. Жмыс конструктивті жне технологиялы шешімдерді ажет етпейді. Себебі ол теорияа негізделіп, практикаа тікелей жол ашады. Барлы мселелерді табылан шешімдері математикалы анализді аналитикалы дісіне негізделген.
Жмыста негізгі сипаттамалар шін деформациия модулі, Пуассон коэффициенті, плитаны атадыы, сонымен атар материалдарды серпімді жне серпімдіжылжымалы асиеттерін анытайтын параметрлер олданылан.
Жмыс нтижелерін ендіру дегейі. Диссертациялы жмысты нтижелері «Южказпроект» ЖИ ЖШС жымына берілді. Ол трт жне он абатты имараттарды фундаменттері мен топыра негіздерін жоспарлау шін олданылды. Мнда бес жне он абатты йді жалпы экономикалы тиімділігі 2,7 млн. тенгені рады. Сонымен атар жмысты нтижелері М.уезов атындаы Отстік азастан Мемлекеттік Университетіні оу процесінде олданылып жатыр.
Жмыс нтижелерін енгізу сыныстары немесе ылыми-зерттеу жмыстарын ендіру нтижелері. Аныталан есептеу формулалары рылыс блшектері топыра негізімен байланыста болан кездегі оны иілуін, иіуші моментін, июшы кш пен реактивті ысымды жне біртекті, біртекті емес топыра негізіні аншалыты отыруыны сан мндерін табуа ммкіндік береді.
Жмыс нтижелері кп абатты имараттарды іргетастары мен топыра негіздерін жоспарлау шін, деформацияланатын атты денелер механикасы пні бойынша дріс пен практика сабатарын беруге жне студенттермен ылыми-зерттеу жмыстарын жргізуге сынылды.
олдану саласы. Зерттеу нтижелерін топыра негізіне орналасатын гидротехникалы, клік, азаматты жне мелиоратив рылыстарын ран кезде жне оларды пайдалануа берілгеннен кейінде олдануа болады. сіресе бл серпімді, серпімдіжылжымалы кпабатты плиталар біртекті жне біртекті емес серпімді, серпімдіжылжымалы топыра негіздеріні бетінде жатан кездегі жанасу есептеріні есептелу дістемесімен байланысты.
Жмысты маыздылыы. Плиталар мен біртекті емес топыра негізіні жылжу асиеттерін жне иілетін плиталар арасындаы толдырушыларды бір кезде еске алынуы ішкі кштерді зара блісуіне алып келеді. Сонымен атар толдырушыны атадыыны суі жоары плитаны иіуші моментті суіне, ал тменгі плитаны иіуші моментті азаюына келтіреді. Бл жадайда толдырушыны физикалы жне геометриялы сипаттамаларын тадай отырып, плиталарда пайда болатын ішкі кштерді алдын-ала реттеуге болады.
Бл рылыс имараттарыны беріктілігін жне орнытылыын сатай отырып, оан жмсалатын рылыс заттарын немдеуге ммкіншілік береді.
Зерттеу нысанын дамытуды жобалы болжамы. азіргі кезде крделі рылысты негізгі мселесі, ол жаа технологияа жне техникаа сйене отырып Казастанны ндірісіні потенциалын сіру. Бл рылыс саласына жмсалатын кімет аржысыны дрыс олданылуы деген сз. Міне осыан бл жмысты, яни кпабатты балкалы, дгелек плиталарды сызыты деформацияланатын негіз бетіне орналасан кездегі жне оларды реологиялы асиеттері есепке алынан шатаы шешілген мселелері жауап береді деген міттеміз.
Uralov Baidulla Kidirbayevich
“Calculation of multilayer plate on ground base with a glance of its elasticity and flexible creeping properties”
- 02. 04.-Mechanics of deformed solid substances for the researching degree candidate of technique
SUMMARY
Object of research work is elastic and flexible creeping composite plates and flexible creeping homogeneous or heterogeneous ground base.
The aim of the work is to solve the problems according to the theory of elasticity and flexible creeping plates connected with tough ground base and on the basis of received solutions to develop calculation method such as “construction-basement”.
Method and methodology of realization: Estimation methods of composite elastic and flexible creeping plates on the tough homogeneous and heterogeneous foundation base are developed. Solutions of contacting problems of the elasticity theory and flexible creeping are represented in the list of Hegenbauer or Chebyshev. However, on the basis of continuity inclusive unknown coefficient is revealed.
Results of the work are contacting problems of elasticity theory and creeping in a particular edge conditions are solved; impact of heterogeneity of ground base on the strain-stressed state of “construction-basement” system is established; influence of ground base creeping strain-stressed state of construction elements connected with compatible basement possessing various rheological properties are revealed; calculation formulas accordingly reflective change bend of construction elements, interacted with thicken homogeneous and heterogeneous elastic ground base and bending moment of flexion, internal force, reaction pressure and setting ground.
Basic constructive, technological and technical operating characteristics: modules of deformation Poisson coefficient and stiffness ratio of a board; elastic and flexible creeping parameters like bending plates and ground basement are accepted as the main properties.
Bending of two or three-layered plates located on the deformed ground base. However, plate materials and basement can be both elastic and flexible. Research work does not demand constructive and technological solutions because they are based on the theoretical research of a problem with practical attachment.
With the help of analytical method of mathematical analysis solutions of all problems are received.
Degree of introduction: the results of the research work are realized in “Uzhkazproekt” Co ltd PI with economic effect in 2.7 million tenge and basement and they are applied in projecting of 4-10 storey houses and also we use it in teaching process at M. Auezova SKSU.
Recommendations for introduction and the results of scientific-research work are the calculation formulas to estimate the deflection elements of constructions interacted with the basement to define moment of flexion, lateral force, reaction of pressure and setting homogeneous and heterogeneous compatibility of ground base are applied.
Results of work in designing stored ground base of five and ten storey house in the course of lecture and practical lessons of mechanics of strain-stressed state of solid body and scientific-research work are introduced.
The area of application: in the process of constructing hydro technical traffic and public constructions which are built on the ground base in the results of research work might be applied. Mainly, it is connected with the calculation of elastic and flexible creeping multilayer plates lying on elastic and flexible creeping homogeneous or heterogeneous ground base.
Economic efficiency and significance of work: simultaneous account of creeping plate material or heterogeneous of ground base of an aggregate leads to the redistribution of stress. However, by increasing aggregate of the stiffness moment of flexion of a top plate increases and in the low plat it decreases. In this case, by means of physical and geometric properties of an aggregate it regulates the distribution of stress in plates.
Prognostic recommendations of development of research object: nowadays the main problem of capital construction is the further lengthening of an industrial potential of Kazakhstan in a new technical basis. It is necessary here to develop efficiency of capital investment on the basis of using achievements of scientific-technical progress. This work can give an answer to the calculation of multilayer beam slabs and circular plates interacted with linear elastic basement according to its properties.
Подписано в печать 09.01.2010г. Формат бумаги 60х84 1/16
Бумага типографическая. Печать офсетная. Объем 1,25пл.
Тираж 100 экз. Заказ №1620
