Колебания крыла в сверхзвуковом потоке газа
САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
На правах рукописи
АРСЕНТЬЕВ Тимофей Петрович
КОЛЕБАНИЯ КРЫЛА В СВЕРХЗВУКОВОМ ПОТОКЕ ГАЗА
01.02.05 — Механика жидкости, газа и плазмы
АВТОРЕФЕРАТ
диссертации на соискание ученой степени
кандидата физико-математических наук
Санкт-Петербург
2008
Работа выполнена на кафедре гидроаэромеханики математико-механического факультета Санкт-Петербургского государственного университета.
Научный руководитель: доктор физико-математических наук,
профессор БАРАНЦЕВ Рэм Георгиевич
Официальные оппоненты: доктор физико-математических наук,
профессор ЕРШОВ Борис Александрович
кандидат физико-математических наук,
доктор технических наук,
доцент ПОЛЯКОВА Екатерина Владимировна
Ведущая организация: Московский Авиационный Институт
Защита состоится "_____" _____________ 2008 г. в _____часов на заседании совета Д 212.232.30 по защите докторских и кандидатских диссертаций при Санкт-Петербургском государственном университете по адресу: 198504, Санкт-Петербург, Старый Петергоф, Университетский пр., д. 28, ауд. ____
С диссертацией можно ознакомиться в Научной библиотеке им. М. Горького Санкт-Петербургского государственного университета по адресу: Санкт-Петербург, Университетская набережная, д. 7/9.
Автореферат разослан " " 2008 г.
Ученый секретарь диссертационного совета,
доктор физико-математических наук, профессор С. А. Зегжда.
ОБЩАЯ ХАРАКТЕРИСТИКА РАБОТЫ
Актуальность темы. Некоторые типы колебаний крыльев самолета и рулевых поверхностей наблюдались с первых дней полета самолета. Для того чтобы описать физическое явление, рассмотрим свободнонесущее нестреловидное крыло без элерона, смонтированное под малым углом в аэродинамической трубе и жестко закрепленное у корня. Когда поток воздуха в аэродинамической трубе отсутствует и модель возбуждается, например, толчком с помощью тяги, то возникает колебание, которое потом постепенно затухает. При постепенном увеличении скорости потока в трубе скорость затухания колебания возбужденного профиля сначала увеличивается. Однако по мере дальнейшего увеличения скорости достигается такой момент, когда скорость затухания быстро уменьшается. При критической скорости флаттера колебание может продолжаться с постоянной амплитудой. При скоростях потока несколько превышающих критическую, небольшое случайное возмущение профиля может служить толчком к возникновению очень сильного колебания. Такие колебания даже если и не приведут к разрушению крыла и крушению самолета, то могут существенно ухудшить управляемость.
В ранние периоды развития авиации устойчивость конструкции относительно флаттера могла быть достигнута за счет незначительных изменений конструкции и за счет незначительного увеличения веса. Новая тенденция к оптимальной конструкции самолетов с высокими летными качествами создает совершенно иную картину. Обычно желают создать самолет с минимальным весом, должным образом соответствующий заданным проектным требованиям (нагрузка, геометрия и т. п.). Эти и другие проблемы, связанные с развитием авиации, остаются актуальными и по сегодняшний день. И дальнейшее развитие авиации влечет за собой дальнейшие исследования задач, связанных с флаттером.
Целью работы является постановка и решение задач, связанных с процессом колебания крыла в сверхзвуковом потоке идеального сжимаемого газа. А именно, исследование аэродинамической задачи и применение полученных в аэродинамике результатов для нахождения асимптотического решения связанной аэроупругой задачи на малых и больших частотах.
Методы исследования. В работе применяются асимптотические методы, основанные на использовании малости относительной толщины профиля крыла и малости амплитуды его колебаний, а также основанные на рассмотрении задачи при малых и больших частотах. Для решения задач используются метод Римана, общее решение для телеграфного уравнения, общее решение для однородного волнового уравнения и формула для решения неоднородного волнового уравнения при нулевых граничных условиях. Также используются методы решения обыкновенных дифференциальных уравнений.
Научная новизна. Найдено аналитическое решение аэродинамической задачи о колебании крыла в сверхзвуковом потоке газа с помощью метода Римана и общего решения телеграфного уравнения. Также найдено второе приближение стационарной части задачи. Получено асимптотическое решение аэроупругой задачи о колебании крыла в сверхзвуковом потоке газа при малых и больших частотах на основе результатов, найденных при решении аэродинамической задачи.
Достоверность полученных результатов обеспечивается корректным применением асимптотических методов, методов математической физики и теории дифференциальных уравнений.
Практическая и теоретическая ценность. Результаты исследования могут представлять интерес для специалистов, занимающихся проектированием летательных аппаратов, движущихся со сверхзвуковой скоростью. Полученные аналитические решения могут быть использованы для расчета скорости и давления на профиле крыла, совершающего произвольной формы колебания. Найденные формулы также позволяют рассчитать скорость и давление в области между профилем крыла и характеристикой. Еще могут представлять интерес найденные частоты, при которых возникают колебания определенной формы.
Апробация работы. Основные результаты, полученные в данной работе, были доложены на международных конференциях «Пятые Окуневские Чтения» (Санкт-Петербург, 2006) и «Шестые Окуневские Чтения» (Санкт-Петербург, 2008), на XXI Всероссийской конференции по аналитическим методам в газовой динамике «САМГАД-2006» (Санкт-Петербург, 2006), на Всероссийском семинаре по аэрогидродинамике, посвященном 90-летию со дня рождения Сергея Васильевича Валландера (Санкт- Петербург, 2008) и на 6-ой Европейской конференции по нелинейной динамике «ENOC 2008» (Санкт-Петербург, 2008).
Публикации. Основные результаты опубликованы в работах [1-8]. Работа [5] опубликована в рецензируемом научном журнале «Вестник Санкт-Петербургского Университета», входящем в перечень ВАК.
В работах [3, 4] соавтору принадлежит постановка аэродинамической задачи о колебании крыла в сверхзвуковом потоке газа. Также соавтором предложен метод Римана для решения задачи на профиле крыла. Диссертантом решена задача на профиле крыла методом, предложенным соавтором и произведен расчет амплитуды колебаний давления на профиле крыла при переходе через критическую частоту. Асимптотика найденного решения и асимптотика колебаний давления на профиле крыла принадлежит обоим авторам.
В работе [8] соавтором показана возможность расщепления стационарной и нестационарной частей задачи на одном уровне точности, получено уравнение и граничные условия во втором приближении стационарной задачи. Диссертантом получено аналитическое решение стационарной задачи во втором приближении.
Вклад соавторов в подготовку докладов и материалов для конференций (см. [1, 2, 6]) такой же, как и в [3, 4, 8].
Структура работы. Работа состоит из двух частей, содержит введение, заключение и список литературы, состоящий из 94 наименований. Общий объем работы составляет 59 страниц текста и 10 иллюстраций.
Результаты, выносимые на защиту.
- Аналитическое решение аэродинамической задачи о колебании крыла в сверхзвуковом потоке газа, полученное на профиле крыла методом Римана.
- Аналитическое решение аэродинамической задачи о колебании крыла в сверхзвуковом потоке газа, найденное в области между профилем крыла и характеристикой с помощью общего решения телеграфного уравнения.
- Второе приближение стационарной задачи.
- Выражение для аэродинамического давления, возникающего при колебании крыла в сверхзвуковом потоке и его асимптотика на профиле крыла при малых и больших частотах.
- Асимптотическое решение связанной аэроупругой задачи на малых и больших частотах.
СОДЕРЖАНИЕ РАБОТЫ
Во введении дается краткая история исследований проблемы флаттера и приведен обзор литературы, посвященной аэродинамике колебаний крыла и связанным аэроупругим задачам о колебании крыла. Также во введении обосновывается актуальность и научная новизна диссертации. Формулируются цель работы, указывается практическая и теоретическая ценность её результатов. Приводится краткое содержание диссертации и результаты, выносимые на защиту.
В первой части работы исследуется аэродинамика колебаний крыла в сверхзвуковом потоке газа. Рассматривается крыло (см. рис. 1), испытывающее поперечные колебания, амплитуда которых мала по сравнению с его толщиной, так что профиль крыла можно представить в виде:
, |f | << |f 0| << 1,
где 
и 
малые параметры, обеспечивающие выполнение указанных неравенств, а частота 
произвольна.
Нестационарное сверхзвуковое течение идеального газа около тонкого крыла описывается известным уравнением для потенциала скоростей 
при соответствующих граничных условиях на профиле крыла и характеристиках, в которые вырождается ударная волна. Представление искомого потенциала 
в соответствующей форме
, |
| << |
|,
позволяет расщепить решение задачи на два последовательных этапа: сначала найти 
, а затем 
. Упрощая уравнение для потенциала с помощью найденных порядков возмущенных величин, для стационарной задачи было получено однородное волновое уравнение. Решение стационарной задачи известно и имеет вид
,
где 
, 
– число Маха.
Рисунок 1. Профиль крыла.
Был рассмотрен случай, когда
, 
Уравнение для 
при этом сводится к виду:
.
Условие на профиле, снесенное на ось y=0, и условие на ударной волне, снесенное на характеристику, принимают вид:
Решение данной задачи на профиле крыла найдено методом Римана
.
И получена его асимптотика при малых и больших
, 
,
, 
.
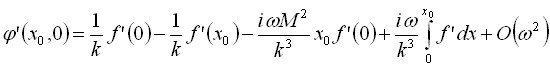Пользуясь интегралом Лагранжа и полученной асимптотикой, была найдена амплитуда колебаний давления на профиле крыла в следующем виде:
Следовательно, при малых 
амплитуда колебаний в асимптотике пропорциональна наклону профиля и не зависит от частоты, при больших 
амплитуда пропорциональна ординате профиля и частоте колебаний.
а б
Рисунок 2. Амплитуда колебаний давления на профиле крыла (M=2, f (x,)=0,1x(1-x)). На рисунке а кривая 1 соответствует значению =0,5, кривая 2 - =1, кривая 3 =3, кривая 4 - =5. Звездочками показана асимптотика при малых . На рисунке б кривая 1 соответствует значению =3, кривая 2 - =5, кривая 3 =8, кривая 4 - =11, кривая 5 - =15. Точками показана асимптотика при больших (=15).
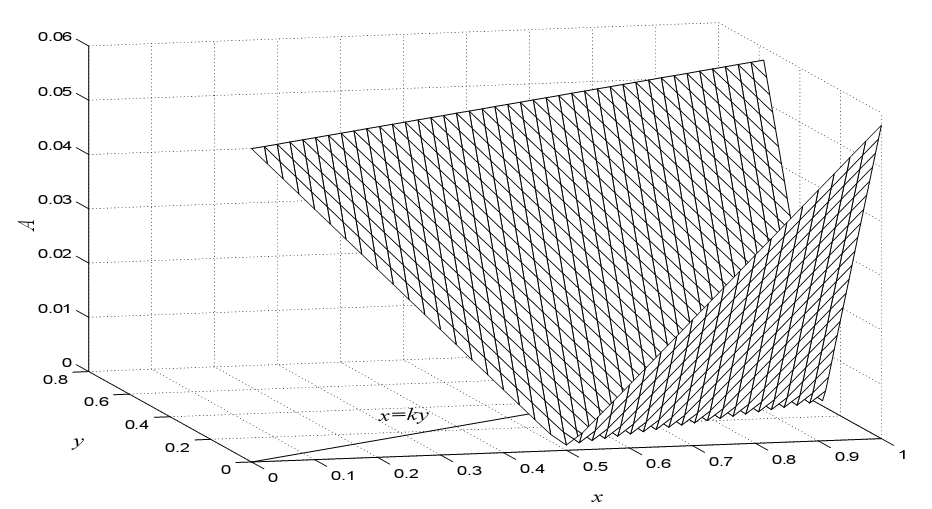
а б
Рисунок 3. Амплитуда колебаний давления на профиле крыла (M=2; f (x,)=0,1x(1-x); а - =0,1; б - =1).
На рисунке 2 представлена амплитуда колебаний давления на профиле крыла для случая, когда крыло совершает колебания по закону f (x,)=0,1x(1-x). Также показана асимптотика при больших и малых 
.
Для решения задачи в области между профилем крыла и характеристикой, уравнение для 
с помощью замены сводилось к уравнению 
. Решение этого уравнения имеет вид
,
где 
и 
- произвольные функции, которые были найдены из условий на профиле крыла и характеристике. В результате в области между профилем крыла и характеристикой получено решение
.
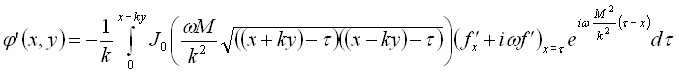а б
Рисунок 4. Амплитуда колебаний давления на профиле крыла (M=2; f (x,)=0,1x(1-x); а - =5; б - =15).
На рисунках 3 и 4 представлена амплитуда колебаний давления в области между характеристикой и профилем крыла при различных 
. Рисунки 2, 3 и 4 показывают, как меняется характер колебаний при переходе через критическую частоту порядка единицы.
В случае, когда потенциал скоростей имеет форму
,
более высокие приближения 
становятся сравнимыми с 
и при этом естественно обе части задачи решать на одном уровне точности.
Подставляя выражение для 
в известное уравнение для потенциала скоростей и допуская, что
,
для 
получили волновое уравнение
,
для 
- неоднородное волновое уравнение
(39)
а для 
- уравнение
.
Подставляя разложения для
и 
в условия на профиле, получили (после сноса на 
)
,
,
.
Полагая
и подставляя в условия динамической совместности разложения для 
и 
, получили
,
В результате после сноса условия для 
на характеристику 
имеем
,
,
.
Таким образом, показано, что расщепление стационарной и нестационарной задач сохраняется и на одинаковом уровне точности.
Первое приближение стационарной части задачи хорошо известно
.
Для 
получили задачу, которая уже была рассмотрена ранее в этой работе. Решение задачи для 
искалось в виде суммы 
, где 
- решение неоднородного волнового уравнения с нулевыми граничными условиями
- решение однородного волнового уравнения с ненулевыми граничными условиями
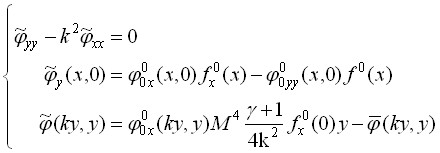
По известной формуле было найдено 
.
,
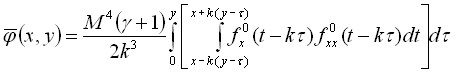где 
.
Решение для 
было получено с помощью общего решения однородного волнового уравнения. Складывая полученные для 
и 
решения и, используя результаты первого приближения, для 
имеем следующее выражение:
.
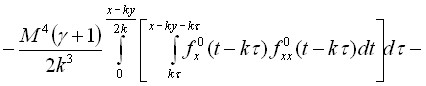
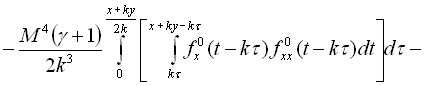
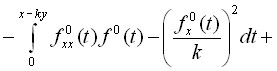
Во второй части работы исследуется форма колебаний гибкого профиля в сверхзвуковом потоке идеального сжимаемого газа. Решается связанная задача аэроупругости. Для постановки задачи вводится модель несущей поверхности и используется модель потока, принятая в первой части.
В качестве модели крыла была рассмотрена тонкая пластина постоянной толщины. И мгновенное положение верхней и нижней поверхности колеблющегося профиля представлено в следующем виде
,
,
где 
малый параметр, определяющий толщину крыла-пластины. Функция, 
определяет форму колебаний профиля крыла-пластины.
Уравнение поперечных колебаний пластины постоянной толщины имеет вид
,
где 
- цилиндрическая жесткость, E, v, - модуль Юнга, коэффициент Пуассона и плотность материала пластины, h - толщина пластины, w(x,t) - прогиб пластины, 
- избыточное давление, возникающее вследствие колебаний профиля.
В наших обозначениях уравнение поперечных колебаний пластины примет следующий вид
,
где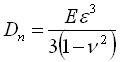 
. Имея крыло со свободными концами, получим следующие граничные условия
при 
, 
.
При малых 
.
Допустим, что 
. Тогда для 
и 
получим соответственно уравнения
,
,
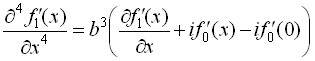где 
.
И граничные условия
при 
, 
,
при 
, 
,
Общее решение уравнения для 
имеет вид
Подставляя общее решение в граничные условия, получим
Дифференциальное уравнение для 
в таком случае примет вид аналогичный уравнению для 
. Решая его так же, как и уравнение для 
, получим
.
В результате было получено следующее решение связанной задачи аэроупругости о колебании крыла в сверхзвуковом потоке сжимаемого газа на малых частотах
.
При больших частотах
.
Из уравнения колебаний пластины получим
. (52)
Здесь 
. Функция 
искалась в виде 
. В первом приближении из уравнения колебаний пластины получено следующее характеристическое уравнение
.
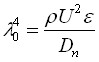Найдя корни которого, можно выписать общее решение
,
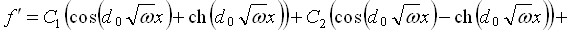
где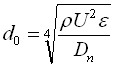 
.
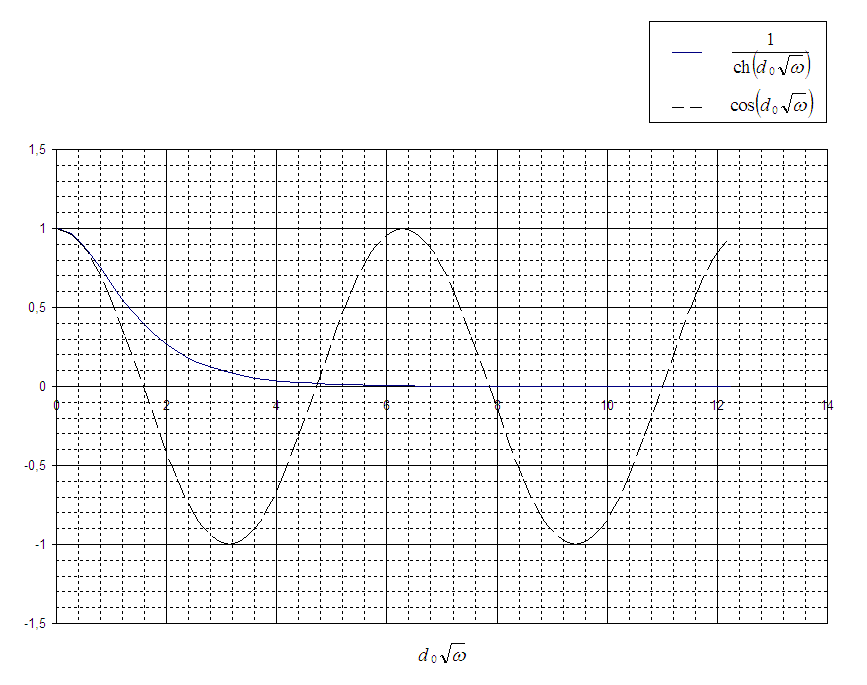
Рисунок 5. Графики функций
и 
.
Из граничных условий в нуле находим, что
. Из условий при 
получим частотное уравнение 
, определяющее частоты, при которых задача может иметь решение. На рисунке 5 точки, соответствующие пересечениям графиков 
и 
являются корнями частотного уравнения. Первые пять значений 
, удовлетворяющих частотному уравнению, будут такими
=0; 4,730; 7, 853; 10,996; 14,137.
В следующем приближении из уравнения колебаний пластины получено
.
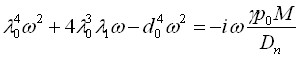Общее решение в этом случае имеет вид:
,
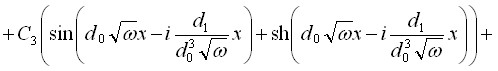
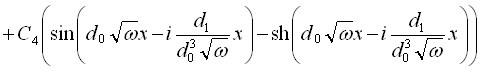где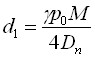 
.
Из граничных условий при 
получим 
. Из условий при 
- уравнение 
.
Так как рассматривается случай при больших 
, то предыдущее уравнение можно записать следующим образом
, 
.
В полученном выражении выделим вещественную и мнимую части
, 
.
, 
.
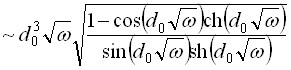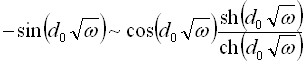Первые три значения 
показаны на рисунке 6.
=0; 2,36; 5,50.
Соответствующие им значения 
будут следующими:
=0; 2,67
; 5,47
.
Таким образом, при заданном параметре 
можно определить частоты, при которых возникают колебания определенной формы. Кроме того, появляется условие для определения параметра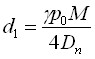 
.
Рисунок 6. Графики функций 
и 
.
Заключение. В работе рассмотрена задача о колебании крыла в сверхзвуковом потоке газа. В первой части исследуется аэродинамика колебаний крыла. Показано как методом Римана, не прибегая к общему решению, может быть найдено решение на профиле крыла, поскольку для решения связанной аэроупругой задачи будет достаточно этого решения. Внутри потока, между характеристикой и профилем решение найдено, используя общее решение телеграфного уравнения. Показана также возможность расщепления стационарной и нестационарной частей задачи на одном уровне точности. Для стационарной задачи во втором приближении было получено неоднородное волновое уравнение с ненулевыми граничными условиями и найдено его аналитическое решение. С помощью интеграла Лагранжа найдено аэродинамическое давление и его асимптотика на профиле крыла при малых и больших частотах.
Во второй части работы рассмотрена связанная аэроупругая задача о колебании крыла в сверхзвуковом потоке газа. Для постановки задачи вводится модель несущей поверхности такая же как в и используется модель потока, принятая в первой части. Опираясь на результаты первой части работы, из системы уравнений связанной аэроупругой задачи получено интегродифференциальное уравнение и его асимптотическое решение на малых и больших частотах. Оказалось, что на малых частотах функция, характеризующая форму колебаний, не зависит от упругих свойств крыла. При больших частотах появились частотные уравнения, определяющие частоты, при которых существует ненулевое решение задачи.
СПИСОК ОПУБЛИКОВАННЫХ РАБОТ ПО ТЕМЕ ДИССЕРТАЦИИ
- Арсентьев Т.П., Баранцев Р. Г. Колебания крыла в сверхзвуковом потоке газа // Международн. конфер. «Пятые Окуневские чтения». 26-30 июня 2006 г., Санкт-Петербург: Тезисы докладов / БГТУ - СПб, 2006. с.36.
- Арсентьев Т.П., Баранцев Р. Г. Решение задачи о колебании крыла в сверхзвуковом потоке газа // XXI Всероссийская конференции по аналитическим методам в газовой динамике «САМГАД-2006». 5-10 июля 2006 г., Санкт-Петербург, Тезисы докладов с.12.
- Арсентьев Т.П., Баранцев Р. Г. Решение задачи о колебании крыла в сверхзвуковом потоке газа. // Дальневосточный Математический Журнал. Том 7. № 1-2. Владивосток Дальнаука 2007. с.30-34.
- Арсентьев Т.П., Баранцев Р. Г. Колебания крыла в сверхзвуковом потоке газа. // Международн. конфер. «Пятые Окуневские Чтения». 26-30 июня 2006 г., Санкт-Петербург: Материалы докладов Том II СПб.: БГТУ, 2007. с.26-31.
- Арсентьев Т. П. Колебания крыла в сверхзвуковом потоке газа // Вестник Санкт-Петербургского Университета, Сер 1, вып. 4, 2007. с.100-107.
- Арсентьев Т.П., Баранцев Р. Г. Аэродинамика колебаний крыла в сверхзвуковом потоке газа. // Всероссийский семинар по аэрогидродинамике, посвященный 90-летию со дня рождения Сергея Васильевича Валландера. 5-7 февраля 2008 г., Санкт-Петербург: Тезисы докладов СПб.: Санкт-Петербургский Государственный Университет, 2008 с.96.
- Арсентьев Т.П., Асимптотика колебаний упругого крыла в сверхзвуковом потоке на малых и больших частотах. // Международн. конфер. «Шестые Окуневские Чтения». 23-27 июня 2008 г., Санкт-Петербург: Материалы докладов Том I СПб.: БГТУ, 2008. с.26-30.
- Arsent’ev Т. P., Barantsev R. G. The account of second terms in steady solution of the wing oscillation problem in supersonic gas flow. // 6th European Nonlinear Dynamics Conference, june30-july4, 2008, Saint-Petersburg, Russia. http://lib.physcon.ru/?item=1534
