О расчете полей температур и скоростей двухкомпонентной среды при термическом расширении графита
На правах рукописи
Бахтин Кирилл Геннадьевич
О РАСЧЕТЕ ПОЛЕЙ ТЕМПЕРАТУР И СКОРОСТЕЙ
ДВУХКОМПОНЕНТНОЙ СРЕДЫ ПРИ ТЕРМИЧЕСКОМ
РАСШИРЕНИИ ГРАФИТА
Специальность 01.02.05 – Механика жидкости, газа и плазмы
Автореферат
диссертации на соискание ученой степени
кандидата физико-математических наук
Саратов – 2006
Работа выполнена на кафедре «Высшая математика и механика» Энгельсского технологического института (филиал) Саратовского государственного технического университета
Научный руководитель:
доктор физико-математических наук,
профессор Ольшанский Владимир Юрьевич
Официальные оппоненты:
доктор технических наук,
профессор Есин Александр Иванович
кандидат физико-математических наук,
доцент Шевырёв Сергей Павлович
Ведущая организация:
Ульяновский государственный технический университет
Защита состоится 21 декабря 2006 г. в 17 ч. 30 мин. на заседании диссертационного совета К 212.243.02 при Саратовском государственном университете по адресу: 410012, Саратов, ул. Астраханская, 83, IX корпус, ауд. 218.
С диссертацией можно ознакомиться в Зональной библиотеке Саратовского государственного университета им. Н.Г. Чернышевского.
Автореферат разослан «___»____________ 2006 г.
Ученый секретарь диссертационного совета
кандидат физико-математических наук,
доцент ___________ В.В.Корнев
ОБЩАЯ ХАРАКТЕРИСТИКА РАБОТЫ
Актуальность темы. Изделия из терморасширенного графита (ТРГ) за последнее десятилетие приобрели большую популярность в различных отраслях промышленности, в первую очередь, как уплотнительный материал для оборудования, работающего в условиях высоких температур и агрессивных коррозийных сред. Терморасширенный графит (другие названия: пенографит, терморасщепленный графит) также используют как теплоизоляционный и огнезащитный материал. Производством окисленного графита (ОГ) и ТРГ, а также материалов на их основе занимается ряд фирм и организаций. Ведущую роль в нашей стране в данной отрасли занимает ЗАО «Унихимтек» (г. Москва).
С помощью достаточно нового метода терморасширения интеркалированного (окисленного) графита в газопроницаемой пресс-форме с заданными размерами (химическое прессование) можно получать изделия заранее определенной формы с регулируемой плотностью. Важным при разработке технологии изготовления изделий с заданными свойствами и формой является моделирование процесса и определение его основных характеристик.
Механизм терморасширения, а также теплофизические свойства пенографита изучены достаточно мало. Одна одномерная модель вспенивания в свободном объеме огнезащитного покрытия рассмотрена в [5]. В ней не рассматривается движение вещества и постоянны теплофизические параметры. Актуальным является создание математической модели процесса вспенивания графита в ограниченном объеме, когда процесс образования ТРГ представляется как фазовый переход с учетом движения графита [6].
Задачи теплопереноса с подвижными границами, вызванными изменением агрегатного состояния вещества, получили название задач типа Стефана [4,7]. Этот класс задач относится к одним из наиболее сложных задач математической физики. Классический вариант задачи Стефана, сформулированный для фазовых переходов типа плавление–кристаллизация, сводится к уравнению теплопроводности в области с заранее неизвестной границей, разделяющей твердую и жидкую фазы и имеющей температуру, равную температуре фазового превращения. Нелинейность задачи обусловлена наличием подвижной границы раздела фаз.
Существует небольшое число аналитических решений подобных задач, ограничивающихся простейшими случаями. Наибольшее развитие получили численные методы решения, значительный вклад в разработку которых внесли в разное время А.А. Самарский [9], Б.М. Будак [1,2], П.Н. Вабищевич [3]. К особенностям математической постановки задачи терморасширения ОГ относится отличие на порядок теплофизических параметров фаз графита и необходимость учета конвективных членов. Для эффективного применения математической модели и оценки влияния конвективных членов в этом случае актуальным является разработка модификаций существующих численных методов.
Целью работы является построение математической модели процесса химического прессования окисленного графита, разработка методов расчета характеристик процесса. Для достижения поставленной цели необходимо решить следующие задачи:
- построение математической модели процесса терморасширения окисленного графита;
- разработка методов расчета характеристик процесса при существенном различии теплофизических параметров агрегатных состояний графита;
- разработка модификации численных методов для решения задачи типа Стефана.
Методы исследования. Основные результаты работы получены на основе идей и подходов кинетической теории и механики сплошной среды для описания движущихся сред при учете фазовых переходов и тепловых воздействий. При построении модели процесса с учетом конвективного тепломассопереноса используются классические уравнения гидромеханики вязкой жидкости. Для решения возникающих задач используется конечно-разностный метод сквозного счета со сглаживанием теплофизических параметров в окрестности подвижной границы раздела фаз.
Научная новизна работы заключается в следующем:
- построена математическая модель процесса химического прессования с учетом движения графита;
- показана возможность замены в построенной модели стенок пресс-формы некоторым граничным условием третьего рода;
- разработан алгоритм совместного решения задач определения полей температур и скоростей движения частиц среды;
- осуществлена оценка влияния конвективных членов на процесс теплопередачи;
- создана программа численного определения полей температур и скоростей.
Достоверность полученных результатов обеспечивается корректностью и строгостью применяемых математических методов, проверкой используемых численных методов на тестовых задачах, имеющих точное аналитическое решение, соответствием основных теоретических результатов и выводов экспериментальным данным и общефизическим представлениям о характере процесса получения терморасширенного графита.
На защиту выносятся следующие результаты и положения:
- процесс вспенивания порошка окисленного графита в ограниченном объеме представлен как тепломассоперенос с фазовым превращением;
- разработана модификация метода сквозного счета для определения параметров вспенивания в технологической форме;
- разработан численный алгоритм определения полей температуры и скоростей вещества и движения границы раздела фаз;
- в численном эксперименте показана необходимость учета в построенной модели конвективных членов.
Практическая и теоретическая ценность. Результаты предложенной работы вносят вклад в теорию гидромеханических задач тепломассопереноса с фазовыми превращениями и могут быть использованы в дальнейших исследованиях по применению методов сквозного счета для численного решения задач типа Стефана. Результаты можно использовать в учебном процессе при чтении спецкурсов и при разработке технологий производства материалов из терморасширенного графита.
Апробация результатов диссертации. Основные результаты диссертации докладывались на семинаре кафедры «Высшая математика и механика» ЭТИ СГТУ (2003 – 2006 гг.), на конференциях «Актуальные проблемы математики и механики» механико-математического факультета СГУ (2004 – 2006 гг.), на VII Международной научно-технической конференции «Динамика технологических систем» (Саратов, 2004 г.), на III и IV Международных конференциях «Континуальные алгебраические логики, исчисления и нейроинформатика в науке и технике» (Ульяновск, 2005 – 2006 гг.), на Международной конференции «Проблемы и перспективы прецизионной механики и управления в машиностроении» (Саратов, 2006 г.).
Публикации. Основные положения диссертации отражены в 8 работах, в том числе в одной статье в журнале «Вестник СГТУ», включенном в перечень ведущих рецензируемых журналов и научных изданий, утвержденный президиумом ВАК.
Структура и объем диссертации. Диссертационная работа изложена на 96 страницах машинописного текста и состоит из введения, трех глав, заключения, списка литературы, содержит 15 рисунков и 2 фотографии. Библиографический список состоит из 61 наименования работ отечественных и зарубежных авторов.
КРАТКОЕ СОДЕРЖАНИЕ РАБОТЫ
Во Введении дается обоснование актуальности темы, сформулированы цель и направления исследования, приводятся необходимые определения, методы, кратко излагается содержание работы и основные результаты, выносимые на защиту.
В главе 1 описана физическая модель процесса терморасширения окисленного графита в ограниченном объеме (метод химического прессования). При определенных допущениях сформулирована математическая модель рассматриваемого процесса. Описан метод решения возникающей задачи с подвижной границей раздела фаз и решены некоторые тестовые задачи. Результаты этой главы служат необходимым базисом при постановке и последующем решении двумерной задачи определения поля температур и скоростей движения графита при его терморасширении.
В параграфе 1.1 приводится описание процесса вспенивания окисленного графита в замкнутом объеме.
В параграфе 1.2 построена математическая модель теплофизического процесса вспенивания графита в одномерном случае. В модели не учитывается наличие стенок пресс-формы, в которую на практике помещают порошок ОГ. В каждой из двух областей 
(ОГ) или 
(ТРГ) справедливо однородное уравнение теплопроводности без учета конвективных членов, характеризующих теплоперенос вследствие движения частиц ОГ/ТРГ. Дополнительно для нестационарного процесса теплопередачи задаются начальное и граничные условия, а также условия Стефана, выражающие постоянство температуры на межфазной границе и изменение величины теплового потока при переходе через нее с учетом количества тепла, затрачиваемого на фазовый переход.
В параграфе 1.3 проводится анализ существующих методов решения задач типа Стефана. Основное внимание уделено численным методам. Существующие методы численного решения данного класса задач можно условно разделить на две группы: с явным выделением подвижной границы и сквозного счета. Методы, основанные на явном выделении фронта (метод выпрямления фронтов, ловли фронта в узел сетки и др.), обладают высокой точностью определения межфазной границы, но, как правило, чрезвычайно громоздки алгоритмически и для получения решения многомерных задач требуют значительных вычислительных затрат. По этим причинам они зачастую неприменимы для многомерных задач. Методы сквозного счета основаны на принципиально ином подходе. Их идея состоит в отказе от непосредственного поиска неизвестной межфазной границы и замене его процедурой сглаживания («размазывания» по температуре) теплофизических параметров.
Метод сглаживания имеет преимущество перед остальными методами, поскольку не зависит от размерности задачи и числа фаз. Сама задача рассматривается в обобщенной формулировке в виде одного нелинейного параболического уравнения, записанного в едином для всей области 
виде:
(1)
Дополнительно заданы краевые условия:
(2)
, (3)
где u – температура, 
– температура фазового перехода; 
– удельная теплоемкость, плотность и коэффициент теплопроводности среды соответственно; 
– удельное количество тепла, затрачиваемое на переход ОГ – ТРГ (аналог скрытой теплоты плавления в задаче плавления-кристаллизации); 
- дельта-функция Дирака, Г – граница области 
.
Можно показать, что из уравнения (1) следуют условия Стефана на межфазной границе 
:
(4)
, (5)
где 
– скорость движения границы 
. Величины, относящиеся к области 
(ОГ), где 
, обозначаем индексом 1, к области 
(ТРГ), где 
, – индексом 2. Сама граница 
при необходимости определяется как изотерма
.
В параграфе 1.4 описано численное решение задачи (1)-(3) с помощью метода сквозного счета. Согласно ему, для перехода к разностной схеме входящая в уравнение (1) дельта-функция на некотором интервале температур 
заменяется приближенно дельтаобразной, или размазанной, дельта-функцией. Также вводится сглаженная, или эффективная, удельная теплоемкость. Например, если 
и 
не зависят от u, то на интервале сглаживания можно взять 
. После такой замены никаких особых элементов в условии задачи уже нет и можно строить консервативную конечно-разностную схему, например, при помощи интегроинтерполяционного метода. В работе использовалась чисто неявная схема, которая является абсолютно устойчивой. Получающаяся после дискретизации нелинейная система алгебраических уравнений решается итерационно с применением на каждой итерации формул прогонки.
Из-за отличия на порядок коэффициентов теплопроводности для ОГ и ТРГ удобным является сведение исходной задачи к поиску новой функции 
, которая является преобразованием Кирхгофа от 
.
Для проверки применимости численного метода решена задача, имеющая точное аналитическое решение, когда закон движения границы имеет вид 
. При расчетах начальное и граничные условия брались совпадающими с точными. Показано, что лучшее совпадение результатов с точным решением удается получить для функции 
.
В параграфе 1.5 задача отыскания поля температур и межфазной границы формулируется уже для многокомпонентной области, состоящей, кроме ОГ/ТРГ, из металлических пластин – стенок пресс-формы. В этом случае обычным образом ввести функцию 
нельзя, т.к. коэффициент теплопроводности является функцией координаты. С целью возможности применения метод сквозного счета модифицируется путем введения новой независимой переменной 
. В результате задача сводится к решению уравнения
, (6)
где
,
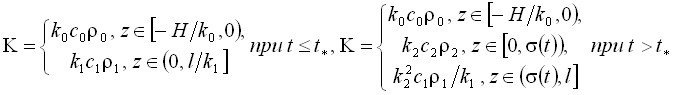с соответствующими краевыми условиями и условием на границе 
.
Индексом 0 отмечены параметры пластины, 
– время достижения температуры фазового перехода на поверхности контакта пластины с областью ОГ. Исходная область 
, где H – толщина стенки формы.
Непрерывному решению уравнения (6) с непрерывной производной по z соответствует непрерывное решение исходной задачи с непрерывным тепловым потоком 
на поверхности контакта пластины с ОГ/ТРГ.
В такой формулировке решена тестовая задача, имеющая точное решение. Результаты численного эксперимента хорошо согласуются с аналитическим решением.
Далее показано, что учесть тонкую пластину можно, задав на поверхности контакта пластины с графитом граничное условие третьего рода
, (7)
где 
– заданная температура внешнего нагрева. Для этого при нескольких значениях толщины стенки формы при одних и тех же входных параметрах
Рис. 1. Сравнение результатов
- при учете пластины,
+ - при замене пластины условием (7),
1: 
, 2: 
,
3: 
, 4: 
решены задачи с учетом пластины и с заменой ее условием (7). На рис. 1 показано сравнение результатов. Получено, что при достаточно тонкой пластине ее можно приближено учесть этим граничным условием. В итоге указана возможность упростить решение, исключив в дальнейшем из рассмотрения стенки пресс-форм и решая ее как задачу типа Стефана методом сквозного счета только в области, занимаемой веществом.
Глава 2 посвящена моделированию процесса вспенивания порошка графита в двумерном случае и численному решению соответствующей задачи типа Стефана также и при учете полей скоростей движения ОГ/ТРГ как сплошной среды.
В параграфе 2.1 описана модель процесса химического прессования ОГ в двумерной области. Приведены определяющие уравнения модели, а также показано, как учитывается скрытая теплота фазового перехода при учете конвективных членов. Обобщенное нелинейное уравнение теплопроводности в данном случае имеет вид:
. (8)
Из него следует условие для теплового потока на границе
,
где 
– нормальная составляющая (по отношению к границе 
) скорости вещества.
В параграфе 2.2 описан алгоритм численного решения поставленной задачи методом сквозного счета. Аппроксимация исходной дифференциальной задачи произведена с помощью локально-одномерной конечно-разностной схемы [8]:
(9)
, 
, (10)
(11)
, 
, (12)
при 
. (13)
Используются следующие обозначения:
, 
,
– шаги сетки по x и y, 
.
Значения коэффициентов 
определяются из соответствующих роду граничных условий формул. Причем они могут быть функциями координат и времени.
Суть схемы состоит в поэтапном решении сначала по одной пространственной переменной, а затем по другой одномерных уравнений теплопроводности при помощи безусловно устойчивых неявных схем.
Выбор схемы с переменным шагом по времени обусловлен трудностью расчетов при первоначальном формировании фазового фронта у внешних границ исходной области, что требует более мелкого шага.
По данной схеме решены две тестовые задачи, имеющие точное решение при определенных допущениях на условия задачи. Для первой задачи граница раздела фаз имеет вид косого фронта, для второй – вид окружности. Основное допущение состояло в принятии конвективных членов равными нулю. Результаты численного эксперимента показывают, что полученные значения поля температур и межфазной границы с приемлемой точностью согласуются с имеющимся точными значениями. Это свидетельствует, что метод вполне пригоден для практических целей при условии значительной разницы теплофизических параметров в различных фазах графита.
При моделировании вспенивания ОГ открытым остается вопрос более точного определения поля скоростей ОГ/ТРГ при терморасширении. Точно его задать практически не представляется возможным, поскольку сам процесс вспенивания еще недостаточно изучен. В параграфе 2.3 выполнена приближенная оценка влияния движения вещества на процесс теплопереноса. Рассмотрена упрощенная модель, в которой предполагается равномерное расширение ТРГ от внешних границ исходной прямоугольной области к центру области.
Из уравнения неразрывности, выражающем условие сохранения баланса массы, можно определить зависимость плотности вещества каждой из фаз от площади, занимаемой ОГ или ТРГ. Формулы для компонентов вектора скорости частиц среды задаются априорно.
Результаты численного эксперимента показывают, что абсолютные значения конвективных членов в уравнении теплопроводности (8) и скорость изменения температуры в узлах расчетной сетки являются величинами одного порядка. Поэтому важной является задача более точного определения поля скоростей движения ОГ/ТРГ при дальнейшем моделировании процесса терморасширения ОГ.
В главе 3 проведен более точный учет движения графита при терморасширении. Краевая задача для нахождения поля температур остается прежней при условии, что при решении поле скоростей может быть достаточно точно вычислено в любой момент времени. Этого можно добиться, если одновременно с отысканием распределения температуры находить скорости вещества. С этой целью за основу приняты уравнения гидромеханики вязкой жидкости. В параграфе 3.1 ставится задача определения поля скоростей графита. Используем уравнения Навье-Стокса для данной модели
.
Положим, что инерционные члены и массовые силы мало существенны. Такое упрощение можно сделать, поскольку скорости движения частиц графита малы и между частицами происходит значительное трение. Из этих уравнений и уравнения неразрывности получим, что после возникновения подвижной границы функции 
в каждый момент времени в каждой из областей 
должны удовлетворять следующей системе уравнений:
, (14)
где 
– давление, 
– вязкость.
Дополнительно имеет место уравнение неразрывности
(15)
и условие на внешней границе области
. (16)
Предполагая линейную зависимость плотности ТРГ от площади, которую он занимает, из условия сохранения массы вещества можно получить согласованные между собой законы изменения плотностей. Считаем, что в областях 
плотность есть функция только времени 
при 
.
Выполнив перекрестное дифференцирование в (14) для определения 
совместно с (15) и (16) получим уравнение
. (17)
С вычислительной точки зрения вместо функции 
удобно находить потенциал скоростей 
. Тогда для потенциальной функции 
уравнение (17) выполнено тождественно, и для определения потенциала 
при данном значении t нужно решить следующую упрощенную задачу:
, (18)
. (19)
В параграфе 3.2 обсуждается способ задания разности плотности графита за малый промежуток времени, в течение которого найдутся точки области, в которых изменится фазовое состояние графита. Такое рассмотрение необходимо для корректного решения задачи Неймана (18), (19), поскольку при задании плотности обособленно необходимо выполнение условия сохранения массы.
В параграфе 3.3 приводится разностная схема решения задачи Неймана, которая учитывает способ задания плотности, описанный в параграфе 3.2. Для приведенной схемы разностный аналог условия сохранения массы выполнен.
В параграф 3.4 описан метод решения разностной задачи для потенциала скоростей. За основу принят алгоритм матричной прогонки. Чтобы получить единственное частное решение задачи Неймана (18), (19), значение потенциала предварительно задается в некотором узле сетки.
Алгоритм совместного численного решения краевой задачи определения температуры и скорости приведен в параграфе 3.5. Используются описанные в предыдущих параграфах схемы численного счета. Решение на новом слое уточняется итерационно.
В параграфе 3.6 построена модель терморасширения графита в двумерном осесимметричном случае при учете влияния на теплоперенос движения частиц среды. Определяющие уравнения записаны в цилиндрических координатах. Приведены необходимы разностные схемы для решения задачи Стефана и Неймана и выполнены численные расчеты.
а)
б)
в)
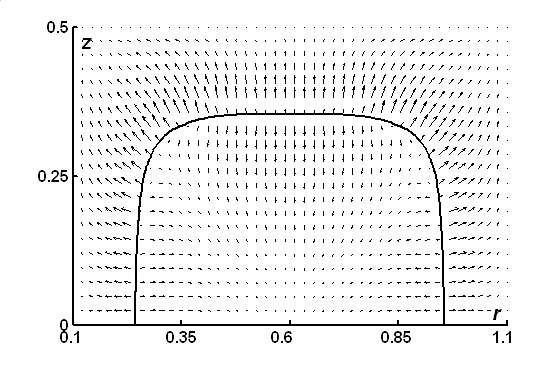
Рис. 2. История межфазной границы и поле скоростей для моментов времени
а) 
, б) 
, в) 
На рис. 2 жирным показаны кривые, соответствующие положению границы раздела компонентов вещества в области 
, полученные в результате численного решения задачи, а также поля скоростей графита. Моментам времени 
соответствуют рисунки а), б) и в) соответственно. Расчеты показывают, что абсолютные значения конвективных членов в уравнении теплопроводности (8) и скорость изменения температуры, являются величинами одного порядка. В связи с этим при моделировании процесса терморасширения ОГ необходимо учитывать движение самого вещества. Из рисунка видно, что, хотя область ТРГ равномерно расширяется, поле скоростей в этой области направлено в противоположную сторону движения межфазной границы. Это объясняется тем, что в выбранной модели процесса плотность в области 
меньше плотности ОГ в области 
.
ОСНОВНЫЕ ВЫВОДЫ ДИССЕРТАЦИИ
- Построена математическая модель процесса терморасширения окисленного графита в ограниченном объеме (метод химического прессования). Основой модели является краевая задача для уравнения теплопроводности с условием типа Стефана на подвижной межфазной границе. Модель учитывает движение фаз окисленного графита и терморасширенного графита в виде конвективных членов в уравнении теплопроводности.
- Для решения возникающих задач разработана модификация численного метода сквозного счета со сглаживанием теплофизических параметров. В частности, показано, что учесть влияние стенок на процесс теплопередачи можно заданием некоторого граничного условия третьего рода.
- Построенный алгоритм определения нестационарных полей температур и скоростей и закона движения границы раздела фаз позволил выполнить анализ зависимости основных характеристик процесса от значений теплофизических параметров.
СПИСОК ПУБЛИКАЦИЙ ПО ТЕМЕ ДИССЕРТАЦИИ
1. К.Г. Бахтин, В.Ю. Ольшанский, А.В. Серебряков. Метод сглаживания в задаче расчета терморасщепления графита // Математика. Механика. Сб. научн. тр. Саратов: Изд-во Сарат. ун-та, 2004.– Вып. 6.– С. 162-165.
2. Ольшанский В.Ю., Серебряков А.В., Бахтин К.Г. Метод сквозного счета в задаче нагрева многослойной среды с подвижными внутренними границами // Проблемы прочности элементов конструкций под действием нагрузок и рабочих сред. Межвуз. науч. сб. Саратов: Изд-во Сарат. гос. тех. ун-та, 2004.– С. 87-91.
3. Ольшанский В.Ю., Серебряков А.В., Бахтин К.Г. Метод сглаживания при моделировании термического расщепления графита в ограниченном объеме // Сб. тр. VII Межд. научно-техн. конф «Динамика технологических систем 2004». Саратов: Изд-во Сарат. гос. тех. ун-та, 2004. – С. 286-290.
4. Бахтин К.Г., Ольшанский В.Ю. О влиянии конвективных членов на процесс терморасщепления графита // Математические модели и методы в прикладных задачах науки и техники. Сб. тр. межд. конф. «Континуальные алгебраические логики, исчисления и нейроинформатика в науке и технике». Ульяновск, 2005: Изд-во Ульяновск. гос. тех. ун-та, 2005. – С. 19-23.
5. Бахтин К.Г., Ольшанский В.Ю. Оценка конвективных членов в одной модели терморасщепления графита // Математика. Механика. Сб. научн. тр. Саратов: Изд-во Сарат. ун-та, 2005. – С. 155-158.
6. Бахтин К.Г., Ольшанский В.Ю. Расчет полей температур и скоростей двухкомпонентной среды в процессе термического расширения графита // Математические модели и методы в прикладных задачах науки и техники. Сб. тр. межд. конф. «Континуальные алгебраические логики, исчисления и нейроинформатика в науке и технике». Ульяновск, 2006: Изд-во Ульяновск. гос. тех. ун-та. 2006. – С. 29-33.
7. Бахтин К.Г., Ольшанский В.Ю. Расчет движения границы раздела в задаче терморасширения графита при учете конвективных членов // Вестник СГТУ: Изд-во Сарат. гос. тех. ун-та, 2006. – №. 3(15). Вып. 2. – С. 7-12 (журнал включен в перечень ведущих рецензируемых журналов и научных изданий, утвержденный президиумом ВАК).
8. Бахтин К.Г., Ольшанский В.Ю. Программа «Метод сквозного счета» // Регистрация программы в фонде ОФАП Госкоорцентра РФ, №50200601944, 10 ноября 2006 г.
Личный вклад Бахтина К.Г. в выполненных в соавторстве перечисленных работах состоит в следующем:
- Бахтин К.Г., Ольшанский В.Ю., Серебряков А.В. «Метод сглаживания в задаче расчета терморасщепления графита» – в численном эксперименте показана эффективность перехода к переменной Кирхгофа в одномерной задаче Стефана при нагреве пакета, подобраны параметры сглаживания, выполнен переход к новым пространственным переменным.
- Ольшанский В.Ю., Серебряков А.В., Бахтин К.Г. «Метод сквозного счета в задаче нагрева многослойной среды с подвижными внутренними границами» – в численном эксперименте показана возможность замены внешних слоев из тонких металлических пластин соответствующими условиями третьего рода.
- Ольшанский В.Ю., Серебряков А.В., Бахтин К.Г. «Метод сглаживания при моделировании термического расщепления графита в ограниченном объеме» – построено точное решение задачи Стефана для многослойного пакета и проведена оценка погрешности метода сквозного счета путем сравнения закона движения границы с данным решением.
- Бахтин К.Г., Ольшанский В.Ю. «О влиянии конвективных членов на процесс терморасщепления графита» – построена разностная аппроксимация двумерной задачи распространения тепла в двухфазной среде при заданной внешней температуре, введены упрощающие предположения о поле скоростей и оценено влияние конвективных членов на скорость движения границы раздела фаз.
- Бахтин К.Г., Ольшанский В.Ю. «Оценка конвективных членов в одной модели терморасщепления графита» – построена разностная аппроксимация при заданных условиях третьего рода на внешней границе, при дополнительных допущениях о поле скоростей выполнена оценка вклада конвективных членов.
- Бахтин К.Г., Ольшанский В.Ю. «Расчет полей температур и скоростей двухкомпонентной среды в процессе термического расширения графита» – построена разностная аппроксимация задачи, определена скорость движения границы раздела фаз для различных теплофизических параметров.
- Бахтин К.Г., Ольшанский В.Ю. «Расчет движения границы раздела в задаче терморасширения графита при учете конвективных членов» – построена разностная аппроксимация задачи совместного определения поля температур и скоростей, реализован алгоритм матричной прогонки, выполнен анализ характеристик процесса.
- Бахтин К.Г., Ольшанский В.Ю. «Метод сквозного счета» – разработан алгоритм реализации метода сквозного счета при совместном решении задачи распространения тепла и определения поля скоростей в двумерной двухфазной задаче Стефана.
СПИСОК ЛИТЕРАТУРЫ
[1]. Будак Б.М., Гольдман Н.Л., Егорова А.Т., Успенский А.Б. Метод выпрямления фронтов для решения задач типа Стефана в многомерном случае // Вычислительные методы и программирование. М.:МГУ, 1967. – Вып. 8. – С. 103-120.
[2]. Будак Б.М., Соловьева Е.Н., Успенский А.Б. Разностный метод со сглаживанием коэффициентов для решения задачи Стефана // Журнал вычислительной математики и математической физики. – 1965. – Т.5, № 5. – С. 828-840.
[3]. Вабищевич П.Н. Численные методы решения задач со свободной границей. – М.: Изд-во Моск. ун-та, 1987. – 164 с.
[4]. Мейрманов А.М. Задача Стефана. Новосибирск: Наука СО АН СССР, 1986. – 239 с.
[5]. Жеребятьев И.Ф., Лукьянов А.Т. Математическое моделирование процессов тепло- и массообмена с подвижными границами. Алма-Ата.: Гылым, 1992. – 264 c.
[6]. Ольшанский В.Ю. Математическое моделирование процесса терморасширения графита с учетом фазовых переходов // IX Всероссийский съезд по теоретической и прикладной механике. Сб. аннотац. докладов. Н.-Новгород, 23-28 августа 2006г.: Н.Новгород, 2006.
[7]. Рубинштейн Л.И. Проблема Стефана. Рига: Звайзгне, 1967. - 457 с.
[8]. Самарский А.А., Вабищевич П.Н. Аддитивные схемы для задач математической физики. – М.: Наука, 2001. – 319 с.
[9]. Самарский А.А., Моисеенко Б.Д. Экономичная схема сквозного счета для многомерной задачи Стефана // Журнал вычислительной математики и математической физики. – 1965. – Т.5, № 5. – С. 816-827.
