Исследование свойств волн возмущения и капиллярной ряби в дисперсно-кольцевом течении.
На правах рукописи
Черданцев Андрей Викторович
ИССЛЕДОВАНИЕ СВОЙСТВ ВОЛН ВОЗМУЩЕНИЯ И КАПИЛЛЯРНОЙ РЯБИ В ДИСПЕРСНО-КОЛЬЦЕВОМ ТЕЧЕНИИ.
01.02.05 - механика жидкости, газа и плазмы
АВТОРЕФЕРАТ
диссертации на соискание ученой степени
кандидата физико-математических наук
Новосибирск - 2006
Работа выполнена в Институте теплофизики им. С.С. Кутателадзе Сибирского отделения Российской академии наук (г. Новосибирск)
Научный руководитель: доктор физико-математических наук,
ст. н.с. Маркович Дмитрий Маркович
Официальные оппоненты: доктор физико-математических наук, профессор Цвелодуб Олег Юрьевич
кандидат физико-математических наук,
Ерманюк Евгений Валерьевич
Ведущая организация: Институт проблем безопасного развития атомной энергетики РАН, г. Москва
Защита состоится 27 декабря 2006 г. в 9 30, на заседании диссертационного совета Д 003.053.01 при Институте Теплофизики Сибирского отделения РАН по адресу: 630090, г. Новосибирск, пр. Лаврентьева, 1.
С диссертацией можно ознакомиться в библиотеке ИТ СО РАН.
Автореферат разослан ____ __________ 2006 г.
Ученый секретарь
диссертационного совета, д.ф.-м.н. Кузнецов В.В.
Актуальность проблемы.
Дисперсно-кольцевое течение представляет собой совместное течение пленки жидкости, высокоскоростного потока газа и дисперсной фазы – капель, уносимых с поверхности пленки в ядро газового потока и осаждающихся обратно. Течение такого типа реализуется в широком спектре промышленных установок: в тепловых трактах АЭС, очистных пленочных аппаратах, химической промышленности.
В настоящее время реализованы лишь достаточно грубые приближения к математическому описанию дисперсно-кольцевого течения. Это связано, прежде всего, со сложной гидродинамической структурой таких потоков. Интенсивный газовый поток взаимодействует с пленкой через турбулентные касательные напряжения на межфазной границе и содержит дисперсную фазу в виде капель с широким спектром размеров. Поверхность пленки в таких течениях имеет сложную структуру волн, разделяющихся на капиллярную рябь и волны возмущения, амплитуда которых в несколько раз превосходит толщину остаточного слоя. Структура дисперсной фазы определяется непрерывными процессами слияния капель и разбиения на более мелкие капли, а также массообменом с пленкой.
Существуют модели, позволяющие выполнить расчет осаждения капель в строгой постановке и дающие удовлетворительное согласие с экспериментальными данными (Алипченков, Зайчик и др. 2001). Для описания срыва и уноса капель с поверхности пленки в ядро потока газа в настоящее время моделирование проводится только в рамках полуэмпирических подходов. При этом, в силу сложности явления, работы по экспериментальному исследованию срыва капель носят единичный характер, и полученных экспериментальных данных не достаточно. Экспериментально установлено, что наличие уноса всегда сопровождается наличием на поверхности пленки волн возмущения, и все предлагаемые исследователями гипотезы, описывающие механизм уноса, так или иначе связаны с этими волнами. Однако число моделей для описания уноса, опирающихся на характеристики волн, невелико из-за недостаточной теоретической и экспериментальной изученности волновой динамики.
Теоретические модели, описывающие волны на пленке в присутствии потока газа, как правило, рассматривают периодические, слабонелинейные волны при достаточно малых напряжениях со стороны потока газа, и не годятся для прямого сравнения с экспериментом. Большинство экспериментальных работ ограничивается измерением средних характеристик волн возмущения, хотя свойства волн при одних и тех же параметрах течения могут очень сильно различаться. Экспериментальное исследование свойств капиллярной ряби выполнялось при помощи методов, которые, как будет показано в данной работе, малоприменимы для исследования мелкомасштабных волн.
Целью работы является:
- детерминистское исследование свойств волн возмущения;
- исследование свойств волн капиллярной ряби при помощи новых экспериментальных методик.
Научная новизна работы заключается в том, что автором впервые:
- Применен метод условного осреднения для обработки экспериментальных записей локальной толщины пленки жидкости, позволяющий получать зависимости свойств волн возмущения от амплитуды с высокой точностью.
- При помощи этого метода получена зависимость скорости волн возмущения от амплитуды при фиксированных параметрах течения в широком диапазоне амплитуд и предложены соотношения, удовлетворительно описывающие коэффициенты этой зависимости.
- Показано, что расстояние между волнами возмущения не зависит от скорости газа и вязкости жидкости.
- Получены обобщенные портреты волн возмущения, исследовано влияние параметров течения на форму волн возмущения.
- Впервые к исследованию дисперсно-кольцевого течения применен метод флуоресцентной визуализации, при помощи которого показано, что использовавшиеся ранее экспериментальные методы малоприменимы для исследования свойств капиллярной ряби в дисперсно-кольцевом течении.
- Получены новые данные по амплитудным и частотным свойствам ряби, поведению шероховатости пленки с изменением параметров течения и скорости волн ряби.
Достоверность результатов основывается на использовании отработанных на других объектах экспериментальных методик, тщательной проверке калибровочных зависимостей, использовании новых статистических методов обработки данных, стабильной воспроизводимости результатов опытов.
Практическое значение
Полученные автором результаты по влиянию параметров течения на свойства волн возмущения могут быть использованы при построении моделей, описывающих форму и динамику волн возмущения, в частности, для упрощения моделей, возможному благодаря экспериментальным данным об инвариантности отдельных волновых характеристик относительно конкретных параметров течения. Данные по шероховатости покрытой рябью пленки и длине волны ряби могут использоваться для коррекции эмпирических корреляций по касательному трению со стороны газа.
На защиту выносятся
- Экспериментальные результаты по влиянию параметров течения волн на характеристики волн возмущения в зависимости от их амплитуды: формулы, описывающие зависимость скорости волн возмущения от амплитуды; независимость числа волн на единицу длины от скорости газа и вязкости жидкости; универсальность зависимости крутизны волн возмущения от амплитуды для разных скоростей газа.
- Экспериментальные результаты по свойствам капиллярной ряби: полученные зависимости амплитуды, длины, крутизны и скорости волн ряби от параметров течения.
- Метод условного осреднения волновых характеристик для исследования свойств волн возмущения и применение метода флуоресцентной визуализации для исследования дисперсно-кольцевого течения.
Апробация работы
Результаты диссертационной работы докладывались и обсуждались на: V мировой конференции “Experimental Heat Transfer, Fluid Mechanics and Thermodynamics” (Салоники, Греция, 2001); III международной конференции «Transfer Processes in Multiphase Flow» (Кельце, Польша, 2002); III Российской национальной конференции по теплообмену (Москва, Россия, 2002); XXXIX, XL, XLI международных студенческих конфренциях «Студент и научно-технический прогресс» (Новосибирск, Россия, 2001-2003); VII, VIII, IX Всероссийских конференциях молодых ученых «Актуальные вопросы теплофизики и гидрогазодинамики» (Новосибирск, Россия, 2002, 2004, 2006); 16м международном конгрессе «Chemical and process engineering» (Прага, Чехия, 2004); 3м международном симпозиуме “Two-Phase Flow: Modelling and Experimentation” (Пиза, Италия, 2004).
Публикации
Результаты работы опубликованы в 9 печатных работах.
Личное участие автора
Данная работа выполнена в 2000-2006 гг. в лаборатории физических основ энергетических технологий Института теплофизики СО РАН. Постановка задач иследований осуществлена диссертантом совместно с научным руководителем Д.М. Марковичем и С.М. Харламовым. Подготовка экспериментальной установки и проведение экспериментов проводились автором совместно с С.М. Харламовым. В проведении экспериментов по измерению интегральных характеристик потока также участвовали В.А. Антипин и В.В. Гузанов. Обработка и интерпретация экспериментальных материалов проводились автором самостоятельно.
Объем работы
Диссертационная работа состоит из введения, пяти глав, выводов и списка литературы. Работа содержит 95 страниц, включая 43 рисунка. Список литературы состоит из 110 наименований.
СОДЕРЖАНИЕ РАБОТЫ
Во введении описывается актуальность изучения волновой динамики дисперсно-кольцевого течения, формулируются цели исследования.
Первая глава содержит обзор литературы, посвященной исследованию дисперсно-кольцевых течений. В обзоре литературы
рассматриваются
- экспериментальные данные по влиянию параметров течения на интенсивности уноса и осаждения капель, поведению уноса, осаждения и перепада давления с расстоянием от входа в канал.
- режимные карты перехода к уносу и появления волн возмущения,
- гипотезы, предлагаемые в литературе для описания механизма уноса.
- использовавшиеся ранее методики для измерения локальной толщины пленки и статистические подходы к исследованию свойств волн возмущения,
- основные экспериментальные результаты по свойствам волн возмущения, теоретические модели для описания волн возмущения и интенсивности уноса.
- экспериментальные результаты по свойствам капиллярной ряби.
Вторая глава содержит описание экспериментальной установки и методов измерений. Рабочий участок установки (рис. 1) представляет собой вертикальный оргстеклянный цилиндр, по внутренним стенкам которого стекает пленка жидкости. Внутренний диаметр цилиндра – 15 мм, длина – 1 м. Жидкость подается на стенки канала через кольцевой щелевой зазор, газ – через установленную соосно с цилиндром тонкостенную трубу.
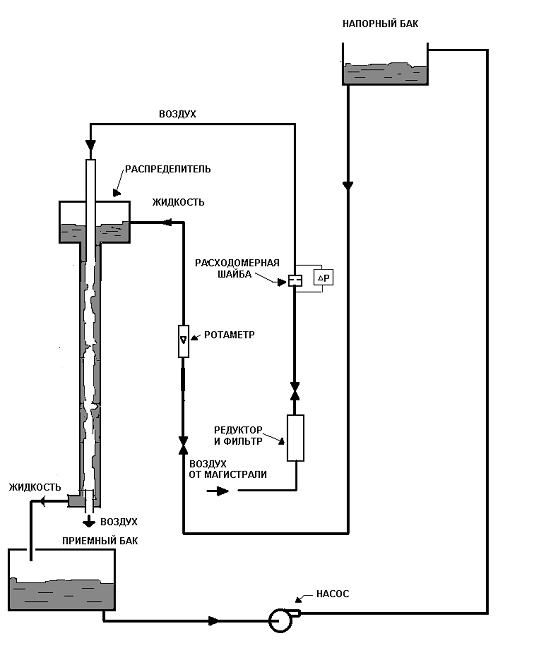 |
| Рисунок 1. Схема экспериментальной установки |
Канал выполнен разборным, что позволяет менять расстояние, на котором располагаются датчики для измерения свойств течения, исследуя, таким образом, изменение этих свойств с расстоянием.
Управляемыми параметрами течения являются:
- входное число Рейнольдса жидкости;
- среднерасходная скорость потока газа;
- свойства рабочей жидкости;
- расстояние от входа в канал, на котором располагаются датчики.
В качестве рабочих жидкостей использовались дистиллированная вода и водоглицериновые растворы с вязкостью в 2 и 3 раза больше вязкости воды. Для определения расхода дисперсной фазы измерялся массовый расход капель жидкости через зонд-пробоотборник, установленный по центру канала. Локальный перепад давления измерялся при помощи дифференциального манометра, через введенные заподлицо в стенку канала патрубки, расстояние между которыми составляло 50 мм (рис. 2).
 | 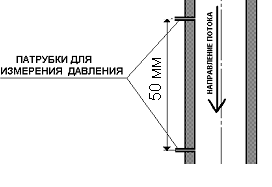 |
| Рисунок 2. Измерение расхода дисперсной фазы и локального перепада давления. | |
 |
| Рисунок 3. Схема датчиков проводимости |
Толщина пленки жидкости измерялась двумя методами, первый из которых – метод локальной электропроводности. Метод основывается на зависимости проводимости электролитической жидкости от толщины слоя. Для измерений использовались датчики проводимости с коаксиальными электродами, вмонтированными заподлицо в стенку канала (рис. 3).
Калибровка датчиков производилась путем измерения проводимости жидкости в зазоре фиксированной толщины, выполненном при помощи специально изготовленных вставок. Погрешность измерения толщины пленки жидкости не превышала 5%.
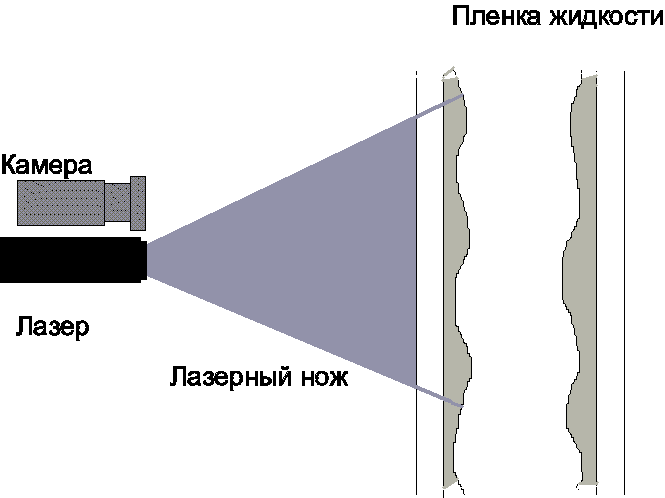 |
| Рисунок 4. Схема метода флуоресцентной визуализации |
Вторым методом измерения локальной толщины пленки, используемым в работе, является метод флуоресцентной визуализации (международное название - «laser induced fluorescence» (LIF)). Принцип метода основан на зависимости интенсивности свечения растворенного в жидкости флуоресцентного вещества от толщины пленки.
Для проведения измерений рабочий канал освещался лазерным ножом, сфокусированным на ближней внутренней стенке канала (рис. 4). Переизлучаемый свет фиксировался цифровой камерой, оснащенной светофильтром, пропускающим только свет в области частот, близких к частоте переизлучения.
Эксперименты проводились с пространственным разрешением 0,1 мм. Использование системы из двух спаренных лазеров позволяло измерять скорости волн. Погрешность измерения толщины пленки жидкости не превышала 3%.
 |
| Рисунок 5. Сравнение сделанных в разное время записей толщины свободно стекающей пленки, полученных разными методами |
На рис. 5 представлено сравнение разных записей толщины пленки при безобдувном течении, полученных методами локальной электропроводности и флуоресцентной визуализации.
Метод электропроводности осредняет мелкомасштабные волновые структуры на поверхности пленки (в частности, капиллярный предвестник волн). Тем не менее, этот метод адекватно описывает крупномасштабные волны и применим для исследования волн возмущения.
Метод флуоресцентной визуализации имеет свои ограничения: если радиус кривизны волны сравним с толщиной слоя жидкости, распределение интенсивности света, отраженного от границы раздела, может сильно искажаться. В частности, метод в данной его реализации неприменим к исследованию свойств волн возмущения, поскольку поверхность волны возмущения покрыта волнами капиллярной ряби.
Таким образом, волновая картина на поверхности пленки исследовалась при помощи двух методов: метод локальной электропроводности применялся для исследования свойств волн возмущения, а метод флуоресцентной визуализации – для исследования свойств волн ряби.
Третья глава посвящена измерению интегральных параметров потока и исследованию возникновения крупных волн.
 |  |
| Рисунок 6. Зависимости расхода дисперсной фазы (а) и локального перепада давления (б) от расстояния. | |
На рис. 6 приведены примеры зависимостей отношения расхода дисперсной фазы к полному расходу жидкости и локального перепада давления от
расстояния. На исследуемых расстояниях расход жидкой фазы линейно растет с расстоянием. Переход к уносу происходит тем раньше, чем выше расходы жидкости и газа.
На больших расстояниях перепад давления незначительно меняется с расстоянием. В близкой к распределителю области, качественно совпадающей с областью образования волн возмущения и начала уноса, перепад давления испытывает рост, который тем сильнее, чем выше расходы газа и жидкости. Измеренные значения перепада давления позволяют оценить среднее значение касательного напряжения со стороны газа на поверхности пленки жидкости.
На рис. 7 представлен пример эволюции распределения максимумов волн с расстоянием от входа в канал. Видно, что на малых расстояниях от входа распределение имеет один горб, который вниз по потоку распадается на два четко различимых горба, один из которых соответствует максимумам волн ряби на подложке, а второй – максимумам волн возмущения. Далее средняя амплитуда волн возмущения нарастает, но вскоре достигает равновесных значений. Также на этих расстояниях крайне слабо меняется частота следования волн. Таким образом, доля волн, взаимодействующих друг с другом, в этой области мала, и волны в этой области можно считать уединенными.
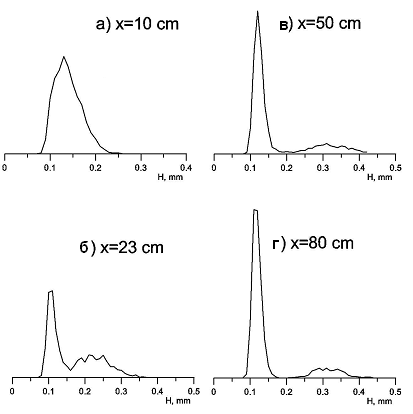 |
| Рисунок 7. Эволюция распределения максимумов волн с расстоянием от входа в канал. Вода, Re=142, Vgas=64 м/с. |
В четвертой главе приведены результаты статистического исследования свойств волн возмущения при помощи метода условного осреднения. Метод основывается на предположении, что свойства волны возмущения при фиксированных параметрах течения однозначно определяются ее амплитудой. В распределении волн по амплитудам выделялся узкий интервал, и для дальнейшей обработки из записи толщины пленки отбирались только волны, амплитуда которых лежит в этом интервале (рис. 8). Совокупность измерений для нескольких интервалов позволяла получить зависимость свойств волн возмущения от их амплитуды при фиксированных параметрах течения, измеренную с высокой статистической достоверностью.
 |
| Рисунок 8. Выделение волн с амплитудами, лежащими в заданном узком интервале: а) преобразованная запись толщины пленки; b) соответствующее распределение максимумов волн по высотам |
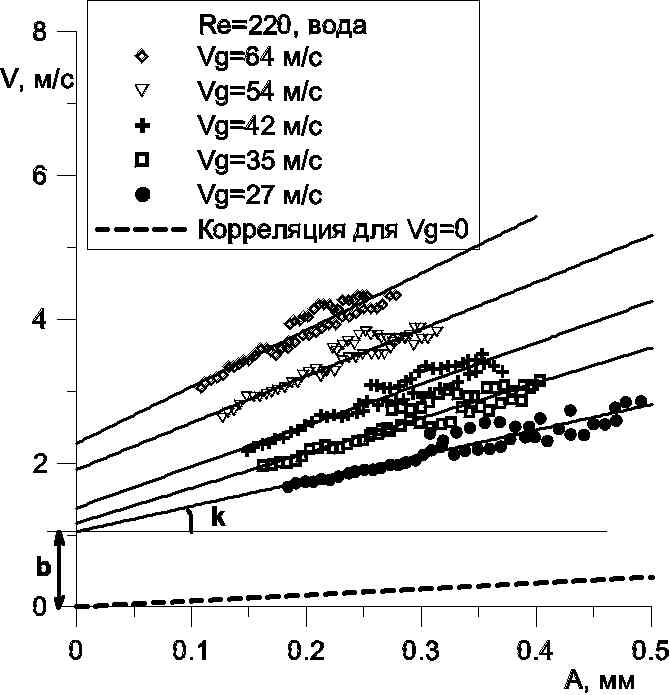 |  |
| Рисунок 9. Зависимость скорости волн возмущения от их амплитуды. Вода, Re=220, скорости газа 27-64 м/с, расстояние от входа 23, 50, 80 см. | Рисунок 10. Влияние вязкости жидкости на скорость волн возмущения. |
На рис. 9 представлены измеренные при помощи метода условного осреднения зависимости скорости волн возмущения от амплитуды для разных скоростей потока газа. Представленные на графике экспериментальные точки получены на расстояниях 23, 50 и 80 см от входа в канал. При фиксированной паре значений расходов жидкости и газа эти точки описываются единой линейной зависимостью ![]() для всего диапазона исследуемых расстояний.
для всего диапазона исследуемых расстояний.
Были предложены соотношения, описывающие коэффициенты этой зависимости. Предполагалось, что коэффициент b, означающий не зависящую от амплитуды постоянную добавку к скорости волны, определяется средней скоростью подложки, по которой распространяются волны возмущения. Средняя скорость подложки определялась, исходя из предположений как о ламинарном профиле скорости в подложке: ![]() , так и о турбулентном профиле скорости в подложке:
, так и о турбулентном профиле скорости в подложке:  , где
, где ![]() . Здесь
. Здесь ![]() и
и ![]() - экспериментально определяемые касательное напряжение на поверхности пленки и толщина подложки,
- экспериментально определяемые касательное напряжение на поверхности пленки и толщина подложки, ![]() - динамическая вязкость жидкости.
- динамическая вязкость жидкости.
За основу для расчета коэффициента k была принята известная из литературы экспериментальная корреляция , описывающая зависимость скорости от амплитуды для нелинейных стационарных волн на поверхности свободно стекающей пленки жидкости. Эта корреляция экстраполировалась на случай наличия потока газа подстановкой в нее расхода, построенного по амплитуде волны с учетом наличия газа: (
, описывающая зависимость скорости от амплитуды для нелинейных стационарных волн на поверхности свободно стекающей пленки жидкости. Эта корреляция экстраполировалась на случай наличия потока газа подстановкой в нее расхода, построенного по амплитуде волны с учетом наличия газа: (![]() ), где
), где ![]() . В этом случае коэффициент k описывается следующей формулой:
. В этом случае коэффициент k описывается следующей формулой:
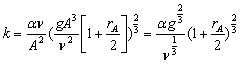 (1)
(1)
На рис. 10 показано влияние вязкости жидкости на скорость волн возмущения. Увеличение вязкости приводит к увеличению коэффициентов зависимости скорости от амплитуды.
На рис. 11 представлено сравнение экспериментальных значений коэффициентов b и k с результатами оценок, описанных выше. Коэффициент b удовлетворительно описывается соотношением для средней скорости подложки, причем для малых чисел Рейнольдса и скоростей газа ближе к экспериментальным данным лежит оценка по ламинарному профилю, тогда как для больших расходов жидкости и газа оценка по ламинарному профилю дает завышенные значения.
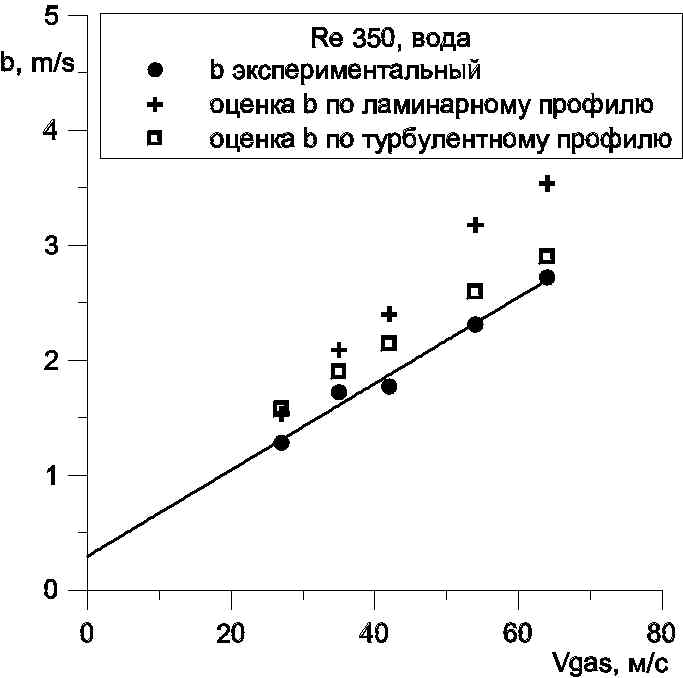 | 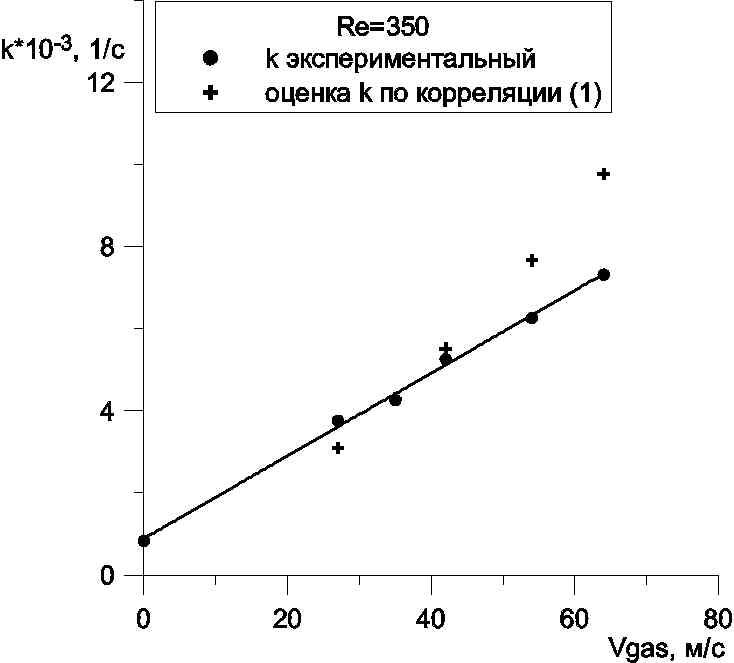 |
| Рисунок 11. Оценки коэффициентов зависимости скорости волн возмущения от амплитуды | |
Коэффициент k удовлетворительно описывается корреляцией (1) для малых и умеренных значений скорости газа. Однако при высоких скоростях газа оценка дает завышенные значения.
Другим параметром, представляющим интерес с точки зрения описания динамики волн и непосредственно используемым в ряде теоретических моделей для описания явления уноса (например, Holowach et al. 2002), является среднее расстояние между волнами.
 |
| Рисунок 12. Частота следования волн и число волн на единицу длины для разных чисел Рейнольдса жидкости. |
Метод условного осреднения позволяет определить эту величину на основе данных по скорости и частоте следования волн из узкого интервала амплитуд. На рис. 12 (а) показана обратная среднему расстоянию величина - количество волн возмущения на единицу длины. Видно, что число волн на единицу длины не зависит от скорости газа. Это означает, что увеличение частоты следования с ростом скорости газа (рис. 12 (б)) происходит исключительно благодаря увеличению скорости волн. На рис. 13 представлены аналогичные зависимости для жидкостей различной вязкости при близких числах Рейнольдса жидкости. Видно, что число волн на единицу длины не зависит от вязкости жидкости, и увеличение частоты следования с вязкостью жидкости вызвано лишь увеличением скорости волн.
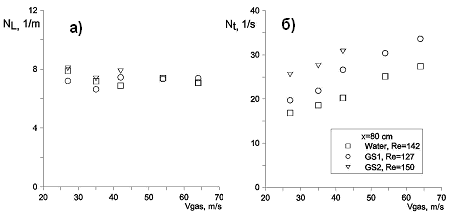 |
| Рисунок 13. Число волн на единицу длины и частота следования волн для разных значений вязкости жидкости. |
Метод условного осреднения также позволяет детально исследовать влияние параметров течения на форму волн возмущения и построить обобщенные портреты волн возмущения, которые являются удобным материалом для сравнения с теоретическими моделями. Для получения обобщенных портретов профили всех волн возмущения из заданного интервала амплитуд суммировались с переносом максимума волны в начало координат.
 |
| Рисунок 14. Обобщенные портреты волн возмущения |
На рис. 14 представлены обобщенные портреты волн разной амплитуды при
фиксированных параметрах течения (а), а также портреты волн
наиболее вероятной амплитуды при различных расстояниях от входа (б), различных скоростях газа (в), числах Рейнольдса жидкости (г) и различных вязкостях жидкости при близких числах Рейнольдса (д).
Для количественного описания формы волн был выбран параметр «крутизна волны» (отношение амплитуды волны к ее полуширине). На рис. 15а представлена зависимость крутизны волн возмущения от амплитуды.
 |
| Рисунок 15. Зависимость крутизны волн возмущения от их амплитуды: а) Для разных скоростей газа, при Re=142, x=23 см и при Re=350, x=50 см; b) для разных значений кинематической вязкости жидкости при близких числах Рейнольдса, x=80 см. |
С увеличением амплитуды крутизна волн линейно нарастает. При фиксированном числе Рейнольдса жидкости зависимость крутизны от амплитуды является единой для всех скоростей газа.
Также можно видеть, что с ростом числа Рейнольдса жидкости и расстояния от входа волны одинаковой амплитуды становятся более пологими. Такое же влияние на крутизну волн оказывает увеличение вязкости жидкости (рис. 15 (б)).
В пятой главе описано исследование свойств капиллярной ряби в дисперсно-кольцевом течении. На рис. 16 представлены записи толщины пленки для течения при низком числе Рейнольдса жидкости, при котором отсутствуют волны возмущения. С ростом скорости газа уменьшается длина волн ряби, что приводит к уменьшению амплитуды ряби, измеряемой датчиками проводимости, вследствие ограниченной пространственной разрешающей способности метода. В реальности амплитуда ряби может достигать высоких значений, зачастую сравнимых с амплитудой волн возмущения.
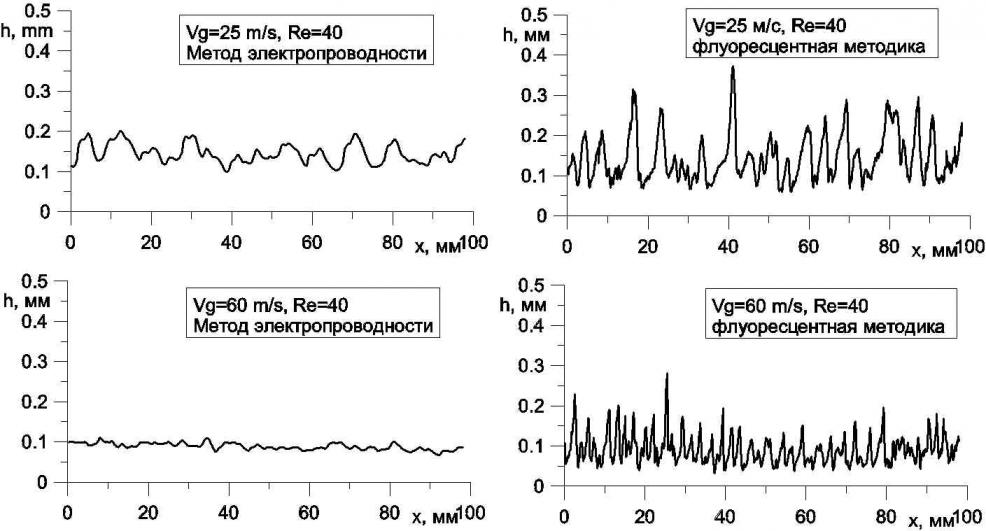 |
| Рисунок 16. Сравнение записей толщины пленки, полученных методами локальной электропроводности и флуоресцентной визуализации. |
 |
| Рисунок 17. Влияние параметров течения на амплитуду волн ряби и сравнение средней толщины пленки, измеренной разными методами. |
На рис. 17 представлено сравнение зависимостей амплитуды волн ряби и средней толщины пленки от скорости газа, полученных при помощи разных экспериментальных методов. Амплитуда волн ряби, измеренная методом LIF, в несколько раз превосходит амплитуду, измеренную методом проводимости как в экспериментах данной работы, так и в работе Chu, Dukler (1974). Амплитуда волн ряби линейно уменьшается с ростом скорости газа и слабо зависит от числа Рейнольдса жидкости. Средняя толщина пленки, измеренная разными методами, с хорошей точностью совпадает.
Необходимо отметить, что при малых числах Рейнольдса жидкости отношение амплитуды ряби близко к средней толщине пленки жидкости. С ростом числа Рейнольдса жидкости это отношение уменьшается. Таким образом, практикуемое во многих эмпирических корреляциях использование средней толщины пленки в качестве параметра шероховатости оправдано только для малых чисел Рейнольдса.
На рис. 18 представлены данные по длине волны ряби. Видно, что длина волны ряби растет с увеличением числа Рейнольдса жидкости, и для высоких чисел Рейнольдса жидкости ее величина слабо зависит от скорости газа.
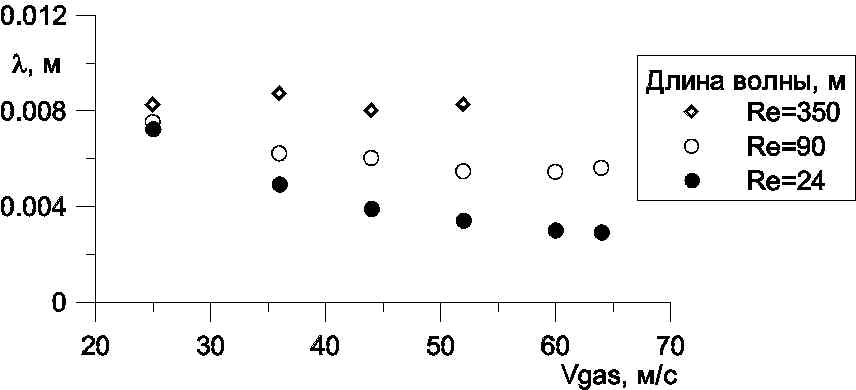 |
| Рисунок 18. Длина волн ряби. |
Одним из параметров, использовавшихся для описания шероховатости пленки, является отношение амплитуды к длине волны (Andritsos, Hanratty 1987). На рис. 19 представлены значения этого параметра для волн ряби в зависимости от скорости газа и числа Рейнольдса жидкости.
Видно, что зависимость крутизны волн ряби от скорости газа не является монотонной и имеет максимум, который смещается в сторону меньших скоростей газа с ростом расхода жидкости. Также необходимо отметить, что крутизна волн ряби сравнима по величине с крутизной волн возмущения.
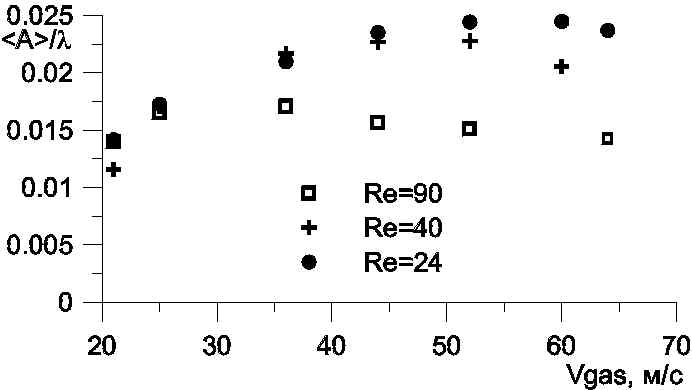 |
| Рисунок 19. Крутизна волн ряби. |
Кросскорреляционное сравнение пар кадров, снятых с небольшой задержкой, позволило измерить среднюю скорость волн ряби. Эти данные представлены на рис. 20. Видно, что скорость волн ряби линейно нарастает с увеличением скорости газа и несколько увеличивается с ростом числа Рейнольдса жидкости.
 |
| Рисунок 20. Скорость волн ряби |
ЗАКЛЮЧЕНИЕ
Получены следующие основные результаты:
1. Для исследования свойств волн возмущения применен новый метод условного осреднения, позволивший с высокой точностью измерить скорость волн возмущения, число волн на единицу длины и параметры формы волн в широком диапазоне параметров течения.
2. Показано, что зависимость скорости волн возмущения от амплитуды едина для всех расстояний от входа в канал, и что коэффициенты прямой, описывающей эту зависимость, линейно растут с увеличением скорости потока газа. Предложены соотношения, описывающие эти коэффициенты.
3. Показано, что число волн на единицу длины для исследуемого диапазона расстояний не зависит ни от скорости газа, ни от вязкости жидкости. Таким образом, увеличение частоты следования волн возмущения с этими параметрами вызвано лишь увеличением скорости волн.
4. Построены обобщенные портреты волн возмущения в широком диапазоне параметров. Показано, что крутизна фронтов волны линейно растет с увеличением амплитуды волны, и что эта зависимость едина для всего диапазона скоростей газа.
5. Впервые применен метод флуоресцентной визуализации для исследования течения пленки жидкости, обдуваемой интенсивным потоком газа. Показано, что метод локальной электропроводности малоприменим для исследования свойств высокочастотной капиллярной ряби. Показано, что амплитуда волн ряби в несколько раз выше амплитуды ряби, измеряемой методом электропроводности.
6. Показано, что амплитуда волн ряби линейно уменьшается с увеличением скорости газа и слабо зависит от числа Рейнольдса жидкости. Показано, что отношение амплитуды волн ряби к средней толщине пленки близко к единице при малых числах Рейнольдса жидкости, но падает с увеличением числа Рейнольдса.
7. Показано, что скорость волн ряби линейно растет с ростом скорости газа и по своему значению близка к оценке средней скорости подложки. Показано, что с увеличением числа Рейнольдса жидкости растет длина волн ряби и ослабляется зависимость длины волн ряби от скорости газа.
8. Показано, что зависимость крутизны волн ряби от скорости газа не является монотонной и имеет максимум, который смещается в сторону меньших скоростей газа с ростом расхода жидкости. Показано, что крутизна волн ряби сравнима с крутизной волн возмущения.
Литература:
1. Алипченков В.М., Зайчик Л.И., Зейгарник Ю.А., и др. Разработка трехжидкостной модели двухфазного потока для дисперсно-кольцевого течения в каналах. М.: 2001. Объединенный институт высоких температур РАН.
2. Andritsos N., Hanratty T.J. Influence of Interfacial Waves in Stratified Gas-Liquid Flows. // AIChE Journal, Vol. 33, No. 3, pp. 444-454, 1987.
3. Chu K.J., Dukler A.E. Statistical characteristics of thin, wavy liquid film // AIChE Journal, 1974, v. 20, № 4, p. 695-706
4. Holowach M.J., Hochreiter L.E., Cheung F.B. A model for droplet entrainment in heated annular flow. // Int. J. Heat and Fluid Flow, Vol. 23, pp. 807-822, 2002.
Результаты диссертации опубликованы в следующих работах:
- Alekseenko S., Cherdantsev A., Kharlamov S., Markovich D. Characteristics of liquid film in a vertical pipe in presence of gas flow. Fifth World Conference on Experimental Heat Transfer, Fluid Mechanics and Thermodynamics, Thessaloniki, Greece, 24-28 September, 2001. V. 3, pp. 1991-1996.
- Alekseenko S.V., Cherdantsev A.V., Kharlamov S.M., Markovich D.M. Linear waves on a falling liquid film in presence of turbulent gas stream. Proceedings of The Third International Conference "On transport phenomena in multiphase systems”, Kielce, Poland, 23-27 of June, 2002. Pp. 349-355.
- Черданцев А.В. Волновое течение пленки жидкости, обдуваемой потоком газа, в области линейного роста волн. VII всероссийская конференция молодых ученых "Актуальные вопросы теплофизики и гидрогазодинамики" (апрель 2002 г., ИТ СО РАН, Новосибирск, с. 130-131).
- В.А. Антипин, Л.И. Зайчик, Ю.А. Зейгарник, Д.М. Маркович, С.Л. Соловьев, О.Г. Стоник, С.М. Харламов, А.В. Черданцев. Развитие трехжидкостной модели двухфазного потока для дисперсно-кольцевого режима течения в каналах. Толщина пленки и перепад давления //Теплофизика высоких температур, 2003, т. 41, №3, с. 455-460.
- Алексеенко С.В., Маркович Д.М., Харламов С.М., Черданцев А.В. Линейная устойчивость стекающей пленки жидкости в присутствии турбулентного потока газа. // "Известия РАН. Серия МЖГ". №4, 2004, с. 119-129.
- Alekseenko S.V., Antipin V.A., Cherdantsev A.V., Kharlamov S.M., Markovich D.M. Gas-driven disturbance waves on vertical liquid film. CD-ROM Proceedings of 3rd international symposium on two-phase flow modeling and experimentation (Pisa, 22-24 of September 2004), ven. 46, 7 pages.
- Alekseenko S.V., Antipin V.A., Cherdantsev A.V., Kharlamov S.M., Markovich D.M. Waves on vertical liquid film sheared by turbulent gas flow. CD-ROM Proceedings of 16th International Congress of Chemical and Process Engineering (Praha, 22-26 of August 2004), paper P5.205, 12 pages.
- Черданцев А.В. Свойства волн возмущения на поверхности пленки жидкости, обдуваемой турбулентным потоком газа. VIII всероссийская конференция молодых ученых "Актуальные вопросы теплофизики и гидрогазодинамики" (октябрь 2004 г., ИТ СО РАН, Новосибирск), с. 80-81.
- Черданцев А.В. Исследование свойств мелких волн в дисперсно-кольцевом течении методом флуоресцентной визуализации. IX всероссийская конференция молодых ученых "Актуальные вопросы теплофизики и гидрогазодинамики" (октябрь 2006 г., ИТ СО РАН, Новосибирск), с. 137-138.

