Напряженно-деформированное состояние многослойных материалов с краевой трещиной нормального разрыва под воздействием внешних температур
На правах рукописи
Татьяна Николаевна Алексеева
НАПРЯЖЕННО-ДЕФОРМИРОВАННОЕ СОСТОЯНИЕ МНОГОСЛОЙНЫХ МАТЕРИАЛОВ С КРАЕВОЙ
ТРЕЩИНОЙ НОРМАЛЬНОГО РАЗРЫВА
ПОД ВОЗДЕЙСТВИЕМ ВНЕШНИХ ТЕМПЕРАТУР
Специальность: 01.02.04 – Механика деформируемого твердого тела
Автореферат диссертации
на соискание ученой степени кандидата технических наук
![]()
![]()
![]()
Москва - 2013
Работа выполнена в Московском государственном открытом университете имени В.С. Черномырдина.
Научный руководитель - доктор физико-математических наук,
профессор Кулиев Валех Джафарович
Официальные оппоненты:
- доктор технических наук, профессор Власов Николай Михайлович
Подольский институт (филиал) Московского государственного открытого университета имени В.С. Черномырдина;
- доктор технических наук, профессор Дудченко Александр Александрович Московский авиационный институт (национальный исследовательский университет).
Ведущая организация - ЗАО «Координационный центр по надежности, безопасности и ресурсу оборудования и трубопроводам атомных электростанций», г. Москва
Защита состоится « 30 » января 2013г. в 16.00 на заседании диссертационного совета Д212.137.02 при Московском государственном открытом университете имени В.С. Черномырдина по адресу: 107996, г. Москва, ул. Павла Корчагина, 22.
E-mail: [email protected]
С диссертацией можно ознакомиться в библиотеке МГОУ имени В.С.Черномырдина
Автореферат разослан __ декабря 2012 г.
Ученый секретарь
диссертационного совета Лукашина Н.В.
![]()
ОБЩАЯ ХАРАКТЕРИСТИКА РАБОТЫ
Актуальность темы. В современной технике широкое применение нашли многослойные материалы. Подобные конструкции из многослойных композитов широко используются в авиакосмической области, судостроении и других отраслях. Многослойные системы представляют собой чередование слоев повышенной твердости (несущих), воспринимающих внешнее воздействие (в частности, механическое) и демпфирующих слоев, перераспределяющих усилия между несущими слоями. Кроме того, предусматривают слои, обеспечивающие защиту несущих элементов от коррозионного, теплового и радиационного воздействия.
Примерами многослойных материалов являются многие природные минералы и искусственные композиты, включая нанотехнологические, а также важнейшие для жизнедеятельности животных и человека ткани. Анализ тепловых воздействий на них представляет практический интерес не только для технических, но и для медицинских приложений. В частности, биомеханику костных систем и технических конструкционных материалов объединяет единый механизм разрушения многослойного материала.
Необходимость решения проблемы прочности, например, исследование процессов трещинообразования в таких системах, важно для повышения их ресурса при экстремальных условиях эксплуатации.
В большинстве работ при моделировании трещины в выбранных местах систем многослойные материалы представляют полосами различных толщин и упругих свойств, жестко сцепленных между собой. В этом случае процесс разрушения многослойных (![]() -слойных) материалов с трещиной исследуется в три этапа: трещина полностью находится на одном из боковых слоев; трещина образована разрывом в этом слое и ее вершина находится на границе раздела разорванного и соседнего целого слоев; на третьем этапе направление роста трещины и ее тип, согласно теоретическим и экспериментальным исследованиям зависит: от Gj, vj, где Gj – модуль сдвига j-го слоя, vj – коэффициент Пуассона того же слоя; от прочности адгезии на границах раздела (прочность адгезии, согласно теории адгезии при сдвиге аналогичной теории Гриффитса – Ирвина, определяется одной новой постоянной – вязкостью скольжения контактного слоя
-слойных) материалов с трещиной исследуется в три этапа: трещина полностью находится на одном из боковых слоев; трещина образована разрывом в этом слое и ее вершина находится на границе раздела разорванного и соседнего целого слоев; на третьем этапе направление роста трещины и ее тип, согласно теоретическим и экспериментальным исследованиям зависит: от Gj, vj, где Gj – модуль сдвига j-го слоя, vj – коэффициент Пуассона того же слоя; от прочности адгезии на границах раздела (прочность адгезии, согласно теории адгезии при сдвиге аналогичной теории Гриффитса – Ирвина, определяется одной новой постоянной – вязкостью скольжения контактного слоя ![]() , а также размером дефекта или слабого места на контакте двух материалов); от микроструктуры пограничного слоя, примыкающего с одной или двух сторон к границе раздела.
, а также размером дефекта или слабого места на контакте двух материалов); от микроструктуры пограничного слоя, примыкающего с одной или двух сторон к границе раздела.
Как правило, при создании и эксплуатации биметаллов в пограничном слое возможны сложные релаксационные процессы, такие как рекристаллизация, образование новых фаз и другие, изменяющие его физико-механические свойства. Для того чтобы в более точном приближении оценить влияние пограничного слоя на прочность материала, необходимо определить толщину этого слоя – например, определить границы зоны диффузии при диффузионной сварке, т.е. смещение поверхности Киркендалла, а также изменение его механических характеристик слоя при удалении от первоначальной границы раздела.
Существует ряд задач, имеющих важное теоретическое и прикладное значение, которые не нашли достаточного освещения в отечественной и зарубежной литературе. В частности, определение напряженно-деформированного состояния многослойного материала с трещинами, находящегося под воздействием температурных полей различного вида. Решение таких вопросов необходимо при создании и эксплуатации современных и перспективных конструкций из биметаллов и композитов, из чего вытекает актуальность темы диссертации.
Целью диссертационной работы является разработка метода определения напряженно-деформированного состояния многослойного материала с краевой трещиной нормального разрыва, находящегося под воздействием внешней температуры, на основе которого можно определить прочность несущих элементов конструкций и принять меры к повышению их надежности. Эта цель достигается решениями и анализами следующих задач:
1. Построение адекватной математической модели, описывающей напряженно-деформированное состояние многослойного материала без трещины, допускающей аналитическое решение исходных дифференциальных уравнений в частных производных при заданных граничных условиях в виде температурных полей.
2. Построение численно-аналитического решения задачи о краевой трещине нормального разрыва с вершиной в первом слое многослойного материала на основе решения задачи без трещины.
3. Определение коэффициента интенсивности напряжений ![]() при заданном нагружении берегов трещины.
при заданном нагружении берегов трещины.
4. Исследование комплексного влияния теплофизических свойств многослойных материалов и внешней температуры на коэффициент интенсивности напряжений ![]() .
.
Научная новизна заключается в следующем:
1. Разработан численно-аналитический метод, позволяющий построить решение новой задачи механики разрушения многослойных материалов с трещиной нормального разрыва, внешняя боковая поверхность которых подвержена действию температуры, удовлетворяющей известным постулатам линейной теории упругости.
2. Впервые получена аналитическая зависимость, позволяющая учитывать комплексное влияние теплофизических свойств многослойных материалов и конкретный вид температурных полей на коэффициент интенсивности напряжений ![]() .
.
3. Установлены условия, при которых происходит торможение трещины, связанные с изменением теплофизических свойств многослойных материалов.
Достоверность полученных результатов подтверждает апробированность исходных положений работы в постановках задач теории термоупругости и теории трещин, математическая точность и строгость в решении и удовлетворении граничных условий рассматриваемых задач, сравнение результатов частных случаев с теоретическими данными других авторов.
Практическая ценность и применение результатов: разработанный метод расчета коэффициента интенсивности напряжений позволяет оценить прочность конструкций и принять меры к повышению их надежности. Аналитический метод позволяет без натурных образцов и макетов оптимизировать прочностные характеристики конструкций из многослойных материалов.
На защиту выносятся следующие основные результаты работы:
1. Численно-аналитический метод решения задач линейной термоупругости многослойных материалов с трещиной нормального разрыва, находящихся под воздействием внешних температурных полей.
2. Решение конкретной задачи механики разрушения многослойных сред с краевой трещиной нормального разрыва, находящихся под воздействием внешней температуры. Нахождение коэффициента интенсивности напряжений ![]() .
.
3. Анализ комплексного влияния теплофизических свойств материалов и заданной внешней температуры на коэффициент интенсивности напряжений ![]() , и тем самым на прочность несущих элементов конструкций.
, и тем самым на прочность несущих элементов конструкций.
4. Условия, при выполнении которых происходит торможение краевой трещины нормального разрыва в многослойных материалах, находящихся под воздействием внешних температурных полей.
Результаты диссертационной работы внедрены в расчетную практику заинтересованных предприятий и используются при проектировании изделий, что подтверждено двумя актами внедрения от организаций: 1.ЗАО НТЦ «Бакор», г. Щербинка Московской области, 2012 г.; 2. ООО «Инструмент», г. Подольск Московской области, 2012 г.
Апробация работы. Основные положения и результаты диссертационной работы докладывались и обсуждались на следующих научных форумах: 1. Межвузовская научная конференция студентов, аспирантов, молодых ученых и специалистов «Новые технологии и разработки в машиностроении, автоматике, экономике, юриспруденции и образовании» при Коломенском институте МГОУ, Коломна, 2005 г.; 2. II Региональная научно-практическая конференция студентов, аспирантов, молодых ученых и специалистов «Наука, экономика, общество», филиал МГОУ в г.Воскресенске, 2008 г.; 3. XVII Международная конференция «Математика, компьютер, образование», Дубна, 2010 г.; 4. XVIII Международная конференция «Математика, экономика, образование», Ростов на Дону, 2010 г.; 5. Общеуниверситетский научный семинар по механике деформируемого твердого тела при МГОУ им. В.С. Черномырдина, 2012 г.
Публикации. По теме диссертационной работы опубликованы 10 научных работ, включая 3 статьи, входящих в перечень ведущих рецензируемых журналов, рекомендованных ВАК РФ.
Структура и объем работы. Диссертационная работа состоит и введения, трех глав, заключения, списка используемой литературы и приложения, содержащего акты внедрения результатов диссертации. Объем диссертации: 126 страниц. В диссертации 9 рисунков, 4 таблицы. Список используемой литературы включает 120 наименований.
ОСНОВНОЕ СОДЕРЖАНИЕ РАБОТЫ
Во введении обосновывается актуальность проблемы исследований, и излагаются основные научные положения, которые выносятся на защиту.
В первой главе сформулированы основные проблемы механики разрушения многослойных сред с трещинами (метод В.Д. Кулиева для решения канонических сингулярных задач теории упругости кусочно-однородных сред, задача Вильямса-Черепанова, задача Зака-Вильямса) дан обзор работ по теме диссертации, указана цель и обоснована структура диссертационной работы.
Во второй главе исследуется задача нахождения поля напряжений в многослойном материале, находящемся под воздействием внешних температурных полей (рис. 1).
Первая часть данной главы посвящена уравнениям термоупругости.
Во второй части формулируется и решается следующая задача: на плоскость действует заданная температура, необходимо определить напряжение в двухслойном материале.

Рисунок 1
Предполагается, что две однородные изотропные полосы жестко сцеплены вдоль плоскости ![]() . Внешняя боковая поверхность двухслойного материала подвержена воздействию некоторой заданной температуры. Материал каждого из слоев является термоупругим. Задача считается симметричной относительно плоскости
. Внешняя боковая поверхность двухслойного материала подвержена воздействию некоторой заданной температуры. Материал каждого из слоев является термоупругим. Задача считается симметричной относительно плоскости ![]() . На бесконечности напряжения отсутствуют, а смещения исчезают.
. На бесконечности напряжения отсутствуют, а смещения исчезают.
1. Начальные условия
![]() . (1)
. (1)
2. Граничные условия
![]() ,
,![]() , (2)
, (2)
![]() ,
,![]() ;
;
![]() ,
, ![]() , (3)
, (3)
 ;
;
![]() , (4)
, (4)
![]() ;
;
![]() , (5)
, (5)
![]() .
.
3. Условия на бесконечности
![]() ,
, ![]() ,
, ![]() ,
,  , (6)
, (6)
 ;
;
![]() ,
, ![]() ,
, ![]() ;
;
![]() ,
, ![]() ,
, ![]() .
.
Здесь ![]() - коэффициент теплопроводности j-го слоя,
- коэффициент теплопроводности j-го слоя, ![]() - коэффициент температуропроводности j-го слоя,
- коэффициент температуропроводности j-го слоя, ![]() - термоупругий потенциал перемещений.
- термоупругий потенциал перемещений.
Всюду в дальнейшем считается, что изменения функции ![]() во времени происходит с достаточно малой скоростью, когда влиянием инерционных членов в уравнениях движения теории упругости можно пренебречь, рассматривая движение как последовательность состояний равновесия (принцип Дюамеля).
во времени происходит с достаточно малой скоростью, когда влиянием инерционных членов в уравнениях движения теории упругости можно пренебречь, рассматривая движение как последовательность состояний равновесия (принцип Дюамеля).
Решение строится из интегральных преобразований Лапласа и Фурье.
Найдем распределение температуры ![]()
![]() в каждом слое с помощью уравнения теплопроводности
в каждом слое с помощью уравнения теплопроводности
 . (7)
. (7)
Термоупругий потенциал перемещений Папковича-Гудьера ![]() для квазистатического случая определяется уравнением Пуассона
для квазистатического случая определяется уравнением Пуассона
 , (8)
, (8)
где ![]() - коэффициент линейного расширения,
- коэффициент линейного расширения, ![]() - коэффициент Пуассона.
- коэффициент Пуассона.
Как известно, термические напряжения и смещения выражаются через термоупругий потенциал ![]() . Применяя обратные преобразования Фурье и Лапласа, можно получить термические напряжения
. Применяя обратные преобразования Фурье и Лапласа, можно получить термические напряжения ![]() ,
, ![]() ,
, ![]() и смещения
и смещения ![]() ,
, ![]() вследствие действия термических напряжений.
вследствие действия термических напряжений.
Для решения плоской задачи теории упругости с трещиной нормального разрыва особый интерес представляет нахождение нормального напряжения ![]() , поэтому рассмотрим следующий частный случай:
, поэтому рассмотрим следующий частный случай: ![]() ,
, ![]() . Здесь
. Здесь ![]() - амплитуда, являющаяся постоянной функцией,
- амплитуда, являющаяся постоянной функцией, ![]() - циклическая частота. В этом случае имеем
- циклическая частота. В этом случае имеем
![]()

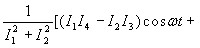
![]() . (9)
. (9)
Здесь
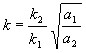 ,
, ![]()
 ,
, ![]()
 ,
, ![]()
 ;
;
![]()
![]()
![]()
![]() ,
,
![]()
![]() ,
,
![]()
![]() .
.
В третьей главе рассматривается задача о краевой трещине нормального разрыва с вершиной в первом слое многослойного материала.
В первой части главы приведен метод В.Д. Кулиева решения данной задачи.
Во второй части рассматривается частный случай: краевая трещина нормального разрыва в двухслойном материале, находящемся под воздействием внешней температуры (рис.2). К берегам трещины приложено заданное напряжение, аналитическое выражение для которого найдено в предыдущей главе.

Рисунок 2
Пусть упругая полуплоскость ![]() , составленная из различных материалов с упругими свойствами
, составленная из различных материалов с упругими свойствами ![]() (
(![]() ), жестко сцепленных вдоль плоскости
), жестко сцепленных вдоль плоскости ![]() , содержит краевую трещину нормального разрыва.
, содержит краевую трещину нормального разрыва.
Трещина перпендикулярна свободной от напряжений границе х=0 и границе раздела слоев ![]() . К берегам трещины приложено заданное нормальное напряжение
. К берегам трещины приложено заданное нормальное напряжение ![]() ,
, ![]() ,
,![]()
![]() , где
, где ![]() интегрируемая на отрезке
интегрируемая на отрезке ![]() функция,
функция, ![]() определяется соотношением (9).
определяется соотношением (9).
На бесконечности напряжения отсутствуют, а смещения исчезают.
Таким образом, приходим к симметричной относительно плоскости ![]() краевой задаче плоской теории упругости для двухслойных материалов с краевой трещиной нормального разрыва, находящихся под воздействием внешней температуры.
краевой задаче плоской теории упругости для двухслойных материалов с краевой трещиной нормального разрыва, находящихся под воздействием внешней температуры.
Граничные условия
![]() ,
, ![]() ,
, ![]() ,
, ![]() , (10)
, (10)
![]() ,
, ![]() ,
, ![]() ,
, ![]() , (11)
, (11)
![]() ,
, ![]() ,
, ![]() ,
, ![]() , (12)
, (12)
![]() ,
, ![]() ,
, ![]() ,
, ![]() , (13)
, (13)
![]() ,
, ![]() ,
, ![]() ,
, ![]() , (14)
, (14)
![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
, ![]() . (15)
. (15)
- Условия на бесконечности
![]() ,
, ![]() , (16)
, (16)
![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, ![]()
![]() ,
,
![]()
![]()
![]() .
.
Условие на конце трещины (дополнительное условие к краевой задаче ((10)-(16)) при ![]() ,
, ![]() имеет вид
имеет вид
![]() .
.
Учитывая симметрию задачи, рассматриваем область ![]() . Решение задачи в указанной области, согласно представлению Папковича-Нейбера перемещений и напряжений через три гармонические функции, примет вид
. Решение задачи в указанной области, согласно представлению Папковича-Нейбера перемещений и напряжений через три гармонические функции, примет вид
при ![]() ,
, ![]() (первая упругая среда:
(первая упругая среда: ![]() )
)


 , (17)
, (17)
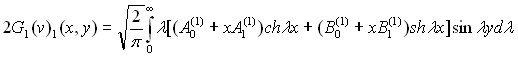 +
+
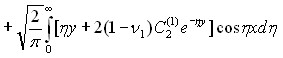 , (18)
, (18)


 , (19)
, (19)


 , (20)
, (20)


 ; (21)
; (21)
при ![]() ,
, ![]() (вторая упругая среда:
(вторая упругая среда: ![]() )
)

 , (22)
, (22)

![]() , (23)
, (23)

 , (24)
, (24)

 , (25)
, (25)

 . (26)
. (26)
Здесь ![]() .
.
Удовлетворяя граничным условиям, получаем систему линейных неоднородных алгебраических уравнений относительно восьми неизвестных функций ![]() ,
, ![]() и с правыми частями, зависящими от неизвестной функции
и с правыми частями, зависящими от неизвестной функции ![]() . В данной системе функция
. В данной системе функция ![]() входит в следующие соотношения:
входит в следующие соотношения:
 ,
,
 ,
,
 ,
,
 . (27)
. (27)
Удовлетворяя оставшимся граничным условиям, приходим к парным (дуальным) интегральным уравнениям
 ,
, ![]() , (28)
, (28)
 ,
, ![]() . (29)
. (29)
Здесь

![]() .
.
Функцию ![]() ищем в виде
ищем в виде

![]() , (30)
, (30)
где ![]() - функция Бесселя первого рода нулевого порядка,
- функция Бесселя первого рода нулевого порядка, ![]() - новая неизвестная функция.
- новая неизвестная функция.
При подстановке (30) в уравнение (28) получаем тождественное равенство. При подстановке (30) в (29) приходим к обобщенному уравнению Абеля, обращение которого позволяет получить выражение для нахождения функции ![]() :
:



![]() . (31)
. (31)
В дальнейшем для решения задачи необходимо все искомые функции ![]() ,
, ![]() , выразить через интегралы
, выразить через интегралы ![]()
![]() .
.
Здесь

![]() ,
,
![]()
![]()
![]() ,
,
![]()
![]()
![]() ,
,
![]() ,
,
![]() ,
,
 ,
,
 ,
,![]() (32)
(32)
где ![]() - модифицированные функции Бесселя первого рода и модифицированные функции Струве.
- модифицированные функции Бесселя первого рода и модифицированные функции Струве.
Представим искомые функции в виде
 ,
,
 ,
,
 ,
,

![]() . (33)
. (33)
Здесь ![]() - новые неизвестные функции.
- новые неизвестные функции.
Таким образом, приходим к системе, состоящей из четырех линейных неоднородных алгебраических уравнений с уже известными правыми частями ![]()
![]()
![]()
![]() относительно новых неизвестных функций.
относительно новых неизвестных функций.
Окончательно получаем интегральное уравнение типа Фредгольма второго рода:

 ,
,


![]() ,
, ![]() . (34)
. (34)
Коэффициент интенсивности напряжений будем искать в виде
![]() , (35)
, (35)
![]()
 . (36)
. (36)
Здесь ![]() определяется из интегрального уравнение типа Фредгольма второго рода (34).
определяется из интегрального уравнение типа Фредгольма второго рода (34).
Для нахождения коэффициента интенсивности напряжений ![]() в вершине краевой трещины
в вершине краевой трещины ![]() ,
, ![]() , находящейся в двухслойной среде под воздействием внешней температуры, достаточно выполнить следующие действия:
, находящейся в двухслойной среде под воздействием внешней температуры, достаточно выполнить следующие действия:
1) в уравнении (34) выполнить замену ![]() ,
,
2) в найденном ранее выражении для нормального напряжения ![]() (9) поменять знак и принять
(9) поменять знак и принять ![]() ,
,
3) полученное соотношение подставить в измененное уравнение (34).
Будем искать ![]() в виде
в виде
![]() ,
,
 ,
,
 .
.
Здесь
 ,
,  .
.
Коэффициент интенсивности напряжений примет вид:
![]() ,
, ![]() .
.
Здесь
 ,
,  ,
,  .
.
Введем следующие обозначения
![]() ,
,  ,
,
тогда
![]() .
.
Благодаря представлению искомых функций в виде (33) появилась практическая возможность вычисления значений ![]() для любых комбинаций свойств материалов и тем самым оптимальном проектировании многослойных конструкций. Для этого средствами аналитической системы Maple разработана вычислительная программа, в которой решение уравнения (34) сведено к решению системы линейных неоднородных уравнений порядка
для любых комбинаций свойств материалов и тем самым оптимальном проектировании многослойных конструкций. Для этого средствами аналитической системы Maple разработана вычислительная программа, в которой решение уравнения (34) сведено к решению системы линейных неоднородных уравнений порядка ![]() . При выполнении расчетов установлено, что для получения трех устойчивых десятичных цифр в значении
. При выполнении расчетов установлено, что для получения трех устойчивых десятичных цифр в значении ![]() достаточно m=20.
достаточно m=20.
Рассмотрим частные случаи общего решения. Пусть ![]() . Результаты численного расчета зависимости
. Результаты численного расчета зависимости 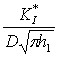 от
от ![]()
![]() при различных теплофизических свойствах материалов представлены на рис. 3, 4, 5, 6. Анализ графиков показывает важность методов неразрушающего контроля.
при различных теплофизических свойствах материалов представлены на рис. 3, 4, 5, 6. Анализ графиков показывает важность методов неразрушающего контроля.

Рисунок 3. Зависимость коэффициента интенсивности напряжений от длины трещины в двухслойном материале
- Кадмиевая бронза – конструкционная сталь 20
- Магниевая бронза Бр Мг 0,3 - конструкционная сталь 20
- Хромовая бронза Бр Х 0,5 - конструкционная сталь 20
- Бериллиевая бронза Бр Б2 - конструкционная сталь 20
- Алюминиевожелезная бронза АЖ9-4 - конструкционная сталь 20
Таблица 1. Свойства материалов
| № | Материал | с | |||||
| Первый слой – различные марки бронзы | |||||||
| 1. | Кадмиевая бронза | 8.890 | 329 | 385 | 0,32-0,35 | 123,6 | 41,2 |
| 2. | Магниевая бронза Бр Мг 0,3 | 8.910 | 242,8 | 381 | 0,32-0,35 | 120,7 | 45,4 |
| 3. | Хромовая бронза Бр Х 0,5 | 8.900 | 176,5 | 385 | 0,32-0,35 | 109,9 | 41,2 |
| 4. | Бериллиевая бронза Бр Б2 | 8.230 | 104,7 | 418,7 | 0,32-0,35 | 128,5 | 50 |
| 5. | Алюминиевожелезная бронза АЖ9-4 | 7.500 | 58,6 | 423 | 0,32-0,35 | 110,7 | 41,6 |
| Второй слой – конструкционная сталь 20 | |||||||
| 7.859 | 52 | 486 | 0,24-0,31 | 213 | 83,9 | ||
Теплофизические свойства:
 - плотность,
- плотность, 
 - коэффициент теплопроводности,
- коэффициент теплопроводности, 
- с - удельная теплоемкость,
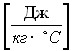
 - коэффициент Пуассона,
- коэффициент Пуассона, - E - модуль продольной упругости,
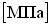
- G – модуль сдвига,
 .
.
На рис. 3 построены графики для двухслойных конструкций, в которых первый слой представлен различными марками бронзы, а второй - конструкционной сталью 20 (табл. 1).
На первом и втором графике с увеличением длины трещины ![]() коэффициент интенсивности напряжений
коэффициент интенсивности напряжений ![]() падает, т.е. происходит торможение трещины. На втором графике небольшой рост рассматриваемого параметра обусловлен близостью границы.
падает, т.е. происходит торможение трещины. На втором графике небольшой рост рассматриваемого параметра обусловлен близостью границы.
На третьем и четвертом графике коэффициент интенсивности напряжений ![]() с увеличением длины трещины падает до некоторой величины
с увеличением длины трещины падает до некоторой величины ![]() =
=![]() , где
, где ![]() - трещиностойкость материала, затем постепенно увеличивается с ростом длины трещины. То есть, нельзя допускать увеличение длины трещины до найденного критического значения во избежание разрушения многослойного материала.
- трещиностойкость материала, затем постепенно увеличивается с ростом длины трещины. То есть, нельзя допускать увеличение длины трещины до найденного критического значения во избежание разрушения многослойного материала.
На пятом графике коэффициент интенсивности напряжений ![]() монотонно увеличивается, т.е. происходит неустойчивый рост трещины.
монотонно увеличивается, т.е. происходит неустойчивый рост трещины.
Таким образом, при заданной тепловой нагрузке наилучшими будут первый и второй материалы. Применение пятого материала нецелесообразно.
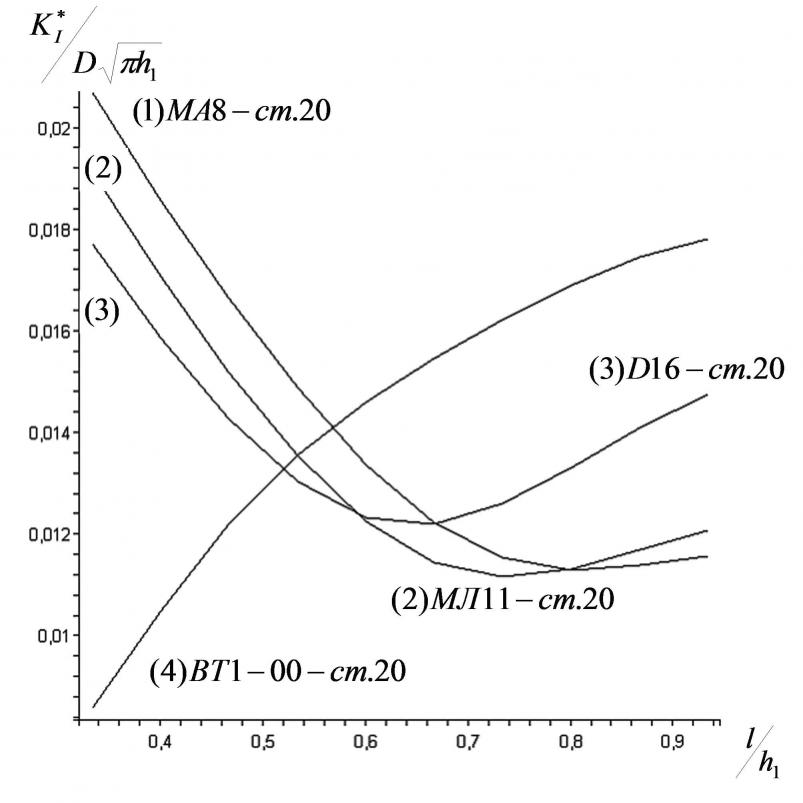
Рисунок 4. Зависимость коэффициента интенсивности напряжений от длины трещины в двухслойном материале
Таблица 2. Свойства материалов
| № | Материал | с | |||||
| Первый слой – различные сплавы легких металлов | |||||||
| 1. | Магний деформируемый МА8 | 1.780 | 133,9 | 1046,7 | 0,31-0,35 | 40,2 | 15,7 |
| 2. | Магний литейный МЛ11 | 1.800 | 117,2 | 1044,7 | 0,31-0,35 | 41,2 | 15,7 |
| 3. | Сплав алюминия D16 | 2.770 | 130 | 992 | 0,32-0,36 | 720 | 26,5 |
| 4. | Титан технический ВТ1-00 | 4.500 | 19,3 | 503 | 0,31 | 110 | 39,2 |
| Второй слой – конструкционная сталь 20 | |||||||
| 7.859 | 52 | 486 | 0,24-0,31 | 213 | 83,9 | ||
На рис. 4 построены графики для двухслойных конструкций, в которых первый слой представлен различными сплавами легких металлов, а второй - конструкционной сталью 20 (табл. 2).
На первом графике с увеличением длины трещины коэффициент интенсивности напряжений ![]() монотонно уменьшается, т.е. происходит торможение трещины. Аналогично, на втором графике анализируемый параметр монотонно уменьшается, близость границы оказывает влияние на небольшое возрастание
монотонно уменьшается, т.е. происходит торможение трещины. Аналогично, на втором графике анализируемый параметр монотонно уменьшается, близость границы оказывает влияние на небольшое возрастание ![]() .
.
На третьем графике коэффициент интенсивности напряжений ![]() с увеличением длины трещины падает до некоторой величины
с увеличением длины трещины падает до некоторой величины ![]() =
=![]() , затем постепенно увеличивается с ростом длины трещины. То есть, нельзя допускать увеличение длины трещины до найденного критического значения во избежание разрушения многослойного материала.
, затем постепенно увеличивается с ростом длины трещины. То есть, нельзя допускать увеличение длины трещины до найденного критического значения во избежание разрушения многослойного материала.
На четвертом графике коэффициент интенсивности напряжений ![]() монотонно увеличивается, то есть происходит неустойчивый рост трещины.
монотонно увеличивается, то есть происходит неустойчивый рост трещины.
Вышесказанное позволяет сделать следующий вывод - при заданных тепловых нагрузках самым прочным будет первый и второй материал, менее прочным – третий. Четвертый материал использовать нецелесообразно.
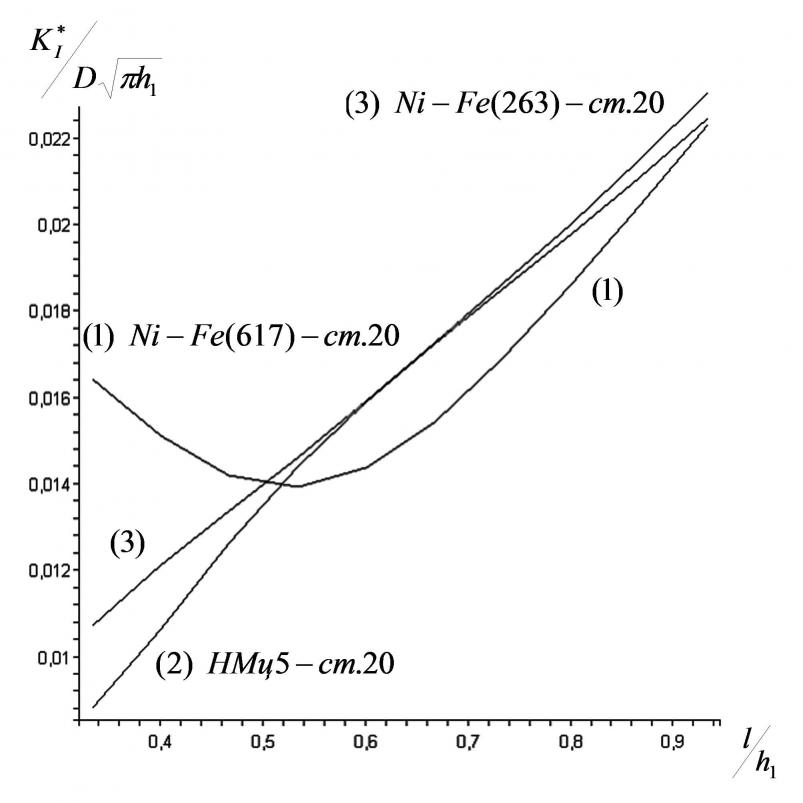 Рисунок 5. Зависимость коэффициента интенсивности напряжений от длины трещины в двухслойном материале
Рисунок 5. Зависимость коэффициента интенсивности напряжений от длины трещины в двухслойном материале
Таблица 3. Свойства материалов
| № | Материал | с | |||||
| Первый слой – различные жаростойкие никелевые сплавы | |||||||
| 1. | Жаростойкий сплав Ni-Fe(617) | 8.400 | 13,4 | 420 | 0,31 | 212 | 80,9 |
| 2. | Никель марганцевый НМц 5 | 8760 | 48 | 544 | 0,31 | 206 | 78,6 |
| 3. | Жаростойкий сплав Ni-Fe(263) | 8.400 | 11,7 | 426 | 0,31 | 222 | 84,7 |
| Второй слой – конструкционная сталь 20 | |||||||
| 7.859 | 52 | 486 | 0,24-0,31 | 213 | 83,9 | ||
На рис. 5 построены графики для двухслойных конструкций, в которых первый слой представлен различными жаростойкими никелевыми сплавами, а второй - конструкционной сталью 20 (табл. 3).
На первом графике коэффициент интенсивности напряжений ![]() с увеличением длины трещины падает до некоторой величины
с увеличением длины трещины падает до некоторой величины![]() =
=![]() , затем постепенно увеличивается с ростом длины трещины. То есть, нельзя допускать увеличение длины трещины до найденного критического значения во избежание разрушения многослойного материала.
, затем постепенно увеличивается с ростом длины трещины. То есть, нельзя допускать увеличение длины трещины до найденного критического значения во избежание разрушения многослойного материала.
На втором и третьем графике коэффициент интенсивности напряжений ![]() монотонно увеличивается, т.е. происходит неустойчивый рост трещины. Таким образом, конструирование материалов вида 2 и 3 нецелесообразно.
монотонно увеличивается, т.е. происходит неустойчивый рост трещины. Таким образом, конструирование материалов вида 2 и 3 нецелесообразно.
Вышесказанное позволяет сделать следующий вывод - из данного набора двухслойных материалов возможно использовать лишь первый материал при заданных тепловых нагрузках.

Рисунок 6. Зависимость коэффициента интенсивности напряжений от длины трещины в двухслойном материале
Таблица 4. Свойства материалов
| Материал | с | ||||||
| Первый слой – тугоплавкие металлы | |||||||
| 1. | Вольфрам | 19.350 | 300 | 134 | 0,26-0,34 | 372,8 | 143 |
| 2. | Молибден | 10.200 | 146,5 | 272 | 0,32-0,35 | 294,3 | 110,6 |
| Второй слой – конструкционная сталь 20 | |||||||
| 7.859 | 52 | 486 | 0,24-0,31 | 213 | 83,9 | ||
На рис. 6 построены графики для двухслойных конструкций, в которых первый слой представлен различными тугоплавкими металлами, а второй - конструкционной сталью 20 (табл. 4).
И на первом, и на втором графике коэффициент интенсивности напряжений ![]() монотонно уменьшается до некоторого значения
монотонно уменьшается до некоторого значения ![]() =
= ![]() , далее увеличивается, т.е. происходит неустойчивый рост трещины. То есть, нельзя допускать увеличение длины трещины до некоторого критического значения во избежание разрушения многослойного материала.
, далее увеличивается, т.е. происходит неустойчивый рост трещины. То есть, нельзя допускать увеличение длины трещины до некоторого критического значения во избежание разрушения многослойного материала.
ОСНОВНЫЕ ВЫВОДЫ
- Построена адекватная математическая модель, описывающая напряженно-деформированное состояние многослойного материала без трещины, допускающая аналитическое решение исходных дифференциальных уравнений в частных производных при заданных граничных условиях в виде температурных полей.
- Разработан численно-аналитический метод, позволяющий построить решение краевой задачи линейной механики разрушения многослойных материалов с трещиной, внешние боковые поверхности которых подвержены воздействию температурных полей различного вида.
- На основе разработанного метода получено решение актуальной задачи о краевой трещине нормального разрыва, находящейся в первом слое многослойного материала под воздействием внешних заданных температурных полей.
- Разработанный численно-аналитический метод практически реализован в виде пакета программ для определения коэффициента интенсивности напряжений
 при оценке процессов разрушения в решении прикладных задач.
при оценке процессов разрушения в решении прикладных задач. - С помощью разработанного пакета программ впервые определен коэффициент интенсивности напряжений
 при решении температурных задач с краевой трещиной нормального разрыва, находящейся в первом слое многослойного материала.
при решении температурных задач с краевой трещиной нормального разрыва, находящейся в первом слое многослойного материала. - Получены новые аналитические зависимости, с помощью которых исследованы комплексные влияния теплофизических свойств многослойного материала и конкретный вид внешней температуры на коэффициент интенсивности напряжений, что дает возможность создания оптимального сочетания теплофизических характеристик материалов с повышенной прочностью.
- На основании разработанного численно-аналитического метода определены оптимальные сочетания теплофизических характеристик многослойных материалов, тормозящих процесс развития трещины, что позволяет повысить прочностную надежность проектируемых конструкций.
ОСНОВНЫЕ РЕЗУЛЬТАТЫ ИЗЛОЖЕНЫ В СЛЕДУЮЩИХ
СТАТЬЯХ:
- Алексеева, Т.Н. Многослойные материалы под воздействием внешней температуры / В.Д. Кулиев, Т.Н. Алексеева // Вестник ЧГПУ им. И.Я. Яковлева. Серия: Механика предельного состояния. - 2011.- №1(9). – С.143-149. (Перечень ВАК РФ).
- Алексеева, Т.Н. Краевая трещина в двухслойных материалах под воздействием внешней температуры / В.Д. Кулиев, Т.Н. Алексеева // Вестник Чувашского государственного педагогического университета им. И.Я. Яковлева. Серия: Механика предельного состояния. - 2011. - № 2(10). - С.3-15. (Перечень ВАК РФ).
- Алексеева, Т.Н. Аналитическая система Maple 8 для решения задач многослойных сред механики разрушения / Алексеева Т.Н., Лясина Е.С, Моос Е.Н. // Вестник ВГТУ. – 2010. - Т.6; №5. - С.70-73. (Перечень ВАК РФ).
- Алексеева, Т.Н. Применение преобразований Лапласа и Фурье к решению некоторых задач математической физики / Т.Н. Алексеева // Материалы межвузовской научной конференции студентов, аспирантов, молодых ученых и специалистов «Новые технологии и разработки в машиностроении, автоматике, экономике, юриспруденции и образовании». - Коломна: Изд-во КИ(ф)МГОУ. – 2005. - С.33-36.
- Алексеева, Т.Н. Задача о нахождении температуры нестационарного теплового поля в многослойном материале / Е.С. Лясина, Т.Н. Алексеева // МГОУ- XXI- новые технологии. – 2007. - №4. - С.4-7.
- Алексеева, Т.Н. Применение преобразований Лапласа и Фурье к решению уравнения Пуассона / Т.Н. Алексеева, Е.С. Лясина // МГОУ- XXI- новые технологии. – 2007. - №6. - С.5-9.
- Алексеева, Т.Н. Применение теории функций комплексного переменного к решению уравнений математической физики / Т.Н.Алексеева // Материалы II региональной научно-практической конференции студентов, аспирантов, ученых и специалистов «Наука, экономика, общество». - Воскресенск: Изд-во филиала МГОУ в г. Воскресенске. - 2008. – С.61-63.
- Алексеева, Т.Н. Аналитические вычисления при решении уравнения теплопроводности / Алексеева Т.Н., Лясина Е.С, Моос Е.Н. // Тезисы докладов XVII Международной конференции «Математика. Компьютер. Образование». – 2010. - вып.17. - С.79.
- Алексеева, Т.Н. Решение интегральных уравнений на основе системы аналитических вычислений Maple 8 / Алексеева Т.Н., Лясина Е.С, Моос Е.Н. // Тезисы докладов XVII Международной конференции «Математика. Компьютер. Образование». – 2010. - вып.17. - С.80.
- Алексеева, Т.Н. Моделирование температурных полей гетерогенных систем / Алексеева Т.Н., Моос Е.Н. // Тезисы докладов XVIII Международной конференции «Математика. Экономика. Образование». - Ростов на Дону: Изд-во СКНЦ ВШ ЮФУ. – 2010. - С.111-112.
![]()
![]()
![]()
![]()
![]()
![]()

