Численное исследование бифуркаций в задаче о конвекции бинарной смеси в замкнутой области
На правах рукописи
Шкарапута Александр Петрович
ЧИСЛЕННОЕ ИССЛЕДОВАНИЕ БИФУРКАЦИЙ В ЗАДАЧЕ О КОНВЕКЦИИ БИНАРНОЙ СМЕСИ В ЗАМКНУТОЙ ОБЛАСТИ
01.02.05 – Механика жидкости, газа и плазмы
Автореферат
диссертации на соискание ученой степени
кандидата физико-математических наук
Пермь 2006
Работа выполнена на кафедре прикладной математики и информатики Пермского государственного университета
Научный руководитель: доктор физ.-мат. наук, профессор
Русаков Сергей Владимирович
Официальные оппоненты: доктор физ.-мат. наук, профессор
Смородин Борис Леонидович
кандидат физ.-мат. наук, доцент
Перминов Анатолий Викторович
Ведущая организация: Тюменский государственный университет
Защита состоится «20» июня 2006 г. в 1515 на заседании диссертационного совета Д 212.189.06 в Пермском государственном университете по адресу: 614990. г. Пермь, ул. Букирева, 15.
С диссертацией можно ознакомиться в библиотеке Пермского государственного университета.
Автореферат разослан «18» мая 2006 г.
Ученый секретарь диссертационного
совета, доцент Г.И. Субботин
Общая характеристика работы
Актуальность работы. Явления тепло- и массопереноса в смесях являются важной составляющей в ряду общих гидродинамических проблем и имеют большую ценность с точки зрения практических приложений, обусловливающих, в свою очередь, интерес к моделированию и теоретическому изучению. В частности, эффект термодиффузии давно уже используется не только для сегрегации смеси, но и для разделения изотопов, а также при выращивании кристаллов. Это же явление лежит в основе изучения множества других проблем от геологии до астрофизики.
Для исследования процессов тепломассообмена большое значение имеют вопросы, связанные с проблемами возникновения и развития конвективного движения (т.е. относящиеся к теории устойчивости равновесия и течений сплошной среды), так как знание закономерностей устойчивости равновесия и течений во многих случаях позволяет управлять механизмами кризиса.
Данная работа представляет собой численное исследование явлений тепло- и массопереноса (важное значение здесь имеет эффект термодиффузии) в замкнутой области на основе хорошо известных уравнений бинарной нереагирующей смеси.
Простая конфигурация изучаемой полости, близкие к реальным внешние условия, а также выбор для исследования наиболее распространенных смесей дают основание полагать, что результаты имеют конкретные практические приложения. С другой стороны, универсальность подходов и выводов позволяют использовать их для более широкого класса задач.
В замкнутой области для построения линейной теории возникают значительные трудности (зачастую непреодолимые). Исследования же нелинейных эффектов, в особенности для осложняющих факторов, таких как эффект термодиффузии и слабое отклонение градиента температуры от вертикального положения, довольно сложны. Важную роль в таких исследованиях приобретает вычислительный эксперимент.
Цель работы. Исследование нелинейных режимов, возникающих в замкнутой области в результате взаимодействия тепловых и концентрационных механизмов. Поиск методов для изучения и описания бифуркационных картин для амплитудных характеристик решения. Построение бифуркационных карт на основе зависимостей для критических чисел.
Научная новизна диссертационной работы.
1. Впервые для ньютоновских жидкостей достаточно детально проведено исследование бифуркационных картин, которым соответствует до пяти стационарных решений.
2. На основании численных расчетов построены зависимости критических чисел Рэлея от числа Cоре и угла наклона, согласующихся в наиболее простых случаях с линейной теорией для массива с теплоизолированными границами.
3. Для исследования конвекции бинарной смеси получено представление зависимости амплитудных характеристик решения от числа Рэлея в виде корней полинома. Проведен анализ зависимостей коэффициентов полинома от параметров задачи. В результате показано, что с их помощью можно:
– находить критические числа (соответствующие точкам бифуркации);
– отслеживать качественные перестройки бифуркационных картин.
Автором представляются к защите:
– результаты численных расчетов для квадратной (в некоторых случаях прямоугольной) полости, подогреваемой сверху и снизу при вертикальном градиенте температуры с учетом нормального и аномального эффектов термодиффузии для жидких и газовых смесей;
– результаты численных расчетов для квадратной полости подогреваемой сверху и снизу при почти вертикальном градиенте температуры с учетом нормального и аномального эффектов термодиффузии для жидких и газовых смесей;
– результаты обработки бифуркационных картин с помощью представления амплитудных характеристик в виде корней полинома.
Достоверность результатов. Результаты согласуются с данными, представленными в работах других авторов, либо в предельных случаях данной задачи (например, в отсутствии эффекта термодиффузии), либо в случаях с близкими задачами (бесконечный слой, замкнутая область с теплоизолированными границами).
Публикации. Основные материалы диссертации изложены в 14 работах. Во всех работах представлены результаты численных расчетов (для конвекции бинарной смеси и их анализ), выполненных А.П. Шкарапутой. Соавтором работ является научный руководитель соискателя, участвующий в постановке исследуемых задач и обсуждении полученных результатов. В работах [2] и [3] соавтором является А.А. Щипанов, исследовавший проблему кристаллизации в цилиндрической области. В работе [6] соавторами являются И.В. Мельников, Д.В. Порошин, A.Н. Шарифулин. Здесь приводится качественное сравнение численных результатов (полученных Шкарапутой А.П.) с результатами слабонелинейной модели, исследуемой данными авторами.
Апробация работы. Результаты работы докладывались на Всероссийской научной конференции «Фридмановские чтения» (Пермь, IX 1998), International Conference. «Advanced problems in thermal convection» (Perm, XI 2003), 14-й Зимней школе по механике сплошных сред. (Пермь, II 2005), Шестом Всероссийском семинаре «Сеточные методы для краевых задач и приложения» (Казань, IX 2005), Конференции молодых ученых «Неравновесные переходы в сплошных средах» (Пермь, XII 2005), а также на Пермском городском гидродинамическом семинаре имени Г.З. Гершуни и Е.М. Жуховицкого и на кафедре прикладной математики и информатики Пермского государственного университета.
Практическая ценность. Полученные результаты могут быть использованы для разделения компонент смеси, где управляющим параметром может являться угол наклона полости, основой (и критерием применимости) построения моделей, связанных с нелинейными эффектами. Также они могут быть полезны для изучения различных явлений, где важную роль играет термодиффузионный эффект.
Содержание и структура работы. Диссертация состоит из введения, четырех глав, приложения и заключения. Общий объем диссертации составляет 130 страниц, включая 73 рисунка. Список литературы содержит 117 наименований.
Общее содержание работы
Во введении обосновывается актуальность работы, ставятся цели и задачи исследования, сформулированы положения, выносимые на защиту, и приведены сведения об апробации работы.
В первой главе представлен обзор публикаций. Так как диссертационная работа тесно связана с такими понятиями, как конвекция в замкнутой области, тепло- и массоперенос в бинарной смеси (в частности, эффект термодиффузии), устойчивость (неустойчивость) равновесия и течений (в свою очередь связанную с терминами: особенности, бифуркации, катастрофы), то в обзоре, с одной стороны, делается попытка охватить явления, связанные с этими понятиями, с другой - рассмотреть работы, которые наиболее близки к исследуемой задаче. На основании обзора делается вывод об актуальности исследования неустойчивости равновесия и конвективных течений в замкнутой области с учетом эффекта термодиффузии.
Вторая глава посвящена исследованию неустойчивости равновесия бинарной смеси в квадратной (в некоторых случаях прямоугольной) полости при строго вертикальном градиенте температуры.
Система уравнений решалась прямым численным интегрированием с помощью параметрической сплайн-схемы. Основные результаты, характеризующие конвективное движение, представлялись в виде зависимостей экстремальной функции тока от числа Рэлея.
Конвективное движение в бинарной смеси осуществляется с помощью двух механизмов: теплового и концентрационного. Из-за взаимодействия этих механизмов корневой закон, соответствующий конвекции в отсутствие эффекта термодиффузии, может изменяться даже в отсутствие наклона полости.
 |  |  |  |
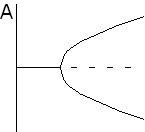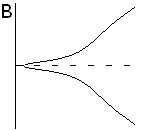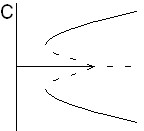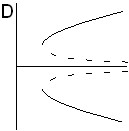| Рис.1. Качественный вид бифуркационных картин при наличии эффекта термодиффузии | |||
Качественный вид бифуркационных картин, полученных для данной постановки задачи, представлен на рис. 1. Рисунку 1,A соответствует обычная корневая зависимость вблизи критической точки. Такая картина соответствует задаче с подогревом снизу и нормальным эффектом термодиффузии при числах Льюиса, сравнимых с единицей (например, для газовых смесей). Аналогичная картина имеет место для задачи с подогревом сверху при аномальном эффекте термодиффузии. На рисунке 1,B представлена бифуркационная картина задачи с подогревом снизу и нормальным эффектом термодиффузии при числах Льюиса, много меньших единицы (например, для жидких смесей). Рисункам 1,C и 1,D соответствует задача с подогревом снизу и аномальным эффектом термодиффузии. На первом из них отображена зависимость при малых (по модулю) числах Соре. В этом случае наблюдается эффект затягивания устойчивости равновесия и имеется критическое число Рэлея, при котором происходит обратная вилочная бифуркация. Рисунку 2 соответствуют большие (по модулю) числа Соре. В этом случае неустойчивые решения не соединяются с осью абсцисс, и их ветви (для газовой смеси при 
) имеют асимптоты.
Бифуркационная карта в случае подогрева снизу для газовой смеси в плоскости «критических» чисел Рэлея (Rac) – числа Соре () представлены на рис. 2. Аналогичные зависимости построены и для жидкой смеси. Показано, что зависимость критических чисел Рэлея (Ra*) от числа Льюиса(Le) и числа Соре с точностью до О() определяется формулой: 
, где коэффициент а=1,5 для квадратной полости, 
соответствует критическому числу Рэлея в отсутствие эффекта термодиффузии.
В области отрицательных чисел Рэлея движение наблюдалось только при аномальном эффекте термодиффузии. Также были построены бифуркационные карты (и эмпирические зависимости) в плоскости критических чисел Рэлея – числа Соре. Для газовых смесей, с ростом числа Соре, в полости вдоль вертикальной оси обнаруживается трехвихревая структура. Средний вихрь вращается в противоположную сторону по отношению к верхнему и нижнему, вследствие этого имеется область, где с ростом числа Рэлея уменьшается эффективный тепловой поток через границы (определяемый числом Нуссельта).
Для более полного исследования эффектов в наиболее интересных случаях представлены зависимости кинетической энергии и числа Нуссельта от числа Рэлея.
В третьей главе рассматривается влияние угла наклона (по отношению к гравитационным силам) на устойчивость равновесия и конвективных течений в квадратной полости.
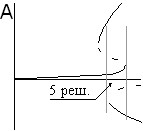
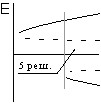
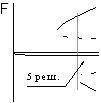
В случае подогрева снизу качественный вид бифуркационных картин с учетом угла наклона при нормальном эффекте термодиффузии показан на рис. 3. Для газовых смесей в этом случае реализуется только ситуация, представленная на рис. 3,D. Для жидких смесей имеют место все четыре ситуации. При соответствующих числах Соре с увеличением угла наклона последовательно реализуются картины под буквами A,B,C и D. На рис. 3,B имеется область гистерезиса между малоамплитудным и высокоамплитудным движением. Этой области соответствует пять стационарных решений.
 |  |  |  |
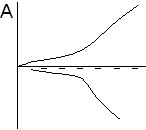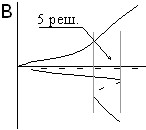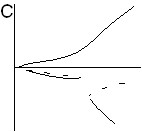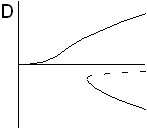| Рис. 3. Качественный вид бифуркационных картин для нормального эффекта термодиффузии при ненулевом угле наклона (подогрев снизу) | |||
Для газовой и жидкой смеси построены бифуркационные поверхности в параметрическом пространстве «критических» чисел Рэлея, чисел Соре и угла наклона. Обозначены границы области, соответствующей пяти решениям (она ограничена не только большими углами наклона, но и большими (по модулю) числами Соре).
 |  |
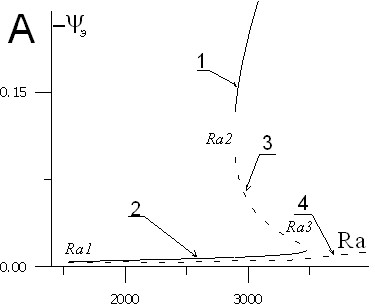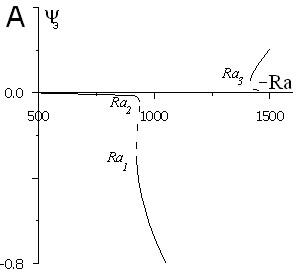
| Рис. 4. A) Зависимость экстремальной функции тока от числа Рэлея для жидкой смеси при угле наклона = 1° и числе Соре = 0.05: 1,2 – устойчивые ветви решения, 3,4 – неустойчивые; B) Зависимости «критических» чисел Рэлея от угла наклона при = 0.05 (1,2,3 – соответствуют Ra1, Ra2 и Ra3) | |
На рис. 4,А представлен количественный вариант бифуркационной картины с явлением гистерезиса при наклоне 1° и 
. На рис. 4,B бифуркационная карта в плоскости «критических» чисел Рэлея – угла наклона при том же значении числа Соре.
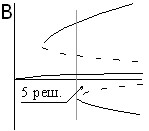
При аномальном эффекте термодиффузии (подогрев снизу) реализуются ситуации, представленные на рис. 5. При появлении угла наклона симметрия пропадает. Бифуркационные картины под буквами A,B,C,D рисунка 5 соответствуют поведению, как газовой, так и жидкой смеси. Из этих картин видно, что в той области, где угол наклона помогает конвекции, движение становится более интенсивным, а вместо нулевого решения (соответствующего механическому равновесию) возникает малоамплитудное. Между малоамплитудным и высокоамплитудным движением может наблюдаться явление гистерезиса (рис. 5,A и рис. 5,С), величина которого меняется с изменением угла наклона. Кроме того, меняется область, соответствующая пяти решениям, и при больших углах наклона она исчезает (рис. 5,С). Если и дальше увеличивать угол наклона, то ветвь малоамплитудного движения сливается с ветвью высокоамплитудного движения и гистерезис между ними пропадает (рис. 5,D).
 |  |  |
 |  |  |
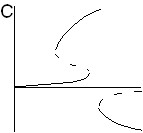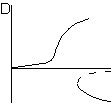| Рис. 5. Качественный вид бифуркационных картин для аномального эффекта термодиффузии при ненулевом угле наклона (подогрев снизу) | ||
В случае малых углов наклона и больших (по модулю) чисел Соре (рис. 5,B) амплитудная характеристика решения, соответствующая малоамплитудному движению, при достаточно больших числах Рэлея становится практически постоянной. Если неустойчивое решение и малоамплитудное решение имеют разные асимптоты, то они не соединяются, следовательно, в этом случае явления гистерезиса не наблюдается. Интересные результаты получаются для газовой смеси при 
. Если
, то малоамплитудное движение пропадает (рис. 5,E), а нулевое решение становится устойчивым при всех значениях числа Рэлея. Картина из-за угла наклона остается несимметричной. Если 
, то наблюдается переворот бифуркационной картины (рис. 5,F) для малоамплитудного движения. Для газовой смеси при 
построены бифуркационные карты в плоскости «критических» чисел Рэлея – угла наклона при различных значениях числа Соре.
 |  |  |  |
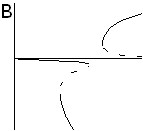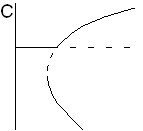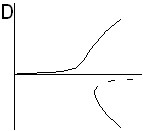| Рис. 6. Качественный вид бифуркационных картин для аномального эффекта термодиффузии при ненулевом угле наклона (газовая смесь, подогрев сверху) | |||
При подогреве сверху и нормальном эффекте термодиффузии в полости возникает течение, причем для газовой смеси с ростом числа Рэлея, как и в случае аномального эффекта термодиффузии, возникает трехвихревое, вдоль вертикальной оси течение. Однако в этом случае все три вихря сонаправлены. В случае аномального эффекта (подогрев сверху) в газовой смеси с ростом (по модулю) числа Соре наблюдается переворот бифуркационной картины (рис. 6, слева направо).
 |  |
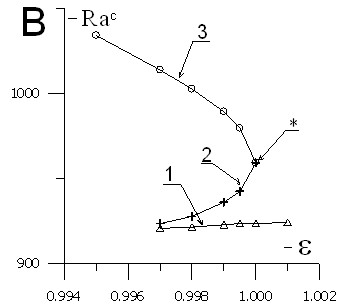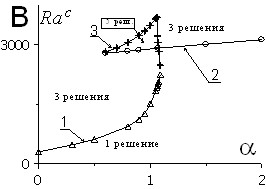
| Рис. 7. A) Зависимость экстремальной функции тока от числа Рэлея для газовой смеси при угле наклона = 20° и числе Соре = –0.999; B) Зависимости «критических» чисел Рэлея от числа Соре при = 20° | |
На рис. 7,А представлен количественный вариант бифуркационной картины с явлением гистерезиса при наклоне 20° и 
, на рис. 7,B бифуркационная карта в плоскости «критических» чисел Рэлея – числа Соре при том же наклоне. Исследованы также зависимости «критических» чисел от числа Соре (в большем диапазоне значений) и от угла наклона полости.
В четвертой главе в тех областях, где число решений равно пяти, зависимости экстремальных значений функции тока от числа Рэлея представляются в виде корней полинома (z z1)(z z2)(z z3)(z z4)(z z5) = 0, где z – амплитудная характеристика решения. В результате строится полиномиальная зависимость z5 Az4 + Bz3 C z2 + D z E = 0, где коэффициенты полинома являются функциями числа Рэлея, числа Соре и угла наклона полости.
Для аномального эффекта термодиффузии, в отсутствии наклона, картина симметрична и полином принимает вид: z(z4 2az2 + b) = 0, где a = B/2 = (z12 + z22 )/2, b = D = z12z22.
Вычисления коэффициентов в этом случае показали, что они имеют линейный (или слабонелинейный) вид (рис. 8). При b=0 число Рэлея совпадает с его критическим значением, если угол наклона этого коэффициента положителен, то неустойчивая ветвь не соединяется с осью абсцисс и имеет асимптоту.
 |  |
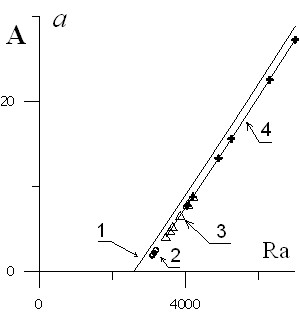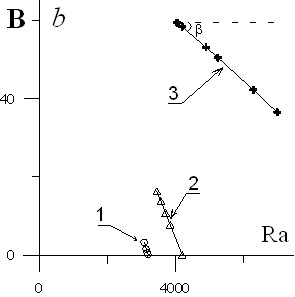Рис. 8. Зависимости коэффициентов для газовой смеси: A) Зависимость а от числа Рэлея: 1 –  , 2 – , 3 –  , 4 –  ; B) Зависимость b от числа Рэлея: 1 – , 2 –  , 3 –  | |
Таким образом, можно записать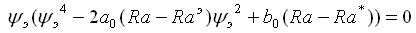 
.
В жидкой смеси 
принимает значения равные 
.
При наличии угла наклона все коэффициенты становятся ненулевыми. Их исследование показало, что они имеют линейный вид. Были проведены расчеты при разных углах наклона и числах Соре. Показано, что зависимости аналогов коэффициентов а и b (В и D соответственно) от числа Рэлея при разных углах наклона ложатся на одну линию. Показано, что с помощью коэффициентов полинома можно исследовать эффект «переворота» с ростом (по модулю) числа Соре. С помощью коэффициентов полинома был исследован и «переворот» при подогреве сверху. Аналогичные расчеты проведены для коэффициентов полинома, полученных при нормальном эффекте термодиффузии для жидкой смеси (в области пяти решений). Во всех случаях коэффициенты полинома имели линейный или слабонелинейный вид.
В этой же главе исследуется применимость лимитационного метода для построения неустойчивых ветвей решения. При использовании этого метода начальные условия строились с помощью комбинации полей (с разными весами), соответствующих устойчивым решениям, между которыми находится неустойчивое решение или с помощью произвольных полей. В результате применения этого метода показано, что он хорошо подходит для построения неустойчивых ветвей решения для бифуркаций разного типа. Приводятся поля функции тока, температуры и концентрации метастабильного решения, с хорошей точностью соответствующего неустойчивому решению.
В приложении рассматривается используемая параметрическая сплайн-схема. Оценивается погрешность результатов в зависимости от шага сетки, показывается, что погрешность величин, полученных численно, не превышает 3%. Рассматривается влияние шага по времени на результаты.
Основные результаты и выводы диссертационной работы
1. Обнаружено большое многообразие бифуркационных картин, обусловленное взаимодействием теплового и концентрационного механизмов переноса.
2. В случае подогрева снизу как при нормальном, так и при аномальном эффекте термодиффузии имеются области параметров задачи, где число стационарных решений равно пяти. В жидкой смеси при нормальном эффекте термодиффузии и наличии угла наклона наблюдается гистерезис между малоамплитудным и высокоамплитудным движением.
3. Для аномального эффекта термодиффузии как при подогреве сверху, так и снизу для газовой смеси с изменением числа Соре обнаружен несимметричный «переворот» бифуркационной картины. При = – 1 имеет место двусторонняя бифуркация.
4. В результате численных расчетов получены формулы для критических чисел Рэлея в зависимости от числа Льюиса и числа Соре. Дана оценка их применимости. В наиболее простых случаях показано, что они согласуются с линейной теорией для массива с теплоизолированными границами.
5. Зависимости амплитудных характеристик решения от числа Рэлея представлены в виде корней полинома. Проведен анализ коэффициентов полинома. Показано, что с их помощью можно находить критические числа Рэлея, судить о поведении неустойчивых ветвей, исследовать качественные перестройки бифуркационных картин.
6. Построены бифуркационные карты в параметрическом пространстве «критических» чисел Рэлея, числа Соре и угла наклона.
7. Для газовой смеси при подогреве сверху, с ростом числа Рэлея, обнаруживается трехвихревая (по вертикали) картина течения. Для нормального и аномального эффекта термодиффузии направление центрального вихря противоположно.
Список публикаций
1. Русаков С.В., Шкарапута А.П. Численное исследование конвекции бинарной смеси в квадратной полости при малых углах наклона // Известия РАЕН. Математика. Математическое моделирование. Информатика и управление. Серия МММИУ. Т. 8, №№ 1-2. Самара, 2004. – C. 55-67.
2. Русаков С.В., Шкарапута А.П., Щипанов А.А. Исследование процессов тепло-, массопереноса бинарной смеси с учетом эффекта термодиффузии // Труды Второй Российской национальной конференции по теплообмену. В 8 томах. Т. 3. Свободная конвекция. Тепломассообмен при химических превращениях. М.: Издательство МЭИ, 1998. – C. 132-135.
3. Русаков С.В., Шкарапута А.П., Щипанов А.А. Исследование процессов рудообразования в интрузивах на основе модели термодиффузии // Фридмановские чтения. Всероссийская научная конференция. Тезисы докладов. Пермь: Пермский ун-т, 1998. – C. 67-68.
4. Русаков С.В., Шкарапута А.П. Проблема устойчивости бинарной смеси в горизонтальном слое // Труды V Международной электронной научной конференции. Современные проблемы информатизации в технике и технологиях. Воронеж, 2000. C. 31-32.
5. Русаков С.В., Шкарапута А.П. Численное моделирование устойчивости механического равновесия бинарной смеси с учетом эффекта Соре // Третья Всероссийская научная internet-конференция. Компьютерное и математическое моделирование в естественных и технических науках. Вып. 12. Тамбов, 2001. C. 10-12.
6. I. Melnikov, D. Poroshin, S. Rusakov, A. Sharifulin, A. Shkaraputa. Influence of the Soret effect on convection of binary fluids in closed cavity with moved wall: analytical and CFD modeling // International Conference. Advanced problems in thermal convection. Abstracts. Perm, 2003. P. 180.
7. Русаков С.В., Шкарапута А.П. Численное исследование влияния эффекта термодиффузии на устойчивость равновесия бинарной смеси // Гидродинамика. Межвуз. сб. науч. трудов. Вып. 14. Пермь, 2004. С. 200-214.
8. Русаков С.В., Шкарапута А.П. Свидетельство об отраслевой регистрации разработки № 3575 от 17 мая 2004 года «Программа численного решения уравнений движения нереагирующей бинарной смеси в приближении Буссинеска с использованием параметрической сплайн-схемы».
9. Русаков С.В., Шкарапута А.П. Исследование бифуркационной картины для задачи о неустойчивости равновесия бинарной смеси в замкнутой области // Научно-Образовательный Центр «Неравновесные переходы в сплошных средах». Итоги работы за 2004 год. Пермь. 2005. – С. 46-49.
10. Русаков С.В., Шкарапута А.П. Численное исследование бифуркаций решений в задаче о конвекции бинарной смеси в замкнутой области. // XIV-я Международная Конференция по Вычислительной Механике и Современным Прикладным Программным Системам. Тез. конф., Алушта, Крым, 2005. С. 398-399.
11. Русаков С.В., Шкарапута А.П. Численное исследование бифуркаций решений в задаче о конвекции бинарной смеси. // 14-я Зимняя школа по механике сплошных сред. Тез. конф., Пермь, 2005. С. 257.
12. Шкарапута А.П. Многообразие бифуркационных картин в задаче о конвекции бинарной смеси в замкнутой области. // Конференция молодых ученых «Неравновесные переходы в сплошных средах» Тез. конф., Пермь, 2005. С. 85-86.
13. Русаков С.В., Шкарапута А.П. Применение аппарата теории катастроф для исследования бифуркационных картин решений в задаче о конвекции бинарной смеси в замкнутой области. // Гидродинамика. Межвуз. сб. науч. трудов. Пермь, вып. 15., 2005. С. 136-148.
14. Русаков С.В., Шкарапута А.П. Проблема нахождения неустойчивых решений в конвективных задачах методом сеток. // Материалы Шестого Всеросийского семинара «Сеточные методы для краевых задач и приложения». Казань, 2005. С.187-191.
Подписано в печать 10.05.2006. Формат 6084 1/16.Бум.офс.
Печать офсетная. Тираж 100 экз. Заказ №____
Отпечатано на ризографе ООО Учебный центр «Информатика»
614990, Пермь, ул. Букирева, 15.
