Математическое моделирование нестационарных температурных полей и напряжений в деталях дискового тормоза, обусловленных пульсирующим подводом тепловой мощности

На правах рукописи

МОИСЕЕНКО МИХАИЛ АНАТОЛЬЕВИЧ

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ
НЕСТАЦИОНАРНЫХ ТЕМПЕРАТУРНЫХ ПОЛЕЙ
И НАПРЯЖЕНИЙ В ДЕТАЛЯХ ДИСКОВОГО ТОРМОЗА, ОБУСЛОВЛЕННЫХ ПУЛЬСИРУЮЩИМ ПОДВОДОМ
ТЕПЛОВОЙ МОЩНОСТИ

01.02.06 – Динамика, прочность машин, приборов и аппаратуры

Автореферат диссертации на соискание ученой степени кандидата

технических наук

Орёл - 2012

Работа выполнена в ФГБОУ ВПО «Брянский государственный технический университет».

Научный руководитель - доктор технических наук, профессор

Сакало Владимир Иванович

Официальные оппоненты: Желтков Владимир Иванович

доктор физико-математических наук,

доцент, профессор ТулГУ;

Болдырев Алексей Петрович

доктор технических наук, доцент,

заведующий кафедрой БГТУ

Ведущая организация - Всероссийский научно-исследовательский

конструкторско-технологический институт

подвижного состава ОАО «ВНИКТИ»

Защита состоится «30» мая 2012 года в 10-00 часов на заседании диссертационного совета Д.212.182.03, созданного на базе ФГБОУ «Гоcуниверситет-УНПК» по адресу: 302020, г. Орёл, Наугорское шоссе, д. 29.

С диссертацией можно ознакомиться в библиотеке ФГБОУ ВПО «Гоcуниверситет-УНПК».

Объявление о защите и автореферат диссертации размещён на официальном сайте Высшей аттестационной комиссии при Министерстве образования и науки Российской Федерации по адресу: http://vak.ed.gov.ru и на официальном сайте ФГБОУ ВПО «Госуниверситет-УНПК» по адресу: http://gu-unpk.ru

Автореферат разослан «. … » апреля 2012 года.

Ученый секретарь

диссертационного

совета Д.212.182.03

ОБЩАЯ ХАРАКТЕРИСТИКА РАБОТЫ

Актуальность темы. Совершенствование тормозной техники является одним из приоритетных направлений развития железнодорожного подвижного состава. Наличие надёжных тормозных систем позволяет повысить экономичность железнодорожных перевозок путём повышения скоростей движения поездов и массы перевозимых грузов.

Наибольшее распространение на железнодорожном подвижном составе получили механические (фрикционные) тормоза, которые по прогнозам экспертов сохранят свои лидирующие позиции и в ближайшем будущем. При разработке конструкций этого вида тормозных устройств большие трудности возникают при оценке нагруженности исполнительного звена тормоза: деталей, образующих фрикционные пары, которые преобразуют кинетическую энергию движения поезда в тепловую. Характеристиками их нагруженности являются уровни максимальных температур и напряжений, возникающих в деталях тормоза.

Получение данных о тепловом и напряжённо-деформированном состоянии деталей тормоза экспериментальными методами требует больших затрат средств и времени. Поэтому большие надежды возлагаются на широкое использование при проектировании тормозных устройств методов математического моделирования. Считается, что их внедрение уменьшит риски принятия нерациональных решений и будет способствовать сокращению затрат на доводку конструкций тормозов железнодорожного подвижного состава.

Для реализации возможностей численных методов на практике необходимо располагать моделями, позволяющими с достаточной точностью описывать процессы теплообмена при торможении. Математические модели, применяемые в настоящее время для исследования температурных полей в деталях фрикционных тормозов, не удовлетворяют этому требованию. Их главный недостаток - низкая адекватность. Причиной этого является использование упрощающих предположений, которые нарушают условия подобия.

Таким образом, математическое моделирование нестационарных температурных полей и напряжений в деталях дискового тормоза, обусловленных пульсирующим подводом тепловой мощности, является весьма актуальной темой исследования.

Объект исследования - механические (фрикционные) тормоза железнодорожного подвижного состава.

Предмет исследования - динамика изменения полей температур и напряжений в деталях дискового тормоза, обусловленных пульсирующим подводом тепловой мощности, возникающим при неполном перекрытии диска тормоза тормозной колодкой.

Область диссертационного исследования соответствует п. 9 Математическое моделирование поведения технических объектов и их несущих элементов при статических, динамических, тепловых, коррозионных и других воздействиях Паспорта специальности 01.02.06 - Динамика, прочность машин, приборов и аппаратуры.

Цель исследования. Обеспечение надёжности тормозных систем железнодорожного подвижного состава путём оценки нагруженности деталей дискового тормоза.

Задачи исследования. Для достижения сформулированной цели были поставлены и решены следующие задачи:

• провести анализ известных теоретических подходов к решению проблемы моделирования полей температур и напряжений в деталях механических (фрикционных) тормозов железнодорожного подвижного состава и способов их практической реализации;
• разработать математическую модель, адекватно описывающую процессы теплообмена при сухом трении в дисковом тормозе скоростного вагона, которая является основой для моделирования полей температур и напряжений в деталях фрикционных тормозов;
• предложить наиболее эффективные методы и алгоритмы реализации этой модели;
• создать на основе выбранных алгоритмов и методов специализированный комплекс программ (СКП) для моделирования нестационарных температурных полей при доминирующем конвективном переносе тепла и определения температурных напряжений, вызванных этими полями, в деталях дискового тормоза скоростного вагона;
• выполнить анализ нагруженности деталей дискового тормоза скоростного вагона, выпускаемого Тверским вагоностроительным заводом (ТВЗ) с помощью разработанного СКП;
• исследовать возможные пути снижения максимальных значений температур и напряжений в деталях тормоза конструкции ТВЗ.

Методы исследования. В работе использованы следующие методы: методы теории подобия; численные методы решения задач математической физики; метод конечных элементов; метод расщепления по физическим процессам; методы декомпозиции области (метод суперэлементов и метод Дирихле-Неймана); методы решения жёстких систем обыкновенных дифференциальных уравнений.

Научная новизна работы:

• разработана математическая модель теплообмена в дисковом тормозе скоростного вагона, позволяющая адекватно описывать процессы выделения и распределения тепла при скольжении накладок по поверхности диска, которая, в отличие от известных моделей, позволяет исследовать не только усреднённые за несколько оборотов диска, но и мгновенные значения температур и напряжений, возникающие в деталях дискового тормоза во время торможения, при соблюдении критериев теории подобия;
• предложено использовать для решения уравнения нестационарной теплопроводности с доминирующим конвективным переносом тепла метод расщепления по физическим процессам, который в случае моделирования теплообмена в деталях дискового тормоза при сухом трении реализуется значительно проще, чем стабилизированные схемы галёркинского типа и менее требователен к ресурсам ЭВМ;
• разработан алгоритм построения функций формы переходных элементов сирендипова семейства в виде шестигранных призм, имеющих от 8-ми до 32-х узлов, использование которых позволяет улучшить hpr-сходимость метода конечных элементов в местах высокой нерегулярности полей температур и напряжений путём локального сгущения сетки и повышения порядка функций формы элемента;
• создан специализированный комплекс прикладных программ (СКП), основанный на реализации методов декомпозиции области (метода суперэлементов и метода Дирихле-Неймана) и позволяющий сократить затраты при проведении многовариантных расчётов сложных объектов путём рационального расчленения сложного объекта на подконструкции и исключения при повторном решении задачи расчёта тех подконструкций, в которые не вносились изменения
• исследована динамика изменения температурных полей в деталях дискового тормоза с учётом перераспределения контактных давлений при тепловом расширении деталей, образующих пару трения.

Достоверность полученных результатов и обоснованность научных выводов и рекомендаций следует из теоретически доказанных условий сходимости решений уравнений математической физики, матричного анализа, выбора адекватных математических моделей для рассматриваемых классов задач, методов расщепления по физическим процессам, сходимости методов декомпозиции области (метода суперэлементов и метода Дирихле-Неймана), сходимости неявных схем Рунге-Кутты, и подтверждается результатами тестирования алгоритмов и хорошим совпадением полученных результатов с теоретическими оценками, расчетными и экспериментальными результатами, полученными другими авторами.

Теоретическую значимость диссертационной работы составляют:

• математическая модель, позволяющая адекватно описать процессы теплообмена при сухом трении в дисковом тормозе, которая построена на фундаментальных результатах, полученных Х. Блоком и И. В. Крагельским (в 1937 году Х. Блок указал на необходимость учёта при сухом трении твёрдых тел конвективного переноса тепла, возникающего при их относительном скольжении; в 1939 году И. В. Крагельский установил, что взаимодействие тел при трении локализуется в некотором объёме материала, который может рассматриваться как «третье тело»);
• способ реализации метода расщепления по физическим процессам, использованного для моделирования теплообмена при сухом трении в деталях дискового тормоза;
• алгоритм построения функций формы переходных элементов сирендипова семейства в виде шестигранных призм, имеющих от 8-ми до 32-х узлов, использование которых позволяет повысить точность и сократить затраты при расчёте конструкций с высокой нерегулярностью полей температур и напряжений;

Практическую ценность диссертационной работы составляют:

• специализированный комплекс прикладных программ;
• результаты исследований динамики изменения полей температур и напряжений в деталях дискового тормоза;
• предложения по снижению максимальных температур и напряжений в деталях дискового тормоза.

Основные результаты и положения диссертации, полученные лично автором и выносимые на защиту:

• математическая модель дискового тормоза скоростного вагона, позволяющая адекватно описывать процессы теплообмена при сухом трении в деталях дискового тормоза;
• способ реализации метода расщепления по физическим процессам, использованного для моделирования теплообмена при сухом трении в деталях дискового тормоза;
• алгоритм построения функций формы переходных элементов сирендипова семейства в виде шестигранных призм, имеющих от 8-ми до 32-х узлов, использование которых позволяет улучшить hpr-сходимость метода конечных элементов в местах высокой нерегулярности полей температур и напряжений путём локального сгущения сетки и повышения порядка аппроксимирующих функций.

Апробации работы. Основные научные и практические результаты работы докладывались и обсуждались на научно-практической конференции «Проблемы и перспективы развития вагоностроения» г. Брянск, декабрь 2006 г.; на XII Международном симпозиуме «Динамические и технологические проблемы механики конструкций и сплошных сред» г. Москва. - МАИ, февраль 2006 г.; на IX Всероссийском съезде по теоретической и прикладной механике, г. Нижний Новгород август 2006 г.; на 58-й научной конференции профессорско-преподавательского состава БГТУ (Брянск, БГТУ, 2007 г.), на международной научно-практической конференции «Наука и производство – 2009» (г. Брянск. - БГТУ, март 2009 г.); на VI Всероссийской научно-практической конференции «Перспективы вагоностроения – 2010» (г. Брянск. - БГТУ, май 2010 г).

Публикации. По теме диссертации опубликовано 6 работ, в том числе 3 в рецензируемых журналах, рекомендованных ВАК.

Структура и объём работы. Диссертационная работа состоит из введения, пяти глав, заключения, списка литературы. Общий объём работы – 128 страниц машинописного текста, 50 рисунков, 7 таблиц и список литературы из 197 наименований.

КРАТКОЕ СОДЕРЖАНИЕ РАБОТЫ

Во введении обоснована актуальность темы диссертации. Сформулированы цель работы, научная новизна и практическая значимость. Приведены сведения о достоверности результатов работы, её апробации, личном вкладе и публикациях автора. Дано краткое содержание диссертации.

В первой главе даётся сравнительный обзор фрикционных тормозов, применяемых на железнодорожном подвижном составе. Анализируется состояние и перспективы использования дисковых тормозов на железнодорожном транспорте. Отмечается, что развитие рельсового подвижного состава идёт по пути интенсификации перевозок. Чтобы отвечать постоянно растущим требованиям к увеличению тормозной мощности, вызванных ростом скоростей движения, увеличением нагрузки на ось и длины составов, конструкция тормозных устройств должна постоянно совершенствоваться.

Для многих зарубежных фирм создание надёжных тормозов c высокой энергоёмкостью стало приоритетной задачей. Её решение они видят в поиске новых конструкционных материалов для изготовления деталей тормоза и оптимизации их геометрических форм. И на этом пути они уже достигли значительных успехов. И одной из составляющих этих успехов является широкое использование методов математического моделирования. Применение этих методов на практике позволило существенно сократить затраты на проектирование и доводку новых и модернизацию существующих конструкций тормозов железнодорожного подвижного состава.

Отмечаются успехи отечественной тормозной науки, связанные с именами Н. П. Петрова, Ф. П. Казанцева И. К. Матросова, Б. Л. Карвацкого, В. Ф. Егорченко, В. М. Казаринова, В. Г. Иноземцева, В. И. Крылова, В. В. Крылова и многих других. Современный этап её развития представлен работами Б. А. Мамота, А. И. Туркова, А. В. Чичинадзе, Б. Г. Кеглина, И. А. Жарова, В. К. Першина, Л. А. Фишбейна, П. А. Тищенко, Д. В. Титарёва и др.

В тоже время анализ тормозных систем, которыми оснащён отечественный подвижной состав, показывает, что они уже не отвечают возросшим требованиям к тормозной мощности. Это негативно сказывается на положении дел в отрасли. Чтобы ускорить процессы проектирования и доводки новых тормозных устройств, необходимо располагать моделями, способными с высокой точностью описывать процессы теплообмена при торможении. Математические модели, которые используются в настоящее время для оценки нагруженности деталей тормозов, не удовлетворяют этому требованию из-за использования упрощающих предположений, которые нарушают условия подобия при моделировании процессов теплообмена при торможении.

Проблема построения модели, адекватно описывающей теплообмен при сухом трении, была решена Х. Блоком в 1937 году. В своей теории распределения тепла при трении он показал, что такая модель должна строиться с учётом конвективного переноса тепла, обусловленного относительным скольжением деталей, образующих пару трения. Для этого случая уравнение теплового баланса имеет вид:

, (1)

где - температура в области ; - время; , и - теплоёмкость, плотность и теплопроводность материала среды соответственно; - скорость движения среды; - источник тепла; – оператор набла.

При торможении интенсивность процесса переноса тепла конвекцией во много раз превышает интенсивности процесса диссипации тепла при теплопроводности. Получение решения уравнения (1) при доминирующем конвективном переносе тепла требует применения специальных численных методов, обладающих большой вычислительной сложностью. Несмотря на это, такой способ моделирования полей температур при торможении широко используется в работах зарубежных авторов. Он позволяет с высокой точностью исследовать температурные поля в деталях тормозов, в том числе, и при термоупругой нестабильности (Thermoelastic Instability Phenomenon), приводящей к появлению зон с аномально высокой температурой (hot-spots). В работах этих авторов для решения уравнения (1) используются стабилизированные схемы галёркинского типа, среди которых предпочтение отдаётся методу Streamline Upwind Petrov-Galekin (SUPG). Недостатками этого метода являются большие затраты на вычисление стабилизирующих членов и сложность выбора оптимального значения параметра стабилизации.

При внешнем трении твердых тел задача транспорта тепла решается сравнительно просто. Для этого случая метод расщепления по физическим процессам оказывается более эффективным способом получения решения уравнения (1), чем метод SUPG. В этом методе уравнение (1) расщепляется на два уравнения, которые описывают процессы более простой физической структуры: первое описывает процесс переноса (транспорта) тепла без теплообмена; второе - процесс теплопроводности (диссипации тепла).

Для областей со сложными геометрическими формами получить решение этих уравнений можно только численными методами, среди которых наибольшей популярностью пользуется метод конечных элементов (МКЭ).

Эффективность применения МКЭ для исследования сложных физических процессов и объектов значительно возрастает при использовании его совместно с методами декомпозиции области (МДО). На основе МДО уже созданы эффективные методы решения задач большой и сверхбольшой размерности, а также задач механического контакта, допускающие глубокое распараллеливание вычислительного процесса.

Первая глава завершается постановкой задачи.

Вторая глава посвящена построению и обоснованию математических моделей теплообмена при фрикционном торможении и выбору наиболее эффективных методов решения задач: нестационарной теплопроводности в движущейся среде, несвязанной термоупругости и механического контакта. Цель решения этих задач: найти распределение температур и температурных напряжений в деталях дискового тормоза скоростного вагона.

Вопросы моделирования теплообмена при торможении рассматриваются применительно к расчёту конструкций тормозов с неохлаждаемыми дисками, в которых практически всё тепло, выделяемое в зоне фрикционного контакта, отводится в детали тормоза. Для этих конструкций тормозов моделирование температурных полей в их деталях сводится к решению двух фундаментальных проблем. Проблемы определения количества тепла, выделяющегося в зоне фрикционного контакта, и проблемы распределения этого тепла между деталями тормоза.

Модель теплообмена в зоне фрикционного контакта строится на основе фундаментального результата полученного И. В. Крагельским и опубликованного в 1939 году в его основополагающей работе «О трении несмазанных поверхностей». В ней И. В. Крагельский обосновал тот факт, что взаимодействие тел при трении локализуется в некотором объёме материала. Этот объём может рассматриваться как «третье тело».

На основе этого результата была построена модель, описывающая теплообмен при сухом трении (рис. 1). В ней условия взаимодействия между накладками и диском тормоза описываются параметрами промежуточного («буферного») слоя, такими, как: - толщина буферного слоя; - теплоёмкость; - плотность; - теплопроводность материала среды и - объёмная интенсивность тепловыделения.

Предложенная методика вы­числения этих параметров позво­ляет учесть влияние шероховатости поверхностей и распределения кон­тактных давлений на теплофизические свойства материала «буферного слоя».

Тепловыделение при трении моделировалось заданием в буферном слое объёмного источника тепла, интенсивность которого эквивалентна интенсивности поверхностного источника :

, (2)

где - коэффициент трения; - линейная скорость; - распределение контактных давлений.

Разработанная модель теплообмена в дисковом тормозе скоростного вагона позволила упростить решение задачи внешнего трения и свести её к решению задачи нестационарной теплопроводности в неоднородной движущейся среде. Для её решения был выбран метод расщепления по физическим процессам. Его алгоритм можно представать в операторном виде. После расщепления уравнение (1) примет вид:

(3)

где ; ;; .

Алгоритм решения операторного уравнения (3) состоит в последовательном выполнении следующих шагов:

(4)

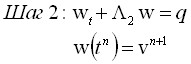(5)

На шаге 1 решается гиперболическое уравнение (4), описывающее конвективный перенос тепла (без теплообмена между частицами тела (среды)). На шаге 2 решается уравнение нестационарной теплопроводности в неподвижной среде (без конвективного члена) (5), которое описывает процессы теплопроводности (диссипации тепла) в теле (среде). Переход на новый временной слой происходит на шаге 3.

Решение задачи (4) при эйлеровом способе описания движения тепла, переносимого диском тормоза, относительно его неподвижной конечноэлементной сетки сводится к нахождению значений температур в узлах этой сетки, смещенных в положение, которое они занимали на предыдущем шаге по времени. В случае равномерной сетки решение этой задачи тривиально. Реализация алгоритма решения этой задачи для нерегулярных сеток при переменном шаге по времени тоже очевидна и не вызывает особых сложностей.

В рассматриваемом алгоритме наибольшие трудности связаны с решением задачи (5). Для её решения использовался метод частичной дискретизации, в котором дискретизация по пространству и по времени осуществляется разными методами.

Для дискретизации по пространству использовался МКЭ. В результате конечноэлементной дискретизации уравнение (5) было преобразовано в систему обыкновенных дифференциальных уравнений (ОДУ):

, (6)

где С - глобальная матрица теплоёмкости; U - вектор узловых температур; - вектор производных по времени узловых температур; K - глобальная матрица теплопроводности; f - глобальный вектор тепловых сил.

Сложность решения системы уравнений (6) состоит в её высокой жёсткости. Для решения жёстких систем ОДУ необходимы специальные методы. Их эффективность зависит от свойств системы (6), поэтому была реализована библиотека методов решения жёстких ОДУ. В неё вошли -методы и неявные многостадийные методы Рунге-Кутты 2-го и 3-го порядков точности, которые были разработаны для решения задачи нестационарной теплопроводности с быстро меняющимися граничными условиями.

Для описания процесса теплоотдачи от деталей тормоза во внешнюю среду использовались граничные условия 3-го рода:

, (7)

где - коэффициент теплоотдачи; - температура поверхности детали; - температура окружающей среды.

Граничные условия в форме (7) позволяют описать теплоотдачу конвекцией и излучением, поэтому коэффициент является нелинейной функцией температуры.

Из формулы (2) следует, что для вычисления тепловыделения в зоне фрикционного контакта необходимо задать контактные давления между диском тормоза и накладками. Контактные давления определялись из решения задачи механического контакта. При этом учитывались тепловые деформации деталей тормоза, которые приводят к перераспределению давлений в зоне фрикционного контакта.

Для определения тепловых деформаций деталей тормоза использовалось уравнение несвязанной термоупругости в перемещениях:

, ,

где - вектор перемещений; - коэффициенты Ляме, характеризующие упругие свойства среды; - коэффициент линейного расширения; - температура; - область определения.

Для решения контактной задачи использовался апробированный и хорошо зарекомендовавший себя метод, основанный на алгоритме Дирихле-Неймана. В известных реализациях он используется в форме «точка-точка». Для конечных элементов высоких порядков точности более удобной оказывается реализация этого алгоритма в форме «точка-сегмент», которая позволяет работать и с несогласованными конечноэлементными сетками контактирующих деталей.

Третья глава посвящена описанию специализированного комплекса программ, реализующего алгоритмы и модели, разработанные во второй главе.

Для задачи нестационарной теплопроводности с доминирующим конвективным переносом тепла, отличающейся высокой нерегулярностью решений, проблема оптимального разбиения деталей тормоза на конечные элементы стоит особенно остро. Один из путей её решения – это использование переходных элементов, которые позволяют строить конечноэлементные сетки, состоящие из элементов различных порядков точности. С этой целью автором был разработан и реализован алгоритм, позволяющий генерировать функции формы переходных элементов сирендипова семейства в виде шестигранных призм с 1-го по 3-й порядки точности. Для этого случая подмножество элементов этого семейства состоит из 531441-го (312) типа переходных элементов, которые могут иметь от 8-и до 32-х узлов. Элементы этого семейства относятся к классу неполных элементов и имеют минимальное число узлов по сравнению с элементами других семейств при одинаковом порядке функций формы.

Другой особенностью СКП является реализация его в виде виртуальной машины, которая программируется путём задания сценария сборки сложного объекта из подконструкций. Достоинством такого подхода является сокращение затрат на проведение многовариантных расчетов сложной конструкции.

Комплекс программ состоит из 6 автономных модулей, которые автоматизируют основные этапы подготовки и проведения вычислений, начиная с генерации конечноэлементной сетки и заканчивая визуализацией результатов расчёта.

В четвертой главе представлены результаты анализа нагруженности деталей механической части дискового тормоза скоростного вагона Тверского вагоностроительного завода (ТВЗ), которые показаны на рис 2. Во время торможения клещевой механизм с усилием 23 кН воздействует башмак 3, который прижимает накладки 2 к диску 1.

Зеркальная симметрия конструкции тормоза позволяет ограничиться анализом теплового и напряжённо-деформированного состояний только одной из её симметричных половин. Конечноэлементная модель, которая использовалась для анализа нагруженности деталей тормоза, показана на рис. 3. Она состоит из 24644 переходных элементов и имеет 117836 узлов.

Тепловыделение и неидеальный термический контакт между деталями тормоза моделировался с помощью контактных элементов.

Оценка нагруженности деталей тормоза выполнялась для режима экстренного торможения: скорость начала торможения - 160 км/ч; время торможения до полной остановки - 52 с.

Распределение температур и интенсивностей температурных напряжений на поверхности диска тормоза для этого режима торможения в зависимости от времени торможения показаны на рис. 4 и рис. 5 соответственно.

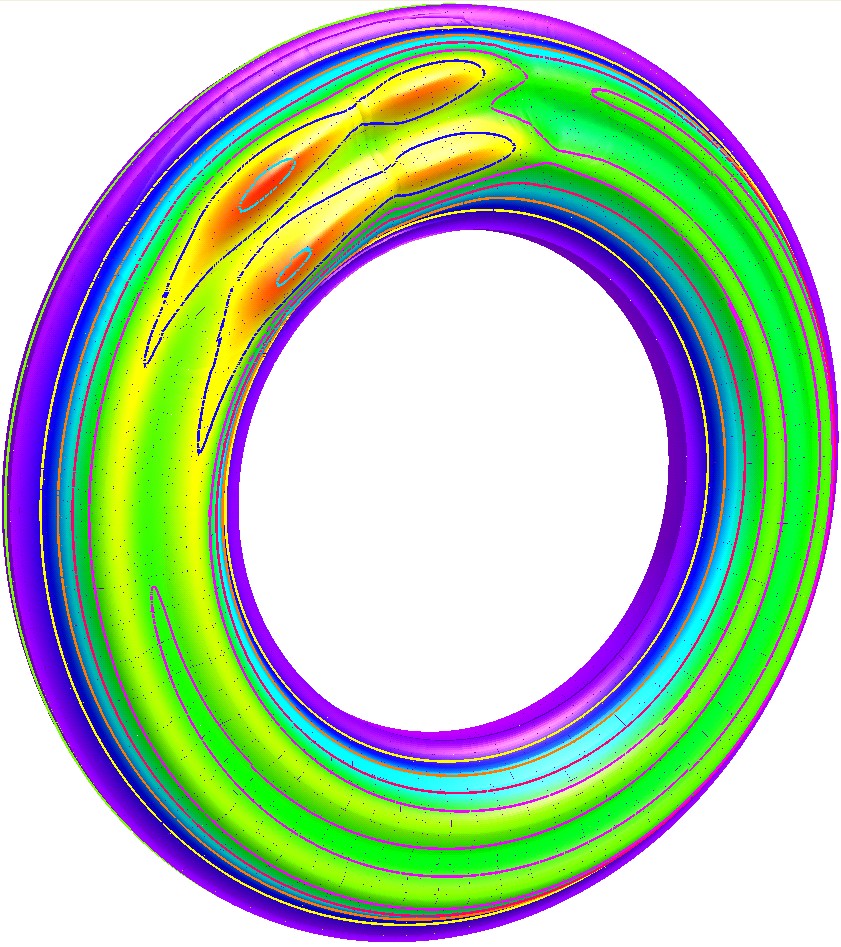
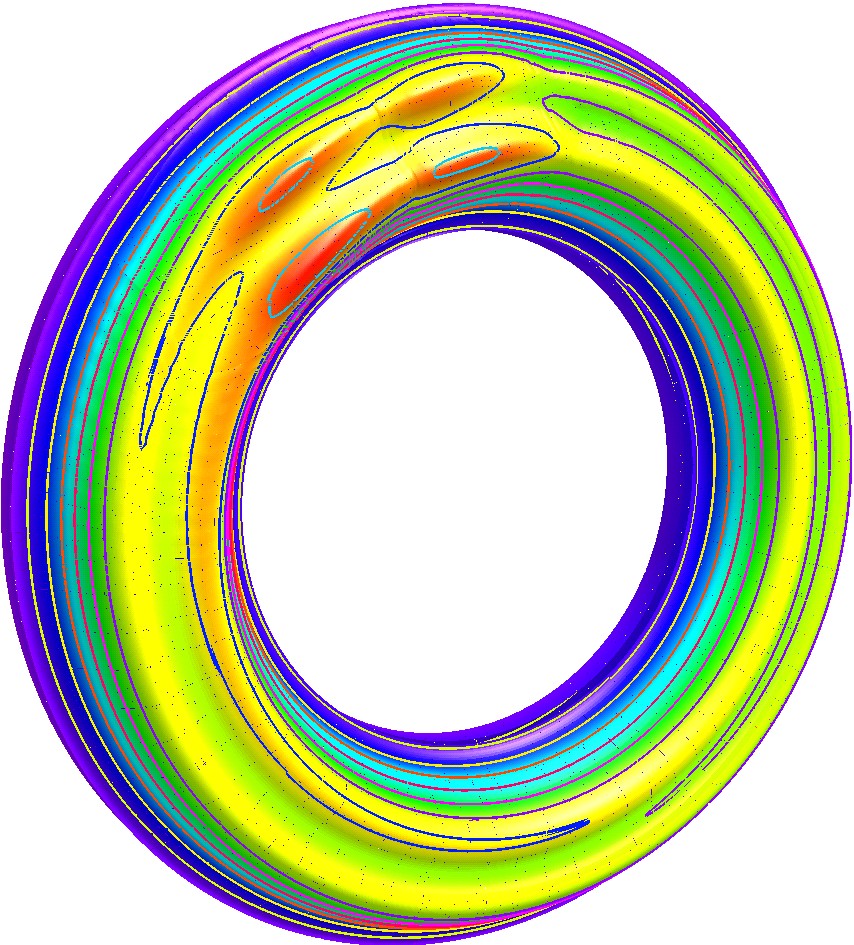
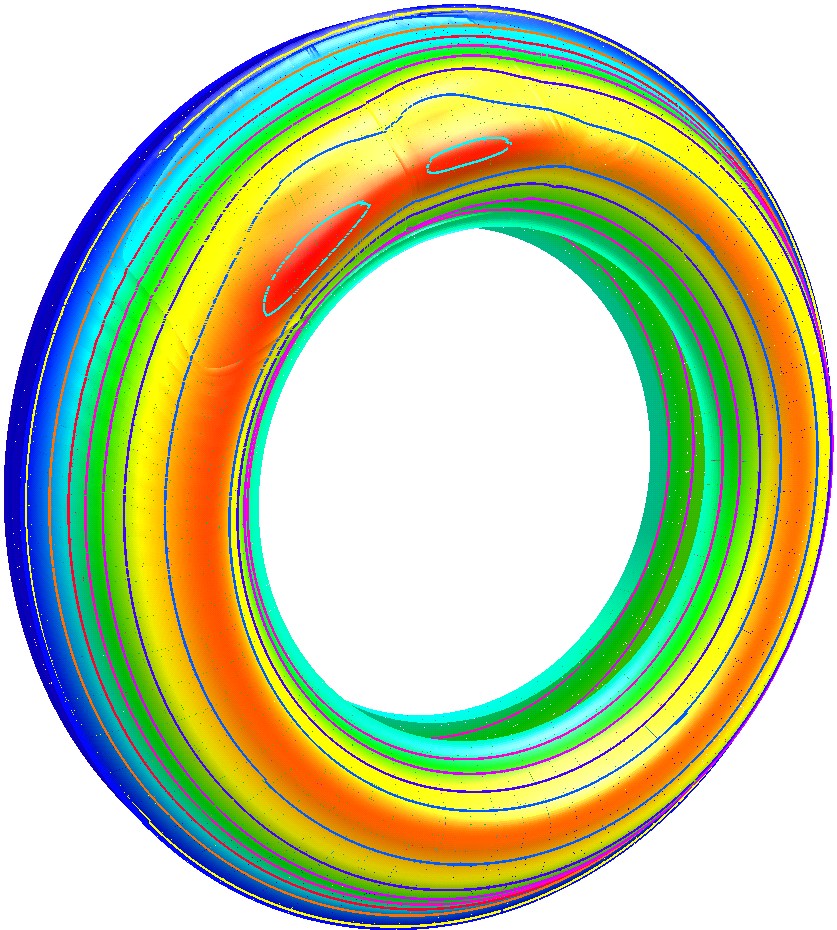
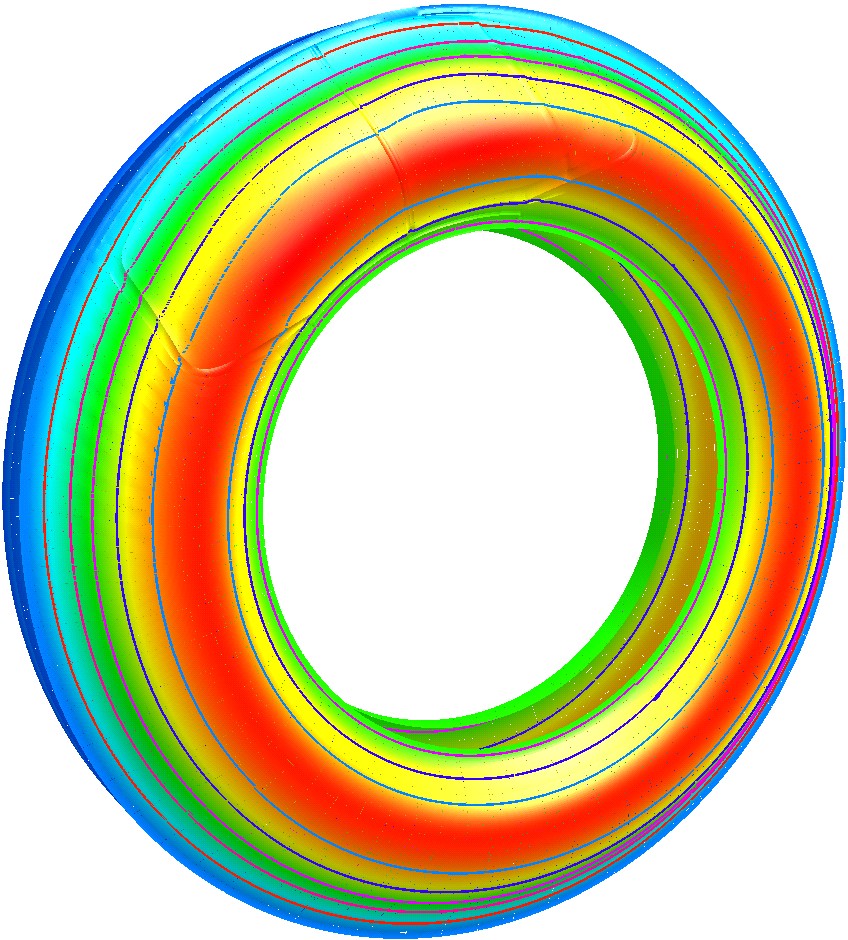
Расчет температурных полей выполнялся с переменным шагом по времени: в начале торможения он составлял 2,4 мс; в конце торможения он соответствовал времени поворота диска на угол равный 3-м градусам.

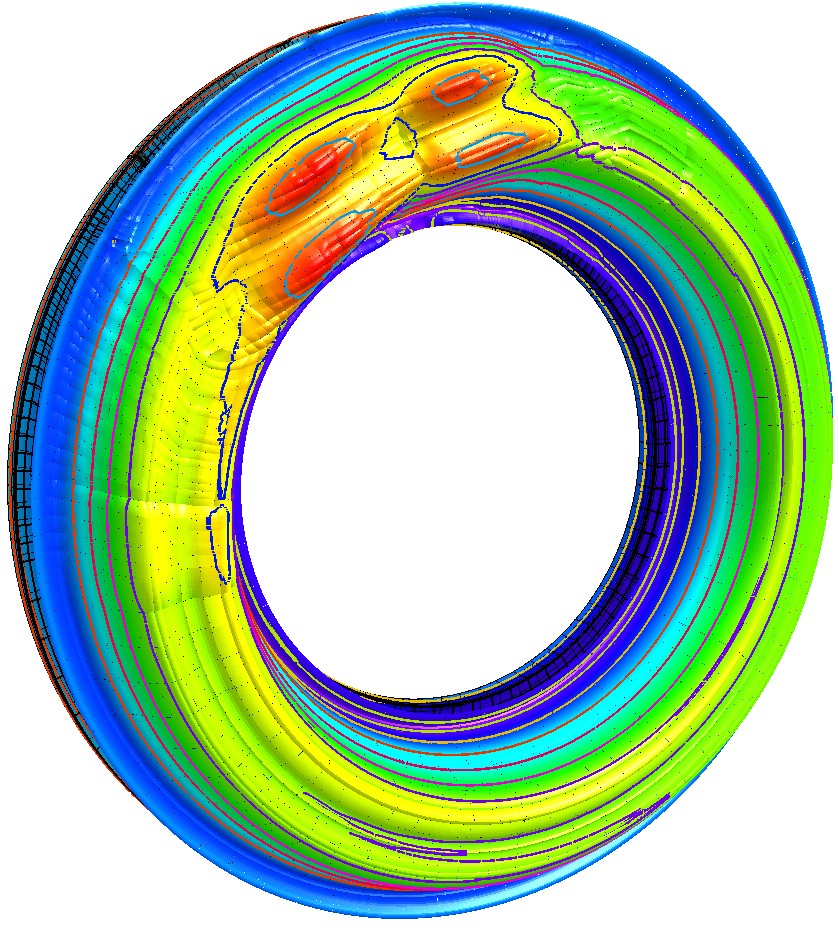
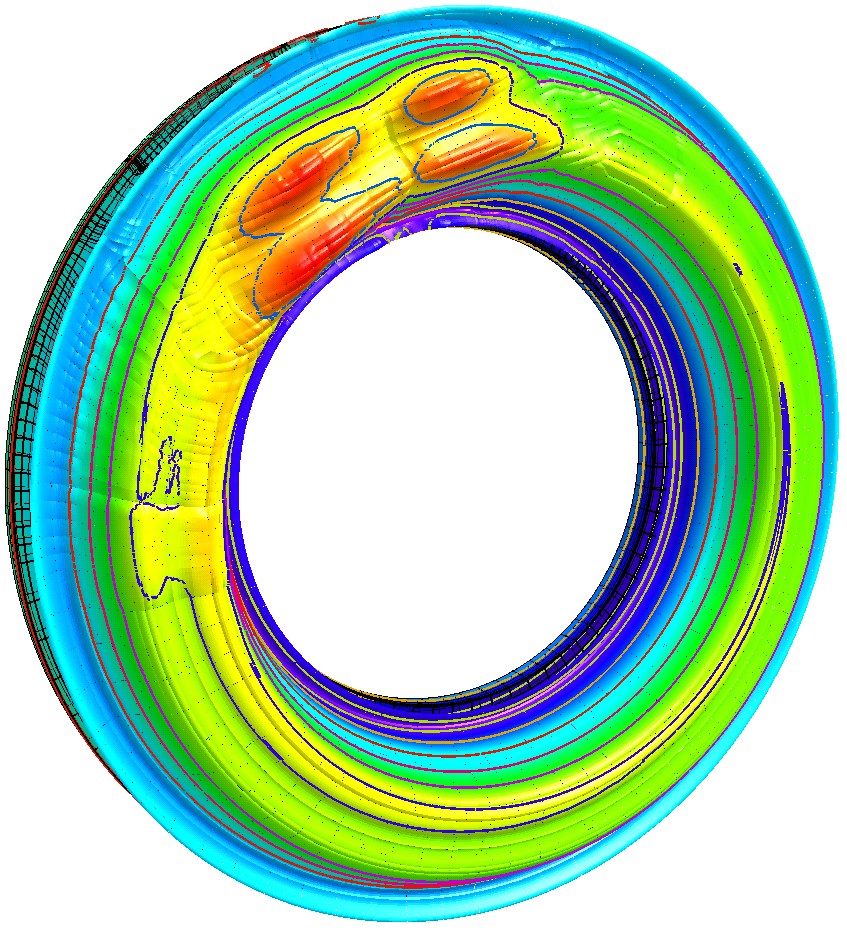
Согласно представленным данным уже на первых секундах торможения на поверхности диска тормоза возникают большие температурные напряжения. Своего максимума они достигают на 7-й секунде торможения. В этот момент времени значение максимума интенсивности температурных напряжений составляет 902 МПа. Напряжения на поверхности диска, где интенсивность температурных напряжений достигает максимума, сжимающие: в тангенциальном направлении они достигают -907 МПа, а в радиальном - -897 МПа. В этот момент времени температура на поверхности диска составляет 382С, что на 100С ниже, чем её абсолютный максимум, которого она достигает на 31-й секунде торможения. Далее напряжения начинают снижаться, хотя температуры на поверхности диска продолжают расти. Своего максимума 492С они достигнут к концу 31-й секунды торможения, после чего начнут снижаться. В конце торможения на 52-й секунде их максимум составит 391С, а максимум интенсивности температурных напряжений – 437 МПа.

Изменение температур и напряжений по толщине и окружности диска на 7-й секунде торможения показаны на рис. 6. На нём видно, что размах колебаний температуры достигает максимума на поверхности диска и быстро уменьшается с удалением от поверхности диска. На глубине 1,5…2,0 мм колебаний температуры уже нет.

Рассмотренные колебания температуры опасны тем, что колебания температуры с размахом в несколько десятков градусов могут вызывать колебания температурных напряжений с размахом в несколько сотен мегапаскалей. Так, на 7-й секунде торможения размах колебаний температуры на поверхности диска составляет 90С, а размах колебаний интенсивности температурных напряжений - 327 МПа.

Согласно представленным данным диск тормоза является высоко нагруженной деталью даже при относительно невысоких скоростях торможения. Максимальные значения интенсивности напряжений на поверхности диска достигают 902 МПа. Однако продолжительность действия напряжений такой величины составляет несколько десятых долей секунды. В том месте материал детали испытывает всестороннее сжатие: главные напряжения и имеют значения -4, -897 и -907 мегапаскалей соответственно. Минимальное значение интенсивности температурных напряжений в этом месте составляет 595 МПа.

Значения температурных напряжений, возникающие в этих деталях, значительно ниже, чем в диске тормоза. Из-за большой толщины накладок в них возникают высокие значения интенсивности напряжений. Это сжимающие напряжения. Они не оказывают существенного влияния на работоспособность этой детали.

В пятой главе рассмотрены пути снижения нагруженности деталей дискового тормоза скоростного вагона.

Общепризнанной рекомендацией, позволяющей снизить нагруженность деталей тормоза, является выбор материала с высокой теплопроводностью.

В качестве материалов, которые могут стать альтернативой стали 20Х13, являются чугуны и алюминиевые сплавы. Их механические свойства не уступают сталям, а коэффициент теплопроводности значительно выше. Например, бейнитный чугун имеет хорошее сочетание теплофизических и прочностных свойств: коэффициент теплопроводности k =45 Вт/(мК), удельная теплоёмкость c=500 Дж/(кгК), плотность =7250…7350 кг/м3, коэффициент линейного расширения =1,0110-5 К-1, коэффициент Пуассона =0,267, модуль упругости при растяжении E=1,6…2,01011 Па, временное сопротивление в=900…1500 МПа, предел текучести 0,2=700…1260 МПа. По наиболее важным показателям (k, в, 0,2) этот чугун в 1,2…2,0 раза превосходит сталь 20Х13.

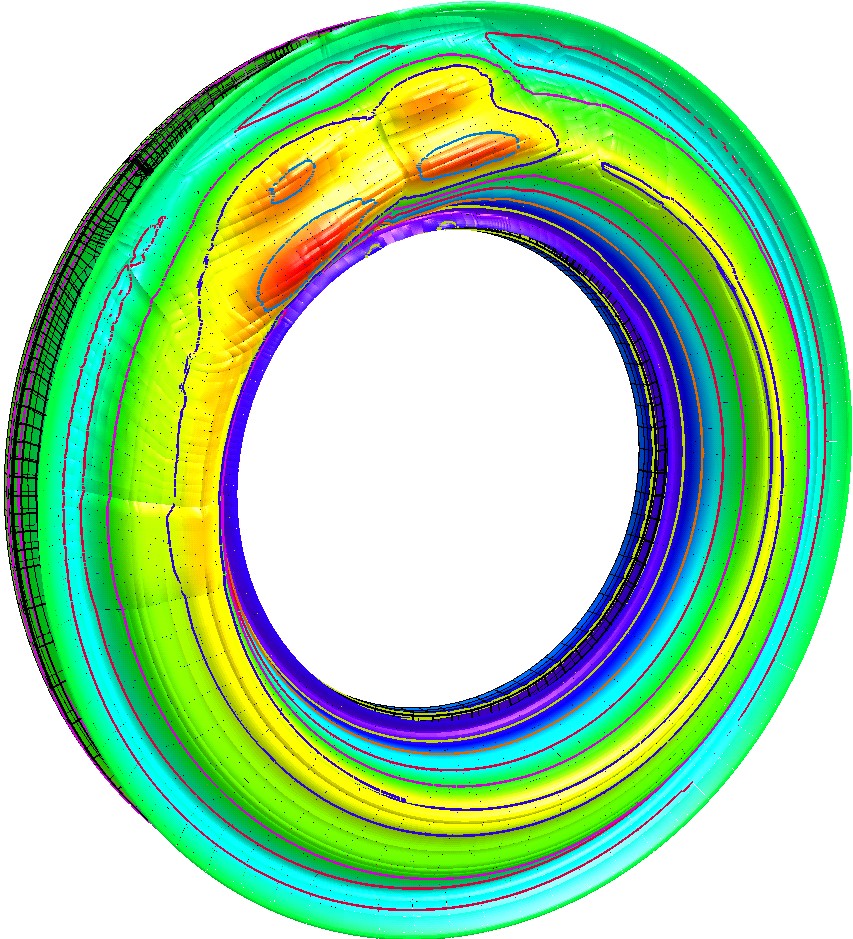
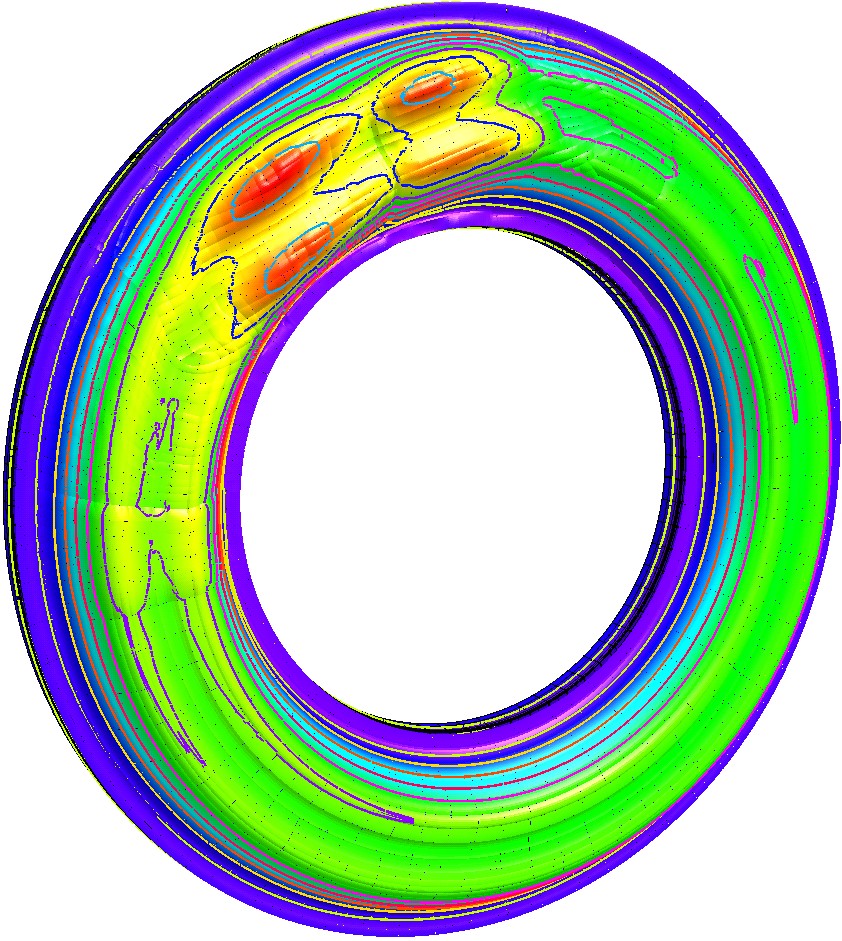
На рис. 7 и 8. представлены результаты исследований полей температур и напряжений в чугунном и стальном дисках тормоза. Параметры торможения те же, что и в предыдущем разделе: скорость начала торможения - 160 км/ч; время торможения до полной остановки - 52 с.

Своих максимальных значений 902 МПа в стальном и 742 МПа в чугунном дисках интенсивности температурных напряжений достигают на 7-й секунде торможения. Максимальные температуры в этот момент времени на поверхности стального диска составляют 382С, на поверхности чугунного диска - 346С.

Представленные данные показывают, что в чугунном диске тормоза значения максимальных температур и максимальной интенсивности температурных напряжений ниже, чем в стальном диске на 12% и 18% соответственно. Это говорит о том, что использование чугунов в качестве материалов для изготовления дисков тормозов является очень перспективным направлением.

Наряду с применением материалов с высокой теплопроводностью оптимизация геометрической формы деталей тормоза является одним из эффективных путей снижения их нагруженности.

В настоящем разделе представлены результаты исследования нагруженности диска тормоза при изменении его толщины. Для простоты сопоставления результатов расчёта моделирование температур и напряжений в деталях тормоза осуществлялось при тех же параметрах торможения, что и ранее: скорость начала торможения - 160 км/ч; время торможения до полной остановки - 52 с.

На рис. 9 представлены значения максимальных температур и интенсивностей температурных напряжений на поверхности стального диска при уменьшении его толщины с 40 мм до 30 мм.

Согласно представленным данным, максимальные значения температур при уменьшении толщины диска на 10 мм увеличились в среднем на 3%, а интенсивность температурных напряжений снизилась в среднем на 8%. Максимального значения 762 МПа на поверхности диска интенсивность напряжений достигает на 7-й секунде торможения. Это на 143 МПа меньше, чем в диске толщиной 40 мм. Более быстрый прогрев диска с меньшей толщиной приводит к тому, что максимум температурных напряжений 512С достигается уже на 25-й секунде торможения.

ЗАКЛЮЧЕНИЕ

В результате проведённых исследований была решена актуальная научно-техническая задача, имеющая существенное значение для развития страны. Её решение создало условия для широкого использования методов математического моделирования на практике, что позволит сократить сроки и затраты при разработке новых и совершенствовании существующих конструкций дисковых тормозов железнодорожного подвижного состава. Основные результаты диссертационной работы состоят в следующем:

1. Разработана математическая модель, позволяющая адекватно описывать процессы теплообмена при торможении и определять действительные (мгновенные) значения температур и напряжений в деталях дискового тормоза при любых режимах торможения.
2. Предложено для сокращения затрат на решение уравнения нестационарной теплопроводности с доминирующим конвективным переносом тепла использовать метод расщепления по физическим процессам.
3. Разработан и реализован алгоритм формирования переходных элементов высоких порядков точности, использование которых делает возможным построение экономичных hpr-схемы конечных элементов при исследовании полей температур и напряжений в деталях дискового тормоза, которые отличаются высокой нерегулярностью полей температур и напряжений.
4. Создан специализированный комплекс прикладных программ (СКП), автоматизирующий весь цикл проведения моделирования, начиная от генерации конечноэлементной сетки и заканчивая графическим представлением результатов расчёта
5. Исследована динамика изменения полей температур и напряжений в диске тормоза Тверского вагоностроительного завода, которую можно охарактеризовать следующим образом:

1. колебания температуры и напряжений наблюдаются в тонком поверхностном слое, толщина которого составляет 1,5…2 мм;
2. при экстренном торможении со 160 км/ч размах колебаний температуры на поверхности диска через 2,4 мс после начала торможения составляет 138С и постепенно снижается: на 1-й секунде торможения он равен 97С; на 5-й - 95С; на 10-й - 50С; на последних секундах торможения (50…52с) размах колебаний температуры практически равен нулю;
3. размах колебания температуры в несколько десятков градусов вызывают колебания интенсивности напряжений с размахом в несколько сотен мегапаскалей; так на 7-й секунде торможения размах колебаний температуры составляет 90С, а размах колебаний интенсивности напряжений достигла 327МПа;
4. максимумы температур и напряжений не совпадают по времени: максимум интенсивности напряжений 902 МПа достигается на 7-й секунде торможения, а максимум температуры 492С – на 31-й секунде;
5. действие пульсирующих сжимающих напряжений, величина которых превосходит предел текучести стали 20Х13, наблюдается в интервале 0,2…0,3 секунды; при этом на поверхности диска тормоза возникают сжимающие напряжения: в окружном направлении они достигают значения -907 МПа, а радиальном - -897 МПа.

6. Установлено, что достичь снижения температур и напряжений в диске тормоза можно:

1. путём замены материала диска тормоза, который изготавливается из жаропрочной стали 20Х13, на бейнитный чугун; в результате моделирования было установлено, что в этом случае максимальные значения температур и интенсивности напряжений в чугунном диске ниже, чем в стальном на 48С и 162 МПа соответственно;
2. путём уменьшения толщины диска тормоза; исследования показали, что при уменьшении толщины диска на 10 мм максимальных значений интенсивности температурных напряжений уменьшаются в среднем на 8%, а значения максимальных температур при этом возрастают в среднем на 3%.

Таким образом, разработанная математическая модель теплообмена в дисковом тормозе скоростного вагона учитывает все основные факторы, влияющие на тепловое и напряжённо-деформированное состояние деталей дискового тормоза. Объёма выходных данных, получаемых при её использовании, достаточно для оценки надёжности и прогнозирования ресурса деталей дискового тормоза.

ОСНОВНЫЕ ПУБЛИКАЦИИ ПО ТЕМЕ ДИССЕРТАЦИИ

В рецензируемых научных журналах, рекомендованных Высшей аттестационной комиссией при Министерстве образования и науки

Российской Федерации:

1. Моисеенко, М. А. Моделирование температурных полей в деталях дискового тормоза / М. А. Моисеенко, В. И. Сакало // Вестник Брянского государственного технического университета. – 2009. - №2(22). – С. 57-64.
2. Моисеенко, М. А. Моделирование процессов теплообмена в дисковом тормозе скоростного вагона / М. А. Моисеенко // Вестник Брянского государственного технического университета. - 2011. - № 4. - С. 65-70.
3. Моисеенко, М.А. Анализ нагруженности деталей дискового тормоза скоростного вагона // Современные проблемы науки и образования. – 2012. – № 2; URL: http://www.science-education.ru/102-5906 (дата обращения: 03.04.2012).

Статьи в научных журналах, сборниках научных трудов и материалов конференций

4. Моисеенко, М. А. Использование переходных элементов высоких порядков точности для расчёта нестационарных полей в деталях дискового тормоза / М. А. Моисеенко, В. И. Сакало // Материалы III Всероссийской научно-практической конференции «Проблемы и перспективы развития вагоностроения». – Брянск: БГТУ.- 2006. – С. 61-64.
5. Моисеенко, М. А. Решение задачи термоупругости с использованием переходных конечных элементов высокой точности / М. А. Моисеенко, Г. А. Неклюдова // Материалы XII Международного симпозиума «Динамические и технологические проблемы механики конструкций и сплошных сред». Избранные доклады. – М.: Изд-во МАИ, 2006. – С. 121-124.
6. Моисеенко, М. А. Использование элементов высокой точности для рас­чета нестационарных полей в деталях дискового тормоза / М. А. Мои­сеенко, Г. А. Неклюдова, В. И. Сакало // IX Всероссийский съезд по теоретической и прикладной механике. Аннотации докладов. Т. III. – Нижний Новгород.: Изд-во Нижегородского ун-та, 2006. – С. 15.

Подписано к печати 23.04.2012 г. Формат 60х84 1/16.

Объем 1,0 усл. п.л. Тираж 100 экз. Заказ № 1457

---------------------------------------------------------------------------------------------------------------------

Отпечатано с готового оригинал-макета на полиграфической базе

ФГБОУ ВПО «Государственный университет – учебно-научно-производственный комплекс»

302020, г. Орел, Наугорское шоссе, 29.