Математическое моделирование нестационарной нелинейной динамики электр о механической системы вибротранспортирующая машина
На правах рукописи
АЗАРОВ Евгений Борисович
МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ
НЕСТАЦИОНАРНОЙ НЕЛИНЕЙНОЙ ДИНАМИКИ
ЭЛЕКТРОМЕХАНИЧЕСКОЙ СИСТЕМЫ
«ВИБРОТРАНСПОРТИРУЮЩАЯ МАШИНА»
Специальность 01.02.06 – Динамика,
прочность машин, приборов и аппаратуры
Автореферат
диссертации на соискание ученой степени кандидата
технических наук
Екатеринбург
2007
Работа выполнена в Государственном образовательном учреждении высшего профессионального образования «Уральский государственный университет путей сообщения» (УрГУПС) Федеральное агентство железнодорожного транспорта
Научный руководитель – доктор технических наук
Румянцев Сергей Алексеевич
Официальные оппоненты:
доктор технических наук, профессор Афанасьев Анатолий Ильич кандидат технических наук Спевак Лев Фридрихович
Ведущая организация – Государственное образовательное учреждение высшего профессионального образования «Уральский государственный технический университет» (УПИ).
Защита состоится 08 мая 2007 г. в 14 часов на заседании Диссертационного совета Д 004.023.01 при Институте машиноведения УрО РАН по адресу: 620219, г. Екатеринбург, ул. Комсомольская, 34.
С диссертацией можно ознакомиться в библиотеке института
Автореферат разослан «06» апреля 2007 г.
Отзывы на автореферат, в двух экземплярах, заверенные гербовой печатью, просим направлять в адрес диссертационного совета по почте.
Ученый секретарь диссертационного совета Харламов В.В.
ОБЩАЯ ХАРАКТЕРИСТИКА РАБОТЫ
Актуальность. В горнодобывающей промышленности, на металлургических предприятиях и транспортных узлах широко применяются всевозможные вибрационные машины, и в частности вибротранспортирующие машины (ВТМ): вибротранспортеры, вибрационные конвейеры и питатели, вибрационные грохоты и т.п. (рисунок 1).
а) 
б)
Рисунок 1 – Вибротранспортирующие машины
В последнее время большое распространение получили машины, в которых вибровозбудители (ВВ) механически не связаны друг с другом, а синхронный режим их вращения обеспечивается за счет явления самосинхронизации (рисунок 1, б). первые исследования динамики вибрационных машин с самосинхронизирующимися ВВ принадлежат отечественным ученым. в основном их работы были посвящены установившемуся синхронному движению или установившемуся принудительно синхронизированному движению.
В последние годы стали появляться первые работы, в которых рассматриваются не только установившиеся, но и переходные динамические процессы, т.е. нестационарная нелинейная динамика, приводящая к синхронизации ВВ. В большинстве работ, посвященных динамике ВТМ, вращающий момент приводных двигателей представлен как некоторая функция, зависящая только от скорости вращения ротора (т.н. статические механические характеристики приводных двигателей).
Между тем, при пуске и при ударных нагрузках на машину в двигателях могут возникать (и возникают) переходные динамические процессы, при которых зависимость вращающего момента от угловой скорости весьма сильно отличается от статической характеристики. Учет этих явлений позволяет не только более точно описать влияние двигателей на нестационарную динамику ВТМ, но и влияние динамики ВТМ на электромагнитные процессы в двигателе, и, как следствие, оценить энергозатраты, возникающие при работе машины.
В данной работе сформулирована задача построения комплексной синтетической математической модели электромеханической системы, состоящей из двух приводных электродвигателей и ВТМ.
Анализ взаимной динамики ВТМ и двигателей позволяет уже на стадии проектирования машины оценить длительность переходных процессов, длительность и величины протекающих по обмоткам двигателей токов. Известно, что на практике имеют место случаи, когда двигатели выходят из строя из-за длительного переходного процесса в ВТМ. длительность этого переходного процесса зависит от ряда физических и геометрических параметров самой ВТМ и приводных электродвигателей. Неправильный набор параметров приводит к чрезмерному затягиванию переходного процесса. Поэтому очень важно исследовать совместную динамику машины и двигателя, выяснить те значения параметров и те условия, при которых переходные процессы протекают быстрее, с наименьшими потерями и наименьшей опасностью перегрева обмоток двигателей.
Известны специфические условия пуска ВТМ, когда при пуске двигателям необходимо поднять массивные дебалансы, находящиеся в нижнем положении под действием силы тяжести, на достаточно большую высоту и начать их дальнейшую раскрутку. На практике для скорейшего пуска часто устанавливают на ВТМ двигатели завышенной мощности. Это приводит к тому, что стадия пуска проходится легко, но затем в ходе всего остального рабочего времени расходуется избыточное количество электроэнергии.
Таким образом, задача исследования и математического моделирования совместной динамики ВТМ и электродвигателей как единой электромеханической системы актуальна не только в теоретическом, но и в практическом смысле, поскольку позволяет выработать рекомендации по проектированию машин, потребляющих в рабочем режиме меньшее количество электроэнергии.
В данной работе построенная ранее математическая модель динамики ВТМ* дополнена системой уравнений, описывающей переходные процессы в асинхронных двигателях, и получена новая математическая модель – модель электромеханической системы «вибротранспортирующая машина». исследование динамики полученной системы осуществлялось методом численного эксперимента с математической моделью.
Идея работы. Исследование динамики ВТМ как единой электромеханической системы методом математического моделирования.
Цель работы
1. Построить математическую модель электромеханической системы «вибротранспортирующая машина», позволяющую на стадии проектирования оценить влияние вибротранспортирующей машины на приводные электродвигатели.
2. Оценить энергозатраты, сопровождающие пуск электромеханической системы «вибротранспортирующая машина» и ударные нагрузки на машину.
3. Выработать рекомендации по подбору типа и мощности приводных электродвигателей с целью уменьшения расхода электроэнергии в рабочем режиме.
научная новизна и практическая ценность
1. сформулирована система дифференциальных уравнений электромеханической системы «вибротранспортирующая машина» для случаев установки приводных электродвигателей на неподвижном основании и непосредственно на рабочем органе ВТМ для достаточно широкого набора возможных двигателей, включая разную полюсность, двигатели с короткозамкнутым и с фазным ротором, основного исполнения и модификаций с учетом эффекта вытеснения тока в стержнях обмоток роторов. Все это определяется параметрами, входящими в систему.
2. построена математическая модель, описывающая не только стационарные, но и все механические переходные процессы как в ВТМ, так и в двигателях. Данная
*Румянцев С. А. Динамика переходных процессов и самосинхронизация движений вибрационных машин. – Екатеринбург: УрО РАН. – 2003. – 135 с. – ISBN 5–7691–1366–9
модель позволяет оценить токи, состояние электромагнитного поля при всех нестационарных режимах, т.е. толчках, рывках и т.п., возникающих при работе ВТМ.
3. Разработаны рекомендации по подбору типа, исполнения и мощности приводных электродвигателей с целью уменьшения потребляемой электроэнергии.
Достоверность научных положений, выводов и рекомендаций диссертации обусловлена: использованием фундаментальных положений динамики системы твердых тел, теории колебаний и удара; использованием фундаментальных положений теории электрических машин; применением хорошо апробированных современных вычислительных методов; соответствием полученных качественных и количественных вычислительных результатов характеру функционирования вибропитателей-грохотов в производственных условиях; сравнением результатов моделирования динамики лабораторного вибрационного стенда с измеренными параметрами его работы и паспортными характеристиками; использованием результатов диссертационной работы конструкторскими организациями.
Реализация работы. Полученные рекомендации по подбору типа и мощности приводных электродвигателей реализованы АОЗТ НППЦ «Уралмеханобр-инжиниринг» при проектировании новых вибротранспортирующих машин.
Апробация работы. Основные положения данной работы и результаты исследований докладывались и обсуждались на: IX всероссийском съезде по теоретической и прикладной механике, Н. Новгород, 2006; международной конференции «Вычислительные и информационные технологии в науке, технике и образовании», ВИТ-2004, Алматы, Казахстан; международной конференции XXXII Summer School –Conference “Advanced Problems in Mechanics”, APM 2005, С-Петербург; международной конференции XXXIII Summer School –Conference “Advanced Problems in Mechanics”, APM 2006, С-Петербург; научно-технической конференции «Молодые ученые – транспорту», Екатеринбург, УрГУПС, 2006; научном семинаре ИМаш УрО РАН 2006; расширенном заседании кафедры электротехники и электротехнологических систем УГТУ-УПИ 2006 г.; научных семинарах кафедры «Прикладная математика» УрГУПС 2004 – 2006 г.; научных семинарах кафедры «Электрические машины» УрГУПС 2004 – 2006 г.
Публикации. По теме диссертации опубликовано 7 научных работ, из которых 4 статьи и 3 работы – тезисы в сборниках международных конференций на английском языке и аннотации доклада на съезде по теоретической и прикладной механике.
Структура и объем работы. Диссертация состоит из введения, 4 глав, заключения, списка литературы из 98 наименований, 4 приложений, содержит 126 страниц, 38 рисунков, 3 таблицы.
содержание работы
Во введении обоснована актуальность темы диссертации, сформулированы идея и цель работы, научная новизна, практическая ценность, достоверность и апробация диссертации. Дана характеристика публикаций, структуры и объема работы.
В первой главе выполнен аналитический обзор сведений по динамике вибромашин, об исследованиях в области динамики вибромашин, теории синхронизации механических систем и электромагнитных переходных процессов в асинхронных электродвигателях, приведены основные задачи исследования, проведенного автором.
Работа посвящена исследованию нестационарной динамики вибрационных машин с независимо вращающимися дебалансными ВВ. Принцип работы этих машин основан на использовании явления самопроизвольной синхронизации движений механических систем. Явление самосинхронизации механических дебалансных вибраторов, установленных на одном вибрирующем органе, было экспериментально обнаружено в 1948 г. Д.А. Плиссом. В 1953 г. И.И. Блехман дал физическое объяснение и математическое описание этого явления. В дальнейшем теория синхронизации вибромашин (синхронизации вращений вибровозбудителей) была обобщена и развита в работах И.И. Блехмана, О.П. Барзукова, Л.А.Вайсберга, Л.Б. Зарецкого, Б.П. Лаврова, А.И. Лурье, Р.Ф. Нагаева, В.М. Потураева, К.М. Рагульскиса, К.В. Фролова, К.Ш. Ходжаева, Р. Миклашевского, В. Богуша и З. Энгеля, Л.Шперлинга, Араки Иосиаки, Иноуэ Дзюнкити, Хаяси Сэцуко и других исследователей.
В работах С.А. Румянцева описывается динамика переходных процессов, сопровождающих пуск машины из состояния покоя, а также воздействия на нее различных возмущений, в том числе ударных, вызванных падением на рабочий орган монолита. В его работах вращающие моменты приводных электродвигателей также задаются функциями, представляющими собой статические характеристики двигателей, т.е. модель описывает нестационарную динамику только самой ВТМ без учета переходных динамических процессов в двигателях.
при пуске и при ударных нагрузках на машину в двигателях могут возникать (и возникают) переходные динамические процессы, при которых зависимость вращающего момента от угловой скорости весьма сильно отличается от статической характеристики. Учет этих явлений позволяет не только более точно описать влияние двигателей на нестационарную динамику ВТМ, но и влияние динамики ВТМ на электромагнитные процессы в двигателе, и, как следствие, оценить энергозатраты, возникающие при работе машины.
В области исследования переходных процессов в асинхронных двигателях ведущее место занимают МЭИ, УГТУ-УПИ, ОПИ. В развитии теории электромагнитных переходных процессов асинхронных машин большую роль сыграли работы Р. Парка, А.А. Горева, Г. Стенлея, Г.Крона, Е.Я. Казовского, А.А. Янко-Триницкого, С.В. Страхова, К.П. Ковача, И. Раца, Л.Н. Грузова, А.Т. Голована, В.А. Шубено, А.В. Иванова-Смоленского, В.Я. Беспалова, М.М. Соколова, Л.Б. Масандилова, Л.П. Петрова, В.А. Ладензона, И.П. Копылова и других ученых. Разработанная в их трудах методика составления и исследования дифференциальных уравнений машин переменного тока дает возможность проводить глубокий анализ электромагнитных переходных процессов в асинхронных машинах.
При выполнении данной работы автор ставил перед собой следующие задачи:
– построить комплексную синтетическую математическую модель, описывающую совместную нестационарную динамику системы ВТМ – электродвигатели и рассматривать в дальнейшем ВТМ как единую электромеханическую систему;
– оценить взаимное влияние ВТМ и электродвигателей при различных режимах работы машины (при пуске, стационарном режиме работы и при ударных нагрузках на рабочий орган ВТМ) в случае применения асинхронных электродвигателей различных модификаций;
– выработать рекомендации по проектированию ВТМ, в частности подбору типов и модификаций асинхронных двигателей с целью уменьшения энергозатрат при эксплуатации ВТМ.
Вторая глава посвящена описанию математической модели динамики ВТМ как электромеханической системы.
| а) | 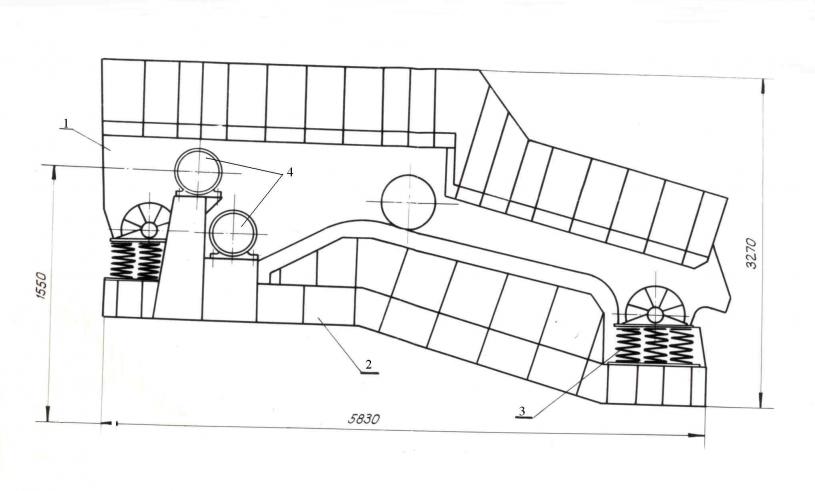 | б) |  |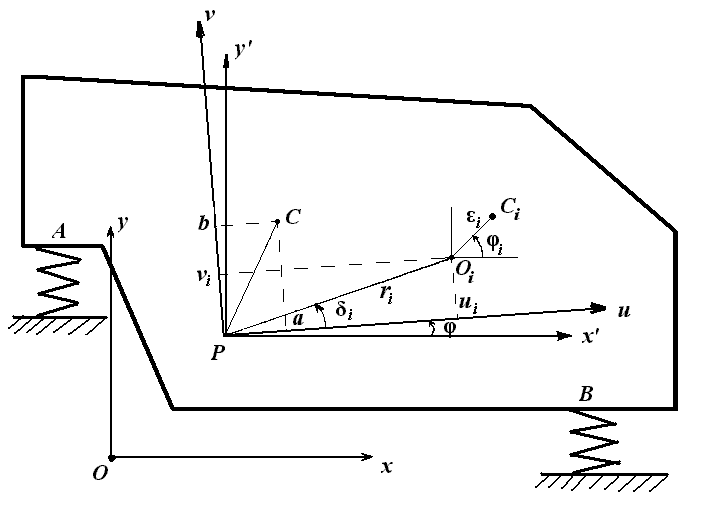
 |
Рисунок 2 – а) вибропитатель-грохот ГПТ; б) расчетная схема ВТМ
Система дифференциальных уравнений движений одномассной ВТМ получена И.И. Блехманом. В работах С.А. Румянцева, полученная система дополнена слагаемыми, позволяющими более точно описывать неустановившиеся движения:
Здесь n – количество вибровозбудителей, установленных на рабочем органе (РО) вибромашины; (х, у) – координаты центра масс РО в некоторой неподвижной декартовой системе координат; – угловая координата РО, то есть угол поворота подвижной системы координат (u, v), жестко связанной с РО относительно неподвижной системы координат (отсчитывается против часовой стрелки); i – угловые координаты (отсчитываются против часовой стрелки) i-го ВВ, другими словами, углы поворота центров масс дебалансов по отношению к неподвижной оси Ох; 
– вращающий момент электродвигателя i-го ВВ и момент сил сопротивления вращению системы «i-й электродвигатель – передающий механизм – вибровозбудитель»; Ii – индексы направления, то есть коэффициенты, принимающие значения «+1», если вращение данного ВВ происходит против часовой стрелки, и значение «–1» в противном случае; М – масса машины; J – момент инерции РО; Ji – момент инерции i-го ВВ; mi – масса i-го ВВ; i – эксцентриситет (расстояние от оси вращения до центра масс i-го ВВ); 
и т.д. – коэффициенты жесткости упругих опорных элементов; 
и т.д. – коэффициенты вязкого сопротивления, соответствующие указанным в индексах обобщенным координатам; g – ускорение свободного падения; i – углы, задающие положения осей дебалансов; Fуд и Муд – сила и момент относительно центра масс ударного воздействия соответственно.
форма импульса ударной силы считается прямоугольной (П-образной). В этом случае величина ударной силы постоянна в течение всего времени удара, и ее значение определяется соотношением
, (2)
где — длительность удара (время действия ударной силы Fуд и ее момента), т — масса падающего монолита, h — высота падения.
Таким образом, сила Fуд и ее момент Муд мгновенно возникают в системе в момент времени t = Tуд, действуют в течение промежутка времени и мгновенно исчезают в момент времени t = Tуд +. Длительность удара может изменяться в довольно широких пределах — это зависит от материала и механических свойств монолита. В дальнейшем эта величина рассматривается как параметр моделирования.
Система (1) построена для случая установки приводных двигателей на неподвижном основании. В случае установки приводных двигателей непосредственно на рабочем органе машины в уравнения для ВВ вместо величины 
входит величина 
.
При переходных динамических процессах, особенно при пуске, происходит активное взаимодействие приводных двигателей, вибровозбудителей и рабочего органа ВТМ друг с другом. Это взаимодействие может описать совместная система дифференциальных уравнений ВТМ как единой электромеханической системы.
Для этого необходимо помимо дифференциальных уравнений, описывающих движение рабочего органа и вибровозбудителей ВТМ, рассмотреть также дифференциальные уравнения приводных электродвигателей, поскольку они являются неотъемлемой частью ВТМ.
Для построения математической модели вибротранспортирующей машины как электромеханической системы совмещена система дифференциальных уравнений динамики вибромашины (1) с системой дифференциальных уравнений асинхронного электродвигателя. Выписаны системы дифференциальных уравнений динамики электромеханической системы ВТМ с линейными и нелинейными уравнениями асинхронных электродвигателей для случаев установки приводных электродвигателей на неподвижном основании и непосредственно на рабочем органе машины.
Система дифференциальных уравнений с постоянными значениями активных и индуктивных сопротивлений роторов асинхронных двигателей для случая установки приводных электродвигателей на неподвижном основании принимает следующий вид:
В полученной системе дифференциальных уравнений первые три уравнения описывают движение рабочего органа машины, последующие – вращение i-го ВВ (ротора электродвигателя). Таким образом, в общем случае, система дифференциальных уравнений будет содержать 3 + 5n уравнений, где n – количество ВВ. В наиболее часто применяемом частном случае, при использовании на ВТМ двух ВВ, система будет состоять из 13 дифференциальных уравнений.
Величины угла поворота i-го ВВ (ротора двигателя) 
, либо их производные, входят в состав всех уравнений, за исключением 2n, описывающих электромагнитные процессы в статорах двигателей. С другой стороны, величины потокосцеплений i-го электродвигателя 
, входят в состав уравнений углового ускорения ВВ. Таким образом, система представляет собой жестко связанную систему дифференциальных уравнений. Решить какие-либо уравнения этой системы отдельно от остальных невозможно, вся система должна интегрироваться совместно.
Система дифференциальных уравнений ВТМ с учетом эффекта вытеснения тока в роторах приводных двигателей в случае применения двигателей с глубокими пазами на роторе записана в виде
(4)
| где |    ;  ;  | (5) |
в случае применения двигателей с фигурными пазами на роторе и с двойной беличьей клеткой
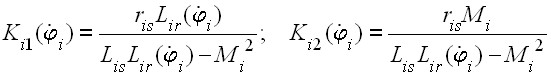 ;    ;  ;  . | (6) |
Величины, входящие в выражения для 
, 
, 
и 
и расчет их числовых значений приведены в приложениях А и Б.
В полученной системе дифференциальных уравнений коэффициенты Ai и Ki1 – Ki4 уже не являются постоянными, а представляют собой нелинейные функции угловой скорости вращения роторов приводных электродвигателей. Величины 
и их производные входят во все уравнения системы (4), тем самым степень связанности системы дифференциальных уравнений еще больше повышается.
Таким образом, получена новая система дифференциальных уравнений, описывающая нестационарную динамику электромеханической системы «вибротранспортирующая машина – электродвигатели», существенно нелинейная не только в механической, но и в электрической части и позволяющая более точно описывать пусковые переходные процессы.
При установке приводных двигателей непосредственно на рабочий орган ВТМ вращающий момент двигателей зависит не только от угловой скорости вращения роторов, но и от угловой скорости самого рабочего органа ВТМ
. (7)
С учетом (7) система (3) примет следующий вид:
(8)
Система дифференциальных уравнений с учетом эффекта вытеснения тока в стержнях обмоток роторов асинхронных двигателей (4) в случае установки приводных двигателей непосредственно на рабочий орган ВТМ и соответствующие коэффициенты (5) и (6) запишутся в виде:
(9)
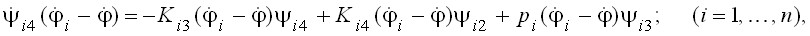
где
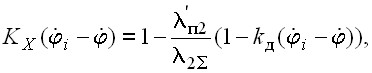   ;  ; | (10) |
либо
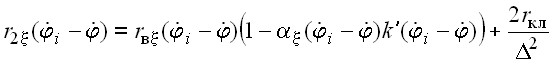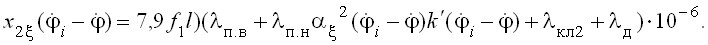   ;  ;  | (11) |
Таким образом, во все дифференциальные уравнения системы (9) и во все уравнения, за исключением 2n, описывающих электромагнитные процессы в статорах двигателей системы (8) кроме величины угла поворота i-го ВВ (ротора двигателя) 
, либо ее производных, входит величина угла поворота рабочего органа 
, либо ее производная. в качестве начального момента времени для систем дифференциальных уравнений (3) и (4) всегда выступает момент включения двигателей в сеть в состоянии покоя машины. При этом все фазовые переменные системы кроме 
в начальный момент времени равны нулю. В качестве начальных значений переменных 
обычно принимают 
, что соответствует свободному положению ВВ под действием силы тяжести. Тем не менее, математическая модель позволяет давать этим переменным и другие начальные значения.
Системы дифференциальных уравнений (3) и (4) с соответствующими начальными условиями интегрировались численно методом Рунге-Кутта.
Построенная математическая модель совместной динамики ВТМ и электродвигателей как единой электромеханической системы реализована в виде программного комплекса.
В третьей главе приведены результаты исследования динамики лабораторного вибрационного стенда как единой электромеханической системы с помощью математической модели. лабораторный вибрационный стенд представляет собой одномассную зарезонансную ВТМ. По своим габаритным размерам вибрационный стенд примерно в 5 – 6 раз меньше ВТМ тяжелого типа (рисунок 3).
Рисунок 3 – Внешний вид вибрационного стенда
Привод вибрационного стенда состоит из двух дебалансных вибраторов, вращение которых осуществляется при помощи двух асинхронных электродвигателей мощностью 120 Вт, установленных непосредственно на рабочем органе вибростенда.В главе приведен конкретный вид системы дифференциальных уравнений электромеханической системы ВТМ для вибрационного стенда в случае привода от двух электродвигателей, установленных непосредственно на рабочем органе машины. В качестве приводных электродвигателей на реальном вибрационном стенде используются двигатели типа ИР-127. Однако автору не удалось найти точных значений некоторых параметров данного двигателя, поэтому в математической модели использованы параметры аналогичного двигателя типа 4АА56А4УЗ, совпадающего с ИР-127 по типу исполнения, мощности, скорости вращения ротора, числу пар полюсов, номинальному току статора и ряду других параметров.
В работе представлены графики пускового и послеударного переходного процесса вибрационного стенда (рисунок 4)
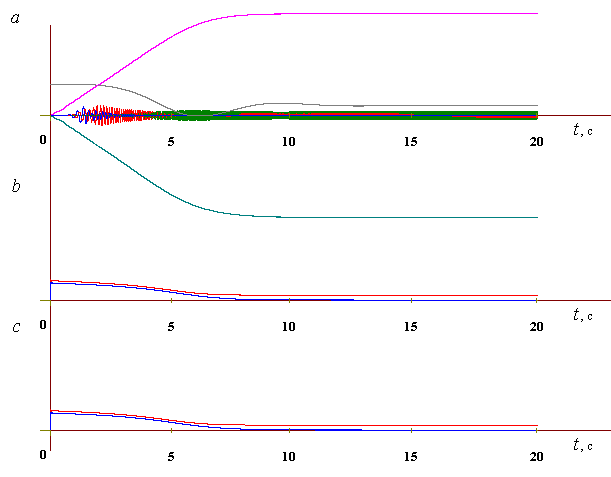
Рисунок 4 – Динамика механического пускового переходного процесса (a), токи
статора и ротора первого (b) и второго (c) двигателей вибрационного стенда
Одним из подтверждений точности построенной модели является факт постоянства направления вынуждающей силы: суммарная фаза поворота ВВ в синхронном движении не зависит от начальных положений дебалансов и большинства других параметров задачи. Она определяется только геометрическими параметрами машины (и равна половине того угла, который составляет с горизонталью прямая, проходящая через центр масс машины и середину отрезка, соединяющего центры вращения ВВ).
Этот результат с высокой точностью (±0,1°) совпадает с явлением, надежно установленным экспериментально. Сюда же можно добавить изменение угла вибрации после удара (проявление адаптивного свойства), которое получено при моделировании и также совпадает с надежно установленным экспериментальным фактом.
Следует отметить, что этот, совершенно очевидный с точки зрения динамики, геометрии и здравого смысла результат, никаким образом не был заложен в модель. То, что он неизменно воспроизводится во всех расчетах, говорит о точности построенной математической модели.
При сопоставлении результатов численного моделирования динамики вибрационного стенда с результатами экспериментальных исследований следует отметить следующее.
1. Суммарная фаза поворота ВВ в синхронном движении, о чем было сказано в начале данной главы, полученная по результатам моделирования, с высокой точностью соответствует взаимному расположению ВВ и центра масс вибрационного стенда (30,050 и 30,00 соответственно). Изменение угла вибрации после удара также соответствует новому положению центра масс.
2. Максимальное значение тока статора при пуске путем численного эксперимента составляет 2,18 А, величина максимального тока при пуске вибрационного стенда – 1,85 А.
3. Амплитудное значение тока в стационарном режиме путем численного эксперимента составляет 0,585 А, величина амплитудного значения тока в стационарном режиме вибрационного стенда – 0,602 А.
4. Время разгона ВВ на модели составляет 6 с, что соответствует времени пуска ВВ вибрационного стенда.
некоторое различие результатов объясняется тем, что в модель были заложены исходные данные двигателей, аналогичных применяемым на вибрационном стенде, но, тем не менее, не являющихся точным их подобием.
Таким образом, значительная часть результатов численного моделирования показывает хорошее соответствие геометрическим и паспортным данным вибрационного стенда и приводных двигателей.
Можно ожидать, что точность остальных данных численного моделирования не уступает точности проверенных, поскольку при решении связанной системы дифференциальных уравнений численным методом точность вычисления величин не может отличаться слишком сильно.
В четвертой главе приведены результаты расчета динамики пусковых и послеударных переходных процессов конкретных вибротранспортирующих машин.
Исследования динамики электромеханической системы «вибротранспортирующая машина» проводились методом численного решения систем (3), (4). При этом в качестве физических, геометрических и прочих параметров использовались данные по ВТМ ГПТ-3.
В главе приведен конкретный вид систем дифференциальных уравнений электромеханической системы ВТМ с линейными и нелинейными уравнениями двигателей для машины типа ГПТ-3 с двумя ВВ, установленными на неподвижном основании.
с помощью полученных моделей исследованы пусковые переходные процессы и динамические процессы при ударе, вызванном падением на рабочий орган ВТМ монолита массой 2 т с высоты 2 м. При этом рассматривалась работа ВТМ с различными типами двигателей.
Информация, как и в главе 3, представлена в графическом виде, позволяющем анализировать переходные динамические процессы и в электродвигателях, и в самой машине (рисунки 5, 6).
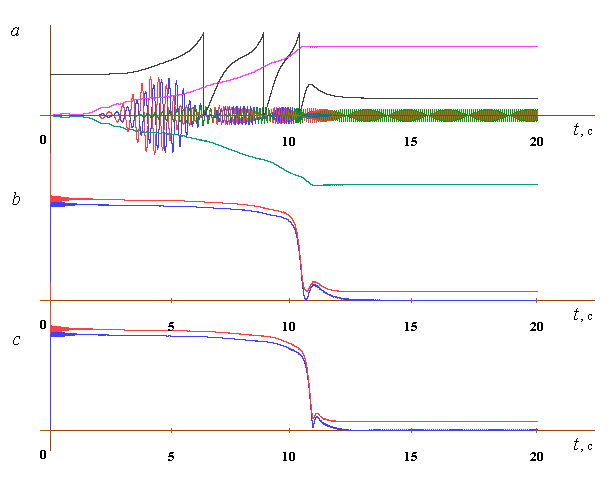
Рисунок 5 – Динамика пускового переходного процесса ВТМ (a), токи статора и ротора
первого (b) и второго (c) двигателей с использованием двигателей основного исполнения мощностью 45 кВт с учетом эффекта вытеснения тока (нелинейная модель двигателей)
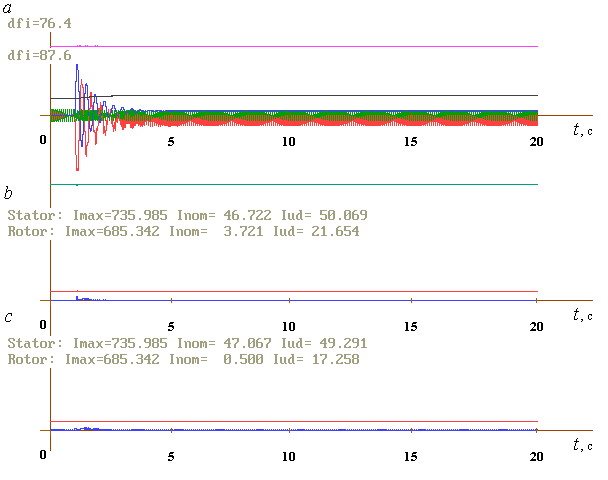
Рисунок 6 – Динамика послеударного переходного процесса ВТМ (a), токи статора и ротора первого (b) и второго (c) двигателей с использованием двигателей основного исполнения мощностью 45 кВт с учетом эффекта вытеснения тока (нелинейная модель двигателей)
Из графиков видно, что характер полученных путем численного эксперимента механических переходных процессов ВТМ тяжелого типа, аналогичен характеру переходных процессов, описанных в предыдущей главе для менее массивного вибрационного стенда. При этом переходные процессы в приводных двигателях носят более сложный характер.
В таблице 1 представлены результаты исследований динамики ВТМ при использовании асинхронных двигателей различных типов и исполнений.
Таблица 1 – Параметры ВТМ с применением двигателей различных типов
| Параметры | Тип двигателя | |||||||
| с фазным ротором 30 кВт | с фазным ротором 45 кВт | с повышенным скольжением 36 кВт | с повышенным скольжением 26,5 кВт | основное исполнение 45 кВт с учетом эффекта вытеснения тока | основное исполнение 55 кВт с учетом эффекта вытеснения тока | с повышенным пусковым моментом 30 кВт | с повышенным пусковым моментом 22 кВт | |
| Максимальное значение тока при пуске, А | – | 805,6 | 498,087 | 400,776 | 735,985 | 857,777 | 499,386 | 348,579 |
| Значение тока в стационарном режиме, А | 35,747 | 49,213 | 32,402 | 30,965 | 46,722 | 58,668 | 38,571 | 28,724 |
| Максимальное значение тока при ударе, А | 37,535 | 53,517 | 34,332 | 31,369 | 50,069 | 67,952 | 41,069 | 30,551 |
| Время выхода ВВ на синхронный режим при пуске, с | – | 7,3 | 10,1 | 12,9 | 13,2 | 7,8 | 8,8 | 14,6 |
| Время выхода ВВ на синхронный режим после удара, с | 0,9 | 0,8 | 2,3 | 2,2 | 1,6 | 1,0 | 0,7 | 1,0 |
При анализе полученных результатов сделаны следующие выводы.
1. Наиболее тяжелым режимом работы для приводных двигателей вибротранспортирующей машины является ее пуск, т.е. подъем дебалансов из нижнего положения и их последующая раскрутка. После раскрутки ВВ двигатели работают в режиме, близком к холостому ходу и большая мощность двигателей не требуется.
2. Падение монолитной массы на рабочий орган вибротранспортирующей машины не вызывает значительных бросков тока в двигателях, способных привести к выходу их из строя.
3. При использовании двигателей с фазным ротором мощностью 45 кВт удается запустить ВВ даже без дополнительного пускового сопротивления, но при этом после выхода на стационарный режим, потребляемые токи остается достаточно большим. Кроме того, в реальных условиях эксплуатации такие двигатели требуют применения дополнительных пусковых сопротивлений, а так же внешнего (ручного или автоматического) управляющего воздействия для их переключения в момент пуска.
4. При применении двигателей основного исполнения показана принципиальная возможность пуска ВВ с двигателями мощностью 45 кВт, но при этом пусковой процесс протекает тяжело и медленно. Использование двигателей основного исполнения большей мощности позволяет осуществить процесс пуска ВТМ быстрее, применение двигателей подобного типа заведомо завышенной мощности приводит к неоправданно завышенному расходу электроэнергии по сравнению с двигателями, описанными ниже.
5. Двигатели с повышенным скольжением осуществляют раскрутку ВВ при мощности 26,5 кВт. При этом токи в стационарном режиме почти вдвое меньше, чем при использовании двигателей основного исполнения мощностью 55 кВт. Однако применение двигателей с повышенным скольжением целесообразно только при равномерной безударной работе ВТМ.
6. Двигатели с повышенным пусковым моментом мощностью 30 кВт легко проходят режим пуска, обладают наименьшим временем выхода на синхронный режим после удара, однако потребляют несколько большие токи в стационарном режиме по сравнению с двигателями с повышенным скольжением.
7. При дальнейшем уменьшении мощности двигателей с повышенным пусковым моментом сохраняется достаточный для подъема и раскрутки ВВ пусковой момент, однако увеличивается время раскрутки, что приводит к чрезмерно длительному протеканию по обмоткам двигателей больших пусковых токов, способных вывести двигатели из строя.
Основной целью данной работы является совершенствование динамики ВТМ, и, как следствие, решение задачи энергосбережения в рабочем режиме ВТМ при выполнении машиной ее основных функций. В этом случае основным критерием подбора приводных электродвигателей является условие наименьшего потребления электроэнергии в установившемся режиме. При этом, в качестве ограничивающего, выступает условие уверенного пуска ВТМ из состояния покоя, т.е. за время, не вызывающее перегрев обмоток двигателей выше допустимых пределов.
Опираясь на этот критерий, при проектировании новых ВТМ и для снижения потребляемой электроэнергии в процессе работы уже существующих машин можно сформулировать следующие рекомендации по подбору электродвигателей. Отметим, что приведенные ниже рекомендации сформулированы для машин с массой рабочего органа порядка 23 т (ВТМ типа ГПТ), однако математическая модель и предложенная методика позволяют выработать рекомендации для ВТМ любых других типов. Отметим так же, что все типы двигателей, рассмотренных в работе, серийно выпускаются отечественной промышленностью.
Несмотря на сложный и энергоемкий пусковой переходный процесс, основное количество электроэнергии ВТМ потребляет в рабочем (стационарном) режиме. В связи с этим, применение двигателей основного исполнения высокой мощности, потребляющих в стационарном режиме большие токи, экономически неоправданно.
Для ВТМ, работа которых не связана с частыми ударными воздействиями и значительными перекосами рабочей нагрузки, можно рекомендовать применение двигателей с повышенным скольжением низкой мощности, например, 26,5 кВт. При этом амплитудное значение тока в стационарном режиме у таких двигателей в 1,9 раза ниже, чем у двигателей основного исполнения мощностью 55 кВт.
Для машин, работающих в условиях частых ударных воздействий, достаточно применить двигатели с повышенным пусковым моментом, мощностью порядка 30 кВт, при этом амплитудное значение тока в стационарном режиме у таких двигателей в 1,5 раза ниже, чем у двигателей основного исполнения мощностью 55 кВт.
Двигатели с фазным ротором при наличии пускового реостата позволяют осуществить пуск ВТМ при мощности в 30 кВт. Наличие пускового реостата дает возможность осуществить разгон вибровозбудителей при характеристиках, близких по характеру к характеристикам двигателей с повышенным скольжением, а в стационарном режиме, при отключенных пусковых реостатах, характеристики двигателей с фазным ротором близки по характеру к характеристикам двигателей основного исполнения или с повышенным пусковым моментом. При этом за счет включения и отключения пусковых реостатов, в одном двигателе удается совместить положительные свойства различных типов двигателей. Амплитудное значение тока в стационарном режиме двигателей с фазным ротором мощностью 30 кВт в 1,6 раза ниже, чем у двигателей основного исполнения мощностью 55 кВт. Однако двигатели с фазным ротором имеют более высокую себестоимость, по сравнению с двигателями с повышенным скольжением и с повышенным пусковым моментом, более трудоемки и дороги в обслуживании.
Таким образом, путем правильного подбора необходимых модификаций двигателя можно не только улучшить пусковую динамику ВТМ, но и существенно сократить потребление электроэнергии в установившемся режиме, что приводит к уменьшению эксплуатационных расходов. Окончательное решение по выбору того или иного типа двигателя принимается в каждом конкретном случае в зависимости от поставленных целей и условий эксплуатации машины.
заключение
В диссертации поставлена и решена задача исследования совместной нестационарной динамики ВТМ и электродвигателей как единой электромеханической системы. построена комплексная синтетическая математическая модель нестационарной динамики электромеханической системы «вибротранспортирующая машина», позволяющая описывать все стадии движения машины, включая неустановившиеся, характерные для переходных динамических процессов.
Построенная математическая модель реализована в виде программного комплекса. Программный комплекс снабжен окном интерфейса, позволяющим формировать любые геометрические и физические параметры вибромашины и параметры электродвигателей. Это дает возможность задавать параметры, как реальных машин, так и вновь проектируемых и даже гипотетических машин.
Программный комплекс представляет собой мощный инструмент, помогающий конструктору на стадии проектирования новых ВТМ получить представление о динамике будущей машины и заблаговременно решить вопрос об оптимальном подборе приводных электродвигателей. Он может быть полезен также для студентов механических специальностей в качестве учебного пособия, иллюстрирующего нестационарную динамику ВТМ.
С помощью программного комплекса поставлен ряд численных экспериментов, позволяющих выявить зависимости длительности синхронизации, величины токов в обмотках двигателей при протекании пусковых и послеударных переходных процессов от параметров электродвигателей различных типов и исполнений. Сформулированы рекомендации по проектированию ВТМ, в частности подбору типов и модификаций асинхронных двигателей с целью уменьшения энергозатрат при эксплуатации ВТМ.
Основные выводы и результаты работы сводятся к следующему.
1. Построена и реализована в виде программного комплекса математическая модель совместной динамики ВТМ и приводных асинхронных двигателей как единой электромеханической системы.
2. Обоснована необходимость использования в математической модели нелинейных дифференциальных уравнений двигателей для более точного описания пусковых переходных процессов.
3. Исследована динамика пусковых переходных процессов и переходных процессов, вызванных падением на рабочий орган монолита, сопоставимого по массе с массой самой машины. Оценены величины токов в обмотках двигателей при различных переходных процессах в электромеханической системе ВТМ.
4. Сформулированы рекомендации по подбору типов и исполнений двигателей, а так же их мощностей с целью уменьшения расхода электроэнергии. Отмечено, что при выборе исполнения асинхронных двигателей необходимо учитывать возможность ударной либо безударной работы ВТМ.
Публикации по теме работы
1. Румянцев, С. А., Азаров, Е. Б. Математическая модель нестационарной динамики электромеханической системы «вибротранспортирующая машина – электродвигатели» [Текст] // Изв. ВУЗов. Горный журнал. – 2006 – № 6. – С. 106 – 109. – ISSN № 0536–1028.
2. Румянцев, С. А., Азаров, Е. Б. Математическая модель нестационарной динамики системы «вибромашина – электропривод» в случае привода от асинхронных двигателей с короткозамкнутым ротором [Текст] // Транспорт Урала. – 2005. – №1. – с. 2 – 7. – ISSN № 1815–9400.
3. Румянцев, С. А., Азаров, Е. Б. Исследование нестационарной динамики вибротранспортирующих машин с использованием математической модели электромеханической системы «вибромашина – электропривод» [Текст] // Транспорт Урала. – 2005. – №4. – с. 45 – 50. – ISSN № 1815–9400.
4. Румянцев, С. А., Азаров, Е. Б. Уравнения нестационарной динамики системы «вибротранспортирующая машина – асинхронные электродвигатели» [Текст] // Проблемы прикладной математики: Сб. научных трудов. – Екатеринбург, УргУПС. – № 41 (124). В 2-х т.: Т.1. – 2005 – 2006. – С. 213 – 228.
5. S. Rumyantsev, E. Azarov. Mathematical model of non-stationary dynamics “The vibration machine-the electric drive” system in case of a drive from asynchronous engines with a short-circuited rotor [Текст] // XXXII Summer School –Conference “Advanced Problems in Mechanics”, APM 2005. – Book of Abstracts. – P. 24.
6. S. Rumyantsev, E. Azarov. Mathematical model of non-stationary dynamics of "vibration machine - electric motors" system by application of asynchronous motor drives with raised starting properties [Текст] // XXXIII Summer School –Conference “Advanced Problems in Mechanics”, APM 2006. – Book of Abstracts. – P. 18.
7. Азаров, Е. Б. Динамика пусковых и ударных переходных процессов в вибротранспортирующих машинах с самосинхронизирующимися вибровозбудителями [Текст] / Азаров Е.Б., Васильева Г.В., Румянцев С.А., Таран С.В., Тарасов Д.Ю. // IX Всероссийский съезд по теоретической и прикладной механике. Аннотации докладов. Т.1. – 2006. – С. 10.
АЗАРОВ Евгений Борисович
МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ
НЕСТАЦИОНАРНОЙ НЕЛИНЕЙНОЙ ДИНАМИКИ ЭЛЕКТРОМЕХАНИЧЕСКОЙ СИСТЕМЫ
«ВИБРОТРАНСПОРТИРУЮЩАЯ МАШИНА»
Специальность 01.02.06 – Динамика,
прочность машин, приборов и аппаратуры
| Подписано к печати 05.04.07 | |
| Формат бумаги 60 х 84 1/16 | Объем 1,2 п.л. |
| Заказ | Тираж 100 экз. |
Типография УрГУПС, 620034, г. Екатеринбург, ул. Колмогорова, 66
