Математическое моделирование напряженно-деформированного состояния и устойчивости пластин и пологих оболочек с построением систем аппроксимирующих функций
На правах рукописи
Абросимов Алексей Анатольевич
МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ
НАПРЯЖЕННО-ДЕФОРМИРОВАННОГО СОСТОЯНИЯ
И УСТОЙЧИВОСТИ ПЛАСТИН И ПОЛОГИХ ОБОЛОЧЕК
С ПОСТРОЕНИЕМ СИСТЕМ АППРОКСИМИРУЮЩИХ ФУНКЦИЙ
Специальности 05.13.18 – Математическое моделирование,
численные методы и комплексы программ;
01.02.04 – Механика деформируемого твердого тела
Автореферат
диссертации на соискание ученой степени
кандидата физико-математических наук
Саратов 2009
Работа выполнена в ГОУ ВПО «Саратовский государственный технический университет»
Научный руководитель: доктор технических наук, профессор
Филатов Валерий Николаевич
Официальные оппоненты: доктор физико-математических наук, профессор
Землянухин Александр Исаевич
доктор технических наук, профессор
Кузнецов Валентин Николаевич
Ведущая организация: Санкт-Петербургский государственный
архитектурно-строительный университет
Защита состоится «29» июня 2009 года в 13![]() ч на заседании диссертационного совета Д 212.242.08 при ГОУ ВПО «Саратовский государственный технический университет» по адресу: 410054, г. Саратов, ул. Политехническая, 77, Саратовский государственный технический университет, корп. 1, ауд. 319.
ч на заседании диссертационного совета Д 212.242.08 при ГОУ ВПО «Саратовский государственный технический университет» по адресу: 410054, г. Саратов, ул. Политехническая, 77, Саратовский государственный технический университет, корп. 1, ауд. 319.
С диссертацией можно ознакомиться в научно-технической библиотеке ГОУ ВПО «Саратовский государственный технический университет».
Автореферат разослан « 29 » мая 2009 года.
Ученый секретарь
диссертационного совета Терентьев А.А.
ОБЩАЯ ХАРАКТЕРИСТИКА РАБОТЫ
Актуальность работы. Тонкостенные оболочечные конструкции находят широкое применение в кораблестроении, самолетостроении, приборостроении, строительстве и других областях. Нелинейная теория оболочек, когда прогиб конструкции соизмерим с толщиной, стала интенсивно развиваться с начала XX века в связи с потребностями кораблестроения. Выдающийся вклад в эту теорию внесли ученые-кораблестроители И.Г.Бубнов и П.Ф.Папкович. Толчком к дальнейшему развитию нелинейной теории оболочек послужил возросший в начале 30-х годов ХХ в. интерес инженеров, прежде всего самолетостроителей, к вопросам устойчивости оболочек под действием разного рода нагрузок. Большой вклад в развитие нелинейной теории пластин и оболочек внесли Н.А. Алумяэ, С.А.Амбарцумян, В.В.Болотин, В.З.Власов, А.С.Вольмир, И.И.Ворович, К.З.Галимов, А.Л.Гольденвейзер, Э.И.Григолюк, Т.Карман, Б.Я.Кильчевский, М.А.Колтунов, М.С.Корнишин, А.И.Лурье, Х.М.Муштари, В.В. Новожилов, П.М.Огибалов, Д.Ю.Панов, И.В.Свирский, В.И.Феодосьев, Чен Вей-Цанг и др.
Для придания большей жесткости и более оптимального распределения напряжений пластины и оболочки могут иметь переменную толщину. Конструкции подвергаются не только механическим, но и тепловым воздействиям. Поведение тонкостенных конструкций постоянной и переменной толщины, находящихся в температурном поле и допускающих прогибы, соизмеримые с толщиной, исследованы недостаточно и требуют дальнейших исследований. При расчете пластин и оболочек вариационными методами необходимо задавать вид базисных функций для искомых переменных, удовлетворяющих граничным условиям на кромках конструкции. В случаях закреплений сторон контура, отличных от шарнирного, полные системы функций, достаточно хорошо реализуемые в расчетах, отсутствуют. Разработка теории и методики решения задач и проведение исследований напряженно-деформированного состояния (НДС) и устойчивости пластин и оболочек постоянной и переменной толщины, в том числе находящихся в температурном поле, является актуальной задачей. Актуальным является создание расчетных алгоритмов, расширяющих круг решаемых задач и уточняющих решение ранее решенных задач. Изложенное определило актуальность темы данной работы и ее цели.
Целью диссертационной работы является создание математической модели НДС и устойчивости пластин и пологих оболочек переменной толщины при воздействии внешней нагрузки и температурного поля, построение систем функций, аппроксимирующих искомые составляющие перемещения, подбор и реализация на ЭВМ алгоритма, позволяющего апробировать построенные системы функций и решить на их основе новые задачи.
Научная новизна:
– На основе функционала потенциальной энергии для кинематической модели Кирхгофа-Лява построена математическая модель НДС и устойчивости пластин и пологих оболочек переменной толщины, находящихся под воздействием нагрузки и температурного поля.
– Предложена модификация статического метода В.З.Власова подбора аппроксимирующих функций, позволяющая строить полные системы аппроксимирующих функций для искомых составляющих перемещения, удовлетворяющих различным закреплениям сторон контура пластин и оболочек прямоугольного плана. С помощью этой методики осуществлено построение трех систем функций для составляющих перемещения: систем, базирующихся на синусах, базирующихся на косинусах и систем полиномиального вида.
– Разработаны алгоритм и комплекс программ для решения нелинейных задач теории пластин и пологих оболочек, базирующиеся на комплексном методе линеаризации исходных нелинейных дифференциальных уравнений в частных производных, с последующим приведением систем линейных дифференциальных уравнений к системам алгебраических уравнений с использованием высоких приближений метода Бубнова-Галеркина при аппроксимировании составляющих перемещения построенными системами функций.
– Путем численного исследования построенные в работе системы функций апробируются на решении тестовых задач, ранее решенных другими авторами и иными методами, и на решении одних и тех же задач с использованием разных систем аппроксимирующих функций. Из сравнения показываются возможность и эффективность использования всех построенных в работе систем функций.
– С использованием предложенной математической модели показано, что при рассмотрении НДС и устойчивости весьма пологих оболочек, различным образом закрепленных по сторонам прямоугольного контура, следует вести расчет с учетом всех возможных вариантов закрепления сторон контура оболочки и выбирать наименее выгодный вариант с меньшим уровнем критической нагрузки, поскольку реальные контурные закрепления могут отличаться от идеальных закреплений расчетной схемы.
– Показано, что для оболочек постоянной толщины в случае большой кривизны на графике «нагрузка – прогиб в центре» наблюдаются петлеобразования. В случае оболочек, шарнирно-неподвижно закрепленных по контуру, эти эффекты наблюдались другими авторами; в случае оболочек, жестко заделанных по контуру такие эффекты более рельефны и они наблюдались автором впервые.
– Показано, что для оболочек с утолщением в центре петлеобразования прекращаются. При этом уровень критической нагрузки значительно возрастает, а критические внутренние усилия понижаются.
– При рассмотрении задач комбинированного нагружения (нагрузка плюс температура), ярко показывается, что для нелинейных задач принцип независимости действия сил не работает.
Достоверность и обоснованность полученных результатов определяются корректностью и строгостью применяемых математических методов, соответствием результатов и выводов, полученных в численных экспериментах, результатам других авторов, полученным иными методами; общефизическим представлениям о характере процессов НДС и устойчивости пластин и оболочек.
Практическая значимость работы заключается в том, что построенная математическая модель и программное обеспечение могут быть использованы в других областях науки и техники, в учебном процессе.
На защиту выносятся:
1. Математическая модель НДС и устойчивости пологих оболочек переменной толщины от действия механических нагрузок и температуры.
2. Модификация статического метода В.З.Власова подбора систем аппроксимирующих функций; системы аппроксимирующих функций, построенные с помощью этой методики.
3. Расчетный алгоритм и программное обеспечение решения нелинейных задач теории пластин и оболочек, базирующиеся на комплексном методе линеаризации исходных нелинейных дифференциальных уравнений с последующим сведением получающихся линейных дифференциальных уравнений к системам линейных алгебраических уравнений с помощью метода Бубнова-Галеркина при аппроксимировании искомых величин системами построенных функций.
4. Результаты численных экспериментов, их сравнительный анализ с известными в литературе решениями и с решениями, выполненными с разными системами аппроксимирующих функций, который показал возможность и эффективность использования всех построенных в работе функций.
5. Результаты решения новых задач, полученные с использованием по-строенных в работе систем функций, в частности: петлеобразований на графике «нагрузка – прогиб в центре» для подъемистых оболочек постоянной толщины; исчезновение петель для оболочек с утолщением в центре и возрастание при этом уровня критической внешней нагрузки и др.
Апробация работы. Основные результаты работы докладывались на ежегодных научно-технических конференциях Саратовского государственного технического университета (Саратов, 2004-2008 гг.); на семинаре кафедры вычислительной математики и информатики СПб ГАСУ под руководством доктора физико-математических наук, профессора Вагера Б.Г. (февраль 2005 г.); на XII, XIII и XV Международных симпозиумах «Динамич. и технологич. пробл. механики конструкций и сплошных сред», Москва, МАИ, 2006-2007, 2009 гг.
Полностью работа докладывалась на научном семинаре кафедры «Математика и моделирование» СГТУ под руководством заслуженного деятеля науки и техники РФ, д.т.н., профессора Крысько В.А. (октябрь 2008 г.); на научном семинаре кафедры «Механика деформированного твердого тела» СГТУ под руководством академика Российской академии архитектуры и строительных наук, профессора Петрова В.В. (ноябрь 2008 г.).
По результатам исследования опубликовано 9 печатных работ.
Структура и объем диссертации. Текст диссертации изложен на 125 страницах, состоит из введения, четырех глав, заключения, списка использованной литературы из 162 наименований, и содержит 58 рисунков и 6 таблиц.
КРАТКОЕ СОДЕРЖАНИЕ РАБОТЫ
Во введении обосновывается актуальность темы диссертации, сформулированы цель и задачи исследования, положения, выносимые на защиту, практическая ценность работы, краткое содержание по главам и проведен анализ работ по теме диссертации.
В первой главе строится нелинейная математическая модель упругой пологой оболочки переменной толщины, находящейся в напряженно-деформированном состоянии под действием нагрузок и температурного поля.
Рассматривается тонкая пологая оболочка прямоугольного плана с размерами ab. Некоторая внутренняя поверхность тела оболочки принимается за координатную поверхность. Оси OX и OY направляются по линиям главных кривизн координатной поверхности оболочки, OZ – по нормали к координатной поверхности в сторону вогнутости (вниз). Оболочка находится в температурном поле ![]() и под действием заданных внешних нагрузок интенсивностью
и под действием заданных внешних нагрузок интенсивностью ![]() , приложенных к элементу оболочки по направлениям x, y и z соответственно. Толщина оболочки переменна и задается ограничивающими ее в вертикальном направлении поверхностями zв (x, y) и zн (x, y). Для кинематической модели прямой недеформируемой нормали Кирхгофа – Лява линейные
, приложенных к элементу оболочки по направлениям x, y и z соответственно. Толщина оболочки переменна и задается ограничивающими ее в вертикальном направлении поверхностями zв (x, y) и zн (x, y). Для кинематической модели прямой недеформируемой нормали Кирхгофа – Лява линейные ![]() ,
, ![]() и угловые деформации
и угловые деформации ![]() при наличии температурного поля связаны следующими соотношениями с составляющими перемещения U,
при наличии температурного поля связаны следующими соотношениями с составляющими перемещения U, ![]() и
и ![]() соответственно в направлении осей OX, OY, OZ:
соответственно в направлении осей OX, OY, OZ:
![]() ,
, ![]() ,
,
![]() . (1) Здесь
. (1) Здесь ![]() и
и ![]() – кривизны оболочки в направлении осей OX и OY соответственно. Индексы x и y при переменных означают дифференцирование по соответствующей координате.
– кривизны оболочки в направлении осей OX и OY соответственно. Индексы x и y при переменных означают дифференцирование по соответствующей координате.
Физические соотношения связи напряжений с деформациями имеют вид: ![]() ,
, ![]() ,
, ![]() , (2)
, (2)
где ![]() – модуль упругости,
– модуль упругости, ![]() – коэффициент Пуассона.
– коэффициент Пуассона.
Потенциальная энергия деформации
 . (3)
. (3)
Подставляя в выражение потенциальной энергии (3) значения деформаций и напряжений через перемещения U, V и W по формулам (1), (2) и проводя интегрирование в (3) по переменной ![]() , получим выражение потенциальной энергии деформации через компоненты перемещения. Приравнивая на основании вариационного принципа Лагранжа полную вариацию потенциальной энергии
, получим выражение потенциальной энергии деформации через компоненты перемещения. Приравнивая на основании вариационного принципа Лагранжа полную вариацию потенциальной энергии ![]() элементарной работе внешних сил
элементарной работе внешних сил 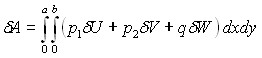 , получаем полное вариационное уравнение для кинематической модели Кирхгофа-Лява. Из полного вариационного уравнения, на основании произвольности вариаций
, получаем полное вариационное уравнение для кинематической модели Кирхгофа-Лява. Из полного вариационного уравнения, на основании произвольности вариаций ![]() ,
, ![]() ,
, ![]() , строятся разрешающие дифференциальные уравнения равновесия, которые в случае, если
, строятся разрешающие дифференциальные уравнения равновесия, которые в случае, если ![]() , при введении начальной поверхности имеют вид:
, при введении начальной поверхности имеют вид:
![]() ,
, ![]() ,
,
![]()
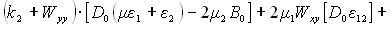
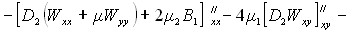
![]()
![]() (4)
(4)
В (4) ![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
, 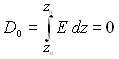 ,
, 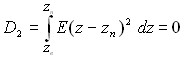 ,
,  ,
, 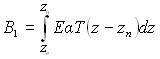 ,
, ![]() – аппликата начальной поверхности, которая определяется из уравнения:
– аппликата начальной поверхности, которая определяется из уравнения:  . (5)
. (5)
Система (4) – система нелинейных дифференциальных уравнений восьмого порядка в частных производных. В работе выводятся также уравнения в смешанной форме, обсуждаются граничные условия на кромках контура оболочки, следующие из контурных интегралов полного вариационного уравнения. Все результаты приводятся в безразмерных параметрах:
![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
;
![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Во второй главе производится подбор расчетного алгоритма.
Для решения задачи отыскания НДС пологой оболочки в нелинейной постановке необходимо провести линеаризацию нелинейных уравнений и свести дифференциальные зависимости к алгебраическим уравнениям.
С этой целью на предварительном этапе расчета применяется метод последовательных нагружений (МПН) с довольно крупным (порядка 0,20h) шагом решения по приращению прогиба в центре. Далее решение улучшается с использованием метода последовательных приближений (МПП). Такой подход позволяет с помощью МПН при малых затратах машинного времени получить хорошее начальное приближение для использования МПП, находящееся в достаточно малой окрестности истинного решения исходной не-линейной задачи и гарантирует сходимость МПП, значительно сокращая количество итераций до полной сходимости последовательных приближений.
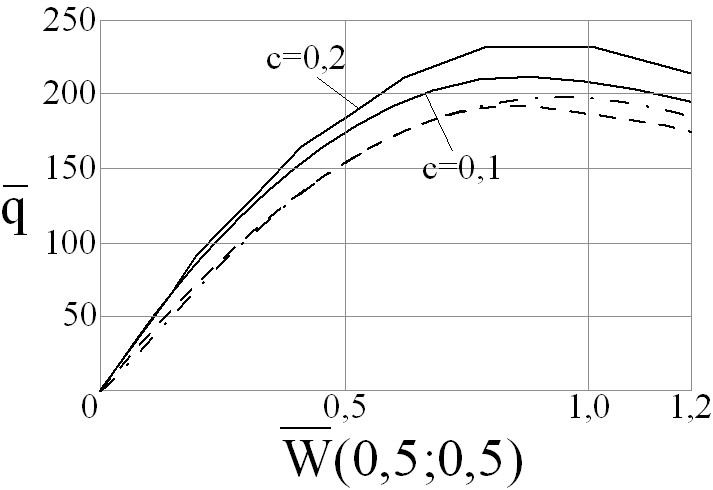
На рис. 1 приводятся графики «![]() » для оболочки постоян-ной толщины, с
» для оболочки постоян-ной толщины, с ![]() , шарнир-но-неподвижно закрепленной по конту-ру. Решения здесь строятся с исполь-зованием 16-го приближения метода Бубнова-Галеркина при аппроксими-ровании составляющих перемещения
, шарнир-но-неподвижно закрепленной по конту-ру. Решения здесь строятся с исполь-зованием 16-го приближения метода Бубнова-Галеркина при аппроксими-ровании составляющих перемещения
системами синусов. Кривая ![]() построена с использованием МПН с шагом по прогибу в центре
построена с использованием МПН с шагом по прогибу в центре ![]() ; кривая
; кривая ![]() – с шагом
– с шагом ![]() ; штриховой линией приводится наше решение, построенное с использованием МПП до полной сходимости последовательных приближений из точек кривой МПН с
; штриховой линией приводится наше решение, построенное с использованием МПП до полной сходимости последовательных приближений из точек кривой МПН с ![]() . Видно, что точки полной сходимости МПП лежат ниже точек лежащих на ломаной с
. Видно, что точки полной сходимости МПП лежат ниже точек лежащих на ломаной с ![]() , как это и должно быть в этой задаче. Штрихпунктирной кривой на этом рисунке показано решение Карпова В.В., построенное во втором приближении вариационного метода Власова-Канторовича при аппроксимировании составляющих перемещения подобранными им полиномами и линеаризации исходных уравнений с использованием схемы Рунге-Кутта в МПН. Приводящееся сравнение последних двух кривых вполне удовлетворительно. Имеющееся расхождение при подходе к верхней критической точке, на наш взгляд, в большей степени объясняется использованием разных вариационных методов, разных приближений.
, как это и должно быть в этой задаче. Штрихпунктирной кривой на этом рисунке показано решение Карпова В.В., построенное во втором приближении вариационного метода Власова-Канторовича при аппроксимировании составляющих перемещения подобранными им полиномами и линеаризации исходных уравнений с использованием схемы Рунге-Кутта в МПН. Приводящееся сравнение последних двух кривых вполне удовлетворительно. Имеющееся расхождение при подходе к верхней критической точке, на наш взгляд, в большей степени объясняется использованием разных вариационных методов, разных приближений.
С использованием принятой методики линеаризации в высоких приближениях метода Бубнова-Галеркина с последующим решением систем линейных алгебраических уравнений методом Гаусса проведено исследование сходимости высоких приближений метода Бубнова-Галеркина и показано, что для достижения приемлемых результатов достаточно расчетов в девятом приближении. При этом установлено, что на разных этапах нагружения и эпюры прогибов, и эпюры напряжений не ведут себя геометрически подобно. В большей степени изменяется качество эпюр напряжений.
В третьей главе строятся и апробируются системы функций, аппроксимирующих искомые составляющие перемещения U, V и W, для оболочек прямоугольного плана, различным образом закрепленных по сторонам прямоугольного контура.
Для решения уравнений теории пластин и оболочек методом Ритца или Бубнова-Галеркина необходимо представлять искомые составляющие перемещения в виде разложений по системам аппроксимирующих функций
![]() ;
; ![]() ;
;
![]() .
.
Здесь ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() – системы функций аппроксимирующие составляющие перемещения в направлении соответствующих координатных осей.
– системы функций аппроксимирующие составляющие перемещения в направлении соответствующих координатных осей.
Для построения систем функций, аппроксимирующих составляющие перемещения, с помощью модификации статического метода В.З.Власова, упростим разрешающую систему уравнений (4) с учетом безразмерных параметров для пластины постоянной толщины. В этом случае ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , и уравнения в перемещениях имеют вид:
, и уравнения в перемещениях имеют вид:
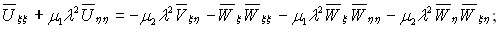
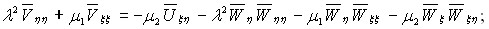
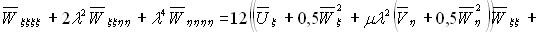 (6)
(6)
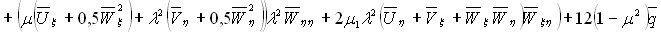 .
.
Обозначая правые части системы (6) соответственно ![]() ,
, ![]() ,
, ![]() , перепишем ее в виде:
, перепишем ее в виде:
![]() ;
; ![]() ;
; ![]() . (7)
. (7)
Вырежем, следуя статическому методу подбора аппроксимирующих функций В.З.Власова, балочку с осью ![]() , тогда из третьего уравнения системы (7) при обозначениях
, тогда из третьего уравнения системы (7) при обозначениях ![]() ,
, ![]() , получим
, получим ![]() . Назовем
. Назовем ![]() в последнем дифференциальном уравнении нагрузочным членом. Пусть функция
в последнем дифференциальном уравнении нагрузочным членом. Пусть функция ![]() такова, что допускает разложение ее в тот или иной ряд. Так, если
такова, что допускает разложение ее в тот или иной ряд. Так, если ![]() – разложима в ряд по синусам на отрезке [0; 1], то, ограничиваясь первыми M членами ряда разложения, будем иметь
– разложима в ряд по синусам на отрезке [0; 1], то, ограничиваясь первыми M членами ряда разложения, будем иметь ![]() . Представляя далее
. Представляя далее ![]() и, используя метод гармонического баланса (ставя в соответствие каждой гармонике синусов вид прогиба), получим обыкновенное дифференциальное уравнение четвёртого порядка относительно
и, используя метод гармонического баланса (ставя в соответствие каждой гармонике синусов вид прогиба), получим обыкновенное дифференциальное уравнение четвёртого порядка относительно![]() :
: ![]() .
.
Общее решение этого обыкновенного дифференциального уравнения
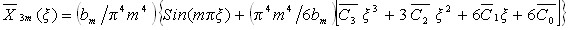 .
.
Следуя статическому методу В.З.Власова, при новых обозначениях произвольных постоянных ![]() ,
, ![]() ,
, ![]() ,
, ![]() , получим для систем аппроксимирующих функций общий вид
, получим для систем аппроксимирующих функций общий вид
 . (8)
. (8)
Значения констант ![]() ,
, ![]() ,
, ![]() ,
, ![]() будут зависеть от способа закрепления рассматриваемой балочки на кромках
будут зависеть от способа закрепления рассматриваемой балочки на кромках ![]() и
и ![]() .
.
a) Если кромки ![]() и
и ![]() закреплены шарнирно, тогда
закреплены шарнирно, тогда
 .
.
Реализуя эти граничные условия, получим ![]() .
.
Теперь функции, аппроксимирующие прогиб в направлении оси ![]() :
:
![]() (9)
(9)
(9) – изученная и широко применяемая в расчетах полная система функций.
б) Кромки ![]() и
и ![]() жестко защемлены, тогда
жестко защемлены, тогда ![]()
![]()
![]() . Реализуя эти граничные условия в (8), имеем
. Реализуя эти граничные условия в (8), имеем
![]() ;
; ![]() ;
; ![]() ;
; ![]() .
.
Теперь 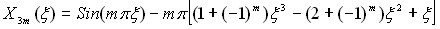 . (10)
. (10)
в) Кромка ![]() жестко заделана, кромка
жестко заделана, кромка ![]() шарнирно закреплена:
шарнирно закреплена:
 . Тогда
. Тогда
![]() (11)
(11)
Рассуждая формально, так же, как с третьим уравнением, с первыми двумя уравнениями системы (7) и реализуя граничные условия неподвижного в тангенциальных направлениях закрепления кромок пластины, получим ![]() . (12)
. (12)
Таким же образом строятся функции ![]() , аппроксимирующие составляющие перемещения в направлении оси
, аппроксимирующие составляющие перемещения в направлении оси ![]() .
.
Аналогично в работе строятся системы функций, базирующиеся на косинусах при разложении нагрузочного члена в ряд Фурье по системе косинусов на отрезке [0; 1], системы полиномиального вида при разложении нагрузочного члена в степенной ряд в окрестности точки ![]() .
.
Построенные в работе системы функций являются полными в классе функций, удовлетворяющих соответствующим граничным условиям, исходя из способа их построения, который базируется на разложении нагрузочных членов в ряды по полным системам функций.
Для апробирования построенных функций с использованием предложенного алгоритма решались задачи отыскания НДС квадратного плана оболочек и пластин постоянной толщины под действием равномерно распределенной нагрузки перпендикулярной плану для конструкций, шарнирно-неподвижно закрепленных и жестко заделанных по контуру, как в линейной, так и в геометрически нелинейной постановках.
Для реализации математической модели был составлен комплекс программ на языке C# с использованием технологии.NET компании Microsoft.
В линейной постановке для оболочек с ![]() выполнялись расчеты со всеми подобранными системами аппроксимирующих функций в четвертом, девятом и шестнадцатом приближениях. Сравнение для оболочек, шарнирно неподвижно закрепленных по контуру, проводилось с эталонным решением, в качестве которого принималось 25-е приближение, выполненное с аппроксимацией по системе синусов. Установлено, что кривые эпюр напряжений, полученные в 16-м приближении для решения, выполненного с аппроксимацией по полиномам, подходят ближе к кривым эталонного решения, чем соответствующие кривые 16-го приближения по синусам, что подтверждает мысль И.К.Даугавета о том, что полиномиальные аппроксимации обеспечивают более быструю сходимость, чем тригонометрические.
выполнялись расчеты со всеми подобранными системами аппроксимирующих функций в четвертом, девятом и шестнадцатом приближениях. Сравнение для оболочек, шарнирно неподвижно закрепленных по контуру, проводилось с эталонным решением, в качестве которого принималось 25-е приближение, выполненное с аппроксимацией по системе синусов. Установлено, что кривые эпюр напряжений, полученные в 16-м приближении для решения, выполненного с аппроксимацией по полиномам, подходят ближе к кривым эталонного решения, чем соответствующие кривые 16-го приближения по синусам, что подтверждает мысль И.К.Даугавета о том, что полиномиальные аппроксимации обеспечивают более быструю сходимость, чем тригонометрические.
Проведены расчеты гибких пластин, шарнирно неподвижно закрепленных по контуру. Расчеты проведены с использованием всех трех систем фун-кций в высоких приближениях. Построенные нами решения сравниваются с решением Корнишина М.С. и Исанбаевой М.С., полученным методом конеч-ных разностей повышенной точности. Сравнение решений, построенных с разными системами аппроксимирующих функций между собой и сравнение с решением, выполненным методом конечных разностей, говорит в пользу возможности и эффективности применения всех построенных систем функций в рассмотренных задачах.
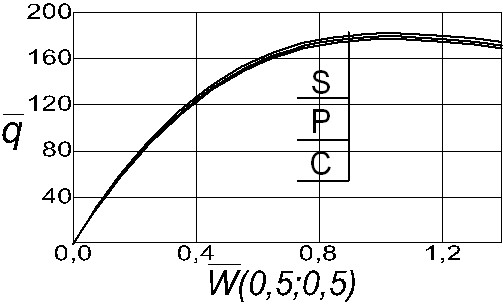
Проведены расчеты гибких пологих оболочек, шарнирно-неподвижно закрепленных и жестко заделанных по контуру с ![]() . Расчеты проведены с использованием всех трех систем функций в 16-х приближениях. Ниже кривыми S (аппроксимирующие функции, базирующиеся на синусах), C (базирующиеся на косинусах) и P (полиномиального вида) на рис. 2 для оболочек, жестко заделанных по контуру, приводятся графики «
. Расчеты проведены с использованием всех трех систем функций в 16-х приближениях. Ниже кривыми S (аппроксимирующие функции, базирующиеся на синусах), C (базирующиеся на косинусах) и P (полиномиального вида) на рис. 2 для оболочек, жестко заделанных по контуру, приводятся графики «![]() ». Разница представленных расчетов с разными системами аппроксимирующих функций трудноуловима.
». Разница представленных расчетов с разными системами аппроксимирующих функций трудноуловима.
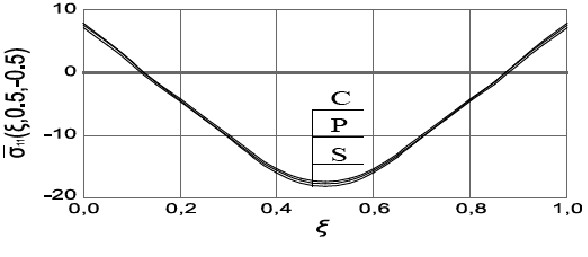
На рис. 3 приводятся эпюры напряжений ![]() на верхнем волокне по сечению
на верхнем волокне по сечению ![]() в верхней критической точке, когда прогиб в центре
в верхней критической точке, когда прогиб в центре ![]() 1,0, а уровень критической нагрузки при аппроксимировании с производящими синусами равен
1,0, а уровень критической нагрузки при аппроксимировании с производящими синусами равен ![]() , с производящими косинусами –
, с производящими косинусами – ![]() , с аппроксимирующими полиномами –
, с аппроксимирующими полиномами – ![]() 179,3. Эпюры прогибов в верхней критической точке по разным расчетам совпадают.
179,3. Эпюры прогибов в верхней критической точке по разным расчетам совпадают.
На основе приведенных решений тестовых задач можно сделать вывод, что для достижения приемлемых результатов для таких конструкций необходимы расчеты в 9-м приближении. Показывается, что если по точности, получающихся решений трудно отдать предпочтение тем или иным системам функций, то по затратам машинного времени следует отдать предпочтение системам, базирующимся на синусах, и системам полиномиального вида. Отмечается, что для оболочек при решении задач в нелинейной постановке конфигурация эпюр напряжений существенно меняется с ростом прогибов, конфигурация эпюр прогибов изменяется в меньшей степени.
В четвертой главе с использованием подобранного алгоритма и построенных систем аппроксимирующих функций решен ряд новых задач.
Решены задачи отыскания НДС и потери устойчивости для оболочек с ![]() квадратного плана со смешанными закреплениями по контуру, когда любая из четырёх сторон может быть или шарнирно закреплена, или жёстко заделана. Возможные схемы закрепления не смещаемого в тангенциальных направлениях сторон контура квадратного плана оболочки приводятся на рис. 4. На схеме 1 – оболочка, шарнирно закрепленная по контуру, на схеме 6 – жестко заделанная по контуру, на схемах 2-5 – оболочки со смешанными закреплениями.
квадратного плана со смешанными закреплениями по контуру, когда любая из четырёх сторон может быть или шарнирно закреплена, или жёстко заделана. Возможные схемы закрепления не смещаемого в тангенциальных направлениях сторон контура квадратного плана оболочки приводятся на рис. 4. На схеме 1 – оболочка, шарнирно закрепленная по контуру, на схеме 6 – жестко заделанная по контуру, на схемах 2-5 – оболочки со смешанными закреплениями.
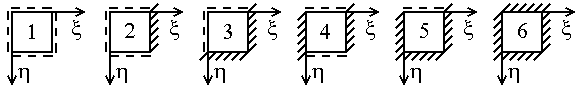
Рис. 4 Схемы закрепления краев контура
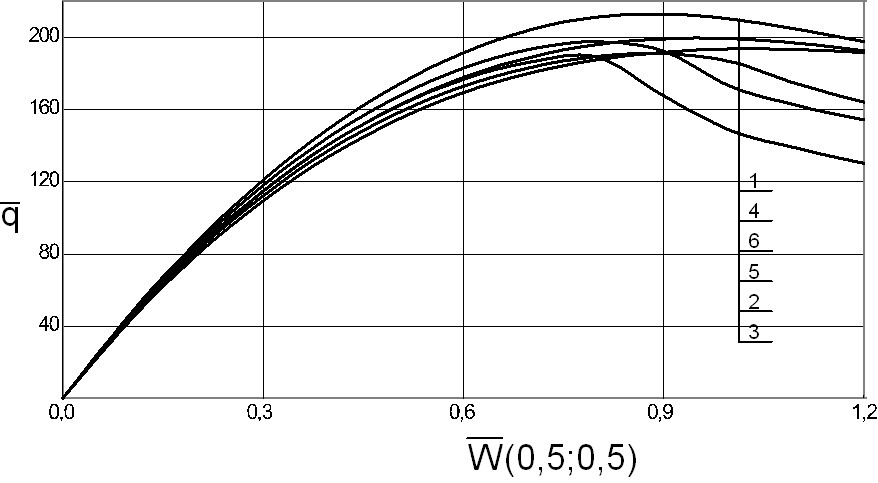
На рис. 5 представлены графики зависимости поперечной нагрузки ![]() , от прогиба в центре оболочки
, от прогиба в центре оболочки ![]() . Номера кривых соответствуют номерам расчетных схем рис. 4. По рис. 5 можно определить положение верхних критических точек (ВКТ), координаты которых приводятся ниже. Первой координатой приводится значение прогиба в центре
. Номера кривых соответствуют номерам расчетных схем рис. 4. По рис. 5 можно определить положение верхних критических точек (ВКТ), координаты которых приводятся ниже. Первой координатой приводится значение прогиба в центре ![]() , вторая координата – значение критической равномерно распределенной нагрузки
, вторая координата – значение критической равномерно распределенной нагрузки ![]() . Схеме 1 контурных закреплений рис. 4 соответствует ВКТ – (0.9; 213); cхеме 2 – (0.8; 198); cхеме 3 – (0.8;189); cхеме 4 – (1.0; 199); cхеме 5 – (0.9; 191); cхеме 6 –(1.0; 194). Видно, что наименьшую критическую нагрузку имеет оболочка с закреплением, выполненным по схеме 3, наибольшую – по схеме 1. В диссертационной работе приводятся эпюры прогибов и эпюры напряжений по сечениям
. Схеме 1 контурных закреплений рис. 4 соответствует ВКТ – (0.9; 213); cхеме 2 – (0.8; 198); cхеме 3 – (0.8;189); cхеме 4 – (1.0; 199); cхеме 5 – (0.9; 191); cхеме 6 –(1.0; 194). Видно, что наименьшую критическую нагрузку имеет оболочка с закреплением, выполненным по схеме 3, наибольшую – по схеме 1. В диссертационной работе приводятся эпюры прогибов и эпюры напряжений по сечениям ![]() и
и ![]() , которые чутко реагируют на характер контурных закреплений. Обращает на себя внимание значительное изменение качества эпюр напряжений на разных стадиях нагружения во всех рассмотренных случаях. В реальных конструкциях закрепление сторон контура может отличаться от идеального закрепления расчетной схемы. Поэтому следует вести расчет на всевозможные закрепления сторон контура и выбирать наименее выгодное с точки зрения момента потери устойчивости закрепление сторон. В нашем случае таким наименее выгодным вариантом закрепления сторон контура является вариант схемы 3 на рис. 4. Этот невыгодный вариант отличается от наиболее выгодного случая, когда оболочка закреплена шарнирно по всем сторонам, на
, которые чутко реагируют на характер контурных закреплений. Обращает на себя внимание значительное изменение качества эпюр напряжений на разных стадиях нагружения во всех рассмотренных случаях. В реальных конструкциях закрепление сторон контура может отличаться от идеального закрепления расчетной схемы. Поэтому следует вести расчет на всевозможные закрепления сторон контура и выбирать наименее выгодное с точки зрения момента потери устойчивости закрепление сторон. В нашем случае таким наименее выгодным вариантом закрепления сторон контура является вариант схемы 3 на рис. 4. Этот невыгодный вариант отличается от наиболее выгодного случая, когда оболочка закреплена шарнирно по всем сторонам, на ![]() по величине верхней критической нагрузки. Такая подстраховка даст оправданный коэффициент запаса при расчете оболочечных конструкций.
по величине верхней критической нагрузки. Такая подстраховка даст оправданный коэффициент запаса при расчете оболочечных конструкций.
С использованием подобранных систем аппроксимирующих функций в работе решаются задачи отыскания НДС квадратных в плане подъемистых оболочек с ![]() и
и ![]() , шарнирно-неподвижно закрепленных и жестко заделанных по всему контуру, от действия равномерно распределенной нагрузки, перпендикулярной плану оболочки. Решения строятся в 16-м приближении метода Бубнова-Галеркина при аппроксимировании составляющих перемещения подобранными функциями полиномиального вида с использованием КМЛ на каждом шаге нагружения. На приводимых в диссертационной работе графиках для шарнирно-неподвижно закрепленных по контуру оболочек видно, сколь значительно отличается конфигурация кривых «
, шарнирно-неподвижно закрепленных и жестко заделанных по всему контуру, от действия равномерно распределенной нагрузки, перпендикулярной плану оболочки. Решения строятся в 16-м приближении метода Бубнова-Галеркина при аппроксимировании составляющих перемещения подобранными функциями полиномиального вида с использованием КМЛ на каждом шаге нагружения. На приводимых в диссертационной работе графиках для шарнирно-неподвижно закрепленных по контуру оболочек видно, сколь значительно отличается конфигурация кривых «![]() -
-![]() » для оболочек с
» для оболочек с ![]() от класссической конфигурации такой кривой для весьма пологой оболочки с
от класссической конфигурации такой кривой для весьма пологой оболочки с ![]() . На кривых с
. На кривых с ![]() имеют место петлеобразования. Такого типа петлеобразования отмечались в работах других авторов, в частности в работах В.В. Карпова. Значительно разнится качество эпюр напряжений для оболочек с
имеют место петлеобразования. Такого типа петлеобразования отмечались в работах других авторов, в частности в работах В.В. Карпова. Значительно разнится качество эпюр напряжений для оболочек с ![]() и для оболочек с
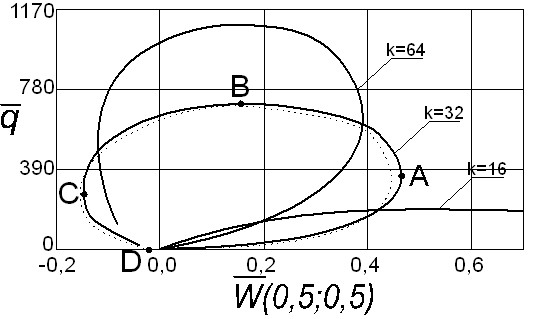
и для оболочек с ![]() . Еще больший контраст в расчетных параметрах для подъемистых и весьма пологих оболочек наблюдается у жестко заделанных по контуру оболочек. На рис. 6 приводятся графики «
. Еще больший контраст в расчетных параметрах для подъемистых и весьма пологих оболочек наблюдается у жестко заделанных по контуру оболочек. На рис. 6 приводятся графики «![]() » для жестко заделанных по контуру оболочек с кривизнами
» для жестко заделанных по контуру оболочек с кривизнами ![]() . Штриховой кривой показан график решения для оболочки с
. Штриховой кривой показан график решения для оболочки с ![]() , построенный при аппроксимации составляющих перемещения системами, базирующимися на синусах. Как видим, это решение практически повторяет сплошную кривую для
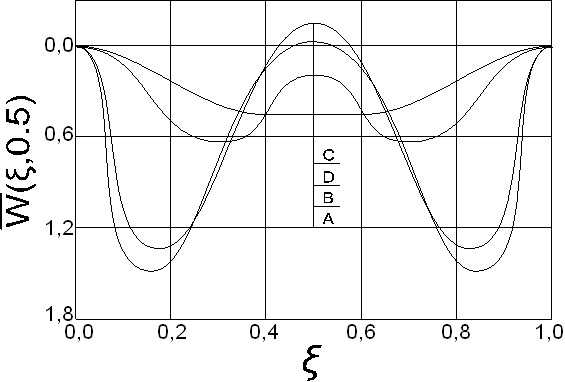
, построенный при аппроксимации составляющих перемещения системами, базирующимися на синусах. Как видим, это решение практически повторяет сплошную кривую для ![]() , построенную с полиномами. Для выяснения характера распределения прогибов по плану оболочки на разных фазах нагружения на рис. 7 построены эпюры прогибов по сечению
, построенную с полиномами. Для выяснения характера распределения прогибов по плану оболочки на разных фазах нагружения на рис. 7 построены эпюры прогибов по сечению ![]() соответственно в точках A, B, C и D сплошной кривой с
соответственно в точках A, B, C и D сплошной кривой с ![]() на рис. 6. Из приводимых на рис. 7 кривых видно, что на начальных фазах нагружения наибольший прогиб был в центре оболочки и при последующем деформировании максимум прогибов сместился в четверти, а прогиб в центре стал уменьшаться, приняв в точке C отрицательное значение. Таким образом, за счет провала оболочки в четвертях центр оболочки не опустился, а вспучился.
на рис. 6. Из приводимых на рис. 7 кривых видно, что на начальных фазах нагружения наибольший прогиб был в центре оболочки и при последующем деформировании максимум прогибов сместился в четверти, а прогиб в центре стал уменьшаться, приняв в точке C отрицательное значение. Таким образом, за счет провала оболочки в четвертях центр оболочки не опустился, а вспучился.
В работе также приводятся эпюры безразмерных напряжений ![]() , на верхней поверхности оболочки (
, на верхней поверхности оболочки (![]() ) в ВКТ для оболочек с кривизнами соответственно
) в ВКТ для оболочек с кривизнами соответственно ![]() . Для оболочки с
. Для оболочки с ![]() это точка
это точка ![]() , для оболочки с
, для оболочки с ![]() точка – (
точка – (![]() ) на рис. 6, для оболочки с
) на рис. 6, для оболочки с ![]() – (
– (![]() ). Из сравнения качества эпюр при разных кривизнах видно, что к моменту потери устойчивости (в ВКТ) оболочка с
). Из сравнения качества эпюр при разных кривизнах видно, что к моменту потери устойчивости (в ВКТ) оболочка с ![]() в рассматриваемом сечении на опорах растянута, напряжение изменяется по сечению по закону, близкому к параболическому, максимум усилий сжатия находится в центре оболочки. В случае оболочек с
в рассматриваемом сечении на опорах растянута, напряжение изменяется по сечению по закону, близкому к параболическому, максимум усилий сжатия находится в центре оболочки. В случае оболочек с ![]() напряжения у опор близки к нулю, максимум сжимающих напряжений сдвинулся в четверти, а в центре оболочка растянута. Таким образом, качество и эпюр прогибов, и эпюр напряжений у оболочки с
напряжения у опор близки к нулю, максимум сжимающих напряжений сдвинулся в четверти, а в центре оболочка растянута. Таким образом, качество и эпюр прогибов, и эпюр напряжений у оболочки с ![]() и у оболочек с
и у оболочек с ![]() различное.
различное.
При обходе петель вместо МПН использовался расширенный «метод продолжения решения по параметру», когда программа автоматически меняет параметр продолжения решения (либо нагрузка, либо прогиб в центре).
Были рассмотрены НДС оболочек переменной толщины как в линейной, так и в геометрически нелинейной постановке, когда толщина оболочки менялась только вдоль одной оси OX по параболическому закону симметрично относительно центра плана оболочки, достигая максимума в центре оболочки. При этом показано, что и в том, и в другом случаях напряжения вдоль оси OX распределяются более рационально, чем вдоль оси OY. Напряженное состояние вдоль оси OX более близко к равнонапряженному, чем вдоль оси OY. Кроме того, в геометрически нелинейной постановке оболочки с ![]() не имеют петель на графике «
не имеют петель на графике «![]() (ц)», что ведет к значительному увеличению критической нагрузки на оболочку.
(ц)», что ведет к значительному увеличению критической нагрузки на оболочку.
Далее приводятся расчеты оболочек переменной толщины, когда толщина изменяется по синусоидальному закону и в направлении оси OX, и в направлении оси OY : ![]() ,
,![]() . (13)
. (13)
При этом параметры распределения толщины (![]() и H ) таковы, что объем материала, затрачиваемый на изготовление оболочки переменной толщины, равен объему материала оболочки постоянной толщины. Тогда
и H ) таковы, что объем материала, затрачиваемый на изготовление оболочки переменной толщины, равен объему материала оболочки постоянной толщины. Тогда ![]()
![]()
![]() , (14)
, (14)
где ![]() . Полагая коэффициент
. Полагая коэффициент ![]() (толщина в центре в два раза больше, чем на опорах), имеем
(толщина в центре в два раза больше, чем на опорах), имеем ![]() . При
. При ![]() ,
, ![]() . В случае
. В случае![]() имеем оболочку постоянной толщины с
имеем оболочку постоянной толщины с ![]() .
.
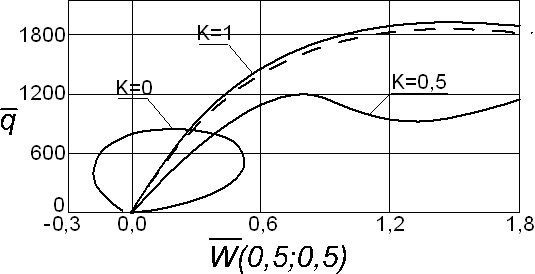
На рис. 8 приводятся графики «![]() (ц)» для квадратных в плане, жестко заделанных по контуру оболочек кривизны
(ц)» для квадратных в плане, жестко заделанных по контуру оболочек кривизны ![]() , находящихся под действием равномерно распределенной нагрузки
, находящихся под действием равномерно распределенной нагрузки ![]() , перпендикулярной плану оболочки. Линия с
, перпендикулярной плану оболочки. Линия с ![]() соответствует оболочке постоянной толщины. Линии с
соответствует оболочке постоянной толщины. Линии с ![]() и
и ![]() соответствуют оболочкам переменной толщины с соответствующим значением
соответствуют оболочкам переменной толщины с соответствующим значением ![]() в формуле (14). Расчеты здесь проводились в 16 приближении метода Бубнова-Галеркина с аппроксимацией составляющих перемещения системами, базирующимися на синусах. Видно, что кривые оболочек переменной толщины идут без петлеобразования. Верхняя критическая нагрузка у кривой с
в формуле (14). Расчеты здесь проводились в 16 приближении метода Бубнова-Галеркина с аппроксимацией составляющих перемещения системами, базирующимися на синусах. Видно, что кривые оболочек переменной толщины идут без петлеобразования. Верхняя критическая нагрузка у кривой с ![]() стала больше таковой для оболочки постоянной толщины почти в полтора раза (1200 против 840). У оболочки с
стала больше таковой для оболочки постоянной толщины почти в полтора раза (1200 против 840). У оболочки с ![]() верхняя критическая нагрузка более чем в два раза превосходит верхнюю критическую нагрузку аналогичной оболочки постоянной толщины (1900 против 840). В работе приводятся эпюры прогибов по сечению
верхняя критическая нагрузка более чем в два раза превосходит верхнюю критическую нагрузку аналогичной оболочки постоянной толщины (1900 против 840). В работе приводятся эпюры прогибов по сечению ![]() для оболочки с
для оболочки с ![]() . Показывается, что на разных этапах нагружения оболочка в центре под действием приложенной нагрузки прогибается, а не вспучивается, как оболочка постоянной толщины под действием той же нагрузки.
. Показывается, что на разных этапах нагружения оболочка в центре под действием приложенной нагрузки прогибается, а не вспучивается, как оболочка постоянной толщины под действием той же нагрузки.
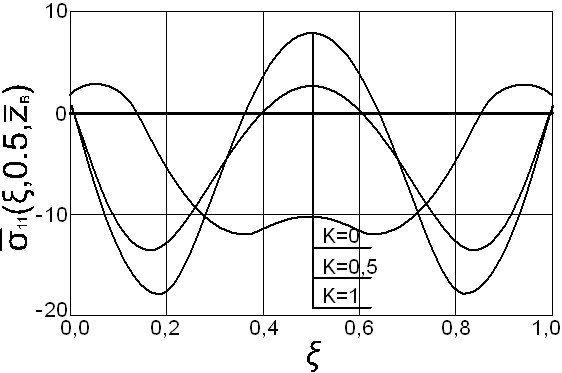
На рис. 9 приводятся эпюры суммарных напряжений на верхней поверхности оболочек (![]() ) по сечению
) по сечению ![]() в верхних критических точках. Видно, что, хотя критическая нагрузка для оболочки переменной толщины с
в верхних критических точках. Видно, что, хотя критическая нагрузка для оболочки переменной толщины с ![]() более чем в два раза выше, чем для оболочки постоянной толщины, напряжения в верхней критической точке меньше у оболочки переменной толщины. Здесь меньше и напряжения сжатия, и напряжения растяжения. Характер распределения напряжений у оболочки переменной толщины с
более чем в два раза выше, чем для оболочки постоянной толщины, напряжения в верхней критической точке меньше у оболочки переменной толщины. Здесь меньше и напряжения сжатия, и напряжения растяжения. Характер распределения напряжений у оболочки переменной толщины с ![]() подобен характеру распределения напряжений у оболочки постоянной толщины. Совсем другой характер распределения напряжений у оболочки переменной толщины с
подобен характеру распределения напряжений у оболочки постоянной толщины. Совсем другой характер распределения напряжений у оболочки переменной толщины с ![]() .
.
Штриховая линия на рис. 8 соответствует расчету для оболочки переменной толщины по (13) с ![]() в (14), выполненному с системами полиномиального вида. Видно, что это решение практически повторяет решение сплошной линии с
в (14), выполненному с системами полиномиального вида. Видно, что это решение практически повторяет решение сплошной линии с ![]() на этом рисунке, выполненное с аппроксимирующими функциями, образующими которых являются синусы. Это еще раз подтверждает мысль о том, что разные функции, подобранные в работе, одинаково хорошо работают в решаемых задачах.
на этом рисунке, выполненное с аппроксимирующими функциями, образующими которых являются синусы. Это еще раз подтверждает мысль о том, что разные функции, подобранные в работе, одинаково хорошо работают в решаемых задачах.
В работе приводится аналогичное решение для оболочек с ![]() . Здесь также демонстрируется, что утолщение оболочки в центре дает график «
. Здесь также демонстрируется, что утолщение оболочки в центре дает график «![]() (ц)» без петлеобразования и приводит к большим значениям верхней критической нагрузки по сравнению с оболочкой постоянной толщины, причем разница в верхних критических нагрузках еще более значительна, чем у оболочек с
(ц)» без петлеобразования и приводит к большим значениям верхней критической нагрузки по сравнению с оболочкой постоянной толщины, причем разница в верхних критических нагрузках еще более значительна, чем у оболочек с ![]() .
.
Исследовалось НДС пластин и оболочек в температурном поле. Рассмотрены потеря устойчивости и закритическое поведение пластины постоянной толщины, квадратного плана, шарнирно неподвижно закрепленной по контуру и находящейся под действием равномерного все возрастающего температурного поля. Результаты решения этой задачи, выполненные в 16-м приближении с аппроксимирующими функциями полиномиального вида, сравниваются с известным решением В.Н.Филатова, полученным в первом приближении вариационного метода В.З.Власова с улучшением аппроксимирующих функций методом вариационных итераций. Показывается, что кривые графиков «температура (![]() ) – прогиб в центре (
) – прогиб в центре (![]() (ц))» по этим двум расчетам практически совпадают. Приводимые эпюры напряжений также хорошо согласуются в количественном плане, однако конфигурация эпюр изгибных напряжений различна, что демонстрирует достоинства расчетов в высоких приближениях перед «хорошим» решением, но выполненным в первом приближении.
(ц))» по этим двум расчетам практически совпадают. Приводимые эпюры напряжений также хорошо согласуются в количественном плане, однако конфигурация эпюр изгибных напряжений различна, что демонстрирует достоинства расчетов в высоких приближениях перед «хорошим» решением, но выполненным в первом приближении.
Решаются две задачи комбинированного воздействия на квадратного плана оболочки постоянной толщины, жестко заделанные по контуру с ![]() . В первой задаче оболочка сначала грузится равномерно распределенной нагрузкой, перпендикулярной плану оболочки, до уровня
. В первой задаче оболочка сначала грузится равномерно распределенной нагрузкой, перпендикулярной плану оболочки, до уровня ![]() , когда прогиб в центре оболочки достигает
, когда прогиб в центре оболочки достигает ![]() (ц)=0,6, далее оболочка нагревается равномерной температурой до уровня
(ц)=0,6, далее оболочка нагревается равномерной температурой до уровня ![]() . Во второй задаче оболочка сначала нагревается до
. Во второй задаче оболочка сначала нагревается до ![]() , чему соответствует
, чему соответствует ![]() (ц)
(ц)![]() , а затем нагружается равномерно распределенной нагрузкой, перпендикулярной плану оболочки, до уровня
, а затем нагружается равномерно распределенной нагрузкой, перпендикулярной плану оболочки, до уровня ![]() . Таким образом, на финише имеем одинаковое суммарное внешнее воздействие на оболочку. В первой задаче оболочка под действием нагрузки прогибается, и прогибы продолжают далее возрастать при последующем нагревании оболочки, достигая на финише прогиба в центре
. Таким образом, на финише имеем одинаковое суммарное внешнее воздействие на оболочку. В первой задаче оболочка под действием нагрузки прогибается, и прогибы продолжают далее возрастать при последующем нагревании оболочки, достигая на финише прогиба в центре ![]() (ц)
(ц)![]() ; во второй задаче при первоначальном на
; во второй задаче при первоначальном на
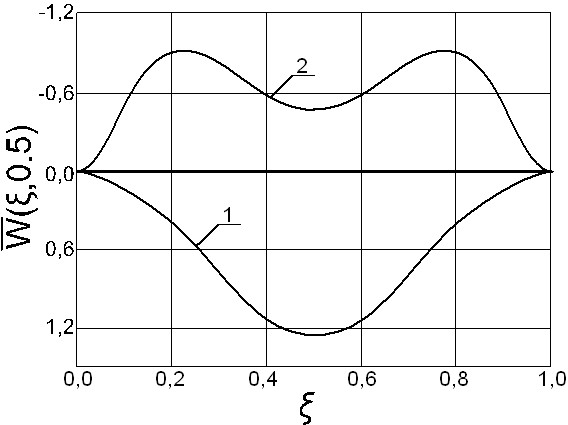
гревании оболочка вспучивается и при последующем нагружении прогибается вниз, достигая на финише прогиба в центре ![]() (ц)
(ц)![]() . Таким образом, от одинакового суммарного внешнего воздействия, деформированное состояние в обеих задачах различное. На рис. 10 приводятся эпюры прогибов по сечению
. Таким образом, от одинакового суммарного внешнего воздействия, деформированное состояние в обеих задачах различное. На рис. 10 приводятся эпюры прогибов по сечению ![]() в конечной точке; по первой решаемой задаче ((
в конечной точке; по первой решаемой задаче ((![]() )+(
)+(![]() ))– кривая 1; по второй решаемой задаче ((
))– кривая 1; по второй решаемой задаче ((![]() )+(
)+(![]() )) – кривая 2. Таким образом, от одинакового суммарного внешнего воздействия деформированное состояние в обеих задачах различное. Значительно разнятся и напряженные состояния в этих двух задачах.
)) – кривая 2. Таким образом, от одинакового суммарного внешнего воздействия деформированное состояние в обеих задачах различное. Значительно разнятся и напряженные состояния в этих двух задачах.
Таким образом, решенные задачи ярко показывают, что в случае решения нелинейных задач принцип суперпозиции не работает.
Основные результаты и выводы
1. Построена математическая модель напряженно-деформированного состояния и устойчивости пологих оболочек переменной толщины, находящихся под действием нагрузки, перпендикулярной плану оболочки, и температурного поля, для кинематической модели Кирхгофа-Лява.
2. Построены три типа полных систем функций, аппроксимирующих искомые ![]() и
и ![]() , служащие для расчета различным образом закрепленных по сторонам контура оболочек прямоугольного плана. Построенные функции удобны для реализации в расчетах, поскольку при изменении граничных условий меняются не сами функции, а лишь четыре константы внутри них.
, служащие для расчета различным образом закрепленных по сторонам контура оболочек прямоугольного плана. Построенные функции удобны для реализации в расчетах, поскольку при изменении граничных условий меняются не сами функции, а лишь четыре константы внутри них.
3. Разработан и реализован на ЭВМ расчетный алгоритм с использованием подобранных систем аппроксимирующих функций, на базе которого решен ряд тестовых задач и несколько новых задач.
4. При решении тестовых задач из сравнения полученных нами результатов с решениями других авторов, выполненных иными методами, и из сравнения наших результатов, выполненных с разными системами аппроксимирующих функций, делается вывод о возможности и эффективности применения всех построенных систем функций.
5. Из новых задач решены задачи напряженно-деформированного состояния и устойчивости от действия внешней нагрузки, перпендикулярной плану оболочки: для весьма пологих оболочек постоянной толщины различным образом закрепленных по контуру; для оболочек большой кривизны (подъемистых оболочек) постоянной и переменной толщины, шарнирно-неподвижно закрепленных и жестко заделанных по контуру; задачи о комбинированном воздействии на оболочку нагрузки и температурного поля. При рассмотрении подъемистых оболочек, жестко заделанных по контуру, нами впервые наблюдались эффекты петлеобразования на графике «![]() », которые пропадают при рассмотрении оболочек переменной толщины. При этом в случае оболочек переменной толщины уровень критической нагрузки значительно возрастает, а уровень критических внутренних усилий понижается. При рассмотрении комбинированного нагружения ярко показывается, что принцип независимости действия сил (принцип суперпозиции) в нелинейных задачах не работает.
», которые пропадают при рассмотрении оболочек переменной толщины. При этом в случае оболочек переменной толщины уровень критической нагрузки значительно возрастает, а уровень критических внутренних усилий понижается. При рассмотрении комбинированного нагружения ярко показывается, что принцип независимости действия сил (принцип суперпозиции) в нелинейных задачах не работает.
Основное содержание диссертации отражено в публикациях:
Публикации в изданиях, рекомендованных ВАК РФ
1. Абросимов А.А. Потеря устойчивости и закритическое поведение пологих оболочек, различным образом закрепленных на прямоугольном контуре / А.А. Абросимов, Г.А. Айрапетьянц, В.Н. Филатов // Вестник Саратовского государственного технического университета. – 2007. – № 3 (26). – Вып. 1. – С. 7-12.
2. Абросимов А.А. Расчеты подъемистых оболочек с разными системами
аппроксимирующих функций / А.А. Абросимов, В.Н. Филатов // Вестник Саратовского государственного технического университета. – 2009. – № 2 (38). – Вып. 1. – С. 49-57.
Другие публикации
3. Абросимов А.А. Расчеты оболочек переменной толщины с разными системами аппроксимирующих функций / А.А. Абросимов, К.В. Молодчиков, В.Н. Филатов / СГТУ. Саратов, 2004. 22 c. Деп. в ВИНИТИ, №2064-В.
4. Абросимов А.А. Граничная задача для уравнений термоупругости гибких пологих оболочек переменной толщины при зависимости механических характеристик материала от температуры / А.А. Абросимов, К.В. Молодчиков, Е.А. Попов, В.Н. Филатов // Мат. моделир., числен. методы и комплексы программ : сб. науч. тр. / СПбГАСУ. – Вып.11. – СПб., 2005. – С. 78-89.
5. Абросимов А.А. Исследование НДС оболочек переменной толщины с использованием разных систем аппроксимирующих функций / А.А. Абросимов, К.В. Молодчиков, В.Н. Филатов // Мат. моделир., числен. методы и комплексы программ : сб. науч. тр. / СПбГАСУ. – Вып.11. – СПб., 2005. – С. 89-103.
6. Абросимов А.А. Применение различных методов линеаризации уравнений при исследовании НДС гибких пологих оболочек / А.А. Абросимов, Г.А. Айрапетьянц // Молодые ученые – науке и производству : материалы конференции молодых ученых. – Саратов: СГТУ, 2007. – С. 5-7.
7. Абросимов А.А. Исследование НДС гибких пологих оболочек с разными системами аппроксимирующих функций / А.А. Абросимов, Г.А. Айрапетьянц, Н.А. Добрюха // Молодые ученые – науке и производству : материалы конференции молодых ученых. – Саратов: СГТУ, 2007. – С. 51-53.
8. Абросимов А.А. Исследование НДС пластин переменной толщины в геометрически нелинейной постановке с разными системами аппроксимирующих функций / А.А. Абросимов, В.Н. Филатов // Прикладная математика и механика: сб. науч. тр. – Ульяновск: УлГТУ, 2007. – С. 3-8.
9. Абросимов А.А. Исследование возможности применения аппроксимирующих функций разного вида к расчетам оболочек защемленных по контуру / А.А. Абросимов // Молодые ученые – науке и производству : материалы конференции молодых ученых. – Саратов: СГТУ, 2008. – С. 5-8.
Подписано в печать 25.05.09 Формат 6084 1/16
Бум. офсет. Усл. печ. л.1,0 Уч.-изд. л.1,0
Тираж 100 экз. Заказ 258 Бесплатно
Саратовский государственный технический университет
410054, Саратов, Политехническая ул., 77
Отпечатано в РИЦ СГТУ. 410054, Саратов, Политехническая ул., 77

