Анализ параметрических колебаний в элементах машин и конструкций при неконсервативном нагружении
На правах рукописи
Васина Валентина Николаевна
АНАЛИЗ ПАРАМЕТРИЧЕСКИХ КОЛЕБАНИЙ В ЭЛЕМЕНТАХ МАШИН И КОНСТРУКЦИЙ ПРИ НЕКОНСЕРВАТИВНОМ НАГРУЖЕНИИ
01.02.06 – Динамика, прочность машин, приборов и аппаратуры
Автореферат диссертации на соискание ученой степени
кандидата технических наук
Москва – 2008
Работа выполнена в Московском энергетическом институте (техническом университете) на кафедре динамики и прочности машин
Научный руководитель: кандидат технических наук, доцент
Радин Владимир Павлович
Официальные оппоненты: доктор технических наук, профессор
Потапов Вадим Дмитриевич
доктор физико-математич. наук, профессор
Кирсанов Михаил Николаевич
Ведущая организация Институт Проблем Механики РАН
Защита состоится «28» мая 2008 г. в 1400 в аудитории Б-112 на заседании диссертационного совета Д 212.157.11 при Московском энергетическом институте (техническом университете) по адресу: 111250 Москва, Красноказарменная ул., д. 17.
С диссертацией можно ознакомиться в библиотеке Московского энергетического института (технического университета)
Автореферат разослан «__» _________ 2008 г.
Учёный секретарь
диссертационного совета
доктор технических наук, профессор О.В. Трифонов
Общая характеристика работы
Актуальность проблемы. Динамические расчеты машин и конструкций при параметрических воздействиях имеют ряд особенностей, главная из которых состоит в необходимости исследования устойчивости положений равновесия, а для нелинейных систем – в анализе закритического поведения. В настоящее время можно считать, что динамическое поведение канонических систем при параметрических воздействиях исследовано достаточно подробно. Менее изученными остаются вопросы параметрических колебаний линейных и нелинейных систем при наличии неконсервативных нагрузок. Подобного рода задачи возникают при действии на механические системы переменных во времени следящих сил, учете сил внутреннего трения (параметрические колебания вращающихся валов), учете непостоянства скорости протекания жидкости (расчеты трубопроводов) и т.д.
Цель работы. Целью диссертационной работы является систематический анализ параметрических колебаний различных механических систем при действии неконсервативных нагрузок. На основе разработанного программного продукта провести анализ параметрических колебаний таких систем, как двухзвенный маятник и консольный стержень при действии переменных по величине потенциальных и следящих сил, исследовать влияние сил внутреннего трения на параметрические колебания вращающегося вала, а также проанализировать динамическое поведение участка гибкого трубопровода при протекании по нему жидкости с переменной скоростью.
Методы исследования. Для построения областей параметрического резонанса используется метод матриц монодромии с применением численного интегрирования уравнений движения. Характер движения нелинейных систем в закритической области исследуется путем построения сечений Пуанкаре. В некоторых случаях динамические системы анализируются методами имитационного моделирования. Параметрические колебания систем с распределенными параметрами исследуются с использованием метода главных координат.
Научная новизна. В работе впервые проведен систематический анализ параметрических колебаний ряда неконсервативных систем с использованием современных средств вычислительной математики и техники. Обнаружены новые эффекты, присущие неконсервативным системам при параметрических воздействиях. В части исследования колебаний консольного стержня при одновременном действии мёртвой и следящей сил обнаружены новые комбинационные резонансы. А в задаче колебаний трубопровода с протекающей жидкостью проиллюстрировано сложное взаимодействие различных форм колебаний системы при её приближении к критическому состоянию.
Достоверность полученных результатов. Достоверность результатов обеспечивается применением строгих математических методов исследования, сопоставлением результатов, полученных различными методами, решением большого числа тестовых задач и сравнением ряда результатов с результатами, приведенными в известных справочниках.
Практическая ценность. Полученные в работе результаты имеют теоретическое и практическое значение. Они позволяют уточнить существующее представление о характере поведения параметрических систем при одновременном действии потенциальных и неконсервативных нагрузок. Могут быть использованы при проектировании и динамическом расчёте элементов конструкции, находящихся при сложном нагружении.
Апробация работы и публикации. Материалы диссертационной работы докладывались и обсуждались:
на Одиннадцатой Международной научно – технической конференции студентов и аспирантов «Радиотехника, электротехника и энергетика». 1 – 2 марта, 2005 г., Москва.
на Двенадцатой Международной научно – технической конференции студентов и аспирантов «Радиотехника, электротехника и энергетика». 2 – 3 марта, 2006 г., Москва.
По теме диссертации опубликованы 3 статьи.
Структура и объем диссертации. Диссертационная работа состоит из введения, пяти глав, сводки результатов и выводов, списка литературы из 75 наименований. Объем работы – 128 страниц основного текста, включая 55 рисунков.
Краткое содержание работы
Во введении приводятся определение понятия параметрические колебания и примеры механических систем, математические модели, движения которых описываются дифференциальными уравнениями с переменными (периодическими) коэффициентами. Проводится обзор основных литературных данных и формулируется постановка задачи об исследовании параметрических систем. Дается краткое содержание диссертации, обоснование важности и актуальности темы исследования параметрических колебаний в неконсервативных системах.
В первой главе в матричной форме излагается теория ФлокеЛяпунова и метод матриц монодромии для построения границ областей параметрического резонанса. С целью верификации алгоритмов и программ, применяемых в дальнейших вычислениях, в данном разделе проводятся вычисления областей параметрического резонанса для классических систем с одной и двумя степенями свободы, уравнения движения которых имеют вид
,
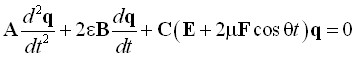где 
вектор обобщённых координат, 
и 
симметричные, положительно определенные постоянные матрицы;
единичная матрица; 
постоянная матрица произвольной структуры, характеризующая структуру параметрического возбуждения. Интегрирование уравнений движения с целью построения матриц монодромии проводилось с использованием системы имитационного моделирования Simulink. Блоксхема для уравнения движения представлена на рис. 1.
Рис. 1. Блок – схема имитационного моделирования для исследования параметрических колебаний системы с двумя степенями свободы
Результаты определения границ параметрического резонанса сравнивались с данными справочника1 (глава VII). В некоторых случаях имеются несоответствия графиков, полученных в диссертационной работе, с графиками, представленными в справочнике. Это касается, например, областей неустойчивости для системы с одной степенью свободы, приведенных на рис. 2, для системы с двумя степенями свободы при 
, изображенных на рис. 3.
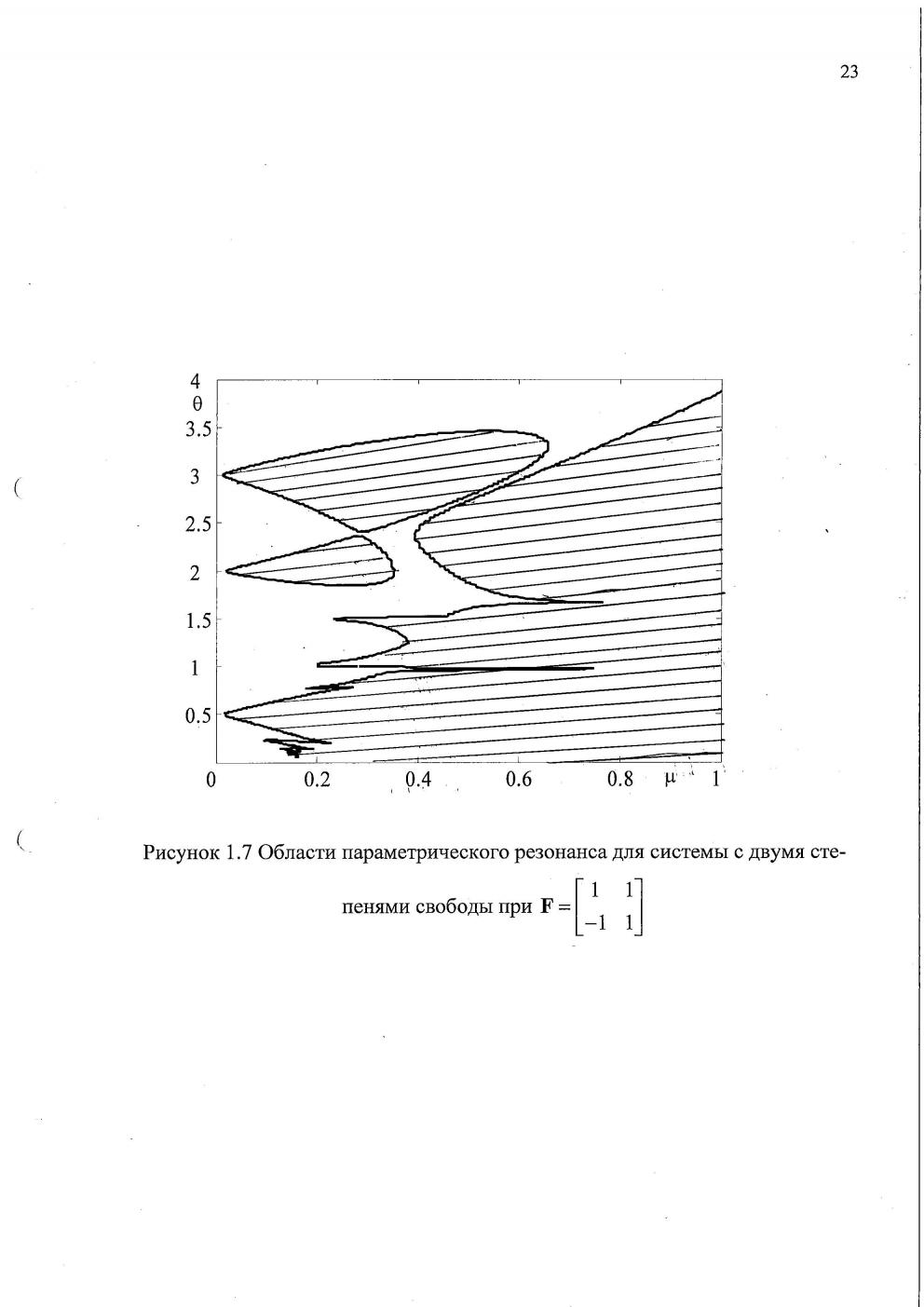
Рис. 2. Области параметрического Рис. 3. Области параметрического
резонанса для системы с одной резонанса для системы с двумя
степенью свободы степенями свободы
Как и в вышеупомянутом справочнике, исследованы параметрические резонансы в системах, находящихся под действием позиционных неконсервативных сил. Построены области параметрической стабилизации динамически и статически неустойчивых систем.
В конце первой главы сформулирована цель диссертации.
Вторая глава посвящена исследованию плоских колебаний двухзвенного маятника (рис. 4), находящегося под действием силы 
, не изме-
1 Вибрации в технике: Справочник. Т.1. Колебания линейных систем / Под ред. В.В. Болотина.- М.: Машиностроение. – 1999. – 504 с.
няющей своего направления, и следящей силы 
, направленной вдоль оси второго звена при любых отклонениях маятника.
Рис. 4. Двухзвенный маятник под действием
потенциальной и следящей сил
Матричная форма уравнений движения относительно вектора угловых перемещений 
имеет вид:
,
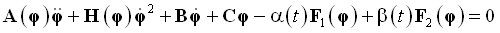где введены обозначения
, 
,
, 
, 
,
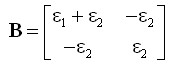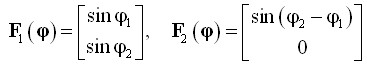Для линеаризованного уравнения движения построены области неустойчивости при постоянных параметрах нагружения 
,
и области параметрического резонанса при 
, 
на плоскости 
. Изучались траектории движения мультипликаторов при изменении параметров. Рассматривались различные случаи нагружения: воздействие только периодической мёртвой силы 
, воздействие только периодической следящей силы 
и одновременное синфазное изменение сил 
и 
с одинаковой частотой. В первом случае главные параметрические резонансы наблюдаются на частотах 
и 
(
и 
первая и вторая собственные частоты маятника), а комбинационный резонанс суммарного типа имеет место в окрестности частоты 
(рис. 5). Изучение траекторий мультипликаторов для 
и 
показало, что на границе областей неустойчивости имеются 
периодические решения, так как мультипликаторы выходят за единичную окружность через значения 
, и почти периодические решения для комбинационного резонанса суммарного типа. Во втором случае нагружения (рис. 6) кроме главных параметрических резонансов 
и 
наблюдается параметрический резонанс разностного типа 
. Здесь также выхода мультипликатора из единичной окружности через значение 
не происходит, так как кроме почти периодических решений в окрестности частоты 
возможны только 
периодические решения. Аналогично система себя ведёт и в третьем случае нагружения.
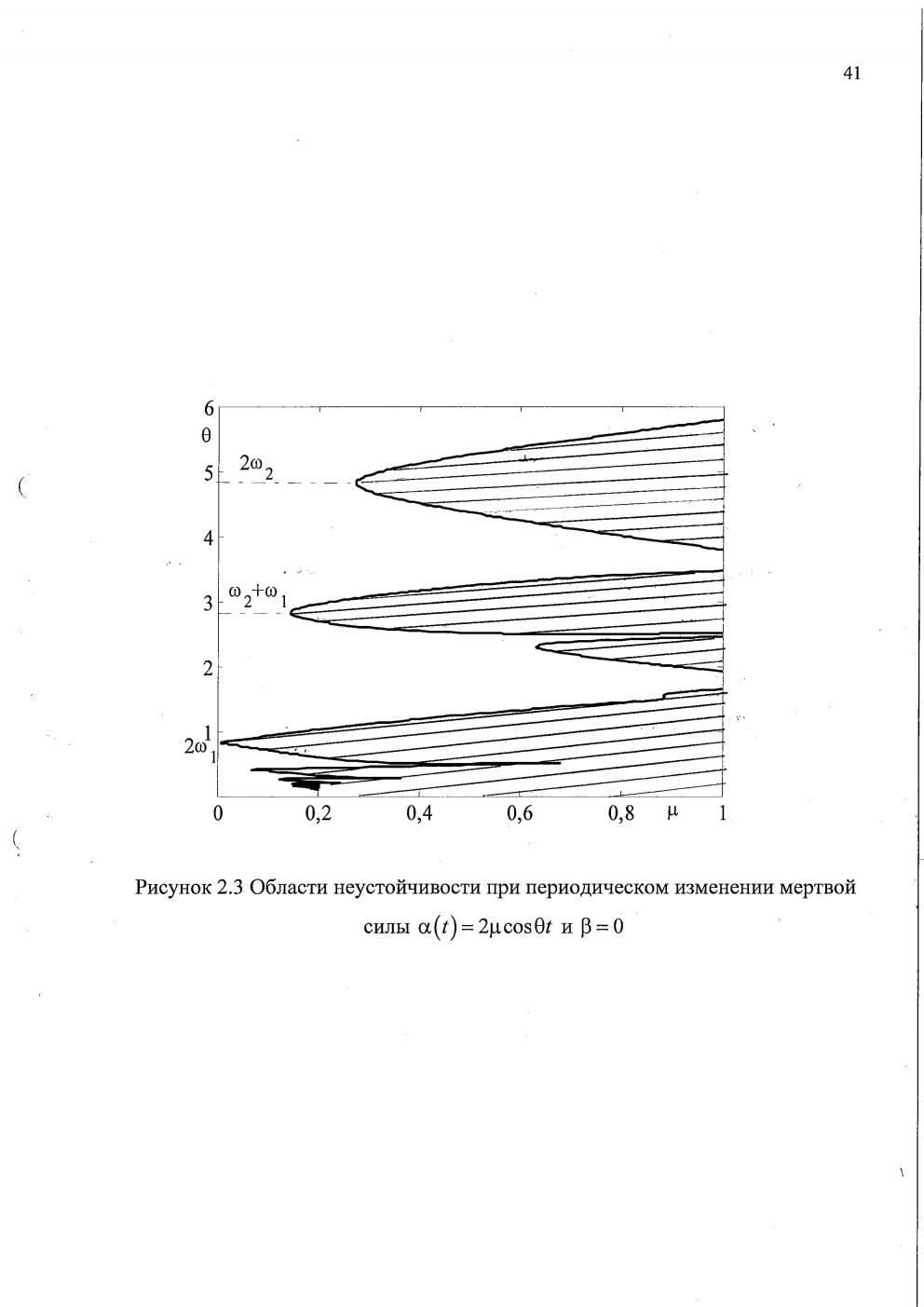
Рис. 5. Области неустойчивости Рис. 6. Области неустойчивости
при периодическом изменении при периодическом изменении
мёртвой силы и постоянной по следящей силы и постоянной по
величине следящей силе величине мёртвой силе
Рассматривалась возможность параметрической стабилизации неустойчивости. Исследование проводилось для величин параметров задачи, близких или равных их критическим значениям. Показано, что при постоянной по величине следящей силе 
, 
, 
и изменяющейся по гармоническому закону мёртвой силе стабилизировать систему возможно даже при невысоких значениях амплитуды параметрического воздействия (рис. 7). Изучалась эволюция границы области устойчивости, построенная при постоянных по величине значениях мёртвой и следящей сил на плоскости 
(рис. 8), при переходе к периодической мертвой силе для некоторых значений частоты 
(кривая 
), 
и 
. Очевидно, что при соответствующем выборе частоты параметрического воздействия область устойчивости может быть существенно расширена.
Исследовалось динамическое поведение нелинейной системы в области параметрического резонанса. Строились амплитудно-частотные характеристики при 
для различных вариантов параметрического нагружения двухзвенного маятника, фазовые портреты и сечения Пуанкаре, по которым можно судить о характере динамического поведения. Задавалось значение 
и брался ряд значений 
с продвижением вглубь параметрического резонанса. Для построения фазовых портретов и сечений Пуанкаре уравнения движения интегрировались на протяжении 
(безразмерное время). После исключения переходного участка дискретная выборка для фазовых переменных формировалась как их значения в моменты времени 
. При малых значениях параметра 
, т.е. в окрестности границы неустойчивости, фазовый портрет замкнутая кривая, а сечение
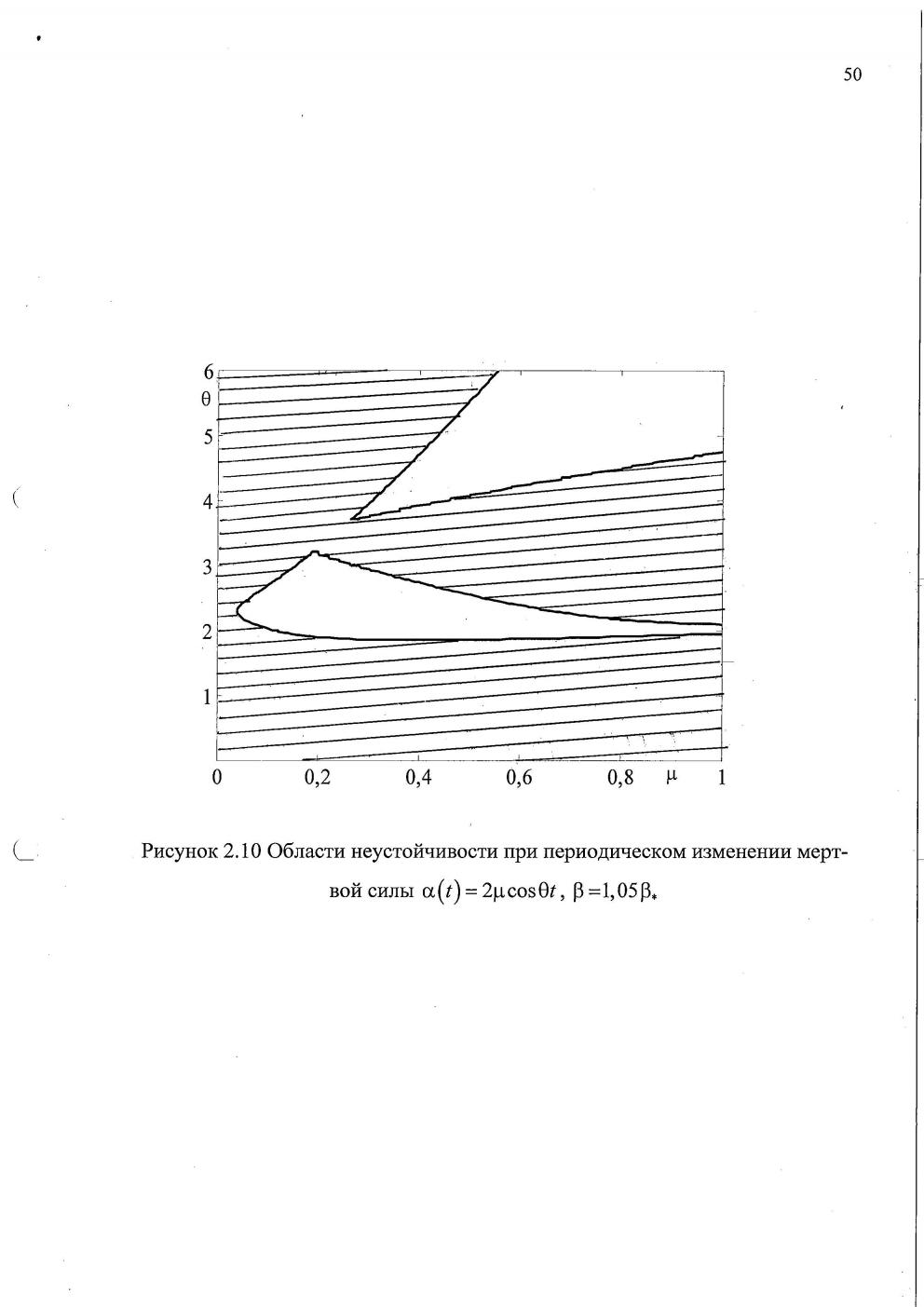
Рис. 7. Области неустойчивости Рис. 8. Границы области устойчи-
при периодическом изменении вости на плоскости параметров
мёртвой силы и величине следящей нагружения при различных значениях
силы, превышающей своё частоты мёртвой силы
критическое значение
Пуанкаре представляет собой конечный набор точек. Движение является периодическим. При возрастании 
фазовый портрет также замкнутая кривая, а сечение Пуанкаре – отрезки линий. Движение в этом случае квазипериодическое и представляет собой сумму гармоник с несоизмеримыми периодами.
На рис. 9 приведены фазовые портреты и сечения Пуанкаре для далеких закритических областей 
(а, б) и 
(в, г). Здесь в первом случае фазовый портрет аналогичен неустойчивому предельному циклу, стремящемуся к некоторому замкнутому аттрактору. Это подтверждает и сечение Пуанкаре, представляющее собой компактный случайный набор точек. При 
в области параметрического резонанса реализуются хаотические движения. Это наблюдается на фазовом портрете и на сечении Пуанкаре, образующем фрактальный набор точек. Таким образом, по мере удаления от границы параметрического резонанса происходит переход характера движения системы от периодического к хаосу.
В третьей главе проводится анализ устойчивости стержня с изгибной жесткостью 
, погонной массой 
и длиной 
, жестко защемленного на одном конце и нагруженного на другом переменными во времени нагрузками 
, направление которой неизменно, и 
, направление которой при любых перемещениях совпадает с направлением касательной к изогнутой оси стержня в точке приложения этой силы. Силы изменяются во времени по
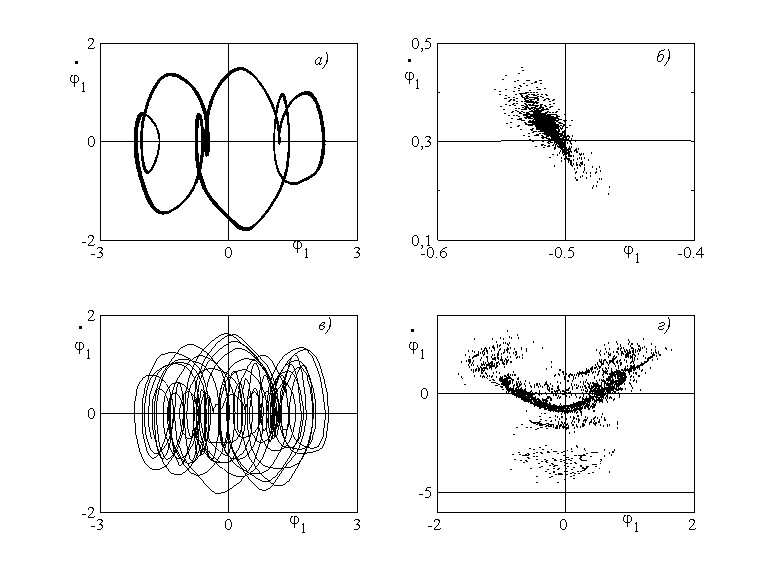
Рис. 9. Фазовые портреты и сечения (а, в) Пуанкаре (б, г) далеких
закритических областей 
(а, б) и 
(в, г)
гармоническому закону. Представим прогиб в виде ряда по формам собственных колебаний консольного стержня, и для удобства вычислений с помощью дельтафункции перенесем проекцию силы 
в уравнение
.
Приходим к системе обыкновенных дифференциальных уравнений с периодическими коэффициентами
,
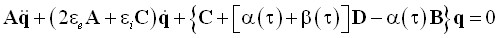где обозначено
.
Матрицы, входящие в уравнение, вычисляются по формулам
На рис. 10 представлена блок-схема имитационного моделирования для исследования параметрических колебаний консольного стержня, с помощью которого интегрировались уравнения движения, и строилась матрица монодромии.
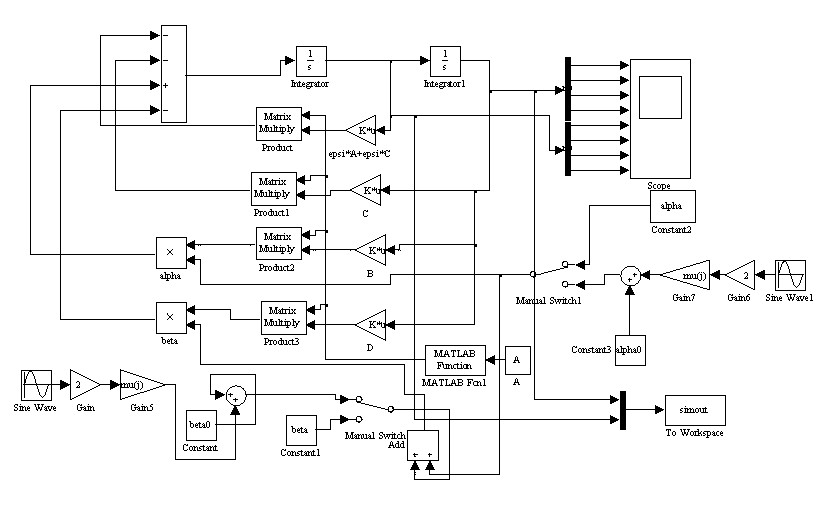
Рис. 10. Блок – схема имитационного моделирования для исследования параметрических колебаний консольного стержня
Некоторые результаты вычислений представлены на рис. 11 и 12. На рис. 11 изображены границы параметрических резонансов при действии только периодической силы 
при 
. Как и следовало ожидать, существенными здесь являются главные параметрические резонансы на частотах 
и комбинационные резонансы суммарного типа на частотах 
. Причем области неустойчивости различного типа могут накладываться друг на друга. При синфазном изменении параметров нагрузки 
и 
области неустойчивости показаны на рис. 12. Здесь присутствуют различные параметрические резонансы: главные, комбинационные суммарного и разностного типа. Обнаружен также кратный параметрический резонанс суммарного типа 
.
Изучались возможности параметрической стабилизации динамически неустойчивой системы, т.е. для случая, когда один из параметров нагрузки постоянен и равен или превышает критическое значение. На рис. 13 построены границы области параметрической стабилизации для случая 
и 
. При превышении следящей силой своего критиче-
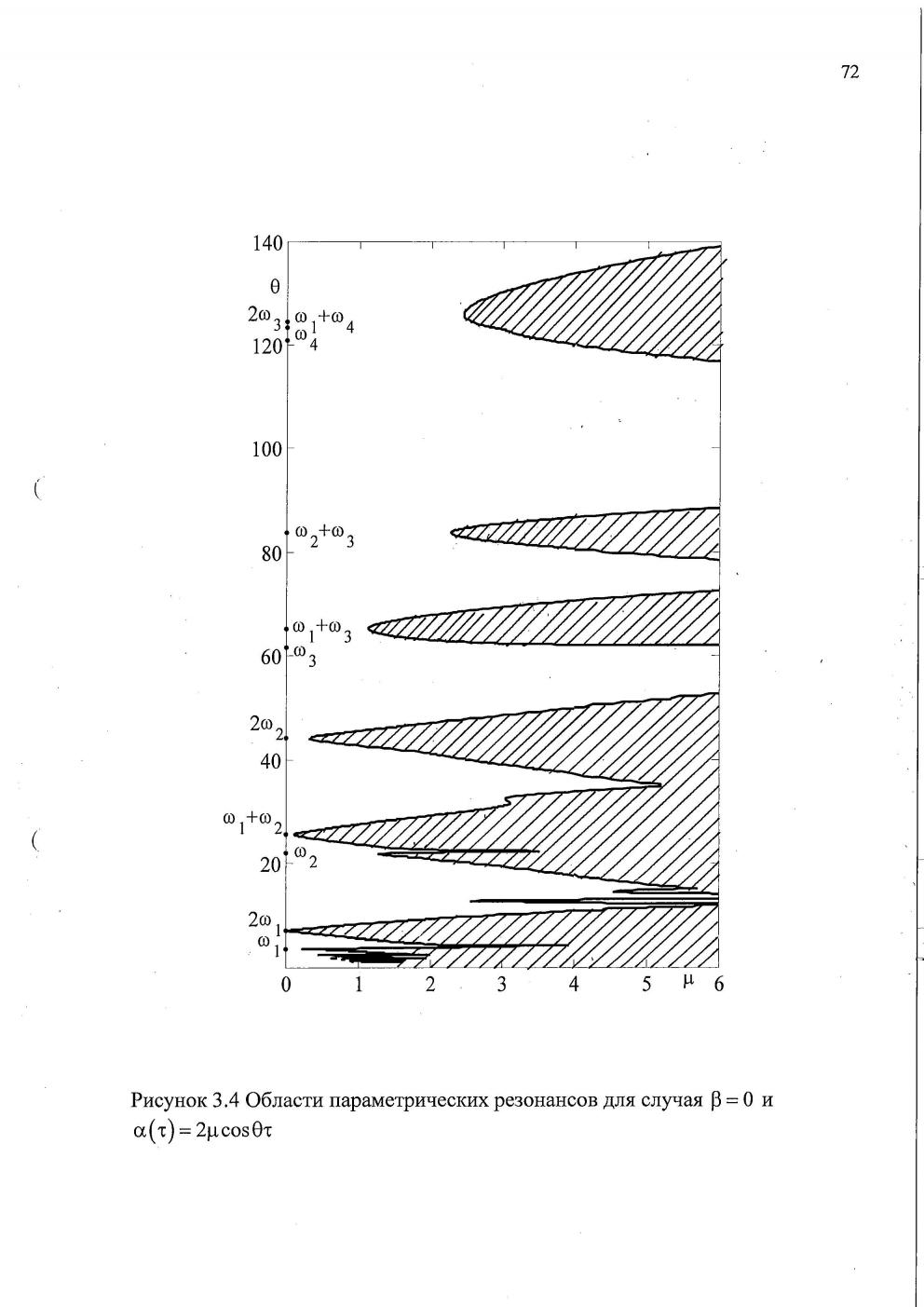
Рис. 11. Области параметричес- Рис. 12. Области параметричес-
ких резонансов при действии ких резонансов при синфазном измене-
только периодической мёртвой силы нии параметров нагрузки
Рис. 13. Области параметрической стабилизации
ского значения 
приложение периодической силы 
стабилизирует систему в окрестности частот 
и 
. Наиболее близка к оси ординат, т.е. реализующаяся при малых значениях амплитуды параметрического воздействия, область в окрестности 
Четвертая глава посвящена исследованию влияния внутреннего трения на параметрические колебания вращающегося вала. Обозначим через 
вектор поперечных перемещений сечений вала относительно оси вращения 
в неподвижной системе координат и применим метод главных координат 
, где вектор 
состоит из форм собственных изгибных колебаний вала, обобщенные координаты включены в матрицу 
.
Для неизотропного вала изгибные колебания будут описываться уравнением с периодическими коэффициентами. При отсутствии присоединенных масс и с учетом нелинейности за счет продольной силы, возникающей в вале при поперечных смещениях и неподвижных опорах, это уравнение будет иметь вид
,
где
,
, 
,
.
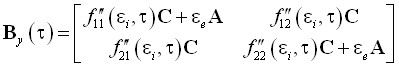В этих формулах элементы матриц 
и 
вычисляются как интегралы от собственных форм и их производных, а также обозначено
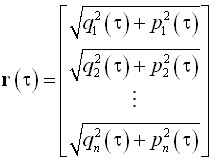
Для случая 
на рис. 14 построены зависимости критической частоты вращения 
от коэффициента внутреннего трения 
при различных значениях коэффициента внешнего трения 
. Вид кривых подтверждает формулу для 
, полученную В.В. Болотиным для безинерционного вала с диском 
, где 
собственная частота изгибных колебаний. Аналогично этой формуле из рис. 14 следует, что при неограниченном росте 
критическая частота приближается к первой собственной частоте изгибных колебаний вала, составляющая для рассматриваемой системы 
.
Для исследования параметрических резонансов линеаризованное уравнение движения интегрировалось 
раз на одном периоде 
при начальных условиях, соответствующих столбцам единичной матрицы размерностью 
. Из значений решений в конце периода составлялась матрица монодромии и вычислялись ее собственные числа мультипликаторы. По теории ФлокеЛяпуноваЧетаева тривиальное решение уравнения будет устойчивым, если все мультипликаторы по модулю меньше единицы, и неустойчивым, если модуль хотя бы одного мультипликатора превысит единицу. На основе этого метода строились границы области неустойчивости на плоскости параметров: 
амплитуда параметрического воздействия и 
частота вращения вала. Параметр 
характеризует степень неизотропности жесткостных свойств вала. Указанные на рис. 15 границы построены для случая коэффициента внешнего трения, равного 
, при различных значениях коэффициента внутреннего трения. Области неустойчивости, расположенные справа от границ, состоят из двух частей: область параметрического резонанса, отмеченная на рис. 15 горизонтальной штриховкой, и область автоколебаний, возникающих за счет действия неконсервативных сил внутреннего трения. Для случая 
эта область отмечена вертикальной штриховкой.
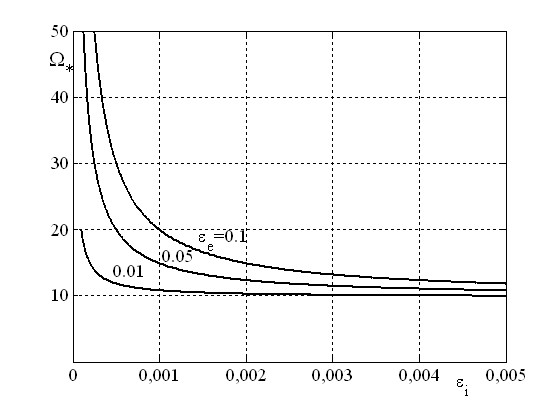
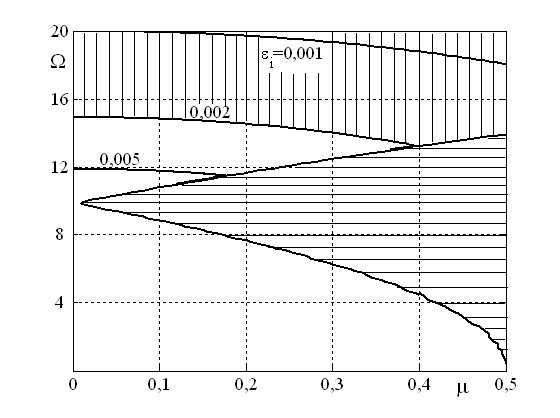
Рис. 14. Зависимость критической Рис. 15. Области неустойчивости
скорости вращения вала от и параметрического резонанса при
коэффициента внутреннего трения 
и различных значениях
коэффициента внутреннего трения
Из рисунка следует, что величина внутреннего трения, существенно снижая верхнюю границу критических частот вращения, практически не влияет на положение границы параметрического резонанса.
Для исследования характера движения системы в области неустойчивости проводилось интегрирование нелинейного уравнения. На рис. 16 построена амплитудночастотная характеристика при 
, 
, 
и 
. По оси ординат здесь отложена амплитуда изгибных колебаний вала 
в установившемся режиме. Амплитуда 
отлична от нуля в области параметрического резонанса в диапазоне частот 
и при 
в
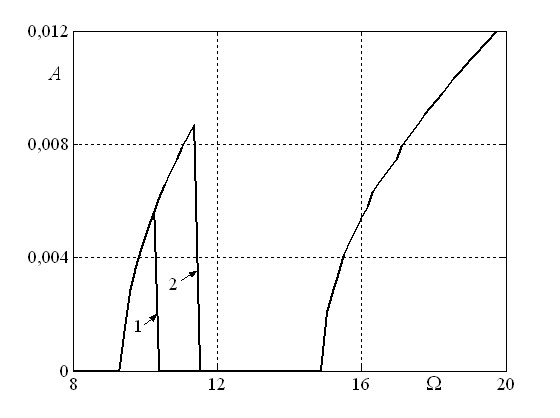
Рис. 16. АЧХ для среднего сечения вала при 
, 
, 
, 
.
области динамической неустойчивости из-за наличия внутреннего трения. Для области параметрического резонанса имеет место явление затягивания, что проявляется в зависимости решений для амплитуды колебаний в окрестности правой граничной точки вышеуказанного частотного диапазона от начальных условий (эффект забрасывания). Кривая 1 на рис. 16 построена для начальных отклонений среднего сечения вала, равных 0,0005 при нулевой начальной скорости, кривая 2 для начальных отклонений 0,005. На рис. 17 представлены траектории движения среднего сечения вала в областях неустойчивости прямолинейной формы при частоте вращения 
(рис. 17,а) и при 
(рис. 17,б) и указанных выше значениях остальных параметров. Тонкими линиями показаны начальные этапы движения, которые при 
стремятся к установившимся движениям круговой формы (жирные замкнутые линии). Более подробный анализ с помощью сечений Пуанкаре показал, что в области параметрического резонанса устанавливается периодическое движение с частотой 
, т.е. имеет место прямая синхронная прецессия. В этом случае сечение Пуанкаре представляет собой единственную изолированную точку. При частотах вращения, больших критических, движение является квазипериодическим, состоящим из гармоник с несоизмеримыми периодами. Соответствующее сечение Пуанкаре замкнутая кривая.
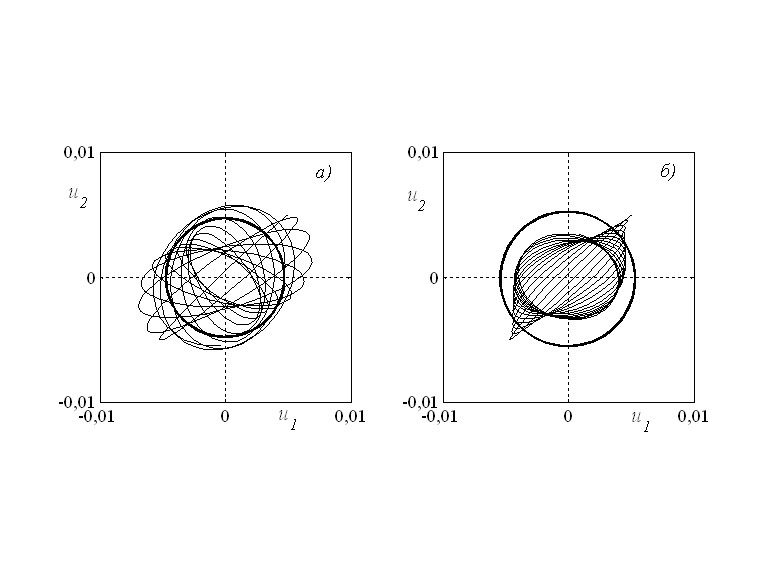
Рис. 17. Траектории движения среднего сечения вала в областях неустойчивости прямолинейной формы при 
(а), 
(б)
В пятой главе проводится исследование параметрических колебаний трубопровода с протекающей жидкостью. Рассматривается прямолинейный участок трубопровода, защемлённый на одном конце, наполненный невязкой жидкостью, которая движется с невозмущённой скоростью 
(рис. 18).
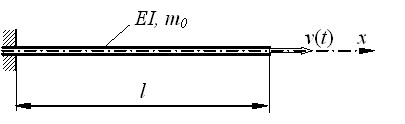
Рис. 18. Участок трубопровода с протекающей жидкостью
Уравнения движения системы принимается в виде
,
где 
прогиб трубопровода, 
масса жидкости, приходящаяся на единицу длины, и введены следующие параметры
Решение уравнения движения представлялось в виде разложения по формам собственных колебаний консольного стержня, в результате приходим к уравнению относительно вектора обобщенных координат 
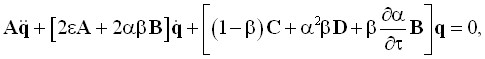
где элементы матриц 
и 
вычисляются как интегралы от собственных форм и их производных.
Для случая постоянной скорости протекания жидкости на рис. 19 для 
представлена зависимость критических значений параметра скорости 
, соответствующая границе, пересечение которой приводит к колебательной неустойчивости трубопровода (флаттеру). Область под кривой 
можно трактовать как область устойчивости на плоскости 
. На этом же рисунке приведена зависимость частоты флаттера 
, соответствующая значениям мнимой части характеристических показателей, переходящих в правую полуплоскость при критических значениях параметров.
Рис. 19. Граница области устойчивости и частота флаттера при потере устойчивости
Рассмотрен случай периодического изменения скорости протекания жидкости, т.е.
.
Здесь 
круговая частота изменения периодической составляющей скорости, связанная с периодом 
известным соотношением 
, 
амплитуда флуктуаций скорости в долях от среднего значения 
.
Методом матриц монодромии исследовалось влияние параметра модуляции 
и частоты 
параметрического воздействия на положение границ области устойчивости на плоскости 
. На рис. 20 представлены границы области устойчивости трубопровода на плоскости 
при частоте параметрического воздействия (пульсаций скорости протекания жидкости) равной 
и различных значениях параметра модуляции параметрического воздействия 
. Эти значения указаны на рис. 20 у соответствующих кривых. Штриховая линия – граница области устойчивости при постоянной скорости протекания жидкости. Кроме несущественных участков стабилизации системы при малых значениях параметра 
в окрестности 
, непостоянство скорости жидкости сужает область устойчивости и тем больше, чем больше параметр модуляции 
. Следует также отметить весьма сложный вид границ устойчивости, характерный для случая, когда неконсервативная система подвергается параметрическому воздействию. На рис. 21 границы области устойчивости построены при постоянной степени модуляции 
для различных частот параметрического воздействия. Здесь существенное влияние на положение границы наблюдается для малых значений (
) относительной массы жидкости. Причем проявляется как стабилизирующее влияние параметрического воздействия (
, 
), так и дестабилизирующее немонотонное влияние параметрического воздействия.
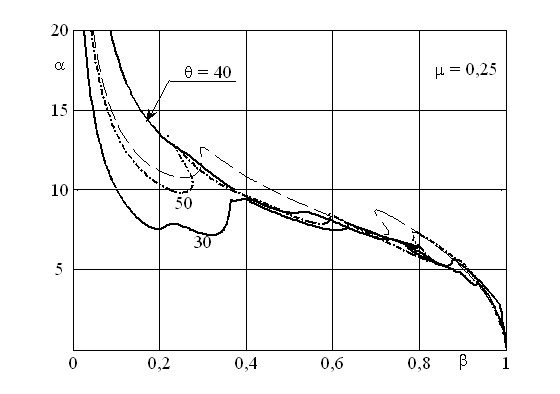
Рис. 20. Границы области устой- Рис. 21. Границы области устой-
чивости при 
и различных чивости при 
и для различных
значениях 
частот параметрического воздействия
Рис. 22 иллюстрирует динамическое поведение системы на границе области устойчивости. Для относительной массы жидкости 
, пульсаций скорости с частотой 
и различных коэффициентов модуляции 
(рис. 22,а), 
(рисунок 22,б), 
(рис. 22,в) и 
(рис. 22,г) построены фазовые портреты движения конца участка трубопровода (
) для установившегося участка движения. При 
критические значения параметров системы приводят к образованию устойчивого предельного цикла с частотой 
. На фазовой плоскости такому предельному циклу соответствует эллипс (рис. 22,а). Введение в систему параметрического воздействия с малой амплитудой 
приводит к бифуркации типа удвоения периода, движение существенно усложняется, оставаясь периодическим (рис. 22,б). Частота движения становится равной 10. При 
и 
периодические движения на границе области устойчивости происходят с частотой 
.
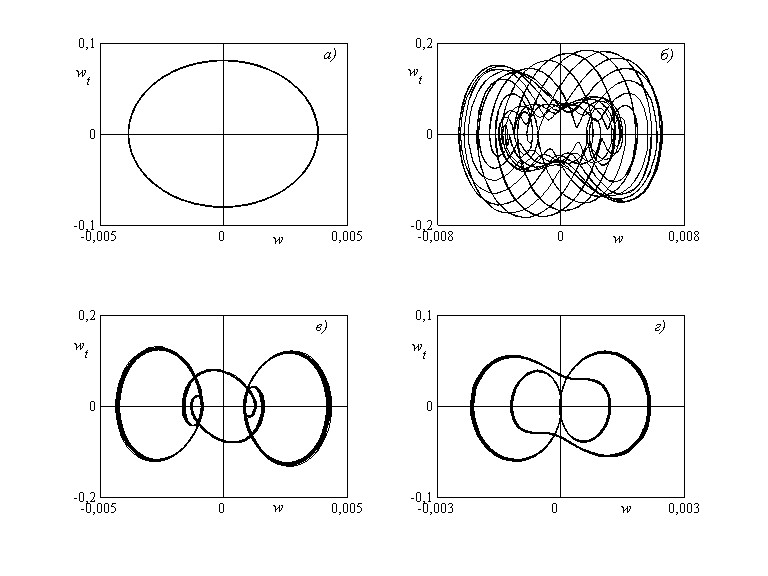
Рис. 22. Фазовые портреты движения конца трубопровода при 
, 
для различных значений коэффициента модуляции
Сводка результатов и выводы
1. Проведен пересчет и дополнительные численные исследования областей параметрического резонанса для систем с одной и двумя степенями свободы. В последнем случае, как и в справочнике (см. ссылку на стр. 5 автореферата), проведен анализ структуры коэффициентов возбуждения. Рассмотрены параметрические резонансы в некосервативной системе с двумя степенями свободы. Вычисления проводились с использованием метода матриц монодромии с проверкой точности положения границы параметрического резонанса непосредственным интегрированием уравнений движения. Интегрирование уравнений параметрических колебаний проводилось с использованием соответствующих схем имитационного моделирования. Получены уточнения некоторых графиков, приведенных в упомянутом выше справочнике.
2. Построены границы области устойчивости и определена частота флаттера при постоянных по величине действующих силах для нелинейного уравнения движения двухзвенного маятника, находящегося под действием потенциальной и следящей сил. Проведено исследование положения границ параметрического резонанса для двухзвенного маятника при различных вариантах периодического изменения величины потенциальной и следящей силы. Кроме главных параметрических резонансов получены комбинационные резонанс суммарного типа при действии периодической мертвой силы и комбинационный резонанс разностного типа при действии периодической следящей силы. Изучены траектории мультипликаторов на комплексной плоскости. Численно проанализирована возможность параметрической стабилизации статически и динамически неустойчивой системы. Проведено исследование динамического поведения нелинейной системы в области параметрического резонанса. Показано, что в области неустойчивости в зависимости от близости к границе существуют периодические, квазипериодические и хаотические движения.
3. Проведено исследование параметрических колебаний консольного стержня при одновременном нагружении мертвой и следящей силами. Применением метода разложения по формам собственных колебаний уравнение движения стержня сведено к системе обыкновенных дифференциальных уравнений. Для случая постоянных по величине нагрузок построена граница устойчивости на плоскости параметров и определена частота флаттера при динамической потери устойчивости. Для построения границ неустойчивости при периодическом изменении нагрузок была разработана схема имитационного моделирования в системе Simulink. Рассмотрены различные варианты параметрического нагружения стержня с построением границ областей неустойчивости и изучением поведения мультипликаторов. Здесь для системы, находящейся под действием только периодической следящей силы, получен суммарный резонанс. А для случая синфазного изменения следящей и мёртвой сил обнаружен кратный параметрический резонанс суммарного типа. Проанализирована возможность параметрической стабилизации статически и динамически неустойчивой системы.
4. Рассмотрены нелинейные уравнения движения вращающегося вала с распределенной массой и имеющего различные главные моменты инерции с учетом неконсервативных сил внутреннего трения. Методом главных координат проведена редукция системы к системе с конечным числом степеней свободы. Исследована устойчивость вращающегося вала, определены критические скорости. Показано, что область неустойчивости является совокупностью области параметрического резонанса и области автоколебаний, возникающих за счет действия неконсервативных сил внутреннего трения. Для нелинейной системы проведено построение амплитудночастотной характеристики и исследован характер движения вала в области неустойчивости при вращении с закритической частотой.
5. Рассмотрены параметрические колебания участка трубопровода с жидкостью, протекающей по нему с непостоянной скоростью. Для случая постоянной скорости протекания жидкости на плоскости параметров относительная массаскорость течения построена граница области устойчивости и определена частота флаттера. Для гармонических флуктуаций скорости проведено подробное исследование положения границ устойчивости на указанной выше плоскости параметров, а также на плоскости коэффициент модуляции–частота. Проведено исследование динамического поведения системы на границе области устойчивости. Показано, что введение в систему параметрического воздействия с малой амплитудой приводит к бифуркации типа удвоения периода, движение системы существенно усложняется, оставаясь периодическим.
Публикации по теме диссертации
- Васина В.Н. Параметрические колебания участка трубопровода с протекающей жидкостью // Вестник Московского энергетического института, 2007. №1. С. 5-12.
- Болотин В.В., Васина В.Н., Радин В.П., Чирков В.П. Параметрические колебания в неконсервативных системах // «Проблемы прикладной механики, динамики и прочности машин». Сборник статей. Изд-во МГТУ им. Н.Э.Баумана, 2005. С. 22-31.
- Васина В.Н., Окопный Ю.А., Радин В.П. Исследование влияния внутреннего трения на параметрические колебания вращающегося вала // Инженерный журнал. Справочник. Машиностроение, 2005, №11. С. 19 - 24
- Васина В.Н., Радин В.П. Исследование устойчивости и послекритического поведения роторной системы // Радиоэлектроника, электротехника и энергетика. Одиннадцатая междунар. науч.-техн. конф. студентов и аспирантов. Тез. докл. В 3-х т. М.: Издательство МЭИ, 2005. Т.3. С.230.
- Васина В.Н., Радин В.П. Исследование влияния внутреннего трения на параметрические колебания вращающегося вала // Радиоэлектроника, электротехника и энергетика. Двенадцатая междунар. науч.-техн. конф. студентов и аспирантов. Тез. докл. В 3-х т. М.: Издательство МЭИ, 2006. Т.3. С.284.
Подписано в печать Зак. Тир. П.л.
Полиграфический центр МЭИ (ТУ)
Красноказарменная ул., д.13
