Динамический контакт ударника и тонких тел с учетом волновых процессов
На правах рукописи
Локтев Алексей Алексеевич
ДИНАМИЧЕСКИЙ КОНТАКТ УДАРНИКА И ТОНКИХ ТЕЛ С УЧЕТОМ ВОЛНОВЫХ ПРОЦЕССОВ
Специальность 01.02.04 – Механика деформируемого твердого тела
АВТОРЕФЕРАТ
диссертации на соискание ученой степени
доктора физико-математических наук
Москва – 2010
Работа выполнена в
Московском государственном университете путей сообщения (МИИТ)
Официальные оппоненты: доктор физико-математических наук,
старший научный сотрудник
Айзикович Сергей Михайлович
доктор технических наук,
старший научный сотрудник
Дементьев Вячеслав Борисович
доктор физико-математических наук,
профессор
Коузов Даниил Петрович
Ведущая организация: Научно-исследовательский институт механики и прикладной математики имени Воровича И.И. Федерального государственного образовательного учреждения высшего профессионального образования "Южный федеральный университет"
Защита состоится 14 октября 2010 года в 14 часов 00 минут на заседании диссертационного совета Д 002.075.01 при Институте проблем машиноведения РАН по адресу: 199178, Санкт-Петербург, Большой пр. В.О., 61.
С диссертацией можно ознакомиться в ОНТИ Института проблем машиноведения РАН.
Автореферат разослан 8 июля 2010 года.
Ученый секретарь
диссертационного совета
доктор технических наук В.В. Дубаренко
ОБЩАЯ ХАРАКТЕРИСТИКА РАБОТЫ
Актуальность темы. Использование в различных областях хозяйственной деятельности человека конструкций и их элементов сложной геометрической формы, композитных материалов заставляет исследователей идти по пути усложнения математических моделей процессов и объектов.
Наиболее интересными и сложными в механике деформируемых тел и ее инженерно-технических приложениях являются динамические задачи, в том числе связанные с ударным взаимодействием тел. Они актуальны как с точки зрения развития фундаментальных разработок по механике твердого деформируемого тела, так и с точки зрения практического применения результатов их решения. С подобными задачами сталкиваются в строительной индустрии на этапе возведения зданий и сооружений, в машиностроении – при рассмотрении различных режимов работы механизмов, а также при эксплуатации механизмов в нормальных и экстремальных условиях.
Потребности инженерной практики заставляют совершенствовать реологические модели соударяемых тел, более детально описывать характер их ударного взаимодействия и учитывать волновые явления, происходящие в них, что, в свою очередь, приводит к созданию более совершенных средств противоударной защиты конструкций и их элементов, к выявлению таких управляемых параметров, изменение которых будет сказываться на конечных характеристиках динамического контакта.
Учет нелинейно упругих, вязкоупругих, термоупругих, пластических и анизотропных свойств соударяемых тел обуславливает более точное представление о характере протекания данного процесса.
Задачи о соударении двух тел решал Ньютон И., учитывая, что изменение количества движения за время удара равно ударному импульсу, приложенному к телу. Сен-Венан Б.Д. впервые рассмотрел задачу о продольном ударе двух стержней, он учел распространение волн в соударяемых телах, но не учел местное смятие материалов ударника и мишени. Основной вклад в теорию удара внес Герц Г., который распространил свою задачу о статическом контактном взаимодействии упругих тел на их ударное взаимодействие. Однако он не учитывал в процессе удара колебательные движения тел вне их области контакта. Это сделал Тимошенко С.П. в 1928 году, объединив колебательные движения балки конечной длины с контактной теорией Герца в единую стройную теорию удара. Zener С. в 1941 г. обобщил эту задачу на случай балки бесконечной длины. В дальнейшем теория удара типа Тимошенко развивалась для стержней и балок Crook А.W., Yamamoto S.A., Россихиным Ю.А., для пластин – Mindlin R.D., Conway H.D, Lee H.C., Уфляндом Я.С., Кильчевским Н.А., Филлиповым А.П., Филлиповым И.Г. Горшковым А.Г., Тарлаковским Д.В. и для оболочек – Hammel J., Kenner V.N., Koller M.G., Yang J. C. S., Сеницким Ю.Э., Кадомцевым И.Г. и др. учеными.
Волновой подход к теории поперечного удара был впервые предложен Филлиповым А.П. в 1968 году и получил дальнейшее развитие в последующие годы: были получены результаты решения задач ударного взаимодействия, связанных с учетом волновых свойств мишени (Филлипов А.П., Скляр В.Л. 1971), многослойности конструкции пластинки (Choi I.H., Lim C.H. 2004, Егорычев О.О. 2005), различных форм ударника и методов решения (Россихин Ю.А., Шитикова М.В. 1994), термоупругих свойств ударника (Гонсовский В.Л. и др. 1993), вязкоупругих свойств ударника (Сеницкий Ю.Э. 1982), наличия начальных напряжений на границе пластинки (Филиппов И.Г., Филиппов С.И. 2007, Товстик П.Е. 2008) и т.д.
Несмотря на значительные достижения в решении проблем, связанных с ударным взаимодействием, вопросы учета нелинейности, вязкости, анизотропии и предварительного напряжения, равно как и использование расчетно-обоснованных средств защиты от удара, до последнего времени являются недостаточно хорошо изученными. В связи с вышеизложенным, исследования, проведенные в рамках данной работы, по изучению влияния перечисленных факторов на процесс ударного взаимодействия твердых тел и пластинок и оболочек следует признать весьма актуальными.
Актуальной является также проблема создания достаточно простой методики решения задач ударного взаимодействия с учетом различных свойств и процессов в контактирующих телах, которой могли бы пользоваться инженеры-проектировщики при расчете конструкций и их элементов, а также для сравнения с результатами, полученными с помощью новейших программных комплексов.
Основными целями диссертационной работы являются:
1) исследование ударного взаимодействия твердых тел с пластинками и оболочками с учетом волновых явлений;
2) изучение влияния вязкоупругих, термоупругих и анизотропных свойств материала пластинки на динамические характеристики контактного взаимодействия;
3) исследование упругих, вязкоупругих, нелинейно упругих и упругопластических свойств буфера, который используется для моделирования контактной силы и может быть средством противоударной защиты;
4) изучение влияния предварительных напряжений мишени на процесс распространения волновых поверхностей в ней и на динамические характеристики удара;
5) создание методики расчета конструкций на ударное воздействие, которая может учитывать различные физические и геометрические свойства соударяющихся тел, на основе использования аналитических и численных методов.
Научная новизна. В процессе проведения исследований были получены аналитические решения и дан численный анализ следующих задач:
1) об ударном взаимодействии упругого, нелинейно упругого, упругопластического и вязкоупругого ударника с упругой изотропной пластинкой;
2) об ударном взаимодействии упругого, нелинейно упругого и вязкоупругого ударника с вязкоупругой изотропной пластинкой;
3) об ударном взаимодействии упругого цилиндрического и сферического ударника с упругой ортотропной пластинкой;
4) о распространении термоупругих волн в пластинке от нагретого ударника;
5) о динамическом контакте ударника и предварительно-напряженной пластинки, к которой приложены внешняя продольная сила, изгибающий и крутящий моменты;
6) о поперечном ударе твердого тела по сферической оболочке с учетом распространения волн.
Получены теоретические результаты, наиболее приближенные к данным экспериментов (Гольдсмит В. 1965, Зукас Д.А. и др. 1985). В совокупности выполненные исследования и проведенный анализ результатов позволили доработать системный волновой подход к задачам ударного взаимодействия.
Достоверность полученных результатов базируется на корректной математической постановке задач, сравнении результатов аналитических решений и численных расчетов, сопоставлении теоретических решений с экспериментальными данными, применении современных программных вычислительных средств. Полученные в работе численные результаты согласуются с общими физическими представлениями. Правильность полученных результатов определяется корректностью математических выкладок и сопоставлением с известными результатами других авторов.
Практическая ценность. Полученные в диссертационной работе результаты могут быть использованы проектными и научно-исследовательскими организациями в процессе проектирования плит и оболочек, на которые возможно действие ударной нагрузки. Результаты диссертационного исследования вошли в курс «Введение в волновую механику» кафедры теоретической механики Института фундаментального образования Московского государственного строительного университета.
На защиту выносятся:
1) метод решения задач ударного воздействия, основанный на представлении динамического контакта как суперпозиции двух задач: местного смятия в зоне взаимодействия и деформирования тел вне ее с учетом волновых процессов;
2) результаты исследования ударного воздействия ударника на пластину с учетом распространяющихся в последней волновых поверхностей;
3) результаты исследования влияния линейно упругих, вязкоупругих, нелинейно упругих и упругопластических свойств ударника на динамические характеристики удара;
4) результаты изучения влияния вязкоупругих свойств материала пластинки на динамические характеристики контактного взаимодействия;
5) результаты изучения влияния анизотропии материала пластинки на динамическую контактную силу и прогиб;
6) результаты анализа влияния термоупругих свойств пластинки на динамические характеристики удара, определение скорости температурной волны;
7) результаты анализа влияния предварительного напряжения пластинки на динамические характеристики удара и скорости распространения продольных и поперечных волн в ортотропной пластинке;
8) результаты анализа значений напряжений на фронтах волн в различных точках мишени, определение их максимальных значений;
9) результаты исследования динамического контакта ударника и сферической оболочки с учетом продольной волны растяжения-сжатия в ней.
Апробация работы. Основные положения диссертационной работы докладывались и обсуждались на научных конференциях профессорско-преподавательского состава Воронежского государственного архитектурно-строительного университета в 2003-2004 годах; на семинаре по теоретической и прикладной механике Воронежского государственного технического университета в 2003 году; на Воронежских школах-семинарах «Современные проблемы механики и прикладной математики» в 2002 и 2004 годах; на 4-ом Международном симпозиуме по строительству среди аспирантов «4th International Ph.D. Symposium in Civil Engineering”. Мюнхен. Германия. 2002; на Международной конференции «34th Solid Mechanics Conference». Закопан, Польша, 2002; на Международной конференции по проблемам механики «6th International Conference on Vibration Problems 2003». Либерец. Чехия. 2003; на 11-й, 12-й и 13-й Международных конференциях «Математика. Компьютер. Образование» в 2004, 2005 и 2006 годах в г. Дубна и г. Пущино; на Международной конференции «4-ые Окуневские чтения». Санкт-Петербург. 2004; на Международных конференциях «Days of Diffraction». Санкт-Петербург. 2004, 2005; на Международных летних школах «Advanced Problems in Mechanics» в 2004, 2005, 2006, 2007, 2008 годах в п. Репино г. Санкт-Петербург; на Международной научно-технической конференции «Научная работа в университетских комплексах». Воронеж. 2005; на Второй Всероссийской научной конференции «Математическое моделирование и краевые задачи». Самара. 2005; на Всероссийской научной конференции студентов и аспирантов «Молодые исследователи – регионам». Вологда. 2005; на Международной конференции, посвященной 75-летию со дня рождения В.И. Зубова «Устойчивость и процессы управления». Санкт-Петербург. 2005; на Международной конференции по вычислительной пластичности. Основы и приложения «Computational plastisity VIII. Fundamentals and applications». Барселона. Испания. 2006; на 14-й и 15-й зимних школах по механике сплошных сред. Пермь. 2005, 2007; на Международной конференции «Лаврентьевские чтения по математике, механике и физике». Новосибирск. 2005; на Международных молодежных научных конференциях «Гагаринские чтения». Москва. 2005, 2007; на Международной финно-угорской конференции по механике «Finno-Ugric international conference of mechanics». Ракив. Венгрия. 2005; на Международном форуме молодых ученых (6-ая Международная конференция). Актуальные проблемы современной науки. Самара. 2005; на Международной конференции «Авиация и космонавтика 2006». Москва. 2006; на Международном форуме молодых ученых (7-ая Международная конференция) «Актуальные проблемы современной науки». Самара. 2006; на Международном конгрессе Сербского общества механики «International Congress of Serbian Society of Mechanics». Капаоник. Сербия. 2007; на 3-й Тематической конференции интеллектуальных конструкций и материалов «III ECCOMAS Thematic Conference Smart Structures and Materials». Гданьск. Польша. 2007; на Всероссийских научно-практических конференциях «Математика, информатика, естествознание в экономике и обществе». Москва. 2007, 2009; на Международных научно-практических конференциях «Теория и практика расчета зданий, сооружений и элементов конструкций. Аналитические и численные методы». Москва. 2008, 2009; на Двенадцатой межвузовской научно-практической конференции молодых ученых, докторантов и аспирантов. Москва. 2009; на семинарах Донского государственного технического университета в 2006 и 2008 годах. Ростов-на-Дону; на городских семинарах по механике в г. Санкт-Петербурге в 2007, 2008; на 16-ом симпозиуме «Динамика виброударных (сильно нелинейных) систем». Звенигород. 2009; на семинаре Института механики сплошных сред. Пермь. 2009; на семинаре кафедры теории пластичности Московского государственного университета. Москва. 2009; на VII Всероссийской научно-практической и учебно-методической конференции «Фундаментальные науки в современном строительстве». Москва. 2010; на XVI Международном симпозиуме "Динамические и технологические проблемы механики конструкций и сплошных сред" им. А.Г. Горшкова. Ярополец. 2010.
Публикации. По теме диссертации автором опубликовано 59 печатных работ, в том числе одна монография и 32 статей в отечественных и зарубежных журналах и сборниках научных трудов и материалов конференций.
Структура и объём работы. Диссертация состоит из введения, шести глав, заключения и списка литературы. Работа изложена на 271 странице машинописного текста, содержит 68 рисунков, 3 таблицы, список использованных источников из 260 наименований.
Поддержка. Исследования автора на различных этапах работы поддерживались грантами РФФИ. В 2003 году автор стал лауреатом именной стипендии Правительства РФ.
КРАТКОЕ ИЗЛОЖЕНИЕ ДИССЕРТАЦИИ
Во введении обоснована актуальность темы диссертации. Приводится краткий исторический обзор решения задач, связанных с ударным взаимодействием и распространением волн в контактирующих телах, описываются этапы эволюции теории удара и отдельных ее направлений для стержней, балок, пластин и оболочек, основные элементы волнового подхода к задачам динамического контакта твердых тел, методы определения характеристик взаимодействия внутри контактной области и вне ее, методы исследования распространяющихся волновых поверхностей и определения их параметров, вопросы, недостаточно хорошо изученные при решении задач ударного взаимодействия тел с разными свойствами и различными начальными условиями; также приводятся некоторые приложения решаемых задач в строительстве и машиностроении. Указаны основные цели работы, кратко изложена структура диссертации, охарактеризована ее научная новизна, научная и практическая значимость, сформулированы основные положения, выносимые на защиту, а также показаны результаты различных частей и всей работы в целом, представленные научной общественности на конференциях, семинарах и симпозиумах.
В первой главе описывается общая постановка задач ударного взаимодействия твердых тел, одно из которых – тонкое, используемые методы, начальные и граничные условия, их влияние на процесс решения, приводятся основные положения подходов к задачам динамического контакта с точки зрения фундаментальных исследований по механике деформируемого твердого тела и инженерных приложений в различных отраслях хозяйственной деятельности человека.
В §1 приводятся основные вехи в развитии теории удара с указанием имен и работ отечественных и зарубежных ученых, внесших наиболее весомый вклад в построение единой стройной теории. Указываются трудности, с которыми сталкиваются инженеры проектных и изыскательских организаций при постановке задачи, выборе расчетной модели, методов и средств расчета конструкций и их элементов, в том числе связанные с отсутствием достаточной нормативной базы для проведения полноценного анализа динамических задач. Для классификации существующих подходов может быть выбрано множество критериев: в данной работе основными считаются: контактная сила, действующая в месте взаимодействия тел, и уравнения движения точек мишени вне этой области. Здесь также указываются методы, наиболее подходящие для каждого подхода.
В §2 описываются все приведенные ранее подходы с указанием характерных особенностей в постановках задач и методах решения. В качестве модели, описывающей контактное взаимодействие тел, используются: модель Герца, упругопластические модели Кильчевского и Александрова-Кадомцева, линейно упругая, нелинейно упругая, вязкоупругая модели, а также некоторые иные модели. В качестве уравнений, описывающих динамическое поведение мишени, используются уравнения Бернулли-Эйлера и Тимошенко – для балок, Кирхгофа-Лява и Уфлянда-Миндлина – для пластинок, для оболочек уравнения рассматриваются также с учетом деформации поперечного сдвига и инерции вращения поперечных сечений и без них.
В качестве определяющего в данной работе используется следующий подход: предполагается, что в результате поперечного удара по мишени в ней распространяются продольные и сдвиговые волны, фронты которых являются поверхностями сильного разрыва. Отметим, что в изотропной пластинке поверхности сильного разрыва представляют собой цилиндрические поверхности-полоски, образующие которых параллельны нормали к срединной поверхности, а направляющие, расположенные в срединной плоскости, представляют собой окружности, расширяющиеся с нормальными скоростями (рис.1). Для остальных типов мишеней вид волновых поверхностей определяется геометрией самой мишени и свойствами ее материала. Ударник моделируется как груз некоторой массы и буфер, свойства и геометрия бьющего конца которого определяет контактную силу в месте удара. В общем случае процесс ударного взаимодействия представлен на рис. 1.
Фактически выбор подхода зависит от начальной скорости взаимодействия тел, свойств их материалов, геометрии области контакта. После начала процесса взаимодействия практически во всех подходах перемещение ударника характеризуется известным функциональным уравнением
, (1.1)
где 
полное перемещение ударника, imp(t), tag(t) – местные смятия материалов ударника и мишени в месте контакта соответственно, P(t) – контактная сила, m – масса ударника, t – время, отсчитываемое с момента соприкосновения ударника и мишени, t1 – переменная интегрирования.
При небольших скоростях удара (меньших или равных 5 м/с) считается, что местное смятие материала пластинки происходит квазистатическим образом, т.е. можно использовать результаты решения контактной задачи для случая статического взаимодействия тел. В случае больших скоростей необходимо учитывать динамическую составляющую контактного процесса.
В зависимости от рассматриваемого типа мишени волны поперечного сдвига и продольного растяжения-сжатия распространяются либо с бесконечно большой скоростью (балка Бернулли-Эйлера, пластинка Кирхгоффа-Лява), либо с конечной скоростью (балка Тимошенко, пластинка Уфлянда-Миндлина).
а) до взаимодействия
б) после взаимодействия
в) вид сверху
Рис. 1 Схема ударного взаимодействия твердого тела с буфером и мишени
В данной работе основными являются подходы, учитывающие влияние волновых явлений на деформирование контактирующих тел, т.е. используются волновые уравнения, описывающие динамическое поведение мишени.
Решение за фронтом волны сильного разрыва строится при помощи лучевого ряда
(1.2)
где Z – искомая функция, Z,(k) = kZ/tk, 
, знаки «+» и «-» относятся к значениям производной Z,(k), подсчитанным перед волновой поверхностью и за ней соответственно, G – нормальная скорость волны, Н(t-s/G) – единичная функция Хевисайда, s – длина дуги, отсчитываемая вдоль луча, t – время.
Если время протекания процесса очень мало, то в степенном ряде по времени и поверхностной координате (1.2) можно ограничиться только первым членом. В этом случае задача сводится к решению одного нелинейного дифференциального уравнения относительно величины, характеризующей местное смятие материалов пластинки и тела, или относительно контактной силы. Чтобы уточнить и детализировать решение, полученное этим способом, учитывают последующие члены лучевого ряда. Для этого определяющие уравнения контактирующего тонкого тела дифференцируют k раз по времени, записывают на различных сторонах волновой поверхности и берут их разность. Затем используют условие совместности
(1.3)
где ( = r, ) – пространственные координаты, одна из которых направлена вдоль прямого луча, а другая является одновременно и поверхностной координатой на волновой поверхности, при этом обе координатные линии являются взаимно ортогональными, 
(
,
) – компоненты вектора нормали к волновой поверхности, / t – -производная по времени.
Другой модификацией метода асимптотических разложений является представление искомых функций в пространстве изображений в виде степенного ряда по полиномам Лежандра
, (1.4)
где 
- некоторая функция, связывающая координату точки на мишени с размерами этой мишени, p – параметр пространства изображений.
Можно также использовать представление неизвестных функций в виде разложений в ряды по функциям Бесселя или численные методы совместно с программно-аппаратными вычислительными комплексами.
В §3 приводятся выводы о границах и условиях применимости тех или иных подходов и методов, а также демонстрируются их преимущества при решении практических задач с различной степенью точности.
Вторая глава посвящена методам решения задач ударного взаимодействия ударника и тонкой мишени. Большинство таких задач может быть разделено на две части: построение решений внутри контактной области (контактная задача) и вне ее (задача распространения волн). В случае использования аналитических методов можно получить искомые функции в виде конечных выражений, но при этом практически всегда необходимо использовать дополнительные условия, которые накладывают ограничения на область применения полученных результатов. При использовании численных методов и современных вычислительных комплексов можно уменьшить количество дополнительных условий, но при этом конечные характеристики динамического контакта тел будут представлены либо в виде таблиц, либо в виде графиков, что не позволит проектировщикам при решении практических задач пользоваться конечными формулами, а результаты предыдущих расчетов могут быть использованы только как тестовые данные. Поэтому различные методы и их группы нужно рассматривать в комплексе применительно к конкретной задаче.
В §1 проводится классификация методов решения внутри контактной области и вне ее. Для определения искомых функций часто используются асимптотические разложения в степенные ряды по функциям Бесселя (Филлипов А.П. 1971), полиномам Лежандра (1.4) (Бирюков Д.Г., Кадомцев И.Г. 2002), по пространственной координате и времени (1.2) (Россихин Ю.А., Шитикова М.В., 1992). Для представления неизвестной нагрузки можно использовать двойные ряды Фурье по координате и времени (Malekzadeh K. et.al 2007), после определения входящих в них коэффициентов находится контактная сила и напряжение в различных точках многослойной пластинки. Поскольку в волновых уравнениях мишени присутствуют производные и по времени, и по поверхностным координатам, то для их замены используется преобразование Лапласа и условия совместности (Томас, 1961) соответственно. Результатом решения уравнений, описывающих динамическое поведение, является определение скоростей волн, неизвестных перемещений и напряжений (в зависимости от того, в каком базисе записаны первоначальные уравнения) с точностью до постоянных интегрирования. Они, в свою очередь, находятся при приравнивании решений, полученных внутри и вне контактной области на ее границе; также используются граничные условия. Для определения неизвестных величин в произвольных точках мишени можно использовать метод регуляризации асимптотических разложений (Россихин Ю.А., Шитикова М.В. 1994) или разложение искомых величин в ряды Лорана вблизи данной точки.
§2 посвящен лучевому методу, в нем приведены волновые уравнения, описывающие динамическое поведение упругой изотропной, вязкоупругой изотропной и упругой ортотропной пластинок с учетом инерции вращения и деформации поперечного сдвига. Используя описанную в первой главе процедуру, из уравнений движения получим систему рекуррентных уравнений, которая для упругой изотропной пластинки примет вид:
(2.1)
где (k)=[r,(k+1)], X(k)=[W,(k)], b=KhD -1, r = r0+Gt, - плотность материала пластинки, r – полярный радиус, r0 – радиус буфера,, 
, Е и – модуль упругости и коэффициент Пуассона материала пластинки соответственно, - модуль сдвига пластинки, 
– угловая скорость вращения нормали к пластинке в направлении r, W – скорость поперечных перемещений точек срединной плоскости (скорость прогиба), D = Еh3/12– цилиндрическая жесткость, 
(i = 1,2) – функции, зависящие от скачков искомых величин k–1 – го и более низких порядков, точка над величинами означает производную по времени.
Для вязкоупругой изотропной пластинки система рекуррентных дифференциальных уравнений записывается следующим образом:
(2.2)
где – ядро релаксации, g (t) – функция релаксации для модели Максвелла, – ядро релаксации в начальный момент времени.
Аналогичные соотношения для упругой ортотропной пластинки принимают вид:
где 
Dr - жесткость изгиба для направления r, Еr, Е и r, - модули упругости и коэффициенты Пуассона для направлений r,, Grz – модуль сдвига в плоскости rz, w(r,) – нормальное перемещение срединной плоскости, (r,) – угол поворота нормали в направлении радиуса r.
Если рассматривать распространение термоупругих волн в мишени от нагретого ударника, то в систему (2.3) добавляются слагаемые, учитывающие температурные свойства мишени, и рекуррентное соотношение, полученное из уравнения теплопроводности гиперболического типа
(2.4)
где 
, k – коэффициент теплоотдачи между пластиной и средой в месте нагрева, с – удельная теплоемкость, q – время запаздывания в установлении теплового потока.
Если в качестве мишени рассматривать сферическую оболочку, то система рекуррентных определяющих уравнений примет вид
(2.5)
Здесь 
, 
R1 – радиус оболочки.
В результате решения систем уравнений (2.1) – (2.5) находятся с точностью до произвольных постоянных интегрирования 
разрывы величин 
, 
и 
, которые являются коэффициентами лучевого ряда (1.2). Выражения для искомых функций W и Qr можно привести в виде лучевых рядов:
– для упругих изотропной и ортотропной пластинок
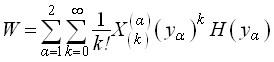, (2.6)
, (2.7)
– для вязкоупругой изотропной пластинки (W определяется формулой (2.6))
, (2.8)
– для термоупругой пластинки скорость изменения температуры определяется следующим степенным рядом
, (2.9)
– для сферической оболочки к выражению (2.6) добавляются
, (2.10)
, (2.11)
, (2.12)
где, величины 
, 
и 
подсчитываются при y=0, 
, 
и 
- растягивающие усилия в оболочке, индекс 
указывает на порядковый номер волны: 
=1 – квазипродольная волна, 
=2 – квазипоперечная, 
и 
- для упругой изотропной и вязкоупругой пластинок, 
и 
- для ортотропной пластинки; упругие модули, входящие в формулу (2.8), являются нерелаксированными.
Полученные лучевые ряды и скачки искомых величин используются в последующих главах при решении задач об ударном воздействии твердого тела на тонкую мишень.
В §3 решение системы уравнений, описывающих динамическое поведение мишени, предлагается искать в виде разложения в ряды по полиномам Лежандра (1.4), где искомая величина х может представлять собой любое линейное или угловое перемещение, входящее в первоначальную систему; для круглой пластинки 
, для сферической оболочки 
, R – радиус пластинки, 0 – угол раскрытия оболочки.
Нагрузка от сосредоточенной силы взаимодействия в месте контакта P(t) также представляется в виде разложения в ряд по полиномам Лежандра
, (2.13)
где r1 – координата точки, в которой происходит динамический контакт.
Выражения (1.4) и (2.13) подставляются в определяющие уравнения, и с учетом свойств ортогональности системы косинусов на отрезке [-, ] получается система уравнений относительно 
. Для определения коэффициентов рядов (1.4) воспользуемся их представлением вблизи искомой точки в виде рядов Лорана
, (2.14)
здесь 
, р – параметр Лапласа.
Выражения для 
вычисляются для конкретного места удара и точки определения неизвестных величин, т.е. r и принимают определенные значения. После обратного преобразования Лапласа перемещения можно записать как функцию времени, двух координат и силы воздействия на пластинку
В §4 описываются некоторые численные методы, используемые в задачах ударного взаимодействия, и процедуры для решения нелинейных интегро-дифференциальных уравнений, полученных из уравнений движения точек мишени при помощи динамических условий совместности. В данной работе используется итерационная схема Тимошенко, реализованная на ЭВМ, которая предполагает, что в пределах одного интервала 
контактная сила изменяется линейно:
, (2.16)
где - шаг интегрирования.
Результаты, полученные с помощью методов конечных и граничных элементов, используются только для сравнения полученных характеристик контактного взаимодействия.
В третьей главе содержатся результаты решения задач ударного взаимодействия твердого тела с линейно упругим буфером (§1), вязкоупругим буфером (§2, 3), нелинейно упругим буфером (§4) и упругой изотропной и вязкоупругой изотропной пластинкой с помощью многочленных лучевых разложений.
Для определения постоянных интегрирования в выражениях (2.6) – (2.8) необходимо составить систему уравнений, характеризующую поведение ударника и контактной области после начала взаимодействия. Движение ударника после его касания мишени описывается уравнением (1.1), уравнение движения контактной области имеет следующий вид:
(3.1)
Зависимость контактной силы от местного смятия материала мишени принимает следующий вид:
– для линейно упругой модели взаимодействия
P(t)= E1 ( - w), (3.2а)
– для вязкоупругого буфера
(3.2б)
– для нелинейно упругого буфера
P(t)= E1 ( - w)+E2 ( - w)3, (3.2в)
где E1 и Е2 – упругие модули пружины, 1 – время релаксации демпфера.
Для определения динамических характеристик удара к выражениям (1.1) и (3.1) необходимо добавить условие непрерывности тангенса угла наклона касательной при переходе через границу области контакта
(3.2)
и начальные условия
. (3.3)
Величина местного смятия не определяется из решения системы уравнений, определяющих динамическое поведение мишени, – для нее необходимо использовать отдельное степенное разложение
, (3.4)
где 
- пока неизвестные константы.
Подставляя формулы (2.6), (3.4) и (2.7) или (2.8), а также выражение для контактной силы в уравнения (1.1), (3.1), (3.2) и приравнивая в полученных соотношениях коэффициенты при одинаковых степенях t, найдем на каждом шаге три алгебраических уравнения для определения трех неизвестных констант: две константы при каждом t входят в лучевые ряды W и Qr и одна константа при каждом t содержится в выражении (3.4). Зная перечисленные константы с учетом (3.3), можно определить контактную силу, которая записывается с точностью до t5 в следующем безразмерном виде:
– для упругой изотропной пластинки и линейно упругого буфера
(3.5)
– для вязкоупругой изотропной пластинки и линейно упругого буфера
(3.6)
– для упругой изотропной пластинки и вязкоупругого буфера
– для вязкоупругой изотропной пластинки и вязкоупругого буфера
(3.8)
– для упругой изотропной пластинки и нелинейно упругого буфера
(3.9)
– для вязкоупругой изотропной пластинки и нелинейно упругого буфера
(3.10)
где 
, 
, 
, 
, 
, 
, 
, 
, 
, 
, 
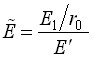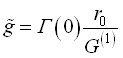- безразмерный параметр вязкости пластинки.
На рис. 2 исследуется зависимость безразмерной контактной силы от безразмерного времени и безразмерных параметров, входящих в выражения (3.5) – (3.10). На рис. 2а приводятся зависимости максимальной контактной силы от безразмерного параметра 
при различных значениях безразмерной скорости удара 
, указанных цифрами у кривых, при этом сплошной линией показаны значения максимальной контактной силы для стальной пластинки, а пунктиром – для алюминиевой. На рис. 2б показывается зависимость контактной силы от времени для различных значений параметра вязкости пластинки 
, которые указаны цифрами у кривых.
Остальные параметры принимают следующие значения: 
=25, = 0.3, 
=1, 
=1.110-6, 
=8.510-3. Рис. 2в и рис. 2г иллюстрируют зависимость контактной силы от времени при разных значениях безразмерных параметров 
и 
соответственно. На рис. 2д изображена нелинейная зависимость максимальной контактной силы от скорости удара: кривая 1 подсчитана при 
, кривая 2 – при 
, кривая 3 – при 
, кривая 4 – при 
(эта кривая соответствует линейно упругому буферу), кривая 5 – при 
, кривая 6 – при 
. На рис. 2е изображена зависимость максимальной контактной силы от обобщенного параметра нелинейно упругого буфера для разных параметров вязкости пластинки 
: кривая 1 подсчитана при 
, кривая 2 – при 
, кривая 3 – при 
, кривая 4 – при 
, кривая 5 – при 
.
Как показали исследования, максимум контактной силы увеличивается при увеличении безразмерного параметра 
, скорости удара 
и плотности материала пластинки (рис. 2а). Из рис. 2б можно увидеть, что максимальная контактная сила уменьшается с увеличением безразмерного параметра вязкости пластинки 
. При его неограниченном уменьшении кривая контактной силы бесконечно близко приближается к кривой, построенной для случая упругой пластинки.
а) б)
в) г)
д) е)
Рис. 2 Зависимость контактной силы от различных параметров взаимодействия
При воздействии на пластинку массивного тела (
) контактная сила увеличивается, при воздействии легкого тела значение контактной силы уменьшается по сравнению со значениями на кривой, соответствующими равным массам контактной области и ударника (рис. 2в). Максимальная безразмерная контактная сила уменьшается с уменьшением безразмерного времени релаксации, при неограниченном увеличении времени кривая контактной силы приближается к кривой, которая соответствует максимальной контактной силе линейно упругого буфера (рис. 2г). При увеличении K (для жестких нелинейных характеристик буфера) максимум контактной силы увеличивается, а при уменьшении K (для мягких нелинейных характеристик буфера) – уменьшается по сравнению с максимумом для линейно упругого буфера (рис. 2д). Из рис. 2е видно, что с уменьшением обобщенного параметра нелинейно упругого буфера контактная сила уменьшается. Как следует из рис. 2е, при увеличении параметра 
максимальные значения контактной силы уменьшаются для любых K и характеристика нелинейности смягчается.
Для мягких нелинейных характеристик (К < -1.5910-6) максимальная контактная сила уменьшается, для жестких характеристик (К > -1.5910-6) максимальная контактная сила увеличивается по сравнению с контактной силой для линейно упругого буфера, которому соответствует значение К = -1.5910-6.
В главе 4 рассматриваются вязкоупругая и упруго-пластическая модели взаимодействия ударника и пластинки. В §1 описывается постановка задачи, а для представления неизвестных величин используется первый член лучевых рядов (2.6) – (2.8), что позволяет избежать разложения в ряд экспоненциальной функции ядра релаксации. Также в этом случае можно обойтись без граничного условия (3.2).
В §2 рассматривается контакт ударника с вязкоупругим элементом Максвелла и упругой изотропной пластинки. Из определяющих уравнений для мишени при предположении абсолютной твердости контактного диска и учете только нулевых членов ряда (1.2) можно получить не только скорость сдвиговой волны, но и динамическое условие совместности для перерезывающей силы и скорости прогиба:
. (4.1)
Подставляя в уравнения (1.1) и (3.1) выражения (3.2б) и (4.1), получим систему интегро-дифференциальных уравнений относительно и w, которая в пространстве Лапласа примет вид:
(4.2)
Решая данную систему, находим выражения для смятия и прогиба мишени в пространстве изображений. Для перехода к оригиналам необходимо решить характеристическое уравнение
(4.3)
в котором 
. Данное уравнение может иметь два комплексно сопряженных и один действительный корень или три действительных корня. В зависимости от этого будут меняться конечные выражения для прогиба и местного смятия и, соответственно, для контактной силы.
Для иллюстрации полученных результатов рассмотрим численный пример и исследуем зависимость контактной силы от вязкоупругих свойств ударника. Параметры взаимодействия в примере принимают следующие значения: m=10г, h=13мм, V0=10м/с, Е1=250кН/м. На рис. 3а построены зависимости контактной силы от времени для различных значений времени релаксации вязкоупругого элемента, которые указаны цифрами у кривых. На рис. 3б представлены зависимости контактной силы от времени для следующих частных случаев динамического взаимодействия: 1) ударник является упругим телом; полагая, получим кривую 1 для упругой контактной силы; 2) пренебрегая инерцией контактного пятна (в уравнении (3.1) отсутствует левая часть), получим кривую 2 при =0.001; 3) пренебрегая инерцией контактной области и считая ударник упругим, получим зависимость 3; кривая 4 построена для общего случая вязкоупругого ударника при =0.001; кривая 5 построена при учете 5-ти членов лучевого ряда (1.2).
а) б)
Рис. 3 Зависимость контактной силы от времени
В §3 рассматриваются следующие модели контакта для сферического ударника:
– упругая модель Герца
, (4.4)
– упругопластическая модель Александрова-Кадомцева
(4.5)
– упругопластическая модель Кильчевского:
(4.6)
где 
, 
, 
, 
, m – наименьшая из пластических констант взаимодействующих тел, 
, =5.7, 
, 
, 
, 
, 
, 
, 
, 1 – коэффициент Пуассона ударника, E1 – модуль упругости ударника.
Используя выражения (1.1), (3.1) и (4.1), приходим к нелинейному интегро-дифференциальному уравнению относительно и Р:
. (4.7)
После подстановки выражений (4.4)-(4.6) в формулу (4.7) получаем интегро-дифференциальные уравнения относительно контактной силы, которые решаются численно с помощью ЭВМ и итерационной схемы, описанной в главе 2.
На рис. 4а кривые 1, 2, 3 построены при использовании соотношений (4.4), (4.5) и (4.6) соответственно, а кривая 4 взята у Голдсмита, начальная скорость удара 
10 м/с. На рис. 4б кривые 1,2 соответствуют 
20 м/с, кривые 3, 4 - 
15 м/с, кривые 5,6 - 
10 м/с, кривые 1, 3, 5 были посчитаны при помощи соотношений (4.4), а кривые 2, 4, 6 - при помощи соотношений (4.5). Из рис. 4а видно, что модель (4.5) дает наилучшее приближение к результату эксперимента и что при скоростях 
10 м/с упругопластические свойства мишени заметно влияют на контактную силу. Из рис. 4б следует, что при увеличении начальной скорости воздействия разница между значениями максимальных контактных сил, полученных при использовании зависимостей (4.4) и (4.5), растет.
а) б)
Рис.4 Зависимость контактной силы от времени
§4 содержит численные исследования полученных аналитических выражений для контактной силы, при этом параметры конструкции принимаются как в некоторых экспериментальных исследованиях, после сравнения делаются выводы о влиянии параметров взаимодействия и модели на точность решения.
В пятой главе рассматривается динамический контакт ударника и ортотропной пластинки, обладающей криволинейной анизотропией. В §1 исследуется влияние анизотропии на динамический прогиб и контактную силу, выражения в безразмерном виде для которых получаются после подстановки (2.6), (2.7), (3.4) и (3.2а) в систему уравнений (1.1), (3.1) и (3.2):
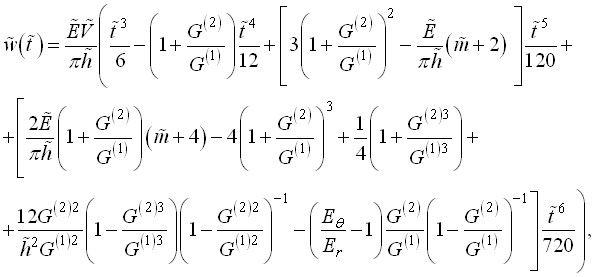(5.1)
где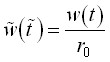 
, 
, 
.
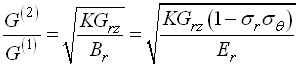На рис.5а приведены зависимости максимального прогиба от соотношения 
для различных значений 
: кривая 1 – для 
=3.410-6, кривая 2 – для 
=2.310-6, кривая 3 – для 
=1.110-6; другие параметры в расчетах принимают следующие значения: 
=25, 
=1, 
=8.510-3. На рис. 5б показаны зависимости максимального прогиба от соотношения скоростей скачков сильного разрыва 
, которое пропорционально отношению 
для различных значений 
, указанных цифрами у кривых.
Анализируя рис. 5а,б, можно сделать вывод об уменьшении максимального прогиба при увеличении соотношений 
и 
, а также о том, что максимальный прогиб увеличивается при увеличении линейной жесткости буфера 
.
В §2 исследуется влияние термоупругих свойств ортотропной пластинки на контактную силу и динамический прогиб, определяются параметры температурной волны с помощью многочленных лучевых разложений, как и в §1.
а) б)
Рис. 5 Зависимость динамических характеристик от параметров анизотропии
На рис. 6а и на рис. 6б приведены зависимости контактной силы и динамического прогиба соответственно от времени для различных значений обобщенного температурного коэффициента аТ, которые указаны цифрами у кривых. Кривые при аТ = 0 соответствуют ударному воздействию без учета распространения тепла. Остальные параметры изучаемой конструкции принимают следующие значения: m = 0.3 кг, r0=100 мм, h=200 мм, E1=25 кН/м, 
ГПа, V0 =10 м/с, 
, 
кг/м
.
а) б)
Рис. 6 Зависимость динамических характеристик от температурного коэффициента
Из рис. 6а,б видно, что увеличение температурного коэффициента, т.е. увеличение температуры ударника, приводит к росту динамического прогиба и контактной силы в месте взаимодействия. Также можно увидеть, что изменение аТ сильнее влияет на динамический прогиб, чем на контактную силу.
Из анализа полученных зависимостей следует, что температурная волна опережает упругие ударные волны, процессы распространения тепла в мишени вначале влияют на продольную волну растяжения-сжатия и, только при последующих приближениях, на поперечную волну сдвига. Процесс распространения тепла в мишени значительно влияет на динамические характеристики контактного взаимодействия: при учете распространения термоупругой волны динамический прогиб в месте контакта и контактная сила увеличиваются, но сила увеличивается менее интенсивно.
В §3 рассматривается математическое моделирование ударного воздействия шара на ортотропную пластинку, обладающую криволинейной анизотропией и предварительно-напряженную продольной силой N, изгибающим Mr и крутящим Mz моментами. Исследуется влияние предварительного напряжения на скорости распространения продольных и поперечных волн, на контактную силу и динамический прогиб. Принимаются во внимание пять уравнений движения для трех линейных и двух угловых перемещений мишени, поскольку удар является неосесимметричным.
Для определения скоростей упругих волн с учетом внешних сил определяющие уравнения дифференцируются k раз по времени, записываются в скачках неизвестных величин на волновой поверхности, и для перехода от производных по поверхностным координатам к производным по времени используется условие (1.3); Z принимает значения,, w, u, v; величина принимает значения r,. Используя процедуру, описанную в главе 3, от полученных уравнений при k = -1 приходим к системе относительно перемещений и скоростей волн. Результат решения данной системы представлен на рис. 7 в виде графических зависимостей 
.
На рис. 7а изображены графические зависимости скоростей упругих волн от внешней продольной силы. Номера 1, 2 соответствуют продольным волнам растяжения-сжатия, распространяющимся в направлениях r и соответственно, номер 3 соответствует волне сдвига продольных сечений в плоскости r, номера 4, 5 соответствуют поперечным волнам сдвига в плоскостях rz, z соответственно. Видно, что сила N практически не влияет на скорости продольных волн 1 и 2, связанных с перемещениями,, и существенно влияет на скорости поперечных волн 3,4,5. Если увеличивать внешнюю сжимающую продольную силу, то скорости поперечных волн уменьшаются до нуля, т.е. волны запираются. Если же увеличивать внешнюю растягивающую силу, то скорости волн растут, т.е. волны разгоняются, причем скорость пятой волны увеличивается до некоторого критического значения, определяемого свойствами материала мишени.
На рис. 7б представлены графические зависимости скоростей упругих волн от внешнего изгибающего момента. Изгибающий момент Mr на скорости волн, связанных с перемещениями u, v, оказывает практически одинаковое влияние. При увеличении абсолютного значения момента поперечные волны запираются, продольные волны практически не зависят от значения Mr.
