Моделирование деформационного поведения вязкоупругих материалов для расчета деталей конструкций
РОССИЙСКАЯ АКАДЕМИЯ НАУК
ИНСТИТУТ МАШИНОВЕДЕНИЯ им. А.А.Благонравова
на правах рукописи
МОСИН АЛЕКСАНДР ВАЛЕНТИНОВИЧ
МОДЕЛИРОВАНИЕ ДЕФОРМАЦИОННОГО ПОВЕДЕНИЯ ВЯЗКОУПРУГИХ МАТЕРИАЛОВ ДЛЯ РАСЧЕТА ДЕТАЛЕЙ КОНСТРУКЦИЙ
Специальность 01.02.04
Механика деформируемого твердого тела
АВТОРЕФЕРАТ
диссертации на соискание ученой степени
кандидата технических наук
Москва
2007
Работа выполнена в Институте машиноведения им. А.А.Благонравова РАН и в компании Alfa Laval (Швеция).
Научный руководитель
доктор технических наук, профессор Ю.В. Суворова
Научный консультант
профессор Н.-Г.Ульсон
Официальные оппоненты:
доктор физикоико-математических наук, профессор, академик АН Латвии В.П. Тамуж
доктор технических-математических наук, профессор А.М.Локощенко
доктор технических наук, профессор В.Л.Данилов
Ведущая организация:
ООО «НТЦ АпАТэК-Дубна»
Защита диссертации состоится «14» марта 2007 года в 15.00 на заседании диссертационного совета Д 002.059.01 при Институте машиноведения им. А.А. Благонравова РАН в помещении конференц-зала по адресу: 101990, Москва, Малый Харитоньевский переулок, 4.
С диссертацией можно ознакомиться в библиотеке Института машиноведения им. А.А. Благонравова РАН по адресу: Москва, ул. Бардина, 4.
Автореферат разослан «09» февраля 2007 года
Ученый секретарь
диссертационного совета,
кандидат технических наук В.М. Бозров
ОБЩАЯ ХАРАКТЕРИСТИКА РАБОТЫ
Актуальность темы
Центробежные сепараторы предназначеныМоделирование поведения вязкоупругих материалов и расчет деталей конструкций в данной работе непосредственно связаны с анализом работы центробежных сепараторов, предназначенных для очистки минеральных масел, гидравлических рабочих жидкостей, дизельных топлив, промывочного керосина, воды и других веществ от механических примесей. Они находят широкое применение на различных промышленных предприятиях, в автохозяйствах, железнодорожных депо, на автозаправочных станциях, на электростанциях, на речном и морском флоте, на нефте- и газопроводах и во многих других сферах деятельности. Исследование эксплуатационных особенностей центробежных сепараторов и долговечности самой конструкции, несомненно, является актуальной задачей.
Материалами, используемыми для изготовления сепараторов, как правило, являются нержавеющие стали. Однако достаточно часто переносные сепараторы небольших размеров изготавливаются целиком из полимеров с целью создания облегченной конструкции, не требующей специальных средств для перевозки к месту использования. Кроме того, некоторые детали даже стационарных сепараторов изготавливаются в настоящее время также из полимеров, обеспечивающих податливость работы соответствующих элементов конструкции. Анализу поведения используемых в производстве сепараторов полимерных материалов в конкретных условиях эксплуатации, а также оценочному расчету отдельных элементов конструкций из этих материалов и посвящена настоящая работа.
Актуальность выбранной тематики подтверждается также тем, что исследования проводились в рамках грантов: РФФИ (01-01-00455а, 04-01-00745а, 06-08-08155офи-а), ФЦНТП 02.442.11.7421, МКНТ № ГА – 38/05.
Настоящая работа выполнялась совместно с компанией Alfa Laval, занимающейся изучением сепараторов различного типа и назначения, выбором материалов, пригодных для их изготовления, исследованием условий эксплуатации на поведение элементов конструкций сепараторов, а также непосредственно производством, составляющим порядка 90% всей мировой продукции.
Основные результаты работы были премированы на конкурсе научных работ «Новая генерация», проводимом среди молодых ученых РАН, других учреждений и организаций России.
Целью работы является изучение характеристик, анализ определяющих соотношений и построение методов численного моделирования для выявления рациональных областей применения полимерных материалов (POM, PEEK, Nylon 6), а также осуществление экспериментов и расчет для конкретных элементов конструкций.
Поставлены следующие задачи:
- анализ вязкоупругих характеристик используемых в производстве сепараторов полимерных материалов (POM, PEEK, Nylon 6) при различных эксплуатационных режимах нагружения;
- исследование влияния температуры и влажности на долговечность и характеристики ползучести исследуемых материалов;
- анализ определяющих соотношений, основанных на представлениях о наследственном характере деформирования вязкоупругих материалов, включающих учет различных режимов нагружения, в том числе циклического (с учетом саморазогрева), а также температуру и влажность;
- разработка методов численного моделирования нелинейно-наследственного определяющего уравнения с различными ядрами ползучести с целью определения параметров уравнения и построения методов расчета при кратковременном и длительном нагружении;
- решение некоторых практических задач деформирования осесимметричных элементов конструкции сепаратора, находящихся в условиях сложного напряженного состояния.
Научная новизна работы состоит в следующем:
- получены новые экспериментальные данные о деформационном поведении при различных режимах нагружения с учетом температуры и влажности для материалов POM, PEEK и Nylon 6 и даны рекомендации по безопасной эксплуатации этих материалов;
- для оценки полученных экспериментальных данных для случая возврата ползучести применена модель наследственного типа с небольшой модификацией;
- установлена зависимость температуры саморазогрева от параметров цикла (в том числе, разрушающего напряжения) и от параметров материала – на основе анализа процессов разгрузки, являющихся составной частью циклического нагружения;
- разработаны численно-аналитические методы моделирования для определения параметров двух- и трехпараметрических ядер в определяющем уравнении для дальнейших расчетов деформационного поведения материалов, определены границы применимости этих ядер.
Достоверность полученных результатов
Достоверность полученных результатов подтверждается сопоставлением расчетных и экспериментальных данных, как полученных автором, так и приведенных в литературе, а также строгостью математических формулировок и обоснованностью применяемых численных методов.
Практическое значение
Результаты работы используются в серийном производстве центробежных сепараторов и позволяют оценивать деформационные характеристики элементов конструкции сепараторов, изготовленных из вязкоупругих полимерных материалов, в течение заданного периода эксплуатации при заданных режимах работы (температура, влажность), что подтверждается приложенным Сертификатом Центра производства сепараторных систем компании Alfa Laval об использовании результатов данной работы.
На основе экспериментальных исследований, позволяющих определить параметры материалов, а также разработанных методов моделирования решены две практические задачи о деформировании элементов конструкций центробежных сепараторов (деформирование цилиндрического элемента и круглой мембраны).
Апробация работы
Основные положения работы докладывались и обсуждались на следующих конференциях и семинарах: XII Конференция молодых ученых и студентов (Москва, 2000 г.), XIII Конференция молодых ученых, аспирантов и студентов «Современные проблемы машиноведения» (Москва, 2001 г.), Московская конференция молодых ученых «Научно-технические проблемы развития Московского мегаполиса» (Москва, 2002 г.), Московская конференция молодых ученых, аспирантов и студентов «Научно-технические проблемы развития Московского мегаполиса» (Москва, 2003 г.), Международный симпозиум “Structure Sensitive Mechanics of Polymer Materials. Physical and Mechanical Aspects” (Moscow, 2004), Научно-технические совещания отдела Solid Mechanics & Material Science компании Alfa Laval (Швеция, Стокгольм), семинар молодых ученых и студентов по проблемам машиноведения (СМУСМ) (Москва, 2006 г.), семинары лаборатории механики композиционных материалов ИМАШ РАН.
Публикации. Основное содержание работы отражено в 9 печатных трудах, список которых приведен в конце автореферата.
Структура и объем работы. Диссертационная работа состоит из введения, четырех глав, заключения и списка литературы из 112 наименований. Работа изложена на 150 страницах машинописного текста, содержит 50 рисунков и 12 таблиц.
Автор выражает глубокую благодарность сотрудникам отдела Solid Mechanics & Material Science компании Alfa Laval (Швеция) за помощь в постановке и осуществлении экспериментов.
КРАТКОЕ СОДЕРЖАНИЕ РАБОТЫ
Во введении изложена общая характеристика работы, обоснована актуальность темы исследования, сформулированы цели и задачи, изложены основные идеи, развитые в диссертации, определена ее структура.
В первой главе дана характеристика центробежных сепараторов, представляющих собой наиболее эффективный способ очистки и увеличения срока годности технологической жидкости на производстве. Первоначально центробежный сепаратор применялся исключительно в пищевой промышленности. В настоящее время он занял заметное место на предприятиях многих других отраслей и используется для очистки промышленных жидкостей от различных эмульсий, примесей и сточных вод. Наиболее уязвимым местом в конструкции сепаратора являются элементы, изготовленные из полимерных материалов, такие, как диски, кольца, мембраны и пр. Анализ поведения некоторых из этих элементов конструкции при длительной эксплуатации и определение их долговечности представляют собой задачу исследований данной работы.
Описаны материалы, используемые для изготовления элементов конструкций сепараторов. В качестве объектов исследовании выбраны три типа полимеров, качественно отличающихся по своему поведению: полиэфирэфиркетон (PEEK) – жесткий полимер, практически нечувствительный к изменению температуры и влажности, Nylon6 – материал с сильно выраженной ползучестью и чувствительностью к внешним факторам и полиоксиметилен (POM) – стабильный вязкоупругий материал, характеристики которого достаточно хорошо могут быть описаны математической моделью, которую в дальнейшем удобно использовать в расчетах.
Для анализа поведения исследованных полимерных материалов использовались представления о вязкоупругом деформировании. В данной главе указано, что наиболее перспективным подходом к описанию вязкоупругого поведения материалов является подход, основанный на представлениях о наследственном характере этого процесса. Его развитию посвящены классические работы Л. Больтцмана и В.Вольтерра, которые построили математическую модель для описания наследственно упругого деформирования, представленную в конечном счете интегральным уравнением Вольтерра 2-го рода с разностным ядром. Наследственой механикой занимались также Ю.Н.Работнов, А.А.Ильюшин, В.В.Москвитин, М.А.Колтунов, В.П.Тамуж, Ю.С.Уржумцев, Н.Н.Малинин, Н.И. Малинин, М.И.Розовский, С.И.Мешков, Ю.В.Суворова, Б.Е.Победря, С.А.Алексеева, B.Coleman, R.Christensen, W.N.Findley, J.S.Lai, G.Duffing, H.Leaderman R.A.Schapery, T.Shirakashi, C.Trusdell и многие другие.
В настоящей работе используется нелинейное уравнение Ю.Н. Работнова
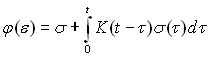 | (1) |
Дано его описание и характеристики используемых двух- и трехпараметрических ядер.
В этой же главе представлен принцип введения температуры и влажности в определяющее уравнение (1):
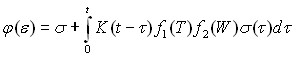 | (2) |
Здесь в уравнение введены дополнительные степенные функции, характеризующие влияние температуры и влажности
 ,  |
Величина 
является эмпирической константой, которая вычисляется на основе экспериментальных данных, а переменная 
характеризует величину прибавления веса при влагонасыщении.
Проблема использования уравнений (1) и (2) при расчетах состоит, прежде всего, в определении параметров уравнений. В главе описаны существующие подходы к решению этой задачи и выявлена необходимость в разработке надежных методов расчетов, в особенности, для случая использования трехпараметрических ядер.
Вторая глава посвящена анализу свойств и поведения материалов, применяемых при изготовлении центробежных сепараторов и описанию их поведения с помощью нелинейно-наследственной модели. Выше уже указывалось, что в данной работе рассмотрены три материала: POM, PEEK и Nylon 6. Для этих материалов осуществлялись эксперименты на растяжение с различными скоростями и при различных температурах и степенях влагонасыщения, а также снимались диаграммы ползучести при различных уровнях напряжений.
 Рис. 1. Диаграммы деформирования POM при различных скоростях нагружения, различных температурах и уровнях влажности: 1 – кривая мгновенного деформирования, 2 –  ,  ,  , 3 –  ,  ,  , 4 –  ,  ,  , 5 –  ,  ,  , 6 –  ,  ,  , 7 –  ,  ,  ; сплошные линии – эксперимент, пунктир – расчет. |
 Рис. 2. Кривые ползучести POM при различных уровнях напряжения, различных температурах и уровнях влажности: 1 –  ,  ,  , 2 –  ,  ,  , 3 –  ,  ,  , 4 –  ,  ,  , 5 –  ,  ,  , 6 –  ,  ,  , 7 –  ,  ,  ; сплошные линии – эксперимент, пунктир – расчет. |
В качестве примера на Рис. 1 и Рис. 2 приведены экспериментальные диаграммы деформирования и ползучести материала POM при различных скоростях нагружения, различных температурах и уровнях влагонасыщения. Для описания процессов деформирования и ползучести использовалось определяющее уравнение (2). Процедура определения параметров уравнения описана в главе 3.
В результате осуществленных экспериментов были выявлены характерные особенности процесса деформирования каждого из материалов. Так, для материала POM:
- диаграммы
стабильны. Результаты экспериментов показывают возможность использования модели наследственного типа с высокой степенью надежности; - материал показывает существенную нелинейность, что необходимо учитывать при конструировании модели;
- чувствительность к температуре средняя и обычная для полимерных материалов:
=6.11, чувствительность к влажности невысока: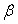 
=1.
Для материала PEEK:
- характерной особенностью процесса деформирования является появление шейки, причем ее возникновение зависит от температуры, см. Табл. 1;
- в отличие от других полимеров, PEEK представляет собой высокомодульный и высокопрочный материал, мало чувствительный к температуре и влажности:
=0.8; 
близко к нулю.
Табл. 1. Зависимость деформации от температуры для материала PEEK
Температура,  | Деформация, % |
| 27 | 5 |
| 70 | 3.5 |
| 125 | 22.5 |
Nylon 6 представляет собой материал, весьма чувствительный как к скорости нагружения, так и к температурно-влажностным воздействиям. Подробное исследование этого материала показало, что при длительном нагружении, а также при повышенных температурах или степенях влажности, свойства материала постепенно меняются; в нем происходят структурные превращения, приводящие к изменению физико-механических свойств, следствием чего является неадекватное поведение материала и значительный рост деформаций. Nylon 6 не может быть рекомендован при длительной эксплуатации конструкции.
В этой же главе показано, что даже такие стабильные материалы как POM, при нагружении проявляют текстурирование (изменение структуры, связанное с переориентацией молекул полимера при его нагружении), что наиболее заметно при анализе процессов разгрузки. Необратимая деформация, возникающая из-за происходящего в процессе нагружения текстурирования материала, зависит как от величины 
, с которой начинается разгрузка, так и от уровня падения напряжения, 
, где 
- тот уровень, до которого происходит разгрузка. Таким образом, в уравнение (1) добавляется некоторая функция 
, а само уравнение для случая возврата ползучести примет вид:
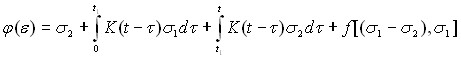 | (3) |
Здесь 
-момент начала разгрузки с величины 
; при 
эксперимент заканчивается.
Все эксперименты проводились для материала POM при различных уровнях величин 
и 
, что дало возможность аппроксимировать функцию 
зависимостью вида
 , |
где 
- экспериментальный параметр. В качестве примера на Рис. 3 приведен один из полученных в экспериментах графиков с соответствующей обработкой данных по формуле (3).
 Рис. 3. Кривые прямой и образной ползучести POM при  =53 МПа, 1 – разгрузка до 35МПа, 2 – разгрузка до 18МПа; сплошные линии – эксперимент, пунктир – расчет по формуле (3). |
Одним из важных разделов главы 2 является раздел, посвященный влиянию циклического нагружения на поведение вязкоупругих полимерных материалов, которое вследствие природы полимера может привести к существенному саморазогреву материала и даже к так называемому температурному взрыву, когда разрушение материала происходит от существенного повышения температуры. При этом потеря элементом конструкции несущей способности происходит не от накопления повреждений, как это обычно бывает при циклическом нагружении (при наличии обеспеченного теплоотвода с его поверхности), а от того, что с ростом температуры прочностные свойства материала значительно снижаются, что и приводит к разрушению.
Анализ тепловыделения при циклическом нагружении приводит к связанной задачи термовязкоупругости, решение которой сопровождается определенными математическими трудностями. Сначала необходимо определить величину работы, совершающуюся в течение одного цикла. Принимается, что тепловыделение 
пропорционально этой работе, т.е. площади петли гистерезиса
 |
Здесь 
- некоторый постоянный уровень нагрузки, на который накладывается вибрация с постоянной амплитудой 
. Значение действующего напряжения при этом
 | (4) |
(
- частота колебаний).
Дальнейший анализ в работе ведется для случая линейной вязкоупругости с ядром Абеля:
 | (5) |
Здесь 
- функция температурного влияния соответственно уравнению (2).
Подставляя в уравнение (5) выражение (4) и принимая функцию 
в виде 
, можно вычислить тепловыделение 
, где
 |
Далее строится функция диссипации
 |
где 
- удельная теплоемкость, 
- плотность материала, 
- количество тепла, выделяемого в единицу времени
 |
Теперь можно перейти непосредственно к решению уравнения теплопроводности
 |
Уравнение решается в предположении, что рассматриваемый элемент достаточно мал и можно пренебречь эффектами теплопередачи. В этом случае получаем
 |
Анализ этого уравнения позволяет получать различные решения в зависимости от параметра 
. Схема полученного решения приведена на Рис. 4.
Видно, что для случая 
существует некоторое значение критического времени, больше которого образец не в состоянии работать:
 |
Решение показывает, что если 
, то увеличение температуры происходит очень интенсивно и может быстро привести к полной потере материалом несущей способности.
Если же образец имеет конечные размеры и в нем происходит перераспределение температуры по координатам и если добавить еще граничные условия, в соответствии с которыми определяется возможность и условия отвода тепла, то решение существенным образом усложняется и требует привлечения численных методов анализа.
 Рис. 4. Изменение температуры во времени при циклическом нагружении и при различных температурных параметрах  |
В главе приведены некоторые экспериментальные результаты, связанные с тепловыделением при циклическом нагружении и дан анализ происходящих процессов разрушения, т.е. устанавливается связь между числом циклов до разрушения N, параметрами цикла: 
(частота), R (коэффициент асимметрии), 
(максимальная нагрузка в цикле) и температурой:
 |
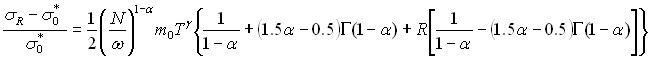Здесь 
и 
- параметры материала.
Третья глава диссертации посвящена анализу нелинейно-наследственного уравнения с различными ядрами. В качестве примера выбраны: наиболее простое и широко распространенное в настоящее время ядро Абеля 
и ядро Работнова, представляющее собой комбинацию свойств слабой сингулярности, свойственной ядру Абеля, и экспоненты, определяющей поведение при 
:
 , 0< <1,  | (6) |
Прежде всего осуществлен анализ кривой мгновенного деформирования, представляющей собой характеристику физической нелинейности рассматриваемой среды. Проанализированы возможные способы аппроксимации кривой мгновенного деформирования и приведены примеры.
При анализе нелинейного уравнения с ядром Абеля разработан алгоритм определения параметров для случаев деформирования и ползучести и его программная реализация. Выбор в качестве алгоритмической среды универсального языка программирования позволил написать компактную программу, предоставляющую достаточно простой и понятный интерфейс для решения данной задачи. В качестве языка программирования был выбран язык Visual C++, средой разработки стал пакет Microsoft Visual Studio 6.0, а базовой операционной системой – Microsoft Windows.
 Рис. 5. Кривая мгновенного деформирования. Кривые деформирования при различных скоростях деформирования: 1 –  , 2 –  , 3 –  , 4 – кривая мгновенного деформирования; сплошные линии – эксперимент, пунктир – расчет |
Подробно описана процедура численного решения поставленной задачи для ядра Абеля, определены параметры 
, рассчитана кривая мгновенного деформирования. Далее эти параметры использованы для расчета диаграмм деформирования, полученных с различными скоростями и кривых ползучести при различных уровнях нагрузки. Результаты расчетов сопоставляются с экспериментами для материала POM. В качестве примера приведен Рис. 5.
Анализ нелинейно-наследственного уравнения с ядром Работнова гораздо более сложен. Функция Работнова представляет собой медленно сходящийся знакопеременный ряд, первым членом которого является функция Абеля с особенностью порядка 
, а на бесконечности она дает логарифмический закон ползучести, хорошо подтвержденный многочисленными экспериментами. В данной работе процедура определения параметров по кривым ползучести использует как аналитические, так и численные методы: интегральное преобразование Лапласа-Карсона, описанную выше компьютерную программу, а также хорошо известные вычислительные средства: Excel, Maple и Curve Expert.
Подход основан на том, что при малых временах нагружения можно воспользоваться только первым членом суммы ряда (6). Тогда
 |
Это выражение может быть использовано для определения параметра сингулярности 
где с помощью программы, описанной выше. Далее считается, что параметр 
– уровень приложенной постоянной нагрузки.
Далее применим преобразование Лапласа-Карсона
будет иметь такое же значение и при использовании всей суммы ряда (5). Для определения параметров 
, предполагаем, что при низком уровне нагрузки материал не выходит за рамки линейного поведения, что позволяет преобразовать уравнение
 |
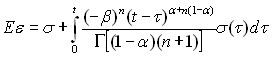к виду
 |
где 
– уровень приложенной постоянной нагрузки.
Далее можно применить преобразование Лапласа-Карсона
 |
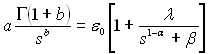при условии, что выбранная кривая ползучести аппроксимирована степенной функцией 
.
Далее осуществляется численная реализация программы определения параметров. В дальнейшем использование уже найденных параметров уравнения корректирует построение кривой мгновенного деформирования на основании любой из изохронных кривых ползучести. Результаты расчетов и сопоставление их с экспериментом для материала Nylon 6 приведено на Рис. 6.
Рис. 6. Кривые ползучести для разных уровней нагрузки: 1 –  , 2 –  , 3 –  ; сплошные линии – эксперимент, пунктир – расчет по формуле (4). |
Здесь кривая мгновенного деформирования аппроксимировалась степенной функцией и расчет кривых ползучести с найденным набором параметров осуществлялся по уравнению
 |
Четвертая глава работы посвящена решению конкретных практических задач о деформировании элементов конструкции сепаратора. При их решении прежде всего возникает проблема обобщения рассмотренной в предыдущих главах модели нелинейно-наследственной среды на случай сложного напряженного состояния. В настоящей диссертации использован подход, разработанный в работах Ю.В.Суворовой и С.И.Алексеевой. Связь между компонентами тензоров напряжений и деформаций записывается в виде
 | (7) |
а связь между интенсивностями напряжений и деформаций аналогична одномерному уравнению
 | (8) |
В соотношениях (7) и (8) 
- интегральный оператор,
 ;  |
 |
 |
Далее модель, основанная на соотношениях (7) и (8) использовалась для расчетов напряженно-деформированного состояния элементов конструкции сепаратора.
В главе рассмотрены две прикладные задачи: одна из них связана с деформированием толстостенного цилиндра конечной длины, а вторая – с деформированием мембраны.
Все расчеты, проведенные для первой задачи, осуществлены численно с использованием системы FEMLAB, представляющей собой мощную интерактивную среду для моделирования, дающую в том числе возможность решать различные виды научных и технических задач, основанных на дифференциальных уравнениях в частных производных. Рассмотрены упрощенные условия, которые позволили проанализировать два случая: осевое растяжение с кручением и осевое растяжение с внутренним давлением. Были осуществлены эксперименты на образцах из двух материалов POM и PEEK, также с использованием FEMLAB были проведены расчеты.
Задача 1. Деформирование толстостенного цилиндра
В качестве примера приведены результаты экспериментов и расчетов для случая растяжения цилиндра с внутренним давлением и осевым растяжением, Табл. 2, Табл. 3, Рис. 7–Рис. 10.
Табл. 2. Эксперимент №1
| Время, с | Внутренее давление, МПа | Осевая нагрузка, МПа | z эксперимент | z расчет, защемленные края | z расчет, свободные края | эксперимент | расчет, защемленные края | расчет, свободные края |
| 200 | 2,5 | 0 | 0,00033 | -0,00049 | -0,00053 | 0,0015 | 0,002 | 0,0022 |
| 465 | 5 | 0 | 0,00063 | -0,0015 | 0,00093 | 0,004 | 0,0049 | 0,0057 |
| 732 | 7,5 | 0 | 0,00087 | -0,0035 | 0,00107 | 0,008 | 0,0098 | 0,0116 |
| 989 | 10 | 0 | 0,0013 | -0,0071 | 0,0018 | 0,014 | 0,0160 | 0,0213 |
| 994 | 10 | 9,1 | 0,005 | -0,0018 | 0,006 | 0,0133 | 0,0145 | 0,0175 |
| 1037 | 10 | 18,1 | 0,0103 | 0,00105 | 0,0108 | 0,012 | 0,0142 | 0,01659 |
| 1063 | 10 | 22,6 | 0,0143 | 0,0035 | 0,0135 | 0,0114 | 0,01397 | 0,0155 |
| 1097 | 10 | 27,2 | 0,0195 | 0,0056 | 0,0170 | 0,0109 | 0,01369 | 0,015 |
| 1151 | 10 | 31,7 | 0,0278 | 0,0078 | 0,0205 | 0,0106 | 0,0136 | 0,0145 |
Табл. 3. Эксперимент №2
| Время, с | Внутренее давление, МПа | Осевая нагрузка, МПа | z эксперимент | z расчет, защемленные края | z расчет, свободные края | эксперимент | расчет, защемленные края | расчет, свободные края |
| 287 | 0 | 9,1 | 0,0013 | 0,0013 | 0,0019 | -0,00035 | -0,00055 | -0,00055 |
| 320 | 0 | 18,1 | 0,0045 | 0,0045 | 0,0046 | -0,00155 | -0,0012 | -0,0012 |
| 334 | 0 | 22,6 | 0,0063 | 0,0063 | 0,0064 | -0,00255 | -0,0016 | -0,0016 |
| 352 | 0 | 27,2 | 0,0085 | 0,0085 | 0,0087 | -0,0038 | -0,0024 | -0,0024 |
| 371 | 0 | 31,7 | 0,0113 | 0,0113 | 0,0114 | -0,005 | -0,00361 | -0,00361 |
| 508 | 2,5 | 31,7 | 0,0127 | 0,0127 | 0,0099 | -0,004 | -0,00129 | -0,00059 |
| 766 | 5 | 31,7 | 0,0148 | 0,0148 | 0,0092 | -0,00075 | 0,00279 | 0,0032 |
| 1034 | 7,5 | 31,7 | 0,0187 | 0,0178 | 0,0091 | 0,0025 | 0,007 | 0,0077 |
| 1290 | 10 | 31,7 | 0,0318 | 0,029 | 0,009 | 0,0093 | 0,01354 | 0,0142 |
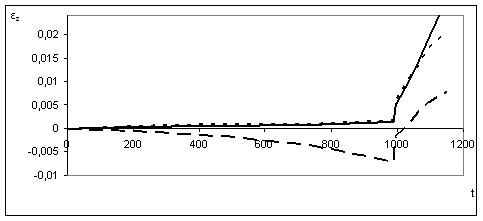 Рис. 7. Экспериментальные и расчетные графики для  по эксперименту №1 с растяжением и внутренним давлением: сплошные линии – эксперимент, черные штрихи – расчет со свободными краями, черный пунктир – расчет с защемленными краями. |
 Рис. 8. Экспериментальные и расчетные графики для  по эксперименту №1 с растяжением и внутренним давлением: сплошные линии – эксперимент, черные штрихи – расчет со свободными краями, черный пунктир – расчет с защемленными краями. |
 Рис. 9. Экспериментальные и расчетные графики для  по эксперименту №2 с растяжением и внутренним давлением: сплошные линии – эксперимент, черные штрихи – расчет со свободными краями, черный пунктир – расчет с защемленными краями. |
 Рис. 10. Экспериментальные и расчетные графики для  по эксперименту №2 с растяжением и внутренним давлением: сплошные линии – эксперимент, черные штрихи – расчет со свободными краями, черный пунктир – расчет с защемленными краями. |
При расчетах рассматривались два варианта граничных условий – защемленные и свободные торцевые поверхности цилиндра. Оказалось, что в основном, как показывают Рис. 7–Рис. 10, расчет более близок к эксперименту для случая защемленных краев. (В действительности точно установить граничные условия работы рассматриваемого элемента конструкции не представляется возможным). Следует подчеркнуть, что в расчетах использовалась модель (7) и (8) и операторы ползучести в виде оператора Абеля с параметрами, определенными для данных материалов по результатам одномерных испытаний (Глава 2).
Задача № 2. Деформирование круглой мембраны
Другим рассмотренным элементом конструкции является круглая мембрана. В данной главе приведен краткий исторический очерк развития теории гибких пластин, который показывает, что начиная с 18-го века этому вопросу уделяется большое внимание в силу, во-первых, сложности корректной постановки задачи и, во-вторых, сложности решения конкретных прикладных задач. В диссертации приводится постановка и роешение задачи об изгибе круглой мембраны, материал которой обладает вязкими характеристиками, что вносит дополнительные трудности в решение. Это конкретная задача, связанная с использованием гибкой круглой пластины из полиоксиметилена в конструкции центробежного сепаратора.
Рассматривается круглая пластина диаметром 620мм и толщиной в 1мм, на которую действует равномерно распределенная нагрузка, приложенная по площади круга диаметром 600мм. Экспериментальный график приложения нагрузки во времени приведен на Рис. 11.
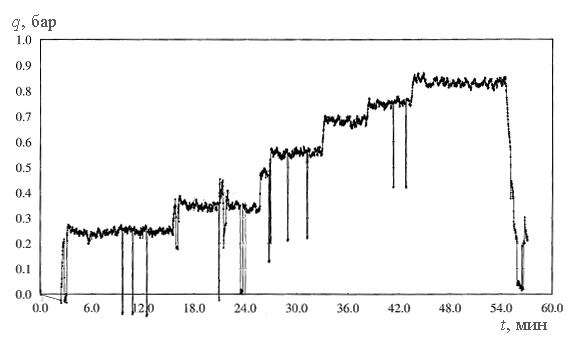 Рис. 11. График приложения нагрузки во времени для эксперимента с мембраной |
При решении задачи принимается случай линейного вязкоупругого тела, используется принцип Вольтера и упругое решение, полученное А.С. Вольмиром.
В результате решения задачи выражения для радиального и тангенциального напряжения в зависимости от безразмерного радиуса 
(с – радиус пластины) записываются следующим образом:
 |
где 
- интенсивность напряжений.
Формулы (7) дают
 |
что позволяет вычислить интенсивность деформаций 
.
Учитывая закон изменения нагрузки, представленный на рис. 6, при котором на каждом из 6-ти этапов можно считать ее постоянной величиной, запишем
 |
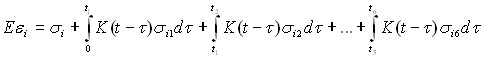или, если принять 
, то
 |
В результате проведенных экспериментов была осуществлена запись деформаций 
и 
практически в центре пластины, при 
= 25 мм, и при 
= 170 мм. Эти значения пересчитывались в значения интенсивностей
 , |
которые и сопоставлялись с осуществленными расчетами. Для расчетов была разработана программа, позволившая выполнить необходимые вычисления и вывести результаты в виде графиков. На Рис. 12 представлены результаты для случая 
, т.е. для центра пластины.
 Рис. 12. Результат расчетов для случая  (центр пластины) |
Максимальное отличие между рассчитанной величиной (1.95%) и экспериментальной (2.2%) в конце опыта составляет 11%. При вычислении интенсивности для радиуса 
= 170 мм расхождение оказывается более значительным и составляет уже 26%. Это можно объяснить тем, что исследуемый радиус находится ближе к границе приложения нагрузки и краю пластины, и, соответственно, граничные условия не могут быть определены точно. Кроме того, полученное решение не учитывает нелинейности материала, что также вносит дополнительные погрешности в расчеты.
ЗАКЛЮЧЕНИЕ
1. Осуществлено экспериментальное исследование вязкоупругих характеристик материалов POM, PEEK и Nylon 6, используемых при изготовлении отдельных деталей центробежных сепараторов, и влияние на поведение этих материалов в условиях длительной ползучести таких факторов, как температура и влажность. Дан анализ характерным особенностям исследованных материалов и обсуждены возможности их использования для изготовления деталей центробежного сепаратора.
2. Показано, что определяющее уравнение, основанное на представлениях о наследственном характере поведения материалов и позволяющее прогнозировать их деформационные характеристики при различных типах нагружения, в условиях разгрузки должно быть дополнено функцией, учитывающей процесс текстурирования, происходящий под нагрузкой и приводящий к появлению дополнительных необратимых деформаций.
3. Решение задачи о циклическом деформировании вязкоупругой среды позволило установить режимы саморазогрева в зависимости от температурной чувствительности материала и значение критического времени, являющегося границей области, в которой значительное и очень быстрое повышение температуры может привести к полной потере материалом несущей способности за короткое время, определяемое параметрами материала и условиями теплоотвода. Установлена зависимость между параметрами циклического нагружения, параметрами материала и температурой.
4. Разработаны методы численного анализа определяющего уравнения и созданы программы, с помощью которых произведено определение параметров определяющего уравнения методами компьютерного моделирования. Рассмотрены случаи наиболее простого ядра Абеля с интегрируемой сингулярностью и наиболее информативного ядра Работнова, позволяющего получать достоверные результаты на больших интервалах времен.
5. Обобщение модели нелинейно-наследственной среды на случай сложного напряженного состояния позволило сформулировать и решить две задачи: об исследовании напряженно-деформируемого состояния толстостенного цилиндра конечной длины и об изгибе круглой мембраны.
6. Численные методы, используемые при решении задач, позволили получить конкретные решения в виде графиков, которые могут служить рекомендациями при проектировании деталей конструкции центробежного сепаратора.
Основные положения диссертации отражены в следующих публикациях:
- Мосин А.В. Использование Visual C++ для определения параметров нелинейного уравнения наследственной модели // «Современные проблемы машиноведения» XII конференция молодых ученых, аспирантов и студентов. Тезисы докладов. Москва. 2000. с. 24.
- Мосин А.В. Использование интегральных преобразований для вычисления параметров определяющего уравнения наследственного типа // «Современные проблемы машиноведения» XIII конференция молодых ученых, аспирантов и студентов. Тезисы докладов. Москва. 2001. с. 22.
- Мосин А.В. Вычисление параметров нелинейного определяющего уравнения наследственного типа // Проблемы машиноведения и надежности машин. 2002. №2, с. 83-88.
- Суворова Ю.В., Мосин А.В. Численные методы определения параметров ядер наследственной модели // Проблемы машиностроения и автоматизации. 2002. №4, с. 34-41.
- Мосин А.В. Определение параметров дробно-экспоненциальной функции Работнова с использованием интегрального преобразования и современного программного обеспечения // Московская конференция молодых ученых, аспирантов и студентов «Научно-технические проблемы развития Московского мегаполиса». Тезисы докладов. Москва. 2002. с. 24.
- Мосин А.В. Использование интегрального преобразования и современной вычислительной техники для определения параметров ядра Работнова // Московская конференция молодых ученых, аспирантов и студентов «Научно-технические проблемы развития Московского мегаполиса». Труды конференции. Москва. 2003. с. 83-89.
- Суворова Ю.В., Алексеева С.И., Мосин А.В. Описание процессов возврата ползучести полимеров с учетом текстурирования // Проблемы машиностроения и автоматизации. Москва. 2003. №4, с. 71-73.
- Алексеева С.И., Мосин А.В. Математическое моделирование процессов деформирования термопластичных полимеров с учетом текстурирования // Труды международного симпозиума «Structure Sensitive Mechanics of Polymer Materials. Physical and Mechanical Aspects». Moscow, 2004. с. 278-279.
- Суворова Ю.В., Мосин А.В. Моделирование напряженно-деформированного состояния при изгибе круглой мембраны из упруго-наследственного материала // Проблемы машиностроения и автоматизации. 2006. №1, с. 81-84.
