Исследование случайных воздействий на вибрационные характеристики стиральных машин барабанного типа при отжиме
На правах рукописи
Фетисов Игорь Валерьевич
ИССЛЕДОВАНИЕ СЛУЧАЙНЫХ ВОЗДЕЙСТВИЙ
НА ВИБРАЦИОННЫЕ ХАРАКТЕРИСТИКИ СТИРАЛЬНЫХ МАШИН БАРАБАННОГО ТИПА ПРИ ОТЖИМЕ
Специальность 05.02.13 Машины, агрегаты и процессы
(коммунальное хозяйство и сфера услуг)
АВТОРЕФЕРАТ
диссертации на соискание учёной степени
кандидата технических наук
Шахты – 2011
Работа выполнена в Федеральном государственном бюджетном
образовательном учреждении высшего профессионального образования «Южно-Российский государственный университет экономики и сервиса» (ФГБОУ ВПО «ЮРГУЭС») на кафедре «Машины и оборудование
бытового и жилищно-коммунального назначения»
Научный руководитель кандидат технических наук, доцент
Алёхин Сергей Николаевич
Официальные оппоненты: доктор технических наук, профессор
Адигамов Касьян Абдурахманович
кандидат технических наук, доцент
Сумзина Лариса Владимировна
Ведущая организация ФГБОУ ВПО «Донской государственный
технический университет», г. Ростов-на-Дону
Защита состоится «24» декабря 2011 г. в 1200 часов на заседании диссертационного совета Д 212.313.01 при ФГБОУ ВПО Южно-Российский государственный университет экономики и сервиса по адресу: 346500, г. Шахты Ростовской области, ул. Шевченко, 147, ауд. 2 247.
С диссертацией можно ознакомиться в библиотеке ФГБОУ ВПО Южно-Российский государственный университет экономики и сервиса.
Текст автореферата размещён на сайте ЮРГУЭС: http: www.sssu.ru
Автореферат разослан «22» ноября 2011 г.
Учёный секретарь
диссертацинного совета Д 212.313.01 Куренова С.В.
ОБЩАЯ ХАРАКТЕРИСТИКА РАБОТЫ
Актуальность темы диссертации. Тенденции и стратегия развития современной техники свидетельствуют о том, что качественные изменения машин и агрегатов достигаются, главным образом, за счёт форсирования скоростных и силовых параметров при одновременном снижении их материалоёмкости. Это обусловливает возрастание динамических нагрузок, механических воздействий и, как следствие, вибрационной активности машин и агрегатов. Установлено, что 70–80 % отказов изделий машиностроения, к которым относятся стиральные машины, являются результатом действия вибрации.
Стиральные машины барабанного типа, представляющие собой наиболее массовые и перспективные устройства для стирки и отжима текстильных изделий, являются одними из наиболее виброактивных изделий в сфере быта и коммунального хозяйства.
Значительные динамические нагрузки, возникающие при вибрации машин в процессе центробежного отжима, ведут к отказам и сокращению сроков эксплуатации машин, увеличивают длительность периода отжима, повышают расход электроэнергии, оказывают негативное вибрационное и шумовое воздействие на человека. Это снижает потребительские свойства машин и их конкурентоспособность на рынке бытовой и коммунальной техники.
Вопросы динамики стиральных машин барабанного типа, методов и технических средств защиты от вибрации рассмотрены в ряде научных работ отечественных и зарубежных авторов (Малыхин В.И., Набережных А.И., Сумзина Л.В., Рябинький Л.М., Кузнецов С.А., Фомин Ю.Г., Лебедев В.С., Ройзман В.П., Малыгин В.И., Spelta C., Lee Jun Young, Matsushima H., Nygards T. и др.). Вместе с тем, изучение динамики стиральных машин осуществлялось, как правило, без учёта влияния случайных воздействий на динамические характеристики машин, которое, как показали дальнейшие исследования, имеет существенное значение при проведении анализа колебательного процесса и разработке на его основе научно обоснованных рекомендаций по совершенствованию виброзащитных систем.
Анализ публикаций, посвящённых исследованию динамики стиральных машин при центробежном отжиме и разработке методов и технических средств их виброзащиты, позволил выявить следующее:
во-первых, подавляющее большинство существующих математических моделей, описывающих колебания стиральных машин, использует в основном известные методы математического моделирования детерминированных колебаний, не учитывая при этом стохастическое поведение системы;
во-вторых, недостаточно полно исследованы методы определения вероятностных характеристик внешних возмущающих сил, действующих на подвесную часть машин при отжиме;
в-третьих, отсутствуют научно обоснованные рекомендации по выбору рациональных конструктивных и режимных параметров стиральных машин, обеспечивающих снижение их виброактивности при случайных внешних воздействиях.
Высокая значимость данных проблем обусловила актуальность и целесообразность выбора направления диссертационного исследования.
Целью диссертационного исследования является исследование виброактивности стиральных машин барабанного типа при случайных динамических воздействиях в процессе центробежного отжима.
В соответствии с указанной целью в диссертационной работе были поставлены и решены следующие основные задачи:
- анализ существующих методов исследования случайных колебаний и способов снижения виброактивности роторных машин, в том числе стиральных машин барабанного типа;
- математическое моделирование динамики колебательной системы стиральных машин при случайных внешних воздействиях с учётом современных положений теории случайных колебаний и конструктивно-режимных особенностей стиральных машин барабанного типа;
- теоретико-экспериментальное определение диапазона значений эксцентриситета центра масс отжимаемых текстильных изделий и внешних случайных воздействий на подвесную часть стиральных машин;
- экспериментальное определение амплитуд случайных колебаний подвесной части и их вероятностных характеристик в зависимости от загрузки стирального барабана;
- разработка рекомендаций по выбору рациональных конструктивных и режимных параметров стиральных машин барабанного типа, обеспечивающих снижение их виброактивности при отжиме.
Объектом исследования являются бытовые стиральные машины барабанного типа, осуществляющие процессы по обработке текстильных изделий при стирке и отжиме в барабане с горизонтальной осью вращения.
Предметом исследования являются колебательные процессы подвесной части, конструктивные и режимные параметры стиральных машин при случайных внешних воздействиях.
Методологической и теоретической основой исследования служат основные положения теории случайных колебаний, труды отечественных и зарубежных исследователей в области совершенствования математических моделей для стиральных машин, устройств и элементов виброизоляции, повышения комфортности и вибронадёжности рассматриваемых объектов.
В диссертации использовались специальные разделы математического и системного анализа, основы теории случайных процессов, численные методы статистической обработки экспериментальных данных, элементы и средства математического и физического моделирования.
Научная новизна диссертации заключается в следующем:
- Доказана целесообразность учёта случайных внешних воздействий на колебания стиральных машин барабанного типа при исследовании их динамики для повышения обоснованности и точности результатов.
- Установлена зависимость диапазона случайных вариаций величины эксцентриситета центра масс отжимаемых текстильных изделий от коэффициента загрузки барабана kз и коэффициента длины барабана kL.
- Установлена функциональная зависимость диапазона возможных значений эксцентриситета центра масс текстильных изделий и возмущающих сил от времени отжима, загрузки машины и периода разгона барабана.
- Теоретически и экспериментально установлен диапазон амплитуд случайных колебаний подвесной части стиральных машин в зависимости от интервала случайных значений эксцентриситета центра масс изделий при отжиме.
- Установлены требуемые значения жёсткости упругих элементов подвески, соответствующие диапазону11,2…15,0 рад/с собственной частоты колебательной системы, а также значение коэффициента длины барабана kL=0,7, соответствующее глобальному минимуму амплитуд колебаний.
Практическая значимость. Для разработки стиральных машин барабанного типа с улучшенными показателями качества, а также при их модернизации, обслуживании и ремонте особую значимость имеют следующие практические результаты диссертационной работы:
- алгоритм теоретического расчёта диапазона случайных значений эксцентриситета центра масс текстильных изделий при центробежном отжиме и его применение при определении динамических характеристик стиральных машин;
- рекомендации по выбору рациональных конструктивных и режимных параметров стиральных машин, обеспечивающих снижение виброактивности при случайных внешних воздействиях и требуемом качестве обработки текстильных изделий;
- программы расчёта рациональных конструктивных и режимных параметров стиральных машин, обеспечивающих снижение виброактивности при случайных внешних воздействиях и требуемом качестве обработки текстильных изделий (свидетельства РФ о государственной регистрации программы для ЭВМ № 2011617524, № 2011617525).
Результаты диссертации представляют интерес для проектно-конструкторских организаций, а также для предприятий по изготовлению, эксплуатации и ремонту как бытовых, так и стиральных машин коммунального хозяйства с целью повышения потребительских свойств машин и их конкурентоспособности на рынке бытовой и коммунальной техники.
Апробация работы. Основные положения диссертации были доложены на ряде Международных и Всероссийских научно-технических конференций: в частности, в Северо-Кавказском государственном университете (г. Невинномысск, 2009 г.), в Южном математическом институте Владикавказского научного центра Российской академии наук (г. Владикавказ, 2008 г. и 2010 г., г. Волгодонск, 2009 г. и 2011 г.), в ФГБОУ ВПО «Южно-Российский государственный университет экономики и сервиса» (г. Шахты, 2009, 2010, 2011 гг.), на Международных научно-практических конференциях МНИЦ ПГСХА (г. Пенза, 2009, 2010, 2011 гг.) и на ряде научных семинаров.
Результаты работы использованы предприятиями ООО «Бытсервис» г. Ставрополь, Торгово-промышленная палата г. Шахты и др.
Материалы диссертации используются в учебном процессе в ЮРГУЭС при изучении дисциплины «Проектирование бытовых машин и приборов», а также рекомендованы магистрантам, аспирантам и преподавателям, занимающимся вопросами динамики стиральных машин.
Публикации. Основное содержание диссертационной работы опубликовано автором в 13 статьях, из них в 4 статьях в журналах, входящих в перечень п. 7 ВАК РФ, а также получены 2 свидетельства РФ о государственной регистрации программ для ЭВМ.
Ряд положений диссертации изложен в отчётах по НИР, выполненных в ЮРГУЭС в 2009–2011 гг.
Структура и объём диссертации. Диссертационная работа состоит из введения, четырёх глав, выводов, приложений, библиографического списка и содержит 167 страниц машинописного текста, 78 рисунков, 10 таблиц и список использованной литературы из 172 наименований.
Диссертация выполнена на кафедре «Машины и оборудование бытового и жилищно-коммунального назначения» Южно-Российского государственного университета экономики и сервиса.
СОДЕРЖАНИЕ РАБОТЫ
Во введении дано обоснование актуальности темы, сформулирована цель и определены основные задачи исследований, приведены сведения о научной новизне, практической значимости и реализации результатов диссертационной работы.
В первой главе проанализированы современные подходы при исследовании динамики машин и механизмов, которые показали, что при воздействии на систему случайных возмущений классические методы расчёта, основанные на детерминизме, становятся неприемлемыми и для получения качественно новых результатов необходимо использовать вероятностные методы. Такая постановка задачи обусловливает актуальность и необходимость применения стандартных и разработки новых вероятностных методов исследования динамики стиральных машин.
Показано, что исследование динамики стиральных машин барабанного типа может базироваться на общетеоретических положениях теории колебаний для твёрдых тел с несколькими степенями свободы и случайным поведением колебательной системы, нашедших применение в различных отраслях техники.
Теоретической основой для исследования случайных колебаний стиральных машин могут служить фундаментальные работы, посвящённые теории случайных процессов и колебаний, таких авторов, как Арнольд В.И., Блехман И.И., Болотин В.В., Купер Дж. и Макгиллем К., Светлицкий В.А., Свешников А.А., Неймарк Ю.И. и др.
Рассмотрены конструктивные особенности и режимные параметры стиральных машин барабанного типа. Показано, что большое значение на величину и характер возмущающих сил при отжиме оказывают такие факторы, как эксцентриситет центра масс текстильных изделий, загрузка машины, коэффициент загрузки барабана, режим отжима. Установлено, что используемые известные методы расчёта эксцентриситета предполагают в основном неизменность его величины в период отжима и не учитывают случайный характер его вариаций.
Такой подход обусловливает динамику вариаций возмущающих сил только в зависимости от частоты вращения барабана и не предполагает учёт диапазона возмущающих сил как случайной величины. Это, в свою очередь, не позволяет исследовать весь диапазон случайных амплитуд колебаний подвесной части при отжиме и ведёт к снижению достоверности результатов исследования динамики стиральных машин.
Таким образом, для повышения достоверности результатов исследования и разработки на их основе эффективных виброзащитных систем необходимо использовать вероятностные методы с учётом стохастического характера внешних динамических воздействий на подвесную часть стиральных машин.
Во второй главе рассмотрены теоретические основы математического моделирования случайных колебаний стиральных машин и вопросы определения диапазона случайных вариаций возмущающих сил.
Для нахождения амплитудно-частотных и вероятностных характеристик процесса случайных колебаний в данной модельной задаче разработана расчётно-аналитическая схема колебательной системы стиральных машин барабанного типа.
Для математического моделирования предложена и решена слабо связанная система шести обыкновенных линейных дифференциальных уравнений второго порядка, описывающая случайные колебания подвесной части стиральной машины барабанного типа (с упругими и диссипативными элементами подвески) вдоль координатных осей неподвижной системы координат О,, и угловые колебания,, вокруг этих осей:

![]()
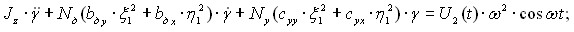
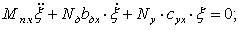
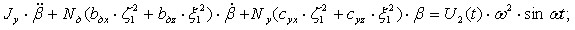

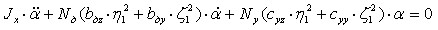 .
.
Здесь Мп.ч – масса подвесной части; Nд – число демпферов; Nу – число упругих элементов; bдх, bду, bдz – коэффициенты демпфирования по осям О1x, О1y, О1z соответственно; cух, cуу, cуz – коэффициенты жёсткости упругих элементов по осям О1x, О1y, О1z соответственно; О1xyz – подвижная система координат, жёстко связанная с центром масс подвесной части; – частота колебаний вынуждающей силы; Jx, Jy, Jz – моменты инерции вдоль осей О1x, О1y, О1z соответственно.
Правые части 1, 2, 4 и 5-го неоднородных дифференциальных уравнений системы (1) представляют собой однотипные произведения случайных процессов U1(t) и U2(t) на неслучайные функции 2sint и 2cost, где U1(t)= m(t)re(t), а U2(t)= m(t)re(t)lx(t). Координатами вектора возмущающих сил f(t) служат случайные величины, такие как масса m=m(t), эксцентриситет re=re(t) отжимаемых текстильных изделий относительно оси вращения барабана, а также смещение lx(t) центра масс изделий вдоль оси вращения барабана относительно инерционной системы координат.
Вышеуказанные координаты вектора возмущающих сил объективно случайны потому, что раскладка текстильных изделий по внутренней поверхности стирального барабана носит случайный характер, а величины масс изделий меняются вследствие отжима и удаления жидкости из загруженных изделий с течением времени случайным образом.
Можно видеть, что все уравнения исходной системы (1) содержат постоянные параметры. Стационарный режим имеет место при стационарных возмущениях после определённого интервала времени от начала колебаний, а, соответственно, нестационарный режим имеет место при разгоне барабана.
Учитывая краткость изложения, приведём итоговые результаты для первого и пятого неоднородных дифференциальных уравнений системы (1) (решения всех остальных уравнений аналогичны). В силу линейности уравнений исходной системы (1), можно считать начальные условия процесса однородными.
Решения первого и пятого дифференциальных уравнений исходной слабо связанной системы (1) позволили получить соответствующие виброперемещения подвесной части стиральных машин с учётом случайного динамического воздействия:
 (2)
(2)
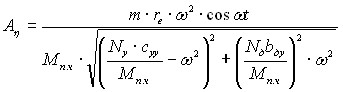 . (3)
. (3)
Вероятностные характеристики виброперемещений при известных математических ожиданиях mf, дисперсиях Df и корреляционных функциях Kf случайных воздействий, где f1(t)=m(t)re(t)2sint, а f5(t)=m(t)re(t)2cost, имеют следующий вид:
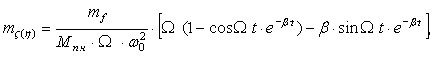 (4)
(4)
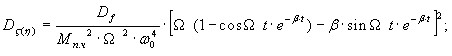 (5)
(5)
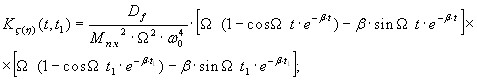 (6)
(6)
где 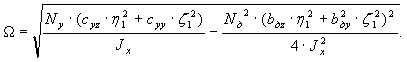
Можно видеть, что при постоянной величине загрузки m=const машины случайность возмущающих сил (внешних воздействий) будет определяться случайной величиной эксцентриситета rе(t), который, в свою очередь, зависит от случайного распределения изделий по обечайке барабана.
Кроме того, при постоянных конструктивных параметрах стирального барабана, условиях его загрузки текстильными изделиями и режиме центробежного отжима случайная величина эксцентриситета rе будет находиться в определённом диапазоне значений, границы которого меняются в зависимости от вида текстильных изделий и режима отжима. Необходимо также учитывать, что в период отжима происходят процессы удаления влаги из изделий и изменения величины их деформации, что также приводит к вариациям величины эксцентриситета rе.
Для решения задачи определения величины и границ диапазона значений эксцентриситета rе в диссертации предложен подход, основанный на допущении о равномерной плотности изделий по всему объёму барабана и крайних возможных положениях кольца изделий в барабане при отжиме, которые зависят от соотношения диаметра барабана DБ и внутреннего диаметра кольца изделий dб. При этом возможны два варианта: 1) dб0,5DБ, 2) dб>0,5DБ. На рис. 1 показаны крайние случаи расположения кольцевого слоя изделий в барабане: на рис. 1а – для 1-го варианта при dб0,5DБ, на рис. 1б – для 2-го варианта при dб>0,5DБ.
Анализ зависимости эксцентриситета rе от диаметров DБ и dб позволил получить семейство графиков функции rе=f(dб) при различных значениях DБ и коэффициента длины барабана kL (рис. 2) (здесь значения rе взяты как средние значения из полученного диапазона rе при различных lОО1).
Как видно из приведённого графика, при увеличении внутреннего диаметра dб кольца изделий (что соответствует снижению коэффициента загрузки kз или увеличению степени деформации изделий при отжиме) величина эксцентриситета rе нелинейно увеличивается. При снижении же диаметра барабана DБ и коэффициента kL значения эксцентриситета rе растут.
Показано, что основными факторами, определяющими границы диапазона возможных случайных значений эксцентриситета центра масс изделий при отжиме, являются: соотношение геометрических параметров стирального барабана, режим его вращения и масса отжимаемых изделий.
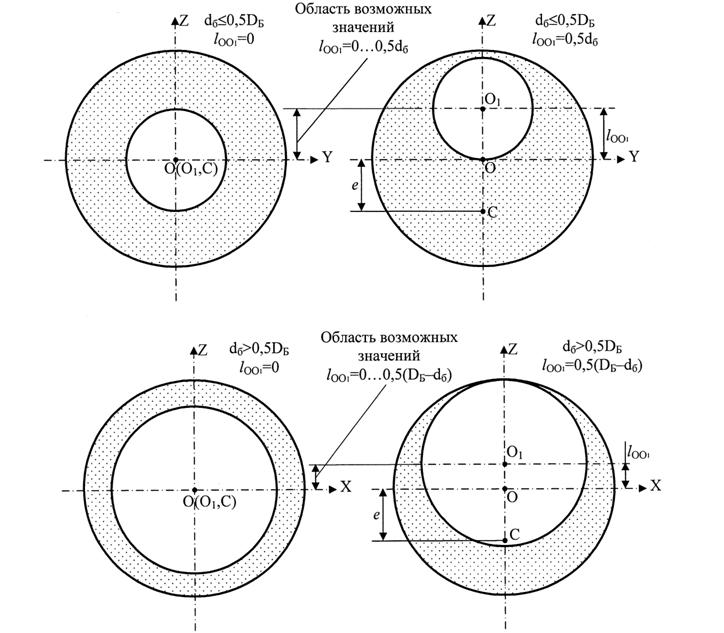
Рис. 1. Расположение кольца изделий в зависимости от соотношения DБ и dб
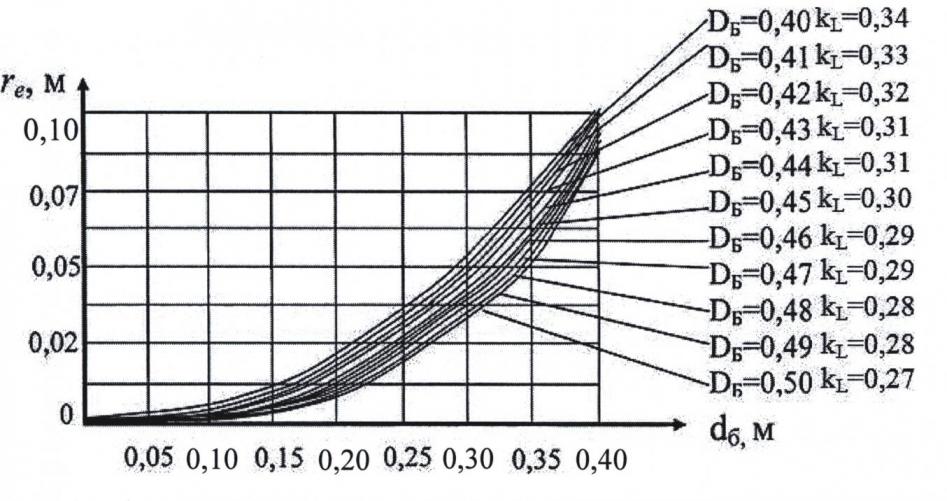
Рис. 2. Графики функции rе=f(dб) при различных DБ
В соответствии с общепринятой в настоящее время методологией описания процесса центробежного отжима, условно разделяемого на два периода, а также с учетом экспериментально полученной в диссертации функциональной зависимости коэффициента деформации изделий от приложенной нагрузки, были рассмотрены качественные изменения и получены формулы для определения частоты вращения барабана Б, влажности W и изменения усадки (деформации) ![]() ткани отжимаемых изделий, их массы mб и объёма Vб в период отжима.
ткани отжимаемых изделий, их массы mб и объёма Vб в период отжима.
Используя полученные формулы, были определены масса mб и объём Vб отжимаемых изделий за период отжима в стиральной машине с диаметром барабана DБ=0,45 м, длиной LБ=0,135 м, угловой скоростью Б=94,2 рад/с (nБ=900 мин-1) при различной загрузке машины mбо. Расчётные зависимости представлены на рис. 3 и 4.
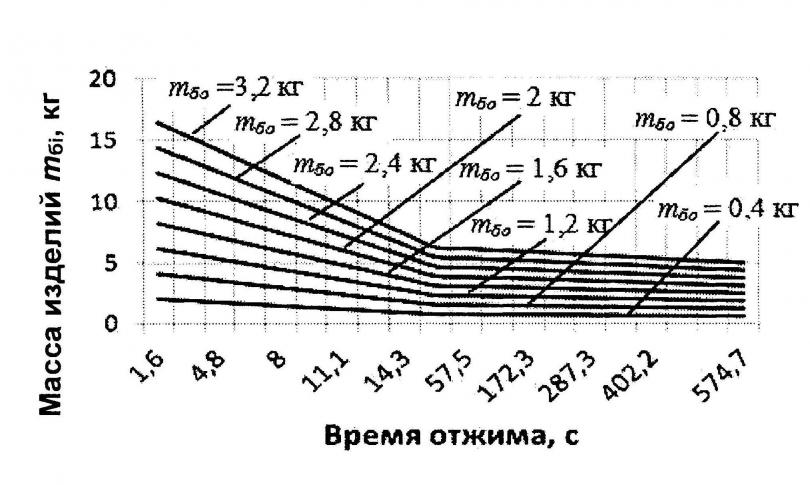 | 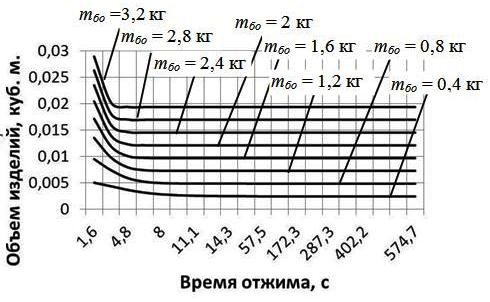 | ||
| Рис. 3. Изменение массы изделий mбi в период отжима при различных значениях загрузки машины mбо | Рис. 4. Изменение объёма изделий | ||
Полученные значения массы изделий являются одним из факторов, определяющих величину возмущающих сил, а объём изделий влияет на величину и диапазон эксцентриситета rе.
Расчётным путём получены диапазоны возможных случайных значений эксцентриситета rе, а также средние его значения при различных значениях загрузки машины mбо. Диапазоны и средние значения эксцентриситета rе при mбо=0,4 кг и mбо=3,2 кг показаны на рис. 5.
На рис. 6 приведены средние значения эксцентриситета rе для масс изделий mбо в интервале от 0,4 до 3,2 кг.
Анализ полученной функциональной зависимости эксцентриситета центра масс изделий от времени отжима и загрузки машины показал, что в течение процесса отжима происходит рост величины эксцентриситета, причём при значениях коэффициента загрузки барабана в диапазоне kз=0,5…0,8 на теоретических кривых зависимостей эксцентриситета rе имеются области с нулевым значением эксцентриситета, расположенные на начальном этапе разгона барабана от 0,3 до 0,8 с.
Здесь также показано значение эксцентриситета rе=0,08RБ=0,0018 м, полученное по традиционному методу расчёта, рассмотренного в первой главе диссертации. При сравнении полученных расчётных значений эксцентриситета со значением rе=0,018ем отклонение составило rе=0,014…0,033 м.
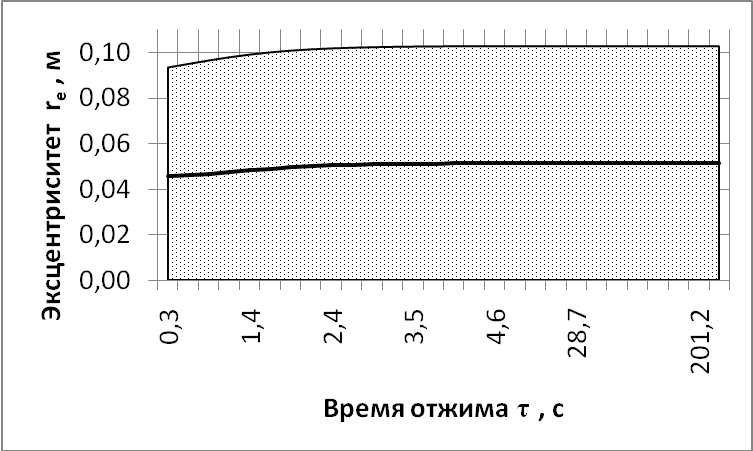
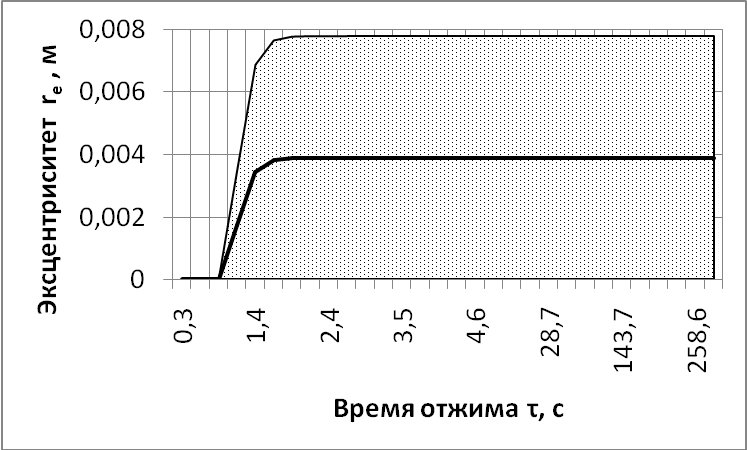
mбо=0,4 кг mбо=3,2 кг
Рис. 5. Зависимости эксцентриситета центра масс изделий rе
и диапазоны его возможных значений в период отжима
при различной массе изделий mбо
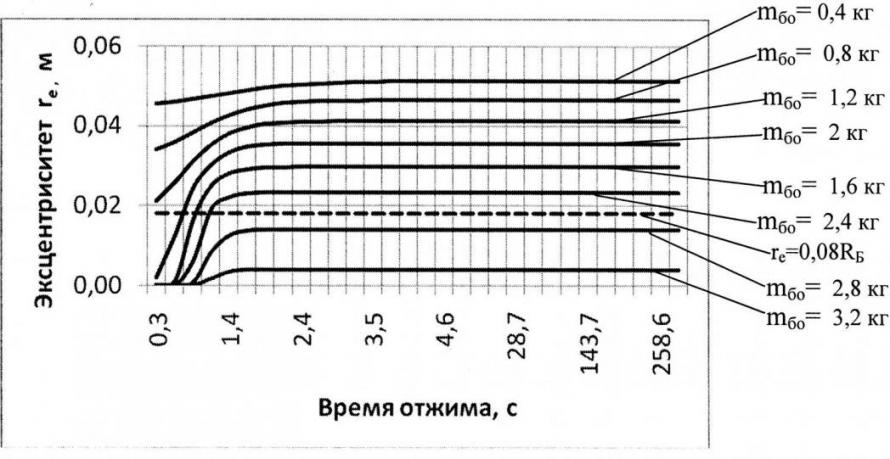
Рис. 6. Средние значения эксцентриситета центра масс изделий rе
в период отжима при различных значениях массы изделий mбо
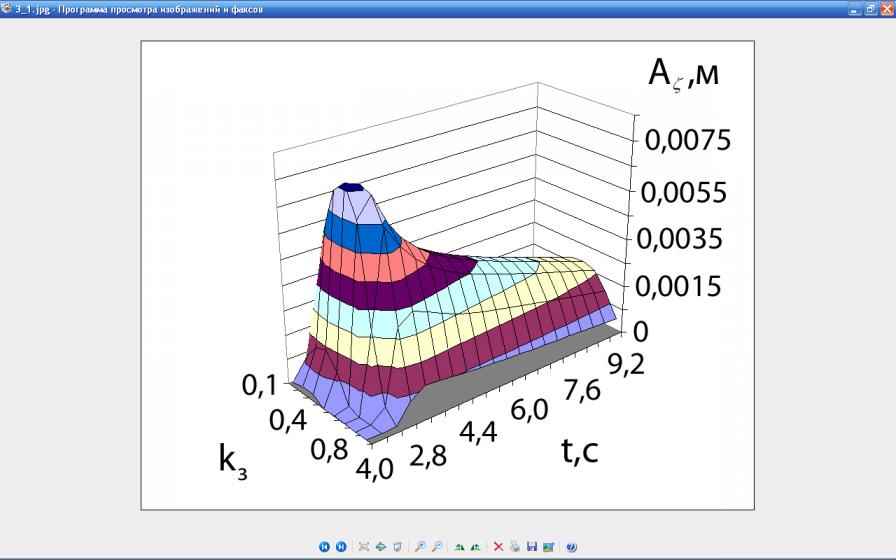
Используя средние значения эксцентриситета rе, были получены зависимости амплитуд случайных колебаний А и А подвесной части вдоль вертикальной и горизонтальной оси при различной загрузке машины mбо (коэффициенте загрузки барабана kз) и различных значений частоты вращения барабана Б. На рис. 7 показаны зависимости амплитуд случай-ных колебаний А и А при различных значениях kз и угловой скорости вращения барабана Б=94,2 рад/с.
Анализ зависимостей амплитуд колебаний показал, что значения амплитуд случайных колебаний определяются влиянием двух факторов, приводящим к локальному максимуму при kз=0,45, причём при 0kз0,45 рост амплитуд обусловлен увеличением загрузки, а при kз0,45 снижение амплитуд обусловлено уменьшением эксцентриситета центра масс отжимаемых изделий.
Обобщение и анализ полученных во второй главе диссертации результатов показал, что при одинаковых условиях загрузки и режима вращения барабана в каждом цикле процесса отжима текстильных изделий диапазон случайных значений возмущающих сил определяется случайными вариациями эксцентриситета центра масс изделий. Установлено, что диапазон случайных вариаций величины эксцентриситета зависит от коэффициента загрузки барабана kз и коэффициента длины барабана kL.

вдоль оси вдоль оси
Рис. 7. Зависимости амплитуд случайных колебаний А и А
подвесной части при различных значениях kз
и угловой скорости вращения барабана Б=94,2 рад/с
Таким образом, предложенный во второй главе диссертации алгоритм по определению диапазона случайных значений эксцентриситета центра масс отжимаемых изделий и соответствующего ему диапазона возмущающих сил позволяет проводить расчёты диапазона амплитуд случайных колебаний подвесной части стиральных машин.
В третьей главе приведены результаты экспериментальных исследований случайных воздействий на колебания подвесной части стиральной машины при центробежном отжиме.
С учётом необходимости использования зависимости деформации текстильных изделий от приложенной нагрузки при разработке алгоритма по определению диапазона значений эксцентриситета rе отжимаемых изделий и соответствующего диапазона возмущающих сил, были проведены экспериментальные исследования для установления функциональной зависимости коэффициента относительной деформации  изделий (где Но – толщина слоя изделий без нагрузки, Нi – толщина слоя изделий под нагрузкой рi) от приложенной нагрузки для условий различных традиционных наборов текстильных изделий разнообразных типов материалов и их массы.
изделий (где Но – толщина слоя изделий без нагрузки, Нi – толщина слоя изделий под нагрузкой рi) от приложенной нагрузки для условий различных традиционных наборов текстильных изделий разнообразных типов материалов и их массы.
На рис. 8 показано поле корреляции между полученными экспериментальными значениями коэффициента деформации и давлением и приведён график функции kотн=f(р).
При определении функции по средним значениям экспериментальных данных была получена следующая регрессионная зависимость:
kотн=0,5455 – 0,5461е-0,001033р, (7)
характеризуемая индексом корреляции R2=0,9998 и средней абсолютной процентной ошибкой аппроксимации МАРE=0,2046 %, что показывает добротность модели более 99 %.
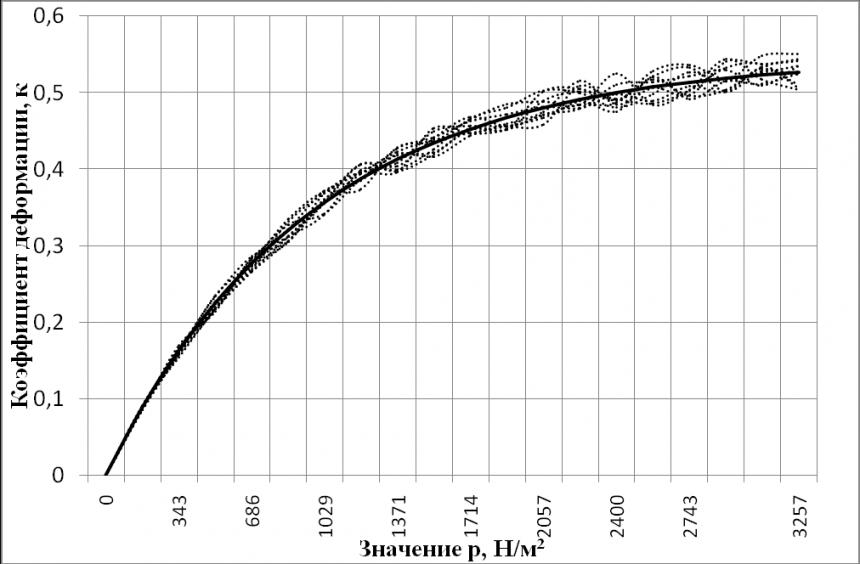
Рис. 8. Поле корреляции между значениями коэффициента деформации и давлением и график функции kотн=f(р)
Полученная зависимость kотн=f(р) позволяет прогнозировать расчётным путём диапазон возможных случайных значений эксцентриситета центра масс изделий и соответствующих возмущающих сил при математическом моделировании случайных колебаний подвесной части стиральных машин в процессе отжима.
В качестве объекта экспериментальных исследований случайных колебаний в данной диссертационной работе использовалась современная бытовая стиральная машина барабанного типа с фронтальной загрузкой Electrolux EWS 1105, колебательная система которой включает виброизоляцию (упруго-диссипативную подвеску) и подвесную часть машины (так называемый моечный узел).
Для определения виброперемещений подвесной части исследуемой стиральной машины в данной работе использовались бесконтактные вихретоковые датчики ДВТ60.20 серии Т-образных, предназначенных для измерения смещений большой амплитуды.
Датчики ДВТ60.20 применялись в комплексе с измерительным преобразователем ИП34, который предназначен для возбуждения обмотки вихретоковых датчиков и преобразования зазора между датчиком и контрольной поверхностью в пропорциональный унифицированный токовый сигнал (1–5 мА, 4–20 мА).
В качестве измерительной и регистрирующей аппаратуры использовался персональный компьютер со стандартным программным обеспечением: ОS Windows XP; MS Office 2007; L-Graph 2.10.
Для преобразования поступающего от датчиков сигнала на компьютер в комплексе с ним использовался внешний модуль АЦП/ЦАП цифрового ввода/вывода на шину USB модели Е14-140.
На рис. 9 показана схема измерительного комплекса экспериментальной установки.

Рис. 9. Схема измерительного комплекса экспериментальной установки:
1 – подвесная часть; 2, 3, 4, 5 – датчики смещений ДВТ60.20;
6, 7 – пружины подвески; 8, 9 – демпферы; ПК – персональный компьютер;
ИП – измерительный преобразователь ИП34;
АЦП/ЦАП – модуль Е14-140 цифрового ввода/вывода на шину USB;
ИПТ – источник постоянного тока Б5-47
При виброперемещениях подвесной части 1 машины сигнал от датчиков смещения 2, 3, 4, 5, формируемый с помощью измерительного преобразователя ИП, поступал через внешний модуль АЦП/ЦАП на шину USB персонального компьютера ПК для регистрации и записи амплитуд и частот колебаний.
Для экспериментального определения зависимости амплитуд случайных колебаний подвесной части от заданных величин внешних возмуща-ющих сил и сопоставления полученных результатов с теоретической базой данных и оценки адекватности математической модели с использованием установленных значений инерционных, упругих и диссипативных коэффициентов были проведены экспериментальные исследования колебаний подвесной части исследуемой стиральной машины с заданными величинами внешних возмущающих сил.
На рис. 10 и 11 приведены итоговые графики амплитуд колебаний подвесной части вдоль вертикальной оси и горизонтальной оси в зависимости от заданной величины центробежной силы Fц.эт и угловой скорости вращения барабана Б.
На графиках сплошной линией обозначены кривые, полученные по экспериментальным данным, а пунктирной линией – по теоретическим расчётам.
Сравнение теоретических и экспериментальных данных показало, что расхождение между ними составило не более 7,5 %, что говорит о хорошей сходимости результатов исследования и позволяет сделать выводы об адекватности разработанной математической модели случайных колебаний подвесной части стиральных машин барабанного типа.
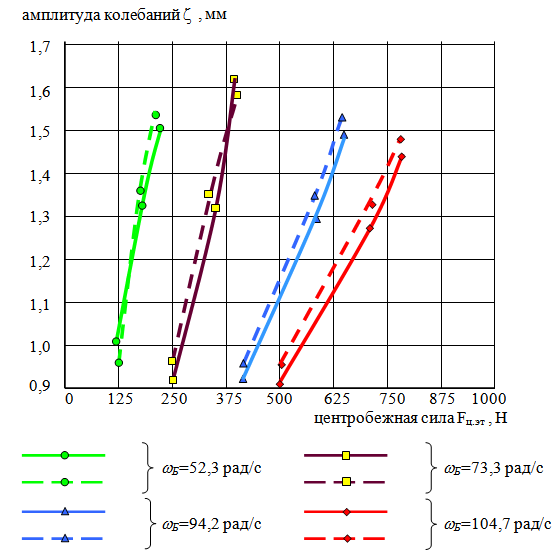
Рис. 10. Графики амплитуд колебаний подвесной части
вдоль вертикальной оси в зависимости от заданных значений
центробежной силы Fц.эт и угловой скорости вращения барабана Б
С целью экспериментального установления диапазона амплитуд случайных колебаний подвесной части, который при равных условиях загрузки стиральной машины и режима отжима определяется вероятностным характером распределения изделий по обечайке барабана, а соответственно, и величиной эксцентриситета центра масс отжимаемых изделий, проведены экспериментальные исследования колебаний подвесной части исследуемой стиральной машины при загрузке барабана текстильными изделиями, выбор которых производился аналогично проведению эксперимента при исследовании деформации изделий под нагрузкой.
На рис. 12 приведены диапазоны экспериментальных значений амплитуд колебаний А подвесной части вдоль вертикальной оси и амплитуд колебаний А подвесной части вдоль горизонтальной оси при загрузке барабана mбо=1,6 кг, при которой наблюдаются максимальные значения амлитуд колебаний, и угловой скорости вращения барабана Б= 94,2 рад/с при отжиме, а также графики математических ожиданий (сплошная линия) и средних теоретических значений амплитуд колебаний (пунктирная линия).
При статистической обработке полученных экспериментальных данных были определены математические ожидания и дисперсии амплитуд случайных колебаний подвесной части в течение всего периода отжима для каждой партии набора текстильных изделий. При этом среднее значение дисперсии составило 2,810-6 м2, а диапазон величин отклонений амплитуд колебаний от математических ожиданий составил 29…32 %.
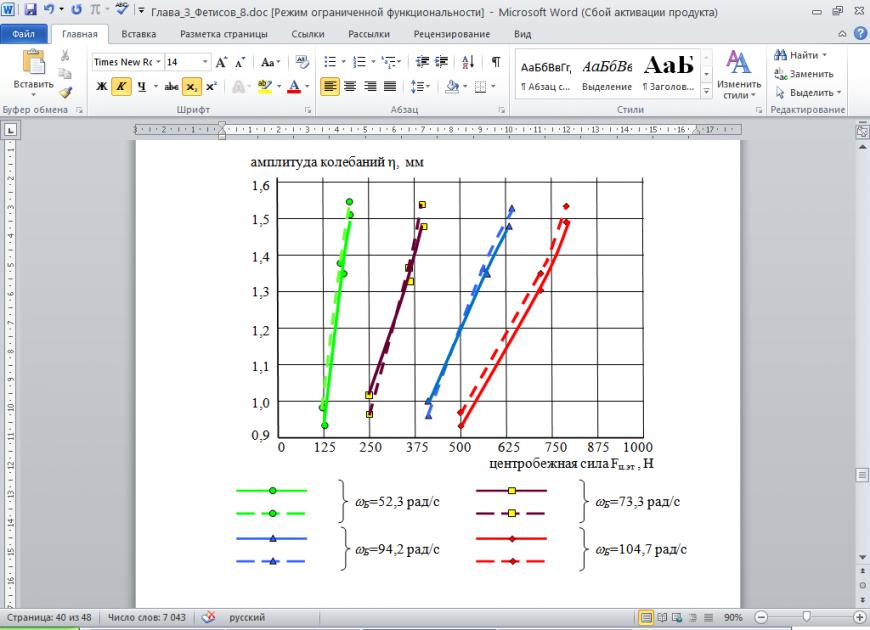
Рис. 11. Графики амплитуд колебаний подвесной части
вдоль горизонтальной оси в зависимости от заданных значений
центробежной силы Fц.эт и угловой скорости вращения барабана Б
Сравнение теоретических средних значений и математических ожиданий экспериментальных величин амплитуд колебаний на всём временном отрезке периода отжима для каждой партии набора текстильных изделий показало, что расхождение между ними не превышает 8 %.
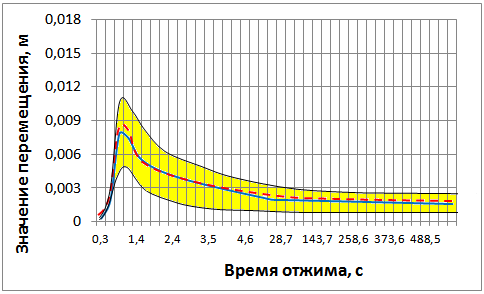
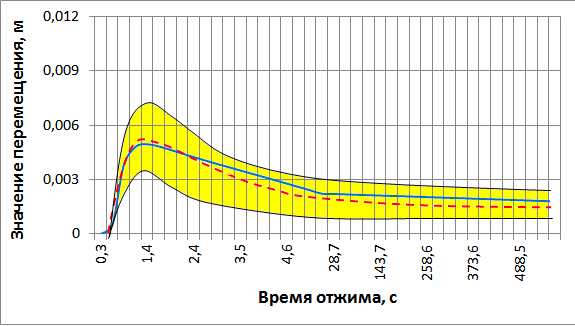
по вертикальной оси по горизонтальной оси
Рис. 12. Экспериментальные диапазоны
и графики математических ожиданий амплитуд случайных колебаний
в период отжима при загрузке mбо=1,6 кг
Эти данные подтверждают адекватность алгоритма определения эксцентриситета центра масс отжимаемых изделий в зависимости от величины массы изделий с учётом конструктивных параметров барабана и режима отжима.
В четвёртой главе диссертации представлены результаты теоретических исследований случайных колебаний подвесной части стиральных машин в зависимости от их конструктивных и режимных параметров при центробежном отжиме.
При этом был установлен характер и определены средние и максимальные значения амплитуд случайных колебаний подвесной части в зависимости от коэффициента длины барабана kL, жёсткости пружин подвески спр и коэффициента диссипации демпферов kд с учётом диапазона значений загрузки машины mбо=0,4…3,2 кг.
Представленные ниже графики исследуемых зависимостей отражают колебания подвесной части вдоль вертикальной оси при mбо=1,6 кг, что соответствует коэффициенту загрузки kз=0,45 и наибольшим амплитудам колебаний.
На рис. 13 приведены графики зависимостей средних и максимальных значений амплитуд колебаний А, полученные для исследуемого диапазона значений коэффициента длины барабана kL=0,2…0,9.
Анализ полученных данных показал, что глобальный минимум функции амплитуд колебаний с учётом всех значений массы изделий mбо из принятого диапазона при отжиме соответствует значению коэффициента длины барабана, равному kL=0,7.
Кроме этого, установлено, что наибольшее влияние на величину амплитуд колебаний коэффициент длины барабана kL оказывает в резонансной области колебательного процесса. Поэтому дальнейшая оценка поведения полученных функциональных зависимостей проводилась по средним и максимальным значениям амплитуд случайных резонансных колебаний.
На рис. 14 приведён график средних и максимальных значений амплитуд резонансных случайных колебаний А подвесной части при kL=0,2…0,9.
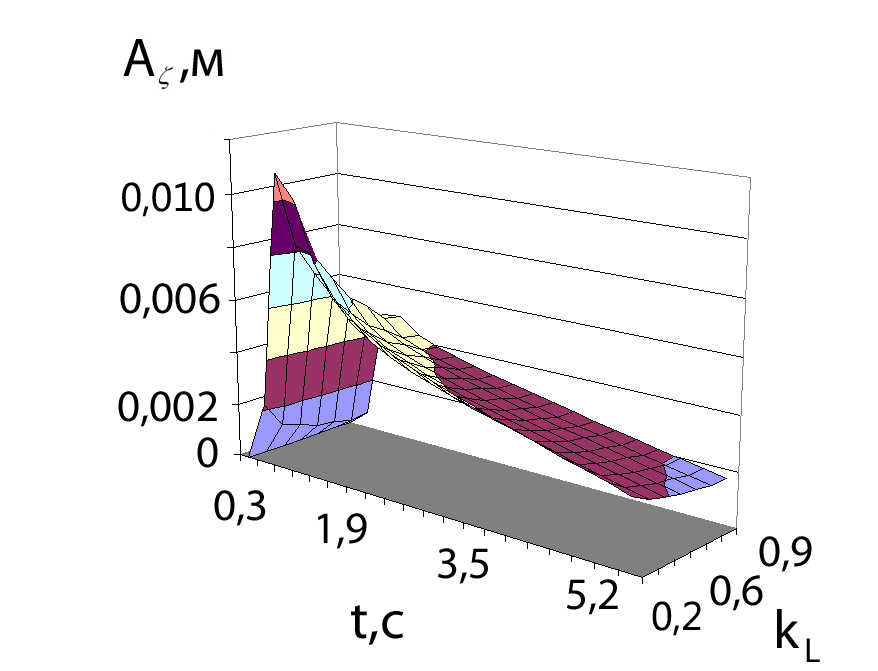 | 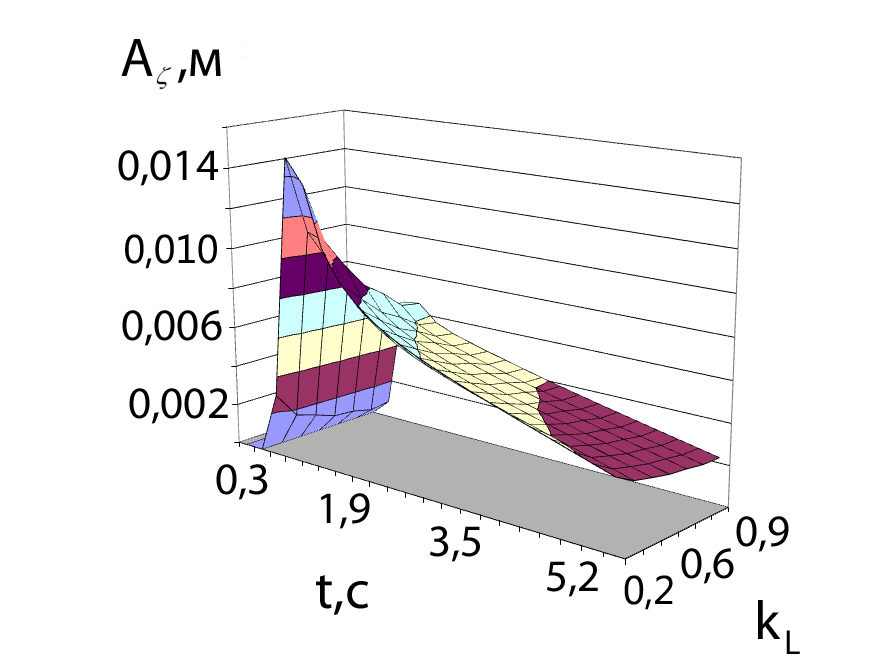 |
а) средние значения амплитуд б) максимальные значения амплитуд
Рис. 13. Амплитуды колебаний А подвесной части
при коэффициенте длины барабана kL=0,2…0,9
Анализ полученных данных показывает, что с учётом максимальных значений из диапазона амплитуд случайных колебаний подвесной части ширина исследуемого диапазона значений коэффициента длины барабана, соответствующего средним значениям амплитуд колебаний, сужается на величину kL=0,1 от kL=0,2 до kL=0,3 и на величину kL=0,24 от kL=0,2 до kL=0,44 в зависимости от установленного уровня колебаний подвесной части машины.
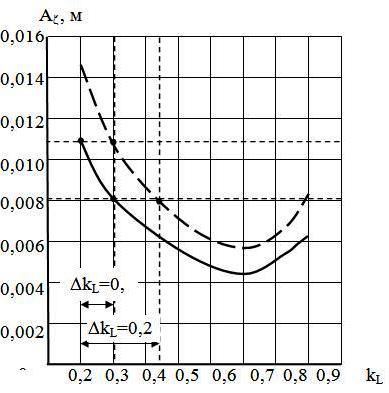
Рис. 14. График средних (сплошная линия) и максимальных (пунктирная линия) значений амплитуд резонансных случайных колебаний А
в зависимости от коэффициента длины барабана kL
На рис. 15 приведены графики зависимостей средних и максимальных значений амплитуд колебаний А в зависимости от диапазона значений жёсткости спр=1000…10000 Н/м, что соответствует диапазону собственной частоты колебаний подвесной части о=5,9…18,7 рад/с (179,1…178,7 мин-1).
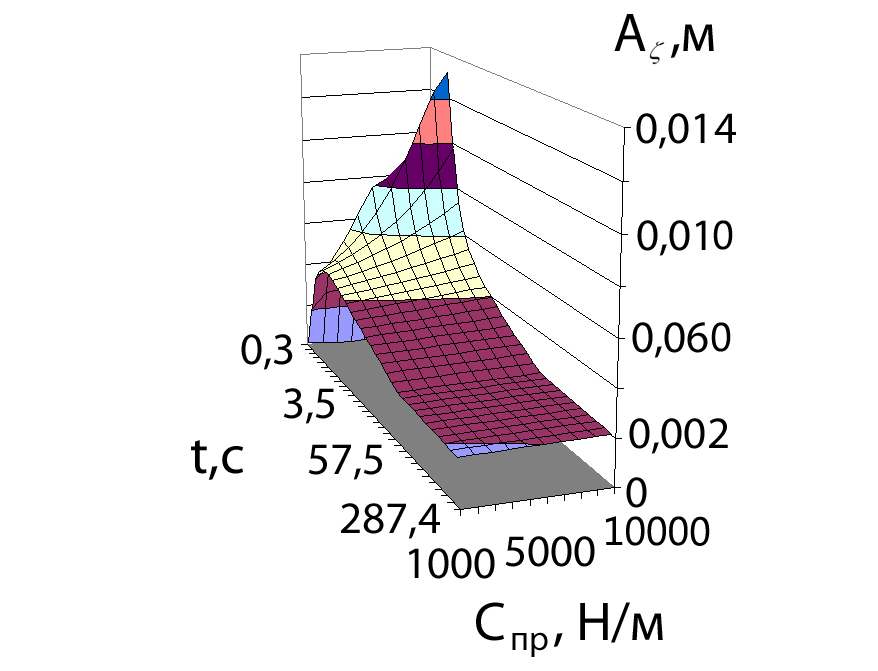 | 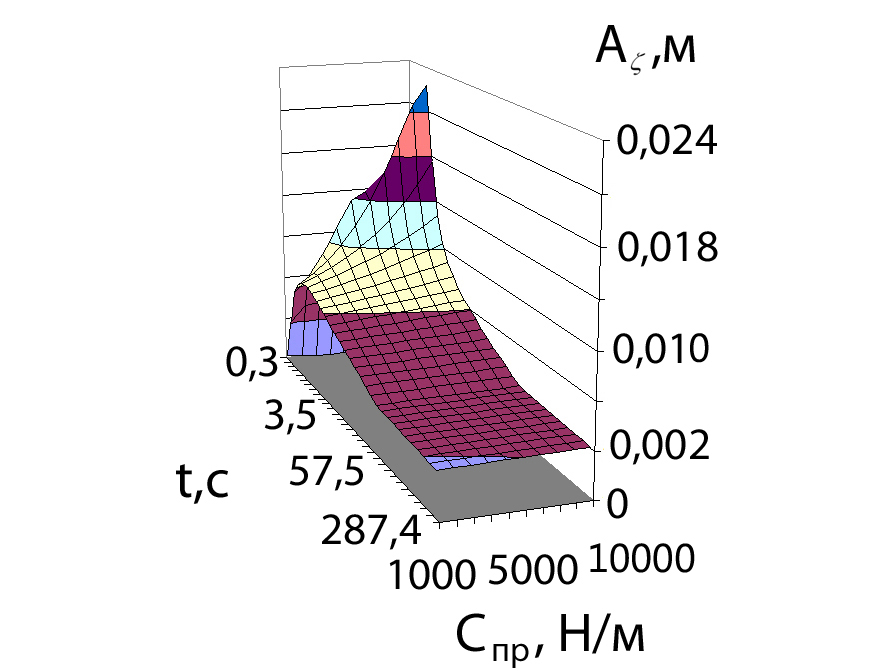 |
а) средние значения амплитуд б) максимальные значения амплитуд
Рис. 15. Амплитуды колебаний А подвесной части
в зависимости от жёсткости пружин подвески спр
Так как наибольшее влияние на величину амплитуд колебаний жёсткость спр оказывает в резонансной области колебательного процесса, то дальнейшая оценка поведения полученных функциональных зависимостей проводилась по средним и максимальным значениям амплитуд случайных резонансных колебаний.
На рис. 16 приведён график средних и максимальных значений амплитуд резонансных случайных колебаний А подвесной части при спр=1000…10000 Н/м.
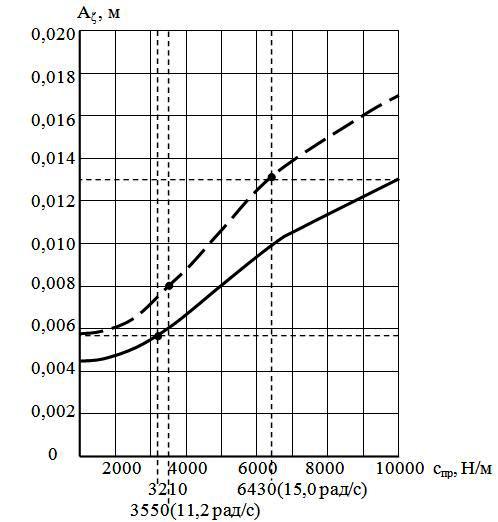
Рис. 16. График средних (сплошная линия) и максимальных (пунктирная линия) значений амплитуд резонансных случайных колебаний А
в зависимости от жёсткости упругих элементов подвески cпр
Анализ полученных зависимостей показал, что с учётом максимальных значений из диапазона амплитуд случайных колебаний подвесной части ширина исследуемого диапазона значений жёсткости упругих элементов подвески, соответствующего средним значениям амплитуд колебаний, сужается от 1000…10000 Н/м до 1000…6430 Н/м в зависимости от установленного уровня колебаний подвесной части машины.
Как показывает практика, снижение жёсткости спр упругих элементов в период разгона барабана приводит к соударениям подвесной части о корпус машины, в связи с чем нижний предел диапазона значений жёсткости необходимо ограничивать. С учётом этого, рекомендуемый диапазон значений жёсткости составляет спр=3550…6430 Н/м, что соответствует собственной частоте колебательной системы 11,2…15,0 рад/с (107,0…143,3 мин-1).
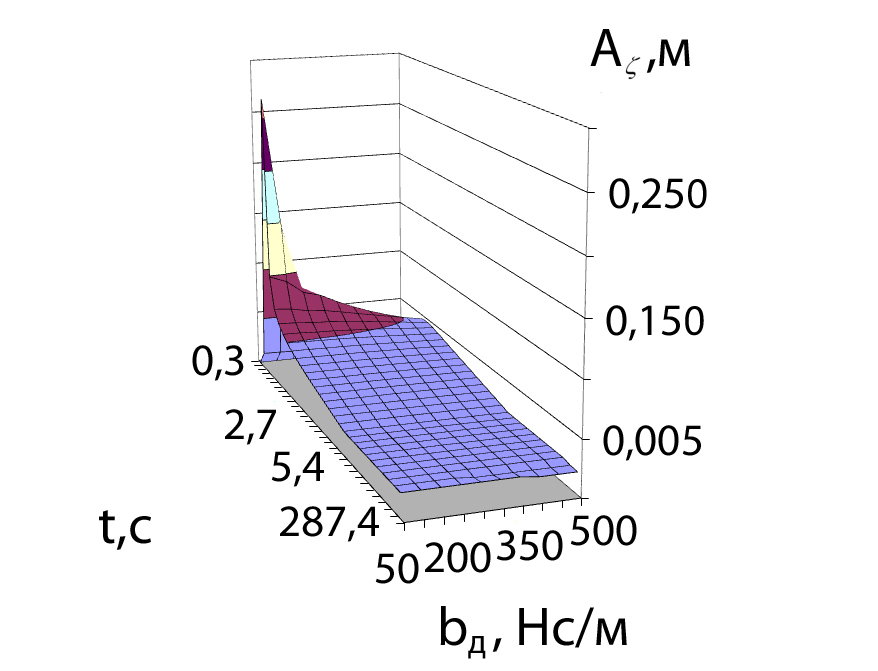
На рис. 17 приведены графики зависимостей средних и максимальных значений амплитуд колебаний А в зависимости от диапазона значений коэффициента диссипации kд=50…500 Нс/м.
 |  |
а) средние значения амплитуд б) максимальные значения амплитуд
Рис. 17. Амплитуды колебаний А подвесной части
в зависимости от коэффициента диссипации демпферов kд
Так как наибольшее влияние на величину амплитуд колебаний коэффициент диссипации kд оказывает в резонансной области колебательного процесса, то дальнейшая оценка поведения полученных функциональных зависимостей проводилась по средним и максимальным значениям амплитуд случайных резонансных колебаний.
На рис. 18 приведён график средних и максимальных значений амплитуд резонансных случайных колебаний А в зависимости от коэффициента диссипации kд.
Анализ полученных данных показал, что с учётом максимальных значений из диапазона амплитуд случайных колебаний подвесной части ширина исследуемого диапазона значений коэффициента диссипации сужается на величину kд=45 Нс/м от kд=50…500 Нс/м до kд=95…500 Нс/м.
Для обеспечения амплитуд резонансных колебаний подвесной части не более 0,008 м, что соответствует виброускорению 71,0 м/с2 и виброскорости корпуса стиральной машины А=30 м/с, являющейся предельной для бытовых стиральных машин в соответствии с ГОСТ 8051–83, установлено, что коэффициент диссипации должен быть не менее kд182 Нс/м по данным графика средних амплитуд колебаний и не менее kд292 Нс/м по данным графика максимальных амплитуд колебаний, что соответствует сужению диапазона коэффициента диссипации для данных амплитуд колебаний kд=110 Нс/м от kд=182…500 Нс/м до kд=292…500 Нс/м.
Таким образом, для обеспечения виброускорения при колебаниях подвесной части аА71,0 м/с2 и, соответственно, виброскорости корпуса стиральной машины А30 м/с для исследуемой машины необходимо выполнение условия kд292 Нс/м.
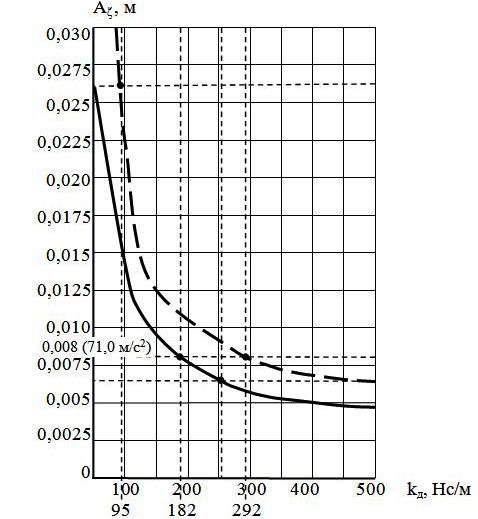
Рис. 18. График средних (сплошная линия) и максимальных (пунктирная линия) значений амплитуд резонансных случайных колебаний А
в зависимости от коэффициента диссипации демпферов kд
Полученные в работе результаты рекомендуются для использования при выборе рациональных конструктивных параметров стирального барабана и системы виброизоляции, обеспечивающих снижение виброактивности стиральных машин барабанного типа.
ОСНОВНЫЕ РЕЗУЛЬТАТЫ И ВЫВОДЫ
1) Анализ работ, посвящённых исследованию динамики стиральных машин, показал, что для повышения эффективности виброзащитных систем выбор их рациональных параметров должен проводиться с учётом стохастического характера колебаний, который определяется случайными внешними воздействиями на подвесную часть машин при отжиме.
2) Доказана целесообразность учёта случайных внешних воздействий на колебания стиральных машин барабанного типа для повышения обоснованности и точности при исследовании их динамики.
3) Установлено, что диапазон случайных возможных значений эксцентриситета центра масс отжимаемых изделий зависит от коэффициента загрузки стирального барабана kз и коэффициента длины барабана kL.
4) Разработан алгоритм теоретического определения диапазона возможных значений эксцентриситета центра масс отжимаемых изделий и возмущающих сил и исследован диапазон амплитуд случайных колебаний подвесной части стиральных машин при отжиме.
5) Установлено, что на теоретических кривых зависимостей эксцентриситета rе при значениях коэффициента загрузки барабана в диапазоне kз=0,5…0,8 наблюдаются области с нулевым значением эксцентриситета rе=0.
6) Получена зависимость амплитуд случайных колебаний подвесной части от загрузки машины с учетом изменения эксцентриситета центра масс отжимаемых изделий rе. При этом максимум амплитуд случайных колебаний подвесной части наблюдается при kз=0,45, причем при 0kз0,45 рост амплитуд обусловлен увеличением загрузки, а при kз0,45 снижение амплитуд обусловлено уменьшением эксцентриситета центра масс отжимаемых изделий.
7) Экспериментально установлен диапазон амплитуд случайных колебаний подвесной части стиральных машин в зависимости от диапазона случайных значений эксцентриситета центра масс изделий при отжиме. При этом среднее значение дисперсии составило 2,810-6 м2, а диапазон величин отклонений амплитуд колебаний от математических ожиданий составил 29…32 %.
8) С учётом максимальных значений амплитуд случайных колебаний подвесной части стиральных машин для обеспечения установленного уровня вибрации рекомендуется принимать значения жёсткости упругих элементов подвески, соответствующие диапазону собственной частоты колебательной системы 11,2…15,0 рад/с, значения коэффициента диссипации демпферов, обеспечивающие виброускорение при колебаниях подвесной части аА71,0 м/с2, а значения коэффициента длины барабана в диапазоне kL=0,44…0,9.
9) Результаты исследования рекомендуются для использования в проектно-конструкторских организациях, на предприятиях по изготовлению, эксплуатации и сервисному обслуживанию стиральных машин, а также в учебном процессе при подготовке высококвалифицированных специалистов в области проектирования и сервиса бытовых машин и приборов.
Основные результаты диссертации изложены в следующих работах
Статьи в ведущих рецензируемых научных журналах
- Алёхин, С.Н. Расчёт энергетических характеристик полезных сопротивлений при вращении барабана / С.Н. Алехин, А.А. Калашников, И.В. Фетисов, Д.П. Махов, А.С. Алёхин // Обзорно-аналитический, научно-техни-ческий и производственный журнал. Технология машиностроения. – 2010. – № 8(98).– 80 с.– С. 40–44.
- Фетисов, В.Г. Исследование процесса колебаний подвесной части стиральной машины при случайных воздействиях / В.Г. Фетисов, С.Н. Алёхин, И.В. Фетисов, А.С. Алёхин // Научно-технический и производственный журнал. Швейная промышленность. – 2010. – № 3. – 50 с. – С. 46–47.
- Алёхин, С.Н. Теоретический расчёт амплитуд случайных колебаний подвесной части стиральных машин при отжиме / С.Н. Алехин, В.Г. Фетисов, С.П. Петросов, И.В. Фетисов, А.С. Алёхин // Научно-технический вестник Поволжья. – Казань : Научно-технический вестник Поволжья. – 2011. – № 3. – 202 с. – С. 44–48.
- Фетисов, И.В. Влияние переходного режима при разгоне барабана на уровень амплитудных значений виброперемещений / И.В. Фетисов // Технология машиностроения.– 2011. – № 5.– С. 45–47.
Публикации в журналах, сборниках трудов, материалах конференций
- Алёхин, С.Н. Особенности формирования случайных внешних воздействий на подвесную часть стиральных машин барабанного типа при отжиме / С.Н. Алёхин, И.В. Фетисов // Сборник докладов Международной конференции «Математическое моделирование и дифференциальные урав-нения». – Владикавказ : ВНЦ РАН и РСО-А. – 2010.– 267 с.– С. 248–250.
- Алёхин, С.Н. Исследование параметров текстильных изделий при отжиме / С.Н. Алёхин, И.В. Фетисов, А.С. Алёхин // Казанская наука: сборник научных статей. – Казань : Казанский Издательский Дом. – 2011. – № 2. – 315 с.– С. 23–25.
- Математическое моделирование снижения виброактивности стиральных машин барабанного типа методом дискретизации : монография / В.Г. Фетисов, С.Н. Алёхин, Д.П. Махов, И.В. Фетисов, А.С. Алёхин. – ГОУ ВПО «Южно-Российский гос. ун-т экономики и сервиса». – Шахты : ГОУ ВПО «ЮРГУЭС», 2009. – 135 с.
- Фетисов, В.Г. Математическое моделирование и исследование процесса оптимальной фильтрации случайных колебаний подвесного блока стиральной машины / В.Г. Фетисов, С.Н. Алёхин, И.В. Фетисов // Математическое моделирование, компьютерные и информационные технологии в технике, экономике и образовании : сб. трудов общерос. науч.-практ. конф. – Невинномысск : Сев.-Кавказ. гос. ун-т. – 2009. – С. 62–65.
- Фетисов, В.Г. Метод статистической линеаризации нелинейных колебаний подвесного блока стиральной машины / В.Г. Фетисов, С.Н. Алёхин, И.В. Фетисов // Информационно-вычислительные технологии и их приложения : сборник статей XI Междунар. науч.-техн. конф. МНИЦ ПГСХА. – Пенза : РИО ПГСХА. – 2009. – 276 с. – С. 244–249.
- Фетисов, В.Г. Модельная задача о поведении подвесного блока стиральной машины, подверженного случайным воздействиям / В.Г. Фетисов, С.Н. Алёхин, И.В. Фетисов // Исследования по дифференциальным уравнениям и математическому моделированию : сборник трудов VII Междунар. конф. «Порядковый анализ и смежные вопросы математического моделирования» (Волгодонск, 24–29 августа 2009 года) / отв. ред. С.Б. Климентов, Е.С. Каменецкий. – Владикавказ : ВНЦ РАН и РСО-А. – 2009. – 156 с. – С. 137–143.
- Фетисов, И.В. Асимптотика поведения эксцентриситета центра масс изделий при отжиме / И.В. Фетисов, С.Н. Алёхин, А.С. Алёхин // Города России: проблемы строительства, инженерного обеспечения, благоустройства и экологии : сборник статей XII Междунар. науч.-техн. конф. МНИЦ ПГСХА. – Пенза : РИО ПГСХА. – 2010. – 168 с. – С. 149–152.
- Фетисов, И.В. Оптимизация параметров подвесной части стиральной машины при случайных воздействиях / И.В. Фетисов, С.Н. Алёхин, В.Г. Фетисов // Теория операторов, комплексный анализ и математическое моделирование : тезисы докладов междунар. науч. конф. (Волгодонск, Россия, 4–8 июля 2011 г.) РАН, Владикавказский научный центр, Южный математический институт. – Волгодонск : ВИС ЮРГУЭС, 2011. – 182 с. – С. 164–166.
- Фетисов И.В. Исследование случайных колебаний подвесной части стиральной машины барабанного типа / И.В. Фетисов, С.П. Петросов, С.Н. Алёхин, А.С. Алёхин // Аналитические и численные методы моделирования естественнонаучных и социальных проблем : сборник статей V Междунар. науч.-техн. конф. – Пенза : Приволжский Дом знаний, 2010. – 324 с. – С. 126–129.
Свидетельства о регистрации программного продукта
- Свидетельство об официальной регистрации программы для ЭВМ: №2011617524, РОСПАТЕНТ, 2011 / Программа расчета резонансной амплитуды колебаний барабана стиральной машины барабанного типа // Фетисов И.В., Калашников А.А., Алехин С.Н., Самоделов А.Н., Кузнецов А.Е.
- Свидетельство об официальной регистрации программы для ЭВМ: №2011617525, РОСПАТЕНТ, 2011 / Программа расчета эксцентриситета центра масс текстильных изделий в стиральных машинах барабанного типа // Фетисов И.В., Калашников А.А., Алехин С.Н., Самоделов А.Н., Кузнецов А.Е.
Личный вклад диссертанта в работах, опубликованных в соавторстве:
П.4 – подготовлен материал и написано 100 % работы;
П.2 – подготовлен материал и написано 80 % работы;
П.1,3,5,6 – предложена идея работы и написано 60 % работы;
П.7,8,9,10,11,12,13 – проведены расчёты, проанализированы исходные данные и результаты расчётов и написано 80 % работы.
ИД № 06457 от 19.12.01 г. Издательство ЮРГУЭС.
Подписано в печать 21.11.2011 г.
Формат 60x90/16. Усл. п.л. 1,75
Тираж 100 экз. Заказ № 579.
ПЛД № 65-175 от 05.11.99 г.
Типография Издательства ЮРГУЭС.
346500, г. Шахты, Ростовская область, ул. Шевченко,147

