Разработка научных основ управления вибрацией гидродинамического происхождения в центробежных насосах магистральных нефтепроводов

На правах рукописи

ПЕРЕВОЩИКОВ СЕРГЕЙ ИВАНОВИЧ

РАЗРАБОТКА НАУЧНЫХ ОСНОВ УПРАВЛЕНИЯ ВИБРАЦИЕЙ ГИДРОДИНАМИЧЕСКОГО ПРОИСХОЖДЕНИЯ В ЦЕНТРОБЕЖНЫХ НАСОСАХ МАГИСТРАЛЬНЫХ НЕФТЕПРОВОДОВ

Специальность 05.02.13 -

Машины, агрегаты и процессы (нефтяной и газовой отрасли)

Автореферат

диссертации на соискание ученой степени

доктора технических наук

Тюмень 2004

Работа выполнена в государственном образовательном учреждении высшего профессионального образования «Тюменский государственный нефтегазовый университет».

Официальные оппоненты: - доктор технических наук,

профессор Грачев Сергей Иванович

- Заслуженный деятель науки

и техники

Российской Федерации,

доктор технических наук,

профессор Поршаков

Борис Павлович

- доктор технических наук,

профессор Мороз

Александр Александрович

Научный консультант - Заслуженный деятель науки

Российской Федерации,

доктор технических наук,

профессор Шабаров

Александр Борисович

Ведущее предприятие: ОАО «Сибнефтепровод».

Защита состоится « 28 » декабря 2004 г. в 14 часов на заседании диссертационного совета Д 212.273.08 при Государственном образовательном учреждении высшего профессионального образования «Тюменский государственный нефтегазовый университет» (ТюмГНГУ) по адресу: 625000, Тюмень, ул. Володарского, 38.

С диссертацией можно ознакомиться в библиотеке ТюмГНГУ.

Автореферат разослан « 26» ноября 2004г.

Ученый секретарь

диссертационного совета Т.Г. Пономарева

ОБЩАЯ ХАРАКТЕРИСТИКА РАБОТЫ

Актуальность проблемы. Надежность и экономичность насосов, как любых машин и механизмов, определяется целым рядом факторов, в том числе условиями их эксплуатации и способностью адаптироваться к изменяющимся условиям работы. К числу факторов, наиболее неблагоприятно сказывающихся на надежности насосных агрегатов, относится повышенная вибрация. На долю отказов центробежных насосов по причине повышенной вибрации приходится 38-45 % всех отказов. Повышенная вибрация сказывается на техническом состоянии торцевых уплотнений и подшипников. Отказы этих узлов составляют 42-53 % от всех отказов насосов. Об этом свидетельствуют известные данные по результатам обследования 32 площадок насосных станций магистральных нефтепроводов с 108 насосами типа НМ 10000-210.

Вибрация насосных агрегатов вызывается причинами механического, электротехнического и гидродинамического происхождения. Наименее изучена и прогнозируема вибрация гидродинамического происхождения, возникающая при работе насосов на пониженных и повышенных подачах. При таких режимах работы происходит интенсивное динамическое воздействие на гидравлическую часть насосов, которое воспринимается механической частью и передается на подшипниковые узлы, корпус и фундаменты агрегатов. Данный вид вибрации сопровождается разрушением подшипников, смещением и биением валов, увеличением вибрации строительных конструкций и примыкающих к насосам трубопроводов. В наиболее тяжелых случаях имеет место разрушение рабочих колес и отводов, улиток крупных насосов и обвязывающих насосы трубопроводов. Следствием вибрации может являться также интенсивный гидроабразивный износ проточной части насосов, что влечет за собой снижение кавитационных характеристик и к.п.д. насосов с последующим ухудшением экономических показателей средств перекачки. Наиболее тяжелыми последствиями от гидродинамической вибрации насосов являются не только материальные потери от разрушения оборудования и временного прекращения транспорта перекачиваемой жидкости, но и значительный ущерб окружающей природе от разлива экологически агрессивных жидкостей из разрушенного оборудования и трубопроводов. Значительный вред повышенная вибрация оборудования несет и обслуживающему персоналу насосных станций, поскольку, как показывает практика, при возникновении вибрации она может превышать допустимые значения, предусматриваемые санитарно-гигиеническими нормами.

Тяжелые последствия от вибрации гидродинамического происхождения требуют дальнейшего более глубокого изучения ее природы. Особенно остро потребность в таком изучении возникла в трубопроводном транспорте нефти, где в связи с сокращением объемов транспорта нефти мощное высокопроизводительное оборудование вынужденно эксплуатируется с недогрузкой по производительности и испытывает вибрацию гидродинамической природы.

Целью диссертационной работы является создание расчетных моделей гидродинамической вибрации центробежных насосов и решение на этой основе крупной народно-хозяйственной проблемы – разработать способы снижения вибрации гидродинамического происхождения в центробежных насосах магистральных нефтепроводов, недогруженных по подаче.

Основные задачи исследований:

-исследовать влияние гидродинамических процессов в проточной части центробежных насосов на их энергетические характеристики;

-создать физическую модель гидродинамической вибрации центробежных и шнеко-центробежных насосов;

-разработать математическую модель гидродинамической вибрации в насосах центробежного и шнеко-центробежного типов;

-провести проверку полученной физико-математической модели гидродинамической вибрации центробежных и шнеко-центробежных насосов путем сопоставления результатов расчета с опытными данными соискателя и с экспериментальными данными других исследователей;

-на основе созданной модели разработать технические решения по снижению вибрации гидродинамического происхождения в центробежных и в шнеко-центробежных насосах, работающих с недогрузкой по подаче;

-выполнить апробацию разработанных технических решений на опытных данных, в том числе полученных в промышленных условиях на насосной станции магистрального нефтепровода.

Методологические основы и достоверность исследований

В диссертационной работе автором использованы классические положения механики по разделам динамики вращательного движения и вибрационных колебаний, классические положения гидродинамики, современные модели и методы расчета квазитрехмерного течения в межлопастном канале рабочего колеса, система интегральных уравнений пристенного слоя, методы системного анализа и теории размерностей. Достоверность результатов исследований подтверждается удовлетворительным совпадением расчетных значений с известными экспериментальными данными, а также с результатами собственных экспериментальных исследований.

Научная новизна диссертационной работы состоит в создании теории гидродинамической вибрации центробежных и шнеко-центробежных насосов, недогруженных по подаче. В работе:

1.Созданы научные основы теории вибрации гидродинамического происхождения в центробежных и шнеко-центробежных насосах, базирующейся на расчетном анализе полей давлений и переменных сил, действующих на рабочие лопасти насоса.

2.Предложена и обоснована физико-математическая модель периодически-квазитрехмерного турбулентного течения вязкой жидкости в рабочих колесах насосов с несимметричным входным устройством.

3.На основе выполненного расчетно-теоретического исследования получена информация о пространственном распределении скоростей, давлений, периодических сил в рабочих колесах насосов магистральных нефтепроводов.

4.Разработан и экспериментально обоснован метод расчета вибрационных характеристик центробежных насосов с несимметричным входом на режимах пониженных подач.

5.Разработаны научно-обоснованные рекомендации по практическому снижению вибрации гидродинамического происхождения у недогруженных по подаче центробежных и шнеко-центробежных насосов.

6.Предложен и обоснован теоретически, на положениях гидродинамики, и опытными данными коэффициент кавитационного подобия центробежных насосов.

Практическая ценность работы заключается в предложении для практического использования технических решений, обеспечивающих насосам центробежного и шнеко-центробежного типов работу с допустимыми уровнями вибрации при эксплуатации их на магистральных нефтепроводах с пониженными объемами перекачки; в разработке методики расчета численных значений конструктивных параметров, создающих насосам условия работы с допустимым уровнем вибрации. Практическая ценность работы заключается также в разработке методики расчета характеристики центробежных насосов, раскрывающей зависимость между подачей насосов и развиваемым ими напором.

Предложенный коэффициент кавитационного подобия центробежных насосов, дает возможность при создании насосов рассмотренного типа обоснованно подходить к конструированию их проточной части, а при эксплуатации подобных машин – более обоснованно проводить модернизацию их конструктивных элементов.

Реализация работы. Результаты исследований и разработок, выполненных автором по гидродинамике центробежных насосов, и в первую очередь насосов магистральных нефтепроводов, нашли свое отражение в трех монографиях (1995г., 1997г. и 2002г.). По результатам работы были разработаны рекомендации для Нефтеюганского управления магистральных нефтепроводов ОАО «Сибнефтепровод» по снижению вибрации гидродинамического происхождения у насосов, работающих с пониженной подачей. Реализация рекомендаций дала годовой экономический эффект по подразделениям управления в 1060 тыс. руб. в ценах 1992 года.

Материалы, положенные в основу диссертации: результаты вибрационных испытаний насосов на действующей нефтеперекачивающей станции; акты вибрационных испытаний насосов магистральных нефтепроводов; результаты теоретических и экспериментальных исследований различных авторов по нестационарным процессам в проточной части центробежных насосов; нормативная документация по технической эксплуатации насосов магистральных нефтепроводов; каталоги и заводские характеристики насосов типа НМ, используемых в магистральном транспорте нефти; научные труды автора, опубликованные при работе над диссертацией за период 1981-2004г.г.; опубликованные работы других авторов, положенные в основу анализа состояния и существа проблемы и использованные для создания методологического подхода к ее решению.

На защиту выносятся: 1.Модель и метод определения вибрационных характеристик гидродинамического происхождения центробежных и шнеко-центробежных насосов, работающих с недогрузкой по подаче. 2.Метод расчета параметров потока в рабочих колесах и переменных гидродинамических сил на основе периодически-квазитрехмерной модели течения.

3.Методика расчета потерь напора в проточной части центробежных насосов и методика расчета напорной характеристики подобных насосов.

4.Коэффициент кавитационного подобия центробежных насосов.

5.Результаты расчетно-экспериментального исследования центробежных насосов магистральных нефтепроводов.

6.Рекомендации по способам снижения вибрации гидродинамического происхождения в недогруженных по подаче центробежных и шнеко-центробежных насосах, основанные на результатах выполненного расчетно-экспериментального исследования.

Апробация работы. Основные положения диссертационной работы и результаты исследований представлялись к обсуждению на научно-технических и научно-практических конференциях, семинарах и совещаниях различного уровня:

-регионального: семнадцатой научно-технической конференции, посвященной 35-летию ТюмГНГУ (г.Тюмень, 1998г.); научно-технической конференции “Научные проблемы Западно-Сибирского нефтегазового региона: гуманитарные, естественные и технические аспекты» (г.Тюмень, 1999г.), девятом, десятом и одиннадцатом Межотраслевом научном и методологическом семинаре под руководством Заслуженного деятеля науки РФ проф. Шабарова А.Б. (г. Тюмень, 2002, 2003, 2004 г.г.);

- Российского и международного: межгосударственной научно-практической конференции “Нефть и газ Западной Сибири. Проблемы добычи и транспортировки” (г. Тюмень, 1993г.), международной научно-практической конференции «Безопасность жизнедеятельности в Сибири и на Крайнем Севере» (г.Тюмень, 1997 г.), международном совещании “Проблемы магистрального и промыслового транспорта углеводородов” (г.Тюмень, 2000г.), международном совещании “Энергоресурсосберегающие технологии в нефтегазовой промышленности России” (г. Тюмень, 2001 г.), международном семинаре “Геотехнические и эксплуатационные проблемы нефтегазовой отрасли” (г. Тюмень, 2002г.), международной научно-практической конференции “Проблемы эксплуатации транспортных систем в суровых условиях” (г.Тюмень, 2002г.).

Публикации. По результатам выполненных исследований опубликовано 39 печатных работ, среди которых три монографии.

Структура и объем работы. Диссертация состоит из введения, семи глав, выводов, списка литературы и 6 приложений. Работа изложена на 347 страницах машинописного текста, содержит 69 рисунков и 28 таблиц. Библиография включает 204 наименования работ отечественных и зарубежных авторов.

ОСНОВНОЕ СОДЕРЖАНИЕ РАБОТЫ

Во введении приводится обоснование актуальности проблемы, которой посвящена диссертационная работа, формулируются цель, задачи и основные направления исследований.

В первой главе диссертации анализируются результаты исследований отечественных и зарубежных авторов в области гидродинамической (технологической) вибрации центробежных насосных агрегатов и в смежных с ней областях, данные промышленных виброиспытаний насосов на действующих нефтепроводах. Анализируются опубликованные работы по изучению параметров потока в рабочих колесах центробежных насосов и работы по пульсациям давления в проточной части рассматриваемых насосов.

Гидродинамические процессы в проточной части лопастных машин, в том числе центробежных насосов, давно являются предметом исследований, начиная с Л.Эйлера. В этой области известны работы Башта Г.М., Грянко Л.П., Зимницкого В.А., Иванюшина В.А., Карелина В.Я., Касьянова В.М., Куфтова А.Ф., Ломакина А.А., Моргунова Г.Н., Наконечного Л.П., Овсянникова Б.В., Повх И.Л., Руднева С.С., Сироткина Я.А., Степанова Г.Ю., Черкасского В.М., Шабарова А.Б., Кamaraswamy S., Krischna R., Knapp R.T., Maray E., Barrett J.A., а также большого количества других исследователей. Много для изучения природы гидродинамических процессов в центробежных насосах магистральных нефтепроводов и, в частности, природы гидродинамической вибрации сделано Бражником В.П., Козобковым А.А., Колпаковым Л.Г., Куценко В.А., Писаревским В.М., Чернышевым Э.А., Шильманом А.Х., Hurst N.W., Ballamy L.J., Geyer T.A. и другими.

Анализ работ перечисленных и других исследователей привел к следующим выводам:

1.Источниками вибрации гидродинамического происхождения центробежных насосов могут служить нестационарные явления, наблюдаемые как в системе “насос - внешняя сеть”, так и внутри самого насоса.

2.Нестационарные гидродинамические процессы в насосах, приводящие к существенным вибрациям, возникают при отклонении режимов работы насосов от оптимальных подач, как в сторону снижения, так и в сторону повышения.

3.Нестационарные гидродинамические процессы в насосах сопровождаются образованием турбулентных вихрей, которые являются следствием неравномерности полей скоростей и давлений потоков, и появлением в определенных режимах обратных токов.

4.Амплитуды и частоты пульсаций давления потоков в проточных частях насосов позволяют предполагать, что с понижением подач насосов вибрация вызывается преимущественно гидродинамическими нестационарными явлениями во входных частях рабочих колес насосов, а при повышении подач (сверх оптимальной) - гидродинамическими нестационарными явлениями на выходе колес. При этом нестационарные процессы на входе колес сопровождаются пульсациями давления с лопастной частотой, кратной количеству лопастей рабочего колеса насоса, а на выходе колес - с лопаточной частотой, кратной произведению лопастной частоты и количеству лопаток отвода.

Заключительная часть первой главы содержит анализ особенностей вибрации насосов магистральных нефтепроводов при их работе с недогрузкой по производительности. Для этого соискателем была собрана и проанализирована информация по результатам вибрационных испытаний насосов 9 нефтеперекачивающих станций Нефтеюганского управления магистральных нефтепроводов ОАО «Сибнефтепровод». Анализ показал, что у всех рассмотренных насосов во время испытаний повышенная вибрация регистрировалась только при их работе с пониженной подачей и на лопастной частоте. На всех остальных частотах, характерных для других причин, способных вызывать вибрацию, повышения уровня вибрации не наблюдалось.

Проведенный анализ работ, выполненных в рассматриваемой области, показал, что объективно существует определенная физическая связь между основными конструктивными параметрами и режимами работы насосов и уровнем вибрации насосных агрегатов при отклонении их режима работы от оптимального. Тот же анализ свидетельствует о том, что существующие по исследуемой проблеме работы, а также работы в смежных с ней областях, не вскрывают конкретных причин технологической вибрации центробежных насосов; имеющиеся в этом направлении исследования носят относительно фрагментарный характер с преимущественно эмпирическим уклоном, не имеют достаточной обобщающей теоретической базы. Такое состояние в исследовании рассматриваемой проблемы требует для достижения более действенных результатов подходить к решению исследуемого вопроса в первую очередь с теоретических позиций, основанных на современных гидродинамических моделях и методах расчета. Теоретический подход может быть реализован несколькими способами на основе нескольких моделей, отражающих реальные процессы с различной степенью адекватности. К числу таких моделей относятся: квазиодномерная модель; модель, основанная на теории пограничного слоя (пространственное невязкое течение в межлопастных каналах, вязкое пристенное течение); модель, основанная на теории «трех моделей» (пространственное квазивязкое течение в межлопастных каналах, деформация характеристик турбулентности в найденном поле скоростей, вязкое безотрывное и отрывное пристенное течение); модель, основанная на трехмерных уравнениях Рейнольдса. Исходя из характера поставленных в работе задач, их решение осуществлялось с использованием двух моделей - квазиодномерной модели и модели, основанной на теории «трех моделей». Первую из них отличает простота использования, что необходимо для инженерной практики, вторую – необходимый научный уровень, так как в его основу положены современные достижения, как в области физики гидродинамических процессов, так и в сфере математического описания данных процессов. Одновременно с этим названный вариант отличается сравнительно небольшой трудоемкостью. Отмеченные варианты модели рассмотрены в главах 2 и 3 настоящей работы.

Вторая глава посвящена расчету гидравлических потерь энергии в элементах проточной части центробежных насосов. Рассмотрение только гидравлических потерь энергии обусловлено целями и задачами данного исследования.

Анализ опубликованных работ по оценке гидравлических потерь энергии в центробежных насосах показывает, что большинство исследователей, результаты работ которых приводятся, в частности, в публикациях Ибатулова К.А., Касьянова В.М., Черкасского В.М, Куфтова А.Ф., Сальникова С.Ю. и многих других, при определении потерь напора в лопастных нагнетательных машинах ограничивается рассмотрением квазиодномерной модели течения, базирующейся на системе уравнений, включающей уравнение неразрывности, уравнение Бернулли, уравнение, отражающее закон изменения момента количества движения, а также на обобщенных в аналитической форме данных о потерях напора в элементах проточной части машин.

В данной главе проводится анализ ранее созданных расчетных зависимостей для нахождения различных видов гидравлических потерь энергии в центробежных насосах по существующей их классификации и выполняется разработка более совершенной методики определения этих видов потерь напора с целью получения более точной информации для поиска конкретных причин вибрации гидродинамического происхождения.

Снижение напора насоса (без энергетических потерь) в результате инерционного движения жидкости в межлопастных каналах рабочего колеса найдено в виде идентификационого параметра , учитывающего уменьшение теоретического вектора скорости инерционным движением жидкости

=, (2.1)

где ; ;

;

- идентификационный параметр, учитывающий инерционное движение жидкости в межлопастных каналах, который при ориентировочных инженерных расчетах может приниматься в пределах 0,92-0,93; остальные величины – параметры, характеризующие геометрические размеры рабочего колеса и его межлопастных каналов, а также величины, входящие в уравнение Л.Эйлера.

Параметр позволяет рассчитывать теоретический напор насоса с учетом инерционного движения жидкости в межлопастных каналах рабочего колеса НТЦ. по формуле

= . (2.2)

Для расчета потерь напора в рабочем колесе от протекающих в нем гидродинамических процессов получена зависимость

, (2.3)

где - идентификационный параметр, учитывающий степень диссипации энергии от взаимодействия различных видов движения жидкости в межлопастных каналах;

;

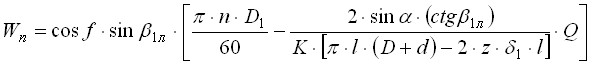f– угол наклона лопастей к дискам рабочего колеса; - угол между лопастью и направлением инерционного движения жидкости в межлопастном канале, находится по эмпирической зависимости

.

Потери напора в отводе находились как сумма потерь от контакта потока с входной кромкой «языка» отвода и потерь, происходящих при движении потока в расширяющемся канале отвода. Для расчета потерь напора от контакта с входной кромкой «языка» отвода получена зависимость

, (2.4)

где = ; - угол наклона вектора абсолютной скорости потока на выходе рабочего колеса; - угол скоса входной кромки «языка» отвода; PD1 - потери давления от вязкостного отрывного течения жидкости в пристенной области у входной кромки «языка» отвода.

Потери напора от расширения потока в отводе согласно выполненным исследованиям определяются зависимостью

, (2.5)

где - угол наклона вектора абсолютной скорости потока на выходе рабочего колеса; - угол наклона стенки спирального отвода или направляющих лопаток отвода; - отношение площади проходного сечения нагнетательного патрубка насоса к площади проходного сечения рабочего колеса на его выходе; PD2 - потери давления от вязкостного отрывного течения жидкости в пристенной области отвода.

Численные значения параметров и PD1 и PD2, входящих в зависимости для расчета , и , определить с достаточной для практики точностью затруднительно. Поэтому потери напора от вязкостного отрывного течения находились сразу для всей проточной части насоса, то есть интегрально. Ставилась задача замыкания проведенных исследований по гидравлическим потерям в насосе на базе энергетического баланса.

Проведенные исследования позволили получить следующую зависимость общего вида для расчета потерь напора от вязкостного отрывного течения жидкости в пристенной области проточной части насоса:

, (2.6)

где - коэффициент гидравлического сопротивления проточной части насоса; FН – площадь поперечного сечения потока (на выходе отвода); bT –идентификационный параметр, учитывающий вихревой характер течения жидкости 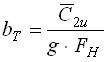; - скорость «вихревого» потока на входе в отвод. Для расчета и bT получены эмпирические зависимости, аппроксимирующие опытные данные для большинства насосов нормального ряда НМ, применяемых в магистральном транспорте нефти.

Заключительный раздел второй главы содержит расчет напорных характеристик насосов по полученным зависимостям на основе формулы

(2.7) и последующее сравнение результатов расчета с опытными характеристиками:

, (2.7)

где - расчетное значение действительного напора насоса;, и - соответствующие потери напора, рассчитываемые без учета потерь в пристенной области, то есть при и PD1 = PD2 = 0. Сравнение расчетных данных с опытными показало, что погрешность расчета напора для насосов, характеристики которых использовались в ходе получения аппроксимирующих зависимостей для нахождения параметров , , и bT, составляет не более 3%. В целом выполненные во второй главе исследования приводят к следующим выводам:

1.На основе известных упрощенных подходов к расчету параметров потока в отдельных элементах проточной части насосов разработана методика квазиодномерного инженерного расчета потерь напора в центробежных насосах типа НМ, применяемых в магистральном транспорте нефти.

2.Расчет по предлагаемой методике для 7 насосов типа НМ ( НМ 2500-230; НМ 5000-210; НМ 7000-210; НМ 10000-210; НМ 10000-210(0,5); НМ 10000-210 (0,7); 10000-210 (1,25) и однотипного с ними по конструктивной схеме насоса 16НД 10х1 показал, что несмотря на сделанные допущения и предположения максимальная погрешность расчета не превысила 3%.

3.Квазиодномерный подход, давший приемлемые результаты в оценке гидравлических потерь в центробежных насосах, не может дать аналогичных результатов при решении задач оптимизационных, связанных с нахождением наиболее совершенной геометрической формы отдельных элементов проточной части насосов, так как не учитывает пространственной формы данных элементов.

4.Анализ рассмотренных в главах 1 и 2 квазиодномерных методов расчета показывает целесообразность перехода к моделям и методам расчета, учитывающим пространственный характер потока, чему посвящена глава 3.

Третья глава содержит разработку гидродинамической модели и метода расчета квазитрехмерного течения в межлопастном канале рабочего колеса центробежного насоса, в том числе модели периодически-квазитрехмерного потока. Создание модели периодически-квазитрехмерного потока проводилось на основе метода, разработанного Степановым Г.Ю. и его последователями, получившего наиболее широкое распространение в практике расчета и проектирования лопастных гидромашин. Вязкость среды учитывалась на основе теории пограничного слоя (Шлихтинг Г., Кутателадзе С.С., Леонтьев А.И, Лойцянский Л.Г., Дорфман Л.А., Шабаров А.Б., и др.) вблизи твердых поверхностей, ограничивающих элементы проточной части гидромашин. Дополнительно учитывались, с использованием обобщенных опытных данных, потери давления в радиальных зазорах и в двухгранных углах, образуемых поверхностью лопастей и меридиональными обводами проточной части.

По принятой к дальнейшим исследованиям модели рассматривалось пространственное установившееся течение несжимаемой вязкой среды, происходящим, согласно работ Степанова Г.Ю., по осредненным поверхностям тока S/1 и S/2, эквидистантным, соответственно, дискам и лопастям рабочего колеса насоса. Данное течение описывалось в цилиндрической системе координат в виде: уравнения движения в проекциях на оси координат и уравнения неразрывности.

Исходная система уравнений первой задачи об осесимметричном течении по осредненной поверхности тока записывалась, следуя Сироткину А.Я., в энергетической форме - посредством уравнения движения в проекции на радиус и уравнения неразрывности. При этом граничные условия для абсолютной и относительной скоростей и w, а также для давления P задавались на входном сечении в рабочее колесо как осесимметричные. Фактическое непостоянство полей параметров потока по окружной координате вблизи «языка» спирального подвода насоса перед входом в рабочее колесо устранялось на основе известных экспериментальных и расчетных данных, согласно которым такая неравномерность наблюдается в пределах угловой координаты , где - разница угловых координат рабочей и тыльной сторон лопастей рабочего колеса насоса. Это обстоятельство позволило в данной работе обосновать, разработать и предложить модель периодически-квазитрехмерного течения в межлопастных каналах центробежных насосов со средним расположением рабочего колеса и с «языком» в спиральном подводе. А на основе предложенной модели - разработать метод расчета параметров периодически- квазитрехмерных потоков.

«Язык» спирального подвода разбивает входное сечение рабочего колеса на две области - область I (в гидродинамической тени «языка») и область II (остальная часть входного сечения). При вращении колеса каждый межлопастной канал периодически попадает в гидродинамическую тень «языка» (область I), что влечет за собой столь же периодическое изменение гидродинамической ситуации в каждом канале.

Полагая, что в пределах областей I и II поток на каждом радиусе r имеет осредненные по угловой координатепараметры (скорость, давление P и угол входа ) для этих областей можно записать:

-область I

; ;

;

-область II

; ;

.

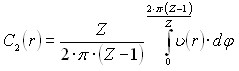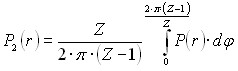В соответствии с выше изложенной гидродинамической моделью полагалось, что в пределах времени поток из области I поступает в рабочее колесо с параметрами , , , и , а за время поток из области II поступает в (Z-1) межлопастной канал рабочего колеса с параметрами , , , и . Эти значения принимались за граничные условия на входе в межлопастные каналы, число которых равно Z. При этом в один межлопастной канал поступает поток с параметрами, имеющими индекс 1 и в (Z-1) канал поступает поток с параметрами, имеющими индекс 2.

Характерный вид скорости, соответствующий областям I и II представлен на рис.3.1.

Рис.3.1.Характерный вид изменения скорости C при входе в рабочее колесо по угловой координате на радиусе r в сечении, нормальном оси вращения колеса

Предложенный метод расчета позволил определить параметры потока в рабочем колесе центробежного насоса и на этой основе переменные гидродинамические силы, действующие на лопасти рабочего колеса центробежного насоса при попадании их в зоны пониженных подач вблизи «языка» спирального подвода насоса, что и является ключевой задачей настоящего диссертационного исследования.

Разработка гидродинамической модели и метода расчета квазитрехмерного течения в межлопастном канале рабочего колеса центробежного насоса выполнялась на основе следующих условий:

1.Массовый расход в пределах каждого элемента проточной части постоянен. 2.Перестройка течения при обтекании всасывающей и напорной кромок лопастей, в том числе и изменение расхода жидкости, происходит в фиксированных контрольных сечениях на фиксированных координатных линиях, соответствующих входу и выходу рабочего колеса. 3. Потери энергии в элементах проточной части насоса учитываются энергетическим способом. При этом в рамках полного расчета загромождение проточной части пограничным слоем, образованным в результате потерь трения, учитывается дополнительным коэффициентом загромождения.

Для получения квази-трехмерной картины течения жидкости в рабочем колесе насоса рассматривалось течение на двух поверхностях – меридиональной и на поверхностях вращения. При этом учитывались потери энергии: в ядре потока - энергетически, в пристенном слое - от вязкого пристенного течения.

Перед началом расчета потока в патрубках и в лопастных решетках было проведено математическое описание области течения, являющейся одним из граничных условий для расчетных уравнений, также были определены параметры на входе в насос (давление Р, плотность и вязкость жидкости, объемный расход Q и частота оборотов ротора насоса n).

При рассмотрении течения в меридиональной плоскости в основу получения итоговых расчетных зависимостей были положены:

- условие равновесия частицы жидкости, находящейся в межлопастном канале вращающегося рабочего колеса

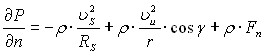; (3.3)

- уравнение расхода через две близкие осесимметричные поверхности тока

; (3.4)

- уравнение для момента силы стационарного течения

. (3.5)

Из уравнения (3.5) определяется сила Fn, входящая в (3.3) , затем из основного уравнения (3.3) исключается давление Р посредством уравнения (3.6), отражающего сохранение обобщенной энтальпии вдоль линии тока в пределах каждой лопастной решетки

, (3.6)

где . В результате получаются уравнения для расчета распределения абсолютной скорости потока в межлопастном канале, первоначально в естественной системе координат Z – r, затем - в полуфиксированной сетке координат L - S. Использовалась полуфиксированная сетка, распространенная в расчетной практике, состоящая их двух семейств криволинейных координатных линий.

Первое семейство подвижных координатных линий (ПКЛ) S было выбрано, совпадающим с расчетными линиями тока в данной итерации. Эти линии пересчитывались заново в каждой итерации.

Другое семейство неподвижных фиксированных координатных линий (ФКЛ) L выбиралось таким образом, чтобы они проходили через начальное сечение рабочего колеса, входную и выходную кромки лопастей колеса, а также через выходное сечение безлопаточного диффузора. Между этими сечениями, являющимися опорными, совпадающими с фиксированными координатными линиями, размещалось заданное количество N промежуточных фиксированных координатных линий. Их границы на периферийном (по переднему диску рабочего колеса) и втулочном (по основному диску колеса) сечениях меридионального контура выбирались из того условия, чтобы они были расположены равномерно по длине соответствующего сечения на расстоянии , где S - длина вдоль линии тока соответствующего элемента периферийного или втулочного сечений.

На основе уравнений в криволинейных координатах была составлена система уравнений для выполнения непосредственных расчетов. При этом использовались рекомендации Куфтова А.Ф. и Сальникова С.Ю., согласно которым для нахождения значения меридиональной составляющей абсолютной скорости в узле расчетной решетки, образованном пересечением i-той фиксированной координатной линией и j-той линией тока (подвижной координатной линией) численно интегрировалось уравнение

, (3.7)

а уравнение расхода (3.4) представлялось в виде:

,

где , , . Последнее условие равного расхода означает, что линии S, проведенные через соответствующие узлы фиксированных координатных линий L, образуют линии тока.

Для решения полученной системы уравнений была выбрана прямая итерационная схема, которая в настоящее время находит широкое применение при расчете течений. Каждое новое (K+1)-ое приближение скоростей по этой схеме определялось непосредственно из уравнения равновесия, а координаты линии тока вычислялись затем по найденному распределению скоростей из уравнения расхода. В качестве критерия сходимости итерационного процесса выбиралась величина максимальной погрешности во всех узлах расчетной сетки

; ; . (3.8)

Процесс расчета принимался завершенным, когда выполнялись следующие условия:

, , ,

где - заданная точность сходимости приближений.

По окончании итерационного процесса определялись локальные производные ,,, а также величины угла наклона и кривизны линий тока в каждом узле расчетной сетки. Вычисления всех производных производилось методом центральных разностей.

Решение второй двухмерной задачи выполнялось в полуфиксированной сетке координат согласно работ Степанова Г.Ю., Сироткина Я.А., Дорфмана Л.А., Подвидза Г.Л., Шабарова А.Б, Куфтова А.Ф., а также других исследователей.

Данная задача решалась приближенным методом расчета двухмерного установившегося течения невязкой жидкости на осесимметричной поверхности тока во вращающихся каналах заданной формы вне пристенной области, в которой проявляется вязкость жидкости. Рассматриваемое течение соответствует относительному течению жидкости в тонком слое переменной толщины на поверхности тока, которая предполагается совпадающей со средней поверхностью тока, определенной в процессе решения первой предельной задачи расчета осредненного осесимметричного течения жидкости.

В отличие от этих подходов, метод предложенный в данной работе заключается в том, что поток рассматривается периодически квазитрехмерным, то есть осесимметричные поверхности тока в разных межлопастных каналах могут отличаться, так как условия при входе в рабочее колесо за «языком» отличаются от условий вдали от него. Поэтому для соответствующего межлопастного канала проводится отдельный расчет течения на осесимметричной поверхности тока.

Для решения поставленной задачи использовались:

- уравнение равновесия частицы жидкости единичной массы (или уравнение вихрей), записанное для полуфиксированной сетки криволинейных координат

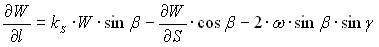, (3.9)

где - угол потока в относительном движении; ; ;

- уравнение расхода на осесимметричной поверхности тока

, (3.10)

где , а численное значение параметров ,, h и (значения коэффициента загромождения, относительной скорости, толщины слоя и угла потока в данной точке) - берутся из результатов расчета осредненного осесимметричного потока, соответствующего межлопастного канала.

В данной задаче координатные линии S первого семейства (ПКЛ) выбирались совпадающими с линиями естественной системы координат (линиями тока). Координатные линии L второго семейства (ФКЛ) выбирались так, чтобы они совпадали с линиями при пересечении осесимметричной поверхности тока с поверхностями вращения, образующими которых являются фиксированные координатные линии первой предельной задачи расчета осесимметричного потока. Направление координаты L выбиралось в сторону противоположную вектору окружной скорости . В качестве границ области течения принимались линии тока (подвижные координатные линии), совпадающие со средними линиями профилей соседних рабочих лопастей, продолженные в области входного устройства и безлопаточного диффузора на величину одного шага расчетной сетки, а также два сечения: одно - отнесенное вверх по потоку в область входного устройства; второе – отнесенное вниз по потоку в область безлопаточного диффузора также на один шаг. В последних двух сечениях задавались граничные условия в виде равноскоростного равнонаправленного потока и равномерного распределения линий тока.

Рассмотрение течения в пристенном слое базировалось на системе интегральных уравнений пристенного слоя, записанного, согласно работ Шабарова А.Б., в виде следующих уравнений:

- интегральное уравнение импульсов в пристенном слое

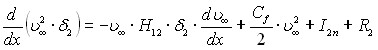; (3.11)

- интегральное уравнение механической энергии в пристенном слое

, (3.12)

где - скорость на внешней границе пристенного слоя, совпадающая со скоростью в ядре потока при данном значении x; x - продольная координата вдоль линии пересечения поверхности вращения с рабочей поверхностью лопасти; - условная толщина потери импульса в пристенном слое; - условная толщина потери механической энергии в пристенном слое;

; ;

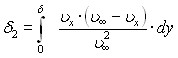y - координата по нормали к стенке; D - интеграл диссипации;

;

I2, I3 – интегралы, зависящие от напряжений Рейнольдса; R2,, R3 -

интегралы отдельных слагаемых уравнений Новье-Стокса, которыми при расчете пристенных течений обычно пренебрегают; H12, H32 – формпараметры профиля скорости в пристенном слое; ; ; Cf - коэффициент трения на стенке.

Для замыкания системы (3.11) – (3.12) использовался двухпараметрический профиль скорости Коулза

, (3.13)

где ; .

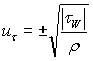Отрицательный знак в последнем выражении соответствует отрывному возвратному течению вблизи стенки.

Параметры Cf, H12,, D, I2,, I3 при принятом профиле скоростей определялись по аппроксимирующим двухпараметрическим зависимостями, приведенным в работах Шабарова А.Б. и Спиридонова В.И.

Расчет пристенного течения производился отдельно для сторон разряжения и давления в межлопастных каналах, соответствующим условиям при входе в рабочее колесо (области I и II). Решение уравнений (3.11) и (3.12) проводилось стандартным методом Рунге-Кутта при начальных условиях:

, , .

В расчете осесимметричного потока углы наклона и кривизна линий тока на кромках лопастей рабочего колеса также рассчитывались по трехточечному шаблону с применением центральных разностей.

В расчете течения на осесимметричной поверхности тока предполагается, что вследствие постоянства давления по ширине межлопастного канала на входе в рабочее колесо величина относительной скорости w постоянна, изменяются лишь углы потока . Учитывались различия условий входа потока в рабочее колесо ( области I и II).

Для определения углов потока и кривизны линий тока на осесимметричной поверхности участок линий тока от левой границы расчетной области течения (предпоследнее сечение входного устройства) до второго сечения (второй фиксированной координатной линии) межлопастного канала рабочего колеса аппроксимировался кубическим сплайном с заданными координатами и первыми производными, определяемыми углами потока .

Для определения углов потока при решении осредненных уравнений осесимметричного потока в рабочем колесе в следующей итерации производится осреднение углов потокана осесимметричной поверхности тока по ширине межлопастных каналов с граничными условиями в областях I и II.

После расчета параметров потока в рабочем колесе насоса производился расчет осесимметричного потока в безлопаточном диффузоре, затем определялись параметры выходной системы. По окончании расчетов первой итерации для каждого осесимметричного элемента проточной части (входного устройства, рабочего колеса и безлопаточного диффузора) уточнялись координаты, углы наклона и кривизна линий тока осесимметричного потока. Эти данные, а также полученные поля скоростей и углов потока в абсолютном и относительном движении, потери во всех элементах проточной части, а также поля давлений, использовались как начальные данные для расчета в следующей итерации.

После того, как была достигнута заданная точность вычислений, производился расчет осредненных по массовому расходу величин в контрольных сечениях по ширине меридионального контура с учетом различных параметров в межлопастных каналах вида I с условиями при входе из области I и вида II с условиями из области II

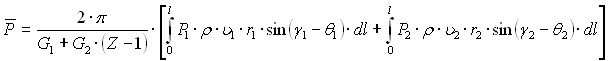, (3.14)

где G1 и G2 - массовые расходы через межлопастной канал с условиями при входе, соответствующими параметрам в области I и II; P- усредняемый параметр; - средний параметр.

В заключении главы 3 приводится блок-схема этапов расчета течения и гидродинамических сил, действующих в центробежном насосе (на основе периодически-квазитрехмерной модели) и приводятся результаты расчета по данной схеме. Расчет включал в себя нахождение распределения скоростей и давлений по обводам проточной части рабочего колеса насоса и выполнялся насоса типа НМ 10000-210 с ротором на подачу 0,7, широко применяемого в магистральном транспорте нефти. Распределение отмеченных параметров находилось для двух подач насоса – 7000 м3/ч и 6000 м3/ч. В результате расчетов были получены данные по изменению вдоль входной кромки лопасти таких параметров, как угол атаки i и средне расходная скорость потока ( частично показано на рис.3.2 и рис.3.3), а также информация по распределению скоростей W и давлений P вдоль лопастей рабочего колеса (с рабочей и с тыльной сторон лопастей, между ними посередине межлопастного канала) для трех областей, примыкающих соответственно к переднему и к основному дискам колеса, а так же для области, расположенной между дисками по середине лопасти (часть результатов расчета представлена на рис.3.4).

Анализ расчетных данных показал, что по мере снижения расхода жидкости происходит: во-первых, увеличение угла атаки потоком входной кромки лопасти i, причем наиболее выражено и значительно у переднего диска рабочего колеса; во-вторых, - изменение распределения вдоль входной кромки лопасти с увеличением , наиболее выраженным у переднего диска колеса. Отмеченные изменения и их масштабы свидетельствуют о формировании на входе в рабочее колесо, и в первую очередь у его переднего диска, отрывных и обратных течений, то есть вихрей, называемых в литературе вихрями торможения.

Изучение результатов расчетов по изменению W и P показало, что при уменьшении подачи относительная скорость потока на рабочей стороне лопасти (WPS ) и преимущественно вблизи выхода из колеса приобретает знак «минус». При этом такое изменение WPS наиболее выражено вблизи основного диска. Отрицательные значения относительной скорости говорят о возникновении зон обратных токов и отрывных пристенных течений.

Образование неупорядоченного вихревого движения жидкости на входе и выходе рабочих колес в отмеченных выше областях у недогруженных по подаче центробежных насосов отмечено авторами многих экспериментальных исследований. Полученные в ходе расчетов результаты согласуются с известными экспериментальными данными. Это свидетельствует о соответствии предложенной модели течения разработанного метода расчета реальной структуре потока в межлопастных каналах насосов.

Четвертая глава включает в себя разработку физико-математической модели гидродинамической вибрации в насосах центробежного и шнеко-центробежного типов на основе выводов, полученных в предшествующих главах работы. На базе данных выводов и дополнительно проведенных в главе 4 исследований было установлено, что вибрация вызывается в значительной мере наличием в спиральном подводе насосов со средним расположением колес «языка», который предназначен для равномерного распределения жидкости по межлопастным каналам. При вращении ротора насоса каждый межлопастной канал (рабочего колеса или шнека соответственно) периодически входит в гидродинамическую тень данного «языка», затем выходит из тени и воспринимает воздействие со стороны входящей в него жидкости, которое временно было существенно ослаблено во время нахождения канала в тени «языка». Возобновление воздействия происходит в короткий промежуток времени и сопровождается образованием ударных сил гидродинамического происхождения, которые, в соответствии с главами 2 и 3 настоящей работы, приложены преимущественно к рабочей стороне второй (по ходу движения) лопасти, из ограничивающих канал лопастей. Все отмеченное приводит к периодическому силовому воздействию на рабочее колесо в области, находящейся вблизи «языка», с частотой, равной частоте прохождения мимо «языка» лопастей рабочего колеса. Эта сила воспринимается ротором в целом, который приходит в колебательное движение и генерирует вибрацию всего насоса.

Изложенное составляет физическую модель вибрации гидродинамического происхождения у центробежных насосов, работающих с недогрузкой по подаче. В эту модель так же входят выражения для расчета сил вибрации.

В результате исследований, проведенных в данной главе, были установлены силы, вызывающие вибрацию как при квазиодномерной модели течения жидкости, так и при квазитрехмерной модели течения. При квазиодномерном взгляде на течение жидкости к силам, вызывающим вибрацию следует отнести: гидродинамическую силу, возникающую при ударном обтекании потоком лопастей рабочего колеса на его входе в результате образования угла атаки и существенного его увеличения с понижением подачи, а также силу, возникающую от взаимодействия в рабочем колесе транзитного и инерционного движений.

Для определения названных сил были получены, на ранее рассмотренных в главе 2 физических основах, расчетные зависимости (4.1) и (4.2):

, (4.1)

где ,

K - коэффициент, учитывающий конструктивные особенности насоса (при одностороннем входе жидкости в колесо К = 1, при двухстороннем -2);

, (4.2)

где .

Кроме центробежных насосов широкое применение, в том числе и в магистральном транспорте нефти, имеют шнеко-центробежные насосы, они отличаются от центробежных наличием у них перед входом в рабочее колесо шнеков. Данные насосы, если они имеют среднее расположение рабочего колеса, также подвергаются вибрации гидродинамического происхождения при понижении их загрузки по расходу жидкости. Проведенные в главе подробные исследования особенностей рассматриваемого вида вибрации у шнеко-центробежных насосов позволили установить, что у данных насосов вибрация вызывается, в основном, возникновением угла атаки на входе в шнек, подобно тому, как это происходит на входе рабочего колеса. После отмеченного контакта поток в шнеке приобретает закрутку по направлению вращения ротора, в том числе и колеса, поэтому при входе в рабочее колесо и в самом колесе не создается условий для возникновения явлений, способных вызвать вибрационные процессы. Зависимость (4.3) для расчета силы, вызывающей вибрацию у шнеко-центробежных насосов, находилась на таких же физических основах, как и сила для центробежного насоса

, (4.3)

где .

Здесь величины В, и i содержат в себе конструктивные параметры шнека (внешний и внутренний диаметры, количество лопастей, угол наклона лопастей и т.п.) и входной части насоса, а также частоту оборотов ротора насоса.

При рассмотрении течения жидкости с позиции квазитрехмерной модели сила, вызывающая вибрацию находится по формуле (4.4), аналитическая форма которой наглядно показывает физический источник ее получения

, (4.4)

где Pps и Pss - давление, действующее соответственно с рабочей и с тыльной стороны лопасти; S - площадь внешней поверхности лопасти, на которую воздействуют давления Pps и Pss; I и II – индексы, показывающие принадлежность параметров соответственно к областям I и II.

Силы , , , и , зависимости для определения которых получены выше, вызывают колебание ротора и последующую вибрацию всего насоса. Таким образом, работающий насос можно рассматривать как систему, участвующую в вынужденных колебаниях с вязким сопротивлением. Колебания такой системы описываются уравнением (4.5)

, (4.5)

где– перемещение при колебательном движении; t - время; h - коэффициент демпфирующей силы; М - масса системы, участвующей в колебании; С - жесткость системы; - начальная фаза колебаний;

; ; ; ;

F –сила, вызывающая вибрацию (сумма и или ; - в зависимости от того, какой насос рассматривается); n – число оборотов ротора насоса в минуту.

У большинства центробежных и шнеко-центробежных насосов, в том числе у насосов типа НМ, исследуемых в настоящей работе, лопасти рабочих колес и шнеков имеют пространственную конфигурацию. Поэтому силы , , и , направленные по нормали к лопасти, имеют три проекции, в качестве которых по сложившейся в вибродиагностике оборудования практике, рассматривают осевую (О), поперечную (П) и вертикальную (В) проекции, ориентированные соответственно вдоль оси ротора, поперек ее и вертикально.

В результате, уравнение (4.5) следует записать для каждой из отмеченных координат. Однако, как показал анализ виброграмм насосных агрегатов магистральных нефтепроводов, полученных автором работы и другими исследователями, координатные составляющие сил вибрации существенно не равноценны – О и В примерно равны друг другу, а П превосходит каждую из них примерно в три раза при любом режиме работы насоса. Отмеченное позволяет ориентироваться на одну, на наибольшую, составляющую П. Поэтому уравнение (4.5) рассматривалось как записанное для координаты П.

В рассматриваемом колебательном процессе наибольшую опасность представляют не промежуточные значения параметров , и , характеризующих данный процесс, а амплитуды этих параметров. При постоянном режиме работы насоса амплитуда силы, вызывающей вибрацию, коэффициент демпфирующей силы h и жесткость системы С полагаются постоянными. В результате из выражений (4.6) будем иметь зависимости, связывающие между собой силу, вызывающую вибрацию, с параметрами вибрации: вибросмещением S = , виброскоростью = и виброускорением = .

Уравнение (4.5) для отмеченных выше условий (постоянный режим работы насоса, постоянство F, h и C) можно представить в виде

или (4.6)

Откуда следует:

или ; (4.7)

или , (4.8)

где , , и - идентификационные постоянные для данной колебательной системы, которые могут быть оценены по известным параметрам h, С и производным от них величинам.

Пятая глава посвящена проверке соответствия опытным данным зависимостей (4.1), (4.2), (4.3), (4.7) и (4.8), моделирующим вибрацию гидродинамического происхождения в центробежных и в шнеко-центробежных насосах. Первоначально проверке подвергался общий характер полученных выражений для центробежных насосов – сравнивались результаты приближенных расчетов силы вибрации для них по формулам (4.1) и (4.2) с известными опытными данными по изменению интенсивности вибрации гидродинамического происхождения в зависимости от подачи насосов.

Проверка показала (рис.5.1), что существует качественное соответствие между расчетным и экспериментальными данным – сила вибрации и интенсивность вибрации минимальны в области, примыкающей к оптимальным значениям подач насосов, а по мере удаления от данной области в сторону повышения или понижения подачи оба параметра возрастают.

Для более глубокой проверки рассматриваемых зависимостей использовались опытные данные, полученные автором, а также данные других исследователей. Опытные данные автора получены на действующей нефтеперекачивающей станции и являются результатом вибрационных испытаний насосного агрегата НМ 10000–210 с ротором на подачу 1,25 ее номинального значения.

В ходе экспериментов измерялись продача и виброскорость агрегата в шести точках конструкции насоса: задний подшипник, передний подшипник, подвод вблизи языка спирали, отвод вблизи языка спирали, всасывающий и нагнетательный патрубки. Для точек, расположенных на подшипниковых узлах, измерение вибрации осуществлялось в трех направлениях: вертикальном, поперечном, осевом.

Анализ полученных виброграмм показал, что при снижении производительности насоса наблюдается увеличение интенсивности вибрации только на лопастной частоте, соответствующей вибрации гидродинамического происхождения. Это обстоятельство позволило использовать полученный экспериментальный материал для проверки зависимостей (4.1), (4.2) и (4.8). Она состояла в нанесении на одно координатное поле опытных значений виброскорости и соответствующих ей, по производительности, расчетных значений силы вибрации F (рис.5.2) с последующим выявлением наличия между и F функциональной взаимосвязи вида (4.8). Согласно рис.5.2 такая взаимосвязь имеет место и она ярко выражена – достоверность аппроксимации составляет 0,9049.

Приведенное на рис.5.2 уравнение содержит численные коэффициенты 0,001 и 0,4318. Они представляют собой постоянные а/ и b/, входящие в формулу (4.8). Найденные таким образом параметры а/ и b/ позволили получить по (4.8) расчетные значения виброскорости. При этом в (4.8) вместо F подставлялась сумма сил, определенных по (4.1) и (4.2). Сравнение расчетных и опытных значений виброскорости показано на рис. 5.3.

Формулы (4.1), (4.2) и (4.8) проверялись также на экспериментальных данных Колпакова А.Л., Писаревского В.М., Покровского Б.В. и Рубинова В.Я., обобщенной информации по вибрации насосных агрегатов НМ 2500-230, НМ 7000-210 и НМ 10000-210 (ротор 1,0), приведенной в РД 153-39ТН-008-96. Проверка в целом показала удовлетворительное соответствие результатов расчета опытным данным, что, в частности, иллюстрирует рис.5.4, который подтверждает наличие выявленной выше корреляционной связи между виброскоростью и вызывающей ее силой, и таким образом свидетельствует, как и прочие, не приводимые здесь упомянутые опытные данные, о соответствии формул (4.1), (4.2) и (4.8) реально наблюдаемым явлениям.

Рис.5.4.Проверка расчетных зависимостей (4.1), (4.2) и (4.8) на опытных данных Писаревского В.М. для насоса НМ 10000-210 с ротором на подачу 1,25 ее оптимального значения

Проверка соответствия опытным данным выражений (4.3) и (4.8) для расчета параметров вибрации гидродинамического происхождения у шнеко-центробежных насосов проводилась на обширном экспериментальном материале Бражник В.П., который был получен им для подпорного насосного агрегата магистральных нефтепроводов НМП 3600-230 (рис.5.5).

Сравнение вибрационных характеристик этого насоса с расчетными значениями вибрации показывает, что расчетные и экспериментальные данные соответствуют друг другу точно так же, как это наблюдается и для центробежных насосов. Существенные отклонения расчетных виброускорений от опытных значений наблюдаются при подачах, больших оптимальной производительности насоса.

Рис.5.5.Сравнение вибрационных характеристик насоса НМ 3600-230 с расчетными значениями силы вибрации:

а) при различных углах установки лопастей шнека

(1 - ; 2 –);

б) при различных диаметрах шнека (3 - D = 0,517 м; 4 – 0,472 м; 5 – 0,427 м);

экспериментальные данные;

расчетные значения

Таким образом, было доказано, что полученные выражения для расчета параметров вибрации гидродинамического происхождения у центробежных и шнеко-центробежных насосов, работающих с недогрузкой по подаче, адекватно отражают описываемые ими физические процессы.

В шестой главе исследуется влияние изменения численных значений параметров, входящих в итоговые выражения (4.1), (4.2), (4.3), (4.4), (4.7) и (4.8) и являющихся параметрами управления вибрацией, на кавитационные характеристики насосных агрегатов, так как большая часть этих параметров способна влиять на всасывающую способность насосов центробежного типа. Для решения поставленной задачи был проведен анализ существующих исследований в области влияния конструктивных параметров перекачивающих агрегатов на их кавитационные характеристики. На основе проведенного анализа установлено, что теоретический путь в решении данной проблемы пока не дает желаемых результатов. Поэтому практикуется эмпирический подход на базе различных параметров подобия, в котором наилучшие результаты достигнуты Рудневым С.С. Им получено выражение, связывающее между собой критический кавитационный запас насосов с параметром С, названным кавитационным коэффициентом быстроходности. Проверка методики Руднева С.С., основывающейся на определении кавитационного подобия насосов по параметру C, на опытных данных для исследованных в работе насосов, а так же для других подобных машин выявила не достаточную адекватность отражения параметром С кавитационных процессов в насосах. Это потребовало выполнения исследований в данной области. Исследования выполнялись на базе, достигнутой Рудневым С.С., наиболее близко подошедшего к решению проблемы. Суть исследований заключается в поиске выражения, раскрывающего зависимость С от особенностей отдельных насосов. Общий вид искомой зависимости представлен в безразмерной форме

, (6.1)

где ;- относительный напор насоса, равный ; H0 – напор, развиваемый насосом при оптимальной подаче; -базовый напор насоса, который можно назвать автомодельным, так как при кавитационный коэффициент быстроходности С будет зависеть только от одного удельного числа оборотов ротора насоса пu или коэффициента быстроходности насоса пs;; n – частота оборотов ротора насоса; Q и H – подача и напор насоса.

Для поиска искомой зависимости использовались опытные данные для подавляющего числа выпускаемых типоразмеров насосов НМ. Коэффициенты быстроходности их составляют 43,54262,39, что охватывает практически весь диапазон коэффициентов быстроходности центробежных насосов (40 300). С целью расширения круга вовлекаемых в анализ опытных данных и придания на этой основе последующим обобщающим выражениям большей достоверности к рассмотрению привлекались данные по одним и тем же маркам насосов, но взятым из различных источников, а также заводские характеристики насосов. При этом рассматривались насосы, как с номинальными, так и со сменными роторами.

Рассмотрение опытных данных для отмеченных насосов в координатах (6.1) (рис.6.1) приводит к выводу, что общая функциональная зависимость(6.1) имеет вид

, (6.2)

где as и bs – безразмерные коэффициенты, постоянные для каждого насоса.

Рис.6.1.Опытные данные по кавитационным характеристикам насосов (представлены частично)

Проведенный анализ опытных данных в функциональной зависимости (6.2) показал, что этой зависимости в равной мере подчиняются все насосы рассматриваемого типа, то есть насосы со всеми возможными значениями пs и пu. При этом разброс опытных данных относительно прямой, описываемой (6.2), минимален и составляет не более 6%.

Отмеченные обстоятельства дают основания считать, что зависимость (6.2) удовлетворительно отражает исследуемое явление, а положенное в ее основу выражение (6.1) имеет под собой вполне определенную физическую базу. Для выяснения этой базы все имеющиеся опытные данные были рассмотрены на одном координатном поле в координатах (6.1) (рис. 6.2).

Анализ рис.6.2 и опытных данных по каждому исследуемому насосу в отдельности, как это показано на рис.6.1, позволил придти к следующим выводам. Во-первых, удельное число оборотов в данном случае представляет собой соотношение кинетической и потенциальной составляющих энергии жидкости и может быть названо коэффициентом кавитационного подобия центробежных насосов или, если опираться только на исследованные насосы, коэффициентом кавитационного подобия центробежных насосов со средним расположением рабочего колеса. Во-вторых, по характеру зависимости от в различных диапазонах можно выделить три специфические зоны. В третьих, границы выделенных зон определяются значениями удельного числа оборотов ротора насоса, соответствующим номинальному режиму работы насоса . В четвертых, выделенные зоны исходя из характера зависимости в них от можно назвать следующим образом:

- при - зона автомодельности кавитационных процессов;

- при 6< - переходная зона от автомодельности к частной

автомодельности кавитационных процессов;

- при 7<<15 - зоной частной автомодельности кавитационных

процессов.

Единство природы исследуемого кавитационного явления в различных центробежных насосах и определенная универсальность полученного параметра позволили обобщить частные эмпирические зависимости для отдельных зон и получить единое расчетное выражение для насосов всего ряда быстроходности

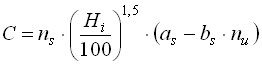, (6.3)

где Hi - напор насоса, имеющий различное значение для вышеприведенных зон; для зоны автомодельности и переходной зоны Hi =Hoo (номинальный напор насоса при установке на нем ротора на номинальную подачу), а для зоны частной автомодельности Hi =Ho (номинальный напор насоса при установке на нем сменного ротора); as и bs - безразмерные коэффициенты, определяемые в зависимости от зоны по соответствующим, полученным в работе, эмпирическим выражениям. На основе формулы (6.3) выведена зависимость для расчета критического кавитационного запаса насосов

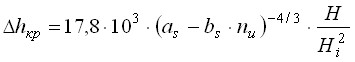. (6.4)

Значения , найденные по формуле (6.4), отличаются от опытных не более, чем на 10%. Зависимость (6.4) использовалась для анализа влияния изменения параметров управления вибрацией на кавитационные характеристики центробежных насосов.

Аналитическая структура формул (4.1), (4.2) и (4.8) показывает, что вибрационные характеристики центробежных насосов в наибольшей степени зависят от численной величины таких параметров, как: диаметр входного отверстия рабочего колеса насоса D1, угол наклона лопастей рабочего колеса на входе в колесо , частота оборотов ротора насоса n, количество лопастей в рабочем колесе Z. Проведенный численный анализ показал, что снижение вибрации путем изменения перечисленных параметров не ухудшает кавитационные характеристики насосов и даже несколько улучшает их.

В седьмой главе разрабатываются способы снижения вибрации у центробежных и шнеко-центробежных насосов, которые вытекают из зависимостей (4.1), (4.2), (4.3) и (4.4) для определения сил ,,и и состоят в изменении входящих в эти зависимости параметров – параметров управления вибрацией.

Анализ отмеченных формул привел к следующим выводам:

1.Для снижения сил, и , вызывающих вибрацию центробежных насосов, необходимо изменять одни и те же конструктивные параметры насосов: уменьшать угол наклона лопастей на входе рабочего колеса , диаметр входного отверстия рабочего колеса и частоту вращения рабочего колеса n; увеличивать количества лопастей рабочего колеса z.

2.Снижение вибрации гидродинамического происхождения у шнеко-центробежных насосов может быть достигнуто: уменьшением внешнего диаметра шнека D, угла установки лопастей шнека , шага шнека S и частоты вращения шнека n; увеличением количество лопастей шнека z.

3.Наибольший эффект для обоих типов насосов (центробежных и шнеко-центробежных) дает уменьшение соответствующих диаметров ( и D), углов установки лопастей ( рабочего колеса и шнека), а также частоты оборотов роторов.

Сделанные на основе расчетно-теоретических данных выводы подтверждены опытными данными, полученными на действующей нефтеперекачивающей станции, и результатами экспериментов различных исследователей.

В заключение главы 7 даются практические рекомендации по использованию результатов исследований. Они представлены методикой, которая позволяет выполнять расчеты требуемых значений параметров управления вибрацией, обеспечивающих насосам допустимый или желаемый уровень вибрации.

ОБЩИЕ ВЫВОДЫ ПО ВЫПОЛНЕННЫМ ИССЛЕДОВАНИЯМ

1.Исследовано влияние гидродинамических процессов в проточной части центробежных насосов на их энергетические характеристики.

По результатам данных исследований разработана методика расчета потерь напора в элементах проточной части центробежных насосов и методика расчета напорной характеристики подобных насосов.

Кроме того, предложена и реализована модель периодически-квазитрехмерного течения в рабочих колесах центробежных насосов; разработаны модель и метод расчета квазитрехмерного течения в рабочих колесах центробежных насосов с определением параметров потока и переменных гидродинамических сил.

2.Создана физическая модель вибрации гидродинамического происхождения у центробежных и шнеко-центробежных насосов.

3.Создана математическая модель вибрации гидродинамического происхождения у центробежных и шнеко-центробежных насосов.

4.Проведена проверка полученной физико-математической модели гидродинамической вибрации центробежных и шнеко-центробежных насосов путем сопоставления результатов расчета с опытными данными соискателя и с экспериментальными данными других исследователей.

5.На основе созданной модели разработаны технические решения по снижению вибрации гидродинамического происхождения в центробежных и в шнеко-центробежных насосах, работающих с недогрузкой по подаче.

В частности, разработаны практические рекомендации по использованию результатов исследований, представленные методикой расчета требуемых значений параметров управления вибрацией, обеспечивающих насосам допустимый или желаемый уровень вибрации; предложен и обоснован теоретически, на положениях гидродинамики, и опытными данными по размерному ряду центробежных насосов типа НМ, охватывающему по удельным оборотам ротора 2,15 12,97, коэффициент кавитационного подобия центробежных насосов.

6.Выполнена апробация разработанных технических решений на

опытных данных, в том числе полученных в промышленных условиях на насосной станции магистрального нефтепровода.

Основные положения диссертации опубликованы в следующих работах:

1.Безус А.А. Влияние схемы соединения насосов на крутизну «кривой выбега» насосных станций / Безус А.А., Перевощиков С.И. // Нефтяное хозяйство. - 1991. - № 7. - С.59-61.

2.Перевощиков С.И. К настройке системы сглаживания волн давления на НПС нефтепроводов / Перевощиков С.И., Безус А.А. // Нефтяное хозяйство. - 1993. - № 11. - С.47-48.

3.Перевощиков С.И. Вибрация насосно-силовых агрегатов магистральных нефтепроводов / Перевощиков С.И., Безус А.А. // Нефтяное хозяйство. - М.: АО "Нефтяное хозяйство", 1994. - № 10. - С.54-55.

4.Перевощиков С.И. Вибрация подпорных насосов магистральных нефтепроводов / Перевощиков С.И., Безус А.А. // Изв. вузов. Нефть и газ. – Тюмень: ТюмГНГУ, 1997.- № 2.- С.75-79.

5.Перевощиков С.И. Снижение гидродинамической вибрации центробежных насосов / Перевощиков С.И. // Изв. вузов Нефть и газ.– Тюмень: ТюмГНГУ, 1997. - № 4.-С.50-56.

6.Перевощиков С.И. Разработка способов снижения гидродинамической вибрации у подпорных насосов магистральных нефтепроводов / Перевощиков С.И. // Изв. вузов Нефть и газ. – Тюмень: ТюмГНГУ, 1997. - № 6.- С.137.

7.Перевощиков С.И. Потери энергии в диффузорных каналах / Перевощиков С.И. // Изв. вузов. Нефть и газ. – Тюмень: ТюмГНГУ, 1998. - № 5.-С.85-89.

8.Перевощиков С.И. Потери энергии в несимметричных диффузорных каналах / Перевощиков С.И. // Изв. вузов. Нефть и газ. – Тюмень: ТюмГНГУ, 1998. - № 6.-С.85-89.

9.Перевощиков С.И. Критерий кавитационного подобия центробежных насосов / Перевощиков С.И. // Изв. вузов. Нефть и газ. – Тюмень: ТюмГНГУ, 2000. - № 1.С.75-80.

10.Перевощиков С.И. Расчет кавитационного коэффициента быстроходности центробежных насосов / Перевощиков С.И. // Изв. вузов. Нефть и газ. – Тюмень: ТюмГНГУ, 2000. - № 2. С. - 63-71.

11.Шабаров А.Б. Модель и метод расчета периодически квазитрехмерного потока в межлопастных каналах рабочих корлес центробежных насосов / Шабаров А.Б., Перевощиков С.И.,Сальников С.Ю. // Изв. вузов. Нефть и газ. – Тюмень: ТюмГНГУ, 2004. - № 4. С. 72-77.

12.Шабаров А.Б. Распределение скоростей и давлений по обводам проточной части рабочего колеса центробежного насоса / Шабаров А.Б., Перевощиков С.И.,Сальников С.Ю. // Изв. вузов. Нефть и газ. – Тюмень: ТюмГНГУ, 2004. - № 5. С. 144-150.

Подписано к печати 25.11.2004 г. Бум. писч. №1

Заказ № 694 Уч. - изд. л.2,00

Формат 60х84 1/16 Усл. печ. л.2,00

Отпечатано на RISO GR 3750 Тираж 100 экз.

Издательство «Нефтегазовый университет»

Государственного образовательного учреждения высшего профессионального образования

«Тюменский государственный нефтегазовый университет»

Отдел оперативной полиграфии издательства «Нефтегазовый университет»

625039, Тюмень, ул. Киевская, 52