Разработка метода оценки герметичности заклёпочных соединений для определения оптимальных конструктивно-технологических решений

На правах рукописи

ШИШКИН Сергей Сергеевич

РАЗРАБОТКА МЕТОДА ОЦЕНКИ ГЕРМЕТИЧНОСТИ

ЗАКЛЁПОЧНЫХ СОЕДИНЕНИЙ ДЛЯ ОПРЕДЕЛЕНИЯ ОПТИМАЛЬНЫХ КОНСТРУКТИВНО-ТЕХНОЛОГИЧЕСКИХ РЕШЕНИЙ

Специальность 05.07.02 – Проектирование, конструкция и производство летательных аппаратов

Автореферат

диссертации на соискание учёной степени кандидата технических наук

МОСКВА – 2010 г.

Работа выполнена на кафедре “Технологическое проектирование и управление качеством” Московского авиационного института (государственного технического университета)

Научный руководитель:

кандидат технических наук, доцент Васильев Сергей Леонидович

Официальные оппоненты:

доктор технических наук, профессор Дудченко Александр Александрович

кандидат технических наук Макаров Александр Федотович

Ведущая организация:

ОАО “Национальный институт авиационных технологий” (НИАТ)

Защита диссертации состоится ____ апреля 2010 г. в ____ часов на заседании диссертационного совета Д 212.125.10 при Московском авиационном институте (государственном техническом университете) по адресу: 125993, Москва, Волоколамское шоссе, д. 4.

С диссертацией можно ознакомиться в библиотеке МАИ.

Автореферат разослан ____ марта 2010 г.

Учёный секретарь диссертационного совета

кандидат технических наук, профессор _____________ Комаров Ю.Ю.

ОБЩАЯ ХАРАКТЕРИСТИКА РАБОТЫ

Актуальность работы. Заклёпочные соединения являются основным видом соединений в современной авиации благодаря высокому ресурсу и живучести, низкой себестоимости, возможности автоматизации сборочных работ и другим факторам. Основными параметрами их качества являются статическая и усталостная прочность, а также герметичность. Обеспечение качества представляется комплексной задачей, решение которой возможно благодаря выбору оптимальных конструктивно-технологических параметров соединения, включая тип крепежа, силовую схему процесса клёпки и величину радиального натяга.

В настоящее время для выполнения потайных и непотайных соединений наибольшее применение находят стержневые заклёпки, широкое внедрение которых определяется наиболее равномерным распределением радиального натяга по толщине пакета. Величина натяга в конструкциях из лёгких сплавов, как правило, не превышает 2.5%. Выбор значения является результатом взаимной увязки и оптимизации заложенных параметров качества. Например, повышение величины натяга способствует увеличению усталостных свойств, однако является причиной значительных деформаций стыкуемых элементов при сборке.

Качество заклёпочных соединений с точки зрения герметичности не всегда адекватно уровню современной техники, что выражается в наличии определённого количества видимых утечек топлива, которые не допускаются требованиями стандартов. Причинами проницаемости является наличие микронеровностей на сопряжённых поверхностях листа и заклёпки, а также потеря сплошности их контакта, причём во втором случае величина расхода уплотняемой среды оказывается существенно выше.

Для устранения проницаемости заклёпочных соединений используется поверхностная герметизация, которая приводит к увеличению веса, а также трудоёмкости и себестоимости сборки узлов и панелей, выходящих на внешний контур. Герметизации подвергаются практически все внутренние объёмы современных самолётов, включая топливный, пассажирский и приборный отсеки. Сокращение объёма данной технологии желательно с точки зрения повышения качества изделий авиационной техники, однако такое решение возможно только при условии обеспечения герметичности другими технологическими мероприятиями.

В настоящее время герметичные свойства заклёпочных соединений в значительной степени исследуются экспериментально, причём на основе качественной оценки. Такой подход, как правило, не позволяет получить численное значение величины утечки уплотняемой среды и, следовательно, оценить её влияние на экологию, пожарную безопасность или предельную дальность полёта. Количественные требования к герметичности заклёпочных соединений не предъявлены. Поскольку наличие проницаемости присуще каждому механическому контакту, результат качественной оценки во многом определяется условиями проведения эксперимента. Качественная оценка устанавливает факт накопления утечки определённой величины, однако не даёт полной информации о причинах её возникновения. Такой подход в ряде случаев не позволяет выявить однозначную взаимосвязь между параметрами соединения и герметичными свойствами, а большое количество факторов различной природы, влияющих на проницаемость, практически исключает эмпирический поиск их оптимального сочетания.

В условиях высокой стоимости количественных методов испытаний на герметичность повышение качества заклёпочных соединений по данному критерию во многом определяется созданием соответствующих расчётных методов, которые позволят наиболее полно описать явления, протекающие в конструкциях, и увязать обеспечение герметичности с другими параметрами качества. В рамках данных методов необходимо установить количественные характеристики проницаемости, определить условия начала разгерметизации и рекомендовать оптимальные конструктивно-технологические решения.

Таким образом, разработка метода оценки герметичности заклёпочных соединений является актуальной задачей, направленной на повышение качества авиационных конструкций.

Цель диссертационной работы – разработка метода оценки герметичности заклёпочных соединений для определения оптимальных конструктивно-технологических решений.

Для достижения поставленной цели необходимо решить следующие основные задачи:

- разработать методику расчёта на герметичность заклёпочных соединений при наличии сплошности контакта;

- построить модель формирования заклёпочных соединений и определить величину контактной нагрузки в исходном состоянии;

- построить модели нагружения заклёпочных соединений и определить опасные уровни внешних нагрузок;

- выявить факторы, значимо влияющие на герметичность заклёпочных соединений, и оценить степень их воздействия.

Методы исследований основаны на классических трудах в области теоретической герметологии, теории упругости и пластичности. Для исследования напряжений разгерметизации проведены численные эксперименты с применением системы символьной математики Waterloo Maple.

Достоверность полученных результатов подтверждается соответствием расчётных значений интенсивности деформаций в листах, окружных остаточных напряжений и опасных уровней внешних нагрузок данным ранее проведённых экспериментальных исследований.

Научная новизна

1. Разработан метод оценки герметичности заклёпочных соединений и определено численное значение расхода топлива через единичное соединение при сохранении сплошности контакта листа и заклёпки;

2. Предложено аналитическое решение задачи о нахождении контактной нагрузки в заклёпочном соединении в исходном состоянии и описано явление обратных пластических деформаций стержня при разгрузке;

3. Получено решение задачи о нагружении клёпаной панели на растяжение или сжатие и установлены опасные уровни внешних нагрузок, приводящие к разгерметизации.

Практическая ценность заключается в создании методики оценки герметичности заклёпочных соединений, которая может непосредственно применяться при проектировании клёпаных конструкций. Её внедрение позволит сократить объёмы испытаний на герметичность и решить вопрос о целесообразности использования герметизации. Полученные результаты численных экспериментов по определению опасных уровней внешней нагрузки и влияния на проницаемость различных конструктивно-технологических параметров являются теоретической базой для повышения герметичности заклёпочных соединений вне использования герметизации. Определение количественных характеристик проницаемости также позволяет оценить влияние утечки на эксплуатационную безопасность изделий авиационной техники.

На защиту выносятся:

- методика расчёта проницаемости заклёпочных соединений при сохранении сплошности контакта на основе теории пористого слоя;

- модель формирования ресурсных заклёпочных соединений для определения контактной нагрузки в исходном состоянии;

- модели нагружения заклёпочных соединений на сдвиг и клёпаных панелей на растяжение и сжатие;

- результаты численных экспериментов по определению опасных уровней внешних нагрузок и влияния технологических факторов на проницаемость;

- методика оценки герметичности заклёпочных соединений.

Личный вклад соискателя заключается в создании методики расчёта контактной нагрузки в ресурсном заклёпочном соединении в исходном состоянии и в результате нагружения, а также в адаптации известной методики расчёта на герметичность к принципиально новому типу конструкций. Автором выполнен весь объём теоретических изысканий, включая создание и отладку приложений при проведении численных экспериментов. В частности, автором получена формула для расчёта радиуса пластической зоны, описан эффект пластической разгрузки и решена задача о нагружении клёпаной панели в постановке Ляме – Кирша.

Работа выполнена в рамках программы целевого финансирования ОЭММПУ РАН № 1002-25-251/ОЭММПУ-12/079-076/100603-558 “Накопление повреждённости, разрушение, изнашивание и структурные изменения материалов при интенсивных механических, температурных и радиационных воздействиях”.

Публикации. Основное содержание работы изложено в 5 публикациях в журналах, входящих в список ВАК РФ.

Структура и объём работы. Диссертация содержит 99 страниц машинописного текста, 34 рисунка, 26 таблиц и состоит из введения, 5 разделов, основных выводов и результатов работы и списка используемой литературы из 58 наименований.

СОДЕРЖАНИЕ РАБОТЫ

В первом разделе проведён анализ конструкции и технологии выполнения заклёпочных соединений, способов герметизации клёпаных конструкций и методов испытаний на герметичность. Выполнен поиск разработок в области обеспечения герметичности заклёпочных соединений.

Герметичность (степень герметичности) – способность конструкции препятствовать истечению уплотняемой среды, под которой понимается объёмный (Q, мм3/с) или массовый (Qm, г/с) расход. Для сравнения герметичности конструкций удобно использовать величину проницаемости G (мкм3). Она определяется внутренними свойствами контакта и не зависит от внешних факторов. Также применяется понятие герметичные свойства, которое характеризует наличие или отсутствие сплошности контакта по всей поверхности стыка.

Анализ работ В.З. Кондрашова, А.И. Ярковца, С.Л. Васильева, В.Ф. Громова и других авторов показывает, что на кафедре “Технологическое проектирование и управление качеством” МАИ накоплен значительный опыт в обеспечении герметичности заклёпочных соединений. Установлено, что их проницаемость определяется конструктивно-технологическими факторами, включая радиальный натяг, точность исполнения отверстий, шероховатость сопряжённых поверхностей листа и заклёпки, величину радиального зазора при постановке заклёпки в отверстие и другие, однако при проектировании конструкций должное внимание уделяется только натягу. При этом нагружение заклёпочных соединений внешними силами нередко приводит к разгерметизации, что отмечается даже при увеличении натягов.

В.З. Кондрашовым предложена методика испытаний заклёпочных соединений на герметичность, а также проведены исследования влияния конструктивных и технологических факторов, включая нагружение. Однако анализ гидростатического метода испытаний, на основе которого создана методика, позволяет предположить, что автором были отмечены только случаи разгерметизации при нарушении сплошности контакта листа и заклёпки.

Анализ известных решений в области теоретической герметологии показывает, что в настоящий момент накоплен достаточный уровень для создания методики количественной оценки герметичности заклёпочных соединений при условии сплошности контакта. Принципы решения герметологических задач описаны в работах В.Т. Бабкина, А.А. Зайченко, В.В. Александрова, Н.Б. Дёмкина, И.В. Крагельского, А.М. Долотова, П.М. Огара, Д.Е. Чегодаева, Л.С. Пинчука и других авторов.

Решение герметологической задачи включает моделирование межповерхностной полости и обоснование механизма массопереноса уплотняемой среды. Для вычисления расхода, как правило, используются уравнения теории эквивалентной щели или пористого слоя. Описание микрорельефа сопряжённых поверхностей производится при замене неровностей телами правильной формы, с помощью опорных кривых или в виде случайной функции. Также необходимым условием является решение соответствующей конструкционно-контактной задачи для определения контактного сближения микронеровностей под нагрузкой и состояния контакта сопряжённых поверхностей.

Второй раздел посвящён созданию методики количественной оценки герметичности заклёпочных соединений при наличии сплошности контакта.

Ресурсные заклёпочные соединения отличаются высокой степенью герметичности благодаря значительным уровням контактной нагрузки при малом перепаде давления. В таких условиях наиболее перспективной для расчёта их проницаемости является модель определения утечек уплотняемой среды через металл-металлический контакт, которая основана на теории пористого слоя при определении коэффициента проницаемости из уравнения Козени. Профиль микронеровностей задаётся с помощью опорных кривых, что позволяет учитывать реальное распределение материала по высоте и получить решение, приемлемое в инженерной практике. Данная методика применима для любых сплошных контактов в широком диапазоне контактной нагрузки и многократно проверена экспериментально для различных конструкций уплотнений.

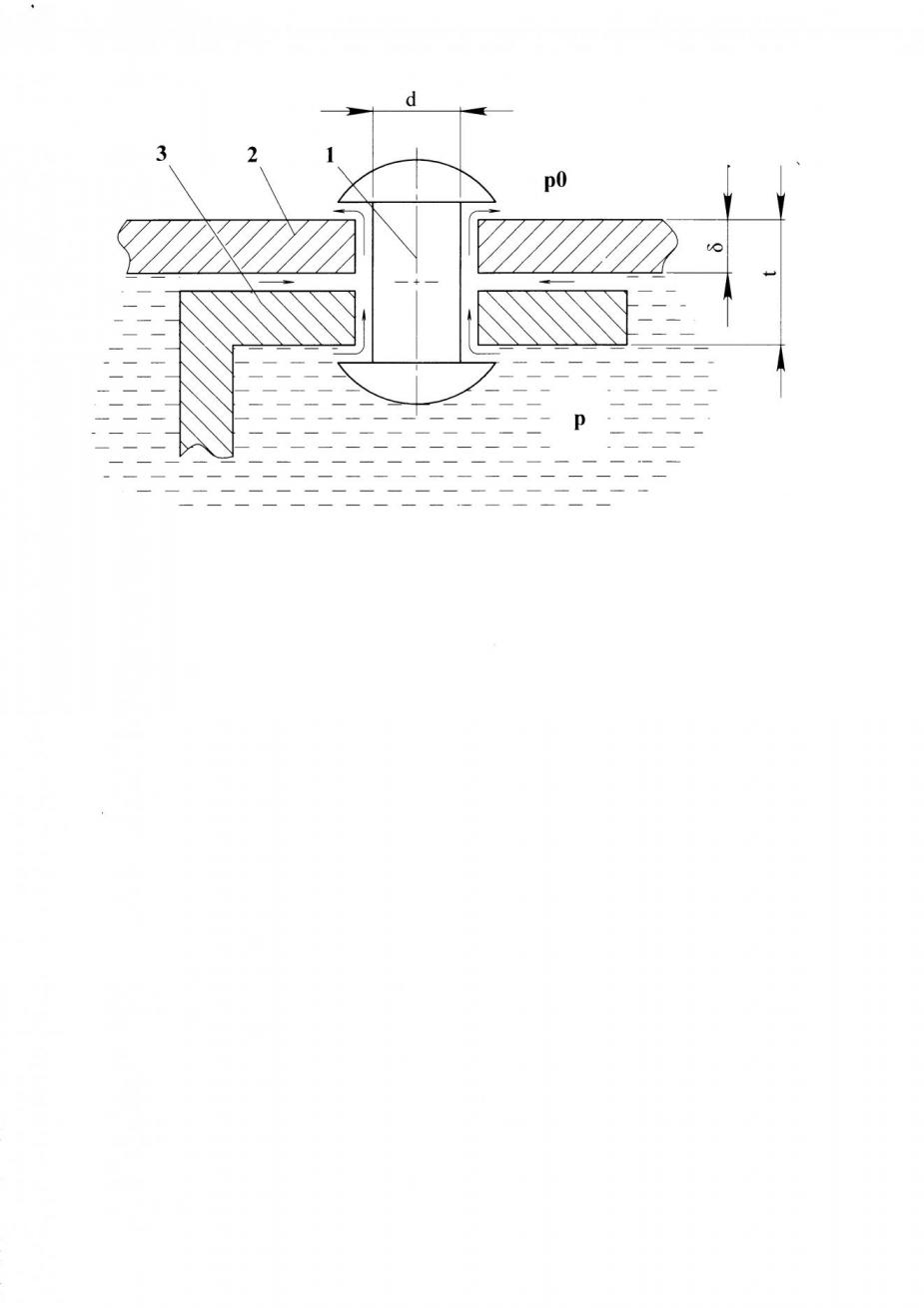
Рисунок 1 – Схема истечения уплотняемой среды через

непотайное заклёпочное соединение при отсутствии герметизации:

1 – заклёпка, 2 – обшивка, 3 – стрингер.

На рис. 1 приведена схема истечения уплотняемой среды через непотайное заклёпочное соединение при отсутствии герметизации. Как правило, такой уплотняемой средой является керосин или воздух. Из механики жидкости и газа известно, что в климатических условиях при давлении в рабочей зоне порядка 0.1 МПа истечение керосина имеет ламинарный характер. Расход топлива через цилиндрический контакт определяется известным уравнением неразрывности фильтрационного потока в условиях стационарного изотермического течения

(1)

где d – диаметр соединения (мм), S – коэффициент динамической вязкости среды (мПа·с), h – эквивалентная толщина пористого слоя под нагрузкой (мкм), lK – эффективная длина продольного контакта (мм), p – давление уплотняемой среды (МПа), p0 – давление вне рабочей зоны (МПа), K – коэффициент проницаемости (мкм2). Поскольку реальный технологический процесс не обеспечивает плотного прилегания листов, величина lK равна толщине обшивки.

Массовый расход воздуха определяется из аналогичных соображений в условиях вязкостного режима истечения

(2)

где M – молярная масса газа (г/моль), T – температура рабочего тела (К), R – Универсальная газовая постоянная, R =8.31 Дж/K·моль.

Отметим, что приведённые соотношения не учитывает возможный нагрев уплотняемой среды в полётных условиях, а также значительные вибрации, которые также приводят к снижению герметичности.

Эквивалентная толщина пористого слоя h под нагрузкой равна

(3)

где – относительное контактное сближение поверхностей листа и заклёпки, Rz – высота микронеровностей (мкм). При дальнейшей записи индекс “1” указывает на листы, “2” на стержень заклёпки.

Численное значение величины определяется с помощью универсальных формул, полученных И.В. Крагельским для случая контактирования двух шероховатых поверхностей без учёта волнистости. Если в процессе нагружения контактная нагрузка достигает максимальной величины q0, а затем снижается до величины q, значение описывается формулой

(4)

где HB – твёрдость по Бринеллю наиболее мягкого материала пары (МПа).

Коэффициент проницаемости K вычисляется из уравнения Козени – Кармана в зависимости от параметра пористости (m) и удельной поверхности соприкосновения микронеровностей с уплотняемой средой (B, мкм-1)

(5)

где U – постоянная Кармана U 0.2.

Выражения для определения значений m и B получены В.Т. Бабкиным и другими авторами исходя из геометрических построений:

(6)

где и – коэффициенты опорной кривой верхнего участка, b и n – коэффициенты опорной кривой нижнего участка, p – относительное сближение в точке перегиба p =0.35, x – среднее значение углов при вершинах продольной шероховатости, y – среднее значение углов при вершинах поперечной шероховатости.

Формулы (6) получены в предположении одинаковой обработки сопрягаемых поверхностей. В противном случае величины Rz,,, b и n можно найти из выражений для эквивалентной шероховатости:

(7)

В практических расчётах удобно принимать стандартизованные значения и для каждой поверхности, а величины b и n находить из предположения о конической форме нижней части микровыступов (n=1). Для коэффициентов b получена следующая зависимость

(8)

Проницаемость контакта в рамках теории пористого слоя равна:

(9)

Анализ полученных выражений показывает, что для определения расхода уплотняемой среды необходимо найти значение контактной нагрузки на всех этапах жизненного цикла соединения (при формировании и эксплуатации). Также необходимо установить краевые условия, при которых сплошность контакта нарушается.

Третий раздел посвящён определению контактной нагрузки в заклёпочном соединении в исходном состоянии.

При образовании заклёпочного соединения происходит осадка стержня вкупе с радиальной раздачей отверстия панели. При этом в листах имеют место упруго-пластические деформации с образованием зоны упрочнения вокруг заклёпки радиусом C, а величина контактной нагрузки достигает значения q0. При снятии усилия клёпки происходит разгрузка соединения, которая приводит к падению давления до величины q1. Полностью сформированное заклёпочное соединение до приложения внешних сил будем называть соединением в исходном состоянии.

Описание НДС в заклёпочных соединениях проводится расчётно-экспериментальными методами или с применением численных решений, (МКЭ и другие). В инженерной практике предпочтительно использование аналитических решений, которые основаны на идентичности процессов радиальной раздачи отверстия панели и нагружения плиты с отверстием внутренним давлением. Такие методики предполагают принятие гипотезы плоского напряженного или плоского деформированного состояния и описаны в работах Н.Н. Малинина, В.М. Долинского, Г.Ю. Джанелидзе, А. Надаи и других авторов.

Технологический процесс выполнения заклёпочных соединений, как правило, предусматривает предварительное сжатие пакета специальными прижимами (рис. 2), что в полной мере соответствует условиям плоской деформации. Для использования такой модели сопряжённые поверхности листов и заклёпки будем считать идеально круглыми, радиальный натяг равномерно распределённым по толщине пакета, а трение при формировании соединения незначительным. Также не учитывается влияние соседних силовых точек, а свойства материалов стыкуемых элементов полагаются идентичными. Отметим, что использование моделей плоского напряжённого состояния, как правило, предусматривает получение на контуре отверстия положительных окружных остаточных напряжений, что противоречит результатам экспериментов.

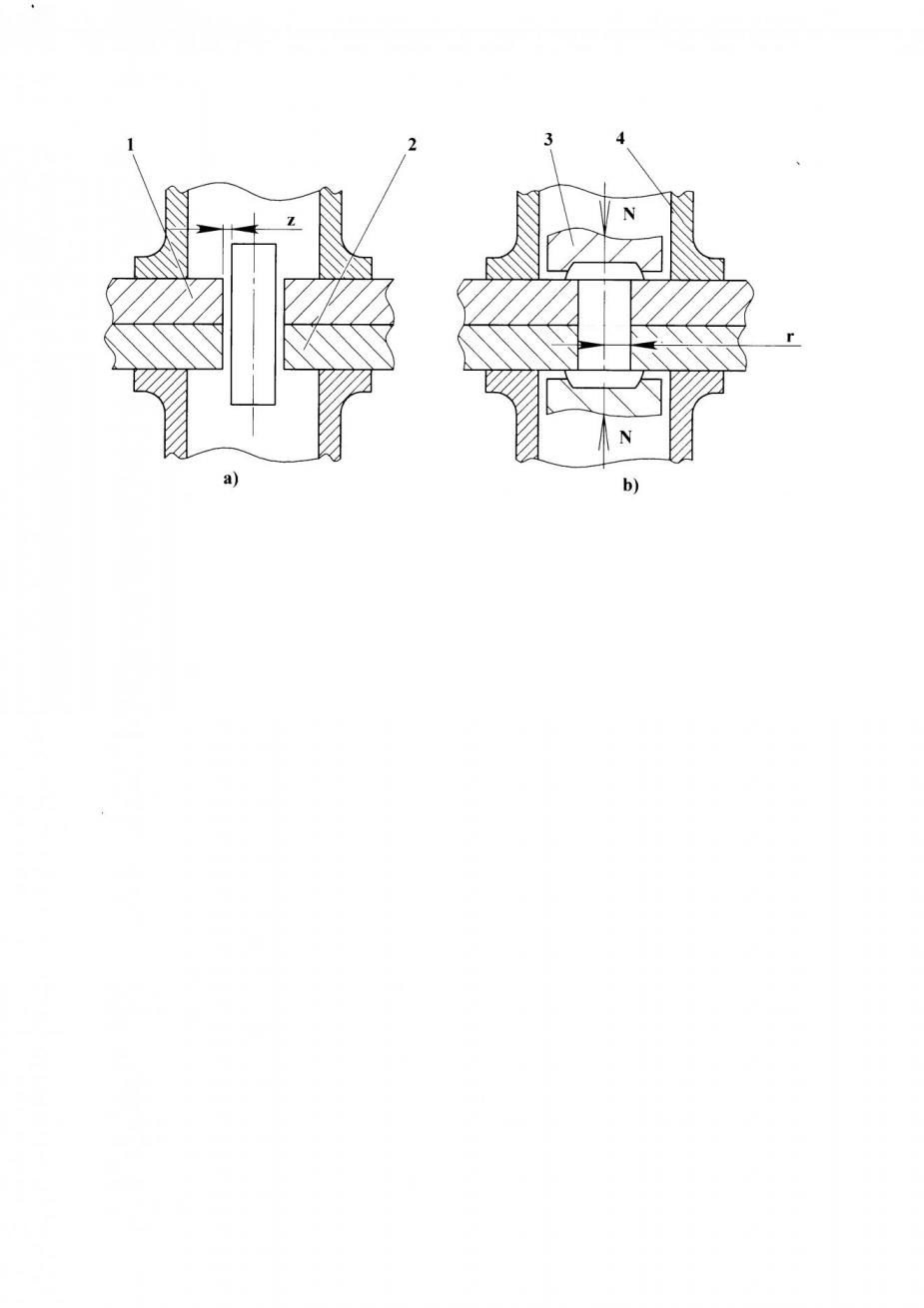
Рисунок 2 – Схема формирования заклёпочного соединения:

a) исходное положение, b) результирующее положение

1 – обшивка, 2 – стрингер, 3 – обжимка, 4 – прижим, N – усилие клёпки.

Для расчёта заклёпочных соединений используется известное решение Н.Н. Малинина о нагружении цилиндра внутренним давлением по теории малых упруго-пластических деформаций с учётом линейного упрочнения материала (рис. 3). Данная модель полностью отражает механику радиальной раздачи отверстия панели и позволяет найти аналитическое выражение для величины контактной нагрузки. При переходе к бесконечной плите автором получены следующие формулы для компонент напряжения в пластической области:

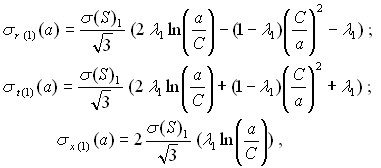(10)

где r – радиальные напряжения (МПа), t – окружные напряжения, x – осевые напряжения, а – текущий радиус начиная от оси отверстия (мм), – коэффициент упрочнения деформационной кривой в квазилинейной форме

(11)

где (S) – предел текучести материала (МПа), (B) – предел прочности, (B) – деформация на пределе прочности, E – модуль упругости (МПа).

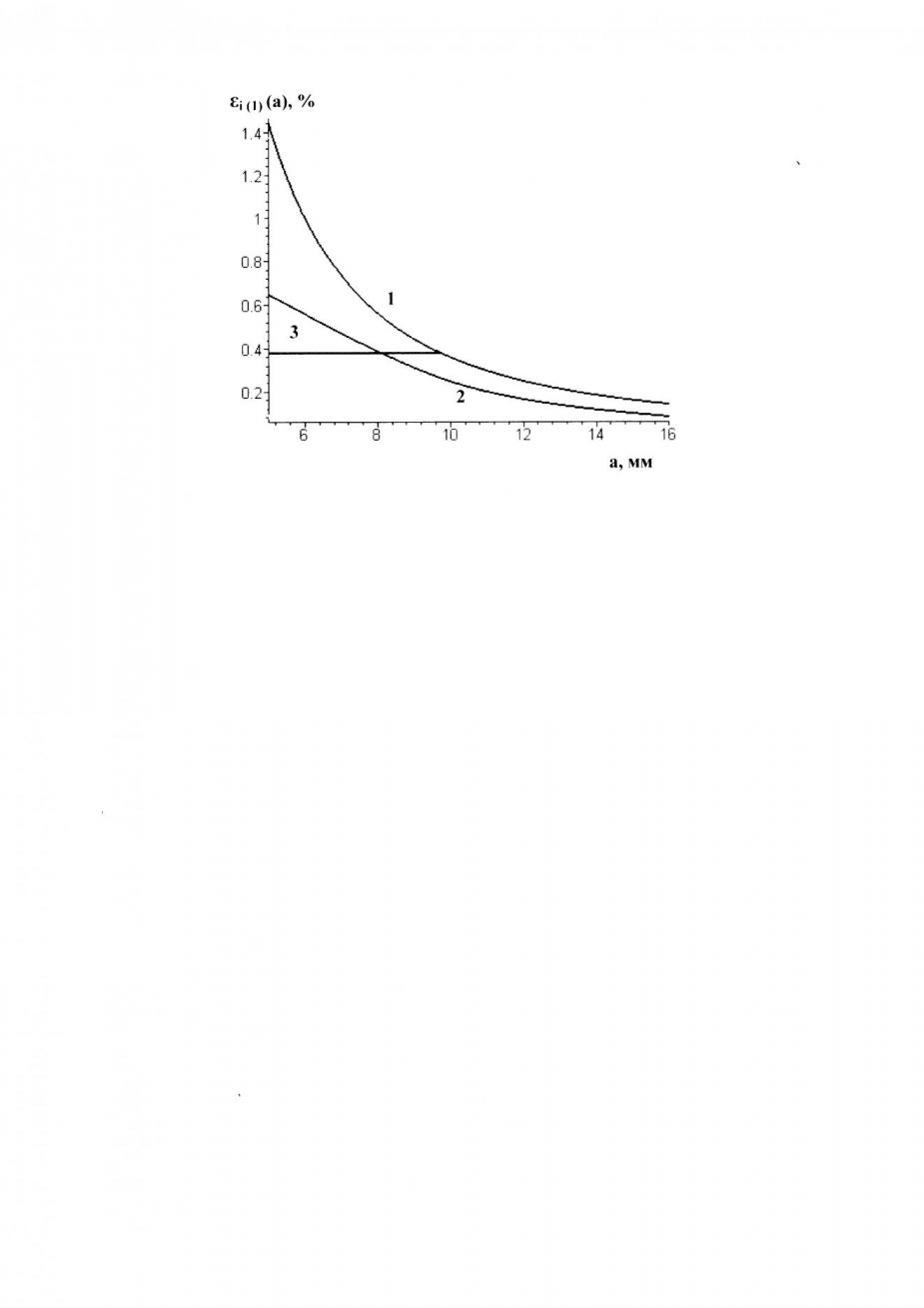
Рисунок 3 – Модель нагружения цилиндра внутренним давлением в условиях плоской деформации: q0 – внутреннее давление (контактная нагрузка), qN – торцевая нагрузка.

Рисунок 4 – Распределение интенсивности деформаций в листах: 1 – расчётная зависимость, 2 – экспериментальная зависимость, 3 – деформация на пределе текучести. Материал заклёпки В65, листов Д16Т. Параметры соединения r = 2.5 мм, = 5%.

Величина контактной нагрузки на контуре отверстия (a = r) равна

(12)

где r – номинальный радиус соединений (мм).

При использовании теории деформаций установлена взаимосвязь между неизвестной величиной радиуса пластической зоны и натяга в соединении

(13)

Для проверки полученных расчётных соотношений использованы результаты прямых измерений компонент деформаций в листах возле заклёпки с помощью малобазных тензодатчиков. Сравнение расчётных и экспериментальных значений показывает удовлетворительную сходимость по величине интенсивности деформаций i (1) и радиусу пластической зоны вокруг заклёпки (рис. 4). Невязка обусловлена, в том числе, различием между истинной величиной натяга и его измеряемым значением.

Разгрузка соединения происходит также в условиях плоской деформации. При этом контакт под выступающими головками непотайных соединений определённо отсутствует, а величина изменения контактной нагрузки определяется из уравнения совместности радиальных перемещений листа и заклёпки. При описании НДС стержня по теории прочности Мизеса для материалов с близкими свойствами (1= 2 и E1=E2) получено следующее выражение

(14)

где z – радиальный зазор при постановке заклёпки в отверстие.

Поскольку при формировании соединения стержень заклёпки находился в условиях всестороннего сжатия, снятие усилия клёпки может приводить к появлению обратных пластических деформаций даже на фоне падающей контактной нагрузки, если текущая интенсивность напряжений превосходит условный предел текучести, достигнутый в ходе формирования соединения. Таким образом, величина q1 также определяется неравенством

(15)

Контактная нагрузка при формировании заклёпочного соединения показана на рис. 5. В момент приложения усилия клёпки значение q0 возрастает с увеличением натягов, однако повышение величины q1 ограничено вследствие эффекта пластической разгрузки стержня. В конструкциях из лёгких сплавов он проявляется уже при ~ 2.5%.

Рисунок 5 – Влияние натяга на распределение контактной нагрузки: q0 – при действии усилия клёпки, q1 – при снятии усилия клёпки. 1 – область упругой разгрузки стержня, 2 – область пластической разгрузки стрежня. Материал заклёпки В65, листов Д16Т. Параметры соединения r = 2.5 мм, z = 0.1 мм.

Рисунок 6 – Распределение окружных остаточных напряжений в листах: 1 – расчётная зависимость 2 – экспериментальная зависимость. Материал заклёпки В65, листов Д16Т. Параметры соединения r = 2.5 мм, = 5%.

Остаточные напряжения в листах можно определить из решения Ляме:

(16)

Для проверки расчётной модели использованы экспериментальные значения окружных остаточных напряжений. Сравнение результатов (рис. 6) показывает удовлетворительную сходимость по всем основным параметрам за исключением глубины залегания, что обусловлено несоответствием расчётных соотношений в упругой зоне. Достоинством модели является определение уровня t (ост) на контуре отверстия, что практически невозможно сделать экспериментально.

Четвёртый раздел описывает нагружение заклёпочных соединений внешними силами.

Анализ конструкции герметичных заклёпочных соединений показывает, что основными видами их нагружения являются сдвиг заклёпки, а также растяжение или сжатие клёпаной панели. При наличии разгрузки и остаточных напряжений материал листов возле заклёпки деформируется упруго. Пластические деформации реализуются при условии

(17)

где i(p) - текущая интенсивность напряжений, (S)1U - условный предел текучести материала листа, достигнутый при формировании соединения

(18)

Нагружение заклёпки на сдвиг и панели на растяжёние или сжатие, как правило, рассматриваются в плоской постановке. При этом не учитывается влияние изгибающих моментов и соседних силовых точек. Интенсивность напряжений, определяемая по теории прочности Мизеса, равна

(19)

Величины, входящие в формулу интенсивности, получают сложением остаточных напряжений и напряжений от внешней нагрузки:

(20)

где r(p) – радиальные напряжения от внешней нагрузки (МПа), t(p) – окружные напряжения, х(p) – осевые напряжения, (p) – касательные напряжения.

При нагружении на сдвиг изменение контактной нагрузки принимается в виде косинусоидальной функции. При определении амплитудного значения из уравнения равновесия получено следующее выражение для контактной нагрузки

(21)

где P – усилие сдвига, – текущий угол, начиная от оси действия силы, – толщина листа.

Компоненты напряжений на контуре отверстия можно найти из решения задачи Н.И. Мусхелишвили о нагружении бесконечной пластинки сосредоточенной силой в условиях плоского напряжённого состояния и предположении о сплошности листа с установленной заклёпкой:

(22)

Отметим, что в области эксплуатационных усилий сдвиг заклёпки, как правило, не приводит к падению контактной нагрузки до нулевой отметки. Таким образом, при упругом нагружении условие сплошности контакта выполняется.

Рисунок 7 – Схема расчётной модели при растяжении клёпаной панели:

a) – постоянная часть, НДС, b) – переменная часть НДС.

При нагружении панели на растяжение или сжатие изменение контактной нагрузки в соответствии с решением Кирша принимается как функция вида

p·(1+k cos 2). В упругости возможно разделение НДС на постоянную (осесимметричную) и переменную составляющие (рис. 7). Расчёт постоянной части проводится по решению Ляме, а переменной с помощью специальной функции напряжения, описанной Киршем и П.Ф. Папковичем. При определении неизвестных значений p и k из уравнения совместности радиальных перемещений листа и заклёпки в условиях сплошности их контакта получено следующее выражение

(23)

где – напряжение растяжения панели.

Компоненты напряжений на контуре отверстия соответственно равны:

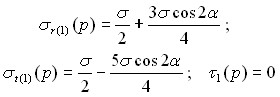(24)

В области эксплуатационных напряжений растяжение или сжатие клёпаных панелей, как правило, не приводит к падению контактной нагрузки до нулевой отметки. При упругом нагружении условие сплошности контакта также выполняется.

В пятом разделе проведены численные эксперименты по определению опасных уровней внешней нагрузки в зависимости от величины натяга, а также влияния различных конструктивно-технологических факторов на проницаемость заклёпочных соединений при сохранении сплошности контакта.

При нагружении заклёпочных соединений будем полагать, что потеря герметичных свойств совпадает с началом пластических деформаций на контуре отверстия. Условие разгерметизации определяется выражением (17), решение которого позволяет найти численные взаимосвязи между величиной натяга и напряжением разгерметизации k для каждого вида нагружения. При растяжении (рис. 8) или сжатии клёпаных панелей из Д16Т при оптимальном натяге = 4% критический уровень внешней нагрузки составляет k =180 МПа. Сравнение полученных расчётных значений (кривая 1) с аналогичными экспериментальными результатами В.З. Кондрашова (кривая 3) показывает удовлетворительную сходимость. Невязка обусловлена низкой чувствительностью метода испытаний на герметичность, который предусматривает накопление утечки, а также реальным расхождением начала обмятия листов и появления течи. Отметим, что расчётные значения также учитывают релаксацию остаточных напряжений (кривая 2), которая проявляется в качестве дефекта негерметичности только при условии знакопеременных нагрузок, что не учитывалось в эксперименте.

При сохранении сплошности контакта расход уплотняемой среды через единичное заклёпочное соединение определяется из выражений (1) или (2). Проведённые численные исследования показали, что изменение величины натяга >2.5% и неравномерность распределения контактной нагрузки не оказывают существенного воздействия на проницаемость вследствие наличия эффекта пластической разгрузки и узкой локализации низких уровней q соответственно. Таким образом, в практических расчётах при условии <k удобно принимать =2.5% и q() =q1.

Наибольшее влияние на герметичность при сохранении сплошности контакта оказывает высота микронеровностей сопрягаемых поверхностей листа и заклёпки (рис. 9). Например, при чистовой обработке зенкерованием проницаемость контакта снижается на 30% относительно сверления, а при развёртывании почти в 8 раз. При этом параметры опорных кривых оказывают куда меньшее воздействие на проницаемость, что позволяет в практических расчётах принимать величины и для отверстия полученного сверлением. Расход авиационного керосина через единичное заклёпочное соединение при Rz1 = 12 имеет порядок Q ~ 1·10-2 мм3/c. Исходные значения высоты микронеровностей и параметров опорных кривых для различных методов обработки отверстия приведены в таблице 1.

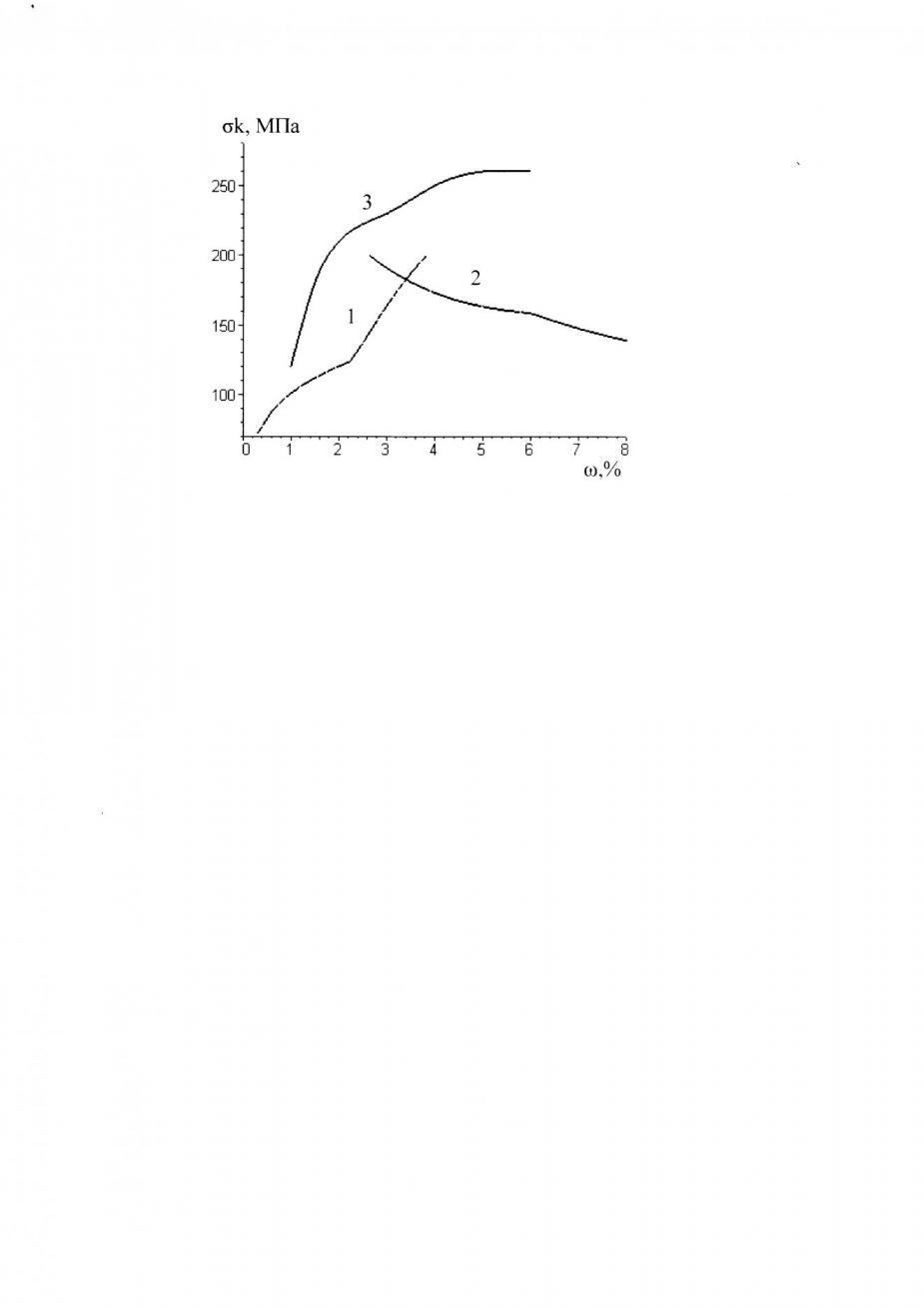
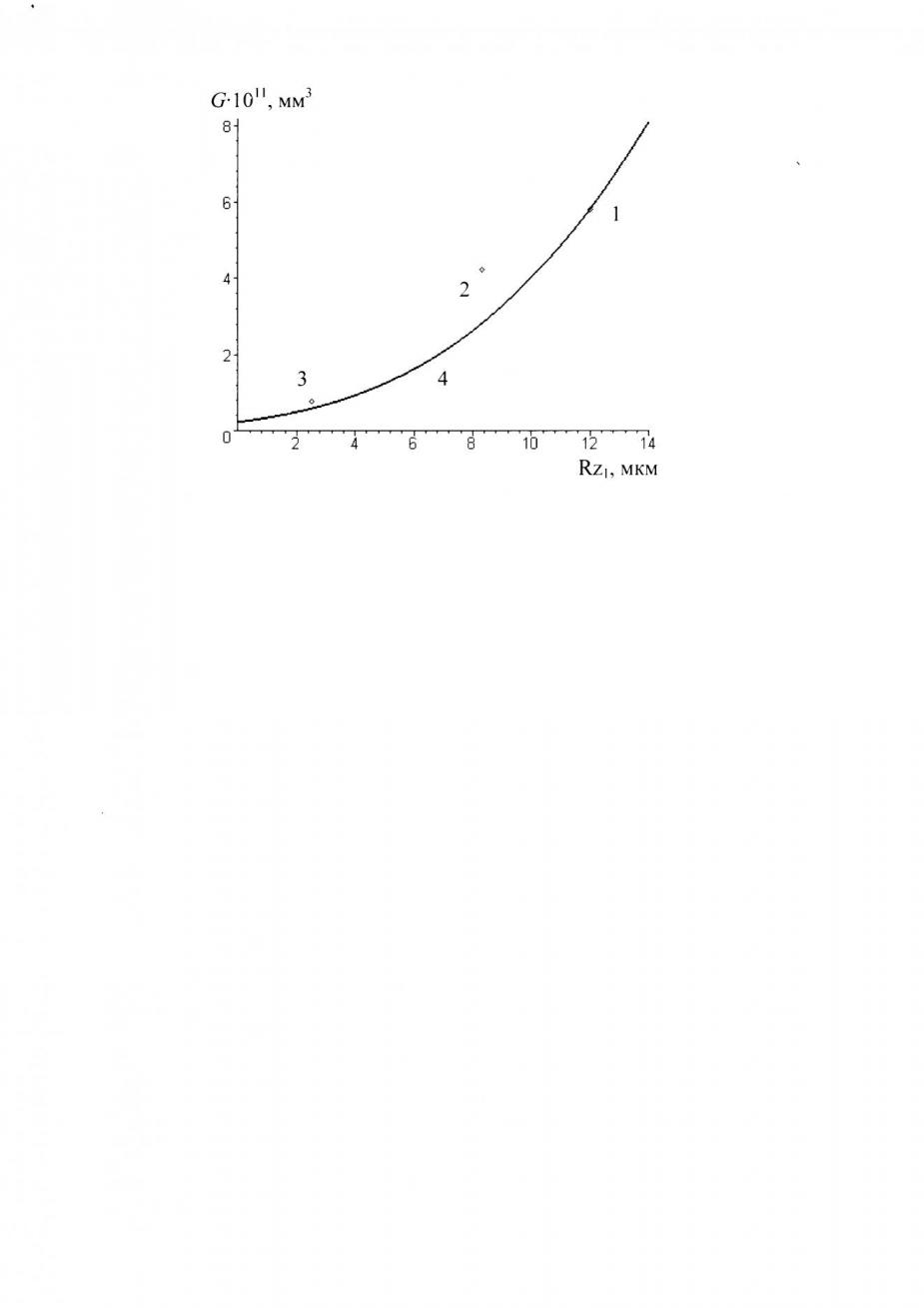
Рисунок 8 - Напряжения разгерметизации при растяжении клёпаной панели: 1 – зона пластических деформаций при =0, 2 – зона пластических деформаций при = /2, 3 – экспериментальная зависимость. Материал заклёпки В65, листов Д16Т. Параметры соединения r = 2 мм, z = 0.12 мм.

Рисунок 9 - Влияние шероховатости отверстия на проницаемость заклёпочных соединений: 1 – сверление, 2 – зенкерование, 3 – развёртывание, 4 – зависимость, полученная при постоянных значениях и для сверления. Материал заклёпки В65, листов Д16Т. Параметры соединения = 2.5 %.

Таблица 1. Высота микронеровностей и коэффициенты опорных кривых.

Вид чистовой обработки	Rz,мкм
сверление	12,0	1,49	1,27
зенкерование	8,3	1,56	1,39
развёртывание	2,5	1,72	1,65
заклёпка	4,0	2,12	1,43

На основе полученных результатов предложена методика оценки герметичности заклёпочных соединений для определения оптимальных конструктивно-технологических решений (рис. 10), под которыми понимается объём поверхностной герметизации, величина радиального натяга, вид чистовой обработки отверстия под заклёпку, а также некоторые геометрические параметры соединения, включая радиальный зазор при постановке заклёпки в отверстие. Данная методика содержит описания воздействий на проницаемость различных конструктивно-технологических факторов, что позволяет увязать обеспечение герметичности и других составляющих качества заклёпочных соединений. Она может применяться непосредственно на этапе проектирования изделий авиационной техники и приемлема для всех типов заклёпок и различных металлических материалов, используемых в производстве клёпаных конструкций.

На первом этапе находится контактная нагрузка в исходном состоянии, остаточные напряжения, интенсивность напряжений под действием внешних сил и напряжения разгерметизации. Далее производится выбор оптимальной величины натяга, который сопровождается проверкой условия < k. При выполнении неравенства сплошность контакта сохраняется, что позволяет отказаться от герметизации при снижении проницаемости посредством улучшения чистоты поверхности отверстия. В противном случае применение герметизации желательно, поскольку при появлении сквозной щели утечки значительно возрастают, а технологические мероприятия по снижению проницаемости не эффективны. Отметим, что выбор чистовой обработки отверстия, в принципе, возможно производить только после появления количественных требований к герметичности заклёпочных соединений.

Рисунок 10 – Схема оценки герметичности заклёпочных соединений.

Рис. 10 показывает, что описанная методика обладает элементарной внутренней структурой. В ходе исследований удалось выявить две принципиально различные картины проницаемости заклёпочных соединений (при наличии и отсутствии сплошности контакта) и установить критерий предельного состояния. В таких условиях оптимизация конструктивно-технологических параметров переходит к рассмотрению нескольких функций одной переменной, а также логических условий границы их применимости. Данные функции имеют ярко выраженный максимум (рис. 8) или монотонно возрастают (рис. 9) в области реальных конструктивных параметров.

Анализ эксплуатационных нагрузок показывает, что растяжение или сжатие клёпаной панели приводит к разгерметизации при любых значениях натягов, тогда как при сдвиге заклёпок, напротив, существует некоторый резерв нагружения. Таким образом, использование герметизации необходимо только в первом случае. Для реальных заклёпочных соединений вопрос о применении данной технологии должен решаться с учётом совместного действия всех внешних сил и уровня знакопеременных нагрузок, однако данная задача выходит за пределы работы.

Отметим, что использование ручной клёпки, иных видов заклёпок кроме стержневых, а также наличие потайной головки, как правило, приводят к ухудшению условий работы материала панели и снижению напряжений разгерметизации.

ОБЩИЕ ВЫВОДЫ

1. Разработан метод оценки герметичности заклёпочных соединений для определения оптимальных конструктивно-технологических решений и предложена соответствующая методика, которая может применяться непосредственно при проектировании клёпаных конструкций.

Установлено, что сокращение роли поверхностной герметизации возможно при сохранении сплошности контакта листа и заклёпки, что достигается выбором оптимальной величины натяга и некоторых геометрических параметров соединения. При этом улучшение чистоты поверхности отверстия под заклёпку позволяет повысить герметичные свойства соединения также только в условиях сплошности контакта.

2. Получено численное значение расхода керосина через единичное заклёпочное соединение при сохранении сплошности контакта, что позволяет определить влияние утечки топлива на эксплутационную безопасность изделий авиационной техники, а также установить количественные требования к герметичности клёпаных конструкций.
3. Получены расчётные значения контактной нагрузки в заклёпочных соединениях в исходном состоянии и под действием внешних сил. Описан эффект пластической разгрузки стержня заклёпки и определены теоретические значения остаточных напряжений в панелях.

Основные положения диссертации опубликованы в следующих работах:

1. Шишкин С.В., Махутов Н.А., Шишкин С.С. Распределение контактной нагрузки в кольцевой модели фланцевого соединения с отклонениями формы герметизируемых поверхностей // Проблемы машиностроения и надёжности машин, №4, 2006 г., С. 62-67.
2. Шишкин С.В., Махутов Н.А., Шишкин С.С. К расчёту пневматической проницаемости фланцевых соединений // Проблемы машиностроения и надёжности машин, №5, 2006 г., С. 42-47.
3. Шишкин С.В., Шишкин С.С. К расчёту авиационных заклёпочных соединений на герметичность // Проблемы машиностроения и надёжности машин, №3, 2008 г., С. 51-59.
4. Шишкин С.С. К расчёту герметичности заклёпочных соединений // Вестник МАИ, т. 16, №15, 2009 г., С. 131-134.
5. Шишкин С.С. К расчёту контактной нагрузки в заклёпочных соединениях // Проблемы машиностроения и надёжности машин, №1, 2010 г., С. 53-57.