Разработка и исследование оптимальной по критерию робастности системы гидроприводов для авиационого тренажер
На правах рукописи
УДК 62-523.3
Таха Али Ахмад
РАЗРАБОТКА И ИССЛЕДОВАНИЕ ОПТИМАЛЬНОЙ ПО КРИТЕРИЮ РОБАСТНОСТИ СИСТЕМЫ ГИДРОПРИВОДОВ ДЛЯ АВИАЦИОНОГО ТРЕНАЖЕР
Специальность 05.04.13 – Гидравлические машины, гидропневмоагрегаты
АВТОРЕФЕРАТ
диссертации на соискание ученой степени
кандидата технических наук
Москва - 2007
Работа выполнена в Московском государственном техническом университете имени Н.Э. Баумана.
Научный руководитель: - доктор технических наук,
профессор Попов Д.Н.
Официальные оппоненты: - доктор технических наук,
профессор Лалабеков В.И.,
- кандидат технических наук, Ситников С.Л.
Ведущая организация: Институт Машиноведения
Им. А.А. Благонравова РАН
Защита диссертации состоится 31 октября 2007 г. В 14 час. 30 мин. на заседании диссертационного совета Д 212.141.16 в Московском государственном техническом университете имени Н.Э. Баумана по адресу: 107005 Москва, 2-я Бауманская ул., д. 5.
С диссертацией можно ознакомиться в библиотеке Московского государственного технического университета им. Н.Э. Баумана.
Ваши отзывы в двух экземплярах, заверенные печатью, просьба выслать по указанному адресу. Желающие присутствовать на защите должны заблаговременно известить Совет письмами заинтересованных организаций на имя председателя совета.
Автореферат разослан “___” 2007 г.
| Ученый секретарь диссертационного совета Д 212.141.16 кандидат технических наук, доцент | Глухов С.Д. |
Общая характеристика работы
Актуальность темы. Электрогидравлический следящий привод (ЭГСП) широко используются в авиационных тренажерах благодаря необходимой динамической жесткости, способности развивать большие силы при высокой точности движения выходного звена и высокому быстродействию. Однако возникающая неопределенность и нестационарность распределения нагрузок, преодолеваемых каждым приводом, ограничивают возможности создания оптимальных систем управления авиационными тренажерами. Проведенные исследования научно обосновывают решение проблемы проектирования робастного по отношению к нагрузке на выходное звено ЭГСП с оптимальными динамическими характеристиками. При этом оптимизация ЭГСП достигается путем синтеза системы управления ЭГСП на основе широко распространенных в современной технике электрогидравлических усилителей (ЭГУ), гидроцилиндров (ГЦ) и насосных станций. Таким образом, совершенствование системы ЭГСП для авиационного тренажера является актуальной задачей.
Цель работы построить алгоритм структурного и параметрического синтеза регуляторов ЭГСП, предназначенных для управления положением и ориентации платформы авиационного тренажера с несколькими степенями подвижности.
Задачи работы:
выбор в результате обзора литературных источников схемы механической части системы, осуществляющей движение платформы авиационного тренажера посредством ЭГСП;
составление и исследование математических моделей ЭГСП авиационного тренажера;
синтез регуляторов ЭГСП, гарантирующих малую чувствительность исследуемой системы к изменению нагруженности приводов, т. е. обеспечивающих робастность ЭГСП по отношению к нагрузкам на выходное звено;
создание алгоритма расчета оптимальной по критериям качества управления и робастности нелинейной системы с ЭГСП для авиационного тренажера;
составление и решение уравнений „обратной кинематики” для определения алгоритмов управления каждым ЭГСП авиационного тренажера;
проверка основных результатов теоретических исследований с помощью экспериментальных данных и численных экспериментов.
Методы исследования. Задачи данной работы решались с использованием методов гидромеханики, механики, методов теорий линейных и нелинейных систем, методов теории оптимального управления, методов проектирования современных систем управления и методов компьютерного моделирования. При расчете переходных характеристик ЭГСП авиационного тренажера применились программные комплексные моделирования процессов управления, позволяющие определить коэффициенты регуляторов и выполнить как моделирование ЭГСП, так и моделирование движения всей платформы тренажера.
Научной новизной в работе являются:
решение задачи проектирования робастного ЭГСП для авиационного тренажера с шестью степенями подвижности;
структура адаптивного регулятора-наблюдателя с эталонной моделью, обеспечивающая робастные свойства системы „шесть ЭГСП - платформа тренажера” при оптимальном качестве процессов управления;
математические модели и алгоритмы управления ЭГСП с учетом различного положения и ориентации платформы тренажера.
Практическая ценность работы:
результаты исследования ориентированы на применение в инженерной практике проектирования и создания авиационных тренажеров с электрогидравлическими приводами в системах управления;
разработанные способы электронного корректирования ЭГСП позволяют избежать излишнего увеличения мощности и габаритных размеров используемого в испытательных установках гидрооборудования (ЭГУ, ГЦ, насосных станций).
Достоверность полученных результатов работы обеспечена тем, что решения задачи синтеза адаптивных регуляторов ЭГСП получены с помощью современных методов теории управления и апробированных методов компьютерного моделирования, а также подтверждены сравнением теоретических исследований с экспериментальными данными и результатами численных экспериментов.
Апробация работы. Разделы работы доложены на научной конференции студентов и аспирантов «Гидравлическая, вакуумная и компрессорная техника» в МГТУ им Н.Э. Баумана 19 апреля 2006 г., представлены на международной научно- технической и научно-методической конференции «Гидрогазодинамика, гидравлические машины и гидропневмосистемы» в Московском энергетическом институте (техническом университете) 14 декабря 2006 г., обсуждены на семинаре кафедры «Гидромеханика, гидромашины и гидропневмоавтоматика» МГТУ им Н.Э. Баумана 22 февраля 2007г.
Реализация работы математические модели и алгоритмы включены в учебные материалы для использования в курсовом и дипломном проектировании на кафедре «Гидромеханика, гидромашины и гидропневмоавтоматика» МГТУ им Н.Э. Баумана.
Публикации по материалам диссертации имеются четыре опубликованные работы.
Объем работы диссертация состоит из введения, четыре глав, заключения, приложений, списка литературы. Работа содержит 156 страницы печатного текста, 4 таблицы, 59 страниц рисунков, список литературы из 79 наименований и 22 страниц приложения.
Основное содержание работы
Во введение обоснована актуальность темы диссертации, определены цель и задачи работы, раскрываются научная новизна и практическая значимость работы.
В первой главе проведен обзор отечественных и зарубежных литературных источников, посвященных вопросам разработки оптимальных ЭГСП. Описаны общие требования и кинематические схемы авиационных тренажеров, представлены основные конструкции ЭГСП, используемых в системе управления платформой тренажера. Затем приводится краткий обзор методов управления ЭГСП, основанных на классической и современной теории управления. Приведены также методы проектирования робастной системы управления и нелинейных систем управления. На основе проведенного обзора сделаны выводы по главе и поставлены задачи исследований.
Во второй главе рассмотрены виды ГЦ и ЭГУ, которые применяются в системе управления платформой авиационного тренажера. Изложены методы оптимизации системы управления с помощью линейных моделей ЭГСП, получена эталонная модель ЭГСП, использованная при синтезе системы управления ЭГСП с учетом нелинейности его характеристик.
Авиационный тренажер в рассматриваемой задаче выполнено в виде платформы Стюарта, имеющей постоянную базу, шесть цилиндрических опор, шесть сферических опор, подвижную платформу и шесть одинаковых звеньев (рис. 1). Каждое звено состоит из ГЦ, датчика перемещения выходного звена и ЭГУ. Вместе эти устройства образуют ЭГСП (рис. 2).
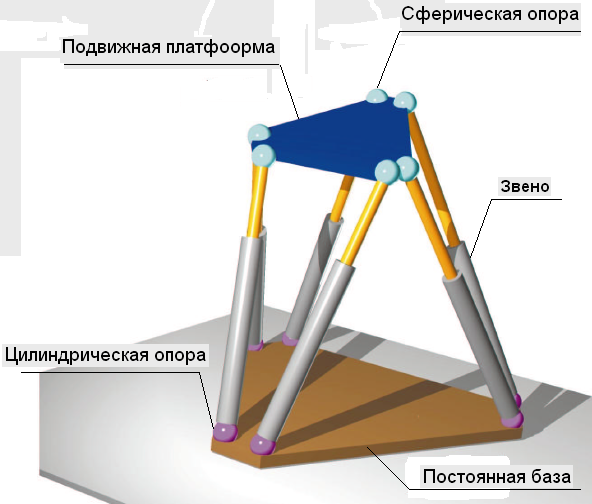
Рис.1
Сначала определены параметры ГЦ и ЭГУ, обеспечивающие требуемые кинематические характеристики платформы. Выбраны два вида ГЦ: симметричный (рис. 2а) для синтеза линейной эталонной модели и дифференциальный (рис. 2б) для реальной системы.
После определения математической линейной модели ЭГСП, для которого необходимо найти эталонную модель (рис. 2а), проведен анализ устойчивости исследуемой системы и оптимизированы её переходные характеристики. Для этого, прежде всего выбраны параметры П- регулятора при наличии обратных связей по трем переменным состояния: перемещение ![]() , скорость
, скорость ![]() и ускорение штока ГЦ. Решение получено с помощью уравнения Риккати и уравнения управления системой:
и ускорение штока ГЦ. Решение получено с помощью уравнения Риккати и уравнения управления системой:
![]() ;
; ![]() ,
,
где ![]() – матрица коэффициентов системы;
– матрица коэффициентов системы; ![]() – матрица входа; P – неотрицательно определенная симметричная матрица; Q и R – положительно определенные симметричные весовые матрицы;
– матрица входа; P – неотрицательно определенная симметричная матрица; Q и R – положительно определенные симметричные весовые матрицы; ![]() – вектор входа размерности;
– вектор входа размерности; ![]() – матрица коэффициентов регуляторов переменных состоянии;
– матрица коэффициентов регуляторов переменных состоянии; ![]() вектор состояния.
вектор состояния.
Оптимальные значения коэффициентов регулятора, проверены по условию обеспечения минимального значения интегрального критерия, учитывающего время и модуль ошибки (ИВМО), при ступенчатом входном сигнале: 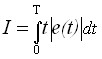 ,
,
где ![]() – верхний предел интегрирования выбирается произвольно так, чтобы интеграл стремился к конечному значению; обычно удобно выбирать
– верхний предел интегрирования выбирается произвольно так, чтобы интеграл стремился к конечному значению; обычно удобно выбирать![]() равным
равным ![]() времени установления;
времени установления; ![]() – ошибка после сумматора (рис. 3а).
– ошибка после сумматора (рис. 3а).
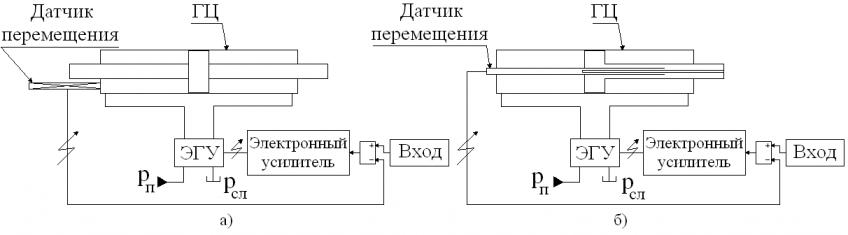
Рис. 2
Для реализации систем с регулированием по переменным состояния, не усложняя схемы контроля состояния привода, можно применить систему управления с «наблюдателем». С помощью наблюдателя управление системой осуществляется не на основе измеренных переменных состояния, а на основе вычисляемых переменных. Уравнение наблюдателя можно записать в виде ![]()
Матрицы ![]() ,
, ![]() и
и ![]() должны быть выбраны таким образом, чтобы значения
должны быть выбраны таким образом, чтобы значения ![]() давали точную оценку
давали точную оценку![]() . Тогда в системе управления вектор
. Тогда в системе управления вектор ![]() используется для формирования сигнала обратной связи
используется для формирования сигнала обратной связи ![]() .
.
Эту процедуру легко реализовать на компьютере, написав несложную программу. С помощью программы получена передаточная функция регулятора – наблюдателя в виде 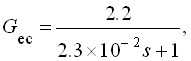
По структурной схеме (рис. 3а) путем компьютерного моделирования вычислена переходная характеристика (рис. 3б). Сравнение этой переходной характеристики с характеристиками, полученными при непосредственном измерении переменных состояния, показывает, что время установления системы в обоих случаях имеет одинаковые значения.

Рис. 3
На рис.3: 1 регулятор-наблюдатель; ![]() передаточная функция обмотки управления ЭГУ;
передаточная функция обмотки управления ЭГУ; ![]() передаточная функция ЭГУ;
передаточная функция ЭГУ; ![]() передаточная функция ГЦ
передаточная функция ГЦ
Для проверки робастности ЭГСП по отношении к нагрузке на его выходное звено, проведена оценка влияния переменной нагрузки на выходное звено ГЦ в соответствии с алгоритмом, блок-схема которого представлена на рис. 4а. При расчетах диапазон изменения нагрузок на выходное звено ЭГСП принят равным ±25% от номинального значения. В результате вычислены переходные и частотные характеристики ЭГСП, которые подтверждают, что динамические характеристики модели практически не изменяются при разных нагрузках на выходное звено (рис. 4б). Таким образом, математическую модель, которая представлена структурной схемой, изображенной на рис. 3а, можно использовать как эталонную модель ЭГСП. Однако модели соответствует дифференциальное уравнение седьмого порядка. Для упрощения эталонной модели необходимо понизить её порядок. С этой целью может быть применен способ, при котором система разбивается на две подсистемы:
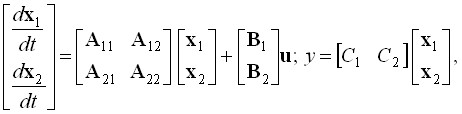
где ![]() сохраняемая часть вектора состояний
сохраняемая часть вектора состояний ![]() ;
; ![]() - часть вектора
- часть вектора ![]() , подлежащая удалению.
, подлежащая удалению.
Приравнивая производную ![]() нулю и подставляя полученное при разрешении уравнения
нулю и подставляя полученное при разрешении уравнения ![]() относительно
относительно ![]() выражение в подсистему, которая соответствует вектору
выражение в подсистему, которая соответствует вектору ![]() , находим пониженного порядка математическую модель в виде
, находим пониженного порядка математическую модель в виде

В результате математическое описание эталонной модели рассмотренного ЭГСП сведено к уравнению третьего порядка и представлено передаточной функцией 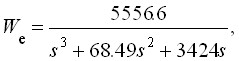
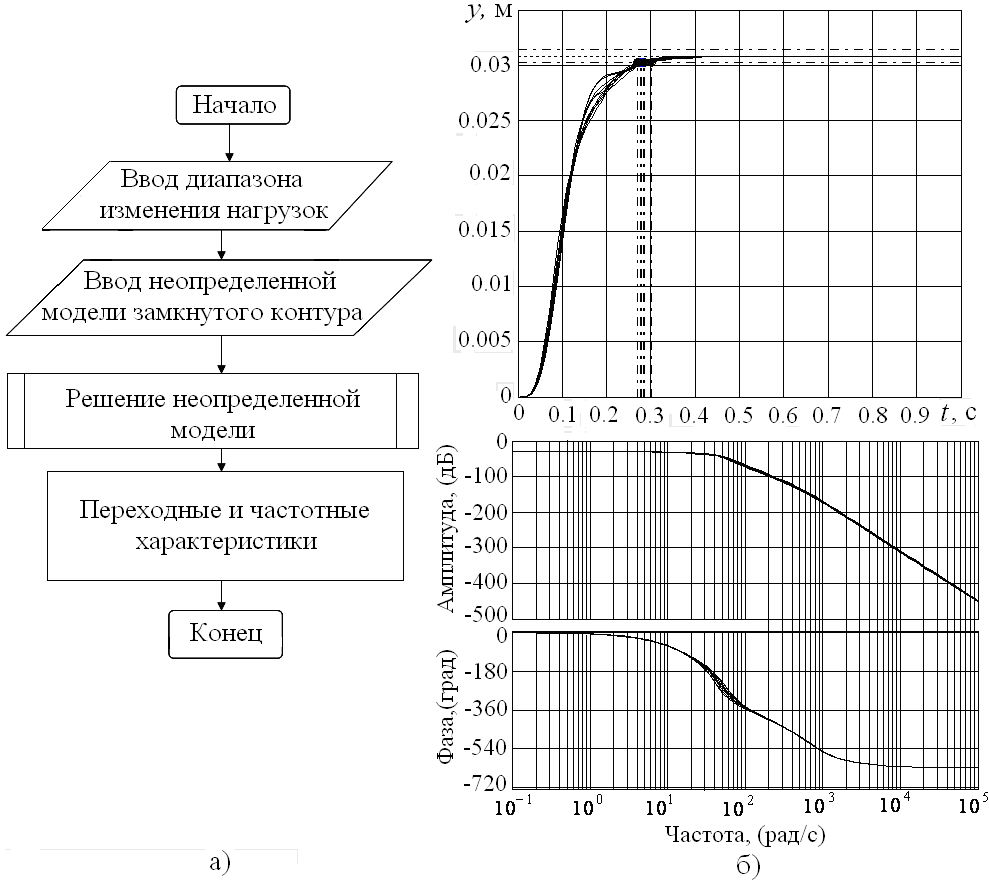
Рис. 4
Третья глава посвящена решению задачи оптимального управления нелинейным ЭГСП, робастным в отношении изменения нагрузки на его выходное звено. Выбран оптимальный регулятор ЭГСП. В регуляторе реализованы алгоритмы адаптации, осуществляемой с помощью эталонной модели.
Схема ЭГСП, для которого необходимо найти оптимальный регулятор, показана на рис. 2б. Нелинейные уравнения для этого ЭГСП преобразованы следующим образом (производные по времени обозначены точкой над переменной):


при ![]()

при ![]()

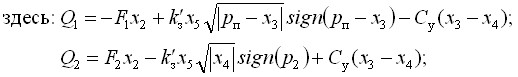

где ![]() – сумма масс поршня, штока ГЦ и приведенной к штоку массы управляемого устройства;
– сумма масс поршня, штока ГЦ и приведенной к штоку массы управляемого устройства; ![]() – коэффициент вязкого трения;
– коэффициент вязкого трения; ![]() – внешняя сила;
– внешняя сила; ![]() – рабочие площади поршня левой и правой полостях ГЦ;
– рабочие площади поршня левой и правой полостях ГЦ; ![]() – модуль объемной упругости жидкости;
– модуль объемной упругости жидкости; ![]() – объемы жидкости в трубках, соединяющих ГЦ с ЭГУ;
– объемы жидкости в трубках, соединяющих ГЦ с ЭГУ;![]() ход штока ГЦ;
ход штока ГЦ; ![]() – удельная проводимость окон распределителя;
– удельная проводимость окон распределителя; ![]() – давления в полостях гидроцилиндра;
– давления в полостях гидроцилиндра; ![]() – давление питания;
– давление питания; ![]() – перемещение золотника ЭГУ;
– перемещение золотника ЭГУ; ![]() – коэффициент утечки жидкости в гидроцилиндре;
– коэффициент утечки жидкости в гидроцилиндре; ![]() и
и ![]() – собственная частота и коэффициент демпфирования ЭГУ;
– собственная частота и коэффициент демпфирования ЭГУ; ![]() – коэффициент преобразования электрического напряжения входного сигнала в перемещение золотника ЭГУ;
– коэффициент преобразования электрического напряжения входного сигнала в перемещение золотника ЭГУ; ![]() напряжение входного сигнала.
напряжение входного сигнала.
Для компьютерного моделирования рассмотренного ЭГСП с помощью приведенных нелинейных уравнений, построена структурная схема (рис. 5а). Использованы коэффициенты ![]() ,
, ![]() для обеспечения разных смещений золотника ЭГУ. В результате моделирования получены переходные характеристики при выдвижении и втягивании штока ГЦ (рис. 5б).
для обеспечения разных смещений золотника ЭГУ. В результате моделирования получены переходные характеристики при выдвижении и втягивании штока ГЦ (рис. 5б).
Переходные характеристики ЭГСП без регулятора (рис. 5б) показывают, что процесс близок к неустойчивому особенно при втягивании штока ГЦ. Для исследования устойчивости ЭГСП был использован второй метод А. М. Ляпунова, потому что функции Ляпунова затем применялись при синтезе алгоритмов адаптации и вычислении коэффициентов регулятора, предназначенного для системы управления ЭГСП. С помощью приведенных выше уравнений определялась функция Ляпунова для ошибки ![]() между переменами
между переменами ![]() состояния реальной системы и переменами
состояния реальной системы и переменами ![]() состояния эталонной модели. Чтобы обеспечить
состояния эталонной модели. Чтобы обеспечить ![]() при
при ![]() , где
, где ![]() функцию Ляпунова имеет смысл выбрать в форме, используемой в критерии оптимизации:
функцию Ляпунова имеет смысл выбрать в форме, используемой в критерии оптимизации:![]() где
где ![]()
Для устойчивости исследуемой системы должно быть выполнено неравенство ![]() , причем
, причем 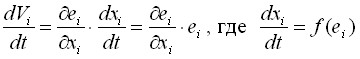 . При применении данного условия и записанных выше нелинейных уравнений законы управления, а также производная от функции Ляпунова получены в приведенном нижнем виде.
. При применении данного условия и записанных выше нелинейных уравнений законы управления, а также производная от функции Ляпунова получены в приведенном нижнем виде.
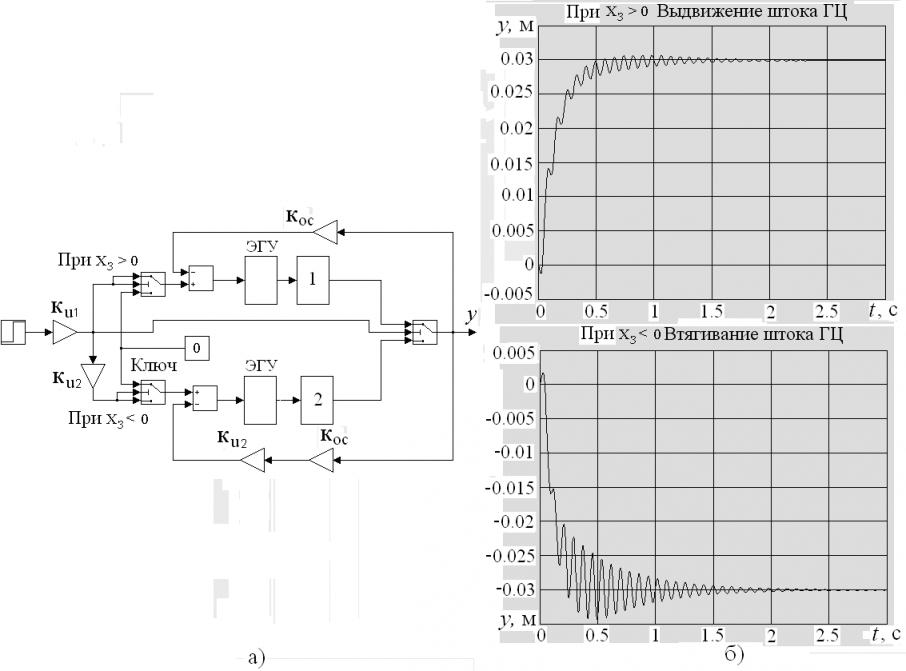
Рис. 5
На рис. 5а: 1 блок для вычисления процесса выдвижения штока ГЦ; 2 блок для вычисления процесса втягивания штока ГЦ
Для выхода эталонной модели ![]() ,
, ![]()
В этом случае:
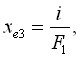
 ,
, 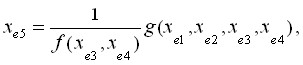
![]()
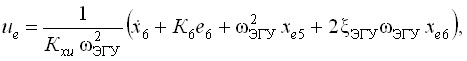
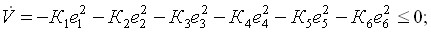
если ![]() , то
, то
![]()
![]()

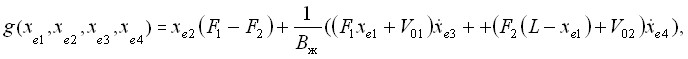
если ![]() , то
, то
![]()
![]()
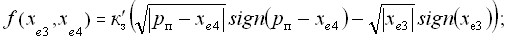
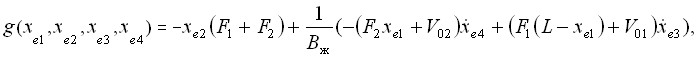
Здесь ![]() – напряжение датчика обратной связи регулятора;
– напряжение датчика обратной связи регулятора; ![]() – коэффициенты усиления регулятора.
– коэффициенты усиления регулятора.
Чтобы найти способы, обеспечивающие у реального ЭГСП переходные характеристики близкие к характеристикам эталонной модели, были рассмотрены два подхода к синтезу алгоритма адаптации для одного ЭГСП. При этом, все переменные состояния ЭГСП считались доступными для измерения.
В первом подходе за эталонную принята математическая модель, структурная схема, которой изображена на рис. 3а. При использовании такой эталонной модели в каждом из шести ЭГСП тренажера, управление движением платформы усложняется, что может вызвать увеличение продолжительности переходных процессов. Поэтому был рассмотрен упрощенный алгоритм, полученный с помощью той же нелинейной математической модели ЭГСП и тех же функций Ляпунова, которые применялись сначала. В таком втором подходе использована пониженного порядка эталонная модель. Чтобы учесть возможную нестабильность нагрузки, уравнение ![]() , действующих на выходное звено сил, было заменено двумя уравнениями:
, действующих на выходное звено сил, было заменено двумя уравнениями:
при ![]()
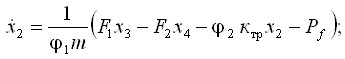
при ![]()
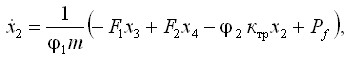
где ![]() и
и ![]() – компоненты фактического вектора
– компоненты фактического вектора ![]() нагрузки.
нагрузки.
При изменении уравнении нагрузки функции Ляпунова изменяются. В результате получен следующий алгоритм адаптации
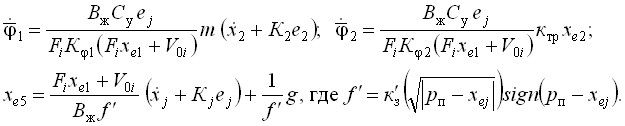
здесь ![]() и
и ![]() компоненты вектора
компоненты вектора ![]() оценки нагрузки,
оценки нагрузки,
В этом алгоритме адаптации:
при ![]()
![]() ;
; ![]() ;
; 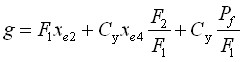 ,
,
при ![]()
![]() ;
; ![]() ;
; 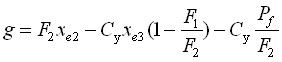 ,
,
Коэффициенты ![]() алгоритма адаптации выбирались так, чтобы сохранялись значения
алгоритма адаптации выбирались так, чтобы сохранялись значения ![]() в допустимом диапазоне изменения нагрузки ±25% от номинального значения. С помощью записанных выше формул построена структурная схема ЭГСП с упрощенным алгоритмом самонастройки адаптивного регулятора (рис. 6). В соответствии с алгоритмом, блок-схема которого представлена на рис. 7а, рассчитывались переходные характеристики ЭГСП с упрощенным адаптивным регулятором (рис. 7б) при различных нагрузках. Характеристики показывают, что с помощью упрощенного алгоритма адаптации можно сохранить вычисленные при первом подходе переходные характеристики ЭГСП, не увеличивая продолжительность процесса адаптации. Упрощенный алгоритм адаптации дает возможность уменьшения продолжительности переходных процессов ЭГСП в реальном времени. При применении этого алгоритма в каждом из шести ЭГСП тренажера, система управления движением платформы тренажера не усложняется и процесс моделирования движения платформы будет близким к процессу в реальном времени.
в допустимом диапазоне изменения нагрузки ±25% от номинального значения. С помощью записанных выше формул построена структурная схема ЭГСП с упрощенным алгоритмом самонастройки адаптивного регулятора (рис. 6). В соответствии с алгоритмом, блок-схема которого представлена на рис. 7а, рассчитывались переходные характеристики ЭГСП с упрощенным адаптивным регулятором (рис. 7б) при различных нагрузках. Характеристики показывают, что с помощью упрощенного алгоритма адаптации можно сохранить вычисленные при первом подходе переходные характеристики ЭГСП, не увеличивая продолжительность процесса адаптации. Упрощенный алгоритм адаптации дает возможность уменьшения продолжительности переходных процессов ЭГСП в реальном времени. При применении этого алгоритма в каждом из шести ЭГСП тренажера, система управления движением платформы тренажера не усложняется и процесс моделирования движения платформы будет близким к процессу в реальном времени.
В четвертой главе для проверки эффективности действия разработанного регулятора ЭГСП было выполнено компьютерное моделирование системы управления платформой с шестью степенями подвижности. В исследуемой системе адаптивный регулятор с эталонной модели и с обратной связью по переменным состояния реальной ЭГСП входит в каждый из шести ЭГСП тренажера.
Чтобы моделировать движение платформы, сначала необходимо решить задачу обратной кинематики платформы авиационного тренажера и построить механическую модель тренажера. При решении задачи обратной кинематики вычисляются перемещения звеньев, обеспечивающих требуемые положение и ориентацию платформы, а также находится механическая модель тренажера, которая состоит из шести цилиндрических опор, закрепленных на постоянной базе, шести сферических опор, платформы и шести звеньев, соединяющие эти платформы (рис. 8). Звено состоит из двух тел. Верхним телом является шток ГЦ, который соединен с подвижной платформой через сферическую опору. Нижнее тело (гидроцилиндр) соединено с базой посредством цилиндрической опоры. Входными сигналами механической модели будут шесть сил, вычисляемых при переходных процессах ЭГСП с помощью уравнений: ![]() при
при ![]() ,
, ![]()
![]() при
при ![]() ,
, ![]()
где ![]() силы, действующие на шток ГЦ.
силы, действующие на шток ГЦ.

Рис. 6
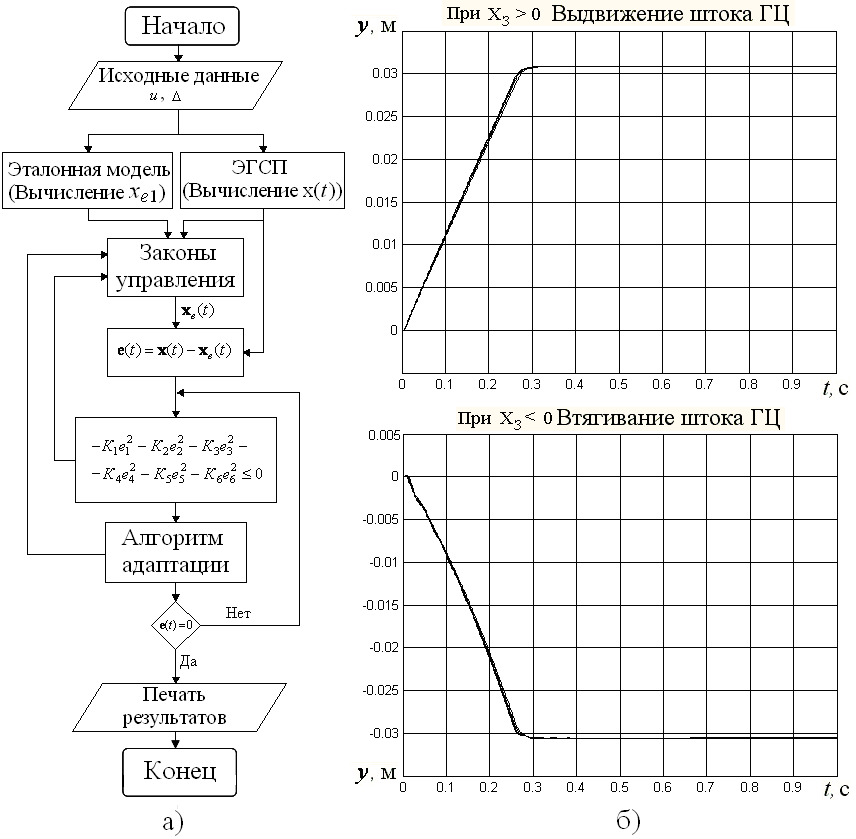
Рис. 7

Рис. 8
Выходными сигналами механической модели являются шесть перемещений верхних тел (конечные значения ![]() перемещений штоков ГЦ).
перемещений штоков ГЦ).
После решения задачи обратной кинематики и создания механической модели тренажера, построена общая структурная схема системы управления платформой тренажера (рис. 9а).
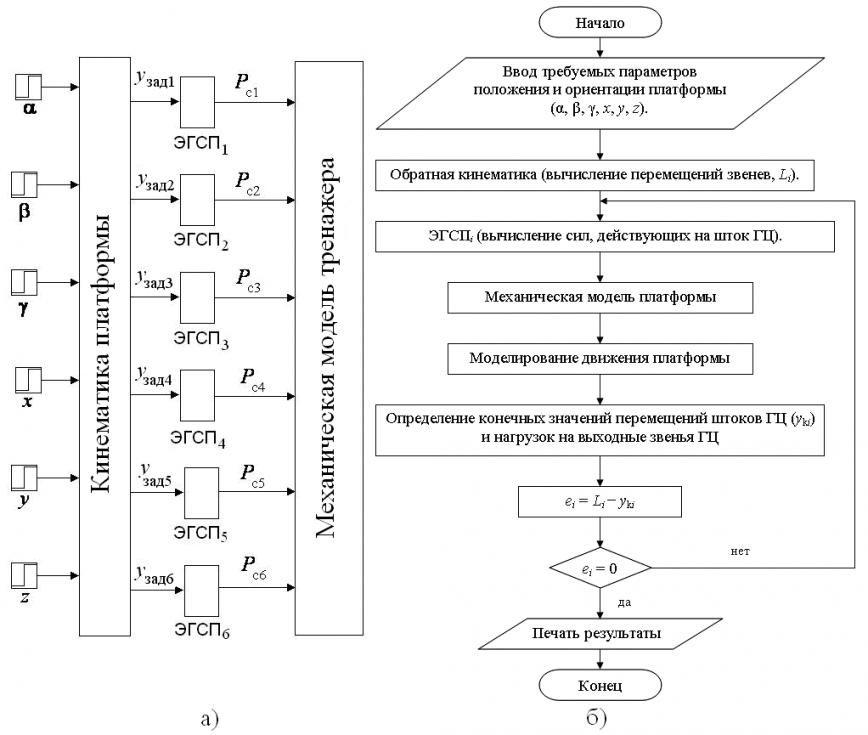
Рис. 9
Сначала компьютерное моделирование движения платформы выполнено без дополнительных регуляторов ЭГСП; вычисленные переходные характеристики шести ЭГСП показывают, что система управления тренажером неустойчива (рис.10). Неустойчивое движение штоков ГЦ создают силы, которые действуют на платформу со стороны каждого ГЦ. Эти силы изменяются в большом диапазоне значений, что вызывает деформацию платформы (рис. 10). Для устранения указанного недостатка применены регуляторы в каждом из шести ЭГСП. В соответствии с алгоритмом, блок-схема которого представлена на рис. 9б, проведено моделирование движения платформы и рассчитывались переходные процессы в шести ЭГСП с адаптивными регуляторами. Изменения нагрузок на выходные звенья ГЦ определялись при заданных конечных значениях координат положения центра массы платформы. Из переходных характеристик (рис. 11) следует, что быстродействие шести ЭГСП значительно увеличились по сравнению с характеристиками, использованными в предыдущем расчете (рис.10).
Результаты компьютерного моделирования подтверждают, что адаптивные регуляторы обеспечивают робастное в отношении нагрузок на выходные звенья ГЦ управление платформой, уменьшая расхождение между требуемыми значениями перемещений штоков ГЦ и конечными значениями этих перемещений в переходных процессах. При компьютерном моделировании проводилась также проверка роли адаптивных регуляторов в случае слежения системы управления за гармоническим входным сигналом. На рис. 12, приведены траектории шести выходных звенья ГЦ при заданной траектории платформы. Траектории показывают, что предложенный адаптивный регулятор с эталонной моделью, действующий в каждом из шести ЭГСП, обеспечивает превосходное слежение системы управления за требуемой траекторией при максимальной частоте, не превышающей ![]() . Ошибка, определяемая разностью входных и выходных сигналов, не больше 2% от максимальной амплитуды сигнала управления.
. Ошибка, определяемая разностью входных и выходных сигналов, не больше 2% от максимальной амплитуды сигнала управления.
Для проверки совершенства предлагаемой в диссертации системы управления ЭГСП выполнено компьютерное моделирование этой системы при параметрах, указанных в двух работах: Chin-I Huang., Li-Chen Fu. Adaptive backstepping tracking control of the Stewart platform//43rd IEEE Conference on Decision and Control. December. -2004. -P. 5228-5233 и Sirouspour M. R., Salcudean S. E. Nonlinear control of hydraulic robots // IEEE Transactions on robotics and automation. -April 2001. -P. 1-11. Результаты компьютерного моделирования показывают, что при использовании предлагаемой в диссертации системы, которая отличается от известных примененными в ней регуляторами, шесть ЭГСП точно воспроизводят траектории, заданные в указанных выше работах. Применение адаптивного регулятора с эталонной моделью дает возможность уменьшить динамическую ошибку и при переходных процессах ЭГСП. В этом случае динамическая ошибка получилась близкой нулю.

Рис. 10
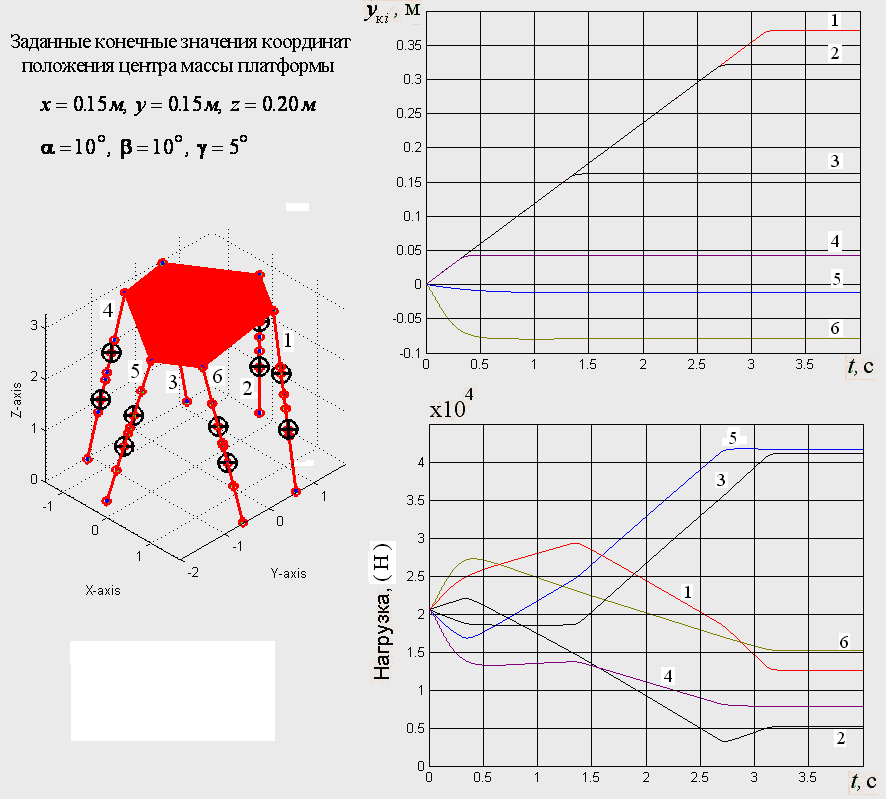
Рис. 11
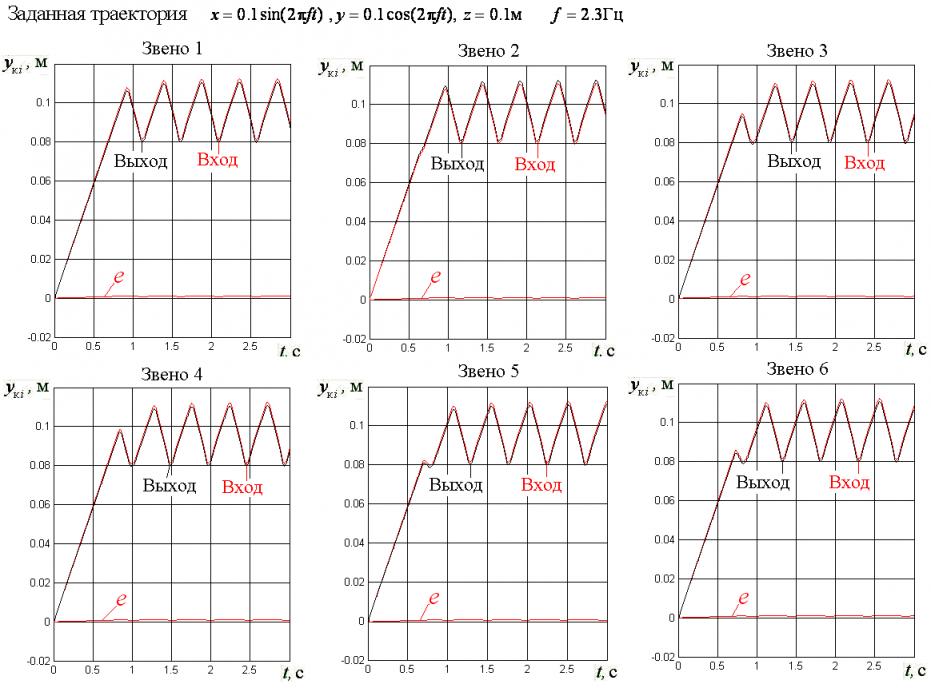
Рис. 12
ОБЩИЕ ВЫВОДЫ
1. В диссертации разработана и исследована система электрогидравлических следящих приводов (ЭГСП) для авиационного тренажера. Предлагаемая система может быть также применена для управления расточным станком с неподвижным центром, хирургическим столом и другими объектами, имеющими несколько степеней подвижности.
2. Особенностью разработанной системы является то, что в ней реализованы комбинированные методы робастно-адаптивного управления. При этом синтез структуры и параметров адаптивного регулятора проведен с помощью эталонной модели, предварительно оптимизированной в результате исследования динамики ЭГСП с линеаризованными характеристиками.
3. Решение задачи синтеза регулятора с учетом нелинейности характеристик ЭГСП получено на основе второго метода Ляпунова.
4. Построенный в диссертации алгоритм беспоисковой самонастройки регулятора позволяет сократить продолжительность переходных процессов, обеспечивая тем самым требуемое быстродействие реальной системы.
5. Для управления всей системой, состоящей из шести ЭГСП, каждый из которых снабжен адаптивным регулятором, в диссертации предложен алгоритм, содержащий расчет в реальном времени обратной кинематики платформы авиационного тренажера. Указанный алгоритм придает разработанной системе свойства интеллектуальной системы.
6. Изложенная в диссертации методика и алгоритмы управления могут служить основой для проектирования современных интеллектуальных ЭГСП различного назначения.
7. Результаты компьютерного моделирования системы управления авиационным тренажером с шестью ЭГСП показывают, что применение в приводе разработанного адаптивного регулятора улучшает качество переходных процессов и повышает точность слежения за заданными траекториями.
8. Адекватность математических моделей и рассчитанных по ним динамических характеристик исследуемой системы, подтверждена сравнением результатов компьютерного моделирования с экспериментальными данными, опубликованными в иностранных литературных источниках по двум системам управления авиационными тренажерами. При этом сравнении установлено, что предлагаемый в диссертации адаптивный регулятор-наблюдатель в каждом ЭГСП обеспечивает управление тренажерами практически с нулевой ошибкой.
Основные результаты диссертации отражены в следующих работах:
1. Таха А.А., Попов Д.Н. Синтез структурной схемы электрогидравлического привода авиационного тренажера // Наука в образовании: Электронное научное издание. Инженерное образование. -2006. -№11. -9с.
2. Попов Д. Н., Таха А.А. Структурный и параметрический синтез электрогидравлического следящего привода авиационного тренажера // Труды международной научно-технической и научно-методической конференции в Московском энергетическом институте (техническом университете). -Москва, 2006. -С 180-183.
3. Попов Д.Н., Таха А.А. Проектирование электрогидравлического следящего привода с неопределенными и нестационарными нагрузками на выходное звено // Вестник МГТУ. Машиностроение. -2007. -№1(66). -С. 99112.
4. Попов Д. Н., Таха А. А. Выбор оптимального регулятора для робастного управления электрогидравлическим следящим приводом авиационного тренажера с шестью степенями подвижности // Известия Вузов. Машиностроение. - 2007. -№ 9.- С. 25-33.

