Разработка способа гибки на малый радиус фланцев облицовочных деталей автомобилей из алюминиевых сплавов и методики расчета его технологических параметров

На правах рукописи

УДК 621.98.044

Горьков Максим Александрович

РАЗРАБОТКА СПОСОБА ГИБКИ НА МАЛЫЙ РАДИУС ФЛАНЦЕВ

ОБЛИЦОВОЧНЫХ ДЕТАЛЕЙ АВТОМОБИЛЕЙ ИЗ

АЛЮМИНИЕВЫХ СПЛАВОВ И МЕТОДИКИ РАСЧЕТА ЕГО

ТЕХНОЛОГИЧЕСКИХ ПАРАМЕТРОВ

Специальность 05.03.05 – Технологии и машины обработки давлением

АВТОРЕФЕРАТ

диссертации на соискание ученой степени

кандидата технических наук

Москва

2007

Работа выполнена в Московском Государственном Техническом Университете им. Н.Э. Баумана.

Научный руководитель: доктор технических наук,

доцент Власов

Андрей Викторович

Официальные оппоненты: доктор технических наук,

профессор Шестаков

Николай Александрович (МГИУ)

кандидат технических наук,

профессор Шпунькин

Николай Фомич (МГТУ МАМИ)

Ведущая организация – АМО “ЗИЛ”

Защита состоится «24» октября 2007 г. в 14 ч. 30 мин. на заседании диссертационного совета Д 212.141.04 в Московском государственном техническом университете им. Н.Э. Баумана по адресу:

105005, г. Москва, 2-ая Бауманская ул., д.5.

Телефон для справок 267-09-63.

Ваш отзыв на автореферат в одном экземпляре, заверенный печатью, просим направлять по указанному адресу.

С диссертацией можно ознакомиться в библиотеке Московского государственного технического университета им. Н.Э. Баумана.

Автореферат разослан «11» сентября 2007 г.

Ученый секретарь

диссертационного совета

кандидат технических наук, доцент Семенов В.И.

ОБЩАЯ ХАРАКТЕРИСТИКА РАБОТЫ

Актуальность работы.

В последние десятилетия автомобильные компании во всем мире проводят научно-исследовательские работы, связанные с уменьшением массы новых автомобилей. Актуальность этих работ растет по мере истощения энергетических ресурсов на нашей планете, в связи с их постоянным удорожанием и неудовлетворительной экологической обстановкой в городах. Несмотря на это количество выпускаемых машин неуклонно растет с каждым годом.

Существует тесная связь между массой автомобиля, расходом топлива и соответственно объемом выхлопных газов. Например, снижение массы на 30% позволило бы уменьшить расход топлива примерно на 50%. Однако масса новых автомобилей постоянно увеличивается.

На кузов автомобиля приходится примерно 26% от общего веса, поэтому снижение его массы является одной из приоритетных задач.

Перспектива внедрения алюминиевых сплавов обусловлена тем, что при сопоставимой со сталью прочности его плотность почти в три раза ниже. При этом алюминиевые детали имеют высокие антикоррозионные свойства и поглощают энергию удара на 50% лучше, чем стальные. К тому же из алюминиевых сплавов можно создать конструктивные элементы наиболее оптимальной формы для повышения жесткости. Однако из-за низкого запаса пластичности внедрение удовлетворяющих требованиям автомобильной промышленности алюминиевых сплавов затруднено. Например, Ford Motor Company использует сплав 6111-Т4.

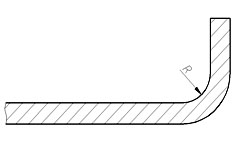
Облицовочные детали автомобилей, такие как капоты, багажники, передние и задние двери, состоят из двух панелей – внутренней и внешней. Традиционным методом их сборки является гибка фланца внешней панели по всему контуру на 180° с охватом фланца внутренней панели. Гибка происходит последовательно на 90°, 135° и 180° (рис.1).

Величина радиуса гиба r на первом этапе должна удовлетворять условию r<0,5t, где t – толщина металла. Таким образом, при толщине панели, равной 1 мм, радиус гиба не должен превышать 0,5 мм. При использовании традиционной технологии выполнение этого условия для стальных деталей не вызывает трудностей, однако при гибке деталей из алюминиевых сплавов трещины образуются уже на первой операции. Многочисленные эксперименты, проведенные на кафедре “Технологии обработки давлением” МГТУ им. Н. Э. Баумана показали, что именно первая операция (гибка на 90°) является ключевой, фактически определяющей качество конечной детали.

а б в

Рис. 1. Операции традиционного процесса сборки:

а – гибка фланца на 90°; б – гибка фланца на 135°;

в – гибка фланца на 180°

В автомобильной, авиационной и аэрокосмической промышленностях существует определенная номенклатура деталей из алюминиевых сплавов, для которых гибка на 90° с малым радиусом является окончательной операцией.

Для реализации в промышленности существующих в настоящее время технологических процессов гибки на малый радиус (здесь и далее под малым радиусом подразумевается величина r<0,5t, где t – толщина заготовки) требуются слишком либо сложная в изготовлении и настройке оснастка, либо специализированное оборудование. Использование сварки в качестве сборочной операции является низкопроизводительным процессом, требующим при этом значительного энергопотребления.

Разработка способа гибки на 90° с малым радиусом для деталей из алюминиевых сплавов с возможностью реализации на стандартном прессовом оборудовании и методики расчета подобных процессов являются на сегодняшний день актуальными проблемами.

Целью работы Разработка нового способа гибки на малый радиус фланцев облицовочных деталей автомобилей из алюминиевого сплава 6111-Т4, позволяющего получить качественную деталь на стандартном прессовом оборудовании, и методики расчета его параметров с учетом прогнозирования разрушения на основе численного моделирования.

Методы исследований.

Теоретическое исследование напряженно-деформированного состо-яния образца в каждый момент деформирования при гибке на малый радиус проведено при помощи метода конечных элементов в программе LS-DYNA.

Результаты теоретического исследования (поля напряжений и деформаций) использованы для расчета степени использования запаса пластичности по деформационному критерию разрушения В.Л. Колмогорова.

Для физического эксперимента была разработана и изготовлена соответствующая технологическая оснастка (штамп и комплект вставок). Эксперименты проведены в лаборатории кафедры “Технологии обработки давлением” МГТУ им. Н. Э. Баумана на испытательной машине INSTRON.

Аппроксимация экспериментальных и теоретических данных, а также построение всех графиков проведено в программе MATHCAD.

Научную новизну имеют следующие результаты:

• метод увеличения пластичности листового металла путем снижения средних напряжений в очаге деформации за счет активных сил трения;
• результаты теоретического и экспериментального анализа второй стадии предложенного способа, показывающие, что при увеличении угла наклона деформирующей поверхности пуансона и трения между заготовкой и инструментами степень использования запаса пластичности снижается, а оптимальным является зазор, равный 5% толщины заготовки;
• механизм смещения очага деформации по предложенному способу гибки, позволяющий повысить ресурс пластичности.

Практическую значимость имеют следующие результаты:

• способ гибки на 90° с малым радиусом как первая операция сборки облицовочных деталей автомобилей из алюминиевых сплавов, позволяющий получить высокое качество поверхности при отсутствии трещин и разрывов на стандартном прессовом оборудовании;
• методика расчета процессов гибки на основе математического моделирования методом конечных элементов с учетом прогнозирования разрушения по критерию В.Л. Колмогорова;
• регрессионная модель, построенная по результатам проведенных теоретических исследований, позволяющая проводить проектный расчет инструмента для гибки на малый радиус.

Апробация работы.

Основные положения и материалы работы доложены и обсуждены на

• конференции “Студенческая весна” на кафедре “Технологии обработки давлением” МГТУ им. Н. Э. Баумана, 2004 г.;
• межвузовской конференции по обработке металлов давлением в МИСиС, 2004 г.;
• II международной научно-технической конференции “Механика пластического формоизменения. Технологии и оборудование обработки материалов давлением”, Тула, ТулГУ, 2004 г.;
• международной выставке-конференции “ExpoScience International”, г. Сантьяго, Чили, 2005 г;
• научном семинаре кафедры “Технологии обработки давлением” МГТУ им. Н. Э. Баумана, 2007 г.

Публикации.

По материалам диссертационной работы опубликовано 7 печатных работ и подана заявка на получение патента на изобретение.

Структура и объем диссертации.

Диссертация состоит из введения, четырех глав, основных выводов и итогов по работе, списка литературы и двух приложений. Работа изложена на 172 страницах машинописного текста, содержит 94 рисунка, 7 таблиц и список литературы из 100 наименований.

Автор защищает:

• методику расчета процесса гибки на малый радиус на основе математического моделирования методом конечных элементов, с учетом прогнозирования разрушения по критерию В.Л. Колмогорова;

• математическую модель процесса гибки, учитывающую свойства материала и его взаимодействие с инструментом и позволяющую полностью определять размеры и напряженно-деформирован­ное состояние заготовки в любой момент деформирования;

• результаты теоретических и физических исследований, показывающие, что активные контактные силы трения снижают среднее напряжение в очаге деформации и позволяют повысить пластичность металла при гибке по предложенному способу;
• результаты теоретических и физических исследований, выявившие влияние геометрии инструмента на конечную форму детали.

КРАТКОЕ СОДЕРЖАНИЕ РАБОТЫ

Во введении обоснована актуальность темы диссертационной работы и сформулирована ее цель.

В первой главе проведен анализ литературных источников, посвященных вопросам сборки облицовочных деталей автомобилей и гибки на малый радиус, методов расчета операций листовой штамповки и критериев разрушения.

В главе рассмотрены существующие схемы деформирования и технические решения, позволяющие проводить гибку на малый радиус. Решением этой проблемы в настоящее время занимается большое количество исследователей. За рубежом это Baartman R., Guohua Zhang, Xin Wu, Guohua Zhang, Livatyali H., Muderrisoglu A. и др. В России этим занимались Власов А.В., Головащенко С.Ф., Коптелов А.А. и Илинич А.М.

Анализ отечественных и зарубежных литературных источников выявил отсутствие в настоящее время способа сборки удовлетворяющего основным требованиям автомобильной промышленности (высокое качество лицевой поверхности детали, возможность получения радиуса гиба r0,5t, применение к деталям, имеющим изогнутую кромку; стойкость инструмента, достаточная для промышленного применения; возможность использования стандартного прессового оборудования). Реализация в промышленности большинства способов требует разработки специализированных единиц оборудования или целых линий, например для горизонтального движения инструмента.

Анализ деформационных критериев разрушения Колмогорова В.Л., Кийко И.А., Деля Г.Д., Мишулина А.А. и Михалевича В.М., Филиппова Ю.К., Калпина Ю.Г. и Беззубова Н.Н. и Джонсона-Кука показал, что наиболее простым в применении является критерий В.Л. Колмогорова. Для его использования необходимо иметь только диаграмму пластичности и поля напряжений и деформаций в каждый момент времени деформирования. Опыт использования критерия В.Л. Колмогорова в практических исследова-ниях показал удовлетворительную сходимость с экспериментальными данными. Остальные критерии требуют постановки дополнительных экспериментов по определению эмпирических коэффициентов.

В соответствии с поставленной целью на основании проведенного литературного анализа сформулированы основные задачи исследования:

1. Разработать способ гибки на прямой угол с малым радиусом для фланцев облицовочных деталей автомобилей из алюминиевых сплавов, позволяющий получать качественную деталь на стандартном прессовом оборудовании.
2. Разработать математическую модель технологического процесса гибки по разработанному способу заготовок на малый радиус с прямой и изогнутой линиями гиба. На основе построенных моделей определить влияние геометрии инструмента на степень использования запаса пластичности.
3. Разработать экспериментальную штамповую оснастку для гибки на малый радиус заготовок с прямой линией гиба. Провести серию экспериментов по гибке как поперек, так и вдоль волокна и доказать возможность получения качественных деталей, применяя разработанный способ.
4. Провести экспериментальное и теоретическое исследование полного процесса сборки участка облицовочной детали автомоби-ля, используя разработанный способ в качестве первой операции.
5. Определить из результатов математического моделирования параметры, влияющие на степень использования запаса пластичности и построить регрессионную модель для проведения проектных расчетов инструмента.
6. Разработать методику расчета технологических процессов гибки, использующую метод конечных элементов, с учетом прогнозирования разрушения.

Во второй главе разработан способ гибки на малый радиус для фланцев облицовочных деталей автомобилей из алюминиевых сплавов. Способ состоит из двух стадий. На первой стадии происходит гибка на радиус, равный 3t (где t – толщина заготовки) (рис.2), а на второй – формирование малого радиуса 0,5t (рис.3).

Рис. 2. Первая стадия предложенного способа гибки на малый радиус

а б в

Рис. 3. Вторая стадия предложенного способа гибки на малый радиус:

а – исходное положение; б – промежуточное положение;

в – конечное положение

На рисунках обозначено: P – сила прижима; V – вектор скорости движения пуансона; R – радиус скругления пуансона; Alpha() – угол наклона деформирующей поверхности пуансона. Первая стадия (традиционная гибка силой) в настоящее время уже хорошо изучена. На второй стадии за счет активных сил трения возникает волна металла, которая при движении пуансона постепенно разглаживается. Наклонной поверхностью пуансона создается подпор и металл как бы ”заталкивается” в зону формирования малого радиуса.

На описанный способ подана заявка на получение патента на изобретение №2006116201(017591) от 12.05.2006 как ”Способ гибки на прямой угол с малым радиусом”.

На современном этапе развития российское автомобилестроение технологически не готово к производству автомобилей с алюминиевыми кузовами, поэтому вопрос об использовании какого-то определенного сплава остается открытым. Глобализация мировой экономики приводит к использованию на отечественных предприятиях качественных материалов, произведенных в других странах. Поэтому в качестве исследуемого материала взят хорошо зарекомендовавший себя в зарубежной практике алюминиевый сплав 6111-Т4, ближайшим российским аналогом которого является АД31. Для сплава 6111-Т4 получены все необходимые для расчета механические характеристики.

Для определения напряженно-деформированного состояния образца и исследования процесса формоизменения построена математическая модель на основе метода конечных элементов и сформулирована методика математического моделирования в программе LS-DYNA. Модель воспроизводит плоское деформированное состояние. Отказ от трехмерных оболочечных элементов обусловлен их непригодностью для расчета гибки на малый радиус. Поведение материала описывается кривой упрочнения, полученной по результатам испытания на растяжение. Модель материала заготовки принята упруго-пластической с нелинейным изотропным упрочнением, а инструменты являются абсолютно жесткими телами, которые перемещаются как единое целое.

В программе LS-DYNA переход в пластическое состояние описывается условием пластичности Мизеса:

, (1)

где sij – компоненты девиатора напряжений; S – напряжение текучести в данный момент; – коэффициент скоростного упрочнения, принимающийся равным единице в рамках диссертационной работы.

Движение сплошной среды описывается при помощи уравнений Лагранжа, удовлетворяющих граничным условиям по напряжениям и перемещениям:

xi= xi(X0,t), (2)

где xi – текущие координаты точки, зависящие от X0 – начальных координат в декартовой системе и времени t; индекс i последовательно принимает значения 1, 2 и 3.

Система уравнений (2) в матричной форме имеет вид:

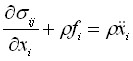, (3)

где ij – тензор напряжений Коши; – объемная плотность материала, fi – вектор плотности объемных сил; – ускорения.

Общий вид конечно-элементной модели (гибка на 180°) показан на рис. 4. Модель описывает непрерывный процесс деформирования, в котором сначала происходит гибка на 90° с радиусом R3t, затем формирование малого радиуса R0,5t, гибка на 135° и 180°.

На рисунке обозначено: 1 – заготовка; 2 – прижим; 3 – матрица гибки на R3 мм; 4 – матрица гибки на R0,5 мм; 5 – пуансон гибки на R3 мм; 6 – пуансон гибки на R0,5 мм; 7 – пуансон гибки на 135°; 8 – пуансон гибки на 180°; 9 – внутренняя панель; 10 – матрица второго и третьего переходов.

По толщине заготовки взято 10 конечных элементов (КЭ), а сетка сделана равномерной по всей длине. Внутренняя панель является абсолютно жестким телом, у которого разрешена только вертикальная степень свободы.

Рассчитано несколько моделей, в которых варьируемыми параметрами являлись угол наклона деформирующей поверхности пуансона (от 10° до 30°), радиус его скругления R (от 10 до 30 мм), суммарный зазор между заготовкой и инструментами (от 0,02 до 0,1 мм) и коэффициент трения по Кулону между заготовкой и инструментами (от 0,05 до 0,3). Наиболее качественные образцы, с точки зрения геометрии подогнутого фланца, получились при =10°, R=10 мм и =0,05 мм.

Результаты математического моделирования (гибка на 90°) позволили детально изучить процесс формоизменения на второй стадии. При традиционной гибке на малый радиус утонение в радиусной области равно 7%, а по предложенному способу получилось утолщение 7,5%. На рис. 5 показаны положения нейтральных линий напряжений (утолщенные линии “A”). Понятие нейтральных линий применимо только к процессу гибки, поэтому на рисунках оставлены границы раздела зон растяжения и сжатия только в зоне гиба. Серым окрашена зона действия растягивающих напряжений. В последний момент деформирования зона растяжения имеет минимальные границы, что объясняет практически полное отсутствие пружинения.

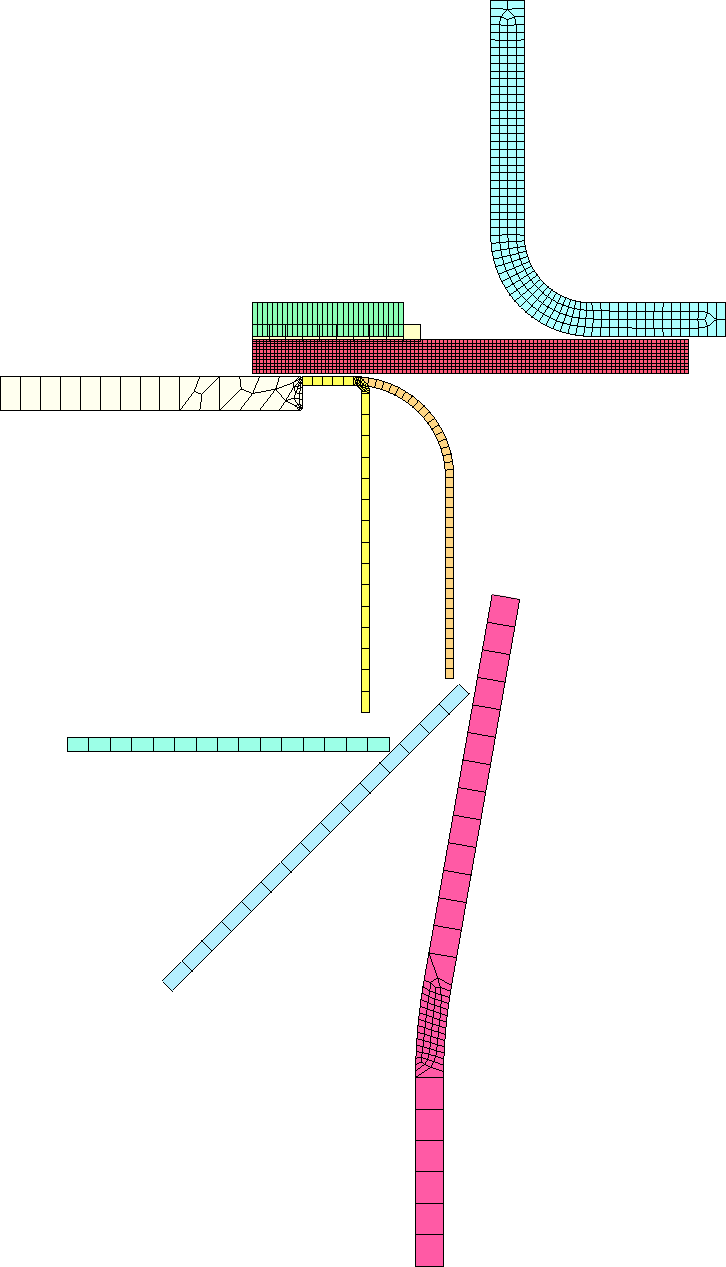
Рис. 4. Конечно-элементная модель полного процесса сборки

При уменьшении угла наклона деформирующей поверхности пуансона подогнутый фланец получается более ровным. Вторым по значимости является коэффициент трения. При превышении значения 0,15 на внешней поверхности образца появляются срезы. Радиус скругления пуансона практически никак не влияет на геометрию подогнутого фланца. На величину радиуса гиба влияет суммарный зазор между заготовкой и инструментами. При значении 0,05 мм его влияние практически исключено, при значениях зазора >0,05 мм величина радиуса увеличивается на величину зазора. При меньших значениях образуется эффект, аналогичный повышению коэффициента трения.

а б

Рис. 5. Положения нейтральных линий напряжений

в конечный момент деформирования на 90° с r0,5t:

а – при традиционной гибке; б – по предложенному способу

Оценка эффективности разработанного способа проведена на основе вычисления степени использования запаса пластичности по критерию Колмогорова В.Л. Суть его сводится к тому, что у недеформированного металла степень использования запаса пластичности равна нулю, а при разрушении – единице. Уравнение имеет вид:

, (4)

где – степень использования запаса пластичности; H – интенсивность скоростей деформации сдвига; р – пластичность металла как функция характеристик напряженного состояния, которая определяется экспериментально; k(t) – показатель напряженного состояния; (t) – показатель Лодэ.

В качестве исходных данных для этого расчета выступают поля напряжений и деформаций в каждый момент деформирования.

Для традиционной гибки получено значение =0,9922, что свидетельствует о начале разрушения, в то время как для предложенного способа =0,8195 (при =10°, R=10 мм и =0,05 мм). Ресурс пластичности увеличен на 17,4%, что свидетельствует об эффективности разработанного способа. Отмечено снижение значения при увеличении угла наклона деформирующей поверхности пуансона и при увеличении коэффициента трения.

В третьей главе описано проведение физических экспериментов, их обработка, а также сравнение с результатами математического моделирования (рис.6 и 7).

а б

Рис. 6. Образец с подогнутым на 90° фланцем с радиусом r3 мм, вид сбоку:

а – эксперимент; б – расчет

а б

Рис. 7. Образец с подогнутым на 90° фланцем с радиусом r0,5t, вид сбоку:

а – эксперимент; б – расчет

Для теоретических расчетов гибки получена кривая упрочнения для алюминиевого сплава 6111-Т4 в лаборатории ОАО ”ТОЧПРИБОР” в МГТУ им. Н. Э. Баумана. Диаграмма пластичности взята для сплава АД31 на основании подобия химического состава сплавов. Экспериментально-аналитическим методом установлено соответствие кривой алюминиевому сплаву 6111-Т4.

Экспериментальное исследование предложенного способа гибки проведено на специально сконструированном штампе с набором вставок. В процессе исследования подтверждено влияние угла наклона деформирующей поверхности пуансона на геометрию конечной детали, при его уменьшении подогнутый фланец получается более ровным, а наиболее качественные образцы получились при гибке пуансоном с углом 10°.

При традиционной гибке на малый радиус алюминиевых заготовок на внешней поверхности были получены трещины, что подтверждает результаты расчета степени использования запаса пластичности.

В четвертой главе описано проведение расчетов и экспериментов по окончательной гибке плоских образцов на 180°. Приведены результаты математического моделирования и эксперимента. Максимальное значение степени использования запаса пластичности в конечный момент деформирования составило =0,9533 (при =10°, R=10 мм и =0,05 мм). На рис.8 показаны результаты расчета при гибке на 135° и 180°, а на рис. 9 – результаты эксперимента. Стоит отметить, что гибка на 180° проведена как вдоль, так и поперек волокна. Окончательные образцы имеют прочное соединение без признаков разрушения.

Большинство участков облицовочных деталей автомобилей имеют кривизну с радиусом скругления более 100 мм. Расчеты криволинейных образцов были проведены в осесимметричной постановке. По результатам расчетов при радиусах 100, 500, 1000 и 2000 мм одна из деформаций (меридиональная) получилась меньше двух других на 1-3 порядка. При этом изменение двух других деформаций составило не более 8% по сравнению с плоским напряженным состоянием. Результаты расчетов степени использования запаса пластичности для вогнутых и выпуклых участков показали, что для плоской и изогнутой кромок с радиусом кривизны свыше 100 мм они отличаются максимум на 4%. На основании этого можно утверждать, что расчет гибки фланца на криволинейных кромках с радиусами кривизны более 100 мм можно проводить при плоском деформированном состоянии. В автомобильной промышленности при радиусах кривизны менее 100 мм, фланец имеет пониженную высоту или не подгибается совсем.

а б

Рис. 8. Результаты расчета гибки на: а – 135°; б – 180°.

а б

Рис. 9. Результаты эксперимента (вид сбоку) на: а – 135°; б – 180°

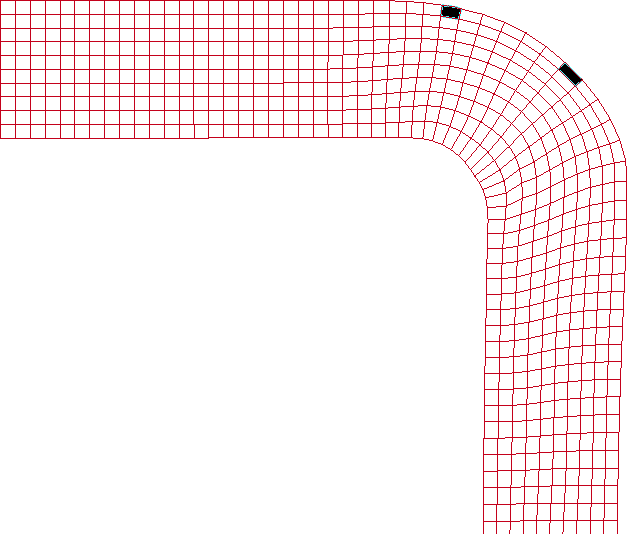
Механика деформирования при гибке на 180° имеет следующие особенности. При гибке на 90° максимальное значение степени использования запаса пластичности получено в КЭ №1 (рис.10а). При этом в дальнейшем он практически не подвергается деформации. В конечный момент деформирования на 180° максимальное значение степени использования запаса пластичности оказалось в КЭ №2 (рис.10б). На рисунке обозначено: 11, 21 – степени использования запаса пластичности при гибке на 90° для КЭ № 1 и 2; 12, 22 – степени использования запаса пластичности при гибке на 180° соответственно.

а б

Рис. 10. Расположение максимальных значений

степеней использования запаса пластичности в конце:

а – первой операции; б – третьей операции

Полученное расположение КЭ с максимальными значениями степеней использования запаса пластичности не зависит от геометрических размеров и трения. Дело в том, что после первой операции в области КЭ №1 упрочнение больше чем в области, граничащей с КЭ №2, поэтому при дальнейшей гибке на 135° возникает изгибающий момент и дальнейшее формоизменение приводит к смещению очага деформации в область, где сопротивление деформированию меньше. Таким образом, на разных операциях интенсивно деформируются разные области, за счет чего и удается получить качественные образцы. При этом схема напряженно-деформированного состояния в радиусной области при традиционной гибке и при гибке по предложенному способу одинаково. Полученное в конце деформирования максимальное значение 22=0,9533, означает почти 5% запас пластичности.

Для проведения проектных расчетов геометрии пуансона второй стадии (формирование малого радиуса) построена регрессионная модель (5) на основе результатов расчетного полнофакторного эксперимента 33=27 с помощью теории планирования эксперимента. Регрессионная модель носит описательный характер области, где возможно получение качественных образцов. Ввиду отсутствия параллельных опытов, оценка каждого коэффициента модели проводилась путем подстановки значений из матрицы планирования эксперимента. В результате модель имеет вид:

=0,8921–0,0066–0,0015R+0,404+0,000095R+0,000052–0,000033R2, (5)

где – степень использования запаса пластичности; – угол наклона деформирующей поверхности пуансона, град; R – радиус скругления пуансона, мм; – коэффициент трения по Кулону.

Для расчета технологических параметров операций гибки разработана специализированная методика, включающая в себя математическое модели-рование, расчет степени использования запаса пластичности по критерию Колмогорова В.Л. и выдачу задания на проектирование инструмента.

ОСНОВНЫЕ ВЫВОДЫ И ИТОГИ

1. Предложенный способ гибки на малый радиус, может быть использован в качестве первой операции для сборки облицовочных деталей автомобилей (капот, крышка багажника, передние и задние двери) из алюминиевых сплавов. Способ позволяет получать высокое качество поверхности без трещин и разрывов на стандарт-ном прессовом оборудовании, а также осуществлять дальнейшее деформирование на угол до 180° без разрушения. На этот способ подана заявка на получение патента на изобретение под названием “Способ гибки на прямой угол с малым радиусом” от 12.05.2006
2. Построенная математическая модель гибки на малый радиус, учитывающая упругопластические свойства материала, контактное трение между заготовкой и инструментами по Кулону, позволяет определять напряженно-деформированное состояние заготовки в любой момент деформирования, распределение степени использования запаса пластичности по поверхности (сечению) образца и пружинение. Сравнение данных численного моделирования с экспериментальными данными показало высокую достоверность разработанной модели, которая правильно определяет место вероятного появления трещины.
3. Использование математического моделирования позволило выявить механизм обеспечения бездефектной гибки на 180° с радиусом гиба, составляющим половину толщины заготовки, заключающийся в том, что утолщение заготовки, достигнутое в опасном сечении на первой операции гибки приводит к возникновению на последующих операциях нового опасного сечения. В результате этого материальные волокна, получившие наибольшие деформации на первой операции, в дальнейшем практически не деформируются, а максимально деформирующиеся волокна на последующих операциях не успевают достичь критических степеней деформации.
4. Проведенное исследование влияния геометрических размеров инструментов на степень использования запаса пластичности и конечную геометрию заготовки выявило оптимальный угол наклона деформирующей поверхности пуансона, составляющий 10° и суммарный зазор между заготовкой и инструментами 0,05 мм, позволяющие получить качественный образец с малым радиусом гиба без трещин.
5. Повышение ресурса пластичности на первой операции предложенного способа (гибке на 90°) по сравнению с традицион-ной гибкой достигается за счет уменьшения тангенциальных деформаций, вызванного противодействующими активными силами трения и снижением средних напряжений в очаге деформации.
6. Разработанная методика расчета технологических параметров гибки на основе математического моделирования позволяет прогнозировать появление трещин и разрывов на этапе проектирования и выбирать наиболее рациональные геометрические размеры деформирующих инструментов, что сводит количество физических экспериментов к минимуму.

Список работ по теме диссертации

1. Власов А.В., Горьков М.А. Оценка предельного формоизменения алюминиевых заготовок при выполнении операции зафланцовки // Известия ТулГУ. Серия. Механика деформируемого твердого тела и обработка металлов давлением. – Тула, 2004. – Вып. 1. – C. 68-77.
2. Власов А.В., Горьков М.А. Технологические процессы сборки кузовных деталей автомобилей из алюминиевых сплавов и методы их расчета // Кузнечно-штамповочное производство: перспективы и развитие. – Екатеринбург, 2005. – С. 194-200.
3. Горьков М.А. Математическое и физическое моделирование процесса зафланцовки деталей из алюминиевых сплавов // Инженерное образование. – 2004. – №6. www.techno.edu.ru.
4. Горьков М.А. Применение метода конечных элементов для расчета технологии зафланцовки // Известия высших учебных заведений. Черная металлургия. – 2005. – №1. – С. 85-86.
5. Горьков М.А. Разработка технологического процесса зафланцовки корпусных деталей из алюминиевых сплавов // Металлофизика, механика материалов и процессов деформирования. Секция 1, Первые шаги в науке: Сборник материалов Второй Международной научно-технической конференции. – Самара, 2004. – С. 12.
6. Горьков М.А., Власов А.В. Моделирование технологического процесса зафланцовки корпусных деталей из алюминиевых сплавов в программном комплексе ANSYS/LS-DYNA // Сборник трудов четвертой российской конференции пользователей программного обеспечения CAD-FEM GMBH. – М., 2004. – С. 155-159.
7. Горьков М.А., Власов А.В. Гибка малопластичных металлов на малый радиус // Заготовительные производства в машиностроении. – М., 2007. – №6. – С. 15-17.