Разработка методик тепловых испытаний элементов композитных стержневых космических конструкций
На правах рукописи
ДЕНИСОВ ОЛЕГ ВАЛЕРЬЕВИЧ
РАЗРАБОТКА МЕТОДИК ТЕПЛОВЫХ ИСПЫТАНИЙ ЭЛЕМЕНТОВ КОМПОЗИТНЫХ СТЕРЖНЕВЫХ КОСМИЧЕСКИХ КОНСТРУКЦИЙ
Специальность 05.07.07 – Контроль и испытания летательных аппаратов
и их систем
АВТОРЕФЕРАТ
диссертации на соискание ученой степени
кандидата технических наук
Москва 2009
Работа выполнена в Московском государственном техническом
университете им. Н.Э. Баумана.
| Научный руководитель: | доктор технических наук, профессор Резник Сергей Васильевич |
| Официальные оппоненты: | доктор технических наук, профессор Петрикевич Борис Борисович кандидат технических наук Юдин Валерий Михайлович |
| Ведущая организация: | ФГУП Научно-производственное объединение им. С.А. Лавочкина, г. Химки, Московская область |
Защита состоится «___»______________2009 г. в ____ часов на заседании
диссертационного совета ДС.212.008.01 в Московском государственном
техническом университете им. Н.Э. Баумана по адресу: 105005, г. Москва,
2-я Бауманская ул., д. 5.
С диссертацией можно ознакомиться в библиотеке МГТУ им. Н.Э. Баумана.
Автореферат разослан «___»_____________2009 г.
Ваш отзыв в одном экземпляре, заверенный гербовой печатью, просьба
направлять по адресу: 105005, г. Москва, 2-я Бауманская ул., д. 5, МГТУ им.
Н.Э. Баумана, диссертационный совет ДС.212.008.01
| Ученый секретарь диссертационного совета, д.т.н., профессор | Калугин В.Т. |
оБЩАЯ ХАРАКТЕРИСТИКА РАБОТЫ
Актуальность работы. При создании перспективных стержневых космических конструкций (КК) из композиционных материалов (КМ) трудно переоценить роль тепловых испытаний. Они служат для проверки результатов теоретических расчетов температурного состояния и способности конструкции выполнять свое назначение. Однако, нередко результаты теории и эксперимента не совпадают. Одно из слабых мест теоретических расчетов – неопределенность данных по теплофизическим свойствам (ТФС) КМ. Восполнять недостатки расчетов с помощью увеличения объемов испытаний нецелесообразно. Причин несколько: высокая сложность и низкая производительность испытаний крупногабаритных натурных конструкций, невозможность испытания масштабно уменьшенных моделей, теряющих представительные качества КМ. Компенсировать недостатки теории и эксперимента за счет увеличения запасов прочности и жесткости затруднительно в силу известных весовых ограничений.
В стержневых композитных КК для обеспечения стабильности формы и размеров в течение эксплуатации должны быть ограничены уровни и перепады температуры, влияющие на температурные деформации. При заданных тепловых нагрузках и размерах КК ее температурное состояние зависит от сочетания ТФС и оптических свойств (ОС) КМ.
Ввиду большого разнообразия и уникальности каждой партии стержней из КМ (различные типы наполнителя и связующего, количество слоев и углы укладки волокон, режимы термообработки) почерпнуть из справочной литературы данные по их ТФС практически невозможно. В традиционных методиках определения ТФС материалов используются образцы в форме круглой или прямоугольной пластин. Приготовление таких образцов из натурной стержневой конструкции затруднительно и может привести к нарушению структуры материала. Продолжительность экспериментов лежит в интервале от нескольких часов до нескольких десятков часов, а результаты испытаний могут иметь значительную погрешность. Очевидно, что назрела необходимость применения более совершенных программно-аппаратных средств для получения данных по ТФС КМ.
Необходима разработка расчетно-экспериментальных методик определения коэффициентов теплопроводности КМ в продольном и окружном направлениях стержней непосредственно на элементах натурных стержневых КК. Новые расчетно-экспериментальные методики могут опираться на существующую материальную базу – термовакуумные камеры, гелиоустановки, установки контактного нагрева, но при этом они должны быть построены на современном математическом аппарате численных методов прогнозирования температурного состояния конструкций. Регистрация экспериментальных данных должна проводиться с помощью быстродействующих и высокоточных автоматизированных средств, а обработка – с привлечением методов решения обратных задач теплопроводности (ОЗТ) и определения методических погрешностей измерения температуры. Методики должны предусматривать определение ОС поверхностей стержней на стандартных оптических приборах.
Цель работы. Повышение точности и производительности тепловых испытаний стержневых композитных космических конструкций на основе применения современных методов и средств математического, физического моделирования и идентификации тепловых процессов.
Тема диссертации отвечала п. 2.6.1 и 2.6.2 Комплексной программы фундаментальных исследований проблем машиностроения, механики и процессов управления, утвержденной РАН на 1995-1999 гг., где значились вопросы разработки теоретических положений, методологии экспериментально-теоретических исследований теплофизических процессов и их комплексной диагностики. Вопросы, рассмотренные в диссертации, были включены в тематические планы важнейших НИР, проведенных в МГТУ им. Н.Э. Баумана по техническому заданию Федерального космического агентства на 2004–2005 гг. в рамках раздела 1 подпрограммы 10, ОКР «Материал» Федеральной космической программы РФ на 2001–2005 гг. на основании контрактов № 810-Т378/04 от 02.03.2004 и № 810-Т378/05 от 18.02.2005. Отдельные результаты получены при финансовой поддержке по гранту РФФИ № 08-08-01065а.
Новизна диссертации.
1. Впервые разработаны методики тепловых испытаний элементов натурных КК на гелиоустановке «ИГУС» ИПМ им. И.Н. Францевича НАН Украины в п. Кацивели в Крыму, на установках контактного нагрева на воздухе во ФГУП ОНПП «Технология» и вакууме в ОАО НПО «Молния», а также в вакуумной камере «СШВ» с электрическими источниками теплового излучения в ОАО ВПК «НПО машиностроения» и выделены области рационального применения установок. Методики позволяют восполнять недостающие данные о коэффициентах теплопроводности КМ с использованием результатов обработки экспериментальных данных на основе решения ОЗТ.
2. При обосновании условий испытаний применена созданная автором система тепловых моделей для численного решения задач теплообмена одиночных и соединенных стержней. Выбор типов и схем размещения датчиков температуры, режимов нагрева был осуществлен на основе исследования закономерностей нестационарных процессов совместного переноса энергии теплопроводностью и излучением в полых стержнях из КМ для условий космического полета и наземных испытаний. Установлено:
а) При частичном затенении элемента стержневой КК сильное влияние на градиенты температуры и ширину зоны «свет-тень» оказывают коэффициенты теплопроводности в плоскости армирования КМ, совпадающей с продольной осью стержня. В частности, для условий полета по геостационарной орбите максимальные градиенты температур, возникающие вдоль оси полого углепластикового стержня с профилем квадратного сечения со сторонами 15х15 мм2 и толщиной стенки = 0,6 мм, возрастают от 2,14 до 5,23 К/мм при изменении величины коэффициента теплопроводности в продольном направлении стержня z от 4,5 до 0,65 Вт/(мК). Для типичных углеродсодержащих полимерных КМ ширина зоны термометрирования на освещенном участке стержня не превышает 100 мм, а на теневом – 300 мм. Для достижения необходимой точности в пределах каждого измерительного участка рекомендуется располагать от 5 до 10 контактных датчиков температуры с шагом не более 5 мм.
в) Влияние внутренней радиации на температурное состояние полых стержней уменьшается при увеличении толщины стенки и коэффициента теплопроводности в окружном направлении. Например, при одностороннем нагреве стержня круглого сечения радиусом 0,04 м, с = 2,5 мм, = 10 Вт/(м·К) потоком излучения плотностью 1400 Вт/м2 температурный перепад в окружном направлении Т в стационарном состоянии, рассчитанный по модели «чистой» теплопроводности, составляет 42,1 К. При расчете по модели радиационно-кондуктивного теплообмена значение Т ниже на 6,3 К. Поэтому определенные с помощью решения ОЗТ зависимости эффективных
(Т) материала тонкостенных стержней будут отличаться не более чем на 10% от «истинных» значений коэффициента теплопроводности КМ.
г) Точность измерения температуры контактными датчиками зависит от тепловой инерции термопары и образца. При близких значениях величин С материалов термопары и образца (С – объемная теплоемкость) методическая погрешность измерения температуры (МПИТ) при испытаниях углепластикового стержня на установке контактного нагрева не превышает 1,2 К в диапазоне 293…423 К.
3. Получены новые данные о температурных зависимостях коэффициентов теплопроводности КМ в продольном и окружном направлениях и об ОС поверхностей для двух типов стержней из углепластика, предназначенных для использования в силовых космических конструкциях.
На защиту выносятся названные выше методики и перечисленные новые научные результаты.
Практическую ценность имеют следующие результаты:
– Вычислительные программы, предназначенные для обоснования условий испытаний стержневых элементов и конструкций, построения планов измерения температуры экспериментальных образцов. Созданные программы были использованы также для оценки теплового режима элементов конструкции тяжелой связной платформы «Энергия», стержневой фермы «СОФОРА» орбитального комплекса «Мир».
– Расчетно-экспериментальные методики определения коэффициентов теплопроводности материала стержней, опирающиеся на существующую материальную базу и современные средства регистрации и обработки экспериментальных данных.
Указанные результаты использованы в НИР и ОКР ФГУП ОНПП «Технология», ОАО НПО «Молния» и ФГУП НПО им. С.А. Лавочкина и в учебном процессе в МГТУ имени Н.Э. Баумана, что отражено в соответствующих актах о внедрении.
Достоверность результатов исследования гарантируется корректностью выбора исходных допущений и ограничений при постановке задач, адекватностью применяемых моделей исследуемым процессам и строгостью использования современного математического аппарата, а также сравнением с результатами других авторов.
Личный вклад автора состоит в разработке методик тепловых испытаний, анализе и обобщении полученных результатов. Все основные результаты и выводы получены лично автором.
Апробация основных результатов диссертации проводилась на научных конференциях и семинарах, в том числе: «Крупногабаритные космические конструкции» (Севастополь, 1990, Новгород, 1993), Молодежной научно-технической конференции «Космонавтика – XXI век» (Москва – Калининград, 1991), семинаре «Математическое моделирование и идентификация параметров процессов переноса в неоднородных средах» (Рига, 1992), 1-й международной конференции «Обратные задачи в технике: теория и практика» (Пам Коуст, США, 1993), 5-м конгрессе по использованию концентрированной солнечной энергии (Москва, 1994), 2-й и 3-й международных конференциях «Ракетно-космическая техника: фундаментальные и прикладные проблемы» (Москва, 2003, 2007), 5-й международной конференции «Обратные задачи: проектирование, идентификация и контроль» (Россия, 2007), 4-м международном научном симпозиуме «Передовые технические системы и технологии» (Севастополь, 2008), 30-м семинаре Европейского космического агентства по использованию антенн для наблюдения Земли, науки, телекоммуникаций и навигации (Нордвейк, Нидерланды, 2008), на научных семинарах в МГТУ им. Н.Э. Баумана, ВИАМ, ФГУП ОНПП «Технология» (1994–2009).
По материалам диссертации опубликовано 10 научных работ. Диссертация состоит из введения, 3 глав, общих выводов и приложения, содержит 117 страниц текста, 54 рисунка, 11 таблиц. Список литературы включает 107 работ.
КРАТКОЕ СОДЕРЖАНИЕ РАБОТЫ
Первая глава носит обзорно-аналитический характер. Рассмотрены особенности стержневых конструкций, вопросы организации тепловых испытаний. Выявлены направления повышения производительности и точности тепловых испытаний. В результате анализа литературных данных сформулирована цель и основные задачи работы.
Вторая глава посвящена математическому моделированию процессов теплообмена стержневых КК для обоснования тепловых испытаний. На основе метода декомпозиции построено семейство тепловых моделей в одиночных стержнях и системе стержней. Данное семейство позволяет исследовать влияние различных факторов (ТФС, ОС, геометрических размеров, внутренней радиации, взаимного затенения и облучения) на температурное состояние стержней при разнообразных видах нагрева излучением. Модели взаимно дополняют друг друга и позволяют в определенных случаях уменьшить размерность задачи.
Во всех моделях считалось, что: направление и плотность переменного во времени падающего потока qW,R() известны; линейные размеры всех стержневых элементов во много раз превосходят их диаметр; наружная e и внутренняя i поверхности стержней диффузно отражают и испускают излучение; начальное распределение температуры T0 и температура окружающей среды Tf известны; объемная теплоемкость C, коэффициенты теплопроводности в продольном z, радиальном r и окружном направлениях зависят от температуры; поглощательные способности, степени черноты поверхностей стержня зависят от температуры и постоянны во всем спектральном диапазоне.
Ниже приведены математические формулировки прямых задач радиационно-кондуктивного теплообмена в стержневых КК.
а) Модель полого бесконечно протяженного стержня (рис. 1)
Рис. 1. К постановке задачи теплообмена полого бесконечно
протяженного стержня
(1)
(2)
(3)
; (4)
(5)
(6)
(7)
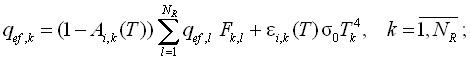(8)
где R1 и R2 – внутренний и наружный радиусы цилиндра; qn,k, qef,k – соответственно, плотности потоков результирующего и эффективного излучения к k-й зоне; 
– угловой коэффициент между k-й и l-й зонами; NR – количество зон, 0 – постоянная Стефана-Больцмана.
б) Модель неравномерно нагретого по длине стержня (рис. 2)
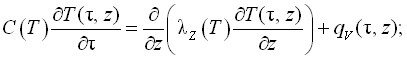(9)
(10)
(11)
, (12)
где 
– удельная мощность объемного тепловыделения; 
z – коэффициент теплопроводности в продольном направлении, l – длина стержня. Плотность потока результирующего излучения qn определена из уравнений (7), (8).
Модели а) и б) можно применить и для исследования температурного состояния элементов конструкций при тепловых испытаниях на воздухе или в другой газообразной среде. В этом случае интенсивность конвективного теплообмена учитывает коэффициент теплоотдачи 
.
в) Модель системы стержней (рис. 3)
(14)
(15)
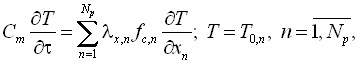(16)
 |  |
| Рис. 2. К постановке задачи теплообмена для неравномерно нагретого по длине стержня | Рис. 3. К постановке задачи теплообмена для системы стержней |
где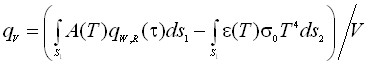 
; Nb – количество стержней, Np – число вершин соединения; fc,n – площадь контакта стержней; xn – локальная пространственная координата, совпадающая с про дольной осью n-го стержня; S1 – поверхность, на которую падает тепловой поток; S2 –излучающая поверхность; Сm – массовая теплоёмкость соединительного узла; V – объем стержня. Тепловой контакт в месте соединения стержней идеальный. Эффекты взаимного затенения и взаимного облучения стержней отраженным, падающим или собственным потоком тепловой радиации пренебрежимо слабы.
Для решения задач (1) – (8), (9 – 12), (14 – 16) применялись методы конечных разностей или конечных элементов, а также зональный метод для описания радиационного теплообмена. Разработанные алгоритмы реализованы в виде Фортран-программ для ПЭВМ.
Ниже представлены результаты теоретических исследований тепловых режимов одиночных стержней и ферменных конструкций для условий космического полета и наземных испытаний.
Изучалось влияние конструктивных размеров, ОС и ТФС материалов на температурные поля в полых стержневых элементах КК. При исследовании перепада температуры 
между освещенной ( = 0) и теневой ( = ) сторонами поверхности цилиндрического стержня (рис. 1) плотность падающего теплового потока считалась распределенной по закону косинуса 
,
. Здесь 
= 1400 Вт/м2 – осредненная плотность потока солнечного излучения в околоземном космическом пространстве.
Видно, что при начальной температуре Т0 = 100 К стержня с = 1 мм в течение первых 300 с происходит резкий «всплеск» температурного перепада в окружном направлении стержня 
, достигающий 150 К (рис. 4). Исходными данными для расчетов были следующие величины: С = 106 Дж/(м3К), r = 0,5 Вт/(мК), = 10 Вт/(мК), А = = 0,9, r1 = 0,04 м. Максимальные темпы нагрева стержня составляют 1 К/c и заметно снижаются с увеличением начальной температуры и толщины стенки. Влияние внутренней радиации на 
существенно при = 1 мм и незначительно при = 2,5 мм. Датчики температуры допустимо размещать только на наружной поверхности стержня, т. к. перепад температуры в радиальном направлении намного меньше, чем в окружном и для =1,0 мм и 2,5 мм не превышает, соответственно, 1,5 и 4,0 К. Ожидаемая продолжительность экспериментов – 400…600 с.
Симплекс относительной теплопроводности К = /r оказывает существенное влияние на значения 
(рис. 5). Для углепластиковых стержней, выполненных методом намотки, значения К могут находиться в интервале 5…15. В стационарном состоянии стержня с r1 = 0,04 м и = 1 мм перепад 
может составлять 80…120 К.
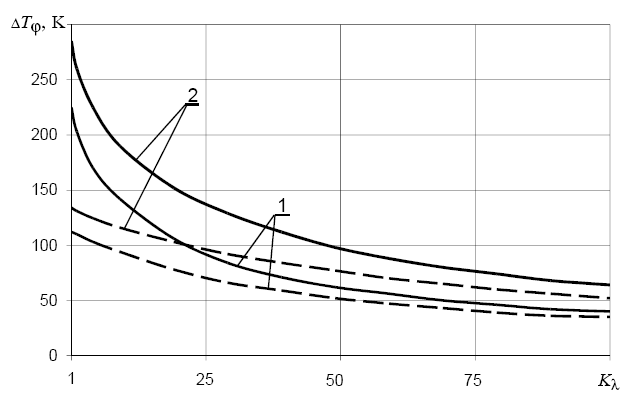 Рис. 4. Влияние начальной температуры и толщины стенки стержня на изменение перепада температуры между освещенной и теневой сторонами стержня во времени: 1 – Т0 = 100 К, = 1 мм; 2 – Т0 = 300 К, = 1 мм; 3 – Т0 = 300 К, = 2,5 мм; = 10 Вт/(мК) ––– без учета внутренней радиации; – – с учетом внутренней радиации |  Рис. 5. Влияние анизотропии коэффициента теплопроводности на перепад температур между освещенной и теневой сторонами стержня: 1 – Ае = 0,5, е = 0,9; 2 – Ае = е = 0,9; r = 0,5 Вт/(мК) ––– без учета внутренней радиации; – – с учетом внутренней радиации |
Исследовано температурное состояние полого стержня диаметром 0,06 м и толщиной стенки 1 мм из углепластика и сплава АМг-6 при движении его по геостационарной орбите после выхода из тени Земли (рис. 6). В начальный момент времени продольная ось стержня была ориентирована перпендикулярно направлению солнечных лучей, а в конечный момент времени – была параллельна солнечным лучам. Для стержня из углепластика перепад температуры в
| окружном направлении может достигать 100 К, температурные градиенты – 1,0 К/мм, а для стержня из сплава АМг-6 соответствующие значения не превышают 3 К и 0,03 К/мм. Немонотонный характер изменения температуры вызван уменьшением угла между направлениями потока солнечного излучения и продольной осью стержня. Примечательно, что максимальные значения температуры стержней, вычисленные для типичного сочетания ОС поверхностей, ниже допустимых, составляющих 425 К для полимерных КМ и 450 К – для алюминиево-магниевых сплавов. Температурные градиенты вдоль |  Рис. 6. Температурное состояние стержня из углепластика и сплава АМг-6 при движении по геостационарной орбите: 1 – сплав АМг-6; 2 – углепластик |
продольной оси углепластиковых стержней, входящих в состав движущейся по геостационарной орбите в период весеннего равноденствия ферменной конструкции, при z = 0,65 Вт/(м·К) и z = 15,0 Вт/(м·К) могут отличаться почти на 50% и составлять, соответственно, 0,62 К/мм и 0,89 К/мм. Темпы изменения температуры не превышают 0,25 К/с. Моделирование проведено для стержней квадратного сечения со сторонами d = 1515 мм2, длиной l = 1500 мм и толщиной = 0,6 мм, степень черноты наружной и внутренней поверхностей стержней = 0,86. Участок, на котором при затенении возникают температурные градиенты вдоль продольной оси, составляет 5–10 калибров стержня. Температура срединной части стержней слабо зависит от значений z, поэтому при декомпозиции конструкции, несмотря на нарушение тепловых связей, можно получить достоверные оценки температуры.
При проведении стендовых тепловых испытаний элементов натурных стержневых КК реализуется схема, когда один из торцов полого стержня нагревается, а другой – теплоизолирован. В модельном примере были заданы: температура торцов: Т1()=Т0+0,42, Т2 = Тf = Т0; температура окружающей среды Тf = 293 К, коэффициент теплоотдачи 
= 2 Вт/(м2·К). Значения d,, ОС и ТФС материалов стержня такие же, как в предыдущем примере, длина l = 300 мм.
Распределение температуры по длине стержня для различных значений z в момент времени = 1000 с показано на рис. 7. Как следует из результатов моделирования по (9) – (12), наибольшее различие температуры с учетом и без учета внутренней радиации составляет, соответственно, 50 К при z = 0,65 Вт/(мК) и 10 К при z = 12,0 Вт/(мК). Длина прогретой зоны не превышает 100 мм.
Третья глава посвящена расчетно-экспериментальным исследованиям элементов натурных стержневых КК на установках контактного и радиационного нагрева. Выявленные выше закономерности учтены при разработке методик тепловых испытаний по определению температурной зависимости коэффициентов теплопроводности КМ в продольном  и окружном (Т) направлениях стержней. Методики предусматривают измерение температур стержневых элементов и последующую обработку экспериментальных данных при помощи апробированных решений коэффициентных ОЗТ. |  Рис. 7. Влияние коэффициента теплопроводности в продольном направлении на температурное состояние стержня: 1 – z = 0,65 Вт/(мК); 2 – 4,5; 3 – 12 ––– без учета радиационного переноса; – – с учетом радиационного переноса |
В методиках предусмотрены три основных этапа: планирование испытаний, проведение испытаний, обработка экспериментальных данных и анализ результатов. Для прогноза температурного состояния экспериментальных образцов использовались программы численного решения систем уравнений (1) – (8) и (9) – (12). С помощью решения этих систем уравнений определялись температурные распределения в окружном направлении и вдоль оси стержней и, тем самым, обосновывались условия эксперимента – определялся участок термометрирования, оценивалось время эксперимента, выбирались датчики, соответствующие ожидаемому уровню температуры.
В качестве образцов должны использоваться тонкостенные стержни с соотношением 
и 
, где l, d, 5 мм – соответственно, продольный, поперечный размеры и толщина.
Объектами исследований служили стержни двух типов: из углепластика серии ОКУП-1 с профилем квадратного сечения со сторонами 15х15 мм2 и толщиной стенки = 0,6 мм, а также из углепластика КМУ-4 в форме полого цилиндра с внутренним диаметром 45,6 мм, толщиной стенки 2 мм, покрытого с двух сторон тканью СВМ-4 толщиной 0,2 мм. На образцах первого типа определялась зависимость 
с использованием установки контактного нагрева (рис. 8) в вакууме и на воздухе, а на образцах второго типа – (Т) при радиационном нагреве на гелиоустановке «ИГУС» и в вакуумной камере «СШВ».
По теоретическим оценкам для условий контактного нагрева температурные градиенты в продольном направлении углепластикового стержня не превышают 3 К/мм, уровни температур – не выше 450 К, темпы нагрева от 0,1 до 0,15 К/с, длина прогретой части стержня – от 30 до 60 мм, а время эксперимента – от 600 до 1000 с.
В диссертации показано, что для уменьшения конвективной составляющей теплообмена размеры камеры спокойного воздуха (2) целесообразно выбирать в интервале 
, 
, где L – длина прогретой части стержня (1). Расчеты по критериальным зависимостям показали, что значения 
коэффициента теплоотдачи 
в зоне термометрирования лежат в широких пределах от 1,0 до 4,3 Вт/(м2·К).
 |  |
| Рис. 8. Схема установки контактного нагрева: 1 – образец; 2 – камера спокойного воздуха; 3 – теплоизоляция; 4 – нагреватель; 5 –термопары | |
Экспериментальные термограммы обрабатывались с помощью программы решения ОЗТ из комплекса «СAR», разработанной П.В. Просунцовым в МГТУ им. Н.Э. Баумана. Установлено, что неопределенность исходных данных по 
и сильно влияет на точность искомых z. Повышение значений 
от 1 Вт/(м2К) до 2 Вт/(м2К) может привести к завышенным результатам определения z КМ на 0,75 Вт/(мК), а использование значений поверхности стержня 0,85 вместо 0,75 – на 0,2 Вт/(мК) (рис. 9).
Для уточнения 
был поставлен дополнительный эксперимент со стержнем из материала с известными ТФС и ОС (кварцевое стекло марки КВ). При обработке экспериментальных данных с помощью программы решения граничной ОЗТ удалось уменьшить неопределенность 
до 1,25
0,5 Вт/(м2·К). Степень черноты поверхности стержня = 0,86 была определена на стандартных оптических приборах во ФГУП ОНПП «Технология» и ОАО «Композит».
В вакуумной камере ОАО НПО «Молния» объемом 8 м3 был проведен нагрев углепластикового стержня при давлении 10-3 Па. Результаты испытаний на воздухе и в вакуумной камере показали, что различие искомых значений 
не превышает 20% (рис. 10), а время испытаний на воздухе в шесть раз меньше. Поэтому на этапах технического предложения и эскизного проекта допустимы эксперименты на воздухе, а на этапе технического проекта – эксперименты в вакуумной камере.
 Рис. 9. Оценка влияния неопределенностей исходных данных по степени черноты и коэффициенту теплоотдачи стержня на точность определения коэффициента теплопроводности: 1 – = 0,8; 2 – f = 2 Вт/(м2·K) | 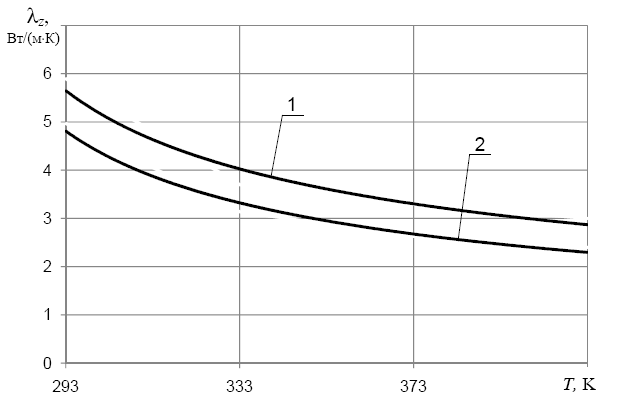 Рис. 10. Результаты определения ко-эффициента теплопроводности в продольном направлении стержня: 1 – эксперимент на воздухе f = 1,5 Вт/(м2·K), = 0,86; 2 – эксперимент в вакуумной камере |
При определении МПИТ на установке контактного нагрева предполагалось, что температура системы «датчик температуры – клей – образец» изменялась в направлениях Y-Z (рис. 11). На торцах были заданы граничные условия первого рода Т1() и Т2(), боковую стенку стержня омывала среда с постоянной температурой Tf. Считалось, что термопара ХА диаметром 0,2 мм расположена на расстоянии l1 = 2 мм от нагреваемого торца стержня длиной l = 300 мм с толщиной стенки = 0,6 мм. Геометрическая модель состояла из 257 элементов.
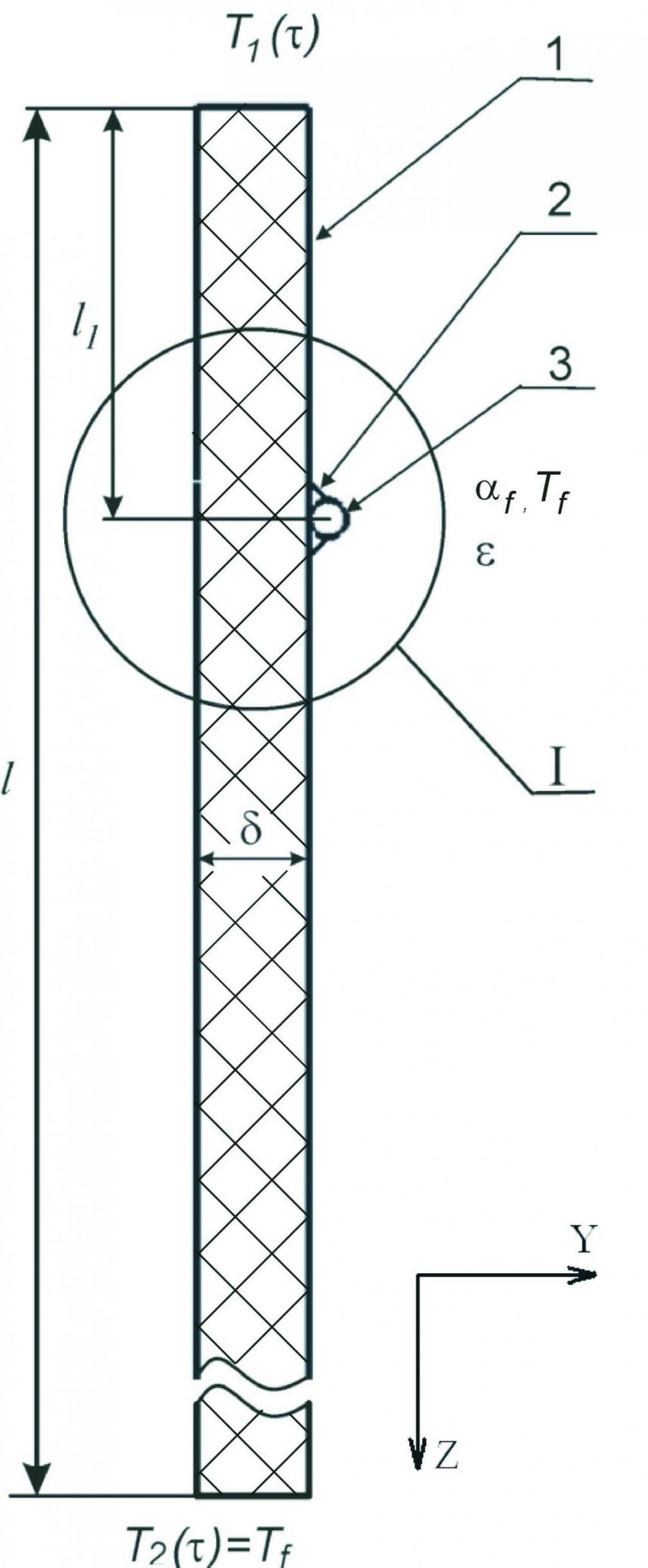 | I 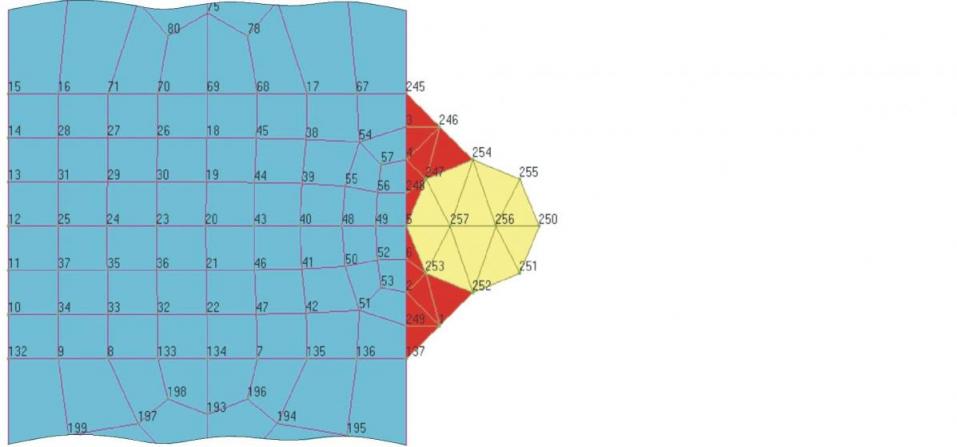 Рис. 11. Геометрическая модель для определения методической погрешности измерения температуры: 1 – образец; 2 – клей; 3 – датчик температуры | |||||
Результаты моделирования показали, что МПИТ на поверхности стержня не превышает 1,2 К для различных значений степени черноты термопары и клея (рис. 12). Погрешность определения  при такой методической погрешности не превышает 1%. По экспериментальным данным, полученным на двух установках радиационного нагрева – гелиоустановке «ИГУС» ИПМ НАН Украины и в вакуумной камере «СШВ» ОАО ВПК «НПО машиностроения», были определены температурные зависимости коэффициента теплопроводности стержня в окружном направлении (Т) (рис. 13). Таким образом, за счет применения современных методов и средств |  Рис. 12. Изменение величины методической погрешности измерения температуры для различных значений степени черноты термопары д и клея к: 1 – д = 0,3; к = 0,5; 2 – 0,3; 0,9; 3 – 0,9; к = 0,5; 4 – 0,9; 0,9 | |||||
| математического, физического моделирования и идентификации тепловых процессов удалось связать воедино математические модели теплообмена композитных стержневых конструкциях и обеспечение их исходными данными, повысить точность определения температурных градиентов и перемещений (рис. 14, 15). | ||||||
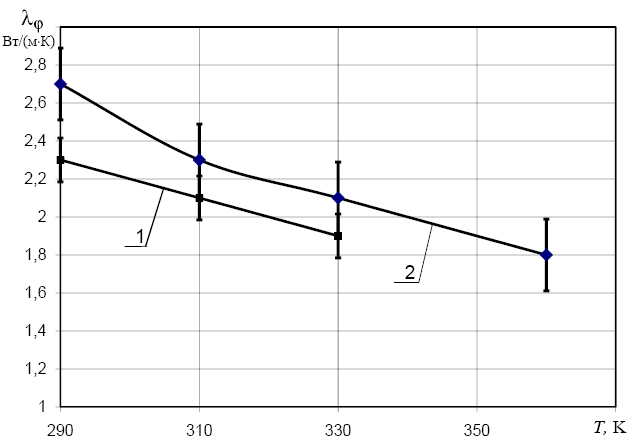 Рис. 13. Зависимости коэффициента теплопроводности КМ стержня в окружном направлении от температуры: 1 – гелиоустановка «ИГУС»; 2 – вакуумная камера «СШВ» |  Рис. 14. Температурные градиенты при остывании углепластикового стержня в теневой зоне: 1 – z = 0,86 Вт/(мК) (ВИАМ); 2 – z (Т), настоящая работа | |||||
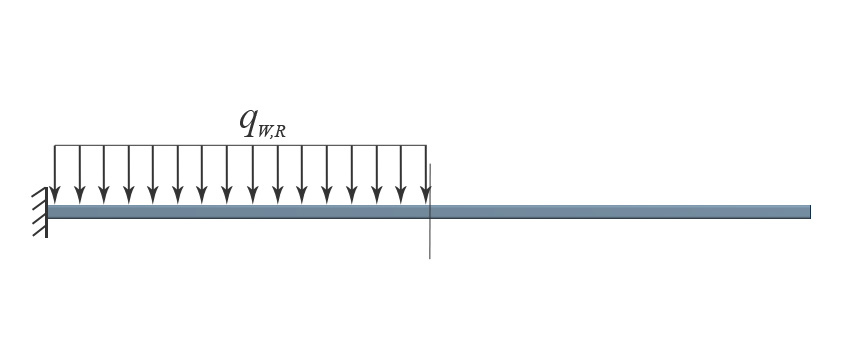  а)  б) | Рис. 15. Распределение поперечных перемещений стержня, закрепленного с одной стороны: а) – z = 0,86 Вт/(м·К), (ВИАМ); б) – z (Т), настоящая работа | |||||
ОСНОВНЫЕ РЕЗУЛЬТАТЫ И ВЫВОДЫ
1. Теоретически обоснованы условия тепловых испытаний элементов композитных стержневых КК. Для этих целей разработано семейство моделей радиационно-кондуктивного теплообмена стержневых космических конструкций. Алгоритмы реализованы в виде программ для ПЭВМ. С помощью указанных моделей исследовано влияние нестационарности тепловых нагрузок, внутренней радиации, анизотропии теплофизических свойств на температурное состояние конструкции. Поведена оценка методических погрешностей измерения температуры тонкостенных стержней контактными датчиками.
2. Впервые разработаны методики расчетно-экспериментального определения коэффициентов теплопроводности КМ в продольном и окружном направлениях стержней, основанные на испытании элементов натурных конструкций и обработке экспериментальных данных с помощью апробированных решений ОЗТ. Эксперименты должны проводиться со стержнями с соотношением 
и 
, где l, d, 5 мм – соответственно, продольный, поперечный размеры и толщина. Методики реализованы на четырех экспериментальных установках: на установке контактного нагрева на воздухе во ФГУП ОНПП «Технология» и в вакууме в ОАО НПО «Молния», гелиоустановке «ИГУС» ИПМ им. И.Н. Францевича НАН Украины в п. Кацивели в Крыму, а также в вакуумной камере «СШВ» с электрическими источниками теплового излучения в ОАО ВПК «НПО машиностроения».
3. Обработка данных сравнительных экспериментов на воздухе и в вакуумной камере показала, что различие искомых значений коэффициента теплопроводности углепластика не превышает 20%, а время испытаний на воздухе в шесть раз меньше. Поэтому для повышения производительности тепловых испытаний на этапах технического предложения и эскизного проекта допустимы эксперименты на воздухе, а на этапе технического проекта – эксперименты в вакуумной камере.
4. С помощью методик по п. 2 впервые определены температурные зависимости коэффициентов теплопроводности в продольном и окружном направлениях и оптических свойств поверхностей для двух типов стержней из углепластиков марок ОКУП-1 и КМУ-4. Полученные результаты по коэффициентам теплопроводности существенно отличаются от данных, используемых на предприятиях отрасли. Например, ранее для тепловых расчетов коэффициент теплопроводности вдоль продольной оси углепластикового стержня принимался равным 0,86 Вт/(м·К), а исследования настоящей работы показали, что в диапазоне температур 293 К – 423 К он меняется от 5,5 до 2,5 Вт/(м·К). Это повысило точность определения температурных градиентов в зоне «свет-тень» в 2,5 раза (с 10 К/мм до 4 К/мм). При частичном затенении закрепленного с одной стороны стержня длиной 1500 мм его поперечные перемещения оказались меньше ожидаемых более чем в 4 раза и составили 1,27 мм вместо 5,18 мм.
5. Результаты диссертации нашли применение в НИР и ОКР ФГУП ОНПП «Технология», ОАО НПО «Молния», ФГУП НПО им. С.А. Лавочкина и используются в учебном процессе в МГТУ имени Н.Э. Баумана, что подтверждено соответствующими актами внедрения.
Труды по теме диссертации:
1. Исследование температурного состояния и оценка температурных деформаций космической платформы в условиях ее эксплуатации: Отчет по теме СМ1-120 НИР, инв. № М 1 – 92 / 5 / НИИ СМ МГТУ им. Н.Э. Баумана; Руководитель С.В. Резник, Исполн. О.В. Денисов, Л.В. Денисова и др. – М., 1992. – 89 с. д.с.п.
2. Алгоритмы и программное обеспечение тепловых расчетов крупногабаритных космических конструкций / С.В. Резник, О.В. Денисов, Л.В. Денисова и др. // Крупногабаритные космические конструкции: Матер. междунар. конф. – Новгород, 1993. – С. 28 – 29.
3. Моделирование температурного состояния композитных космических конструкций / С.В. Резник, Д.Ю. Калинин, О.В. Денисов и др. // Ракетно-космическая техника: фундаментальные и прикладные проблемы: Матер. 2-й междунар. конф. – М., 2003. – Т. 2. – С. 197 – 198.
4. Разработка технологии изготовления тонкостенных элементов космических конструкций из полимерных композиционных материалов. Отчет по контракту № 810–Т378/04 от 02.03.2004 об ОКР, № М 13 – 04 / 1 / МГТУ им. Н.Э. Баумана; Руководитель С.В. Резник, Исполн. О.В. Денисов, Д.Ю. Калинин и др. – М., 2004. – 134 с. д.с.п.
5. Разработка технологии изготовления тонкостенных элементов космических конструкций из полимерных композиционных материалов. Отчет по контракту № 810–Т378/05 от 18.02.2005 об ОКР, № М 13 – 05 / 1 / МГТУ им. Н.Э. Баумана; Руководитель С.В. Резник, Исполн. О.В. Денисов, Д.Ю. Калинин и др. – М., 2005. – 70 с. д.с.п.
6. Методические особенности тепловых испытаний элементов натурных стержневых космических конструкций / О.В. Денисов, П.В. Просунцов, С.В. Резник и др. // Ракетно-космическая техника: фундаментальные и прикладные проблемы: Матер. 3-й междунар. конф. – М., 2007. – Т. 4. – С. 130 – 139.
7. Денисов О.В. , Поспелов И.А. Определение погрешностей измерения температуры тонкостенных элементов стержневых космических конструкций // Ракетно-космическая техника: фундаментальные и прикладные проблемы: Матер. 3-й междунар. конф. – М., 2007. – Т. 4. – С. 140 – 146.
8. Денисов О.В., Калинин Д.Ю., Резник С.В. Моделирование температур-
ного состояния элементов композитных стержневых космических конструкций // Вестник МГТУ им. Н.Э. Баумана. Машиностроение. – 2008. – Спец. выпуск. – С. 183 – 192.
9. Резник С.В., Денисов О.В. Постановка и результаты тепловых испытаний элементов композитных стержневых космических конструкций
// Вестник МГТУ им. Н.Э. Баумана. Машиностроение. – 2008. – № 4. – С. 81 – 89.
10. Reznik S.V., Kalinin D.Y., Denisov O.V. Features of large deployable antennas thermal state in space // Proceed. 30th ESA antenna workshop on antennas for Earth observation, science, telecommunication and navigation space missions. – Nordwijk (The Netherlands), 2008. – P. 335 – 338.
