Совершенствование рабочих органов устройства для модифик а ции льняного волокна
На правах рукописи
ГРИШИН
Александр Геннадьевич
СОВЕРШЕНСТВОВАНИЕ РАБОЧИХ ОРГАНОВ устройства для модификации льняного волокна
Специальности 05.02.13 «Машины, агрегаты и процессы (легкая промышленность)»
Автореферат
диссертации на соискание учёной степени
кандидата технических наук
Кострома - 2009
Работа выполнена в Костромском государственном технологическом университете
Научный руководитель: доктор технический наук, доцент
Разин Сергей Николаевич.
Официальные оппоненты: доктор технических наук, доцент
Титов Сергей Николаевич,
Костромской государственный
технологический университет,
кандидат технических наук
Вихарев Сергей Николаевич,
ОАО «Красная Маёвка»,
г. Кострома.
Ведущая организация: Костромской НИИ льняной
промышленности
(ОАО «КНИИЛП»), г. Кострома.
Защита состоится 25 декабря 2009 года в 12.00 часов на заседании диссертационного совета Д212.093.01 в Костромском государственном технологическом университете по адресу: г. Кострома, ул. Дзержинского, 17, ауд. 214.
С диссертацией можно ознакомиться в библиотеке Костромского государственного технологического университета.
Автореферат разослан 25 ноября 2009 года.
Учёный секретарь диссертационного совета,
доктор технических наук, профессор П. Н. Рудовский.
общая характеристика работы
Актуальность темы диссертации обусловлена тем, что создание методик расчета рабочих органов устройства для модификации льняного волокна в ленте и их совершенствование позволит повысить производительность и надёжность работы устройства.
Проблема обеспечения сырьевой базы отечественной текстильной промышленности, в основном хлопком, после распада СССР приобрела особую актуальность. Даже в географически южных районах России не удается добиться существенного повышения производства хлопка. Попытки смягчить “сырьевой голод” из-за высокой стоимости импортного сырья заставляют обращать внимание на лён, как на традиционный российский продукт.
Использование льна для расширения сырьевой базы при производстве пряжи в текстильной промышленности возможно только за счёт применения технологий его углубленной переработки. Существующая технология переработки льна позволяет получать только 6-8% длинного чёсаного волокна от общей массы перерабатываемого сырья (льнотресты).
Короткое волокно, которого в 3-4 раза больше, используется крайне не эффективно (для производства мешковины, верёвочных изделий, пакли). Поэтому, наряду с традиционным использованием короткого волокна, в последнее время всё больший интерес проявляется к альтернативным способам получения такого короткого льняного волокна (даже из тресты масленичных культур), которое может быть использовано, как один из компонентов при выработке высококачественной пряжи, ваты, нетканых материалов.
В последнее время в Костромском государственном технологическом университете появилось несколько диссертационных работ, направленных на создание новых устройств и технологий для углублённой переработки короткого льняного волокна. Это работы Т.Ю. Смирновой, А.Р. Корабельникова, С.Н. Разина.
Цель этих работ, придать получаемому короткому волокну параметры хлопко- или шерстоподобного волокнистого продукта, который в конечном итоге называют модифицированным (штапелированным) льняным волокном (МЛВ), а иногда – котонином. Это позволяет использовать МЛВ в прядении в смеси с хлопком или шерстью, получать из короткого волокна качественную пряжу и ткани.
В связи с этим работа, направленная на совершенствование рабочих органов данных устройств является актуальной.
Цель и задачи исследований.
Целью работы является увеличение производительности и эксплутационной надёжности работы устройства для модификации льняного волокна на основе совершенствования его рабочих органов.
Поставленная цель исследования обусловила необходимость постановки и решения следующих задач:
1. Проанализировать состояние дел в области теории и практики высокоскоростного трепания.
2. Провести анализ достоверности значения силы натяжения в обрабатываемой ленте при её взаимодействии с бильной планкой в традиционной модели
- разработать альтернативную традиционной модель ленты, учитывающую её гибкость и растяжимость
- разработать модель взаимодействия ленты (гибкой нити) с бильной планкой
- осуществить проверку достоверности созданной модели
- исследовать силовые нагрузки, возникающие в ленте при её взаимодействии с билами
- сравнить полученные силы натяжения с силами, рассчитанными по традиционной модели.
3. Исследовать поведение рабочих органов при эксплуатации, на основе которых дать рекомендации по увеличению производительности и надежности работы устройства.
а) исследовать поведения бильных планок при эксплуатации.
- исследовать возможность применения подвижных бильных планок при модификации льняного волокна.
- исследовать колебания бильных планок в плоскости вращения.
- исследовать колебания бильных планок в поперечном направлении.
- дать рекомендации по выбору геометрических размеров бильных планок.
б) исследовать крутильные колебания вала совместно с бильным барабаном и дать рекомендации по выбору оптимального размера бильного барабана и вала.
Методы исследования. Выполнение диссертационной работы опиралось на труды ведущих учёных в области текстильного машиностроения, первичной обработки лубяных волокон, прикладной механики нити.
Методы теоретической механики, сопротивления материалов, дифференциального и интегрального исчисления, векторного анализа, численные математические методы, теории вероятностей и математической статистики, а также прикладной механики нити, были использованы при проведении теоретических исследований. Численное исследование математических моделей проводилось в среде Delphi7 и MathCad-2000, и электронных таблиц Excel.
Научная новизна работы заключается в том, что впервые:
- создана и обоснована математическая модель гибкой нити (ленты), учитывающая её продольные деформации,
- разработана математическая модель взаимодействия (удара) ленты с билом, позволяющая определять как силы натяжения, возникающие в ленте, так и геометрию движения самой ленты,
- для созданных моделей получены явные разностные схемы пригодные для программирования на ЭВМ, численно получено условие устойчивости явных разностных схем, которое совпало с условием Куранта для волновых уравнений.
- создана и обоснована математическая модель взаимодействия нити с подвижным билом, совершающим как поступательное, так и вращательное движение,
- в рамках модели взаимодействия нити с билом, совершающим вращательное движение, определены условия закрепления бильных планок, при которых возможно возникновение резонансных явлений.
Практическая ценность работы и реализация полученных результатов. Диссертационная работа выполнялась в рамках отраслевой научно-технической программы по развитию техники и технологии переработки лубяных культур на 2001…2010 г.г., тематических планов НИР Всероссийского НИИ по переработке лубяных культур и КГТУ, а также региональной программы «Развитие льняного комплекса Костромской области».
На основе проведённых исследований были даны рекомендации по усовершенствованию рабочих органов модификатора.
- обоснован выбор толщины бильных планок;
- обоснована возможность уменьшения размеров рабочего вала модификатора и бильного барабана;
- обоснована возможность применения подвижных бил при модификации.
Эти рекомендации были использованы при создании новой улучшенной модели модифицирующего устройства. Новая машина – модификатор ММЛ-3 была создана в условиях ООО «ПРОМТЕКС».
Основные положения работы используются в учебном процессе студентами КГТУ.
Апробация работы. Основные положения диссертационной работы были представлены и получили одобрение: на международной научно-технической и практической конференции «Актуальные проблемы переработки льна в современных условиях», г. Кострома, КГТУ, 2004 г.г.; на научно-практической конференции «Прогресс. Актуальные проблемы переработки льна», г. Иваново, ИвГТА, 2004 г.г.; на международных научно-практических конференциях «Актуальные проблемы науки в агропромышленном комплексе», г. Кострома, КГСХА, 2007, 2008 г.; на заседаниях учёного Совета Всероссийского НИИ по переработке лубяных культур (г. Кострома, 2002 г.); на Всероссийском научном семинаре «Научные проблемы агропромышленной переработки лубоволокнистых материалов», г. Кострома, КГТУ, 2009 г.; на семинаре по ТММ кафедры ТММ и ПТМ, г. Кострома, КГТУ, 2009 г.
Публикации. По материалам диссертации опубликовано 9 печатных работ, в том числе 4 публикаций в журналах входящих в перечень ВАК, 5 печатных работ опубликованы в сборниках материалов (трудов) и тезисов докладов на международных, всероссийских конференциях и других изданиях.
Объём работы. Диссертация состоит из введения, четырёх глав, выводов, списка литературы и приложений.
Работа изложена на 125 страницах и содержит 34 иллюстрации, 4 таблицы. Список литературы включает 92 источника.
КРАТКОЕ СОДЕРЖАНИЕ РАБОТЫ
Во введении обоснована актуальность темы диссертационной работы, определены цели и задачи исследований, указана научная новизна и практическая значимость работы.
В первой главе проведен обзор литературных источников, рассмотрена история вопроса, проанализировано текущее состояние проблемы.
В начале главы даны краткие сведения об устройстве для модификации льняного волокна в ленте (модификаторе), его конструкции, назначении, и месте устройства в технологической цепочке переработки льна. Сделан вывод о том, что работ посвящённых модификатору, и процессу модификации с помощью высокоскоростного трепания крайне мало.
Далее отмечено, что процесс высокоскоростного трепания, реализованный в модификаторе, во многом схож с явлениями, происходящими при трепании сырца льнотресты на МТА при традиционном получении длинного волокна, что позволяет использовать результаты работ, полученными такими известными учёными как: Кузьминский А.Б., Неронов Н.А., Суслов Н.Н., Савиновский В.И., Кузнецов Г.К., Ипатов А.М., Пашин Е.Л., Лапшин А.Б., Дьячков В.А., Левитский И.Н., Коновалов В.В., Янушевский Д.А., Корабельников Р.В., Корабельников А.Р., и многими другими работавшими в этой области.
Далее кратко изложена история механики идеальной гибкой нити. Сделаны выводы о том, что имеющиеся немногочисленные, точные, аналитические решения неприменимы для описания процесса трепания, так как они рассматривают только стационарные движения нити. Метод Рахматуллина-Эргашова применим только для расчета ударных нагрузок, то есть первых мгновений после нанесения удара, а разностные методы для счёта на ЭВМ, непрерывной нити в литературе за последние пол века не встречаются.
В конце главы проанализированы существующие модели нити, а также модели ее взаимодействия с рабочими органами. Выделено два принципиально различных подхода к построению моделей нити, дискретный (рис.1 б) и в)) и традиционный континуальный (рис. 1 а)).
рис. 1. Модели нити. а) традиционная - континуальная, б) дискретная, в) дискретная Ляпунова, г) дискретная предлагаемая
Отмечено что континуальный подход позволяет найти силу натяжения нити, после решения уравнения захлёстывания.
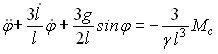
Недостатком этого уравнения является то, что при его выводе использовано спорное допущение о прямолинейности участков нити, что вызывает сомнение в получаемых значениях сил натяжения. Поэтому необходима независимая проверка этих результатов.
В дискретных моделях расчёт на компьютере обычно проводится для малого количества элементов (не более пяти), что не позволяет достаточно точно моделировать гибкую непрерывную нить. Сделан вывод о том, что это связано с нерастяжимостью нити и предложено ввести растяжимость в модель Ляпунова (рис. 1 г)).
Во второй главе для предложенной дискретной модели (рис. 1 г) получена математическая модель движения.
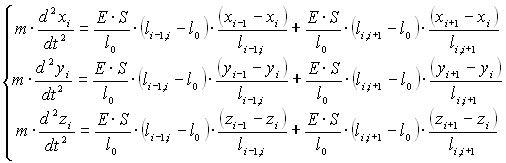(i=1..N).
где: Е – модуль упругости на растяжение, S – площадь поперечного сечения нити, l0 – длина недеформированного упругого элемента, m – масса одной точки, lk,j – длина упругого элемента между точками с номерами k и j.
Показано, что полученная дискретная система в пределе переходит в общие уравнения движения динамики гибкой растяжимой нити.
Отмечено, что однотипность уравнений полученной дискретной системы, позволяет получить явную разностную схему удобную для программирования. Приведён вывод разностной схемы, и её код на языке Pascal.
Показано, что полученную разностную схему можно вывести как из предлагаемой дискретной системы, так и из общих уравнений движения гибкой растяжимой нити, что, и доказывает достоверность полученных дифференциальных уравнений.
Для моделирования удара предложена модель (рис. 2), идея которой заключается в том, что в момент времени t > 0 кромка полуплоскости “растянет” упругий элемент между точками А и С. Поэтому величина силы, действующая на эти точки со стороны “растянутого” упругого элемента изменится. Для предложенной модели получены уравнения движения. Для примера, приведём уравнения движения точки А, расположенной выше била:
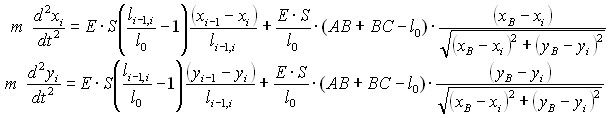
Проведён анализ вопроса о существовании и единственности полученной дифференциальной задачи, а также её корректности по Адамару. Доказано, что при трепании данная задача всегда некорректна по Адамару.
Показано, что частными случаями полученной математической модели являются волновые уравнения, для явных разностных схем которых, критерием устойчивости является условие Куранта. Поэтому полученная разностная схема обязана как минимум удовлетворять этому условию.
При численных экспериментах было установлено, что полученная разностная схема удовлетворяет условию Куранта строго.
В третьей главе представлены результаты тестирования программы и проведено сравнение результатов численных расчетов по традиционной модели и предлагаемой.
Программа тестировалась на волновом уравнении поперечных колебаний струны. Результаты тестирования показали, что с точными аналитическими решениями совпали формы колебаний, периоды (частоты) и амплитуды, если выполнено условие малости колебаний. Если же условие малости не выполнено, то колебания становятся нелинейными и зависят от начальных условий. В частности при увеличении начальной скорости в сто раз, частота колебаний первой формы струны закреплённой в обоих концах, возросла в два раза
Программа также была протестирована на волновом уравнении продольных колебаний упругого стержня, в частности на задаче о прямолинейной нити конечной длины, которую потянули за один конец с постоянной скоростью в вдоль себя (задача Тимошенко). Для начальных мгновений в этой задаче, ударное возмущение рассчитывается по формуле 
. Тестирование разработанной модели на этом решении показало хорошее совпадение результатов, как для ударной нагрузки, так и для последующего движения нити.
Далее программа тестировалась на задаче о прямолинейной нити конечной длины, которую потянули за один конец с постоянной скоростью перпендикулярно нити (задача Эргашова).
Для начальных мгновений в этой задаче есть точное решение. Ударное возмущение рассчитывается по формуле Рахматуллина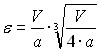 
, кроме того известна форма нити. Тестирование разработанной модели на этом решении показало хорошее совпадение результатов, как формы движущейся нити, так и ударного относительного удлинения рассчитанное по приведённой формуле.
Другой вид задачи Эргашова моделирует удар била по нити и дальнейшее ее взаимодействие с билом в случае, когда оба конца нити свободны, а удар наносится по середине нити конечной длины, перпендикулярно нити. Кроме решения по традиционной континуальной модели, других точных решений у этой задачи не существует. Сила натяжения нити рассчитанная по континуальной модели в этой задаче постоянна, так как угловая скорость вращающейся нити в этом случае не изменяется. Для сравнения приведён график изменения силы натяжения нити в точке закрепления рассчитанной по предлагаемой модели (рис. 3), для случая, когда по традиционной модели сила натяжения в точке закрепления Т = 5 Н.
рис.3. Сила натяжения, рассчитанная по предлагаемой модели. а) первое осреднение, б) полное осреднение по времени.
Отмечено, что сила натяжения в предложенной модели носит колебательный характер (рис. 3 а), и при осреднении приближается к 15 Н (рис. 3 б), что в 3 раза больше, чем при расчёте по традиционной модели. Для того, чтобы силы натяжения совпали, необходимо увеличить начальную угловую скорость нити в традиционной модели в 
раз. Физически это соответствует случаю, когда кинетическая энергия нити в относительном движении, по отношению к билу, в результате нанесения удара не изменяется. Кроме того, из рис. 3б видно, что сила натяжения достигает максимальных значений в самом начале взаимодействия нити с билом. Величину этой силы натяжения можно рассчитать по формуле Рахматуллина. Всплески силы натяжения в процессе движения происходят тогда, когда нить принимает прямолинейную форму. По нашему мнению это вызвано тем, что кинетическая энергия точек нити обусловленная радиальными скоростями, при распрямлении переходят в энергию упругой деформации (натяжение).
В последней части главы рассмотрена модельная задача трепания, когда нить закреплена (рис. 1. а). Сравнение результатов расчётов по традиционной модели и предлагаемой позволяют сделать такие же выводы, что и в задаче Эргашова.
Главный вывод из результатов сравнения двух моделей на последних двух задачах заключается в том, что средние численные значения сил натяжения совпадают. Колебания силы натяжения в предлагаемой модели по нашему мнению в реальности будут быстро затухать, из-за наличия сил внутреннего трения и поэтому процесс осреднения при сравнении натяжения по двум моделям надо считать корректным. Совпадение среднего значения сил натяжения рассчитанного по двум моделям увеличивает достоверность полученных значений и достоверность самих моделей.
Сделан вывод, что при расчётах удобнее пользоваться традиционной моделью, как более простой, но при этом начальная угловая скорость захлестываемого участка нити необходимо полагать равной 
, где V – скорость нанесения удара, l – длина захлестываемого участка нити.
В четвертой главе представлены результаты исследования поведения рабочих органов модификатора при их взаимодействии с обрабатываемой лентой.
В начале главы изучена возможность применения подвижных бил при модификации (рис. 4 а). На рисунке бильная планка 1 прикреплена шарниром 2 к бильному барабану. Это решение, в случае движения бильной планки в момент начала взаимодействия в направлении противоположном вращению бильного барабана (условие «смягчения» удара), позволит увеличить скорость вращения и тем самым увеличить производительность устройства.
Для выявления влияния подвижности бил на силы натяжения, возникающие в ленте, вначале была рассмотрена задача о взаимодействии ленты с поступательно движущемся билом (рис. 4б). На рисунке подвижная бильная планка 2 взаимодействует с нитью 3. Роль восстанавливающей центробежной силы инерции Fи выполняет упругий элемент 1 прикреплённый к движущейся с постоянной скоростью точке О1.
Уравнения, описывающие поведение системы в этом случае имеют вид.
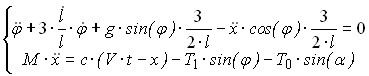
где: 
и 
– силы натяжения в ленте (нити) в сечения набегания и сбегания с кромки бильной планки, 
- скорость точки 
, х – координата кромки бильной планки (точка О), – угловая координата захлёстываемого участка ОА ленты, l – его длина, с – жесткость упругого элемента.
Анализ результатов расчётов по полученной модели показал, что сила натяжения в ленте за одно взаимодействие уменьшается только в том случае, когда масса ленты становится сопоставимой с массой бильной планки, что технически сделать не возможно. Отсюда был сделан вывод, что можно существенно уменьшить массу (размеры) бильных планок и других рабочих органов уже существующего модификатора, с жёстко закреплёнными бильными планками. Другой важный вывод заключается в том, что «смягчение» удара при одном взаимодействии не происходит.
Поэтому далее была рассмотрена модель с многократными взаимодействиями ленты с вращающимся билом (рис. 4 а). В этом случае при совпадении частоты вращения бильного барабана с собственной частотой колебаний бильной планки возможно наступление резонанса, при котором амплитуды колебаний бильной планки станут большими, что приведёт к уменьшению скорости нанесения удара (условие «смягчения» удара). В этом случае увеличения производительности устройства можно достичь за счёт увеличения частоты вращения бильных барабанов, до такого значения при котором скорость нанесения ударов останется прежней.
Для модели (рис. 4 а) получено уравнение движения бильной планки:
,
где: 1 – угол отклонения бильной планки от радиального направления, l – длина бильной планки, а – расстояние между осью вращения бильного барабана и шарнирным закреплением планки, 1 – угловая скорость вращения бильного барабана.
При условии малости колебаний собственная частота колебаний бильной планки вычисляется по формуле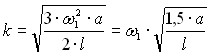 
. В случае, когда l = 1,5 а, получаем k = 1, то есть условие наступления резонанса. А именно, для наступления резонанса необходимо чтобы длина бильной планки была в 1,5 раза больше расстояния между осью вращения бильного барабана и шарнирным закреплением планки.
Из проведённых исследований был сделан вывод, что «смягчение удара» возможно. И что применение подвижных бил при модификации льняного волокна является перспективным направлением исследований, конечной целью которых будет являться увеличение производительности устройства.
Дальнейшие исследования в четвёртой главе были посвящены модификатору с жёстко закреплёнными бильными планками
Жёстко закреплённые бильные планки под действием сил трения со стороны обрабатываемой ленты будут совершать колебания в направлении перпендикулярном плоскости вращения барабана (поперечные колебания). Поэтому при выборе толщины бильных планок необходимо исследовать колебания бильных планок в этом направлении.
Расчётная схема поперечных колебаний бильной планки представлена на рис. 5а, где F(t) – сумма проекций сил натяжения в сечениях набегания и сбегания на ось у.
рис.5. а) расчётная схема исследования колебаний бильной планки,
б) зависимость частоты собственных колебаний планки от её толщины.
Уравнение свободных поперечных колебаний балки известно из литературы и имеет вид:
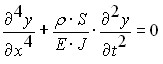
При этом частоту первой формы колебаний можно найти по формуле:
.
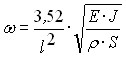где 
– объемная плотность, 
– площадь поперечного прямоугольного сечения балки, 
– модуль упругости на растяжение, 
– момент инерции площади поперечного сечения балки относительно оси являющейся пересечением сечения планки и плоскости у = 0.
Для стали (
,
), получим формулу для определения частоты первой формы колебаний:
Графики, посчитанные по этой формуле для некоторых значений, приведены на рисунке 5б. Анализ графика 5б, позволил установить, что при угловой скорости вращения барабана 
, и длине бильной планки l = 0,15 м, толщина h, бильной планки должна быть не менее 2 мм, поскольку при этой толщине частота собственных колебаний 400 с-1, что в два раза выше частоты возмущающей силы.
В заключительной части последней главы была рассмотрена возможность уменьшения размеров бильного барабана.
Возможность уменьшения радиуса бильного барабана и длины бильных планок, позволит увеличить скорость вращения барабана при сохранении скорости нанесения удара бильными планками по обрабатываемой ленте, что позволит увеличить производительность модификатора.
Для этого были исследованы крутильные колебания вала и критическая частота его вращения.
для определения частоты собственных крутильных колебаний вала с билльным барабаном была использована формула: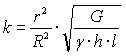 
, где 
– модуль сдвига (модуль упругости второго рода), 
– объёмная плотность, 
– длина вала, 
– толщина барабана, 
– радиус барабана, 
– радиус вала.
Для исследования возможностей изменения геометрических параметров бильного барабана (при неизменных r и l ) была построена зависимость R(h), при которой выполняется условие: 
. Анализ этой зависимости позволил установить, что при увеличении толщины бильного барабана с 15 мм до 25 мм возможно уменьшение радиуса бильного барабана с 21см (первого варианта устройства для модификации) до 17 см.
При расчёте валов, обязательным является определение их критической частоты вращения, что и было сделано в заключительной части главы.
Для определения критической частоты вращения была использована теория колебаний упругого вала в жестких опорах. Была получена зависимость критической угловой скорости вала от его радиуса с учетом гироскопического эффекта.
Анализ этой зависимости позволил установить, что критическая частота вращения вала, при уменьшении радиуса бильного барабана с 21см до 17 см, при одновременном увеличении его толщины с 15 мм до 25 мм снижается незначительно (с 509 с-1 до 431 с-1 ), и остается более чем в два раза выше частоты вращения вала.
ОБЩИЕ ВЫВОДЫ
- Анализ работ, посвящённых исследованию процесса модификации льняного волокна в ленте путём высокоскоростного трепания, позволил сделать следующие выводы: а) работы в основном направлены на изучение влияния режимно-конструктивных параметров модификатора, на качественные показатели МЛВ, б) исследований направленных на изучение движения рабочих органов практически нет, в) математические модели, описывающие взаимодействие волокнистой ленты с рабочими органами модификатора, получены при использовании достаточно грубых допущений и, следовательно, не позволяют достаточно точно определить силы, возникающие при этом.
- Сравнение результатов численного решения полученной математической модели нити с известными точными аналитическими решениями механики нити показало их хорошее совпадение, что позволяет сделать вывод о её адекватности.
- Результаты численных экспериментов, позволили установить, что при исследовании взаимодействия нити с рабочим органом, возможно использование континуальной модели нити, если начальную угловую скорость захлёстываемого участка увеличить в
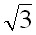раза. - Численное решение математической модели взаимодействия нити с упруго закреплённым, поступательно движущемся билом, позволило установить, что масса бильного барабана, а следовательно и размеры самого устройства могут быть уменьшены.
- Решение математической модели взаимодействия нити с шарнирно закреплённым вращающемся билом позволило установить, что в этом случае многократные воздействия на бильную планку приведут к появлению резонанса, если шарнирные крепления бильной планки установить на расстоянии 2/3 длины бильной планки от оси вращения барабана, что позволяет увеличить производительность устройства без изменения его геометрических параметров.
- Исследование поперечных колебаний бильной планки позволило сделать заключение о том, что её толщина при частоте вращения бильного барабана n=1000..3000 оборотов в минуту должна быть не менее 2 миллиметров.
- Анализ крутильных колебаний вала позволил установить, что при увеличении толщины бильного барабана с 15 мм до 25 мм возможно уменьшение радиуса бильного барабана с 21см (первого варианта устройства для модификации) до 17 см.
- Анализ исследования критической угловой скорости вращающего вала модификатора, позволил установить, что критическая частота вращения вала, при уменьшении радиуса бильного барабана с 21см до 17 см, при одновременном увеличении его толщины с 15 мм до 25 мм снижается незначительно (с 509 с-1 до 431 с-1 ), и остается более чем в два раза выше частоты вращения вала.
ПУБЛИКАЦИИ, ОТРАЖАЮЩИЕ ОСНОВНОЕ СОДЕРЖАНИЕ РАБОТЫ
журналы входящие в перечень ВАК
- Лапшин А.Б., Оценка продольных и поперечных колебаний льняной пряди при сходе с бил в процессе трепания. // Лапшин А.Б., Пашин Е.Л, Гришин А.Г./ Изв. вузов. Технология текстильной промышленности. – 2001. - № 6. – с. 21…25.
- Гришин А.Г., Преобразование двухмерного дискретного представления нити к редуцированным уравнениям континуального представления. // Гришин А.Г., Лапшин А.Б., Пашин Е.Л./ Изв. вузов. Машиностроение. – 2002. - № 8. – с.3…10.
- Разин С.Н., Экспериментальная проверка формулы Эйлера при исследовании взаимодействия гибкой нити с шероховатым цилиндром. // Разин С.Н., Коваленко Н.И, Гришин А.Г./ Изв. вузов. Технология текстильной промышленности. – 2006. - № 4. – с. 45..48.
- Бойко С.В., Моделирование взаимодействия полуплоскости с гибкой нитью. // Бойко С.В., Гришин А. Г. / Изв. вузов. Технология текстильной промышленности. – 2007. - № 4. – с. 113-118.
Сборники материалов (трудов) и тезисы докладов на международных, всероссийских конференциях и других изданиях
- Разин С.Н., Оценка скорости воздушных потоков внутри рабочей камеры модификатора// Разин С.Н., Гришин А.Г./ Материалы межд. науч.- техн. конф. “Актуальные проблемы переработки льна в современных условиях ”. Сборник трудов – Кострома, КГТУ, 2004, с. 21-22.
- Гришин А.Г., Аналитическое решение уравнения захлёстывания ленты при её взаимодействии с билом модификатора// Гришин А.Г., Разин С.Н., Пашин Е.Л../ Материалы 58 межд. науч.- практ. конф. “Актуальные проблемы науки в агропромышленном комплексе ”. Сборник трудов, Том 3 – Кострома, КГСХА, 2007, с. 71-73.
- Гришин А.Г., Поперечные колебания бильной планки при модификации льна // Гришин А.Г., Разин С.Н., Смирнова Т.Ю./ Материалы 59 межд. науч.- практ. конф. “Актуальные проблемы науки в агропромышленном комплексе ”. Сборник трудов, Том 4 – Кострома, КГСХА, 2008, с. 84-87.
- Разин С. Н., Уравнения движения подвижной бильной планки. // Разин С. Н., Гришин А.Г., Пашин Е.Л. / Материалы 59 межд. науч.- практ. конф. “Актуальные проблемы науки в агропромышленном комплексе ”. Сборник трудов, Том 4 – Кострома, КГСХА, 2008, c. 57-159.
- Разин С. Н., Применение подвижных бил в конструкции модификатора ММЛ. // Разин С. Н., Гришин А.Г., Пашин Е.Л./ Вестник Всероссийского НИИ по переработке лубяных культур, ВНИИЛК, №3, Кострома, 2007, c. 104-107.
