Повышение эффективности и качества формообразования полых тонкостенных шаров бесцентровым шлифованием
На правах рукописи
БОЧКАРЕВ Антон Петрович
Повышение эффективности и качества формообразования полых тонкостенных шаров бесцентровым шлифованием
Специальность 05.02.08 – Технология машиностроения
Автореферат
диссертации на соискание ученой степени
кандидата технических наук
Саратов 2013
Работа выполнена в Федеральном государственном бюджетном
образовательном учреждении высшего профессионального образования
«Саратовский государственный технический университет
имени Гагарина Ю. А.»
Научный руководитель:
Официальные оппоненты:
Ведущая организация:
Защита диссертации состоится 11 декабря 2013 г. в 15.00 часов на заседании диссертационного совета Д 212.242.02 в ФГБОУ ВПО «Саратовский государственный технический университет имени Гагарина Ю.А.» по адресу: 410054, Саратов, ул. Политехническая, 77, Саратовский государственный технический университет имени Гагарина Ю.А., корп. 1, ауд. 319.
С диссертацией можно ознакомиться в научно-технической библиотеке ФГБОУ ВПО «Саратовский государственный технический университет имени Гагарина Ю.А.».
Автореферат разослан « 8 » ноября 2013 года
Учёный секретарь
диссертационного совета А. А. Игнатьев
ОБЩАЯ ХАРАКТЕРИСТИКА РАБОТЫ
Актуальность темы. В последние годы как в мировой, так и в отечественной экономике отчетливо проявляется тенденция значительного удорожания природных материальных и энергетических ресурсов. Вследствие технических, экономических и организационных изменений на производственных предприятиях возникает необходимость в соблюдении все более высоких требований по производительности, экономичности и гибкости производственных систем. Поэтому одной из основных задач, стоящих перед машиностроением, является ускоренный переход к ресурсо- и энергосберегающим, малоотходным и безотходным технологиям. Эффективное направление решения этой задачи в металлообрабатывающем производстве – значительное повышение коэффициента использования металла путем максимального приближения заготовки по форме и размерам к готовой детали. В мировой технической науке исследователи и технологи уже много лет пытаются решить сложную техническую проблему – создание полых тел качения сферической формы, имеющих меньшую, чем сплошные шарики, массу, но конкурентоспособных с ними по техническим характеристикам. Использование таких изделий в подшипниках качения позволяет значительно снизить давление на наружные кольца подшипников при высокой частоте их вращения и, тем самым, повысить их надежность, долговечность и ресурс эксплуатации. Кроме того, использование подшипников с уменьшенной массой очень актуально для применения в авиационной и космической технике, где идет борьба за снижение взлетного веса летательного аппарата. Помимо этого, замена сплошных шариков на полые в подшипниках качения при выпускаемых программах позволит значительно снизить металлоемкость производства, сократить время изготовления подшипниковых узлов, а значит, и снизить потребление всех видов используемой энергии, уменьшить основную и дополнительную заработную плату, амортизационные и накладные расходы и еще целый ряд связанных с этим затрат, т.е. позволит адекватно отреагировать на изменяющуюся конъюнктуру рынка. Поэтому работа по созданию теоретических основ в области исследования и создания принципиально новых объектов, вектор которой лежит в плоскости требований современности – перехода на малозатратные технологии, особенно актуальна на современном этапе развития науки.
Целью работы является повышение эффективности и качества изготовления полых тонкостенных шаров в условиях серийного производства.
Методы и средства исследований. Теоретические исследования процесса формообразования сферической поверхности полых шариков осуществлялись с использованием положений, принципов и методов, принятых в технологии машиностроения, теории резания, теории трения и математической статистике, методов моделирования на ЭВМ. В экспериментальных исследованиях использовались методики планирования экспериментов и обработки статистических данных, полученных в результате проведения экспериментов в реальных производственных условиях.
Научная новизна работы:
1. Исследована и обоснована теоретическая схема бесцентрового шлифования полых шаров кругами с дискретной поверхностью, позволяющая повысить производительность их обработки напроход.
2. Обосновано оптимальное сочетание параметров рабочей зоны и режимов обработки на основе исследования механизма формообразования сферической поверхности при бесцентровом шлифовании шаров.
3. Разработана математическая модель формирования геометрических параметров наружной сферической поверхности полого шара бесцентровым шлифованием с учетом кинематических, динамических и стохастических факторов технологического процесса.
4. Получены регрессионные зависимости геометрических параметров наружной сферической поверхности полого шара от основных наладочных параметров технологической системы при бесцентровом шлифовании полых шаров, адекватно отражающие разработанную математическую модель и обеспечивающие оптимизацию условий обработки.
Практическая ценность и реализация работы:
- разработано технологическое оснащение для осуществления нового способа бесцентрового шлифования полых шаров в условиях мелкосерийного производства на серийном станочном оборудовании;
- определены рациональные наладочные параметры рабочей зоны бесцентрово-шлифовального оборудования и режимы резания для обеспечения эффективной и качественной обработки полых шаров;
- разработаны практические рекомендации для производственных предприятий по использованию нового способа бесцентрового шлифования полых шаров в условиях мелкосерийного производства с использованием штатного серийного оборудования.
Результаты теоретических и экспериментальных исследований внедрены в учебный процесс ФГБОУ ВПО СГТУ имени Гагарина Ю.А. при изучении курса «Технология машиностроения», а также в виде методических указаний для выполнения научно-производственной работы студентами 4-го и 5-го курсов.
Обоснованность и достоверность полученных теоретических и экспериментальных результатов, выводов и рекомендаций подтверждается производственными испытаниями способа и установки для бесцентрового шлифования полых шаров с использованием современных методов рационального планирования экспериментов и обработки экспериментальных данных, а также показателями эффективности использования разработанной технологической операции.
Апробация работы. Основные положения и результаты диссертационной работы докладывались и обсуждались на 8 научных конференциях различного уровня, в том числе на 7 международных конференциях: «Технология-2010» (Орел, 2010); «Фундаментальные и прикладные проблемы машиностроения» (Псков, 2009); «Математические методы в технике и технологиях» (Саратов, 2010); «Технологическое обеспечение качества машин и приборов» (Пенза, 2011); «Наука, образование, общество: тенденции и перспективы» (Москва. 2013).
Публикации. По результатам научных исследований опубликовано 12 статей, из которых 4 – в изданиях, рекомендованных ВАК РФ, 1 – в зарубежном издании из базы данных Scopus, получен 1 патент РФ на изобретение.
Структура и объем работы. Диссертация состоит из введения, 5 глав, общих выводов, списка использованной литературы из 103 наименований. Диссертационная работа изложена на 122 страницах, содержит 4 таблицы, 43 рисунка.
Положения и результаты, выносимые на защиту:
- Способ формообразующего бесцентрового шлифования полых шаров.
- Математическая модель формирования сферической поверхности при бесцентровом шлифовании полых шариков.
- Результаты экспериментальных исследований влияния технологических факторов на погрешность получаемой сферической поверхности в виде отклонения от круглости.
- Практические рекомендации для промышленных предприятий по использованию нового способа бесцентрового шлифования полых шариков в условиях мелкосерийного производства с использованием штатного серийного оборудования.
СОДЕРЖАНИЕ РАБОТЫ
Во введении обоснована актуальность темы, сформулированы цель и научная новизна, а также научные положения и результаты, выносимые на защиту.
Первая глава посвящена анализу существующих на настоящий момент способов и устройств по механической обработке сферических тел качения. Рассмотрены способы и устройства, основанные на различных схемах удаления припуска и формообразования сферической поверхности. Принципиально эти схемы можно разделить на две крупные группы – это дисковая обработка шариков и бесцентровая, а также группу, в которой используются иные, реже применяемые схемы обработки. Дисковая, в свою очередь, подразделяется на двух-, трех-, четырех- и более дисковые схемы. Наиболее широко в настоящее время, применяются схемы 2-дисковой обработки для изготовления сплошных монолитных шариков в крупносерийном и массовом производствах подшипниковой промышленности. В таких устройствах для интенсификация процесса удаления припуска используется большая сила прижима (до 10 т) шариков между верхним и нижним дисками. Для нежестких тел качения типа полых тонкостенных шариков это неприемлемо. В многодисковых схемах шарики поджимаются к обрабатывающим дискам с помощью воздушной или жидкостной среды под давлением пружин, жесткой кинематической связи и др. Схемы, основанные на бесцентровой обработке, традиционно содержат ведущий (абразивный или металлический) и шлифовальный абразивный круги, а также опорный нож. В целом ряде схем бесцентрового шлифования шариков используется ведущий круг с выполненной на его периферии винтовой канавкой как постоянного углового профиля, так и с изменяющимся его расположением. Близким аналогом является способ, содержащий шлифовальный круг с нарезанными на его периферии кольцевыми канавками. Проанализирован и ряд других способов и устройств, основанных на центробежной обработке, использовании бесконечного прижимного ремня, качающегося опорного ножа и мн.др.
В диссертации проанализированы работы по шарообработке как российских, так и зарубежных ученых С.М. Андиона, А.А. Мулабаева, М.Л. Цнафа, П.И. Ящерицына, И.П. Филонова, С.Г. Редько, В.Д. Гундорина, И.В. Дунина-Барковского, А.Н. Резникова, С.П. Байкова, М.К. Клебанова, А.Н. Садовникова, А.И. Спришевского, R.I. Parker, H.W. Seibbi, H.H. Coe, T.A. Harrisa и др.
На основе анализа можно сделать вывод, что большинство известных способов и устройств предназначено для обработки сплошных шариков и для изготовления полых шариков использовано быть не может в силу того, что их отличительной особенностью является наличие высоких давлений на обрабатываемые шарики. Ряд других способов не позволяет обеспечить такой характер движения шарика в зоне обработки, который необходим для равномерного наложения следов контакта с инструментом на всю сферическую поверхность, что значительно снижает эффективность и качество обработки. И, кроме того, большая часть существующих в настоящее время устройств для обработки полых шариков имеют низкую производительность.
На основании вышеизложенного можно сформулировать основные задачи исследований:
- Обосновать и исследовать технологическую схему обработки полых шаров бесцентровым шлифованием.
- Исследовать механизм формообразования сферической поверхности полых шаров при бесцентровом шлифовании.
- Определить характер и степень влияния основных технологических факторов и параметров рабочей зоны на точность геометрической формы сферической поверхности.
- Разработать математическую модель процесса бесцентрового шлифования полых шаров, обеспечивающего эффективное формирование их сферической поверхности заданного качества.
- Экспериментально проверить математическую модель и установить зависимость эффективности процесса бесцентрового шлифования полых шаров от условий обработки.
- Разработать практические рекомендации по промышленному использованию результатов теоретических и экспериментальных исследований обработки полых шаров способом формообразующего бесцентрового шлифования.
В связи с этим предложена схема нового способа бесцентрового шлифования шариков (рис. 1), позволяющая использовать для его реализации серийное бесцентрово-шлифовальное оборудование. Сущность способа заключается в следующем. Устройство содержит шлифовальный круг 1 с выполненными на его рабочей поверхности винтовыми канавками 2, абразивный ведущий круг 3 с выполненной на его рабочей поверхности винтовой V-образной канавкой 4 и скошенный опорный нож 5, на котором размещают обрабатываемые шары 6. Шар получает вращение от ведущего круга, а его винтовые канавки перемещают шары вдоль шлифовального круга. При прохождении шаром зоны винтовой канавки шлифовального круга происходит прерывание его контакта со шлифующими участками 7, и шар освобождается от действия на него сил резания. В этот момент происходит изменение динамического состояния технологической системы: шар – ведущий круг – шлифовальный круг – опорный нож, и шар меняет свою ориентацию относительно режущего инструмента. В результате этого происходит мгновенный разворот шара на некоторый угол, величина которого зависит от многих как систематических, так и случайных факторов.
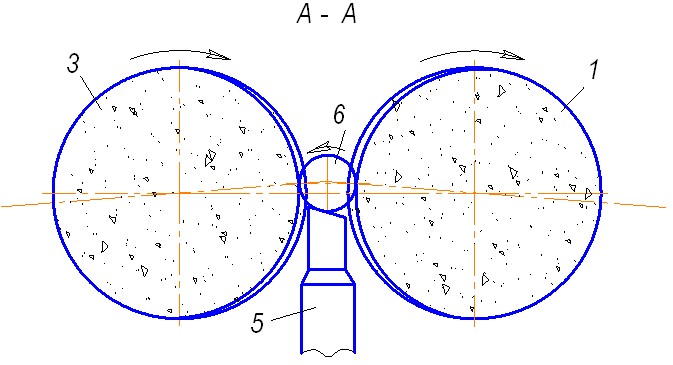
Рис.1. Схема способа бесцентрового шлифования шариков
Выполнение на шлифовальном круге винтовой канавки позволяет многократно прерывать контакт шара со шлифовальным кругом, т.е. вести обработку дискретно, сферическими сегментами, образующими в результате сферическую поверхность.
Во второй главе рассмотрен механизм формообразования сферической поверхности при бесцентровом шлифовании полых шаров с использованием абразивного ведущего круга с винтовой транспортирующей канавкой и шлифовального круга с винтовой разрядной канавкой. Предлагаемый способ сочетает в себе возможности кинематического и динамического регулирования положения шарика в зоне обработки.
Рассматривая условия контактирования шара с боковыми сторонами канавки ведущего круга, отмечаем, что в силу кинематической асимметрии профиля канавки (рис. 2) появляется силовой фактор, способный привести к появлению движения развертывания сферы на плоскость. В технологическом плане это означает, что на поверхности сферы будет обрабатываться не кольцевая, а винтовая поверхность. Покажем такую возможность математически.
Кроме тангенциальных составляющих силы воздействия ведущего круга на заготовку, вращающих ее, имеет место воздействие на заготовку радиальных составляющих FR1 и FR2, действующих на нее по нормалям в точках контакта К11 и К22. Кроме того, в тех же точках контакта на заготовку действует осевая сила подачи, возникающая вследствие воздействия на нее одной из граней (на рис. 3 – правой) призматической канавки, выполненной на поверхности ведущего круга. Источником силового воздействия ведущего круга на заготовку является ее вес, который распределяется между ведущим кругом и ножом. На ведущий круг заготовка шара воздействует суммарной силой
. (1)
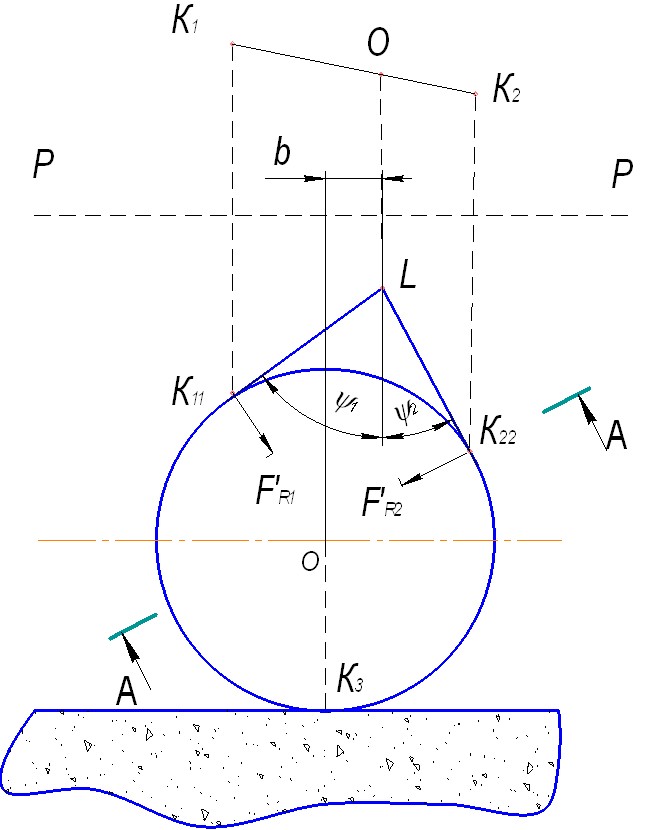
Рис. 2 Рис. 3
Если профиль канавки симметричный, сила, определяемая соотношением (1), распределяется по ее граням поровну. Если же профиль несимметричный, то воздействие силы тяжести шарика на грани неравнозначно: 
. Если 2 < 1, то FR2 > FR1.
Вследствие того, что на грани канавки действуют разные по величине нормальные силы, разными по величине будут и их тангенциальные составляющие: 
. Относительно центра сферической заготовки эти силы создают крутящие моменты: 
. Одна из составляющих каждого момента вращает заготовку вокруг мгновенной оси
К1-К2, другие же составляющие моментов в плоскости, перпендикулярной мгновенной оси вращения К1-К2 и проходящей через центр шарика, направлены противоположно друг другу. Но, имея различные величины и частично компенсируя действие друг друга, они создают момент, который стремится разворачивать заготовку в указанной плоскости в направлении большего момента:
.
После подстановки значений получим
. (2)
Выражение (2) позволяет определить величину разворачивающего момента и определить условия, при которых этот момент преодолеет противодействие моментов трения на гранях канавки. Это приведет к появлению дополнительного кинематического движения – вращения в плоскости, не совпадающей с плоскостью основного вращения, что является условием формообразования сферической поверхности.
Рассмотрим возможность получения дополнительного формообразующего движения заготовки в зоне ее обработки за счет влияния силы продольной подачи. Причиной такого движения является действие тангенциальной составляющей силы FR2 (рис. 4) и тангенциальной составляющей силы осевой подачи:
. (3)
Силу воздействия ведущего круга, обеспечивающую осевую подачу, можно определить следующим образом:
, (4)
Тогда
. (5)
Суммарная сила, создающая момент, разворачивающий заготовку в плоскости радиального сечения ведущего круга через точки его контакта с заготовкой:
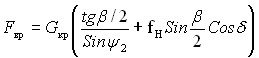. 6)
Величину крутящего момента, возникающего при этом, после проведения преобразований можно записать:
. (7)
Таким образом, крутящий момент (7) стремится разворачивать заготовку в плоскости радиального сечения ведущего круга, проходящего через точки его контакта с заготовкой, а крутящий момент (2) – вокруг оси, лежащей в этой плоскости и являющейся осью симметрии канавки, выполненной на поверхности ведущего круга. Сумма выражений (2) и (7) представляет собой величину крутящего момента, обеспечивающего формообразующую развертку сферической заготовки:
. (8)
Поскольку направление момента (8) не совпадает с направлением основного крутящего момента, вращающего заготовку вокруг оси, параллельной осям ведущего и шлифовального кругов, обеспечивается условие формообразования сферической поверхности.
Из выражения (8) ясно, что если ввести конструктивную асимметрию канавки, выполненной на поверхности ведущего круга, и обеспечить соотношение 
2 < 
1, то момент развертывания сферы будет еще больше по величине. Причем конструктивная асимметрия будет суммироваться с кинематической асимметрией и усиливать эффект развертывания сферы даже без воздействия шлифовального круга. Необходимо отметить, что эффект развертывания будет иметь место только при выполнении соотношения:
М > Мтр, (9)
где Мтр – суммарный момент трения между поверхностью заготовки и поверхностями опорного ножа и граней канавки ведущего круга. Определим условие обеспечения движения развертывания без воздействия шлифовального круга.
, (10)
где
– момент трения заготовки о поверхность опорного ножа; 
– момент трения заготовки о поверхность канавки ведущего круга в точке контакта К1; 
– то же, в точке К2. Определим слагаемые в правой части выражения (10):
; 
; 
.
После подстановки значений сил и преобразований получим
. 
. (11)
Векторы моментов (11) коллинеарны, поэтому суммируются арифметически:
. (12)
Геометрическая сумма выражений Мтр.н. и (12) представляет собой величину момента трения, препятствующего развороту заготовки в направлении действия момента (8):
.
После подстановки значений моментов и соответствующих преобразований получим
. (13)
При М = МТР система находится в состоянии неустойчивого равновесия, когда вращение может начаться, а может и не начаться. Условие, определяющее это состояние:
.(14) Известно, что одним из основных факторов, определяющих поведение сферической заготовки в зоне обработки при бесцентровом шлифовании шариков, является наличие погрешностей формы на ее поверхности и их взаимодействие с вектором силы резания. Если величины погрешностей формы сферы в результате их исправления в процессе удаления припуска становятся одного порядка с зернистостью абразивных кругов: с величиной выступов (впадин) абразивных зерен, контактирующих с обрабатываемой поверхностью, то они начинают играть ту же роль, что и выступы (неровности) на поверхности заготовки. Взаимодействуя друг с другом случайным образом, они управляют поведением заготовки в зоне резания. Следует отметить, что аналогичные неровности на поверхности опорного ножа (меньшие по величине, чем зернистость), с определенного момента времени по мере исправления погрешностей формы заготовки также начинают существенно влиять на этот процесс. Взаимодействие в точках К1, К2 и Кн (рис. 5) обеспечивает опосредованную «подачу» материала в зону резания, а взаимодействие в точке К3 обеспечивает удаление образующегося при этом дополнительного асимметричного припуска. Кроме того, образующийся дополнительный асимметричный припуск во взаимодействии с силой резания вызывает интенсивный разворот заготовки в плоскости, не совпадающей с плоскостью основного вращения, что является формообразующим движением.
Определим величину дополнительного припуска. Он образуется путем перемещения всей заготовки в направлении шлифовального круга (точка К3) при набегании неровностей заготовки с амплитудой Аk на грани канавки ведущего круга в точках К1 и К2 и на поверхность ножа в точке Кн. (рис. 5). При этом неровности поверхности заготовки взаимодействуют с неровностями поверхностей граней канавки ведущего круга в (рис. 6) и с неровностями поверхности опорного ножа н. Все эти взаимодействия являются случайными процессами, а их результат – перемещение заготовки – случайной величиной. Случайные величины суммируются по правилу геометрической суммы. Поэтому при набегании неровности А на неровность поверхности канавки величина перемещения центра масс заготовки в направлении нормали к ее поверхности в точке контакта составит
, 
. (15)
Здесь 
.
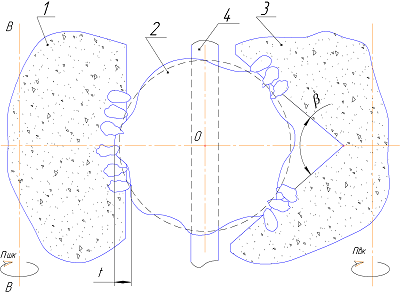
| Рис. 5. Схема контактирования сферической заготовки с элементами рабочей зоны при бесцентровом шлифовании | Рис. 6. Схема взаимодействия неровностей (зерен) шлифовального и ведущего кругов с неровностями (погрешностями формы) сферической заготовки |
В точке контакта заготовки с опорным ножом перемещение в направлении нормали к поверхности ножа:
. (16)
Суммарное перемещение поверхности заготовки в направлении точки К3:
. (17)
Общее увеличение глубины резания из-за наличия погрешностей формы заготовки и погрешностей формы опорного ножа и граней канавки ведущего круга: 
.
Основная цель процесса бесцентрового шлифования шариков – достижение их правильной сферической формы, т.е. удаление всех неровностей на сферической поверхности. Основное препятствие в достижении такого результата – весьма большая зернистость ведущего круга. Значительное пространство между его зернами позволяет размещаться в нем выступам на сферической поверхности заготовки и «уводить» из зоны шлифования соответствующие погрешности. Это обстоятельство диктует необходимость применять в качестве ведущих хорошо заправленные мелкозернистые абразивные круги со связкой, сглаживающей впадины на гранях канавки. В самом деле, если d0 = 0 и н = 0, то
. (18)
Наибольшая эффективность достижения правильной сферической формы будет при
. (19)
Это выражение представляет собой условие обеспечения наибольшей эффективности подачи неровностей в зону шлифования.
Получение точной сферической поверхности в реальном производстве в большинстве случаев связано с максимальным обеспечением случайных условий ее образования. Если же имеет место действие мощных детерминированных факторов, необходимо создавать дополнительные возможности с целью усиления стохастической составляющей процесса. Поэтому на поверхности шлифовального круга мы выполняем винтовую канавку, периодически прерывающую его контакт с заготовкой, разделяя, таким образом, непрерывный случайный процесс на множество независимых случайных эпизодов.
Определим оптимальные соотношения параметров такой канавки. Целесообразно выбрать направление винтовой канавки, противоположное направлению канавки ведущего круга (рис. 7), т.к. в этом случае тангенциальная составляющая силы резания Рт будет создавать благоприятно направленный крутящий момент, способствующий более эффективному развороту заготовки (рис. 8).
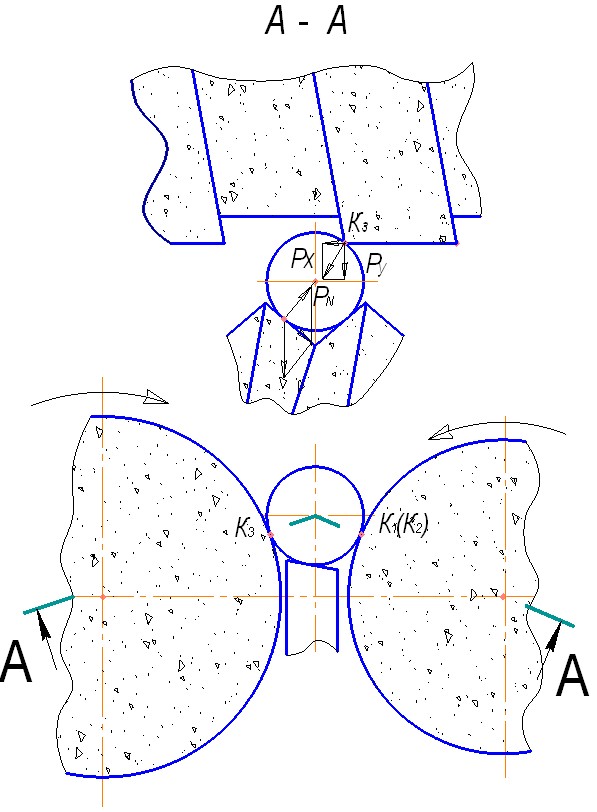
| Рис. 7 | Рис. 8 |
Величину Рт можно определить следующим образом:
. (20)
Тогда крутящий момент от этой составляющей будет равен
. (21)
Этот крутящий момент суммируется с крутящим моментом, возникающим из-за кинематической асимметричности профиля канавки ведущего круга, по правилу геометрической суммы, т.к. эти векторы неколлинеарны:
, (22)
После освобождения от величин второго порядка малости и преобразований получим
. (23)
Если шаг (рис. 9) канавки выполнить чрезмерно большим, неизбежны удары, как при шлифовании цилиндрических поверхностей со шпоночными канавками. Если же шаг принять слишком малым, не удастся обеспечить многостадийный случайный процесс формообразования сферы. Таким образом, представляется логичным выполнить на поверхности шлифовального круга винтовую канавку таким образом, чтобы на расстоянии, равном диаметру заготовки, укладывалось несколько ее шагов. Ширина канавки в этом случае определяется, во-первых, из конструктивных соображений, а, во-вторых, в зависимости от ширины среза участка сферы таким образом, чтобы обеспечить мгновенный разрыв контакта шлифовального круга с заготовкой с последующим мгновенным вступлением в контакт нового участка его поверхности. Минимальную ширину канавки можно определить из
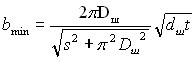. (24)
Максимальная ширина канавки будет равна
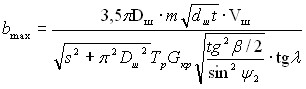. (25)
Т.к. величина шага винтовой канавки шлифовального круга зависит от ширины этой канавки, то для повышения эффективности процесса необходимо математически определить эту зависимость:
S = 
.
Таким образом, выбирая в зависимости от параметров обрабатываемого объекта, шлифовального и ведущего кругов, режимов обработки величину шага винтовой канавки шлифовального круга можно не только повысить эффективность обработки, но и оптимизировать исправляющую способность бесцентрового шлифования шариков. Т.е. выбрать такие условия наладки станка, чтобы и величина овальности и величина огранки отвечали требованиям, предъявляемым к точности размеров и формы шариков.
Третья глава содержит методику экспериментальных исследований, в которой представлен объект исследований, экспериментальная установка, методика планирования одно- и многофакторных экспериментов и обработки экспериментальных данных.
В качестве объекта исследований выбран полый шарик размером 1 дюйм, заготовка которого получена сваркой двух полусфер, проштампованных из стали толщиной 2 мм. Наружный диаметр заготовки равен 25,8±0,025 мм; отклонение от круглости 0,028-0,035 мм; шероховатость Rz 20-25 мкм. Окончательно обработанный полый шарик должен иметь диаметр 25,4±0,01 мм и отклонение от круглости 0,010 мм; шероховатость Rz10-15 мкм.
Для проведения экспериментальных исследований нового способа бесцентрового шлифования полых шариков была разработана и создана экспериментальная установка на базе серийного бесцентрово-шлифовального станка SASL200х500 (рис. 9). Модернизации подверглись шлифовальный и ведущий абразивные круги и правящее устройство. В качестве шлифовального круга использовался абразивный круг с параметрами 500500305 12А16СТ1В (рис. 10). На наружной поверхности шлифовального круга была выполнена винтовая канавка ширина, которой в процессе проведения экспериментальных исследований изменялась от 2 до 8 мм; глубина поддерживалась постоянной – 4-5 мм; шаг – 10 мм.
Ведущий круг имел параметры: 500315203 12А12СТ1В. На его наружной поверхности была выполнена винтовая канавка V-образного профиля с углом при вершине 90; шагом 28 мм (рис. 11). Шпиндель, на который установлен шлифовальный круг, имел постоянную частоту вращения – 1400 об/мин; шпиндель ведущего круга позволял регулировать частоту вращения от 10 до 125 об/мин. Ось вращения ведущего круга выставлялась параллельно оси вращения шлифовального круга.
 Рис. 10 |  Рис. 11 |
В результате проведения предварительных отсеивающих экспериментов были определены 4 наиболее значимых фактора, влияющих на эффективность формирования сферы полого шарика в заданных геометрических пределах – ширина винтовой канавки шлифовального круга, ее шаг, высота центра шарика над осями абразивных кругов и частота вращения ведущего круга. Так как шаг винтовой канавки шлифовального круга тесно увязан с ее шириной (глава 2), то в качестве полного факторного эксперимента выбираем 23.
Граничные значения варьируемых факторов были выбраны по результатам проведения анализа априорной информации и выполненных однофакторных экспериментальных исследований.
Четвертая глава содержит результаты проведения одно- и многофакторных экспериментальных исследований, а также результаты оптимизации режимов обработки и наладочных параметров экспериментальной установки.
Экспериментальные исследования влияния на погрешность формы сферической поверхности полого шарика в виде отклонения от круглости, ширины винтовой канавки шлифовального круга показали (рис. 12), что если ширину винтовой канавки сделать слишком маленькой, то промежуток времени, в течение которого контакт обрабатываемой сферы с поверхностью шлифовального круга будет потерян, будет недостаточным для эффективного разворота шарика вокруг мгновенной оси, не совпадающей с осью основного вращения шарика.
 |  |
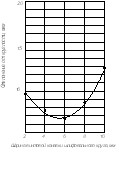| Рис. 12. Зависимость величины отклонения от круглости от ширины винтовой канавки шлифовального круга | Рис. 13. Зависимость отклонения от круглости от шага винтовой канавки шлифовального круга |
Если же ширина винтовой канавки шлифовального круга будет чрезмерно большой, то время потери контакта шарика со шлифовальным кругом будет таким большим, что шарик в этот период может повернуться как в одну, так и в другую сторону на угол значительно больший, чем требуется для обеспечения качественной и полной развертки. Поэтому обеспечить получение качественной сферы весьма затруднительно.
Экспериментальные исследования влияния на погрешность формы сферической поверхности полого шарика в виде отклонения от круглости, шага S винтовой канавки шлифовального круга показали (рис. 13), что с увеличением шага винтовой канавки погрешность формы в виде отклонения от круглости увеличивается. При этом сделать слишком малые значения шага винтовой канавки при соответствующей ее ширине технически невозможно. При чрезмерно большом шаге неизбежны удары, как при шлифовании цилиндрических поверхностей со шпоночными канавками. Если же шаг выполнить слишком малым, не удастся обеспечить многостадийный случайный процесс формообразования сферы. Экспериментальные исследования влияния на погрешность формы сферической поверхности полого шарика в виде отклонения от круглости в диаметральных сечениях сферы, величины превышения h центра шарика над осями ведущего и шлифовального кругов показали (рис. 14), что при малых величинах превышения центра шарика над плоскостью, в которой лежат оси ведущего и шлифовального кругов, превалирует явление формирования погрешностей формы нечетной огранки, овальность же имеет наименьшие значения. С увеличением h нечетные гармоники уменьшаются, зато увеличиваются гармоники четные – овальность увеличивается). Наилучшие значения h приходятся на диапазон 6 ‹ h ‹ 7 мм. Это объясняется практически двухточечным контактом шарика с кругами – на противоположных сторонах хорд, близких по величине к диаметру шарика).
 |  |
| Рис. 14. Зависимость отклонения от круглости от величины превышения центра шарика над осями ведущего и шлифовального кругов | Рис. 15. Зависимость отклонения от круглости от частоты вращения ведущего круга |
Этот фактор проявляется, если точки контакта лежат на хордах, соединяющих площадки контакта. По мере увеличения величины превышения h длина дуги между точками контакта становится некратной длине окружности шарика, что препятствует образованию огранки с малыми гармониками в силу того, что величина съема становится более равномерной по длине окружности. Но этот фактор действует в антагонизме с вертикальными составляющими реакции поверхностей шлифовальных кругов и ножа, которые стремятся вытолкнуть шарик из зоны обработки вверх. Из-за того, что снимаемый припуск по поверхности шарика распределяется неравномерно, величины этих сил переменны во времени и имеют импульсный характер. Это приводит к колебаниям положения центра шарика с амплитудой, величина которой находится в пределах суммарной величины упругих деформаций контактирующих тел. При величине превышения h, составляющей примерно 6-7 мм, эти два фактора уравновешивают друг друга, поэтому отклонения формы являются минимальными. При дальнейшем увеличении h второй фактор начинает превалировать, и при некоторых условиях это может привести даже к многократным мгновенным разрывам контакта шарика с опорным ножом и кругами, т.е. к появлению значительных вибраций. А это, несомненно, приводит к увеличению амплитуды погрешностей формы.
Экспериментальные исследования влияния на погрешность формы сферической поверхности полого шарика в виде отклонения от круглости, частоты вращения n ведущего круга показали (рис. 15), что чем больше частота вращения ведущего круга n, тем меньше время контакта обрабатываемого шарика со шлифовальным кругом, объем снимаемого припуска, количество попаданий заготовки в разрядную винтовую канавку шлифовального круга и, тем самым, меньше число актов ее разворота в зоне резания, а значит эффективность получения развертки и формирования сферы ниже.
Многофакторные экспериментальные исследования позволили получить следующую математическую модель в виде степенной зависимости:
.
Как показывает анализ полученной зависимости наибольшее влияние на погрешность формы сферической поверхности полого шарика в виде отклонения от круглости в диаметральных сечениях сферы оказывает величина превышения h центра шарика над осями ведущего и шлифовального кругов; в меньшей степени ширина винтовой канавки шлифовального круга b и частота вращения ведущего круга n. Кроме того, значимым оказалось взаимовлияние величины h и n.
Оптимизация режимов резания и наладочных параметров установки выполнялась на основе симплекс-метода. Для этого на основе полученных моделей процесса была получена математическая модель бесцентрового шлифования полых шариков. Результаты оптимизации позволили получить рациональную величину настройки опорного ножа h = 6,3 мм и частоту вращения ведущего круга n = 60 об/мин.
В пятой главе представлены практические рекомендации по использованию технологии бесцентрового шлифования полых шариков в серийном производстве и приведен расчет ожидаемого экономического эффекта от практического использования предложенной технологии.
ОСНОВНЫЕ ВЫВОДЫ
- Выполненные в работе теоретические и экспериментальные исследования позволили решить поставленную актуальную задачу по исследованию и обоснованию нового способа бесцентрового шлифования полых шаров, отличающегося пониженными силами резания и высокой эффективностью исправления погрешностей геометрической формы сферической поверхности.
- В работе исследован механизм формообразования сферической поверхности при бесцентровом шлифовании полых шаров, раскрыты причины и установлены виды формообразующих движений шара, определены настроечные параметры установки для бесцентрового шлифования полых шаров.
- В ходе проведения теоретических и экспериментальных исследований раскрыто влияние различных технологических факторов при бесцентровом шлифовании полых шаров на геометрические параметры получаемой сферы.
- Получены экспериментальные зависимости показателя эффективности процесса бесцентрового шлифования полых шаров от геометрических параметров рабочей зоны и наладки станочного оборудования.
- Показано, что наибольшее влияние на погрешность формируемой сферы в виде отклонения от круглости оказывает величина превышения центра шара над плоскостью, проходящей через оси ведущего и шлифовального кругов.
- В результате выполненной оптимизации технологической операции определены оптимальные режимы бесцентрового шлифования полых шаров и наладочные параметры станка, позволяющие обеспечить заданную точность размеров в пределах допуска ±0,01 мм, и отклонение от круглости в пределах 50% от поля допуска на размер, при этом такт обработки составил 1 шар/с.
- Разработаны методические рекомендации по использованию нового способа бесцентрового шлифования полых шариков в условиях серийного производства с использованием штатного серийного оборудования.
Основные научные положения и результаты исследований
опубликованы в следующих работах:
Публикации в рецензируемых изданиях, рекомендованных ВАК РФ:
1. Бочкарев А.П. Совершенствование метода обработки полых тел сферической формы / А.П. Бочкарев // Вестник Саратовского государственного технического университета. 2011. № 3 (58). Вып. 2. С. 17-20.
2. Бочкарев А.П. Математическая модель процесса формообразования при бесцентровом шлифовании пустотелых шаров / А.Н. Васин, Б.М. Изнаиров, А.П. Бочкарев // СТИН: научно-технический журнал. 2013. № 1. С. 28-32.
3. Бочкарев А.П. Повышение эффективности исправления погрешностей формы при бесцентровом шлифовании шариков / А.Н. Васин, Б.М. Изнаиров, А.П. Бочкарев // СТИН: научно-технический журнал. 2013. № 3. С. 17-19.
4. Бочкарев А.П. Взаимодействие заготовки со шлифовальным кругом при бесцентровом шлифовании шариков / А.Н. Васин, Б.М. Изнаиров, А.П. Бочкарев // СТИН: научно-технический журнал. 2013. № 7. С. 18-21.
Публикации в зарубежных изданиях, входящих в базу данных Scopus
5. Bochkarev A.P. Shaping in the Centerless Grinding of Hollow Spheres / A.N. Vasin, B.M. Iznairov, A.P. Bochkarev // Russian Engineering Research. 2013. Vol. 33. № 8. Р. 490-494.
Публикации в других изданиях
6. Бочкарев А.П. Исследования напряжений нежестких тел сферической формы в подшипниках качения / А.П. Бочкарев, П.Ю. Бочкарев, А.Н. Васин // Исследование сложных технологических систем: межвуз. науч. сб. Саратов: СГТУ, 2008. С. 4-14.
7. Бочкарев А.П. Способ получения заготовок полых бесшовных тел сферической формы / А.П. Бочкарев, П.Ю. Бочкарев, А.Н. Васин // Автоматизация и управление машино- и приборостроении: межвуз. науч. сб. Саратов: СГТУ, 2008. С. 4-6.
8. Бочкарев А.П. Кинематические особенности оборудования для шлифования шариков / А.П. Бочкарев, П.Ю. Бочкарев, А.Н. Васин // Инновации и актуальные проблемы техники и технологий: материалы Всерос. науч. практ. конф. молодых ученых: в 2 т. Саратов, 15-16 сент. 2009 г. / СГТУ. Саратов, 2009. Т. 2. С. 69-73.
9. Бочкарев А.П. Расчет контактных напряжений полых тел сферической формы в подшипниковым производстве / А.П. Бочкарев, П.Ю. Бочкарев, А.Н. Васин // Математические методы в технике и технологиях – ММТТ-22: сб. тр. XXII Междунар. науч. конф.: в 10 т. / ППИ. Псков, 2009. Т. 5. С. 13-15.
10.Бочкарев А.П. Три задачи, решаемые при производстве полых тел сферической формы / А.П. Бочкарев, П.Ю. Бочкарев, А.Н. Васин // Фундаментальные и прикладные проблемы машиностроения – Технология 2010: материалы 12-й Междунар. науч.-техн. конф. Орел, 7 ноября 2010 г. Орел: ОрелГТУ, 2010. С. 140-143.
11. Бочкарев А.П. Повышение эффективности исправления погрешностей формы при бесцентровом шлифовании шаров / А.Н. Васин, Б.М. Изнаиров, А.П. Бочкарев // Технологическое обеспечение качества машин и приборов: материалы VI Междунар. науч.-практ. конф. Пенза: ПГУ, 2011. С. 5-7.
- Бочкарев А.П. Процесс формообразования сферической поверхности при бесцентровом шлифовании шаров / А.Н. Васин, Б.М. Изнаиров, А.П. Бочкарев // Технологическое обеспечение качества машин и приборов: материалы VI Междунар. науч.-практ. конф. Пенза: ПГУ, 2011. С. 8-10.
Патент на изобретение РФ
- Патент № 2415004. Способ бесцентрового шлифования шариков / Бочкарев А.П., Бочкарев П.Ю., Васин А.Н. Зарегистрирован в Государственном реестре изобретений Российской Федерации 27 марта 2011 г.
БОЧКАРЕВ Антон Петрович
Повышение эффективности и качества формообразования
полых тонкостенных шаров бесцентровым шлифованием
Автореферат
Подписано в печать 06.11.13 Формат 6084 1/16
Бум. офсет. Усл. печ. л. 1,0 Уч.-изд. л. 1,0
Тираж 100 экз. Заказ 175 Бесплатно
Саратовский государственный технический университет
410054, Саратов, Политехническая ул., 77
Отпечатано в Издательстве СГТУ. 410054, Саратов, ул. Политехническая, 77
Тел. 24-95-70, 99-87-39. E-mail: [email protected]
