Совершенствование методов расчета надежности функциональных систем самолетов гражданской авиации и исследование процессов старения
На правах рукописи
Бойко Оксана Геннадьевна
совершенствование методов расчета Надежности
функциональных систем самолетов гражданской авиации
и исследование процессов старения
Специальность 05.07.02 – Проектирование, конструкция и производство
летательных аппаратов
АВТОРЕФЕРАТ
диссертации на соискание ученой степени
доктора технических наук
Красноярск 2010
Работа выполнена в Государственном образовательном учреждении высшего профессионального образования «Сибирский государственный аэрокосмический университет имени академика М.Ф. Решетнева».
Научный консультант: доктор технических наук, профессор
Шаймарданов Лев Гайнуллович
Официальные оппоненты: доктор технических наук, профессор
Москвичев Владимир Викторович
доктор технических наук, профессор
Головенкин Евгений Николаевич
доктор технических наук, профессор
Смирнов Николай Анатольевич
Ведущая организация: Сибирский научно исследовательский институт
авиастроения им. С.А. Чаплыгина,
г. Новосибирск
Защита состоится 11 ноября 2010 г. в 14 часов на заседании диссертационного совета ДС 212.023.01 при ГОУ ВПО «Сибирский государственный аэрокосмический университет имени академика М.Ф. Решетнева» по адресу: 660014, г. Красноярск, проспект имени газеты «Красноярский рабочий», 31.
С диссертацией можно ознакомиться в библиотеке Сибирского государственного аэрокосмического университета имени академика М.Ф. Решетнева.
Автореферат разослан «_____»_________2010 г.
Ученый секретарь
диссертационного совета
доктор технических наук, профессор А.Е. Михеев
общая характеристика работы
Актуальность темы. Основой обеспечения безопасности полета самолета является надежность его планера, двигателей и функциональных систем. Самолетостроение и авиадвигателестроение являются передовыми отраслями машиностроения и областями науки, в которых трудятся многочисленные научные школы. В этих областях выполнено достаточно большое количество фундаментальных научных исследований, что в значительной степени способствовало созданию высоконадежных самолетов и авиадвигателей. Тяжелые авиапроисшествия последних десятилетий не связаны с отказами планера самолета либо двигателей. Чаще они являются следствием ошибок экипажей, спровоцированных отказами агрегатов функциональных систем.
Многочисленные функциональные системы самолетов включают сотни агрегатов, имеющих различные физические принципы работы и конструктивное исполнение. Их изготавливают сотни различных предприятий разных отраслей промышленности. Разработчики и изготовители агрегатов, к сожалению, не объединены в научные школы, что препятствует решению ряда проблемных вопросов, связанных с надежностью функциональных систем.
Надежность как область науки начала формироваться сравнительно недавно с конца 50-х, начала 60-х годов прошлого столетия. Основные положения, традиционно принятые в теории надежности, не все соответствуют практике. В гражданской авиации, в соответствии с Нормами летной годности самолетов (НЛГС), надежность авиационной техники при проектировании и эксплуатации оценивается в вероятностях отказа за 1 час полета, приводящих к последствиям различной степени тяжести.
Интегральные функции вероятности отказа систем со сложной структурой представляют собой Ѕ-образные кривые, близкие по форме к интегральной функции Нормального закона распределения случайной величины. Поскольку время (налет самолета) измеряется тысячами и десятками тысяч часов, то 1 час по сравнению с налетом является величиной третьего-четвертого порядка малости. Это дает возможность определять вероятность отказа функциональной системы самолета за 1 час в виде производной от интегральной функции вероятности ее отказа. Форма типичной зависимости вероятности отказа за 1 час полета от налета часов для функциональных систем самолетов гражданской авиации (ФСС ГА) приведена на рис. 1. Характер зависимости рис. 1 трудно признать адекватным исходным данным.
Характер изменения вероятно
| Рисунок 1 – Форма зависимости вероятности отказа системы за 1 час полета от налета часов | сти отказа системы за 1 час не соответствует характеру изменения. |
надежности агрегатов. Кроме того, отсутствует однозначность решения, т.к. одно и то же значение вероятности отказа за 1 час достигается при двух существенно различных величинах налетов часов. Отмеченное выше, а также ряд других подобных некорректностей определили в качестве первостепенной задачи анализ традиционного метода расчета надежности сложных систем и разработку альтернативного методологического подхода.
Некорректности сложившихся методов расчета надежности отмечены в монографии Орлова А.И. «Эконометрика» (2003 г), где отмечается, что «… по мнению ряда специалистов, из-за неграмотности разработчиков, государственные стандарты содержат многочисленные ошибки. Для анализа ситуации в 1985 г была организована рабочая группа по упорядочению системы стандартов по прикладной статистике и другим статистическим методам. Оказалось, что существенная часть стандартов по статистическим методам действительно содержала грубые ошибки. Некоторые из них действуют до сих пор. Затем, с целью исправления сложившегося положения, был организован Всесоюзный центр по статистическим методам и информатике. Центр работает в структуре МГТУ им. Н.Э. Баумана. В связи с обнаружением грубых ошибок, 24 из 31 Государственных стандартов по статистическим методам были отменены в 198687 годах….» Следует отметить, что в литературе с 1960 по 2009 гг. методологические подходы к расчету надежности остались неизменными. Не составляет исключение и отраслевой стандарт ОСТ 100132-84 Надежность изделий авиационной техники.
Вторым аспектом надежности авиационной техники, вызывающим тревогу в последние 10-15 лет, является эксплуатация в России стареющего отечественного авиационного парка и поступление из-за рубежа далеко не новой техники иностранного производства. В связи с этим, в диссертационной работе, в качестве второй актуальной задачи, рассматривается влияние на надежность сложных функциональных систем длительности эксплуатации самолетов.
Целью работы является анализ некорректностей традиционного метода расчета надежности сложных функциональных систем самолетов гражданской авиации и его совершенствование путем разработки альтернативного методологического подхода, а также исследование влияния длительности эксплуатации самолетов на надежность функциональных систем.
Основные задачи исследования:
1. Выполнить анализ методологического подхода, заложенного в традиционный метод расчета надежности сложных ФСС ГА авиации. Рассмотреть корректность использования в традиционных методиках математических моделей.
2. Разработать альтернативные математические модели для расчета надежности агрегатов и сложных ФСС ГА.
3. Разработать альтернативный метод расчета надежности сложных ФСС ГА при проектировании и эксплуатации.
4. Разработать обобщенный критерий оценки состояния функциональных систем в процессе длительной эксплуатации. Исследовать в обобщенном виде влияние длительности эксплуатации на надежность функциональных систем.
5. Рассмотреть возможности использования методологии риск-анализа в исследованиях надежности авиационной техники.
Объектом исследования являются функциональные системы самолетов гражданской авиации (ФССГА) и методы расчета их надежности.
Предмет исследования включает методологические подходы, положенные в основу разработки методов оценки надежности систем, процессы, обуславливающие изменение надежности систем при длительной наработке.
Научная новизна состоит в том, что впервые:
1 Поставлена и решена задача о правомерности традиционного подхода к решению задач оценки надежности сложных функциональных систем.
2. Показано, что построение экспоненциальной модели надежности выполнено с нарушениями ряда фундаментальных положений теории вероятностей, что при экспоненциальной модели интегральной функции вероятности отказа агрегатов ФССГА, их вероятность отказа на единицу времени (1 час полета) является убывающей функцией времени и неадекватно отражает деградационные процессы, происходящие в агрегатах в процессе работы.
3. Показана неправомерность использования условных вероятностей и условных плотностей вероятности для одной случайной величины и, как следствие, неправомерность получения экспоненциальной модели надежности агрегатов из представления интенсивности отказов в виде мгновенной условной плотности вероятности.
4. Показано, что решение задачи надежности сложных ФССГА с использованием интегральных функций вероятностей отказов агрегатов, приводит к неправомерному использованию теоремы умножения вероятностей, предусматривающей выполнение операций над вероятностями только дискретных событий (случаев).
5. Разработан методологический подход к решению задач расчета надежности сложных ФССГА, основанный на использовании дискретных значений вероятностей отказов агрегатов за произвольную единицу времени, которая, применительно к самолетам гражданской авиации, определена как 1 час полета, либо за продолжительность типового полета. Разработан метод расчета надежности ФССГА, обеспечивающий возможность оценки надежности, как при проектировании, так и при эксплуатации.
6. Показано, что прямое применение теоремы умножения вероятностей при использовании дискретных значений для ФССГА с различным типом резервирования, допустимо только применительно к системам с однозначным процессом развития отказа. Для систем с индивидуальным резервированием разработан альтернативный подход, учитывающий порядок (сценарий) развития отказов в системе.
7.Показана возможность существенного увеличения надежности ФССГА без увеличения числа агрегатов, за счет замены систем с общим резервированием на системы с последовательно соединенными блоками, имеющими индивидуальное резервирование
8. Решены частные задачи риск-анализа в постановке «затраты-прибыль». Показано, что в этой постановке, получаемые решения обеспечивают возможность анализа стратегических направлений развития техники.
9. Введена обобщенная оценка процесса «старения» функциональных систем. Показано, что системы самолетов гражданской авиации стареют не более чем на 60% вне зависимости от величины налета самолета. Показано, что реализуемый в эксплуатации процесс старения с позиций обеспечения надежности более благоприятен, чем процесс, задаваемый Разработчиком самолета.
Практическая значимость работы заключается в том, что:
1. Совершенствование методов расчета надежности систем обеспечивает Разработчиков, Эксплуатантов и Федеральные авиационные власти достоверной информацией о безотказности авиационной техники и ее соответствии требованиям НЛГС, что способствует повышению безопасности полетов.
2. Выполненные исследования процессов старения функциональных систем показывают, что при действующей системе технического обслуживания, нет оснований для снятия изношенных самолетов с эксплуатации по причине их недостаточной надежности.
3. Решение задач риск-анализа в координатах «затраты-прибыль» может служить практическим ориентиром для выбора эффективных направлений деятельности в развитии техники и обеспечении ее безопасности.
Апробация работы. Основные положения диссертационной работы доложены на НТС института Гражданской авиации Сибирского государственного аэрокосмического университета имени академика М. Ф. Решетнева.2006-2010; на НТС Самарского государственного аэрокосмического университета имени С.П. Королева, Самара, 2009; на III Всероссийской конференции «Безопасность и живучесть технических систем» ИВМ СО РАН, Красноярск, 2009, на НТС кафедры Самолетостроения и эксплуатация авиационной техники Иркутского государственного технического университета, Иркутск, 2010; на НТС Сибирского научно-исследовательского института им. С.А. Чаплыгина, Новосибирск, 2010; на НТС ОАО ИСС 2010 г.
Основные результаты диссертационной работы, изложены в монографии «Надежность функциональных систем самолетов гражданской авиации» (Избранные труды Российской школы, – М.: РАН. 2009), опубликованной по итогам I Всероссийского конкурса молодых ученых, проведенного Межрегиональным советом по науке и технологиям в 2009 г, г. Миасс.
Материалы диссертации использованы в учебном пособии «Надежность функциональных систем самолетов гражданской авиации», СибГАУ, 2010 г.
Публикации. Результаты работы опубликованы в 30 научных работах, в том числе 1 монографии, в 23 статьях в журналах из перечня ВАК.
Структура и объем. Диссертационная работа состоит из введения, 5 разделов, заключения и списка литературы. Работа объемом 194 страницы машинописного текста содержит 66 рисунков, 20 таблиц, список литературы включает 155 наименований.
основное содержание работы
В первом разделе рассмотрены вопросы обеспечения надежности и безопасности полетов Разработчиками и Изготовителями авиационной техники и поддержания ее Эксплуатантами. Показано, что Разработчики и Эксплуатанты существенно разобщены. Они проходят процедуры сертификации деятельности в различных государственных органах. Сертификационные требования к Разработчикам и Эксплуатантам не гармонизированы, как в части перечней особых (неблагоприятных) ситуаций, так и их определениях.
Взаимопонимание Разработчиков и Эксплуатантов отсутствует и в структуре показателей, оценке и контроле надежности авиационной техники. Разработчик оценивает надежность в вероятностях отказов, приводящих к последствиям различной степени тяжести, что соответствует государственным требованиям, заложенным в НЛГС. Эксплуатант контролирует надежность коэффициентом 
(числом отказов, приходящихся на 1000 часов налета). При этом связь 
с требованиями НЛГС неочевидна. Эксплуатант фактически неориентируется в оценках надежности и показателях задаваемых НЛГС. Это снижает мотивацию к поддержанию надежности и препятствует разработке предложений по совершенствованию авиатехники и ее технического обслуживания.
Представление об изношенности самолета в настоящее время основывается на налете часов, либо на календарном сроке службы. До настоящего времени нет критериев оценки изношенности ФСС.
Во втором разделе рассмотрены нормативные методы и методологические основы традиционного расчета надежности, действующие в гражданской авиации и у Разработчиков авиационной техники. Традиционно при расчете надежности сложных ФСС используются:
– математическая модель оценки надежности агрегатов;
– процедура построения математической модели надежности систем, основывающаяся на определенных правилах.
В качестве модели надежности высоконадежных агрегатов (редкий поток событий отказа) используются интегральные функции распределения вероятностей безотказной работы 
в виде экспоненциального распределения
, (1)
где 
- интенсивность отказа, и вероятности отказа 
. (2)
При стационарном процессе эксплуатации 
приравнивают к среднему на интервале значению параметра потока отказов 
, т.е. 
.
Вероятность отказа (2) является монотонно возрастающей функцией времени, асимптотически стремящейся к 1 при 
. Интегральная функция
имеет два существенных, с точки зрения оценки надежности, недостатка:
– интегральная функция не оценивает безотказность агрегата как его свойства, а является оценкой проявления этого свойства во времени;
– интегральная функция определяет вероятность отказа агрегата на интервале времени от 0 до 
, но не определяет момент отказа агрегата и в этом смысле вносит неопределенность.
Вероятность отказа за единицу времени (1 час) определяет безотказность агрегата как свойство и может быть получена как производная от по времени (рис. 2). Она является убывающей функцией времени, что никак не согласуется со здравым смыслом, опытом испытаний и эксплуатацией агрегатов. При испытаниях и в эксплуатации агрегат неизбежно деградирует и вероятность его отказа за 1 час
должна увеличиваться. При стационарном процессе эксплуатации большой совокупности однотипных агрегатов, и при определен ной системе технического обслуживания, параметр потока отказов 
принимают постоянным, поскольку он поддерживается техническим обслуживанием и заменами.
Поскольку 
является математическим ожиданием числа отказов за 1 час, естественно ожидать, что и вероятность отказов за 1 час является величиной, также не зависящей от времени. Экспоненциальное распре-
| Рисунок 2 – Зависимость вероятности отказа за 1 час при экспоненциальном распределении | деление представленное на рис. 2 явно противоречит этим представлениям. В работе рассмотрены два пути появле- |
ния в надежности этого распределения. Первый связан с использованием распределения Пуассона
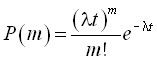, (3)
где 
- математическое ожидание попадания числа точек на единицу длины.
Положив участок 
пустым, т.е. 
(на участок не попала ни одна точка) из (3) сразу получают (1). Но распределение Пуассона определяет вероятность попадания на участок того либо иного числа точек, а «0» не является числом.
Далее из единицы вычитают (1) и получают вероятность отказа, которая вместе с (1) образует полную группу несовместных событий которая, при таких операциях не может не равняться 1, т.к.
(4)
Из распределения Пуассона (3) вероятность отказа 
, с большим основанием, может быть получена при, т.е. вероятность попадания одной точки на участок (рис. 3) будет иметь вид
, (5)
тогда вероятность отказа за 1 час будет вначале возрастать (рис. 3) как производная от 
, а затем примет отрицательные значения.
из (1) и из (5) образуют полную группу несовместных событий, но
| Рисунок 3 – Вероятности отказа агрегата, определенные при различных m |  Поскольку распределение Пуассона |
определяет вероятность попадания того либо иного числа точек на участок определенной протяженности, то адекватной оценки вероятности отказа и безотказной работы агрегата из этого распределения получить не удается. Тем более, что в задаче расчета вероятности отказа агрегата определяется вероятность попадания на участок только первой точки, как первого и единственного отказа. Но Пуассон этой задачи не рассматривал, а в требовании ординарности, наложенном на систему точек, отмечал, что точки распределены по оси с равномерной плотностью
числа точек на единицу длины 
. В монографии Александровской Л.Н. «Безопасность и надежность технических систем» (2008 г) совершенно справедливо отмечается, что для распределения Пуассона случайной переменной является число отказов, а не время. Замена в нем переменной на время, выполненная с использованием преобразования Лапласа, приводит к получению не экспоненциального, а гамма-распределения. Гамма-распределение может быть представлено как сумма экспоненциальных распределений вида (5).
Другой вывод экспоненциального распределения вероятности безотказной работы (Воробьев, В.Г. 1995) получен из представления интенсивности отказов 
как условной плотности вероятности в виде
, (6)
где 
- плотность распределения вероятности безотказной работы.
Поскольку
,
то после преобразований получают выражение вида (1).
Выражение (6) получено из рассмотрения испытания 
агрегатов (Базовский, И.; 1965), когда при времени 
, осталось 
исправных и 
отказавших агрегатов. Выполнив операции дифференцирования дискретных чисел (числа агрегатов) 
и 
автор приходит к выражению (6), которое корректно ровно в той степени, в которой корректны операции дифференцирования дискретных чисел. Однако следует отметить, что в распределении Пуассона (3) 
- математическое ожидание, а в (6) условная плотность вероятности, но результат получен одинаковый в виде (1), что является некорректностью.
Кроме того, в выражении (6) 
определена как мгновенная условная плотность вероятности для одной случайной величины и против такого определения есть ряд возражений:
– во-первых, рассматривается вероятностная задача (в вероятностной трактовке) и в ней по определяющей функции (вероятности отказа) вносится детерминистическая трактовка. Предполагается, что при всех t < t1, отказа не было с вероятностью равной единице, а положение t1 на оси времени никак не ограничено;
– во-вторых, плотность вероятности отказа для отдельного агрегата определяется из статистики испытаний большой группы таких агрегатов и является распределением, ординаты которого определены из опыта и не подлежат изменению даже при необходимости формирования условной плотности;
– в-третьих, как и при определении условной вероятности безотказной работы проигнорирован принцип отсутствия последействия;
– в-четвертых, в теории вероятностей определение условных вероятностей и условных плотностей вероятностей предусматривает наличие системы двух зависимых случайных величин, каждая из которых имеет свою переменную.
Таким образом, в работе показано, что экспоненциальное распределение не может быть принято в качестве математической модели вероятности отказа агрегата ФССГА.
Для анализа процедурных вопросов построения математической модели расчета надежности сложных систем, в работе рассмотрена традиционная процедура построения решения для тестовой системы состоящей из 16 агрегатов. Рассматривались случай общего резервирования, когда 4 цепочки из 4-х последовательно соединенных агрегатов включены параллельно и случай индивидуального резервирования, когда 4 блока из 4-х параллельно включенных агрегатов соединены последовательно. Для упрощения все агрегаты приняты одинаковыми с параметрами потоков отказов равными 
. Интегральные функции вероятностей отказов агрегатов приняты в форме распределения равномерной плотности
. (7)
Тогда интегральные функции вероятности отказа тестовой системы при традиционном подходе для индивидуального резервирования запишутся в виде
, (8)
а для общего резервирования
. (9)
Вид интегральных функций и приведен на рисунке 4, а соответствующие им значения вероятностей отказа за 1 час полета на рисунке 5.
Характер изменения кривых, приведенных на рисунке 4 указывает на то, что они являются интегральными функциями близкими к Нормальному закону распределения случайной величины. Зависимости вероятности отказа за 1 час полета (рис. 5) по виду схожи с плотностью распределения вероятности Нормального закона. Следует отметить, что вид Нормального распределения не зависит от используемого закона.
В соответствии с ОСТ, при использовании для агрегатов распределения равномерной плотности вероятности (7), при 
час будем иметь
| 1 – общее резервирование; 2 – индивидуальное резервирование; 3 – общее резервирование при экспоненциальном распределении Рисунок 4 – Вероятности отказа системы |  , т.е. вероятность отказа за 1 час численно равна параметру потока отказов и не |
зависит от времени. В связи с этим, кривые, приведенные на рисунке 5 трудно признать соответствующими исходной независимости от времени параметров потоков отказов агрегатов. Кроме того вероятности отказа за 1 час полета определены неоднозначно, т.к. каждая из вероятностей реализуется при двух существенно различных значениях времени. В работе показано, что неадекватность моделей реальным процессам, реализуемая при традиционном подходе к решению задачи
оценки надежности системы, является следствием подмены понятий. Так, процедура построения решения в задаче оценки надежности системы основывается на использовании теоремы умножения вероятностей. Теорема умножения вероятностей получена применительно к вероятностям дискретных событий и оперирует с дискретными событиями. При решении задачи расчета надежности сложных систем, при традиционном подходе, процедурам, предусмотренным теоремой умножения вероятностей, подвергают не дискретные события, а инте-
| 1 – общее резервирование; 2 – индивидуальное резервирование; 3 – общее резервирование при экспоненциальном распределении Рисунок 5 – Вероятность отказа системы за 1 час полета: | гральные функции вероятностей отказов агрегатов. Итоговые выражения для расчета надежности систем, вида (8), (9) представляют собой, в развернутом виде, суммы произведений сте- |
пеней от интегральных функций вероятностей отказов агрегатов. В соответствии с центральной предельной теоремой распределение таких сумм стремится к нормальному при увеличении числа членов (рис. 4 и 5). Подмена дискретных событий интегральными функциями при использовании теоремы умножения вероятностей приводит к несоответствиям результатов расчетов и испытаний на надежность. Сложный агрегат может быть представлен как система, состоящая из отдельных элементов с их последовательным и параллельным соединением. Расчет его надежности по традиционной методике неизбежно определит его интегральную функцию вероятности отказа и вероятность отказа за 1 час в форме кривых нормального распределения (рисунки 4 и 5). Вместе с этим, по итогам испытаний на надежность по стандартному плану для него определяют интенсивность отказа 
либо 
и моделируют его надежность однопараметрическим законом, скорее всего экспоненциальным. То же можно сказать и о сложных элементах элементной базы электронных блоков.
В работе отмечено, что интегральная функция вероятности отказа агрегата определяет вероятность отказа на интервале времени 
, и вносит неопределенность относительно конкретного момента времени отказа агрегата. При рассмотрении тестовой системы из 16 агрегатов следует иметь в виду и 16 неопределенностей. Для системы общего резервирования отказ реализуется с вероятностью из (9) (рис. 4) на интервале времени 
только тогда, когда в каждой из 4-х параллельно включенных цепочек, откажут по одному агрегату, т.е. если в системе откажут 4 агрегата. В большинстве источников авторы на этом обстоятельстве не акцентируют внимание. Для отрезка времени протяженностью 
, взятого внутри интервала 
, вероятность отказа традиционно определяют как приращение интегральной функции 
на этом отрезке. Но отказ системы на отрезке 
, естественно с соответствующей вероятностью, возможен только в случае если на 
откажут те же 4 агрегата, что и на интервале 
. К тому же в соответствии с требованием наложенным на систему точек, подчиняющихся распределению Пуассона, вероятность попадания на малый отрезок 
более одной точки (отказа) пренебрежимо мала. Таким образом, если решается задача относительно вероятности отказа на интервале 
, то в этой же постановке не может решаться задача вероятности отказа на отрезке 
. Следовательно, задачи определения вероятности отказа на интервале 
и на малом отрезке 
находящемся внутри этого интервала, при решении задачи расчета надежности системы, несовместны. В связи с этим, результаты приведенные на рисунках 4 и 5 не более чем результаты расчета конечных значений некорректных математических операций, неадекватно отражающих изменение надежности системы, а выражения (8) и (9) не интегральные функции вероятности отказа системы, а результат их некорректного определения.
В третьем разделе приведены результаты разработки альтернативного методологического подхода и метода расчета надежности сложных систем.
Распределение Пуассона получено при наложении условий ординарности, стационарности и отсутствия последействия на совокупность точек на оси. В условии ординарности указывается: «вероятность попадания того либо иного числа точек на отрезок протяженностью 
зависит только от длины этого отрезка и не зависит от его положения на оси. Иными словами, точки распределены на оси с равномерной плотностью с интенсивностью 
, равной математическому ожиданию числа точек на единицу длины». В соответствии с этим определением естественно полагать, что точки должны быть распределены по оси с равномерной плотностью вероятности. Для определения вероятности попадания первой точки (первого и единственно возможного отказа), ужесточим требования к системе точек. Положим, что точки расположены равномерно, т.е. на равном расстоянии 
, тогда вероятность попадания первой точки (первого отказа) выразится как
. (10)
Для перехода от регулярной системы точек к случайной, возвращаемся к системе точек подчиняющихся распределению Пуассона, заметим, что в нем рассто-яние между точками – величина обратная 
, т.е. 
и тогда
, (11)
т.е. получено распределение с равномерной плотностью вероятности на которое и указывал Пуассон в условии ординарности.
Далее в качестве математической модели интегральной функции вероятности отказа агрегатов в работе принято распределение с равномерной плотностью. Поскольку теорема умножения вероятностей предусматривает процедуры над дискретными событиями, то при решении задач надежности сложных систем предложено использовать дискретные значения вероятностей отказа агрегатов на единицу времени 
, а имея в виду, требования НЛГС на 1 час полета.
Разработан метод расчета систем с общим резервированием. Подстановкой 
ч в (8) и (9) найдено альтернативное значение вероятности отказа тестовой системы при общем резервировании за 1 час
. (12)
Остановимся подробнее на существе процедуры определения вероятности отказа на произвольном отрезке времени 
. Традиционно эта вероятность определяется как приращение интегральной функции вероятности отказа системы на этом отрезке. Для рассматриваемой тестовой системы это будет приращение функции (9) при общем резервировании.
При построении интегральных функций вероятностей отказа систем традиционно выполняются процедуры построения решений, не акцентируя внимание на условии реализации отказа в системе. Рассматриваемая система с общим резервированием откажет на интервале [0, t], только если в ней на этом интервале откажут ровно 4 агрегата (по одному в каждой цепочке). Моменты отказов этих агрегатов на рассматриваемом интервале времени никак не определены их интегральными функциями. В соответствии с условием ординарности, на малом отрезке, расположенном внутри интервала 
не может реализоваться более 1 отказа. Это условие подтверждается и статистикой отказов агрегатов систем самолетов в эксплуатации. В связи с этим, на отрезке времени протяженностью в 1 час, меньшем отрезка 
, не могут одновременно отказать 4 агрегата. Тем более условие отказа системы не может быть выполнено на малом 
(
). Это ставит под сомнение правомерность, как дифференциальной функции отказа системы, так и исходной интегральной функции.
С позиций теории вероятностей, процедуры построения традиционного решения, на первый взгляд, представляются оправданными. Но в действительности, при решении задач оценки надежности, проигнорировано как условие применения теоремы умножения вероятностей, так и условие ординарности. Построить решение относительно вероятности отказа системы на интервале 
в дискретных значениях вероятностей отказа агрегатов, как это предусматривает теорема умножения вероятностей, возможно лишь определив эти дискретные значения. Для этого интервал [0, ], где – дискретные моменты времени, необходимо принять за единицу времени и применительно к ней определить параметр потока отказов как
.
Тогда вероятность отказа агрегата за эту новую единицу времени, равную протяженности интервала [0, ], будет иметь вид
,
и вероятность отказа системы определится как
. (13)
Поскольку
, то выражение (13) формально подобно выражению (9), отличие состоит в понимании, трактовке и использовании результатов расчетов. Выражение (9) традиционно воспринимается как интегральная функция вероятности отказа системы с общим резервированием, по которому возможно определить текущее по времени значение вероятности отказа, вероятность отказа на отрезке, и вероятность отказа за 1 час в виде приращения (9) на этих отрезках (рис. 5). Выражение (13) не является и не интерпретируется как интегральная функция. Оно определяет вероятность отказа системы на дискретных интервалах [0, ], в том числе на интервале 
= 1 час.
Таким образом, в выражении (13), при изменении протяженности интервала, всегда понимается изменение параметра потока отказов 
при единичном значении времени. Тогда как в (9) параметр потока отказов 
принимается постоянным, а изменяется время 
.
Сходство выражений (9) и (13) определяет получение одинаковых результатов только при расчетах на равных интервалах, имеющих начало при 
. При определении вероятностей отказа системы на одинаковых отрезках 
(в том числе и при 
протяженностью 1 час) произвольно расположенных на оси 
, результаты расчетов существенно различны.
Рассматриваемая в работе тестовая система, согласно традиционному подходу (9) на отрезке 
=1000 часов имеет вероятность отказа равную:
| Диапазон (ч) |  |  |  |  |
 | 0,014 | 0,2 | 0,0256 | 0,0004 |
При альтернативном подходе в соответствии с (13), вероятность отказа при 
часов равна 0,014 и не зависит от положения отрезка 
на оси 
.
В первом случае выражение (9) рассматривалось как интегральная функция вероятности отказа (рис. 4) и в соответствии с ней на участке 
протяженностью 1000 часов при различных его положениях на оси 
вероятности отказа получены как приращения интегральной функции. Во втором случае, при альтернативном подходе, выражение (13) рассматривается как вероятность отказа на интервалах [0, ].
В рассмотренном примере для агрегатов принято распределение с равномерной плотностью вероятности, при котором вероятности их отказов на отрезке 
зависят только от его длины и не зависят от его положения на оси времени. Это свойство Пуассоновского потока событий. Несмотря на нелинейность выражения (13) и вид рис. 4, при альтернативном подходе это свойство осталось присущим и рассматриваемой системе.
В работе рассмотрена также правомерность использования традиционной интегральной функции вероятности отказа с позиций стационарности процесса эксплуатации и потоков событий отказов агрегатов. Практикой эксплуатации авиационной техники отечественного и зарубежного производства показано, что при действующей системе технического обслуживания потоки отказов агрегатов стационарны, т. е. параметры потоков отказов не зависят от времени работы системы (от налета часов). При этом момент времени принятый за начало отсчета времени в выражении (9) и на рис. 4 является произвольным и может быть выбран любым. Т. е. реализуется не одна функция (9), принятая за интегральную, а поле таких функций. Любому произвольному моменту времени t будут соответствовать вероятности отказа системы 
в интервале значений [0, 1] в зависимости от момента начала отсчета времени. Таким образом, в условиях стационарности потока отказов, интегральная функция вероятности отказа системы теряет смысл. Оправданным является определение вероятностей отказа системы на определенных отрезках времени, которые остаются независимыми от положения отрезка на оси времени (налета часов).
Разработан метод расчета систем с индивидуальным резервированием. Показано, что таким системам присущи некоторые ранее не рассматривавшиеся особенности. Рассматривается система индивидуального резервирования, содержащая n последовательно соединенных блоков, каждый из которых включает m = 2 параллельно соединенных агрегатов. Структурная схема такой системы приведена на рис. 6.
Рисунок 6 – Структурная схема системы с
индивидуальным резервированием
Положим, что параметры потоков отказов всех агрегатов одинаковые равные, а 
. Примем в качестве математической модели вероятности отказа агрегатов распределение с равномерной плотностью. При традиционном подходе к расчету надежности вначале определяется вероятность отказа блоков из параллельно включенных агрегатов в виде
,
и вероятность их безотказной работы
.
Исходная система, таким образом, заменяется на эквивалентную с 
последовательно соединенными элементами, вероятности безотказной работы которых равны 
. Далее определяется вероятность отказа всей исходной системы за 1 ч:
. (14)
Из (14) следует, что вероятность отказа системы с последовательно соединенными блоками возрастает по мере увеличения числа блоков n. Показано, что в действительности это далеко не так, поскольку рассматриваемая система (рис. 6) откажет только в том случае если в одном из блоков (любом) откажут оба агрегата. Так как вероятности отказов агрегатов в 1 час одинаковы и равны, возможны различные сценарии отказов агрегатов, не приводящие к отказу всей системы. Например возможен сценарий когда откажут агрегаты 1, 3, 6, 7 безразлично в какой последовательности. И чем больше n, тем меньше вероятность отказа 2-х агрегатов в одном блоке. В работе эта вероятность определена следующим образом. Поскольку первым может отказать любой агрегат системы с вероятностью, то вероятность того, что вторым откажет агрегат, установленный в одном блоке с отказавшим, равна 
. Тогда, наибольшая из всех возможных (сценарий 1) вероятность отказа рассматриваемой системы, при альтернативном подходе к расчету систем с индивидуальным резервированием, будет
. (15)
Другие возможные сценарии развития отказов в системе определяют существенно меньшие вероятности отказа в соответствии с выражением
, (16)
где i – число отказавших агрегатов приводящих систему к отказу при рассматриваемом сценарии развития отказов.
Таким образом, становится очевидным, что при увеличении числа последовательно соединенных блоков вероятность отказа в соответствии с (15) и (16) уменьшается, а не возрастает, как это определяет традиционный подход (14). Разработанный метод расчета надежности систем с индивидуальным резервированием позволяет по новому взглянуть на возможности повышения надежности систем, за счет изменения подхода к применению сочетания общего и индивидуального резервирования.
Рассмотрим систему (рис. 7), состоящую из 
параллельно работающих подсистем содержащих по 16 последовательно соединенных агрегатов.
Рисунок 7 – Система общего резервирования
Вероятность отказа системы общего резервирования согласно традиционной методики определится как
, (17)
где параметр потока отказов принят одинаковым для всех агрегатов.
Не изменяя числа агрегатов в системе и степень ее резервирования, представим систему как z соединенных последовательно равных частей, например,, (рис. 8)
Рисунок 8 – Схема исходной системы, разделенная на z = 4 части общего резервирования
Рассчитаем надежность полученной системы. Вероятность отказа каждой ветви любой из 4-х частей будет
.
Тогда система представленная на рис. 8 преобразуется к виду представленному на рис. 9, а вероятность ее отказа определится как
. (18)
Рисунок 9 – Схема системы, разделенная на z = 4 частей, преобразованная к схеме индивидуального резервирования
В системе (рис. 9) вероятность отказа каждого элемента равна 
. При альтернативном подходе первая и наибольшая вероятность отказа всей системы (рис. 9) реализуется, когда откажут 2 элемента в одном блоке, и определится как
.
Для сравнения выполнены расчеты вероятностей отказов систем при общем резервировании и после разбиения на z частей с индивидуальным резервированием по традиционному и альтернативному методам. На рис. 10 и 11 приведены зависимости и.
| Рисунок 10 – Отношение вероятностей отказа исходной системы общего резервирования к вероятности отказа системы разделенной на z частей, рассчитанной по традиционной методике при n = 16, m = 2 и = 110-2 | 1) = 110-5 и 2) =110-2 Рисунок 11 – Зависимость от z отношения вероятностей отказа исходной системы к вероятности отказа системы разделенной на z частей и рассчитанной по альтернативной методике при n=16, m=2 |
Из рис. 10 следует, что расчеты, выполненные при традиционном подходе, показывают увеличение надежности системы с общим резервированием, при разделении ее на z частей, что переводит ее в систему, содержащую z блоков с индивидуальным резервированием. Но это увеличение надежности несущественное, так как при z = 2 надежность возрастает в 1,8 раза, а при z = 4 в 3,5 раза (рис. 10). В работе показано, что перевод системы с общим резервированием к системе с z блоками индивидуального резервирования сопряжен с определенными трудностями. Несущественное увеличение надежности, выявляемое при традиционном
подходе, не стимулирует разработчиков систем к преодолению этих трудностей.
При альтернативном методе решения той же задачи увеличение надежности с разбиением системы на z частей существенно больше (рис. 11). При z=4 надежность увеличивается в 100, а при z = 6 в 340 400 раз.
Показано, что для системы с общим резервированием при трех параллельно работающих подсистемах эффект еще выше. При традиционном подходе к рас-
чету надежности он составляет при z = 4 увеличение надежности в 12 раз (рис. 12), а при альтернативном подходе (рис. 13) надежность возрастает в 2800 раз и в 9000 раз при z = 5. Это не может не стимулировать разработчиков к преодолению упомянутых выше трудностей связанных с переходом от систем с общим резервированием к системам имеющим z блоков индивидуального резервирования. При традиционном подходе, при построении решения для расчета надежности сложных систем, не учитывается неоднозначность возможных путей (сценариев) развития отказа в системе. Это также приводит к получению ошибочных результатов.
Практика оценки надежности агрегатов и ФСС ГА опирается на результаты испытаний, программы которых в соответствии с ГОСТами определяются планами испытаний. Поверочные расчеты выполняются по статистической информации о наработках и отказах, собранной в эксплуатационных подразделениях. При этом, планы испытаний на надежность не совпадают с программами технического обслуживания и возникает неоднозначность в толковании результатов. В связи с этим, для получения адекватных оценок на стадии проектирования, необходимо планы испытаний согласовывать с задаваемыми эксплуатантам программами технического обслуживания.
| Рисунок 12 – Отношение вероятностей отказа исходной системы и системы разделенной на z частей, рассчитанные по традиционной методике при n = 20, m = 3 и = 1 10-2 | Рисунок 13 – Отношение вероятностей отказа исходной системы и системы разделенной на z частей, и рассчитанные по альтернативной методике при n = 20, m = 3 и = 110-2 |
В практике технической эксплуатации различают две стратегии: стратегию эксплуатации до выработки ресурса и стратегию эксплуатации по фактическому состоянию. Последняя в свою очередь разделяется на стратегию эксплуатации до предотказного состояния и до безопасного отказа. Каждой стратегии эксплуатации соответствует своя стратегия технического обслуживания. Стратегии эксплуатации до выработки ресурса соответствует стратегия технического обслуживания с контролем наработки. Стратегии эксплуатации до предотказного состояния соответствует стратегия обслуживания с контролем параметров. Стратегии эксплуатации до безопасного отказа соответствует стратегия обслуживания с контролем надежности.
В расчетах надежности часто используют интенсивность отказа 
и параметр потока отказов 
. Планам испытаний, по результатам которых оцениваются 
и 
, в эксплуатации соответствует стратегия эксплуатации до безопасного отказа, но только до той поры, пока не выполнялись мероприятия по поддержанию надежности агрегатов.
С целью пояснения проблемы выбора оценок надежности агрегатов по статистическим материалам эксплуатантов, в работе определено соотношение наработок и отказов для рулевых приводов самолета Ту-154М. Привода эксплуатируются до выработки ресурса равного 12 000 летных часов. По статистике наработок и отказов всех эксплуатирующихся агрегатов определена средняя наработка на отказ 
. Параметр потока отказов 
- величина обратная 
. По статистике наработок и отказов только отказавших агрегатов определены значения 
, 
, 
. Значения указанных оценок приведены в таблице 1
Таблица 1 Значения наработки агрегатов
| Тип агрегата |  |  |  |  |
| РП-55-2А | 40600 | 3999 | 213 | 10000 |
| РП-56-2 | 182700 | 6200 | 2410 | 10640 |
| РП-57 | 121800 | 9180 | 580 | 15800 |
| РП-58 | 162400 | 5758 | 1197 | 12276 |
Значения 
(табл. 1), используемые для определения 
и в расчетах надежности, существенно отличается от 
, 
, 
. Более того при среднегодовом налете самолета 2 000 часов и 
=182 700 часов, календарный срок наработки на отказ для РП-56-2 составит 91 год, а для агрегата РП-55-2А – 20 лет. Рассматриваемые агрегаты являются гидромеханическими с высоким давлением и с резиновыми уплотнительными манжетами. Естественно, что они не смогут безотказно проработать 90 или даже 20 лет.
На первый взгляд, складывается абсурдная ситуация. В расчет закладывается надежность агрегата, определяемая как 
, которая для агрегатов недостижима в принципе. Здесь следует иметь ввиду два аспекта действующей стратегии технического обслуживания. Первый состоит в том, что заменяются не только отказавшие агрегаты, но и все неотказавшие наработавшие 12 000 часов, т.е. реально ни 20 лет ни 91 год агрегаты не эксплуатируются.
Вторым аспектом является стационарность процессов эксплуатации, т.е. приведенные в таблице 1 значения 
остаются в эксплуатации неизменными. В связи с этим, в расчетах на надежность агрегатов и систем необходимо использовать именно эти 
. Но при этом необходимо помнить, что это оценки не только собственных свойств безотказности агрегатов, но и системы их технического обслуживания, а она сильно зависит от принятой стратегии и режимов технического обслуживания. Если рассматриваемым рулевым приводам увеличить ресурсы, например, до 24 000 часов, то их параметры потоков отказов увеличатся. А если уменьшить до значений менее 12 000 часов, то параметры потоков отказов также уменьшатся.
Параметр потока отказов агрегата в эксплуатации следует представить состоящим из двух частей
.
Одна составляющая 
- определяется собственно свойствами агрегата, другая 
- стратегией и режимом обслуживания. В эксплуатации при действующей системе технического обслуживания выделить эти составляющие не представляется возможным.
Для оценки вероятностей пребывания системы в различных состояниях оперативного цикла использования самолета по назначению разработана упрощенная методика использования Марковских моделей.
В четвертом разделе рассмотрены некоторые аспекты риск-анализа авиационной техники. Риск-анализ, как новое направление в области исследования надежности, развивается сравнительно недавно. Под ним понимается анализ произведения вероятности возникновения катастроф на потери, сопровождающие их реализации (А.М. Лепихин, Н.А. Махутов, 2003). Фактически под риск-анализом понимается риск потерь. В работе развивается подход, анализирующий «затраты-прибыль», предложенный в монографии Девида Б.Брауна (1979 г.). Под затратами понимаются средства истраченные на достижение определенного уровня безопасности сложных человеко-машинных систем, а прибыль это нереализовавшиеся потери от аварий и катастроф в функции затрат на безопасность. Кривая «затраты-при-быль», как утверждает Б.Браун, имеет один и тот же характер для всех областей человеческой деятельности (рис. 14)
Отличие состоит в соотношении затрат и прибыли. В соответствии с кривой «затраты-прибыль», на начальном этапе повышения безопасности небольшие затраты обеспечивают получение существенной прибыли. По мере роста затрат на безопасность, эффект неуклонно снижается. Опасность существует всегда и приходит с неожиданной стороны.
Существенен вопрос о том, сколько необходимо и достаточно вкладывать средств в
| Рисунок 14 – Кривая затраты-прибыль | обеспечение безопасности. Б. Браун полагает, что условие необходимости и достаточности |
выполняется если затраты равны прибыли. Считается, что при меньших затратах налогоплательщики теряют из-за недостаточного разрежения потока аварий и катастроф. При больших затратах в обеспечение безопасности общество беднеет поскольку недопроизводит товары и услуги. В настоящее время появились отрасли промышленности, например ядерная энергетика, для которых такое условие необходимости и достаточности представляется сомнительным. Авария на атомной электростанции может уничтожить экономику государства средних размеров, но вложение всего национального дохода государства в безопасность далеко от реальности и бессмысленно.
В работе предпринята попытка построить математическую модель кривой «затраты-прибыль» и наполнить ее содержанием как в части затрат, так и прибыли. на примере частных задач обеспечения безопасности полетов. Для этого рассмотрена статистика 50 катастроф с самолетами и вертолетами на территории Российской Федерации. Установлено, что катастрофы, вызванные отказами функциональных систем, не наблюдались. 97 % катастроф сопряжены с негативными последствиями влияния человеческого фактора. И только 3% катастроф связаны с отказами авиационной техники, по причине КПН. Они определяются отказами двигателей с отягощающими последствиями, к которым относятся нелокализуемый пожар и разрушение двигателя, наносящее самолету повреждения, при которых продолжение полета становится невозможным.
При современном уровне производства надежность двигателей с большей или меньшей тягой одинакова. В этих условиях вероятность отказа двигателя с отягощающими последствиями возрастает с увеличением числа двигателей на самолете. В связи с этим в гражданской авиации наметилась тенденция к увеличению тяги двигателей и к переходу к двухдвигательным самолетам.
Производство двигателя большей тяги существенно дороже, чем меньшей. Так стоимость одного килограмма тяги двигателя примерно пропорциональна степени увеличения каждого килограмма тяги в кубе. Данный факт обеспечивает возможность построения кривой «затраты-прибыль» для оценки безопасности полетов, определяемой безопасностью силовой установки.
В работе рассмотрено влияние стоимости силовой установки самолета на потери от катастроф. Стоимость одного килограмма тяги двигателя принимается пропорциональной степени увеличения его тяги k (k = 23) в n раз. Пусть базовый двигатель имеет тягу Р0 и стоимость Ц0. Если на самолете установлено m базовых двигателей, то тяга всей силовой установки выразится как
,
а стоимость базового варианта силовой установки будет
.
При увеличении тяги двигателя в n раз, стоимость одного килограмма тяги увеличивается в 
раз, а стоимость самого двигателя увеличивается в 
раз. Если в силовой установке использовать двигатели большей тяги, то при фиксированной тяге силовой установки Р на самолете будет установлено в n раз меньше двигателей. Тогда стоимость силовой установки с уменьшенным числом двигателей будет
. (19)
Для оценки потерь от катастроф в соответствии с НЛГС зададимся вероятностью катастрофического отказа двигателя на один час полета 
. Будем считать, что потери, связанные с реализацией одной катастрофы равны Ck и, что базовая силовая установка самолета содержит 
двигателей. Тогда вероятность отказа двигателя за 1 час полета
.
Поскольку увеличение тяги двигателей в n раз позволяет во столько же уменьшить их число в силовой установке, то и вероятность отказа двигателя будет
.
Тогда стоимость потерь от катастрофы составит
. (20)
Выражения (19) и (20) в параметрической форме определяют кривую «затраты на безопасность – уменьшение потерь от катастроф по параметру n». Выразив 
из (19) в виде
,
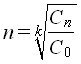и подставив в уравнение (20) окончательно получим
. (21)
Поскольку C0 и Ck нам неизвестны, то характер изменения затрат и уменьшение потерь удобнее исследовать по выражениям (19) и (20) в долях C0 и 
.
Результаты выполненных расчетов для случаев увеличения стоимости одного кг тяги пропорционально второй и третьей степени увеличения тяги двигателя, представлены на рисунке 15. Таким образом из рисунка следует, что с увеличением затрат, их эффективность по уменьшению потерь от катастроф интенсивно снижается, что хорошо согласуется с предложенной в Б Брауном моделью «затраты-прибыль» применительно к безопасности полетов.
В работе рассмотрена задача анализа соотношения затрат и прибыли для самолета при неизменном числе двигателей m и увеличении их тяги. Поскольку при увеличении тяги двигателей в n раз стоимость каждого килограмма тяги увеличивается в nk раз, а стоимость двигателя увеличивается в nk+1 раз, то стоимость силовой установки в этом случае будет
(22)
При этом пропорционально n
| Рисунок 15 – Зависимость потерь от катастроф в функции затрат | возрастает общая тяга силовой установки самолета, а с ней возрастает полетная масса, пассажировмести- |
мость и потери от реализации катастрофы, т. е.
,
где 
- потери от катастрофы при базовом варианте силовой установки.
Тогда, потери от катастрофы с учетом ее вероятности будут
.
Окончательно выражение для расчета потерь определится в виде
(23)
Зависимость потерь связанных с катастрофами в функции затрат на увеличение тяги силовой установки приведены на рис. 16. В противоположность рис. 15 здесь потери от катастроф увеличиваются по мере увеличения затрат на силовую
установку. Увеличение потерь, в этом случае, связано с ростом пассажировместимости самолета при неизменной надежности силовой установки. Таким образом, с увеличением тяги двигателей стоимость силовой установки растет значительно быстрее потерь из-за катастроф.
При этом может сложиться ложное впечатление об уменьшении потерь от катастроф. На самом деле, такой характер зависимости потерь от затрат на силовую установку указывает на то, что начиная с некоторой величины затрат, т. е. тяги силовой установки, затраты возрастают настолько интенсивно, что этот путь следует признать тупиковым.
В диссертационной работе выполнено исследование эффективности затрат на повышение надежности систем самолета за счет увеличения точности
| Рисунок 16 – Зависимость потерь от катастроф в функции затрат на увеличение тяги двигателей | размерной обработки деталей. Вывод подобен приведенным выше. |
В вопросах обеспечения и поддержания надежности и летной годности особое значение имеет понимание основных положений Норм летной годности самолетов. В диссертационной работе положения НЛГС рассмотрены на примере влияния прочности конструкции самолета на его экономическую эффективность.
Так, максимальная взлетная масса самолета Мmax складывается из: массы полезного груза Мп.г. (пассажиры и грузы), массы топлива Мт и массы конструкции самолета Мк. Например, для самолета Ту-204: Мmax = 107,9 т; Мп.г. = 25,2 т; Мт = 32,7 т; Мк = 50 т.
При фиксированных Мт и Мmax, изменение массы полезного груза возможно только за счет массы конструкции или наоборот.
Прочность конструкции самолета и способность противостоять полетным нагрузкам без разрушения, определяется площадью сечения его силовых элементов. При неизменных материалах конструкции, прочность прямо пропорциональна массе конструкции. Прочность определяет риск разрушения, т. е. риск катастроф и однозначно связана с массой полезного груза. Для самолета Ту-204 эта связь определится в виде
Мп.г. = (Мmax – Мт) – Мк = 75,2 – Мк.
Поставлена задача определения связи массы конструкции с вероятностью ее разрушения, т. е. с вероятностью реализации катастрофы. Масса конструкции самолета Ту-204, равная 50 т, определена из условия ее способности противостоять без разрушения воздействию двукратной перегрузке 
, при максимальной массе с коэффициентом запаса прочности 
. При этом, вероятность разрушения 
, в соответствии с НЛГС, должна быть не более 110-9.
Если величину массы конструкции самолета 
=50 т разделить на величину перегрузки 
=2 и величину запаса прочности 
=1,5, то самолет с максимальной взлетной массой разрушится с вероятностью равной 1 при критической массе 
=16,6 т. Рассмотренные условия определяют две точки функциональной зависимости вероятности разрушения от массы конструкции 
= f(Mк). Совершенно очевидно, что при Мк > 50 т вероятность разрушения сохраняется, хотя и становится меньше чем 110-9. Допустимо предположить, что вероятность разрушения будет асимптотически стремиться к нулю по мере увеличения массы конструкции. Это предположение может быть реализовано если зависимость 
= f(Mк) будет иметь экспоненциальный вид.
Тогда, с учетом отмеченных выше условий, для вероятности разрушения конструкции самолета Ту-204 найдено:
= exp 0,6138 (
– 
).
По этому выражению рассчитаны значения вероятности разрушения и массы полезного груза приведенные в табл. 2.
Таблица 2 Массы конструкции, полезного груза и вероятности разрушения самолета
| Мк, т | 16,6 | 20 | 30 | 40 | 50 | 60 | 70 |
| Mп.г., т | 58,6 | 55,2 | 45,2 | 35,2 | 25,2 | 15,2 | 5,2 |
| Q | 1 | 0,124 | 2,610-4 | 5,7810-7 | 110-9 | 2,710-12 | 5,8210-15 |
| Рисунок 17 – Зависимость вероятности разрушения самолета от массы полезного груза Q = е0,6138(16,6 – Mк) | Рисунок 18 – Зависимость вероятности разрушения конструкции от массы самолета |
Построение графической зависимости =f(Mк) в диапазоне ее изменения от 1 до 5,8210-15 затруднительно. Поэтому на рис. 17 приведена зависимость ln=f(Mп.г.). Из табл. 2 и рис. 17 видно, что во всем рассмотренном диапазоне увеличения массы конструкции, вероятность ее разрушения непрерывно уменьшается. Чтобы получить наглядное представление о ха рактере кривой на рис. 18 и рис. 19 показан ее вид на начальном и конечном участках рассмотренного диапазона изменения Mк. Из приведенных рисунков следует, что значение нормируемой вероятности разру шения конструкции 110-9 не является ни особой, ни характерной точкой на кривой 
=f(Mк). Напрашивается вопрос, из каких соображений задано пороговое значение вероятности катастрофической ситуации 110-9? Ответ на него может быть получен из п. 2.4 Руководства по сохранению летной годности ИКАО: «…2.4. Для оценки приемлемости конструкции, было признано необходимым, установить обоснованные значения вероятности, которые были определены на следующей основе:
а) опыт эксплуатации свидетельствует о том, что серьезное авиационное происшествие по причине эксплуатационного и конструктивного характера имеет место примерно один раз за миллион часов налета. В 10 % случаев такое происшествие может быть связано с отказными состояниями, возникающими вследствие отказа самолетных систем. Исходя из этого считалось, что для новых конструкций вероятность серьезных авиационных происшествий, вызванных отказами систем, не должна превышать этого показателя. Поэтому требуется, чтобы вероятность возникновения серьезного авиационного происшествия, вызванного всеми такими отказными состояниями, не превышала одного случая на 10 миллионов часов налета, т. е. вероятность должна составлять менее 10-7;
б) для того, чтобы удостовериться в обеспечении этого заданного показателя, необходимо выполнить комплексный количественный анализ надежно-сти работы всех систем самолета. Для
| Рисунок 19 – Зависимость вероятности разрушения конструкции в диапазоне ее расчетного значения от массы самолета | этого было сделано произвольное допущение о наличии примерно 100 потенциальных отказных состояний, которые будут препятствовать выполне- |
нию продолженного безопасного полета и посадки. Заданная вероятность происшествия, составляющая 10-7, равномерно распределится между этими состояниями, что, в конечном итоге, обусловило вероятность каждого отказного состояния не более 110-9. Таким образом, верхний предел вероятности отдельного отказного состояния, которое не позволит безопасно продолжить полет и выполнить посадку, установлен на уровне 110-9 для каждого часа полета….».
Этот предел естественно установлен и для такого отказного состояния, которое обусловлено недостаточной надежностью и прочностью конструкции планера самолета и любой его системы. Вместе с этим, совершенно очевидно, что в установлении нормативного значения вероятности катастрофической ситуации 110-9 содержатся существенные неопределенности.
Так в п. 2.4 а) Руководства, определение частоты серьезного авиационного происшествия менее 110-7 содержит две, изменяющихся в эксплуатации, предположительных оценки.В пункте 2.4 б) принято произвольное допущение о 100 потенциальных отказных состояниях, которые приводят к катастрофе. В итоге, получена верхняя граница вероятности катастрофических ситуаций, вызванных отказами авиационной техники равная 110-9 на час полета. В целом, эта оценка воспринимается как обобщающая оценка опыта самолетостроения. Очевидно, что точное получение такой оценки из теоретических и экспериментальных материалов не представляется возможным.
Разработчикам самолетов в доказательной документации, подтверждающей соответствие самолета требованиям НЛГС, необходимо подтвердить недопустимость катастрофических отказных состояний с вероятностью не более 110-9. Это тоже крайне непростая задача.
В таблицах 3 и 4 приведены оценки отношения массы конструкции самолетов к максимальной взлетной массе. Среднее значение относительной массы конструкции для ближнемагистральных самолетов оказалось равным 0,586, для среднемагистральных 0,542, и для дальнемагистральных 0,472. Это расхождение для различных классов самолетов вполне объяснимо.
Таблица 3 Соотношение масс для ближнее- и дальнемагистральных самолетов
| Класс | Ближнемагистральные | Дальнемагистральные | |||||||||
| Тип | Ту-134А | Як-42 | МД-81 | В-737 | А-320-100 | Ил-62М | В-707-320В | В-767-200ER | Ил-96-300 | А-340-200 | MD-11 |
| Год внедрения | 1967 | 1980 | 1981 | 1990 | 1988 | 1974 | 1962 | 1984 | 1992 | 1992 | 1990 |
| Мmax | 47 | 57 | 63,5 | 52,4 | 66 | 167 | 151,5 | 175,5 | 216 | 251 | 273,3 |
| Мк | 29 | 33,5 | 35,5 | 31 | 38 | 73,4 | 67,1 | 83,8 | 117 | 118,6 | 126,7 |
| Мк/Мmax | 0,617 | 0,588 | 0,56 | 0,59 | 0,576 | 0,439 | 0,443 | 0,477 | 0,54 | 0,472 | 0,463 |
Таблица 4 Соотношение масс для среднемагистральных самолетов
| Класс | Среднемагистральные | ||||||
| Тип | Ту-154М | В-727-200 | В-757-200 | А-320-200 | Ил-86 | L-1011 | A-330-300 |
| Год внедрения | 1986 | 1971 | 1984 | 1988 | 1980 | 1972 | 1993 |
| Мmax | 100 | 95 | 108,8 | 73,5 | 210 | 195 | 208 |
| Мк | 55 | 46,7 | 58,2 | 39,8 | 117,4 | 108,5 | 117,7 |
| Мк/Мmax | 0,55 | 0,49 | 0,535 | 0,54 | 0,56 | 0,556 | 0,566 |
Ближнемагистральные самолеты имеют продолжительность беспосадочного полета 1-2 часа, а дальнемагистральные 10 –12 часов. При одном и том же ресурсе 60 000 летных часов, ближнемагистральные самолеты испытывают в 5 раз большее число циклов нагружения, определяемых взлетами и посадками, по сравнению с дальнемагистральными. Разброс относительных масс для самолетов одного класса в пределах 11–12 % представляется крайне существенным и труднообъяснимым.
Из таблицы 3 и рис 19 следует, что для рассматриваемого самолета Ту-204 уменьшение вероятности разрушения со значения 5,7810-7 до 110-9 за 1 час требует увеличения массы конструкции с 40 до 50 т, что на практике приведет к уменьшению массы полезного груза с 35,2 т до 25,2 т. Надежность самолета в области значений вероятности отказа 110-9 за 1 час трудно прогнозировать и доказывать, а ее увеличение сопряжено с существенным уменьшением массы полезного груза и коммерческой отдачи, т. е. конкурентоспособности.
Повышение надежности и снижение ущерба от катастроф, в рассматриваемом случае, сопряжено с увеличением стоимости перевозок.
В пятом разделе рассмотрена проблема «старения» функциональных систем самолетов в процессе длительной эксплуатации и влияние старения на надежность систем. В настоящее время основной парк магистральных самолетов России составляют самолеты отечественной постройки, налетавшие от 20 до 45 тысяч летных часов. Самолеты иностранного производства, приобретаемые в собственность, либо эксплуатирующиеся на лизинговой основе, также, в основном далеко не новые.
В последние 10-15 лет в научно-популярной и отраслевой литературе появились публикации сеющие сомнения в надежности стареющего парка самолетов. В связи с этим, в работе выполнены исследования влияния длительности наработки на надежность функциональных систем.
На самолете используется большое число функциональных систем, оказывающих существенное влияние на надежность самолета и безопасность полетов. В таблице 5 приведено распределение доли отказов, вызванных КПН по различным функциональным системам отечественных самолетов, приведших к авиапроисшествиям.
В среднем доля отказов по КПН составляет 75 % от общего числа авиапроисшествий по всем типам самолетов. Следует отметить, что из-за сложности структуры систем, поиск отказов и их устранение сопряжено с существенными потерями времени и экономическим ущербом. Важным является факт того, что 44,3 % от общего числа отказов агрегатов систем проявляются в полете и оказывают влияние на его безопасность.
Функциональные системы самолетов состоят из большого числа агрегатов и комплектующих изделий, которые имеют различные физические основы функционирования и конструктивное исполнение. Так на самолете Ту-154М только до безопасного отказа эксплуатируются 934 агрегата. Естественно, что изучение старения систем на основании рассмотрения деградационных процессов структурных элементов агрегатов и их выходных характеристик является невыполнимой задачей при анализе надежности систем.
Ресурсы агрегатов (до первого ремонта и межремонтный) в определенной степени характеризуют их возможности выполнять свои функции с установленной надежностью. В связи с этим, в работе предложено степень отработки агрегатами своих ресурсов принять за оценку процессов старения функциональных систем. Относительная отработка ресурса i-м агрегатом определится как
,
где 
- наработка i-го агрегата в момент сбора информации; 
- ресурс агрегата межремонтный либо до первого ремонта.
Таблица 5 Перечень систем, отказы которых из-за КПН создают наибольшее число инцидентов (ПАП) (в сумме в среднем – 75 % по каждому типу самолета)
| Наименование системы | Относительное число ПАП, вызванных отказами систем, % | Относительное число в общем числе ПАП, % | |||||||||
| Ан-2 | Л-410 | Як-40 | Ан-24 | Ту-134 | Як-42 | Ту-154 | Ил-62 | Ил-62М | Ил-86 | ||
| Система кондиционирования | 4,43 | 7,30 | 2,49 | ||||||||
| Радиоаппаратура связи | 5,56 | 2,02 | |||||||||
| Система электроснабжения | 9,11 | 5,64 | 3,93 | 4,30 | 4,39 | ||||||
| Система управления самолета | 3,29 | 22,00 | 6,67 | 2,72 | |||||||
| Гидравлическая система | 5,64 | 4,93 | 3,95 | 7,87 | 10,53 | 3,18 | |||||
| Шасси | 42,96 | 54,66 | 21,05 | 36,52 | 12,00 | 31,70 | 6,67 | 11,82 | 37,71 | 25,38 | |
| Пилотажно-навигационная | 6,67 | 4,30 | 1,85 | ||||||||
| Фонарь, окна | 4,49 | 0,93 | |||||||||
| Крыло | 10,00 | 0,81 | |||||||||
| Воздушные винты | 12,50 | 2,20 | |||||||||
| Двигатель | 54,00 | 16,20 | 7,39 | 12,50 | 11,80 | 28,00 | 25,43 | 21,66 | 40,85 | 19.30 | 27,81 |
| Топливная система двигателя | 5,26 | 4,30 | 7,89 | 4,05 | |||||||
| Система зажигания | 5,33 | 1,39 | |||||||||
| Приборы контроля двигателя | 6,34 | 11,18 | 15,67 | 5,83 | |||||||
| Система выхлопа (реверс) | 33,33 | 13,97 | 3,24 | ||||||||
| Навигационная радиоаппаратура | 5,43 | 6,58 | 3,93 | 2,02 | |||||||
| Суммарное относительное число ПАП | 74,00 | 76,78 | 76,86 | 75,31 | 75,84 | 72,00 | 72,8 | 75,00 | 75,24 | 75,43 | 90,31 |
| Число систем с наибольшим числом отказов, приводящих к ПАП | 4 | 5 | 5 | 8 | 7 | 4 | 3 | 5 | 5 | 4 | |
Тогда старение системы, как степень отработки ресурсов ее агрегатами, можно представить в виде средней относительной отработки ресурсов
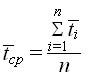
где 
- число агрегатов в системе.
Старение функциональных систем в работе исследовалось на примере гидромеханических и электросистем самолетов Ту-154М, Ан-24 и вертолетов Ми-8. Поскольку в авиакомпаниях не сохраняется «история» налета агрегатов по налету планера, то построить зависимость 
для функциональных систем самолетов в функции налета планера с начала его эксплуатации для произвольных значений налета 
не представляется возможным. Рассмотрены могут быть только те значения по оси времени (налета), которым соответствует налет экземпляров (бортов) самолетов на момент выполнения исследования. Этим объясняется неравномерность интервалов времени между смежными значениями на зависимостях приведенных на рис. 20, 21 и 22.
Из приведенных рисунков видно, что средние относительные отработки ресурсов агрегатами функциональных систем возрастают с увеличением налета планера самолета, но не превышают значения 0,6 (60 %). Предельное значение средней относительной отработки ресурсов агрегатами систем для различных систем достигается при различном налете планера. Это определяется величиной собственных ресурсов агрегатов систем. Стабилизация средней относительной отработки ресурсов агрегатами систем определяется их заменами при эксплуатации вследствие отработки ресурсов, неисправностей, отказов и по организационным причинам.
Рисунок 21 – Средняя относительная отработка ресурсов агрегатами шасси
Таким образом, стабилизация отработки ресурсов агрегатами на 60 % указывает на то, что системы «не стареют» более чем на 60 %, а следовательно не могут являться причиной уменьшения надежности самолетов с большими налетами часов.
Вместе с этим следует помнить, что в структуре системы одновременно работают агрегаты с различной отработкой ресурсов от малой до близкой к 100 %.
Разработчик самолета, задавая требования по ресурсам агрегатов, вместе с этим задает и процесс «старения» систем. Но в этом процессе не учитываются замены агрегатов вследствие отказов, неисправностей и по организационным причинам. Разработчик учитывает замены агрегатов только вследствие отработки ими ресурсов. Представляет интерес рассмотрение этого процесса и сравнение с реализуемыми в эксплуатации процессами.
В таблице 6 приведены значения назначенных ресурсов агрегатов основной системы электроснабжения переменным током (СПЗСЗБ40) и радиодальномера СД-75 самолета Ту-154М.
Таблица 6 Величина ресурсов агрегатов функциональных систем самолета Ту-154М
| Функциональная система | Комплектующие изделия | Назначенный ресурс, ч |
| СП3С3Б40 | ГТ40ПЧ6 | 6000 |
| БЗУ-376СБ | 27000 | |
| БРН-208М7А | 27000 | |
| БРЧ-62БМ | 30000 | |
| БТТ-40Б | 30000 | |
| СД-75 | ЗСД-75 | 20000 |
| ПУР | 20000 | |
| АМ-001 | 50000 | |
| ИСД-1 | 50000 |
На рисунках 23 и 24 приведены зависимости средних относительных отработок ресурсов систем СПЗСЗБ40 и СД-75, заданные Разработчиком самолета.
На приведенных рисунках наклонные линии соответствуют процессам увеличения средней относительной отработки ресурсов агрегатами систем Вертикальные линии мгновенного уменьшения средней относительной отработки 
являются следствием замены агрегата, либо нескольких агрегатов по причине выра ботки ими ресурсов, т.е. в это время их относительная отработка ресурса уменьшается от 1 до 0.
Рисунок 23 – Зависимость средней относительной отработки агрегатов
основной системы электроснабжения переменным
током самолета Ту-154М (по назначенному ресурсу)
Рисунок 24 – Зависимость средней относительной отработки СД-75
самолета Ту-154 М (по назначенному ресурсу)
Из приведенных рисунков следует, что при определенных значениях налета самолета средняя относительная отработка ресурсов всеми агрегатами систем приближается к 1. С точки зрения надежности систем этот случай наиболее неблагоприятен. Если же оценить среднюю относительную отработку ресурсов агрегатами систем по средним значениям за длительный промежуток времени 40-50 тыс. часов налета, то она может быть оценена как 0,6 (60 %), что хорошо согласуется с результатами определенными по эксплуатационным значениям.
Общие результаты и выводы. В результате выполненных исследований впервые получены следующие научно-значимые результаты: 1. Показано, что экспоненциальное распределение вероятности случайной величины не может быть использовано в качестве математической модели надежности агрегатов поскольку оно определяет вероятность отказа за единицу времени работы агрегата как убывающую функцию. Это противоречит как опытным данным, так и представлениям о том, что развитие деградационных процессов с увеличением времени работы увеличивает вероятность отказа.
Показано, что процедуры получения экспоненциального распределения для оценки надежности некорректны
2. Показано, что решение задачи расчета надежности функциональных систем с использованием интегральных функций вероятностей отказов агрегатов неправомерно. Теорема умножения вероятностей, применяемая в решении, предусматривает умножение вероятностей дискретных событий, но не интегральных функций. Зависимость вероятности отказа за единицу времени (1 час полета), получаемая из решения с использованием интегральных функций вероятностей отказа агрегатов, не соответствует опытным данным и не имеет однозначности решения.
3. Разработан методологический подход и метод решения задач оценки надежности функциональных систем самолетов гражданской авиации, при котором вероятность отказа, либо безотказной работы определяется непосредственно за произвольную единицу времени. При этом в решении используются вероятности отказа агрегатов также за произвольную единицу времени, являющиеся дискретными величинами, что обеспечивает правомерность использования в решении операций предусмотренных теоремой умножения вероятностей.
4. Установлено, что решение задачи оценки надежности сложных систем, применительно к дискретным значениям вероятности отказа агрегатов, возможно прямым применением теоремы умножения вероятностей, реализуемом при традиционном подходе, только для систем с однозначным процессом (сценарием) развития отказа.
5. Для систем с индивидуальным резервированием разработан альтернативный подход расчета надежности, учитывающий неоднозначность сценариев развития отказа в системе.
6. Разработанный метод расчета обеспечивает возможность оценки надежности систем как при проектировании, так и в процессе эксплуатации. Показано, что используемые при проектировании оценки надежности агрегатов систем, получаемые при гостированных планах испытаний, не реализуются в эксплуатации, поскольку планы испытаний существенно отличаются от условий, определяемых режимами технического обслуживания при эксплуатации. Рекомендовано испытания агрегатов выполнять по планам согласованным с режимами технического обслуживания.
7. Положено начало развития риск-анализа технических систем учитывающего не только вероятности и потери от катастроф, но и затраты на обеспечение безопасности. На частных примерах показано, что развиваемое направление риск-анализа учитывающего затраты (на обеспечение безопасности) и прибыль (от нереализовавшихся катастроф), может быть использовано для анализа перспективности стратегических направлений развития техники.
8. Исследования процессов «старения» (влияния длительности наработки на надежность) дали возможность установить, что функциональные системы самолетов гражданской авиации стареют не более чем на 60 % и в процессе длительной эксплуатации при действующей системе технического обслуживания не теряют надежность.
1. Бойко, О.Г Надежность и стратегии технической эксплуатации функциональных систем самолетов гражданской авиации./ Л.Г. Шаймарданов., А.Г. Зосимов, О.Г. Бойко // Решетневские чтения: матер. IX Междунар. науч. конф., посвящ. 45-летию СибГАУ. СибГАУ. – Красноярск, 2005. – С. 75–78.
2. Бойко, О.Г. Проблемы и возможности изменения стратегий технической эксплуатации агрегатов самолетов гражданской авиации/ Л.Г. Шаймарданов., А.Г. Зосимов, О.Г. Бойко // Вестник СибГАУ. Сб. науч. тр.: СибГАУ. – Красноярск, 2006. – Вып. №5(12). – С. 30–33.
3. Бойко, О.Г. Методика оценки надежности функциональных систем самолетов гражданской авиации по статистическим материалам эксплуатанта/ Л.Г. Шаймарданов, А.Г. Зосимов, О.Г. Бойко, В.Л. Медведев // Вестник СибГАУ. Сб. науч. тр.: СибГАУ. – Красноярск, 2006. – Вып. №5(12). – С. 159–164.
4. Бойко, О.Г. Особенности анализа надежности функциональных систем самолетов гражданской авиации/ Л.Г. Шаймарданов., О.Г. Бойко// Вестник СибГАУ. Сб. науч. тр.: СибГАУ. – Красноярск, 2007. – Вып. №2(15). – С. 63–67.
5. Бойко, О.Г. Надежность системы электронной индикации самолета ТУ-204/ О.Г. Бойко, В.Б. Краснопеев// Вестник СибГАУ. Сб. науч. тр.: СибГАУ. – Красноярск, 2007. – Вып. №2(15). – С. 58–59.
6. Бойко, О.Г. Анализ отработки ресурсов системами самолета Ту-154М при длительной эксплуатации/ В. Б. Краснопеев, О. Г. Бойко// Вестник Сиб. гос. аэрокосмич. ун-та: сб. науч. тр.: СибГАУ. – Красноярск, 2007. – Вып. №4(17). – С62–64.
7. Бойко, О.Г. Метод расчета надежности функциональных систем самолетов гражданской авиации по статистическим материалам эксплуатантов/ Л.Г. Шаймарданов., А.Г. Зосимов, О.Г. Бойко // Вестник СибГАУ. Сб. науч. тр.: СибГАУ. – Красноярск, 2007. – Вып. № 4(17). – С. 118119.
8. Бойко, О.Г. Методологические особенности расчета надежности функциональных систем самолетов гражданской авиации/ Л.Г. Шаймарданов., О.Г. Бойко // Вестник СибГАУ. Сб. науч. тр.: СибГАУ. – Красноярск, 2007. – Вып. № 4(17). – С. 120124.
9. Бойко, О.Г. Особенности старения одноименных систем различных типов самолетов/ О.Г. Бойко, П.Г. Утенков // Вестник СибГАУ. Сб. науч. тр.: СибГАУ. – Красноярск, 2008. – Вып. №2(19). – С. 123–126.
10. Бойко, О.Г. О возможности Марковской аппроксимации в расчетах надежности функциональных систем самолетов гражданской авиации/ О.Г. Бойко// Вестник СибГАУ. Сб. науч. тр.: СибГАУ. – Красноярск, 2008. – Вып. №2(19). – С. 111–113.
11. Бойко, О.Г. Математические модели и методы расчета схемной надежности функциональных систем самолетов/ Л.Г. Шаймарданов., О.Г. Бойко // Вестник СибГАУ. Сб. науч. тр.: СибГАУ. – Красноярск, 2008. – Вып. № 3(20). – С. 7881.
12. Бойко, О.Г. Задача оптимизации отработки ресурсов самолетов гражданской авиации/ О.Г. Бойко// Вестник СибГАУ. Сб. науч. тр.: СибГАУ. – Красноярск, 2008. – Вып. №3(20). –С. 93–94.
13. Бойко, О. Г., Исследование процессов старения систем электроснабжения и автоматики ТУ-154/ О.Г. Бойко, В.Б. Краснопеев // Вестник СибГАУ. Сб. науч. тр.: СибГАУ.– Красноярск, 2008. – Вып. №4(21). – С. 116–120.
14. Бойко, О. Г. Правомерность использования интегральных функций распределения случайных величин в расчетах надежности функциональных систем/ О.Г. Бойко// Вестник СибГАУ. Сб. науч. тр.: СибГАУ. – Красноярск, 2008. – Вып. №4(21). – С. 109–111.
15. Бойко, О. Г. Анализ и оптимизация использования однотипного самолетного парка на маршрутной сети авиакомпании/ О.Г. Бойко, П.Г. Утенков // Вестник СибГАУ. Сб. науч. тр.: СибГАУ. – Красноярск, 2009. –Вып. №1(22). –С. 99–101.
16. Бойко, О. Г. Направление решения задачи обеспечения исправности функциональных систем самолетов эксплуатантами/ О.Г.Бойко// Вестник СибГАУ. Сб. науч. тр.: СибГАУ. – Красноярск, 2009. – Вып. №2(23). – С. 171–173.
17. Бойко, О. Г. Элементы риск-анализа и безопасность полетов/ Л.Г. Шаймарданов., О.Г. Бойко // Вестник СибГАУ. Сб. науч. тр.: СибГАУ. – Красноярск, 2009. – Вып. № 3(24). – С. 8689.
18. Бойко, О. Г. Математические модели и методы расчета надежности сложных систем/ Л.Г. Шаймарданов., О.Г. Бойко // Вопросы современной науки и практики/ Журнал университета им. В.И. Вернадского.–Тамбов, 2009. – Вып. №8(22). – С. 64–72.
19. Бойко, О.Г. Анализ традиционного и разработка альтернативного методологического подхода к расчету надежности сложных систем/ О.Г.Бойко // Наука и технологии. Итоги диссертационных исследований. Том 1. Избранные труды Российской школы. –М.: РАН, 2009. – С. 326–336.
20. Boyko, O.G. Risk analysis and the elements of flight security/ O.G. Boyko, L.G. Shaymardanov//Vestnik/ Scientific journal of Siberian state aerospace university named after ac. M.F.Reshetnev. – 2009. – Vol. 26. № 5. – P. 87– 91.
21. Бойко, О.Г. Возможности оптимизации структуры функциональных систем самолетов гражданской авиации/ О.Г. Бойко, Е.А. Фурманова, Л.Г. Шаймарданов// Вестник СибГАУ. Сб. науч. тр.: СибГАУ.– Красноярск, 2010. – Вып. № 1(27). – С. 912.
22. Бойко, О.Г. Анализ зависимости прочности, риска катастроф и эффективности перевозок от массы конструкции самолета/ О.Г. Бойко// Вестник СибГАУ. Сб. науч. тр.: СибГАУ. – Красноярск, 2010. – Вып. № 1(27). – С. 114117.
23. Бойко, О.Г. Надежность функциональных систем самолетов гражданской авиации: моногр. Избранные труды Российской школы по проблемам науки и технологий. – М.:РАН. 2009. – 119 с.
24. О.Г. Бойко, Л.Г. Шаймарданов метод расчета надежности авиационных систем с индивидуальным резервированием агрегатов// Вестник СибГАУ. Сб. науч. тр.: СибГАУ. – Красноярск, 2010. – Вып. № 2(28). – С. 116119.
25. О.Г. Бойко, Л.Г. Шаймарданов, О соотношении интегральной, дифференциальной функций вероятностей отказов и вероятности отказа на произвольном отрезке времени в расчетах надежности агрегатов и сложных авиационных систем // Вестник СибГАУ. Сб. науч. тр.: СибГАУ. – Красноярск, 2010. – Вып. № 2(28). – С. 8789.
