Обоснование кинематической и кинетостатической разрешимости шестизвенных шарнирных плоских групп ассура
На правах рукописи
Стариков Степан Павлович
ОБОСНОВАНИЕ КИНЕМАТИЧЕСКОЙ
И КИНЕТОСТАТИЧЕСКОЙ РАЗРЕШИМОСТИ ШЕСТИЗВЕННЫХ ШАРНИРНЫХ ПЛОСКИХ ГРУПП АССУРА
Специальность: 05.02.18 – Теория механизмов и машин
Автореферат
диссертации на соискание ученой степени
кандидата технических наук
Новосибирск - 2008
Работа выполнена на кафедре Теории механизмов и машин и основ конструирования государственного образовательного учреждения высшего профессионального образования «Сибирский государственный индустриальный университет», г. Новокузнецк.
| Научный руководитель: | заслуженный деятель науки РФ, доктор технических наук, профессор Л.Т. Дворников. |
| Официальные оппоненты: | доктор технических наук, профессор В.С. Хорунжин, доктор технических наук, профессор Э.Я. Живаго. |
| Ведущая организация: | Государственное образовательное учреждение высшего профессионального образования «Томский политехнический университет», г. Томск. |
Защита состоится: 23 декабря 2008 г. в 10.00 часов на заседании диссертационного совета Д 212.173.07 при ГОУ ВПО «Новосибирский государственный технический университет» по адресу: 630092, Новосибирск-92, пр. Карла Маркса, 20.
С диссертацией можно ознакомиться в ГОУ ВПО «Новосибирский государственный технический университет».
Автореферат разослан « » ноября 2008 г.
| Ученый секретарь диссертационного совета Д 212.173.07 | Никитин Ю.В. |
Общая характеристика работы
Актуальность исследования.
Экономическое развитие государства напрямую связано с совершенствованием машиностроительной отрасли производства. Создание новых машин и механизмов возможно лишь на основе серьезного научного фундамента, позволяющего обеспечивать высокую эффективность машин уже на стадии их проектирования. Процесс проектирования в обязательном порядке должен включать в себя этапы структурного синтеза кинематических схем машин, их грамотного кинематического и силового расчетов, собственно проектирования и изготовления продукции на основе наиболее высоко зарекомендовавших себя технологий. Все из перечисленных этапов проектирования одинаково важны и не могут быть проигнорированы, в том числе этапы кинематического и силового анализа будущих машин.
Развитие машиностроения определяется естественным усложнением схемных решений и требованием разработки особых, чаще всего принципиально новых подходов к их исследованию. В частности, в практике машиностроения все большее применение получают машины, включающие в свой состав элементы более сложных структур.
Согласно известному принципу создания машин, разработанному профессором Ассуром Л.В., они образуются от ведущих звеньев путем присоединения (наслоения) к ним групп звеньев, обладающих нулевой подвижностью (так называемых групп Ассура).
Наиболее разработанными являются методы исследования двухзвенных групп (диад). Найдены и достаточно известны методы анализа четырехзвенных групп. Группы же Ассура, включающие в свой состав шесть звеньев, требуют своего исследования. Практика машиностроения показывает, что шестизвенные группы уже имели применение в машинах, а в последнее время начинают получать все большее использование. На этом основании можно утверждать, что разработка методов кинематического и кинетостатического исследования шестизвенных плоских групп, является проблемой весьма актуальной.
Целью настоящего исследования является развитие теории структурного анализа и синтеза, методов кинематического и кинетостатического исследований плоских шарнирных шестизвенных групп Ассура.
Для реализации поставленной цели важными являются следующие задачи:
- изучить существующие методы анализа и синтеза групп нулевой подвижности;
- обосновать полный состав шестизвенных плоских шарнирных групп нулевой подвижности;
- идентифицировать группы по следующим признакам: числу используемых звеньев, сложности базисного звена, числу выходов цепи, числу изменяемых замкнутых контуров в группе, сложности использованного в цепи изменяемого замкнутого контура, числу сторон цепи, числу наружных сторон цепи и распределению числа наружных сторон цепи между выходами;
- исследовать кинематику и кинетостатику плоских шарнирных групп нулевой подвижности, в частности на основе методов исследования четырехзвенных групп;
- изучить влияние класса шестизвенных плоских шарнирных групп нулевой подвижности на сложность их кинематической и кинетостатической разрешимости;
- подтвердить реальными техническими решениями возможность широкого применения в технике шестизвенных плоских групп Ассура.
Объектом исследования являются плоские шарнирные шестизвенные группы нулевой подвижности (группы Ассура).
Предметом исследования является - структура, кинематика и кинетостатика плоских шарнирных шестизвенных групп Ассура.
Методы исследования.
В работе использованы методы теории механизмов и машин и теоретической механики.
Достоверность результатов работы подтверждается реальными методами создания структур плоских шестизвенных групп нулевой подвижности, разработкой новых механизмов, подтвержденных патентами РФ, в частности «Кривошипно-ползунного механизма пресса» (патент № 2201348), «Секции механизированной крепи» (патент № 2303699), «Двухщековой дробильной машины» (патент № 2332260).
На защиту выносятся следующие научные положения:
- обоснование необходимых и достаточных условий структурного синтеза шестизвенных плоских шарнирных групп Ассура;
- методы исследования кинематики шестизвенных плоских шарнирных групп Ассура, базирующиеся на известных приемах кинематического решения четырехзвенных групп;
- доказательство теоремы о реакциях в трехшарнирном звене;
- методика силового анализа плоских шарнирных шестизвенных групп Ассура;
- реальное использование шестизвенных плоских групп Ассура, позволяющее создавать новые механизмы с особыми свойствами.
Личный вклад соискателя. В работах, опубликованных в соавторстве, соискателю принадлежит формализация поставленных задач, разработка методов кинематического и кинетостатического исследования групп Ассура, обобщение и анализ результатов.
Научная новизна исследования заключается в развитии теории исследования кинематики и кинетостатики плоских шарнирных шестизвенных групп Ассура. Впервые показана возможность отыскания всего многообразия плоских шестизвенных групп. Разработаны новые механизмы, названные «Кривошипно-ползунный механизм пресса», «Секция механизированной крепи» и «Двухщековая дробильная машина». На эти схемы получены патенты РФ.
Практическая полезность результатов исследования показана на конкретных примерах синтеза механизмов, обладающих широкими возможностями обеспечения заданных траекторий и законов движения рабочих органов. Результаты диссертационной работы в виде методических разработок внедрены в учебный процесс ГОУ ВПО «Сибирского государственного индустриального университета» (кафедра теории механизмов и машин и основ конструирования), г. Новокузнецк.
Апробация работы.
Основные результаты исследования докладывались на:
- Всероссийской научной конференции студентов, аспирантов и молодых ученных, 27 – 28 апреля 2004 г., СибГИУ, г. Новокузнецк;
- Международной конференции «Проблемы теоретической и прикладной механики», Алматы, Казахстан, 1- 2 марта, 2006 г.;
- Всероссийской научной конференции студентов, аспирантов и молодых ученных, 27 – 28 апреля 2006 г., СибГИУ, г. Новокузнецк;
- семнадцатой научно – практической конференции по секции механики и машиностроения, г. Новокузнецк, 3 – 4 июля 2006г.;
- Международной конференции по теории механизмов и механике машин, г. Краснодар, 9 – 15 октября 2006 г.;
- Международной научно-технической конференции «Современные проблемы механики, строительства и машиностроения», 15 – 16 ноября 2006г., г. Павлодар, Казахстан;
- шестнадцатой студенческой конференции по секции теории механизмов, динамике и прочности машин, 27 – 28 апреля 2007 г., СибГИУ, г. Новокузнецк;
- XIII Международной научно-практической конференции студентов, аспирантов и молодых ученых «Современные техника и технологии», 26 – 27 марта 2007г., г. Томск;
- восемнадцатой научно – практической конференции по секции механики и машиностроения, СибГИУ, г. Новокузнецк, 3 – 4 июля 2007г.
Публикации. Всего опубликовано по теме диссертации 18 работ, из них 2 научных статьи в журналах, входящих в перечень изданий, рекомендованных ВАК РФ; 1 научная статья в центральном журнале «Теория механизмов и машин», Санкт-Петербург; 10 публикаций в материалах Международных и Всероссийских конференций; 1 методическое указание; 3 изобретения и 1 полезная модель.
Структура и объем работы. Диссертация состоит из введения, пяти глав, заключения, библиографического списка из 50 наименований и приложения. Общий объем работы составляет 155 страниц, включая 5 таблиц и 80 рисунков.
Основное содержание работы
Во введении обосновывается актуальность работы и дается описание содержания глав диссертации.
В первой главе диссертационной работы проводится анализ известных методов структурного, кинематического и кинетостатического исследования плоских шарнирных механизмов на основе фундаментальных работ Дж. Уатта, П.Л. Чебышева, М.Ф. Грюблера, Л. Бурместера, П.О. Сомова, Х.И. Гохмана, Л.В. Ассура, В.В. Добровольского, И.И. Артоболевского, а также исследований Н.И. Колчина, С.Н. Кожевникова, Г.Г. Баранова, О.Г. Озола, У.А. Джолдасбекова, Л.Н. Решетова, Э.Е. Пейсаха, Л.Т. Дворникова, Л.Н. Гудимовой и других ученных, внесших важный вклад в изучение плоских шарнирных механизмов. Особо показывается роль профессоров В.В. Добровольского и Г.Г. Баранова в нахождении многообразия шестизвенных плоских шарнирных групп нулевой подвижности. На основании изученного материала формулируются задачи настоящего исследования.
Вторая глава диссертации посвящена разработке методов структурного синтеза полного состава шестизвенных плоских шарнирных групп Ассура. Доказывается справедливость утверждения профессора В.В. Добровольского о существовании десяти отличающихся друг от друга шестизвенных плоских шарнирных групп нулевой подвижности. Доказательство основывается на универсальной структурной системе профессора Л.Т. Дворникова, записываемой в виде
 | (1) |
где 
- наиболее сложное - базисное звено кинематической цепи,
- число звеньев, добавляющих в цепь по i кинематических пар,
W - подвижность цепи,
n и p5 - соответственно, число звеньев и шарниров исследуемой цепи.
В (1) третье уравнение - есть известная формула подвижности плоских механизмов П.Л. Чебышева.
Для шестизвенных групп нулевой подвижности (W=0) согласно третьему уравнению системы (1) p5 = 9 и тогда
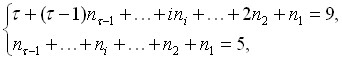 | (2) |
откуда следует, что 
не может принимать значений
более 
. Таким образом, шестизвенные плоские шарнирные группы нулевой подвижности могут быть образованы лишь с базисными звеньями - треугольным (
) и четырехугольным (
).
При 
система (2) получит вид
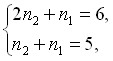 | (3) |
откуда 
, 
. При 
решениями (2) являются 
, 
.
Известно, что число ветвей любой кинематической цепи 
определяется зависимостью
 . | (4) |
Для всех шестизвенных групп Ассура 
. Число ветвей цепи связано с числом выходов цепи 
и числом использованных в ней замкнутых изменяемых контуров 
зависимостью
 . | (5) |
При 
возможны три вида соотношений 
и 
, а именно 
, 
; 
, 
и 
, 
. Цепь с одним выходом не может быть встроена в замкнутую кинематическую цепь.
Простейшим плоским подвижным замкнутым контуром является четырехугольный 
. В шестизвенных цепях могут использоваться контуры 
, 
и 
.
Число всех сторон цепи 
определяется зависимостью
 . | (6) |
Для шестизвенных групп 
.
При замыкании контуров, замыкающие звенья увеличивают число сторон на величину равную числу вводимых контуров, т.е. суммарное число сторон с плоской кинематической цепи определяются как
 . | (7) |
В кинематических цепях с изменяемыми замкнутыми контурами часть сторон звеньев становятся внутренними в, а остальные наружными н. Очевидно, что
 . | (8) |
Таблица 1
Полный состав шестизвенных плоских шарнирных групп нулевой подвижности - групп Ассура (n=6, р5=9, =4).
| № п/п | Обозначение группы | Базисное звено | Число выходов / Число замкнутых контуров | Сложность контура | Суммарное число сторон | Число внутренних сторон | Число наружных сторон | Число сторон между выходами | Схема цепи |
| / | i | c | в | н |  | ||||
| 1 | 6 ГНП.3 | 3 | 4/0 | - | 14 | 0 | 14 | 3-4-3-4 |  |
| 2 | 6ГНП.3 (3-3-5) | 3/1 | 4 | 15 | 4 | 11 | 3-3-5 |  | |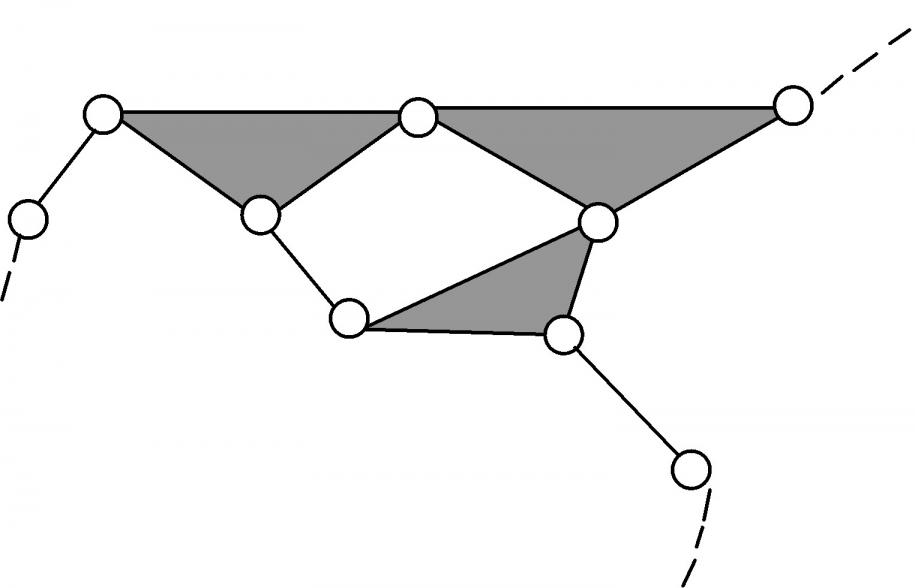
| 3 | 6ГНП.3, (3-4-4) | 3-4-4 |  | ||||||
| 4 | 6ГНП.3, | 5 | 5 | 10 | 3-3-4 |  | |||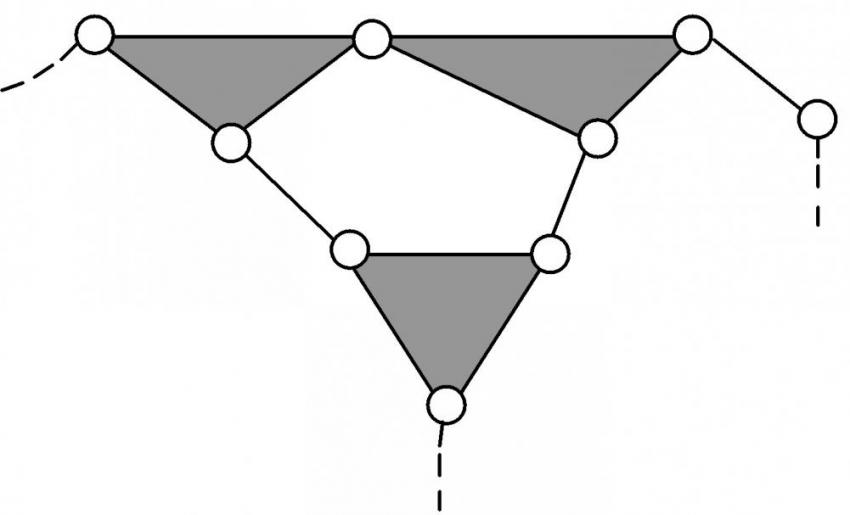
| 5 | 6ГНП.3 | 6 | 6 | 9 | 3-3-3 |  | |||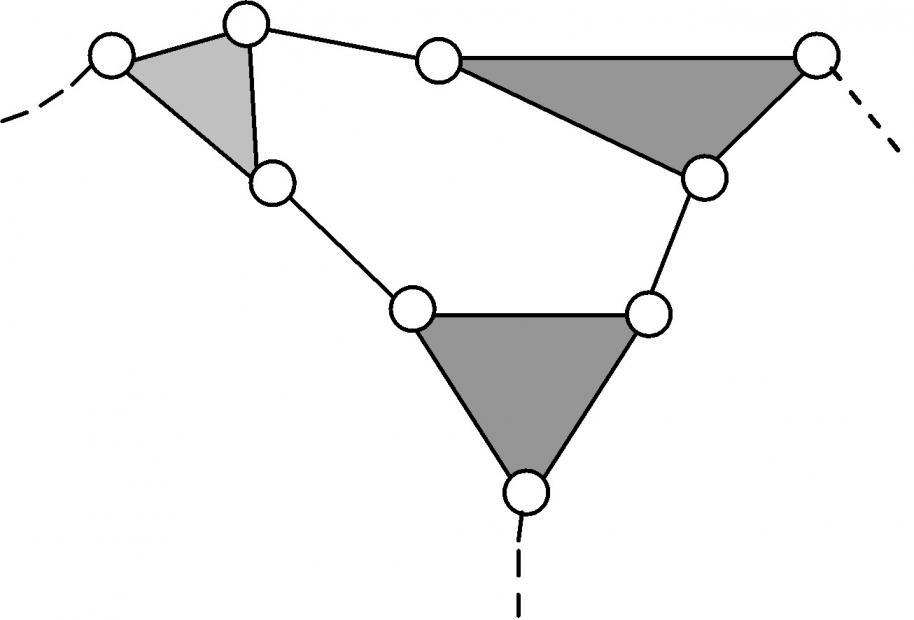
| 6 | 6ГНП.3 , (3-5) | 2/2 | 4+ 4 | 16 | 8 | 8 | 3-5 |  | |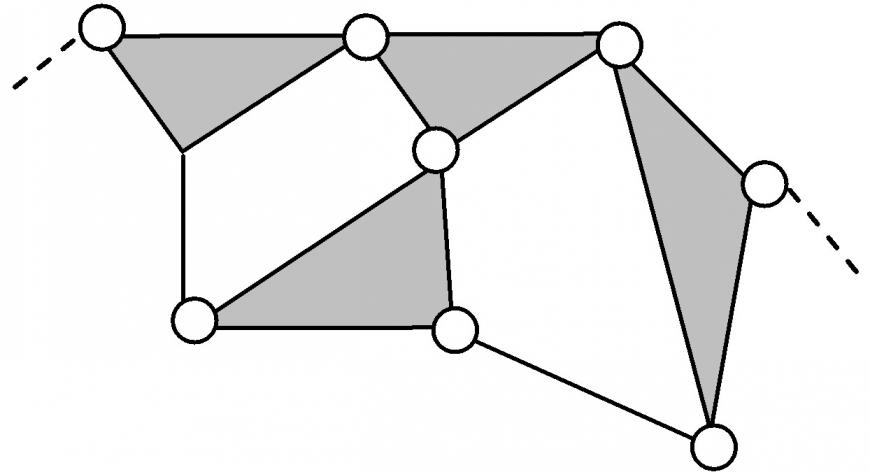
| 7 | 6ГНП.3, , (4-4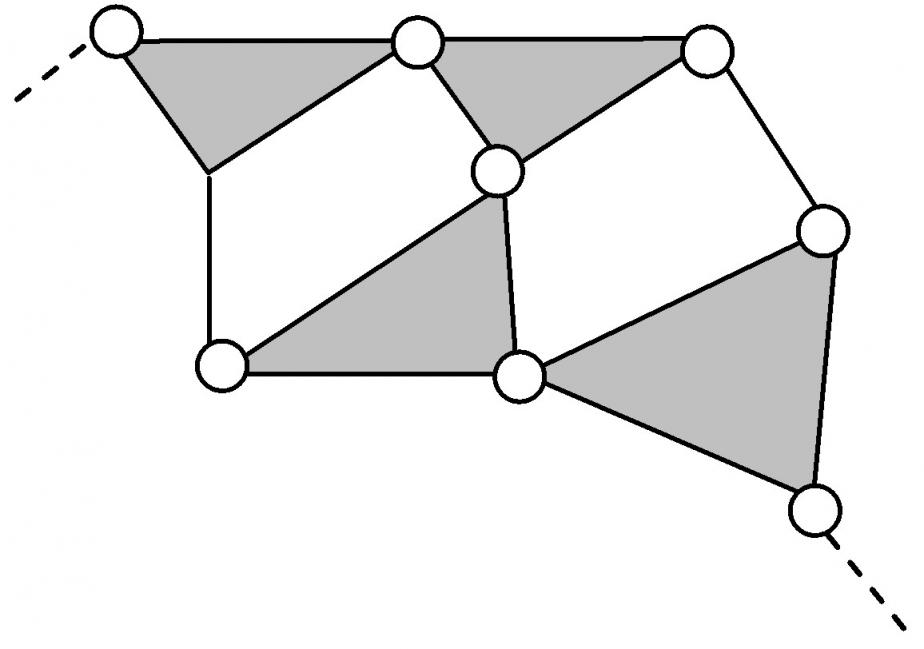) | 4-4 |  | ||||||
| 8 | 6ГНП.3, , | 4+ 5 | 9 | 7 | 3-4 |  | |||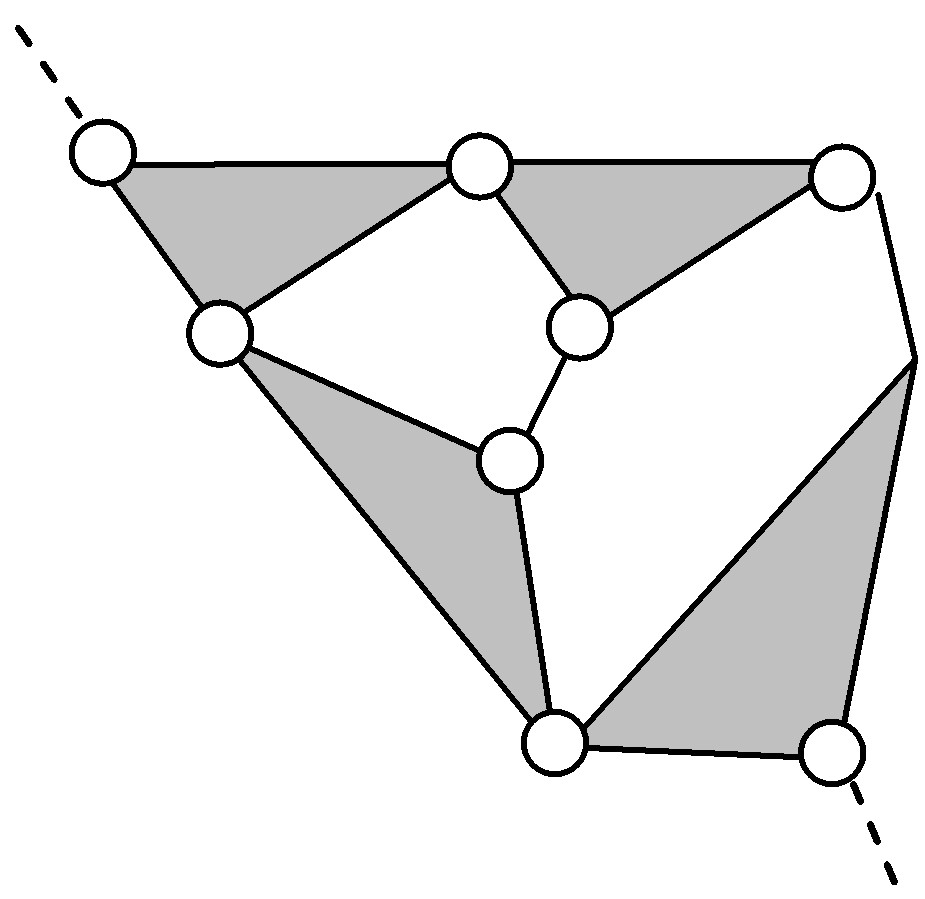
| 9 | 6ГНП.4, | 4 | 3/1 | 4 | 15 | 4 | 11 | 3-4-4 |  |
| 10 | 6ГНП.4, , | 2/2 | 4+ 5 | 16 | 9 | 7 | 3-4 |  |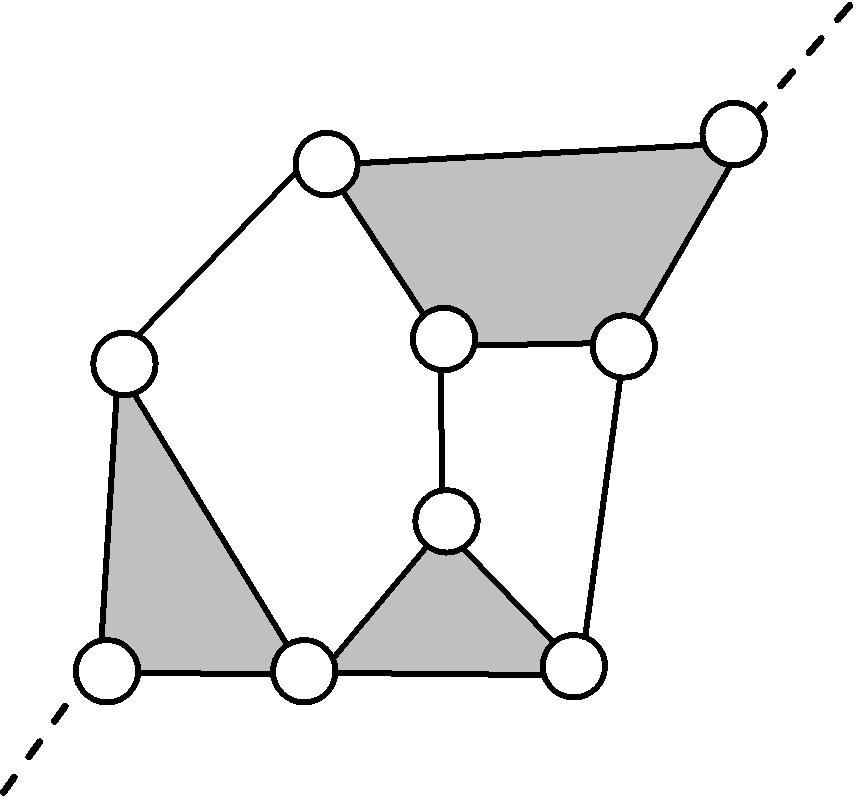
Так как в зависимости от конкретного числа i и их вида параметр в оказывается переменным, изменяющимся по числу, то переменным будет, и число н наружных сторон цепи и это число может быть по разному распределено между выходами цепи. Условно обозначим этот критерий классификации, как 
и из логических соображений, ограничим минимальную «дистанцию» между выходами цифрой 3. Наличие именно трех звеньев между выходами гарантирует группе работоспособность, если даже группа этими выходами будет замкнута на стойку – на неподвижное звено.
Использованные критерии: 
, 
, 
, i, в, н и 
обеспечивают полную идентификацию отличающихся групп. На этом основании удалось доказать, что отличающихся шестизвенных групп нулевой подвижности 10. Все они приведены в таблице 1, где предложено обозначить группы аббревиатурами, например 6ГНП.3
,
(3-5), что означает 6 - шестизвенные группы, ГНП - группы нулевой подвижности, 3 - трехпарное базисное звено (
), 
,
- два замкнутых изменяемых контура, (3-5) в скобках означает, что между выходами группы звеньев распределились как 3 и 4.
Согласно классификации плоских кинематических цепей, предложенной И.И. Артоболевским класс цепей определяется видом используемого в ней контура. Первая из приведенных в таблице 1 групп относится к третьему классу (самое сложное - трехпарное звено), а все остальные группы, относя к цепям высших классов. При 
- к четвертому классу, при
- к пятому классу и при
- к шестому классу.
Третья глава диссертации посвящена обоснованию, разработке и реализации приемов кинематического исследования всех десяти плоских шарнирных шестизвенных групп Ассура графо-аналитическим методом.
Прежде всего, в главе дается полное доказательство кинетической разрешимости плоских групп Ассура.
Показывается, что графо-аналитическое решение кинематики нормальной по Ассуру, т.е. не имеющей замкнутых изменяемых контуров шестизвенной группы (позиция 1 в таблице 1), было найдено еще Л.В. Ассуром, и что кинематические решения остальных девяти групп до настоящего исследования известны не были.
Анализ особенностей строения этих девяти групп показал, что для их разрешения могут быть применены принципиально различные приемы и алгоритмы. Для групп 1, 3, 9; 4, 5, 8 и 6, 7, 10 были разработаны и реализованы отличающиеся алгоритмы. Исследование первой тройки групп было основано на найденном в 2004 г. решении четырехзвенной группы четвертого класса. Разработанный алгоритм рассмотрим на примере шестизвенной группы номер 3 (таблица 1) с четырехугольным замкнутым изменяемым контуром вида (3-4-4), показанной на рисунке 1.
В основе ее решения лежит метод отыскания особой точки 
, являющейся точкой Ассура для двух трехпарных звеньев 1 и 5. Чтобы найти эту точку, прежде по известным скоростям точек A и D найдем скорость точки Ассура S2, лежащей на пересечении линий, продолжающих AB и поводок CD. Скорость точки S2 определится из зависимостей
| (9) |
| Рис.1. Шестизвенная группа с четырехугольным замкнутым изменяемым контуром вида (3-4 -4). | Рис.2. План скоростей группы 6ГНП.3, (3-4-4). |
Аналогично можно найти скорость точки S5, принадлежащей пятому звену, из уравнений
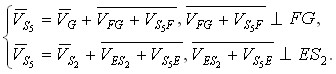 | (10) |
Выделив далее звенья 1, 2, 5 и 6, рассмотрим четырехзвенную группу с четырехугольным замкнутым изменяемым контуром KBEH.
На продолжениях линий звеньев BE и KH найдем точку их пересечения 
- именно эта точка, является одновременно точкой Ассура и для звена 1 и для звена 5. Скорость точки 
может быть найдена из уравнений
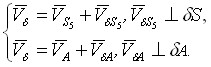 | (11) |
Зная скорость точки 
, можно найти скорости точек K, B, E и H.
Оставшиеся неизвестными скорости точек C и F, находятся из уравнений:
 | (12) |
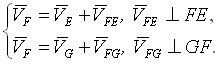 | (13) |
Построенный по приведенным уравнениям план скоростей показан на рисунке 2 с указанием направлений всех векторов.
Из второй тройки групп покажем решение группы 5. Она приведена на рисунке 3.
| Рис.3. Шестизвенная группа Ассура с шестиугольным изменяемым замкнутым контуром. |
Прежде всего сформулируем и докажем следующую теорему: В шестизвенной группе Ассура с шестиугольным замкнутым изменяемым контуром соседние точки Ассура, принадлежащие треугольным звеньям, имеют одинаковые проекции скоростей на линии, соединяющие эти точки.
Отметим, что точки Ассура треугольных звеньев 1 (S1) и 5 (S5) отыскиваются на пересечении линий поводков: для звена 1 - BC и KH, для звена 5 – EF и KH. Докажем, что проекции скоростей точек S1 и S5 на направление линии KH равны. Основываясь на известной теореме о проекциях скоростей двух точек тела, покажем, что проекции скоростей точек K и H звена 6 на соединяющую их линию KH равны 
. Так как точки Ассура S1 и S5, принадлежат соответственно звеньям 1 и 5 по аналогии можно записать, что 
и что 
. Так как левые части этих соотношений равны между собой, то равными являются и правые части соотношений, т.е. 
, что и требовалось доказать. Точно так же доказывается равенство проекций векторов скоростей точек S1 и S3 на соединяющее их направление BC и равенство проекций векторов скоростей точек S5 и S3 на соединяющее их направление EF.
Используя доказанную теорему и учитывая свойство плана скоростей, заключающееся в том, что фигуры на механизме всегда являются подобными фигурам, образованным векторами относительных скоростей звеньев, покажем кинематическое решение шестизвенной группы в виде последовательности процедур:
1) Откладываем на плане скоростей (рис. 4.) в масштабе известные скорости: 
(
), 
(
) и 
(
);
2) Проводим на плане скоростей из концов векторов 
и 
, т. е. из точек a и g линии перпендикулярные AS1 и GS5 соответственно (на плане скоростей эти линии показаны пунктиром). Находим точку их пересечения и обозначаем ее как j;
3) На перпендикуляре S1A произвольно фиксируем точку m и из нее проводим линию перпендикулярную S1S5 до пересечения с перпендикуляром S5G в точке n;
4) Из точек m и n проводим линии, перпендикулярные S1S3 и S3S5 до пересечения их в точке 
;
5) Полученный треугольник mnl замечателен тем, что он подобен треугольнику S1S3S5 на схеме группы. Можно утверждать, что концы векторов скоростей точек S1, S3 и S5 лежат на продолжении линий, соответственно jm, jn и jl. На этом основании проводим линию jl (на плане эта линия показана штрихпунктиром). Именно на этой линии будет лежать конец вектора скорости точки S3;
 |
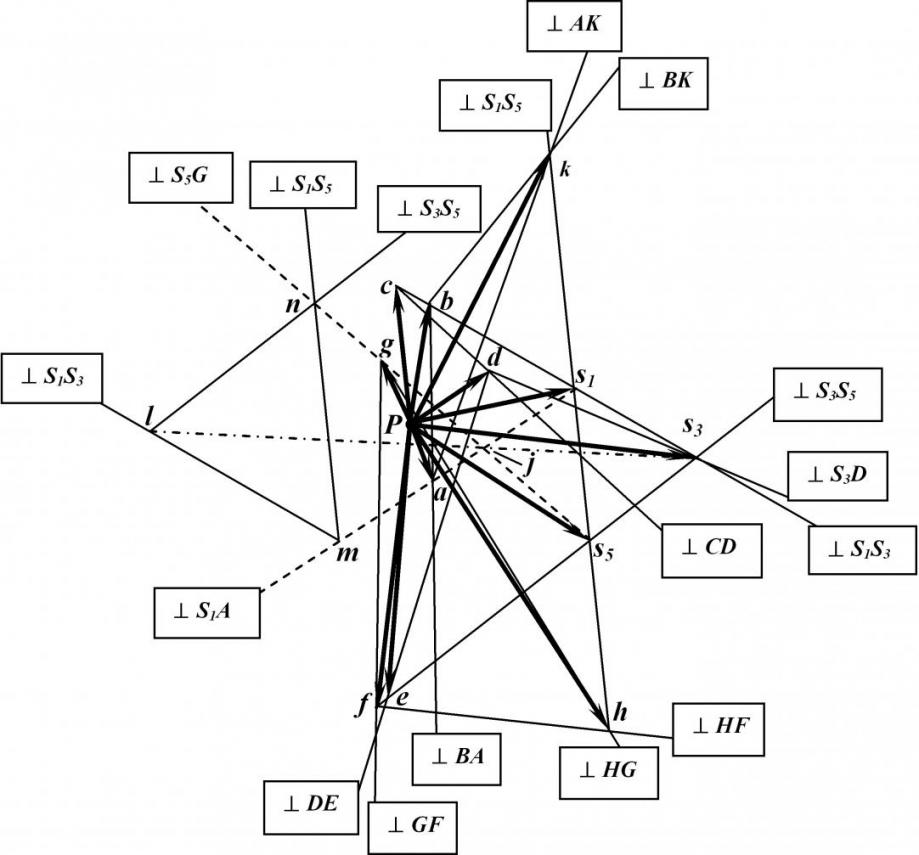Рис. 4. План скоростей группы 6ГНП.3 |
6) Из точки d проводим линию перпендикулярную DS3 и на пересечении ее с линией jl находим точку s3. Соединяя полюс плана скоростей P и точку s3, находим отрезок 
, который в выбранном масштабе определит скорость точки S3;
7) Зная скорость точки S3 и скорость точки D, легко найти скорость точки E на основании следующей системы уравнений
 | (14) |
Дальнейшее нахождение скоростей точек группы Ассура вполне очевидно.
| Рис.5. Шестизвенная плоская группа Ассура с двумя четырехугольными замкнутыми изменяемыми контурами вида (3 – 5). |
Для исследования третей тройки групп был разработан комбинированный метод, включающий определение направления, на котором лежит конец вектора одной из точек Ассура и, далее, методом ложных скоростей - истинного положения этой точки на плане. Сущность применяемого метода покажем на примере группы 6ГНП.3,(3-5) (рис.5.). Выделим на схеме цепи треугольник S1 S3 S5. Через известные скорости и найдем на плане (рис.6.) подобную этому треугольнику фигуру nml. В точке j этот треугольник вырождается в точку. Именно линия jl является линией, на которой лежит конец вектора скорости точки Ассура S5.
Затем, задавая ложные скорости точке B, через векторные уравнения (15), (16) и (17) найдем последовательно ложные скорости H, C и E
| (15) | |
| (16) | |
| (17) |
 |
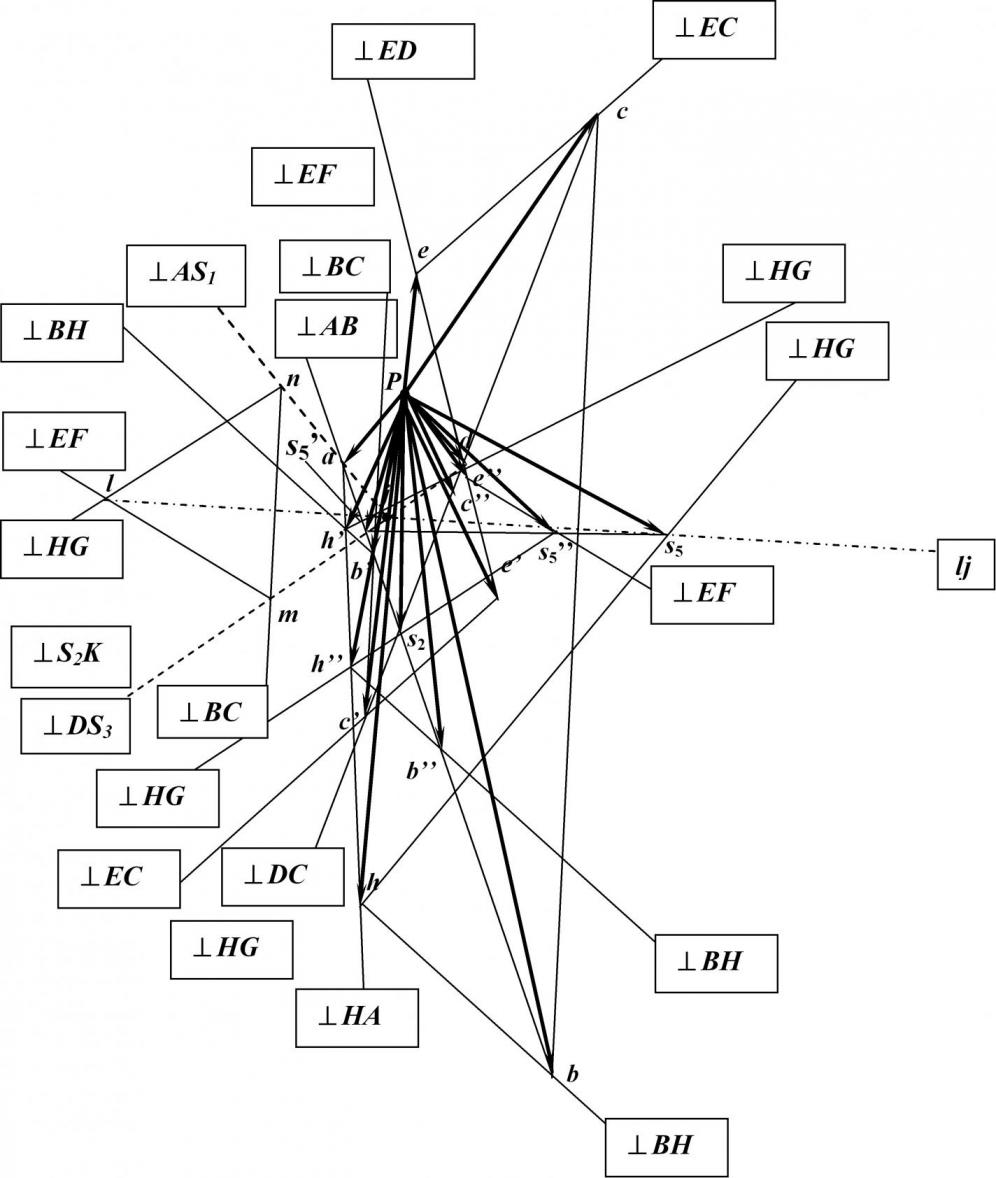Рис.6. План скоростей группы 6ГНП.3 , (3-5). |
После этого скорость точки S5’ определяем через точки H’ и E’ зависимостями
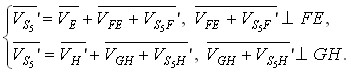 | (18) |
Двойное построение ложного плана позволяет найти направление 
, которое, пересекаясь с направлением jl, определяет истинное положение конца вектора скорости точки S5. После этого обратным образом легко находим истинные скорости точек H и E, а также всех остальных точек группы.
Что касается ускорений точек и звеньев шестизвенных групп, то они могут быть найдены аналогично нахождению скоростей.
Четвертая глава диссертации посвящена разработке методов кинетостатического исследования шестизвенных плоских групп Ассура. В основе подходов был использован, в частности прием, описанный академиком И.И. Артоболевским применительно к трехповодковому звену Бурместера относительно одной из точек Ассура. Этот прием в настоящей работе сформулирован в виде следующей теоремы о трехшарнирном звене безотносительно к точке Ассура.
Если в трехшарнирном звене известны тангенциальные составляющие сил реакций во всех трех кинематических парах и если перпендикулярные к ним направления не пересекаются в одной точке, то известными являются и полные реакции во всех кинематических парах.
Рассмотрим трехшарнирное звено (рис.7.), тангенциальные составляющие реакций во всех трех кинематических парах которого 
, 
и 
известны. На пересечении перпендикуляров к двум из тангенциальных составляющих реакций, например Q и L, зафиксируем точку S, которая принадлежит рассматриваемому звену. Тогда из уравнения суммы моментов сил, действующих на звено, относительно S однозначно находится неизвестная нормальная реакция, т.к. известна и известны плечи h1 и h2 приложения этих реакций.
| Рис.7. Силовой анализ трехшарнирного звена. |
Далее, из векторного уравнения суммы сил, действующих на трехшарнирное звено, определяются нормальные составляющие реакций в шарнирах Q и L
 . | (19) |
Геометрическое сложение составляющих реакций, позволяет определить полные реакции во всех трех шарнирах, т.е. сформулированная теорема оказывается доказанной
На основе этой теоремы был разработан алгоритм кинетостатического исследования шестизвенных групп Ассура, включающий в себя следующие процедуры:
- отыскание двухпарных звеньев (поводков) группы и определение тангенциальных составляющих реакций в их шарнирах;
- отыскание трехпарных звеньев с двумя поводками и через точку Ассура определение тангенциальной составляющей реакции в свободном от поводка шарнире;
- применение к треугольному звену, в котором известны все тангенциальные составляющие реакций, теоремы о реакциях в трехшарнирном звене.
Дальнейшие решения оказываются вполне очевидными.
Покажем применение разработанного алгоритма на примерах трех групп (в диссертации приводится решение всех десяти шестизвенных групп). Шестизвенная группа Ассура с пятиугольным замкнутым изменяемым контуром и приложенными к ней реакциями показана на рисунке 8.
| Рис.8. Шестизвенная группа Ассура с пятиугольным замкнутым изменяемым контуром. |
Выделяются поводки (двухпарные звенья) 6 (HK), 4 (FE), 3 (CD) и для каждого из них из уравнений сумм моментов относительно крайних кинематических пар находятся тангенциальные составляющие реакций в соседних кинематических парах K, Е, C, H, F и D:
 , | (20) |
 , | (21) |
 , | (22) |
 , | (23) |
 , | (24) |
 . | (25) |
На пересечении линий поводков FE и KH фиксируется точка S5. Эта точка принадлежит пятому звену и является для него точкой Ассура. Из уравнения суммы моментов относительно точки S5
 | (26) |
находится тангенциальная составляющая реакции в шарнире G.
Далее на пересечении линий, продолжающих поводок CD и S5G, фиксируется точка 
. Сумма моментов относительно этой точки для всей группы
 | (27) |
позволяет при известных 
и 
найти тангенциальную составляющую реакции в шарнире A.
На пересечении линий поводков CD и FE фиксируется точка S2 звена 2. Из уравнения суммы моментов относительно S2 для звена 2
 | (28) |
определяется тангенциальная составляющая реакции в шарнире B.
Воспользуемся далее теоремой о трехшарнирном звене. На пересечении продолжения поводка HK и линии, соединяющей точки B и S2 (BS2), фиксируется точка 
звена 1, тангенциальные реакции во всех шарнирах которого известны. Из уравнения суммы моментов относительно точки 
для этого звена
 | (31) |
становится возможным определить нормальную составляющую реакции в шарнире A. При известных 
и 
из условия 
определяется полная реакция в шарнире A.
Уравнение суммы сил звена 1
 , | (32) |
позволяет определить полные реакции в шарнирах K и B, а далее и во всех остальных шарнирах группы.
Силовое решение шестизвенной группы Ассура шестого класса (рис.9.) проводится по следующему алгоритму:
Выделяются поводки KH, FE, CB и по уравнениям сумм моментов сил относительно всех шести шарниров K, H, F, E, C и B определяются тангенциальные составляющие реакций (
, 
, 
, 
, 
и 
).
На продолжении линий поводков FE и KH фиксируется точка S5, принадлежащая пятому звену. Уравнение суммы моментов относительно этой точки для пятого звена позволяет определить тангенциальную составляющую реакции в шарнире G.
Аналогично, на продолжении поводков CB и KH фиксируется точка S1, принадлежащая первому звену, и из уравнения суммы моментов сил относительно этой точки определяется тангенциальная составляющая реакции в шарнире A.
Далее, на продолжении направлений AS1 и GS5 фиксируется точка 
. Уравнение суммы моментов относительно 
для всей группы позволяет определить тангенциальную составляющую реакции в шарнире D.
 | |
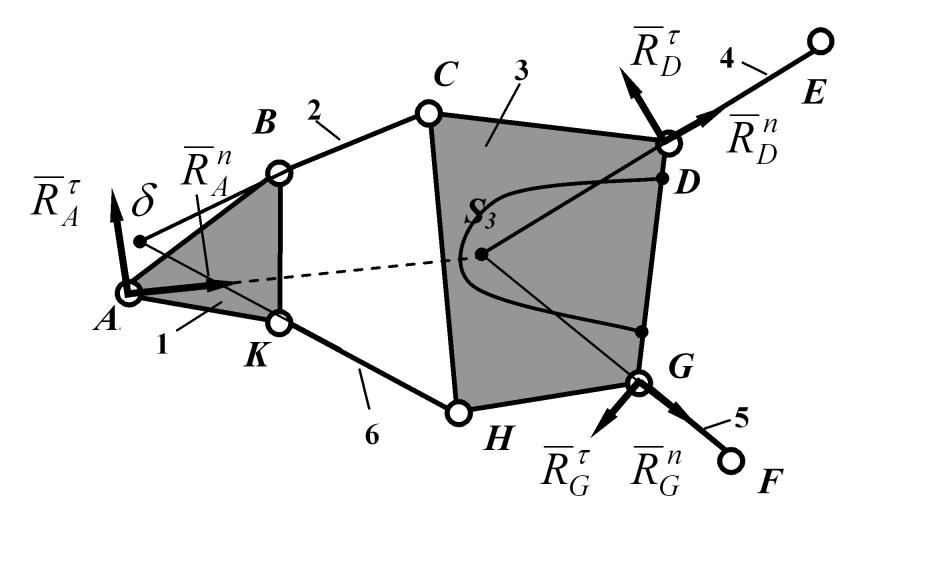| Рис.9. Шестизвенная группа Ассура шестого класса. | Рис. 10. Шестизвенная плоская группа Ассура с четырехугольным базисным звеном и четырехугольным замкнутым изменяемым контуром. |
Так как у звена 3 становятся известными тангенциальные составляющие реакций во всех трех кинематических парах, применим к нему теорему о реакциях в трехшарнирном звене и определим все полные реакции в шарнирах C, D и E (
,
и 
).
Далее, из уравнений сумм сил для поводков BC и EF находятся полные реакции в шарнирах B и F. Процедура определения полных реакций в шарнирах A, K, H и G становится очевидной.
Силовое исследование шестизвенной группы с четырехугольным базисным звеном и четырехугольным замкнутым изменяемым контуром (рис.10.) имеет свои особенности.
Выделяя звенья 4 и 5, по уравнениям сумм моментов сил, действующих на них, находим тангенциальные реакции в шарнирах E, D, F и G.
На пересечении продолжений поводков ED и FG найдем точку S3. Эта точка есть точка Ассура, принадлежащая звену 3.
Отбросим теперь от группы звенья 4 и 5, заменив их реакциями в точках D и G. Для всей оставшейся группы звеньев составим уравнение моментов сил относительно точки S3 и найдем 
.
Выделяя далее звенья 2 и 6 по уравнениям сумм моментов относительно C и H найдем тангенциальные составляющие реакций в шарнирах B и K.
На продолжении направлений звеньев BC и KH найдем точку 
и, используя теорему о трехшарнирном звене, из уравнения суммы моментов найдем нормальную составляющую реакции в точке A, а значит и полную реакцию 
.
После этого, из уравнения суммы сил для звена 1 легко находятся полные реакции в шарнирах B и K. Далее, рассматривая равновесие звеньев 2 и 6, находим полные реакции в шарнирах C и H. Аналогично решается звено 3, а также, звенья 4 и 5.
Разработанные в четвертой главе диссертации алгоритмы позволяют найти полные решения кинетостатики всех десяти шестизвенных групп Ассура.
Пятая глава работы посвящена практической реализации шестизвенных групп Ассура в машинах и устройствах.
  |
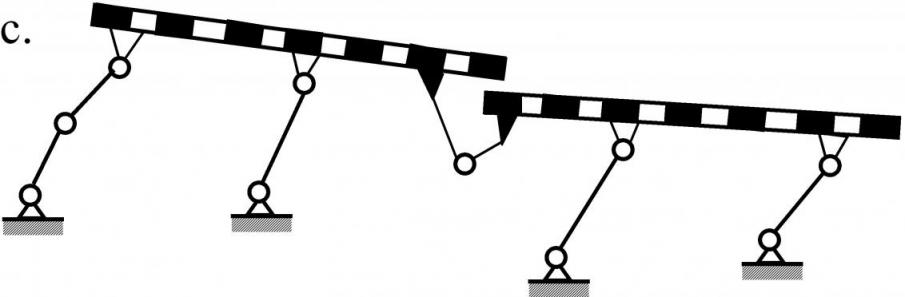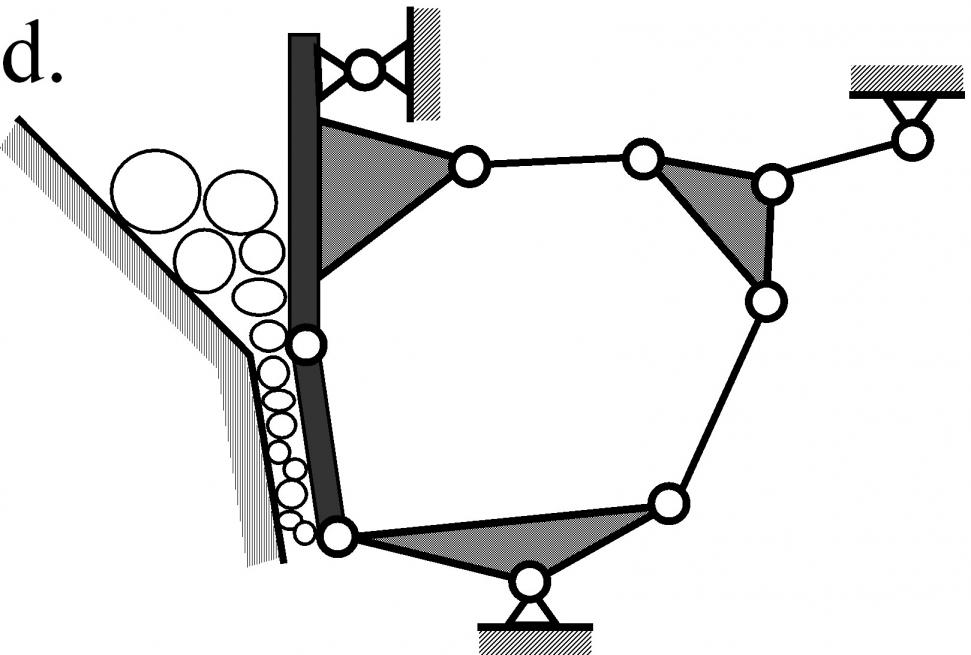| Рис. 11. Новые механизмы, включающие в свой состав шестизвенные группы Ассура. |
Разработанные в настоящем исследовании методы позволили найти ряд принципиально новых схем машин, пригодных для использования в промышленности. На рисунке 11 приведены кинематические цепи разработанных автором новых машин, защищенные патентами РФ на изобретения и полезную модель, в частности, были разработаны «Кривошипно-ползунный механизм пресса» (рис.11.a.), включающий в свой состав группу Ассура 6ГНП.4, (патент № 2201348), «Секция механизированной крепи» (рис.11.b.), включающая в свой состав группу Ассура 6ГНП.3,(3-4-4) (патент № 2303699) «Двухсекционный грохот» (рис.11.c.), включающий в свой состав группу Ассура 6 ГНП.3 (патент на полезную модель № 70168), «Двухщековая дробильная машина» (рис.11.d.), включающая в свой состав группу Ассура 6ГНП.3,
(патент № 2332260).
Шестизвенные группы Ассура, включающие в свой состав изменяемые замкнутые контуры, могут использоваться при создании ответственных строительных конструкций. На рисунке 12 показана строительная ферма, полученная путем связывания особым образом кинематических пар шестизвенной группы Ассура 6ГНП.3,(3-5) в узлы (термин строительной механики).
. |
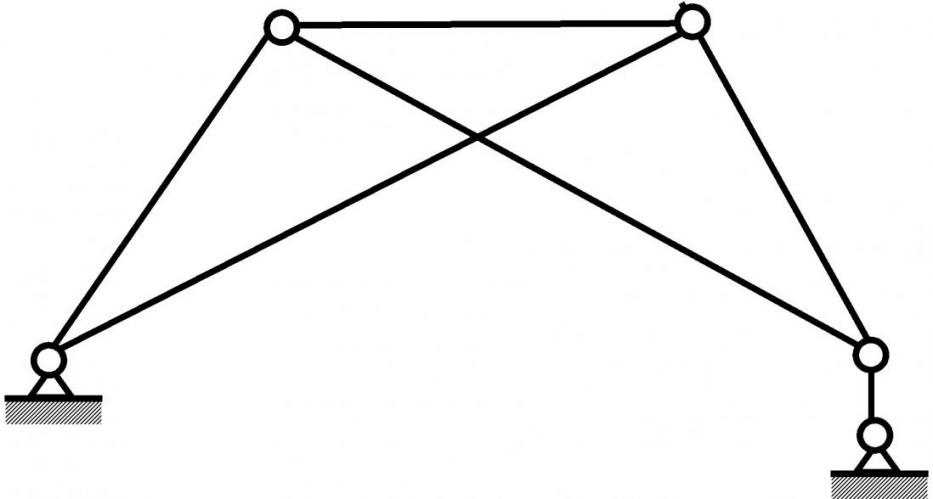| Рис. 12. Пятистержневая ферма. |
Разработанные в настоящей диссертации методы кинематических и кинетостатических исследований позволяют уже на стадии проектирования производить исчерпывающие расчеты приведенных выше и других машин, содержащих в своем составе шестизвенные группы Ассура.
Основные выводы
- На основании изучения существующих методов анализа и синтеза групп нулевой подвижности, обоснован полный состав шестизвенных плоских шарнирных групп нулевой подвижности, что позволило подтвердить правомерность известного предположения профессора Добровольского В.В. о существовании десяти видов шестизвенных плоских шарнирных групп Ассура.
- Идентифицированы все шестизвенные группы по следующим признакам: числу используемых звеньев, сложности базисного звена, числу выходов цепи, числу изменяемых замкнутых контуров в группе, сложности вводимых в цепь изменяемых замкнутых контуров, числу сторон цепи, числу наружных сторон цепи и распределению числа наружных сторон цепи между выходами.
- Исследована кинематика и кинетостатика плоских шарнирных групп нулевой подвижности на основе методов исследования четырехзвенных групп. Разработанное в диссертации доказательство кинематической разрешимости плоских групп Ассура различной сложности позволило найти алгоритмы нахождения линейных скоростей центров шарниров и угловых скоростей звеньев всех десяти шестизвенных групп. В работе обосновано решение задачи силового анализа всех десяти шестизвенных групп. Сформулирована и доказана теорема о разрешимости трехшарнирного звена.
- Изучено влияние класса шестизвенных плоских шарнирных групп нулевой подвижности на повышение сложности их кинематического и кинетостатического решения. Что показало, не зависимость сложности кинематических и кинетостатических решений шестизвенных плоских шарнирных групп Ассура от их класса, определяемого сложностью используемых изменяемых замкнутых контуров. Группы четвертого, пятого и шестого классов решаются одним методом.
- Подтверждена реальными техническими решениями возможность широкого применения в технике шестизвенных плоских групп Ассура. Разработаны «Кривошипно-ползунный механизм пресса» (патент № 2201348), «Секция механизированной крепи» (патент № 2303699) «Двухсекционный грохот» (патент на полезную модель № 70168), «Двухщековая дробильная машина» (патент № 2332260).
Список опубликованных работ по теме диссертации
Основные положения диссертации полностью отражены в 18 публикациях, из них 2 научных статьи в журналах, входящих в перечень изданий, рекомендованных ВАК РФ.
- Дворников Л.Т. Исследование кинематики и кинетостатики плоской шарнирной шестизвенной группы Ассура с четырехугольным замкнутым изменяемым контуром/ Л.Т. Дворников, С.П. Стариков // Известия ВУЗов, «Машиностроение». - 2008. - №4. - С. 3-10.
- Дворников Л.Т. Кинематическое и кинетостатическое исследование двухсекционного грохота/ Л.Т. Дворников, С.П. Стариков // Вестник Кузбасского государственного технического университета. - 2008. - № 1 (65). - С. 44-46.
- Стариков С.П. Кинематическая разрешимость семизвенного кривошипно-ползунного механизма для прессования / С.П. Стариков // Наука и молодежь: проблемы, поиски, решения. Труды Всероссийской научной конференции студентов, аспирантов и молодых ученых/ Под ред. С. М. Кулакова. - Новокузнецк: Из-во СибГИУ, Ч. П. Техн. Науки, 2004. - вып. 8. - С. 264 - 265.
- Стариков С. П. Полный состав простейших плоских групп Ассура / С.П. Стариков // Наука и молодежь: проблемы, поиски, решения. Труды Всероссийской научной конференции студентов, аспирантов и молодых ученых/ Под ред. С. М. Кулакова. - Новокузнецк: Из-во СибГИУ, Ч. П. Техн. Науки, 2005. - вып. 9. - С. 263 - 266.
- Стариков С.П. Кинематика плоской нормальной по Ассуру шестизвенной группы нулевой подвижности / С.П. Стариков // Наука и молодежь: проблемы, поиски, решения. Труды Всероссийской научной конференции студентов, аспирантов и молодых ученых/ Под ред. С. М. Кулакова. - Новокузнецк: Из-во СибГИУ, Ч. П. Техн. Науки, 2005. - вып. 9. - С. 301 - 303.
- Дворников Л.Т. Кинематика и кинетостатика плоской шестизвенной группы Ассура четвертого класса / Л.Т. Дворников, С.П. Стариков // Теория механизмов и машин. - 2006. - № 1, Том 4. - С. 61 - 65.
- Дворников Л.Т. К вопросу об использовании методов теории механизмов применительно к горным машинам / Л.Т. Дворников, С.П. Стариков, А.С. Князев // Наукоемкие технологии, разработки и использование минеральных ресурсов: Материалы Международной научно – практической конференции: сборник научных статей, СибГИУ / Под ред. В. Н, Фрянова, Е. В. Пугачева. - Новокузнецк, 2006. - С. 201 - 203.
- Стариков С. П. Новые решения в задачах кинематического исследования плоских групп Ассура высоких классов / С.П. Стариков, Л.Т. Дворников / Сборник докладов международной конференции по теории механизмов и машин, - Краснодар: Кубан. гос. технол. ун-т, 2006. - 297 с. - С. 63 - 64.
- Стариков С. П. Кинематическое исследование плоской группы Ассура шестого класса / С.П. Стариков // Наука и молодежь: проблемы, поиски, решения. Труды Всероссийской научной конференции студентов, аспирантов и молодых ученых/ Под ред. С. М. Кулакова. - Новокузнецк: Из-во СибГИУ, Ч. П. Техн. Науки, 2006. - вып. 10. - С. 207 - 213.
- Стариков С. П. Кинематика шестизвенной плоской группы Ассура с двумя четырехугольными замкнутыми изменяемыми контурами вида (3 – 5) / С.П. Стариков // Наука и молодежь: проблемы, поиски, решения. Труды Всероссийской научной конференции студентов, аспирантов и молодых ученых/ Под ред. С. М. Кулакова. - Новокузнецк: Из-во СибГИУ, Ч. П. Техн. Науки, 2006. - вып. 10. - С. 228 - 232.
- Дворников Л. Т. Развитие методов кинематического исследования на шестизвенные плоские группы Ассура / Л.Т. Дворников, С.П. Стариков / Труды международной научно-технической конференции «Современные проблемы механики, строительства и машиностроения», Казахстан: Павлодар. - 2006. - том 1. - С. 23 - 31.
- Стариков С.П. Исключение избыточных связей в плоских механизмах / С.П. Стариков, Л.Н. Гудимова / XIII Международная научно-практическая конференция студентов, аспирантов и молодых ученых «Современные техника и технологии» / Сборник трудов в 3-х томах. Т. 1. - Томск: изд-во Томского политехнического университета, 2007. - 547 с. - С. 367 - 370.
- Стариков С.П. Кинетостатическое исследование плоской шестизвенной шарнирной группы Ассура с четырехугольным замкнутым изменяемым контуром / С.П. Стариков, Л.Т. Дворников / XIII Международная научно-практическая конференция студентов, аспирантов и молодых ученых «Современные техника и технологии» / Сборник трудов в 3-х томах. Т. 1. - Томск: изд-во Томского политехнического университета, 2007. - 547 с. - С. 370 – 372.
- Дворников Л. Т. Приемы кинематического исследования плоских групп Ассура высоких классов графо-аналитическим методом / Л.Т. Дворников, С.П. Стариков /методические указания / СибГИУ – Новокузнецк, 2006 - 31 С.
- Пат. № 2201348 РФ, МПК 7 B 30 B 1/06, F 16 H 21/00. Кривошипно-ползунный механизм пресса/Дворников Л.Т., Чужиков О.С., Стариков С.П. - № 2001120227; заяв. 18.07.2001; опубл. 27.03.03., Бюл. № 9 - 5 с.; 1 ил.
- Пат. № 2303699 С1 РФ, МПК E 21 D 23/00. Секция механизированной крепи/ Дворников Л.Т., Князев А.С., Стариков С.П. - № 2005141748/03; заяв. 30.12.2005; опубл. 27.07.2007, Бюл. № 21 - 5 с.; 1 ил.
- Патент на полезную модель № 70168 РФ МПК B07B 1/28, B07B 1/42 Двухсекционный грохот/Дворников Л.Т., Стариков С.П. - № 2006111137/22; заяв. 05.04.2006; опубл. 20.01.2008, Бюл. №2 - 1с.; 1 ил.
- Пат. № 2332260 С1 РФ, МПК B 02 1/04. Двухщековая дробильная машина/ Дворников Л.Т., Стариков С.П. - № 2007101108/03; заяв 09.01.2007; опубл. 27.08.2008, Бюл. №24 - 5с.; 1 ил.
Подписано в печать « » ноября 2008 г.
Формат бумаги 60
84 1/16. Бумага писчая. Печать офисная.
Усл. печ. л. 1. Уч.-изд. л. 1,15. Тираж 100. Заказ
Сибирский государственный индустриальный университет
654007, г. Новокузнецк, ул. Кирова, 42.
Издательский центр СибГИУ
