Построение и исследование дескриптивных алгебр изображений с одним кольцом
На правах рукописи
Яшина Вера Владимировна
Построение и исследование дескриптивных алгебр изображений с одним кольцом
Специальность 05.13.17 – «Теоретические основы информатики»
АВТОРЕФЕРАТ
диссертации на соискание ученой степени
кандидата физико-математических наук
Москва 2009
Работа выполнена в Учреждении Российской академии наук Вычислительный центр им. А.А. Дородницына РАН
Научный руководитель: кандидат физико-математических наук
И.Б. Гуревич
Официальные оппоненты: доктор физико-математических наук,
профессор В.М. Чернов
кандидат физико-математических наук
доцент П.П. Кольцов
Ведущая организация: НИИ Прикладной математики и кибернетики Нижегородского Государственного Университета им. Н.И.Лобачевского
Защита состоится 14 мая 2009 г. в 14:00 на заседании диссертационного совета Д002.017.02 Учреждения Российской академии наук Вычислительный центр им. А.А. Дородницына РАН по адресу: 119333, Москва, ул. Вавилова, 40.
С диссертацией можно ознакомится в библиотеке Учреждения Российской академии наук Вычислительный центр им. А.А. Дородницына РАН.
Автореферат разослан 13 апреля 2009 г.
Ученый секретарь
диссертационного совета
доктор физико-математических наук
профессор В.В. Рязанов
Общая характеристика работы
Актуальность темы
Диссертационная работа посвящена постановке и решению математических задач, возникающих в связи с созданием унифицированного языка для единообразной стандартизированной записи преобразований изображений и преобразований моделей изображений на основе дескриптивных алгебр изображений (ДАИ).
Разработка и исследование математического аппарата, обеспечивающего теоретическую основу автоматизации обработки, анализа, оценивания и понимания изображений, является одной из фундаментальных задач информатики. Автоматизация обработки и анализа изображений должна обеспечить разработчикам автоматизированных систем, предназначенных для работы с изображениями, и конечным пользователям возможность в автоматическом или интерактивном режимах: 1) разрабатывать, адаптировать и проверять методы и алгоритмы распознавания, понимания и оценивания изображений; 2) выбирать оптимальные или адекватные методы и алгоритмы распознавания, понимания и оценивания изображений; 3) проверять качество исходных данных и их пригодность для решения задачи распознавания изображений; 4) использовать стандартные алгоритмические схемы распознавания, понимания, оценивания и поиска изображений. Такая автоматизация, в свою очередь, требует разработки и развития нового подхода к анализу и оцениванию информации, представленной в виде изображений. С этой целью И.Б.Гуревичем [2] осуществлена специализация Алгебраического подхода к задачам распознавания, классификации и прогноза Ю.И.Журавлева [1] на случай представления исходной информации в виде изображений (Дескриптивный подход к анализу и пониманию изображений (ДПАИ)).
ДПАИ задает единую концептуальную структуру для развития и реализации этих моделей и математического языка. Основной целью ДПАИ является структурирование разнообразных методов, операций и представлений, используемых в анализе и распознавании изображений, причем формальные конструкции ДПАИ обеспечивают способы и инструменты представления и описания изображений для их последующего анализа и оценивания.
В рамках развития ДПАИ необходимо разработать и изучить математический язык для единообразного описания: 1) моделей изображений; 2) преобразований, обеспечивающих построение моделей изображений; и 3) преобразований, обеспечивающих решение задач распознавания. Данная задача тесным образом связана с изучением способов представления исходной и промежуточной информации в задачах обработки, анализа и распознавания изображений (моделей изображений), а также с описанием моделей решения задач распознавания в виде стандартизированных алгоритмических схем.
В качестве такого математического языка в ДПАИ выбран аппарат дескриптивных алгебр изображений (ДАИ). Актуальность данной работы определяется тем, что она посвящена конкретизации и развитию математического аппарата ДПАИ в виде ДАИ1К.
Результаты работы вносят существенный вклад в развитие ДПАИ и тем самым в создании математической теории анализа изображений.
1 Ю.И. Журавлев. Об алгебраическом подходе к решению задач распознавания и классификации // Проблемы кибернетики, выпуск 33, Москва, Наука, 1978, - стр. 5-68.
2. I.B. Gurevich. The Descriptive Framework for an Image Recognition Problem // Proceedings of the 6th Scandinavian Conference on Image Analysis.- Pattern Recognition Society of Finland, 1989.- vol. 1. – P. 220 – 227.
Цели и задачи диссертационной работы
Целью диссертационной работы является определение и исследование специализированных версий ДАИ - дескриптивных алгебр изображений с одним кольцом (ДАИ1К).
В рамках поставленной задачи были выделены следующие основные направления исследований: 1) сравнительный анализ алгебр изображений и алгебраических методов, применимых для анализа изображений; 2) построение специализированных ДАИ1К; 3) исследование операндов и операций ДАИ1К; 4) построение алгоритмических схем анализа изображений на основе ДАИ1К; 5) экспериментальное исследование применения ДАИ1К в задачах распознавания изображений.
Научная новизна
Новизна данной работы определяется тем, что как постановки задач исследования, так и получение искомых результатов производились в рамках нового подхода к математическому анализу изображений – ДПАИ. ДАИ являются одним из основных инструментов данного подхода и отличаются от известных АИ тем, что обеспечивает возможность оперировать как с основными моделями изображений, так и с основными моделями тех процедур преобразования, которые обеспечивают эффективный синтез и реализацию базовых процедур формального описания, обработки, анализа и распознавания изображений. ДАИ1К и ее специализированные версии являются новыми типами алгебр. Определение ДАИ1К, метод построения ДАИ1К, необходимые и достаточные условия построения ДАИ1К, классы ДАИ1К, порождающие классы моделей изображений ранее не вводились и не изучались и также являются новыми. В целом все результаты, выносимые на защиту, являются новыми и оригинальными.
Методы исследования
Теоретической основой исследований, проведенных в рамках данной диссертационной работы, являются ДПАИ, общие алгебраические методы, методы обработки изображений и методы математической теории анализа изображений и математической теории распознавания образов.
Практическая ценность
Практическая и инновационная ценность теоретических результатов работы заключается в том, что последние являются основой для разработки новых информационных технологий принятия интеллектуальных решений по информации, представленной в виде изображений, и для создания новых поколений автоматизированных информационных систем и алгоритмическо-программных комплексов (АПК), необходимых для их реализации. Указанные информационные технологии и системы предназначены для использования в: а) автоматизации научных исследований, в частности, биомедицинских; б) медицинской диагностике (ранняя диагностика тяжелых заболеваний, прогнозирование хода болезни и лечения по результатам обследования); в) технической диагностике; г) прогнозировании природных катастроф (наводнения, лесные пожары); д) экологическом мониторинге и во многих других разделах науки и техники.
ДАИ1К могут быть использованы для стандартизации и тестирования алгоритмического наполнения АПК, обеспечивающих поддержку указанных информационных технологий.
Апробация полученных результатов
В основу диссертационной работы положены результаты, полученные автором в ходе исследований, проводимых в рамках НИР по проектам 1) Российского фонда фундаментальных исследований (проекты №№ 01-07-90017, 02-01-00182, 05-07-08000-офи_а, 05-01-00784, 06-01-81009-Бел_а, 06-07-89203, 07-07-13545-офи_ц, 08-01-00469, 08-01-90022-Бел_а); 2) ФЦНТП «Исследования и разработки по приоритетным направлениям развития науки и техники» на 2002-2006 гг. (проект № 37.011.11.0015, 2002-2004; проект № 37.011.11.0016, 2002-2004); 3) Программы фундаментальных исследований Отделения математических наук РАН «Алгебраические и комбинаторные методы математической кибернетики» (проект «Дескриптивные алгебры изображений», 2003-2005; проект «Дескриптивные алгебры с одним кольцом над моделями изображений», 2006-2008); 4) Комплексной программы научных исследований РАН «Математическое моделирование и интеллектуальные системы» (проект № 2.14, 2001-2003; проект № 2.14, 2004-2005); 5) Программы Президиума РАН П-14 «Фундаментальные проблемы информатики и информационных технологий» (проект № 2.14, 2006-2008); 6) Программы Президиума РАН «Фундаментальные науки – медицине» (2008 г.); 7) Программы Президиума РАН «Поддержка инноваций» (2006 г.); 8) Программы Президиума РАН "Поддержка инноваций и разработок" (2008 г.); 9) Программы Международной Ассоциации содействия сотрудничеству с учеными из новых независимых государств бывшего Советского Союза (ИНТАС) (проект № 04-77-7067, 2005-2006); 10) Программы «Участник молодежного научно-инновационного конкурса» (УМНИК-07-9) Фонда содействия развитию малых форм (проект №8067, 2008).
Основные результаты работы докладывались и обсуждались на 12 ведущих конференциях и семинарах: на всероссийской с участием стран СНГ конференции «Методы и средства обработки сложной графической информации» (Нижний Новгород, сентябрь 2003г.); на международных конференциях «Распознавание образов и анализ изображений: новые информационные технологии» (РОАИ-7-2004, Санкт-Петербург, октябрь 2004г.; РОАИ-8-2007, Йошкар-Ола, октябрь 2007г.; РОАИ-9-2008, Нижний Новгород, сентябрь 2009г.); на 8-ом Ибероамериканском конгрессе по распознаванию образов (CIAPR-3-2003, Гавана, Куба, ноябрь 2003 г.); на открытых российско-немецких семинарах «Распознавание образов и понимание изображений» (OGRW-6-2003, Катунь, Российская Федерация, август 2003г.; OGRW-7-2007, Эттлинген, Германия, август 2007г.); на международной конференции «Зрение, моделирование и визуализация 2005» (VMV-2005, Эрланген, Германия, ноябрь 2005 г.); на 2-ой международной конференции «Машинное зрение: теория и приложения» (VISAPP 2007) (Барселона, Испания, март 2007г.); на международной конференции по информатике в здравоохранении (HealthInf 2008, Фуншал, Мадейра, Португалия, январь 2008 г.); на международных семинарах «Извлечение информации из изображений. Теория и приложения» в рамках международных конференций «Машинное зрение. Теория и приложения» (IMTA-1-2008, Фуншал, Мадейра, Португалия, январь 2008г.; IMTA-2-2009, Лиссабон, Португалия, февраль 2009г.).
По теме диссертации опубликовано 22 работы, в том числе 7 в изданиях, входящих в перечень ведущих рецензируемых журналов и изданий, рекомендованных ВАК для публикации основных результатов диссертации на соискание ученой степени доктора и кандидата наук.
Структура и объем работы
Представленная работа состоит из введения, четырех глав, заключения и библиографического списка используемой литературы, содержащего 151 работу. Объем диссертационной работы – 143 страницы.
Результаты, выносимые на защиту
- Определение, метод и необходимые и достаточные условия построения ДАИ1К.
- Специализированные версии ДАИ1К над изображениями, над моделями изображений и над преобразованиями изображений.
- Набор операций стандартной алгебры изображений (АИ), обеспечивающих построение ДАИ1К.
- Классы ДАИ1К, порождающие классы моделей изображений.
- Модель решения задачи распознавания изображений на основе ДМИ.
- Специализация модели решения задачи распознавания, ДМИ и ДАИ1К для создания алгоритмической схемы решения задачи морфологического анализа клеток крови.
Содержание работы
Во Введении обосновывается актуальность выбранной темы; формулируются цель и задачи исследования, показана научная новизна, указаны основные методы исследований. Кратко излагается содержание диссертации по главам.
Первая глава имеет обзорный характер и содержит описание основных стадий «алгебраизации» в области распознавания образов и анализа изображений. В ней описаны общие принципы алгебраического подхода к описанию изображений и алгоритмов, а также основные результаты основополагающих теорий, обеспечивающих представление изображений и преобразований над ними в виде алгебраических структур, позволяющих использовать в анализе и распознавании изображений методы, заимствованные из других областей математики. Конечной целью при этом является сравнительный анализ функциональных возможностей известных АИ и исследование возможностей построения АИ, соответствующих объединению и пересечению множеств операций этих алгебр.
Развитие математической теории распознавания образов и в определенной степени математической теории анализа и распознавания изображений проходило по двум параллельным, по сути взаимосвязанным, направлениям: а) разработка, формализация, исследование и оптимизация методов представления исходной информации в задачах распознавания; б) разработка, формализация, исследование и оптимизация методов преобразования исходной информации, обеспечивающих собственно решение задач распознавания.
В разделе 1.2. описаны основные этапы «алгебраизации» в распознавании образов. Отдельное внимание уделяется двум основополагающим теориям – «Алгебраическому подходу к задачам распознавания и классификации» Ю.И. Журавлева (описание алгоритмов распознавания образов в виде алгебры алгоритмов) и «Теории образов» У.Гренандера (описание исходных данных, как объектов анализа).
Алгебраический подход Ю.И.Журавлева является методической основой для формализованного представления алгоритмов распознавания образов в терминах алгебр над множеством некоторых базисных алгоритмов. Смысл этого подхода состоит в том, что семейство эвристических алгоритмов рассматривается как некоторая алгебра, операции которой позволяют на основе базиса семейства алгоритмов строить такое расширение этого семейства, которое содержит корректный алгоритм, правильно классифицирующий конечную выборку по всем классам.
Наиболее общим подходом к алгебраическому описанию информации для алгоритмов распознавания является общая теория образов У.Гренандера, объединяющая метрическую теорию с теорией вероятности на некоторых универсальных алгебрах комбинаторного типа. Основной упор делается на исследование структуры распознающих элементов. Теория образов У.Гренандера является основой для создания наиболее общего аппарата для работы с образами произвольной природы и их представления как алгебраических структур.
В разделе 1.3. описаны основные этапы «алгебраизации» в анализе изображений. Отдельное внимание в данном разделе уделяется математической морфологии Ж.Серра, алгебре изображений С.Стернберга и стандартной алгебре изображений Г.Риттера.
Математическая морфология Ж.Серра является одной из первых попыток создать теоретический аппарат, позволяющий описать многие распространенные операции обработки изображений в виде композиции достаточно малого набора стандартных простых локальных операций и правил.
На основе операций математической морфологии С.Стернберг ввел понятие “алгебра изображений”. Используя развитую Т.Матероном и Ж.Серра бинарную теорию операций, он создал алгебру для анализа изображений. Невозможность построения универсальной алгебры для задач обработки изображений на основе морфологической АИ объясняется ограниченностью базиса, образуемого теоретико-множественными операциями сложения и вычитания по Х.Минковскому.
Окончательное оформление идея АИ получила в виде стандартной АИ Г.Риттера. АИ Г.Риттера является наиболее детализированным из известных в настоящее время подходов к описанию операций над изображениями в терминах алгебраических операций над базисными операциями с простой структурой. АИ является удобным средством для формирования базисного набора операций для единой алгебраической схемы представления, анализа и распознавания изображений. Узким местом при применении методов АИ в распознавании изображений является выбор последовательности алгебраических операций и «темплейтов» для представления сложных операций обработки изображений.
Раздел 1.4. содержит общие концепции «алгебраизации» анализа и распознавания изображений, выделенные в рамках развития ДПАИ. Описаны основные аспекты ДПАИ И.Б.Гуревича.
Математической основой ДПАИ являются ДАИ, которые позволяют объединять и стандартизировать процедуры построения и обработки моделей изображений и их преобразований. Задачи, объекты и преобразования, рассматриваемые при извлечении информации из изображений, задаются иерархическими структурами, построенными путем применения операций ДАИ ко множеству непроизводных задач, непроизводных элементов изображения и базисных преобразований. При таком подходе существует возможность варьировать методы решения подзадачи, используя операции анализа изображений в качестве элементов ДАИ, сохраняя в целом схему технологии извлечения информации из изображений. Место ДАИ среди основных разновидностей алгебр иллюстрируется на рисунке 1.
Рис.1. Классификация алгебр.
Вторая глава посвящена основным концепциям и определениям, связанными с ДАИ, в частности, с ДАИ1К, и содержит специализированные версии ДАИ1К над изображениями.
В разделе 2.2 вводится определение ДАИ1К.
Определение 1. Кольцо U, являющееся конечномерным векторным пространством над некоторым полем P, является ДАИ1К, если его операндами являются либо модели изображений, либо операции над изображениями.
В разделе 2.3 формулируются необходимые и достаточные условия и описывается метод построения ДАИ1К.
Теорема 1. Пусть P – поле любой природы; U – множество элементов следующей природы: 1. реализации изображений; 2. преобразования изображений, 3. представления изображений; 4. модели изображений; –операции сложения (+), произведения(·) и умножения на элемент поля (·), выбранные из множества операций: 1. стандартные алгебраические операции; 2. преобразования анализа и обработки изображений; 3. алгебраические замыкания, линейные комбинации и суперпозиции этих операций. Математическая конструкция (P, U, ) является ДАИ1К тогда и только тогда, когда элементы множества U с введенным на нем множеством операций и полем P, удовлетворяют следующим свойствам классической алгебры: I. Свойства кольца U (a, b, c U): 1) a, b U, ! (a+b) U: (а) a+(b+c) = (a+b)+c; (б) a+b = b+a; (в) 0U,aU,a+0=a; (г) aU,(a), a+(a)=0; 2) a, b U, ! (a·b) U: (а) a·(b·c)=(a·b)·c; (б) (·a+·b)·c = ·a·c+·b·c; II. Свойства векторного пространства ( P, a U: ·a U): 1) ·(·a)=(·)·a; 2) (+)·a = ·a+·a; 3) ·(a+b) = ·a+ ·b.
Доказательство этой теоремы следует из определения ДАИ1К и определения классической алгебры.
Предложен следующий метод построения ДАИ1К. Шаг 1. Выбирается поле, на котором задается алгебра. Шаг 2. Задаются операнды множества, рассматриваемого как кандидат на ДАИ1К. Шаг 3. Задаются операции множества, рассматриваемого как кандидат на ДАИ1К. Шаг 4. Из заданных операций выбираются следующие: операция сложения элементов заданного множества, операция произведения элементов заданного множества, операция произведения элемента множества на элемент выбранного поля. Шаг 5. Исследуется интерпретируемость выбранных операций ДАИ на предмет физической реализуемости ДАИ1К в контексте анализа и обработки изображений. Шаг 6. Вводятся необходимые ограничения на выбранные поле, операнды и операции заданного множества (шаги 1-4). Шаг 7. В случае возможности наложения ограничений, сформулированных на шаге 6, формулируется и доказывается теорема существования ДАИ1К заданного вида. Доказательство данной теоремы основывается на необходимых и достаточных условиях построения ДАИ1К (смотри теорему 1).
В разделе 2.4 проводится исследование операций стандартной АИ Г.Риттера в контексте их использования для построения ДАИ1К и строятся специализированные ДАИ1К над изображениями.
Условия, определяющие подмножество операций стандартной АИ, обеспечивающее порождение ДАИ1К, устанавливаются в теореме 2.
Теорема 2. Пусть F – некоторое поле. Элементами кольца W являются изображения I, заданные функциями вида {(x, a(x)), xX, a(x)F}, где F- множество значений, X – множество точек (IFX). Введены операции, и умножение на элемент поля. Операции принадлежат множеству операций стандартной АИ. Тогда следующие условия необходимы и достаточны для построения ДАИ1К:
(1) I(RX) или I(Rn)X, тогда в роли операции выступает операция сложения двух изображений; в роли операции выступает операция произведения двух изображений; в качестве умножения на элемент поля выступает скалярное умножение элемента из множества F и изображения;
(2) I(2F)X, тогда в роли операции выступает операция объединения двух изображений или операция пересечения двух изображений; в качестве умножения на элемент поля выступает скалярное умножение элемента из множества F и изображения;
(3) I(R2)X, тогда в дополнении к описанным операциям в (1) в роли операции выступает операция сложения двух изображений; в качестве умножения на элемент поля выступает скалярное умножение элемента из множества F и изображения; в роли операции выступает операция произведения двух изображений или следующая операция:
Пусть 1 и 2 бинарные операции R2xR2R определены как
| (x1, x2) 1 (y1,y2) = x1y1-x2y2, | (1) |
| (x1, x2) 2 (y1,y2) = x1y2+x2y1, | (2) |
тогда если I1, I2 (R2)X представляют два комплексно-значных изображения, тогда произведение I3=I1I2 представляет комплексное произведение:
| I3={(x,c(x)), с(x) = (a1(x)b1(x)-a2(x)b2(x), a1(x)b2(x)+a2(x)b1(x)), xX}. | (3) |
Доказательство основано на необходимых и достаточных условиях построения ДАИ1К (теорема 1) на основе операций стандартной АИ.
При разработке методов автоматизации распознавания изображений необходимо найти способы эффективной формализации изображений, которая бы отражала семантику изображений, информацию, заключенную в его внутренней структуре и структуре внешних связей реального мира (сцены), воспроизводимой с помощью изображения. На основе введенной в ДПАИ формализации строятся ДАИ1К над реализациями изображений. При выборе операций применимых к реализациям изображений учитываются следующие два факта: 1) преобразования изображений должны быть замкнутыми относительно исходных данных; 2) необходимо ввести некоторые специализированные классы ДАИ1К, используемые далее в главе 4 при построении алгоритмической схемы решения практической задачи.
Для построения специализированных ДАИ1К использовался описанный в разделе 2.3 метод. В таблице 1 представлены построенные в разделе 2.4 специализированные ДАИ1К. Таблица содержит: 1) класс: номер класса ДАИ1К; обозначение класса (в случае использования построенной алгебры в главе 4 для построения алгоритмической схемы); 2) операнды алгебры: элементы ДАИ1К; 3) операции алгебры: операции, введенные над операндами ДАИ1К. По каждой специализированной ДАИ1К сформулирована и доказана теорема существования ДАИ1К заданного вида.
Таблица 1. Специализированные ДАИ1К над изображениями
| Класс | Операнды алгебры | Операции алгебры |
| 2.4.3.1 | I={(x,f(x)),xX,f(x)Fi}U1 | I1+I2={(x,a(x)+b(x)),xX} (4) |
| I1·I2={(x,a(x)·b(x)),xX} (5) | ||
| ·I={(x,·f(x)), xX} (6) | ||
| 2.4.3.2 | I={(x,f(x)),xX,f(x)X}U2 | I1+I2 = {(x,a(x)+b(x)), xX} |
| I1· I2 = {(x, a(b(x))), xX | ||
| ·I = {(x, ·f(x)), xX} | ||
| 2.4.3.3 ДАИ 1 | I={((x,y),(r(x,y),g(x,y), b(x,y))}(x,y)XU r(x,y),g(x,y),b(x,y)[0...M-1]; M=256 | I1+I2={((x,y),((r1(x,y)+r2(x,y))modM,…))}(x,y)X |
| I1·I2={((x,y),((r1(x,y)·r2(x,y))modM,…))}(x,y)X | ||
| ·I ={((x,y),([r(x,y)modM],…))} x,y)X | ||
| 2.4.3.4 ДАИ2 | J={((x,y),gray(x,y))}(x,y)XV; gray(x,y) [0...M-1]; M=256 | I1+I2={((x,y),(gray1(x,y)+gray2(x,y))modM)}(x,y)X |
| I1·I2={((x,y),(gray1(x,y)·gray2(x,y))modM)}(x,y)X | ||
| ·I={((x,y),[gray(x,y)modM])} x,y)X | ||
| 2.4.3.5 | I={((x,y),M[x,y])}(x,y)X U4; M[x,y]R; X={1,…,n;1,…,n} | I1+I2={((x,y),(M1+ M2)[x,y])}(x,y)X |
| I1·I2={((x,y), (M1·M2)[x,y])}(x,y)X | ||
| ·I ={((x,y), (· M)[x,y]))} x,y)X |
ДАИ1К 2.4.3.1 интересна методом задания реализации изображения на фиксированной области определения изображения с различными множествами значений изображения в каждой точке определения изображения. Для построения ДАИ1К над реализациями изображений такого вида вводятся ограничения на множество множеств значений изображений. В ДАИ1К 2.4.3.2 демонстрируется использование операции суперпозиции двух функций в качестве операции произведения двух элементов алгебры. ДАИ1К 2.4.3.3-2.4.3.5 вводятся для демонстрации использования различных операций обработки изображений для построения алгебр. ДАИ1К 2.4.3.3 (ДАИ 1) над цветными изображениями и ДАИ1К 2.4.3.4 (ДАИ 1) над тоновыми изображениями вводятся для дальнейшего использования в главе 4.
В качестве примера теорем существования для различных классов ДАИ1К приведем теорему 3 для ДАИ1К 2.4.3.1. Для доказательства вводятся дополнительные ограничения: пусть задано множество множеств 
(ограничим значения множеств n-мерной действительной плоскостью): I. Введена операция сложения двух элементов из Fi, Fj Rn: i, j = 1,2,…, a Fi, b Fj: ! a+b Fk, k=1,2…, Fk Rn, обладающая следующими свойствами ( a Fi, b Fj, c Fy, i, j, y = 1,2,…): 1.1 a+(b+c) = (a+b)+c; 1.2 a+b = b+ a; 1.3 i: a Fi, 0 Fi: a+0=a; 1.4 i: a Fi, (-a) Fi: a+(-a)=0. II. Введена операция умножения двух элементов из Fi, Fj: i,j = 1,2,…, a Fi, b Fj: ! a·b Fk, k=1,2…, Fk Rn, обладающая следующими свойствами ( a Fi, b Fj, c Fy,i,j,y=1,2,…): 1.5 a·(b·c) = (a·b)·c. III. На множестве Fi (i=1,2,…) введена операция умножения на элемент поля действительных чисел R: R, aFi: !·aFi (i=1,2,…), обладающая следующими свойствами ( a Fi, b Fj, c Fy,i,j,y=1,2,…,, R): 1.6 (·a+ ·b)·c = ·a·c+ ·b·c; 1.7 · (·a) = (·)·a; 1.8 ( + )·a = ·a +·a; 1.9 · (a+b) = ·a+ ·b. В случае если все FiF Rn (i=1,2,…), то множество F с введенными так операциями является алгеброй над полем действительных чисел.
Теорема 3. Пусть R - поле действительных чисел; I={(x, f(x)),xX,f(x)F}(F
(множество множеств 
удовлетворяет свойствам 1.1-1.9), F - множество значений, принимаемое изображением I на множестве X) – элементы множества U1. Обозначим I1 = {(x, a(x)), xX, a(x)F1}и I2 = {(x, b(x)), xX, b(x) F2}, (F1,F2
)любые два элемента множества U1. Вводятся операция сложения двух изображений I1, I2 вида (4), операция умножения двух изображений I1, I2 вида (5), операция умножения изображения I на элемент поля действительных чисел R вида (6). Тогда множество U1 с введенными на нем операциями сложения, произведения и умножения на элемент поля действительных чисел является ДАИ1К над полем действительных чисел.
В данном разделе были также приведены логические операции обработки изображений, не порождающие ДАИ1К. В таблице 2 продемонстрированы возможности выбора логических операций, порождающих и не порождающих построение ДАИ1К и построенная дескриптивная группа изображений (ДГИ)-ДГИ 2, которая будет использована в главе 4. Сформулирована теорема существования ДГИ 2.
Таблица 2. Выбор логических операций для построения ДАИ1К
| Класс | Операнды алгебры | Операции алгебры |
| 2.4.3.6 ДГИ 2 | Ib={((x,y),(bool(x,y),bool(x,y),bool(x,y)))}(x,y)XB; bool(x,y){0,1} | Ib1+Ib2={((x,y),((bool1(x,y)+bool2(x,y))mod2,…))}(x,y)X |
| Ib1·Ib2={((x,y),((bool1(x,y)ORbool2(x,y)),…))}(x,y)X | ||
| ·Ib={((x,y),([·bool(x,y)mod2],…)}(x,y)X | ||
| ДАИ1К | Ib={((x,y),(bool(x,y),bool(x,y),bool(x,y)))}(x,y)XB; bool(x,y){0,1} | Ib1+Ib2={((x,y),((bool1(x,y)+bool2(x,y))mod2,…))}(x,y)X |
| Ib1·Ib2={((x,y),((bool1(x,y)AND bool2(x,y)),…))}(x,y)X | ||
| ·Ib={((x,y),([·bool(x,y)mod2],…)}(x,y)X | ||
| ни группа, ни алгебра | Ib={((x,y),(bool(x,y),bool(x,y),bool(x,y)))}(x,y)XB; bool(x,y){0,1} | Ib1+Ib2={((x,y),((bool1(x,y)ORbool2(x,y)),…))}(x,y)X |
| Ib1·Ib2={((x,y),((bool1(x,y)ANDbool2(x,y)),…))}(x,y)X | ||
| ·Ib={((x,y),([·bool(x,y)mod2],…)}(x,y)X |
В соответствии с Теоремой 1 выделены обобщающие классы ДАИ1К: 1) ДАИ1К над реализациями изображений со стандартными алгебраическими операциями; 2) ДАИ1К над реализациями изображений с операциями обработки изображений; 3) ДАИ1К над реализациями изображений с алгебраическими замыканиями, линейными комбинациями и суперпозициями операций; 4) ДАИ1К над преобразованиями изображений; 5) ДАИ1К над представлениями изображений; 6) ДАИ1К над моделями изображений. В главе 2 построены специализированные ДАИ1К из классов 1-3. В главе 3 – из классов 4 и 6.
Третья глава посвящена специализированным версиям ДАИ1К, необходимым для построения алгоритмических схем по модели решения задачи распознавания изображений. Для такого построения необходимо вводить специализированные ДАИ1К над исходной и промежуточной информацией в задачах обработки, анализа и распознавания изображений (ДАИ1К над моделями изображений) и специализированные ДАИ1К над преобразованиями изображений и моделей изображений для порождения новых моделей изображений.
В разделе 3.2 кратко приводятся результаты по математической характеризации и формализации пространства представлений изображений, формулируются теоремы о порождении ДМИ с помощью специализированных классов ДАИ1К и вводятся специализированные ДМИ, необходимые для описания исходных и промежуточных данных в задаче морфологического анализа клеток крови, рассмотренной в главе 4.
На рисунке 2 изображена схема синтеза моделей изображений: с помощью преобразований 
и семантической и контекстной информации 
об исходном изображении I строятся схемы для формального описания объектов и их связей на изображении (множество представлений изображений). Применение построенных схем к реализациям изображения 
, или к реализациям изображения после применения к ним структурирующих элементов 
приводит к построению множества моделей исходного изображения 
.
Рис. 2. Синтез моделей изображения.
В соответствии с представленной схемой 2 выделены специализированные классы ДАИ1К для описания и построения моделей изображений (таблица 3). По каждому классу ДАИ1К сформулированы правила построения ДМИ с помощью этого класса ДАИ1К (формулируются и доказываются теоремы и следствия). Сформулированные теоремы и следствия из них определяют свойства алгебр порождать ДМИ. Ниже приведена одна из теорем и следствия из нее.
Таблица 3. Классы ДАИ1К для описания и построения ДМИ.
| Класс | Операнды алгебры | Операции алгебры | Порождает |
| 1. | Реализации исходного изображения  или реализации фрагментов исходного изображения  | Процедурные преобразования изображений  | T-модели изображений; реализации изображений |
| 2. | Процедурные преобразования изображений  | Операции над процедурными преобразованиями | T-модели изображений; реализации изображений |
| 3. | Параметрические преобразования изображений  | Операции над параметрическими преобразованиями | P-модели изображений |
| 4. | Порождающие преобразования изображений  | Операции над порождающими преобразованиями | G-модели изображений |
| 5. | Представления изображений  | Операции над представлениями изображений | ДМИ; мультимодельные. и многоаспектные представления изображений |
| 6. | Процедурные модели изображений  | Операции над процедурными моделями изображений | T-модели изображений; реализации изображений |
| 7. | Параметрические модели изображений  | Операции над параметрическими моделями изображений | P-модели изображений |
| 8. | Порождающие модели изображений  | Операции над порождающими моделями изображений | G-модели изображений |
Теорема 4. Пусть P – некоторое заданное поле; исходное изображение I задано множеством реализаций 
и множеством контекстной и семантической информации 
; 
- любые реализации из множества реализаций 
исходного изображения I, заданные на одной и той же области определения реализаций изображения 
с некоторыми множествами значений 
реализаций изображения в каждой точке области определения 
; на множестве реализаций изображений заданного вида вводятся операция сложения 
двух реализаций изображения 
; операция умножения 
двух реализаций изображения 
; и операция умножения 
изображения I на элемент поля P; математическая конструкция (P, 
, (
)) является ДАИ1К над реализациями изображений. Тогда множество семантической и контекстной информации 
задает правила применения операций (
) ко множеству реализаций изображений 
для порождения ДМИ.
Следствие 1. Для любого исходного изображения I, заданного множеством реализаций 
, описываемых ДАИ1К над полем P, и множеством контекстной и семантической информации 
, множество 
задает правила применения операций (
) из множества процедурных преобразований ко множеству реализаций изображений 
для порождения процедурных моделей изображений.
Следствие 2. Для любого исходного изображения I, заданного множеством реализаций 
, описываемых ДАИ1К над полем P, и множеством контекстной и семантической информации 
, множество 
задает правила применения операций (
) из множества процедурных преобразований ко множеству реализаций изображений 
для порождения множества I-моделей исходного изображения I (множества новых реализаций изображений).
На основе описанных в главе 2 и в главе 3 ДАИ1К построены 5 специализированных ДМИ (см. таблицу 3).
Таблица 3. Построение ДМИ на основе ДАИ1К.
| Класс | Построение | Назначение |
| 3.2.2.2 Процедурная ДМИ 1 | 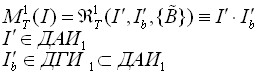  -представление изображения | Описание выделенных фрагментов на изображении с помощью умножения исходного изображения на изображение-маску |
| 3.2.2.2 Процедурная ДМИ 2 |   -представление изображения | Описание процесса сегментации |
| 3.2.2.3 Процедурная ДМИ 3 |   -представление изображения | Снятие разницы в освещенности исходных изображений за счет перевода исходных цветных изображений в тоновые |
| 3.2.2.4 Параметрическая ДМИ 4 |   -представление изображения | Получение описания тонового изображения в виде пары значений  :  - уникальный номер признака в некотором признаковом пространстве;  - значение признака из множества действительных чисел |
| 3.2.2.5 Параметрическая ДМИ 5 |  | Получение описания тонового изображения в виде вектора наиболее информативных признаков |
В разделе 3.4 описываются специализированные ДАИ1К для описания и построения ДМИ, используемые в главе 4 для описания алгоритмической схемы (таблица 4, 5). Формулируются соответствующие теоремы существования ДАИ1К и ДГИ заданного вида.
Таблица 4. Специализированные ДАИ1К над преобразованиями изображений.
| Класс | Операнды алгебры | Операции алгебры |
| 3.3.1.1 ДАИ 3 | Операции f(UV)F конвертирования элементов ДАИ 1 (U) в элементы ДАИ 2 (V) | f1(I)+f2(I)=J1+J2 |
| f1(I)·f2(I)=J1·J2 | ||
| ·f(I)= ·J | ||
| 3.3.1.2 ДГИ 1 | Операции sb((U,C)B)SB получения бинарных масок, соответств. объектам, C – информация о контурах объектов, BU (ДГИ 2) | sb1(I,C)+sb2(I,C)=Ib1+Ib2 |
| sb1(I,C)·sb2(I,C)=Ib1·Jb2 | ||
| ·sb(I)= ·Ib | ||
| 3.3.1.3 ДАИ 4 | Операции g(VP1)G вычисления признаков тоновых изображений (V-ДАИ2, P1–ДАИ5) | g1(I)+g2(I)=p1+p2 |
| g1(I)·g2(I)=p1·p2 | ||
| ·g(I)= ·p |
Таблица 5. Специализированные ДАИ1К над параметрическими моделями изображений.
| Класс | Операнды алгебры | Операции алгебры |
| 3.3.2.1 ДАИ 5 |  P1,n-кол-во признаков;  (i=1,…,n);  - номер признака;  -значение признака: 1) , если  ; 2) ,если |  |
 | ||
 | ||
| 3.3.2.2 ДАИ 6 |  (векторы одинаковой длины) |  |
 | ||
 |
Глава четыре посвящена описанию практического приложения ДПАИ и его основных инструментов, в частности ДАИ1К, для решения задачи морфологического анализа клеток крови. На основе теоретического аппарата ДПАИ, специализированных версий ДАИ1К и ДМИ, введенных и описанных в главах 2 и 3, и модели решения задачи распознавания изображений строятся алгоритмические схемы обучения алгоритмов распознавания для задачи анализа цитологических препаратов и классификации нового изображения по трем диагнозам с помощью распознающего алгоритма с настроенными параметрами.
В основу синтеза алгоритмических схем положена следующая математическая модель решения задачи распознавания изображений на основе ДМИ.
Пусть 
- множество исходных изображений (делится на два множества 
-обучающее множество изображений, 
- распознаваемое множество изображений); 
- множество классов (в некоторых случаях - множество классов эквивалентности изображений); 
-множество представлений изображений, используемых для построения моделей 
и 
обучающего и распознаваемого множества исходных изображений соответственно; множество алгоритмов 
решает задачу распознавания изображений, если оно ставит в соответствие множеству исходных изображений множество предикатов 
, где предикат Pj(Ii)=ij принимает следующие значения: ij=1, если изображение Ii принадлежит классу Kj; ij=0, если изображение Ii не принадлежит классу Kj; ij=, если алгоритм А не может установить принадлежность изображения Ii к классу Kj. p0-настроенные параметры после обучения алгоритмов. Тогда математическая модель задачи распознавания имеет следующий вид (схема 7):
В разделе 4.1 сформулирована постановка решаемой практической задачи, которая состоит в автоматизации классификации ядер клеток лимфатической системы по трем диагнозам: злокачественные опухоли (первичная B-клеточная лимфосаркома (ЛС); саркомная трансформация B-клеточного хронического лимфолейкоза (ТХЛЛ)), доброкачественная опухоль (B-клеточный хронический лимфолейкоз (ХЛЛ)). В качестве исходных данных используются 1) микрофотографии отпечатков лимфатических органов больных с 3 диагнозами; 2) контуры указанных экспертами-морфологами диагностически ценных ядер лимфоидных клеток. Решение этой задачи оформлено в виде информационной технологии, математическая модель которой строится в данной главе. Для построения модели используются специализированные ДМИ и ДАИ1К, построенные в главах 2 и 3.
В разделе 4.2 описаны основные шаги информационной технологии; приведены таблицы использования специализированных ДАИ1К и ДМИ, построенных ранее; и построена математическая модель развиваемой информационной технологии морфологического анализа ядер клеток лимфатической системы, основанная на общей модели распознавания изображений (7) и на специализированных ДАИ1К и ДМИ.
В соответствии со схемой (7) математическая модель состоит из трех этапов: этап 1 – приведение изображений к виду удобному для распознавания; этап 2 обучение алгоритма распознания; этап 3 применение настроенного алгоритма распознавания к моделям исходных изображений. Этап 1 содержит 6 шагов: 1.1. получение масок диагностически важных ядер для всех изображений; 1.2. сегментация диагностически важных ядер на всех изображениях; 1.3. сведение исходных цветных изображений к тоновым; 1.4а. вычисление признаков на построенных моделях обучаемого множества; 1.5а. выбор информативных признаков, описывающих изображения обучаемого множества; 1.6b. вычисление признаков на изображениях распознаваемого множества. На этапе 2 и 3 для решения поставленной задачи был выбран класс алгоритмов распознавания, основанных на вычислении оценок. Этап 2 содержит 2 шага: 2.1. шаг построения оценок по обучающему множеству изображений; 2.2. шаг настройки алгоритма распознавания по построенным оценкам и по истинным информационным векторам, задающим принадлежность изображений обучающего множества к некоторому классу изображений. Этап 3 содержит 2 шага: 3.1. шаг построения оценок по распознаваемому множеству изображений; 3.2 шаг распознавания по построенным оценкам. Каждый шаг математической модели представлен следующим образом: 1) описание шага (назначение и обоснование шага); 2) операнды шага (элементы ДАИ1К или ДГИ); 3) операции шага (элементы или операции ДАИ1К или ДГИ); 4) результаты применения операций шага (ДМИ). Буквами «а» и «б» отмечены места, в которых обработка обучающих и распознаваемых изображений отличается.
Математическая модель представлена в виде двух алгоритмических схем (обучение распознающего алгоритма, классификация нового изображения по трем диагнозом с помощью распознающего алгоритма с настроенными параметрами). На рисунках 3 и 4 представлены алгоритмические схемы обучения и распознавания нового изображения соответственно (в качестве распознаваемого изображения выбирается любое из распознаваемого множества исходных изображений). Серые блоки на схемах соответствуют шагам математической модели.
Рис.3. Алгоритмическая схема обучения алгоритмов автоматизированного анализа цитологических препаратов на основе ДМИ и ДАИ1К.
Рис.4. Алгоритмическая схема распознавания цитологических препаратов на основе ДМИ и ДАИ1К.
Представленное приложение, во-первых, представляет технологию в виде хорошо структурированной математической модели и, во-вторых, показывает, как ДАИ1К могут быть использованы в задаче анализа изображений. Описанная прикладная задача была поставлена специалистами Гематологического центра РАН, в который были переданы результаты решения для практического использования.
В Заключении сформулированы основные научные результаты работы, обсуждаются перспективные направления дальнейших теоретических исследований и прикладная ценность результатов
Список основных публикаций по теме диссертации
По результатам диссертации в реферируемых изданиях опубликовано 22 работы, в том числе 7 работ, опубликовано в изданиях, входящих в список рекомендованных ВАК. Основные результаты изложены в следующих работах:
1. I. Gurevich, I. Koryabkina,V. Yashina, H. Niemann, and O. Salvetti. An application of a descriptive image algebra for diagnostic analysis of cytological specimens. An Algebraic Model and Experimental Study // Proceedings of VISAPP 2007 – Second International Conference on Computer Vision Theory and Applications, Barcelona, Spain, March 8-11, 2007. Volume Special Sessions /Edited by A. Ranchordas, H. Araujo, and J. Vitria. - INSTICC Press, 2007. - P.230-237.
2. I. Gurevich, V. Yashina. Conditions of Generating Descriptive Image Algebras by a Set of Image Processing Operations // Progress in Pattern Recognition, Speech and Image Analysis. Proceedings of the 8th Iberoamerican Congress on Pattern Recognition, November 26-29, 2003, Havana, Cuba /A. Sanfeliu, J. Ruiz-Shulcloper (Eds.): CIARP'2003, LNCS 2905. - Springer-Verlag Berlin Heidelberg, 2003. - pp. 498-505.
3. I.B. Gurevich, V.V. Yashina. Descriptive Image Algebras with One Ring // Pattern Recognition and Image Analysis: Advances in Mathematical Theory and Applications, Vol. 13, No.4., 2003. - pp. 579-599.
4. I.B. Gurevich, V.V Yashina. Algorithmic Scheme Based on a Descriptive Image Algebra with One Ring: Image Analysis Example // Pattern Recognition and Image Analysis: Advances in Mathematical Theory and Applications. - MAIK "Nauka/Interperiodica", 2005. – Vol.15, No.1. - P.192-194.
5. I.B. Gurevich, V.V. Yashina. Generating Descriptive Trees // Proceedings of 10th International Fall Workshop on Vision, Modeling, and Visualization.- Infix, 2005.-P. 367-374.
6. I.B. Gurevich, V.V. Yashina. Operations of Descriptive Image Algebras with One Ring // Pattern Recognition and Image Analysis: Advances in Mathematical Theory and Applications. Pleiades Publishing, Inc. 2006. - Vol.16, No.3. - pp. 298-328.
7. I.B. Gurevich and V.V. Yashina. Computer-Aided Image Analysis Based on the Concepts of Invariance and Equivalence // Pattern Recognition and Image Analysis: Advances in Mathematical Theory and Applications. - MAIK "Nauka/Interperiodica"/Pleiades Publishing, Inc., 2006. - Vol.16, No.4. – pp.564-589.
8. I.Gurevich, V.Yashina. Descriptive Analysis of Image Data. Basic Models // Image Mining Theory and Applications: Proceedings of the 1st International Workshop on Image Mining Theory and Applications -IMTA 2008 (in conjunction with VISIGRAPP 2008), Funchal, Madeira, Portugal, January 2008 / Edited by I.Gurevich, H.Niemann, O.Salvetti. - INSTICC PRESS, 2008. - pp. 3-15.
9. I.B. Gurevich and V.V. Yashina. Descriptive Approach to Image Analysis: Image Models // Pattern Recognition and Image Analysis: Advances in Mathematical Theory and Applications. - MAIK "Nauka/Interperiodica"/Pleiades Publishing, Inc., 2008. - Vol.18, No.4. - P. 518-541.
10. I. Gurevich, V.Yashina. Prolegomena toward Algebraic Image Analysis // Image Mining Theory and Applications: Proceedings of the 2nd International Workshop on Image Mining Theory and Applications - IMTA 2009 (in conjunction with VISIGRAPP 2009), Lisboa, Portugal, February 2009 / Edited by I.Gurevich, H.Niemann and O.Salvetti. – Portugal: INSTICC PRESS, 2009. – P.3-8.
11. I. Gurevich, V.Yashina. Image Representation: From Raw Data to Models // Image Mining Theory and Applications: Proceedings of the 2nd International Workshop on Image Mining Theory and Applications - IMTA 2009 (in conjunction with VISIGRAPP 2009), Lisboa, Portugal, February 2009 / Edited by I.Gurevich, H.Niemann and O.Salvetti. – Portugal: INSTICC PRESS, 2009. – P.20-29.
12. I.B. Gurevich, V.V. Yashina, I.V. Koryabkina, H. Niemann, and O. Salvetti. Descriptive Approach to Medical Image Mining. An Algorithmic Scheme for Analysis of Cytological Specimens // Pattern Recognition and Image Analysis: Advances in Mathematical Theory and Applications. - MAIK "Nauka/Interperiodica"/Pleiades Publishing, Inc., 2008. - Vol.18, No.4. - P. 542-562.
13. I.Gurevich, V.Yashina, H.Niemann, O.Salvetti. Medical Image Mining on the Base of Descriptive Image Algebras. Cytological Specimen Case // Proceedings of the - International Conference on Health Informatics - HEALTHINF 2008, Funchal, Madeira, Portugal, 28-31 January, 2008. - INSTICC PRESS, 2008. - Vol. 2. - P.66-73.
Подписано к печати 10.04.2009г.
Тираж 100 экз. Печ. лист. 1. Заказ № 76.
УОП Института этнологии и антропологии РАН
Ленинский проспект, 32А
