Моделирование влияния тепловых воздействий на характеристики микрополосковых антенн
На правах рукописи
МАКСИМОВ Евгений Юрьевич
МОДЕЛИРОВАНИЕ ВЛИЯНИЯ ТЕПЛОВЫХ
ВОЗДЕЙСТВИЙ НА ХАРАКТЕРИСТИКИ
МИКРОПОЛОСКОВЫХ АНТЕНН
Специальность 05.13.18
Математическое моделирование, численные методы
и комплексы программ
А в т о р е ф е р а т
диссертации на соискание ученой степени
кандидата технических наук
ПЕНЗА 2011
Работа выполнена на кафедре «Конструирование и производство радиоаппаратуры» ГОУ ВПО «Пензенский государственный университет».
Научный руководитель доктор технических наук, профессор
Якимов Александр Николаевич.
Официальные оппоненты: доктор технических наук, профессор
Макарычев Петр Петрович;
кандидат технических наук, доцент
Дрождин Владимир Викторович.
Ведущая организация ОАО «Концерн радиостроения «Вега».
Защита диссертации состоится «__»______2011 г., в «__» часов, на заседании диссертационного совета Д 212.186.04 в ГОУ ВПО «Пензенский государственный университет» по адресу: 440026, г. Пенза, ул. Красная, 40.
С диссертацией можно ознакомиться в библиотеке ГОУ ВПО
«Пензенский государственный университет». Автореферат размещен на сайте университета www.pnzgu.ru
Автореферат разослан «___» __________ 2011 года.
Ученый секретарь
диссертационного совета
доктор технических наук,
профессор Смогунов В. В.
ОБЩАЯ ХАРАКТЕРИСТИКА РАБОТЫ
Актуальность темы. В настоящее время перспективным направлением совершенствования антенн сверхвысоких частот (СВЧ), широко используемых в системах с радиоканалами, является их микроминиатюризация на основе малогабаритных линий передачи. Современные микрополосковые антенны (МПА) обеспечивают высокую повторяемость размеров, низкую стоимость, малые металлоемкость, габаритные размеры и массу.
Антенны являются одним из наиболее важных элементов любой приемопередающей аппаратуры, определяя качественные и количественные характеристики передачи информации по радиоканалу. Обычно антенны располагаются в непосредственном соприкосновении с окружающей средой, испытывая механические и тепловые нагрузки. Это неизбежно приводит к деформациям антенного полотна и, как следствие, к отклонению их электрических характеристик относительно расчетных, что влияет на работу всей системы в целом. Особенно критичными являются деформации антенного полотна вследствие тепловых нагрузок. Так, например, радиосистема охраны периметра объектов, оснащенная микрополосковой антенной и подверженная тепловым деформациям, может допустить ложное срабатывание или пропуск нарушителей в охраняемую зону.
Существующие математические модели не позволяют учесть влияние тепловых воздействий на конструкторские и электрические характеристики МПА, поэтому возникает необходимость математического моделирования и оценки влияния таких воздействий еще на этапе проектирования.
В связи с этим актуальной является задача математического моделирования излучения микрополосковых антенн с учетом тепловых воздействий окружающей среды для оптимизации ее конструкции и достижения устойчивости к этим воздействиям с целью повышения надежности эксплуатации этих систем.
Наибольший вклад в решение проблем математического моделирования излучения, рассеяния и распространения электромагнитных волн внесли Л. Д. Бахрах, А. Б. Борзов, Д. И. Воскресенский, В. В. Никольский, Р. В. Островитянов, Ю. Г. Смирнов, А. В. Соколов,
Л. А. Школьный, А. Н. Якимов и другие ученые.
Развитию методов проектирования с учетом внешних воздействий способствовали работы А. А. Самарского, Ю. Х. Вермишева,
Ю. Н. Кофанова, И. Г. Мироненко, И. П. Норенкова, П. И. Осищера,
Е. Н. Талицкого, А. Н. Якимова и др.
Достижения в области вычислительной техники в настоящий момент предоставляют возможность применить методы моделирования, позволяющие создавать адекватные математические модели и анализировать влияние внешних воздействий на характеристики антенн с высокой степенью точности. Существующие вычислительные методы, например конечных элементов и конечных разностей, на основе которых реализованы алгоритмы в известных коммерчески доступных пакетах прикладных программ – HFSS, Microwave Office,
Microwave studio, ANSYS, T-Flex анализ, Solid Works, Рro engineer
и ряд других – адекватны технологиям сегодняшнего дня, однако
не включают математическое моделирование тепловых воздействий
на характеристики излучения микрополосковых антенн.
Целью диссертационной работы является построение и исследование математической модели микрополосковой антенны, учитывающей влияние тепловых воздействий окружающей среды на ее характеристики, для оптимизации конструкции на этапе проектирования.
Для достижения цели необходимо решить следующие взаимосвязанные задачи:
1 Построить электродинамическую модель микрополосковой антенны, позволяющую рассчитать ее характеристики излучения с учетом деформаций антенного полотна.
2 Построить тепловую модель микрополосковой антенны, позволяющую рассчитать ее геометрические характеристики с учетом влияния тепловых воздействий и оценить возникающие при этом деформации антенного полотна.
3 Разработать обобщенную модель, связывающую тепловую и электродинамическую модели и позволяющую оценить влияние тепловых воздействий на характеристики микрополосковой антенны.
4 Разработать алгоритм и методику построения обобщенной математической модели микрополосковой антенны.
5 Разработать компьютерное приложение, позволяющее реализовать предлагаемые математические модели и проектировать микрополосковые антенны с заданными техническими характеристиками с учетом влияния тепловых воздействий.
6 Провести оптимизацию конструкции микрополосковой антенны по критерию минимального влияния тепловых воздействий с использованием разработанного компьютерного приложения.
Объектом исследования является тепловое воздействие окружающей среды на многослойные излучающие структуры произвольной конфигурации.
Предмет исследования – влияние тепловых воздействий на характеристики микрополосковых антенн.
Методы исследования. При проведении исследований использовались положения линейной теории упругости и теплообмена, векторного и функционального анализа, электромагнитных волн, методы математического моделирования, векторной алгебры, оптимизации.
Достоверность научных положений и выводов, содержащихся в работе, основывается на подтверждении адекватности предложенных моделей посредством вычислительного эксперимента и сравнении
с известными моделями, успешной практической апробации решений, полученных на основе теоретических разработок и подтвержденных актами о внедрении.
Научная новизна диссертационной работы заключаются в следующем:
1 Построена электродинамическая модель микрополосковой антенны, отличающаяся дискретным представлением ее излучающих элементов, что позволяет при деформации учесть влияние изменения пространственного положения отдельных фрагментов этих элементов на характеристики излучения МПА.
2 Построена тепловая модель микрополосковой антенны, отличающаяся стержневым представлением параллелепипедных элементов ее дискретизации, позволяющая рассчитать геометрические характеристики с учетом влияния тепловых воздействий и оценить возникающие при этом деформации антенного полотна.
3 Предложены алгоритм и методика построения обобщенной математической модели микрополосковой антенны, связывающей тепловую и электродинамическую модели, отличающиеся реализацией процедуры автоматического многократного целенаправленного преобразования антенного полотна по результатам исследования его напряженно-деформированного состояния, вызванного тепловым воздействием, что позволяет оценить влияние тепловых воздействий на характеристики микрополосковой антенны.
Практическая значимость работы состоит в использовании разработанных моделей, алгоритма, методики, программного комплекса (свидетельство о регистрации электронного ресурса № 16616
от 05.12.2010 г.) и результатов исследования при решении задач проектирования антенных конструкций, устойчивых к тепловым воздействиям, для систем с радиоканалами.
На защиту выносятся:
1 Электродинамическая модель микрополосковой антенны, позволяющая рассчитать характеристики излучения с учетом деформаций антенного полотна.
2 Тепловая модель микрополосковой антенны, позволяющая рассчитать геометрические характеристики с учетом влияния тепловых воздействий и оценить возникающие при этом деформации антенного полотна.
3 Алгоритм и методика построения обобщенной математической модели микрополосковой антенны, связывающей тепловую и электродинамическую модели и позволяющей оценить влияние тепловых воздействий на характеристики микрополосковой антенны.
Реализация и внедрение результатов работы осуществлялись в виде использования в проектно-конструкторской деятель-ности НИКИРЭТ (г. Заречный Пензенской обл.) и ООО «Автопоиск» (г. Пенза).
Результаты исследований использованы также при построении математических моделей для изучения влияния воздействия тепловых нагрузок на микрополосковые антенны в рамках научно-исследовательской работы «Исследование излучения электромагнитных волн с учетом возмущающих воздействий методами математического моделирования», выполняемой на кафедре «Конструирование и производство радиоаппаратуры» ГОУ ВПО «Пензенский государственный университет» по заданию Минобрнауки России, и использованы для проведения вычислительных экспериментов в учебном процессе этой кафедры при подготовке студентов специальности «Проектирование и технология радиоэлектронных средств» по дисциплине «Техническая электродинамика» в разделе «Антенны СВЧ».
Результаты работы подтверждены актами о внедрении.
Апробация работы. Основные результаты диссертационной работы докладывались и обсуждались на Международной научно-технической конференции «Надежность и качество» (г. Пенза, 2008–2010 гг.); научно-практической конференции ИНФО-2010 «Инновации в условиях развития информационно-коммуникационных технологий»
(г. Сочи, 2010 г.); VII Всероссийской научно-технической конференции «Современные охранные технологии и средства обеспечения комплексной безопасности объектов» (г. Заречный, 2010 г.); I Международной научно-практической интернет-конференции «Молодежь. Наука. Инновации» (г. Пенза, 2010 г.); IV Международной научно-технической конференции молодых специалистов, аспирантов и студентов «Математическое и компьютерное моделирование естественно-научных и социальных проблем» (г. Пенза 2010 г.); IV Всероссийской конференции «Радиолокация и связь» (г. Москва, 2010 г.).
Публикации. Основные положения диссертации опубликованы в 18 печатных работах, из них 4 – в рецензируемых журналах, входящих в перечень ВАК РФ. Получено свидетельство о регистрации электронного ресурса.
Структура и объем работы. Диссертационная работа состоит из введения, четырех глав, выводов по главам, заключения, библиографического списка, включающего 103 наименования, и трех приложений. Основная часть изложена на 165 страницах машинописного текста, содержит 47 рисунков и 5 таблиц.
Личный вклад автора. Основные результаты, выносимые на защиту, получены автором лично. Во всех работах, которые выполнены в соавторстве, соискатель непосредственно участвовал в постановке задач, обсуждении методов их решения, разработке программ расчетов, получении и анализе результатов.
ОСНОВНОЕ СОДЕРЖАНИЕ РАБОТЫ
Во введении обоснована актуальность разработки моделей, алгоритмов и методик, позволяющих учесть и минимизировать влияние тепловых воздействий на характеристики микрополосковых антенн еще на этапе их проектирования. Сформулированы цель и задачи исследований, дана общая характеристика работы, показана научная новизна полученных результатов, сформулированы основные положения, выносимые на защиту.
В первой главе рассмотрены проблемы математического моделирования влияния тепловых воздействий на конструкции микрополосковых антенн и характеристики их излучения. Основная сложность задачи заключается в необходимости моделирования многослойной структуры, где каждый слой обладает собственными характеристиками. Традиционные формулы, применяемые для решения задач с однородными материалами здесь не применимы. Проведен анализ методов моделирования физических объектов, позволяющих решить поставленную задачу. Рассмотрена возможность математического моделирования излучения МПА с помощью строгих и приближенных методов.
Микрополосковые антенны обычно имеют множество излучателей, пространственное положение которых изменяется в процессе деформирования. При этом в силу сложности электродинамической задачи ее решение строгими методами не представляется возможным. Для моделирования МПА целесообразно использование приближенных методов. Анализ приближенных методов (геометрической оптики, физической оптики, апертурного, краевых волн, геометрической теории дифракции, Галеркина, дискретизации) показывает, что для приближенного вычисления электромагнитного излучения больших тел сложной формы, к которым можно отнести и деформированные МПА, наиболее подходящим является метод дискретизации, одной из модификаций которого является метод конечных элементов.
Для решения поставленной задачи возможно применение одного из методов моделирования тепловых воздействий на физические объекты конечных разностей, главных компонент, граничных элементов, конечных элементов. В ходе анализа методов выявлено следующее.
Несмотря на широкие возможности метода конечных разностей, его использование совместно с конечно-элементной электродинамической моделью, полученной дискретизацией объекта моделирования, оказывается затруднительным.
Применимость метода главных компонент для решения данной задачи является ограниченной, поскольку он требует значительного упрощения модели, что приводит к потере точности моделирования.
Метод граничных элементов хорошо подходит для решения задач с границей на бесконечности и задач взаимодействия двух сред на границе. Его применение для моделирования МПА затруднительно, так как требует рассмотрения антенного полотна в равной степени как на границах соприкосновения тел, так и внутри конкретного однородного тела, имеющего строгие границы. Данный метод не дает явного представления о возникающих деформациях модели под воздействием тепловых нагрузок.
Метод конечных элементов позволяет моделировать конструкцию практически любой конфигурации и сложности. Результаты моделирования легко совмещаются с входными данными большинства других методов, что позволяет совместить тепловую модель, полученную с помощью данного метода, с электродинамической моделью.
Таким образом, метод конечных элементов оказывается наиболее удобным для совместного исследования тепловых и электродинамических процессов в микрополосковой антенне.
Во второй главе описывается моделирование влияния теплового воздействия на характеристики микрополосковой антенны.
Микрополосковая антенна представляет собой многослойную структуру, состоящую из нескольких плоских прямоугольных излучателей, симметрично расположенных на диэлектрической пластине, с обратной стороны которой – сплошная заземляющая пластина (рисунок 1).
Излучатели такой антенны имеют прямоугольную форму и возбуждаются микрополосковой линией. При тепловых воздействиях из-за разного температурного расширения диэлектрической подложки и металлической пластины исходное излучающее полотно деформируется, а координаты центров излучающих элементов и их пространственная ориентация изменяются.
 |
| Рисунок 1 – Внешний вид микрополосковой антенны |
Основная проблема построения электродинамической модели заключается в необходимости учета возможных искажений как всей излучающей поверхности, так и отдельных излучателей МПА, вследствие ее деформаций. Для учета деформации излучающих площадок предложена их дискретизация на прямоугольные фрагменты, являющиеся элементарными излучателями Гюйгенса. При этом каждый фрагмент излучающей площадки имеет свою пространственную ориентацию, определяемую нормалью 
, привязанной к локальной системе координат (рисунок 2). Поле отдельной излучающей площадки будет определяться суммой полей ее фрагментов.
 |
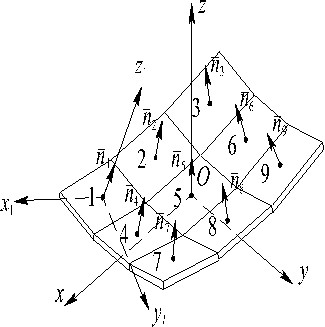| Рисунок 2 – Излучающая площадка под воздействием температурных нагрузок |
Координаты точки наблюдения P, расположенной в дальней зоне излучения МПА, могут быть найдены относительно ее центральной точки, совпадающей с началом системы координат, как
, 
, 
,
где 
– расстояние от центральной точки МПА до точки наблюдения; 
– углы наклона линии, направленной из начала координат в точку наблюдения к осям 
соответственно. Расстояние от центра фрагмента с порядковыми номерами 
до точки наблюдения P определяется выражением
,
где 
, 
и 
– координаты центра фрагмента. Электрическая составляющая поля одного излучателя 
с порядковыми номерами 
будет определяться выражением
,
где 
– напряженность электрического поля в точке P, создаваемая фрагментом с номерами 
; 
– площадь фрагмента; 
– рабочая длина волны антенны; 
– волновое число; 
– порядковые номера фрагментов; 
– число излучателей по осям координат 
.
Общее поле излучения 
в дальней зоне для всей МПА определяется как суперпозиция полей всех ее излучателей:
.
Таким образом, учет кривизны каждого из излучателей МПА позволяет уточнить общее поле МПА при ее деформациях.
Для оценки возможности использования построенной электродинамической модели для учета влияния деформаций излучающей поверхности на характеристики ее излучения решена тестовая задача. Проведено сравнение известного решения электродинамической задачи для цилиндрической формы излучающей поверхности антенной решетки (Воскресенский Д. И., Пономарев Л. И., Филлипов В. С. Выпуклые сканирующие антенны – М. : Сов. радио, 1978. – 304 с.) с результатами расчета при использовании построенной электродинамической модели излучения микрополосковой антенны, приобретающей ту же форму в результате деформации (рисунок 3).
Полученная диаграмма направленности (ДН) цилиндрической решетки (рисунок 3, кривая 1) практически повторяет решение той же задачи, полученное с использованием предложенной модели (рисунок 3, кривая 2). Отклонения по ширине главного лепестка по уровню 0,707 составляют около 2,7 %, а по максимальному уровню бокового лепестка 10 %. Эти результаты позволяют считать математическую модель с разбиением излучающих элементов, используемую для расчета диаграмм направленности микрополосковых антенн, адекватной и применимой для задачи электродинамического моделирования деформируемых МПА.
Рисунок 3 – Диаграммы направленности микрополосковой антенны
при цилиндрической деформации:
1 – рассчитанная по известной формуле для цилиндрической антенны;
2 – рассчитанная с пользованием предложенной модели
Для определения реакции модели на нагрев построена тепловая модель, которая необходима для использования совместно с электродинамической моделью. Тепловая модель МПА получена путем разбиения ее геометрической модели на множество элементов, неразрывно соединенных между собой. Наиболее удобным является применение элемента дискретизации в форме параллелепипеда. Размер каждого ребра элемента дискретизации, прилегающего к излучающей поверхности, должен быть не более половины длины волны рабочего сигнала антенны. В свою очередь, элемент дискретизации заменяется стержнями, соединенными между собой в узлах элемента (рисунок 4). Тепловые коэффициенты линейного расширения и коэффициенты упругости стержней соответствуют тем же коэффициентам моделируемого с помощью элементов дискретизации материала. Стержни не разрушаемы и не оказывают сопротивления при скручивании, но способны растягиваться или сжиматься. Закрепление модели осуществляется в центре заземляющей пластины.
 |
| Рисунок 4 – Силы, воздействующие на стержень, ограниченный узлами 4 и 3, при его нагреве |
Расчет деформаций модели проводится для мгновенного значения тепловой нагрузки. При расчете воздействия переменной во времени тепловой нагрузки требуется дискретизация всего интервала ее воздействия на мгновенные значения, для каждого из которых необходимо решить подобную задачу. При построении тепловой модели МПА, вследствие относительно малого размера антенны, тепловое воздействие считается равномерным. Процессы нагрева стержней, передача тепла по ним и т.п. не оказывают влияния на конечный результат, многократно усложняя расчет. Поэтому делается допущение о том, что все стержни, к которым прикладывается тепловая нагрузка, не передают тепло остальным стержням и нагреваются мгновенно до температуры приложенной нагрузки.
Изменение температуры окружающей среды на 
приводит к изменению линейных размеров стержней и возникновению сил упругости (см. рисунок 4).
В предлагаемой модели в начале расчета при нулевых деформациях в каждом узле 
модели появляются силы упругости 
(на рисунке 4 силы показаны только для узлов 3 и 4), передаваемые стержнем 
. Появление сил упругости в стержне обусловлено разницей длин одного и того же стержня (в результате его расширения или сжатия), находящегося под тепловой нагрузкой и без нее. Длина стержня, находящегося под тепловой нагрузкой, равна
,
где 
– длина стержня 
при отсутствии нагрузки; 
– коэффициент теплового расширения; 
– изменение температуры.
Величина силы упругости стержня 
в узле 
будет равна
,
где 
– коэффициент жесткости стержня 
на растяжение и сжатие. Вектор 
всегда будет параллелен тому стержню, которому он принадлежит. Направление вектора при нагреве будет в сторону увеличения длины стержня, а при охлаждении – в сторону уменьшения.
В каждом узле модели необходимо определить суммарный вектор сил упругости – результирующий вектор. Проекции результирующего вектора на координатные оси определяются как сумма всех соответствующих проекций сил упругости, создаваемых стержнями, соединенными узлом 
:
,
где 
– номер второго узла стержня, начинающегося в 
; 
,
и 
– координаты узла 
. Результирующие векторы сил упругости в каждом узле стержня определяют его вектор узловых усилий 
. Также одной из основных характеристик стержня является его матрица жесткости 
. Она связывает вектор узловых перемещений 
и вектор приложенных к стержню узловых усилий 
соотношением
.
Определив матрицу жесткости стержня 
, можно рассчитать для него вектор узловых перемещений 
. Модель всей конструкции получается алгоритмическим путем. Здесь реализована процедура автоматического многократного целенаправленного преобразования антенного полотна по результатам исследования его напряженно-деформированного состояния, вызванного тепловым воздействием, что позволяет оценить влияние тепловых воздействий на геометрические характеристики микрополосковой антенны. Суть ее заключается в следующем. Для каждого стержня определяем вектор его перемещений 
. Перемещения одного и того же узла от соседних стержней должны совпадать. Сместив стержни в направлении вектора перемещений, получаем новое деформированное состояние модели. Распределение сил в модели изменяется, следовательно, требуется переопределение векторов перемещений 
, по которым стержни снова смещаются. Цикл расчета продолжается до тех пор, пока модель не достигнет равновесия сил упругости (или вектор перемещений 
будет равен нулю).
С использованием построенной тепловой модели был проведен расчет деформации МПА при нагреве на 30 °С относительно исходной температуры, при которой отсутствуют деформации (рисунок 5, кривая 1).
Рисунок 5 – Тепловая деформация модели в ее сечении:
1 – результаты расчета с использованием построенной тепловой модели;
2 – результаты расчета в ANSYS
Для проверки достоверности моделирования тепловая модель МПА (габариты – 1121121,5 мм; материал диэлектрика – фторопласт-4; толщина диэлектрика – 1 мм; толщина заземляющей пластины – 0,5 мм) была построена и рассчитана в пакете ANSYS при нагреве также на 30 °С относительно исходной температуры (см. рисунок 5, кривая 2).
Расхождение в координатах на краях МПА составляет не более 5 %, а на краях центральной площадки – не более 1 %. Отсюда можно сделать вывод, что модель является адекватной и применима для решения поставленной задачи.
Решение задачи о моделировании воздействия тепловой нагрузки на электромагнитные характеристики МПА требует совместного расчета по электродинамической и тепловой модели. В связи с этой необходимостью алгоритмическим путем построена обобщенная модель, связывающая тепловую и электродинамическую модели и позволяющая оценить влияние тепловых воздействий на электромагнитные характеристики микрополосковой антенны. С помощью этой модели можно рассчитывать электродинамические характеристики моделируемой МПА при любом тепловом воздействии. Построение такой модели заключается в совмещении соответствующих узлов электромагнитной и тепловой моделей. При изменении положения узлов тепловой модели узлы электромагнитной автоматически также меняют свое положение, что позволяет получить данные для расчета электромагнитных характеристик МПА, подвергнутой тепловой нагрузке
Важно так построить тепловую и электродинамическую модели, чтобы обеспечить полное совпадение координат площадок Гюйгенса электродинамической модели и излучателей тепловой модели в исходном состоянии (не подвергнутой тепловому воздействию). При верном составлении обобщенной модели координаты узлов в углах излучателей тепловой модели должны совпадать с координатами соответствующих узлов элементов Гюйгенса электродинамической модели при любой тепловой нагрузке. Тогда при расчете ДН по электромагнитной модели учитывается новое пространственное положение узлов тепловой модели, приобретенное в результате воздействия тепловой нагрузки.
С учетом того, что и сама модель МПА и ее излучатели меняют свою форму и пространственное положение при тепловом воздействии, можно сказать, что электромагнитные характеристики будут также отличаться от исходных. На рисунке 6 приведены результаты расчетов с использованием обобщенной модели МПА при исходной температуре и при изменении температуры на 30 °С от исходной.
Здесь наглядно иллюстрируется влияние тепловых нагрузок на ДН МПА. Отклонение ширины главного лепестка на уровне 0,707 при нагреве на 30 °С составляет 8 %, а отклонение уровня боковых лепестков при тех же условиях составляет 30 %. Величина отклонений довольно значительна и требует учета при проектировании МПА.
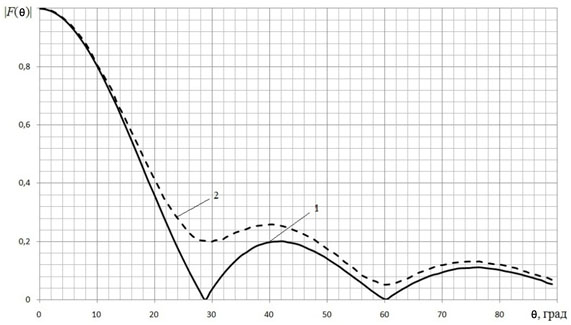
Рисунок 6 – Сравнение диаграммы направленности при исходной
температуре (кривая 1) и при тепловом воздействии (кривая 2)
Таким образом, во второй главе получены следующие результаты:
– построена электродинамическая модель микрополосковой антенны, отличающаяся дискретным представлением ее излучающих элементов, что позволяет при деформации учесть влияние изменения пространственного положения отдельных фрагментов этих элементов на характеристики излучения МПА;
– построена тепловая модель микрополосковой антенны, отличающаяся стержневым представлением параллелепипедных элементов ее дискретизации, позволяющая рассчитать геометрические характеристики с учетом влияния тепловых воздействий и оценить возникающие при этом деформации антенного полотна;
– построена обобщенная модель, связывающая тепловую и электродинамическую модели и позволяющая оценить влияние тепловых воздействий на характеристики микрополосковой антенны.
В третьей главе предложены алгоритм и методика построения обобщенной математической модели микрополосковой антенны, связывающей тепловую и электродинамическую модели, отличающиеся реализацией процедуры автоматического многократного целенаправленного преобразования антенного полотна по результатам исследования его напряженно-деформированного состояния, вызванного тепловым воздействием, что позволяет оценить влияние тепловых воздействий на характеристики микрополосковой антенны. Создан программный комплекс, позволяющий реализовать предлагаемые математические модели и проектировать микрополосковые антенны с заданными техническими характеристиками с учетом влияния тепловых воздействий. Набор управляющих параметров позволяет создать модель микрополосковой антенны с заданными характеристиками. Данные исследования выводятся в графическом виде и хранятся в базах данных.
Пример представления результата расчета ДН микрополосковой антенны приведен на рисунке 7.
Рисунок 7 – Окно вывода результатов
Пример представления результата расчета нагрева тепловой модели приведен на рисунке 8.
Созданный программный комплекс, использующий построенные модели, предложенную методику и алгоритм, расширяет возможности конструктора по оптимизации микрополосковых антенн и позволяет скорректировать любые параметры конструкции еще на этапе проектирования и повысить устойчивость МПА к тепловым воздействиям.
Рисунок 8 – Результат нагрева модели на 30 °С
В четвертой главе проведена оптимизация конструкции микрополосковой антенны по критерию минимального влияния тепловых воздействий на ширину ДН и уровень боковых лепестков с использованием программного комплекса, реализующего предложенные модели, методику и алгоритм. Даны рекомендации по модернизации исследуемых конструкций.
Оптимальные конструкторские решения МПА достигаются в результате изменения управляющих параметров (толщин диэлектрической подложки и заземляющей пластины, их температурных коэффициентов линейного расширения, площади поверхности МПА) по минимальному отклонению уровня боковых лепестков и ширины главного лепестка ДН относительно их состояния без приложения тепловой нагрузки к МПА.
В ходе исследований было выявлено значительное влияние на чувствительность МПА таких параметров, как тепловой коэффициент линейного расширения диэлектрического слоя и толщина заземляющей пластины. Для оптимизации в исходной конструкции МПА были применены следующие изменения. Материал диэлектрика фторопласт-4 был заменен на полистирол ПТ-16, толщина заземляющей пластины уменьшена в 1,42 раза, толщина диэлектрического слоя увеличена в
3 раза. Изменение площади МПА (без изменения излучающей поверхности) оказало минимальное воздействие на ее чувствительность к тепловым нагрузкам и признано неэффективным. Параметры оптимизированной конструкции, полученные при исследовании, являются приемлемыми для большинства конструкций (габариты МПА – 1121123,35 мм; материал диэлектрика – полистирол ПТ-16, тепловой коэффициент линейного расширения которого составляет 
). Диаграмма направленности оптимизированной конструкции микрополосковой антенны, исследованной в данной главе, приведена на рисунке 9.
Рисунок 9 Диаграммы направленности МПА, нагретой на 30 °С,
до оптимизации (1), после оптимизации (2)
и без приложения тепловой нагрузки (3)
Отклонение ширины главного лепестка ДН оптимизированной МПА на уровне 0,707 при нагреве на 30 °С составляет 2 % (см. рису-
нок 9, кривая 2), а отклонение уровня боковых лепестков при тех же условиях составляет 8 %. При сравнении отклонений ДН, нагретой на 30 °С МПА, до оптимизации (см. рисунок 9, кривая 1) и после оптимизации (см. рисунок 9, кривая 2) от ДН МПА без тепловой нагрузки (см. рисунок 9, кривая 1) выявлено, что после оптимизации конструкции МПА отклонения ДН при приложении тепловой нагрузки значительно снизились (отклонение ширины главного лепестка снизилось в 4 раза, а отклонение уровня боковых лепестков в 3,8 раза). Полученные результаты указывают на возможность применения моделей, методики и алгоритма для оптимизации существующих МПА и проектирования новых конструкций МПА, устойчивых к тепловым нагрузкам.
В заключении обобщены результаты работы. Работа нашла практическое применение, что подтверждается актами о внедрении в производственный процесс предприятий НИКИРЭТ и ООО «Автопоиск», в учебный процесс и научные разработки кафедры «Конструирование и производство радиоаппаратуры» ГОУ ВПО «Пензенский государственный университет».
В приложениях приведены тексты программных модулей для моделирования микрополосковых антенн, а также документы, подтверждающие внедрение результатов работы и свидетельство о регистрации программного комплекса.
ОСНОВНЫЕ РЕЗУЛЬТАТЫ И ВЫВОДЫ
1 Проведено исследование методов моделирования физических объектов, позволяющих решить поставленную задачу.
2 Построена электродинамическая модель микрополосковой антенны, отличающаяся дискретным представлением ее излучающих элементов, что позволяет при деформации учесть влияние изменения пространственного положения отдельных фрагментов этих элементов на характеристики излучения МПА.
3 Построена тепловая модель микрополосковой антенны, отличающаяся стержневым представлением параллелепипедных элементов ее дискретизации, позволяющая рассчитать геометрические характеристики с учетом влияния тепловых воздействий и оценить возникающие при этом деформации антенного полотна.
4 Построена обобщенная модель, связывающая тепловую и электродинамическую модели и позволяющая оценить влияние тепловых воздействий на характеристики микрополосковой антенны.
5 Предложены алгоритм и методика построения обобщенной математической модели микрополосковой антенны, связывающей тепловую и электродинамическую модели, и отличающиеся реализацией процедуры автоматического многократного целенаправленного преобразования антенного полотна по результатам исследования его напряженно-деформированного состояния, вызванного тепловым воздействием, что позволяет оценить влияние тепловых воздействий на характеристики микрополосковой антенны.
6 Создано программное приложение на языке программирования Delphi, позволяющее реализовать предлагаемые математические модели и проектировать микрополосковые антенны с заданными техническими характеристиками с учетом влияния тепловых воздействий.
7 Проведена оптимизация конструкции микрополосковой антенны по критерию минимального влияния тепловых воздействий с использованием разработанного компьютерного приложения.
ОСНОВНЫЕ ПУБЛИКАЦИИ ПО ТЕМЕ ДИССЕРТАЦИИ
Публикации в изданиях, рекомендованных ВАК РФ
1. Максимов, Е. Ю. Конечно-элементная модель тепловых воздействий на микрополосковую антенну / Е. Ю. Максимов, А. Н. Якимов // Известия высших учебных заведений. Поволжский регион. Технические науки. – Пенза, 2010. – № 3 (15). – С. 103–113.
2. Максимов, Е. Ю. Методика построения матрицы жесткости конструкции микрополосковой антенны / Е. Ю. Максимов // Известия высших учебных заведений. Поволжский регион. Технические науки. – Пенза, 2010. – № 4 (16). – С. 81–88.
3. Максимов, Е. Ю. Конечно-элементная модель тепловых воздействий на микрополосковую антенну / Е. Ю. Максимов, Н. К. Юрков,
А. Н. Якимов // Измерительная техника. – 2011. – № 2. – С. 65–68.
4. Максимов, Е. Ю. Стержневая модель микрополосковой антенны /
Е. Ю. Максимов, А. Н. Якимов // Новые промышленные технологии. – Пенза, 2010. – № 6. – С. 37–39.
Публикации в других изданиях
5. Максимов, Е. Ю. Моделирование влияния тепловых воздействий на характеристики излучения микрополосковой антенны / Е. Ю. Максимов,
А. Н. Якимов // Надежность и качество : тр. междунар. симп. Т. 1. – Пенза : Информационно-издательский центр ПГУ, 2007. – С. 276–278.
6. Максимов, Е. Ю. Оценка влияния изгиба микрополоскового излучателя на его диаграмму направленности / Е. Ю. Максимов, А. Н. Якимов // Надежность и качество : тр. междунар. симп. Т. 2. – Пенза : Информационно-издательский центр ПГУ, 2008. – С. 160–162.
7. Максимов, Е. Ю. Оценка влияния температурных деформаций на излучение микрополосковой антенны / Е. Ю. Максимов, А. Н. Якимов // Современные охранные технологии и средства обеспечения комплексной безопасности объектов: материалы 7-й Всерос. НТК (Россия, Пенза–Заречный, 7–8 октября 2008 г.). – Пенза : Информационно-издательский центр ПГУ, 2008. – С. 141–144.
8. Максимов, Е. Ю. Оценка влияния тепловых воздействий на излучение микрополосковой антенны / Е. Ю. Максимов, О. Н. Балуков // Цифровые модели в проектировании и производстве РЭС : межвуз. сб. науч. тр. – Пенза : Изд-во ПГУ, 2009. – № 14. – С. 144–150.
9. Максимов, Е. Ю. Оценка влияния изгиба микрополоскового излучателя на его диаграмму направленности / Е. Ю. Максимов, А. Н. Якимов // Цифровые модели в проектировании и производстве РЭС : межвуз. сб. науч. тр. – Пенза : Изд-во ПГУ, 2009. – С. 114–119.
10. Максимов, Е. Ю. Конечно-элементная модель микрополосковой антенны / Е. Ю. Максимов, А. Н. Якимов // Надежность и качество : тр. междунар. симп. Т. 2. – Пенза : Изд-во ПГУ, 2009. – С. 180–184.
11. Балуков, О. Н. Влияние шага дискретизации линейной антенны на ее излучение / О. Н. Балуков, Д. А. Куликов, Е. Ю. Максимов // Цифровые модели в проектировании и производстве РЭС : межвуз. сб. науч. тр. – Пенза : Изд-во ПГУ, 2009. – №. 14. – С. 217–226.
12. Максимов, Е. Ю. Математическая модель теплового воздействия на микрополосковую антенну / Е. Ю. Максимов, А. Н. Якимов // Надежность и качество : тр. междунар. симп. Т. 1. – Пенза : Изд-во ПГУ, 2010. – С. 386–388.
13. Максимов, Е. Ю. Тепловая модель микрополосковой антенны /
Е. Ю. Максимов, А. Н. Якимов // Цифровые модели в проектировании и производстве РЭС : межвуз. сб. науч. тр. ; под ред. Н. К. Юркова. – Пенза : Изд-во ПГУ, 2010. – С. 101–107.
14. Максимов, Е. Ю. Построение матрицы жесткости для модели микрополосковой антенны // Цифровые модели в проектировании и производстве РЭС : межвуз. сб. науч. тр. ; под ред. Н. К. Юркова. – Пенза : Изд-во ПГУ, 2010. – С. 118–123.
15. Максимов, Е. Ю. Моделирование тепловых воздействий на микрополосковую антенну / Е. Ю. Максимов, А. Н. Якимов, Н. К. Юрков // Молодежь. Наука. Инновации : тр. I Междунар. науч.-практ. интернет-конференции. – Пенза : Изд-во Пензенского филиала РГУИТП, 2010. – С. 231–233.
16. Максимов, Е. Ю. Оценка влияния температурных деформаций на излучение микрополосковой антенны / Е. Ю. Максимов, А. Н. Якимов // Современные охранные технологии и средства обеспечения комплексной безопасности объектов : материалы VIII Всерос. науч.-техн. конф. (Россия, Пенза–Заречный, 6–8 октября 2010 г.). – Пенза : Изд-во ПГУ, 2010. –
С. 144–149.
17. Максимов, Е. Ю. Стержневая модель тепловых воздействий на микрополосковую антенну / Е. Ю. Максимов, Н. К. Юрков, А. Н. Якимов // Инновации в условиях развития информационно-коммуникационных технологий : материалы науч.-практ. конф. ИНФО-2010. (Сочи, 1–10 октября 2010). – М. : МИЭМ, 2010. – С. 432–435.
18. Максимов, Е. Ю. Модель микрополосковой антенны с возможностью учета тепловых нагрузок / Е. Ю. Максимов, А. Н. Якимов, В. В. Смогунов, И. В. Астафьев // Радиолокация и радиосвязь : докл. IV Всерос. конф. (Москва, 29 ноября – 3 декабря 2010 г.). Т. 2. – М. : Изд-во ИРЭ РАН, 2010. – С. 76–79.
Научное издание
МАКСИМОВ Евгений Юрьевич
МОДЕЛИРОВАНИЕ ВЛИЯНИЯ ТЕПЛОВЫХ
ВОЗДЕЙСТВИЙ НА ХАРАКТЕРИСТИКИ МИКРОПОЛОСКОВЫХ АНТЕНН
Специальность 05.13.18 Математическое моделирование,
численные методы и комплексы программ
Подписано в печать 26.05.11.
Формат 60841/16. Усл. печ. л. 1,16.
Тираж 100. Заказ № 403.
Издательство ПГУ.
440026, Пенза, Красная, 40.
Тел./факс: (8412) 56-47-33; e-mail: [email protected]
