Математическое моделирование паразитных электромагнитных эффектов в электронных модулях
На правах рукописи
Конников Игорь Аркадьевич
Математическое моделирование
паразитных электромагнитных эффектов
в электронных модулях
05.13.18 - математическое моделирование,
численные методы и комплексы программ
АВТОРЕФЕРАТ
диссертации на соискание учёной степени
доктора технических наук
Санкт-Петербург
2009
Работа выполнена на кафедре компьютерной математики и программирования Государственного образовательного учреждения высшего профессионального образования “Санкт-Петербургский государственный университет аэрокосмического приборостроения”
Научный консультант: Заслуженный деятель науки, доктор
технических наук, профессор Хименко Виталий Иванович
Официальные оппоненты: доктор технических наук, профессор
Анисимов Владимир Иванович
доктор физико-математических наук, профессор
Фарафонов Виктор Георгиевич
доктор технических наук, профессор Фоминич Эдуард Николаевич
Ведущая организация: Закрытое Акционерное Общество “НИТИ “Авангард””
Защита состоится “_____” _____________ 2009 года в ____ ч. ____ мин.
на заседании диссертационного совета Д212.233.02 при Государственном образовательном учреждении высшего профессионального образования “Санкт-Петербургский государственный университет аэрокосмического приборостроения” по адресу: 190000, Санкт-Петербург, ул. Большая Морская, д. 67.
С диссертацией можно ознакомиться в библиотеке Государственного образовательного учреждения высшего профессионального образования “Санкт-Петербургский государственный университет аэрокосмического приборостроения”
Автореферат разослан “___” _______________________ 2009 года.
Учёный секретарь
диссертационногосовета Осипов Л. А.
Общая характеристика работы
Введение. Актуальность работы. Основные тенденции развития современной электронно-вычислительной и радиоэлектронной аппаратуры (повышение быстродействия и степени её интеграции) приводят к усилению влияния конструктивно-технологической реализации на её выходные электрические характеристики. Среди конструктивно-технологических факторов на первое место неумолимо выходят паразитные электромагнитные эффекты, т.е. эффекты, физическая природа которых обусловлена электромагнитным полем, и которые, не будучи предусмотрены принципиальной электрической схемой, являются причиной паразитных наводок, а также задержек, отражений, искажений формы и затуханий сигналов, несущих полезную информацию. Именно такие эффекты в последнее время становятся доминирующей причиной несоответствия выходных электрических характеристик изготовленного конструктива значениям, которые прогнозируются его разработчиком по результатам моделирования с помощью принципиальной схемы. Учёт паразитных электромагнитных эффектов при разработке электронных модулей - сложная наукоёмкая проблема, требующая соответствующего научно-методического обеспечения как в процессе проектирования, так и на стадии предпроектных исследований. По оценкам специалистов, в ближайшие годы до 90% печатных плат будет создаваться для цифровых систем повышенного быстродействия и в дальнейшем проблема будет приобретать всё большую значимость. Поэтому можно полагать, что названные выше тенденции развития современной электроники обуславливают постоянную актуальность разработки и внедрения всё более эффективных методов решения этой проблемы. Имеется настоятельная необходимость повышения размерности задач моделирования, решение которых возможно широко доступными вычислительными средствами. Необходимы новые математические методы, модели и алгоритмы, ориентированные на снижение затрат машинного времени при моделировании конструктивов и одновременно обеспечивающие достаточно высокую точность.
Подход к решению проблемы давно известен. Единственная реальная возможность успешного решения проблемы имеется на пути комплексной автоматизации основных этапов разработки электронных модулей средствами вычислительной техники. Основная идея заклю-чается в том, чтобы по завершении процесса размещения элементов и трассировки цепей в автоматическом режиме переработать информацию о принципиальной электрической схеме и морфологии трасс, реализующих эту схему, в эквивалентную электрическую схему с учётом паразитных электромагнитных эффектов и затем рассчитать выходные электрические характеристики разрабатываемого устройства, нормируемые техническим заданием. Для этого необходимо сначала сформировать математическую модель, позволяющую смоделировать паразитные электромагнитные эффекты, и pассчитать значения параметров этой модели. Главный недостаток такого подхода слишком большая размерность математических моделей, описывающих указанные эффекты, неадекватная возможностям широко доступных вычислительных средств; модели, имеющие достаточно малую размерность, не обеспечивают приемлемой точности. Тем не менее, реализация этого подхода подтвердила на практике его принципиальную эффективность и перспективность; именно на него ориентированы последние разработки крупнейших зарубежных компаний (Mentor Graphics, Quantic EMC, Sigrity, Cadence, Simberian, Zuken и др.).
Предмет исследования и цель работы. Предметом исследования являются паразитные электромагнитные эффекты в коммуникаторе электронного модуля. В качестве физической модели объекта исследования принята слоистая диэлектрическая среда с плоскопараллельными границами раздела слоёв. Как правило, такая модель адекватна электронным модулям нулевого и первого уровней.
Данная работа направлена на решение важной научно-технической проблемы разработку и исследование новых математических методов моделирования паразитных электромагнитных эффектов в электронных модулях и, прежде всего, методов моделирования задержки сигналов, несущих полезную информацию, и методов моделирования взаимных помех сигнальных цепей. Моделирование остальных паразитных электромагнитных эффектов может осуществляться с помощью уже известного математического обеспечения, необходимость их учёта в этом случае не приводит к столь значительному повышению размерности математической модели проектируемого устройства.
В более детальном рассмотрении целью исследования является создание формализованных методов решения комплекса задач модели-рования паразитных электромагнитных эффектов в коммуникаторе электронного модуля и, прежде всего, разработка необходимых матема-тических моделей и аналитических методов их построения (точных и приближённых), ориентированных на использование вычислительной техники, а также методов расчёта параметров этих моделей, в частности:
разработка аналитических методов вычисления поля единичного элементарного источника (т.е. функции Грина) в квази-стационарном приближении, которые могут служить основой для получения математических моделей и методов оценки паразитных электромагнитных эффектов в коммуникаторе;
получение аналитических выражений для параметров математи-
ческих моделей (индуктивностей и емкостей) планарных проводников и резисторов с учётом их размеров и распределения заряда/тока по их объёму, а также конструкции модуля в целом;
разработка математических моделей для оценки задержек и паразитных электромагнитных связей в коммуникаторе и методов построения этих моделей, а также применение разработанных математических моделей для схемотехнического моделирования.
Разработанные решения ориентированы на достижение возможно большей размерности решаемых задач с максимальным использованием аналитических методов, реализуемых заранее при разработке математического обеспечения, в отличие от ориентации на численные методы, предполагающие проведение основного, причём гораздо большего, объёма вычислений в процессе моделирования.
Методы исследования. При решении поставленных задач использованы методы математической физики и электродинамики, теории электрических цепей (прежде всего метод Элмора), вычислительной математики, теории специальных функций, натурный и вычислительный эксперимент.
Положения, выносимые на защиту. Получены лично автором и выносятся на публичную защиту следующие научные результаты, составляющие новизну диссертации:
математическая модель конструкции электронного модуля, предназначенная для использования при расчёте паразитных реактивностей и оценке внутренней электромагнитной совместимости конструктива, и приближённые аналитические методы представления указанной модели, позволяющий снизить её размерность для заданной точности;
приближённые аналитические методы вычисления функции Грина для уравнения Лапласа;
приближённые аналитические методы расчёта параметров математической модели проектируемого модуля паразитных емкостей и индуктивностей проводников и резисторов в слоистой среде на основе аналитических выражений, полученных кратным интегрированием функции Грина, причём первообразные соответствующих четырёхкратных интегралов получены впервые. Аналитическое решение задачи расчёта реактивностей проводников в слоистой среде, вектор тока в которых перпендикулярен плоскостям слоёв коммутации, получено впервые. Предельные значения погрешностей приближения бесконечно тонкого проводника и метода средних геометрических расстояний получены впервые. Аналитический метод двусторонней оценки реактивностей при неизвестном произвольном (в том числе меняющемся) распределении заряда/тока предлагается впервые;
приближённый аналитический метод эквивалентной постоян-ной распространения и математические модели для расчёта электро-магнитного поля в слоистой среде и оценки паразитных электромаг-нитных связей (оценки внутренней электромагнитной совместимости) на основе представленного в виде интеграла Зоммерфельда решения волнового уравнения, в том числе в системе неортогонального монтажа, без пространственной дискретизации на мелкой сетке;
метод трансформации математических моделей, не допус-кающих непосредственную схемотехническую реализацию, в математические модели, ориентированные на схемотехническое моделирование объектов радиоэлектроники и во временной, и в частотной областях. В отличие от известных, предложенный метод позволяет получать универсальные математические модели нового класса, обладающие уникальным свойством точным воспроиз-ведением характеристик переходного процесса, в том числе времени задержки (по Элмору), с возможностью одновременного удовлетворения требований к модели по точности в частотной области (причём не только на постоянном токе, т.е. на частоте = 0);
математические модели беспроводных каналов паразитной связи (горизонтального и вертикального) и канала связи, имеющего проводник. Указанные модели, полученные с помощью предложенного в диссертации метода, в схемотехнической интерпретации обеспечивают, в отличие от известных, точное воспроизведение времени задержки при высокой точности моделирования длительности фронта.
Научная новизна. В совокупности полученные научные результаты позволяют проводить оценку влияния паразитных электромагнитных эффектов в электронных модулях на качественно новом современном научно-техническом уровне, для которого характерны, прежде всего,
использование прямых расчётов электромагнитного поля помехи вместо взаимных емкостей и индуктивностей для получения эквивалентных схем при анализе внутренней электромагнитной совместимости, что ведёт к повышению адекватности математической модели модуля и снижению размерности этой модели;
возможность точного воспроизведения характеристик переходного процесса в коммуникаторе при анализе работы электронного модуля во временной области, что ведёт к повышению адекватности его математической модели;
возможность ориентации на научно-исследовательские и проектные задачи существенно большей, чем прежде, размерности задач за счёт использования математических моделей меньшей размерности при достижении высокой точности, а также использования
более быстрых методов расчёта параметров этих моделей.
Важной особенностью разработанных методов моделирования является то, что они, в отличие от известных, сочетают строгость электродинамической постановки задачи и простоту (малую размерность) получаемых моделей.
Достоверность результатов. Обоснованность и достоверность выносимых на защиту научных положений, выводов и рекомендаций обусловлены и подтверждаются корректностью математического обоснования проведённых исследований и системным подходом к решению задач; результатами натурных и вычислительных экспериментов, согласованностью с известными решениями; комплексной оценкой достоверности при разработке промышленных образцов микроэлектронной аппаратуры и при включении в отраслевые стандарты (акты внедрения прилагаются); апробацией при обсуждении на научно-технических конференциях, симпозиумах и семинарах.
Практическая реализация. В целом для решения актуальной задачи повышения эффективности и качества разработки электронных модулей разработаны научные основы для создания программного обеспечения, с помощью которого реализуется учёт ПЭМЭ при разработке электронных модулей; разработано и внедрено в эксплуатацию программное обеспечение, вошедшее в состав программных продуктов "Рапира 5.3", "ПРАМ 5.3", "Микро 001", "Микро-2005", "TopoR" и “Микро 2008”; разработаны раздел "Определение паразитных реактивных связей в микросборках (машинный и ручной расчёт)" отраслевого стандарта ОСТ4 ГО.010.214 и раздел "Микросборки. Общие требования и нормы конструирования" отраслевого стандарта ОСТ 107.460.084.200-88.
Результаты теоретических исследований, рекомендации по их практическому применению и разработанное на их основе программное обеспечение (в том числе отдельные программы, работающие в автономном режиме) использованы при проведении научно-исследовательских и опытно-конструкторских работ в ЗАО «НИТИ «Авангард» (Санкт-Петербург), в ООО "Эремекс" (Санкт-Петербург), в АНО «Научно-консультационный центр «Аллюр» (Рязань), а также получили внедрение в учебный процесс в Государственном университете аэрокосмического приборостроения (Санкт-Петербург). Практическое внедрение подтверждается соответствующими актами.
Публикации. По материалам диссертации опубликованы 75 печат-ных работ (из них 4 в соавторстве), в том числе 28 статей (из них 1 в соавторстве) опубликованы в изданиях, которые входят в перечень, рекомендованный ВАК РФ для докторских диссертаций по исследуемой проблеме.
Структура и объём работы. Работа состоит из введения, четырёх глав, заключения, оглавления и списка литературы, включающего 184 наименования. Объём работы 378 л., где представлены 40 рисунков и 11 таблиц.
Содержание работы
В первой главе расмотрены методы математического моделирования поля элементарного источника в слоистой среде.
При моделировании ПЭМЭ в электронном модуле в качестве физической модели реального пространства, где рассчитывается поле, принимается слоистая среда, состоящая из произвольного числа плоскопараллельных слоёв, неограниченных в азимутальном направлении. Такая структура, как правило, адекватна конструкции электронных модулей нулевого и/или первого уровня, реже конструкции модулей более высоких уровней. Каждый слой характеризуется своей толщиной и физическими характеристиками; слои считаются гомогенными, изотропными и непроводящими. Первый и/или последний слой может быть ограничен идеально проводящей плоскостью, моделирующей наличие металлического корпуса или экрана. Физические процессы в модели считаются квазистационарными. Потенциал электрического поля во всех точках такой модели (кроме точки, где расположен единичный точечный заряд) описывается уравнением Лапласа 
и граничными условиями. Если считать, что слои расположены перпендикулярно оси аппликат, то в случае задач с осевой симметрией решение уравнения Лапласа для потенциала единичного элементарного источника поля в ?-ом слое модели (т.е. функция Грина в слоистой среде), как известно, даётся формулой
G = 
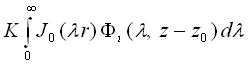, (1)
где K коэффициент, зависящий от физической природы поля: 
при расчёте электростатического потенциала (константа Кулона) и 
при решении магнитостатической задачи (константа Био-Савара); 
, 
абсолютные диэлектрическая и магнитная проницаемости свободного пространства; 
функция Бесселя первого рода нулевого порядка; 
x0, y0, z0 абсцисса, ордината и аппликата точки, где вычисляется поле; x, y, z абсцисса, ордината и аппликата элементарного источника поля. Функция 
определяется из граничных условий для потенциала и поэтому зависит от физической природы поля.
Множество функций (), для всех коммутационных слоёв является тем формальным математическим объектом, который содержит информацию о слоистой структуре физической модели моделируемого конструктива, необходимую и достаточную для расчёта реактивностей проводников. Указанный объект целесообразно использовать в качестве математической модели конструкции моделируемого модуля при расчёте паразитных реактивностей проводников. Эта математическая модель не содержит информации о морфологии и размерах трасс подложки или платы, которая, строго говоря, не является информацией о конструкции модуля в целом. Параметрами такой математической модели будут диэлектрические проницаемости, магнитные проницаемости и толщины слоёв физической модели.
Традиционный метод вычисления функции Грина (1) основан на аппроксимации функции () по степеням переменной u=exp(??) и использовании тождества Вебера-Липшица
(? ¦ 0),
в результате чего функция Грина приводится к виду:
, (2)
где 
, Т
коэффициенты аппроксимации.
Как показали исследования, традиционная методика имеет значительный резерв повышения точности, в публикациях не отмеченный (по сведениям автора). Оказалось, что при заданном значении старшей степени аппроксимирующего многочлена весьма существенное влияние на точность аппроксимации функции () оказывает выбор масштабирующего множителя ?, значение которого предлагается оптимизировать по критерию минимума максимальной абсолютной погрешности аппроксимации функции (). Предлагаемый метод по сравнению с традиционным позволяет достичь значительно более высокой точности, особенно на расстояниях r>1.50. От традиционного метода предлагаемый отличается использованием характеристического размера 0 в качестве масштабирующего множителя (метод экспресс-оценки значения ?=0 предлагается) и улучшенной аппроксимацией математической модели конструкции аппроксимацией в базисе функций Чебышева первого рода, причём такой, чтобы на краях интервала аппроксимации погрешность отсутствовала.
Другой предложенный метод решает задачу вычисления функции Грина без применения аппроксимации полиномами. Для этого выражение (1) представляется в виде суммы:
G = K (I1 + I2),
где I1 =
; I2=
;
произвольный предел интегрирования, выбираемый из условия
. (3)
Учитывая монотонный характер изменения функции (), условие (3) может быть выполнено с любой требуемой степенью точности. Выразив интеграл через первообразную, получим, что
I2 
,
где ( r) =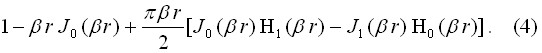 
В выражении (4) J функция Бесселя первого рода -го порядка; функция Струве -го порядка; = 0, 1.
()
1
0.75
0.5
0.25
0
-0.25
-0.5
0 5 10 15 20
Рисунок 1. -функция
Тета-функция (r) с точностью до множителя 
моделирует ошибку, возникающую при замене в выражении для функции Грина (1) верхнего предела интеграла с бесконечного на конечный; множитель 
учитывает специфику конкрет-ной задачи. Как показывает вычисли-тельный эксперимент, функция () имеет колебательный характер и квазипериодична, причём при увеличении аргумента амплитуда колебаний постепенно уменьшается, на бесконечности функция обращается в нуль, а период колебаний стремится к 2. Тета-функция представлена на рис.1, где введено обозначение =r. Первые нули тета-функции (
) и её производные 
(
) протабулированы.
Определяемый для наибольшего расстояния[1] rmax ближайший больший нуль тета-функции ¦rmax даёт величину произведения minrmax, обладающего следующим свойством: для всех расстояний rџrmax может быть взят один и тот же нуль тета-функции, т.к. он соответствует значению предела =/r¦min, а заведомо обеспечивает соотношение (2) и всегда обеспечивает равенство I2=0 при заданной относительной погрешности. Тогда
G(r) = К
. (5)
Равенство (5) в математическом аспекте является практически точным. Вычисление интеграла с конечными пределами в (5) не представляет особых трудностей при численном интегрировании. Учитывая возможность разбиения интервала интегрирования на шаги, значение функции Грина может быть рассчитано с любой требуемой точностью, которая ограничена на практике лишь особенностями языка программирования и техническими возможностями компьютера. Это позволяет полученное с помощью формулы (5) значение условно считать точным (в пределах физических допущений, принятых при математической формализации задачи). Появляется возможность в случае приближённого вычисления функции Грина исходить из требу-емой погрешности вычисления поля в слоистой среде, контролируя эту погрешность, и не ограничиваться контролем точности промежуточных результатов или эвристическим обоснованием точности вычисления функции Грина. Это позволяет использовать метод для разработки новых приближённых вычислительных методов и контроля их точности. В частности, предлагается методика вычисления функции Грина, основанная на аппроксимации её части, не имеющей особенностей, в базисе функций Чебышева первого рода по чётным степеням расстояния r, которая ориентирована на последующее интегрирование функции Грина по координатам и позволяет получать простые аналитические выражения для реактивностей проводников.
Таким образом, исследован традиционный метод вычисления функции Грина, ориентированный на использовании тождества Вебера-Липшица, а также разработаны приближённые аналитические методы для слоистой среды, один из которых основан на использовании предложенной в диссертации специальной функции (тета-функции) и позволяет получать сколь угодно малую погрешность вычисления (т.е. является практически точным), а два других позволяют снизить объём вычислений по сравнению с традиционным методом, особенно на малых расстояниях, характерных для микроэлектроники. Выявлена область предпочтительного использования каждого из методов.
Во второй главе на основе результатов, полученных в первой главе, получены аналитические выражения для потенциальных коэффи-циентов и индуктивностей проводников с учётом закона распределения заряда/тока, размеров проводников и формы их поперечного сечения. Pазработанные в диссертации методы расчёта реактивностей получены на основе развития подхода В. И. Семенцова, в работах которого был совершён прорыв к инженерному решению задачи.
Так например, выражения для потенциального коэффициента а получены кратным интегрированием функции Грина (2) с весом, равным плотности поперечного распределения заряда:
где коэффициент 
; 
плотность заряда вдоль осей аппликат, ординат и абсцисс соответственно; z аппликата -ой границы раздела слоёв модели, где расположен проводник (аппликата того слоя коммутации, для которого рассчитывается ёмкость); l, b, t длина, ширина и толщина проводника, соответственно.
Это значение можно представить состоящим из двух слагаемых:
a = a0 + a,
где a0 потенциальный коэффициент проводника в свободном пространстве; 
поправка, позволяющая учесть влияние слоистой среды.
При равномерном распределении заряда по объёму проводника плотность распределения заряда
Тогда, выразив интеграл через первообразную, получим, что потенциальный коэффициент проводника в свободном пространстве:
a0=
где 
; 
; 
;
s = 
exp (3/2) среднее геометрическое расстояние отрезка прямой, который имеет длину t, от самого себя.
Для тонких проводников (s ^ ) поправка a от толщины провод-ника не зависит; выразив интеграл через первообразную, получим:
,
где 
=; Т
коэффициенты аппроксимации математической модели среды для электростатической задачи. Аппроксимация проводится в базисе функций Чебышева первого рода по предложенной методике так, чтобы обеспечить отсутствие погрешности на краях интервала аппроксимации.
С помощью выражения (5) часть функции Грина, не имеющая особенностей (поправка на слоистость среды), может быть аппроксими-рована в базисе функций Чебышева первого рода по чётным степеням переменной r. Тогда, найдя первообразную четырёхкратного интеграла, с учётом формулы Ньютона для возведения бинома в целую степень получим, что выражение для потенциального коэффициента а можно представить в виде:
+
,
где 
;
k=l/b коэффициент формы проводника (отношение длины проводника к его ширине); D коэффициенты аппроксимации.
Выявлены области предпочтительного использования полученных формул. Аналогично получены аналитические выражения для потенциальных коэффициентов и индуктивностей проводников при равномерном, квадратичном и предельно неравномерном (описываемом импульсной функцией Дирака) законах распределения.
Как известно, распределение заряда/тока по объёму проводника в значительной мере определяется формой его поперечного сечения и потенциалами соседних проводников и может существенно меняться в процессе работы схемы. Это принципиально отличает токоведущие проводники от уединённых пластин известной правильной формы при расчёте реактивностей. Относительное расхождение результатов расчёта ёмкости С при различных распределениях заряда в сравнении с ёмкостью при равномерном распределении для проводника с коэффициентом формы k в однородной среде представлено на рис.2. Неравномерность N оценивалась отношением плотности заряда на кромке проводника к плотности на его осевой линии. На рис.2 кривая 1 соответствует распределению, описываемому d-функцией Дирака; 2 квадратичному распределению, N=Ґ; 3 квадратичному распределению, N = 10; 4 квадратичному распределению, N = 4; 5 квадратичному распределению, N = 2; штрих-пунктирная линия экспоненци-альному распределению для неравно-мерности N=1000.
1 101 102 103 k=l/b
Рисунок 2
Аналогичное исследование было проведено для оценки влияния неравномерности распределения тока на индуктивность (см. рис.3). На рис.3 кривая 1 соответствует квадратичному распределению, N=3; 2 квадратичному распределению, N = 7.77; 3 квадратичному распреде-лению, N=; 4 экспоненциальному распределению, N = 1000; 5 распределению, описываемому 
-функцией Дирака.
,%
30
20
10
1
2
3
4
5
0
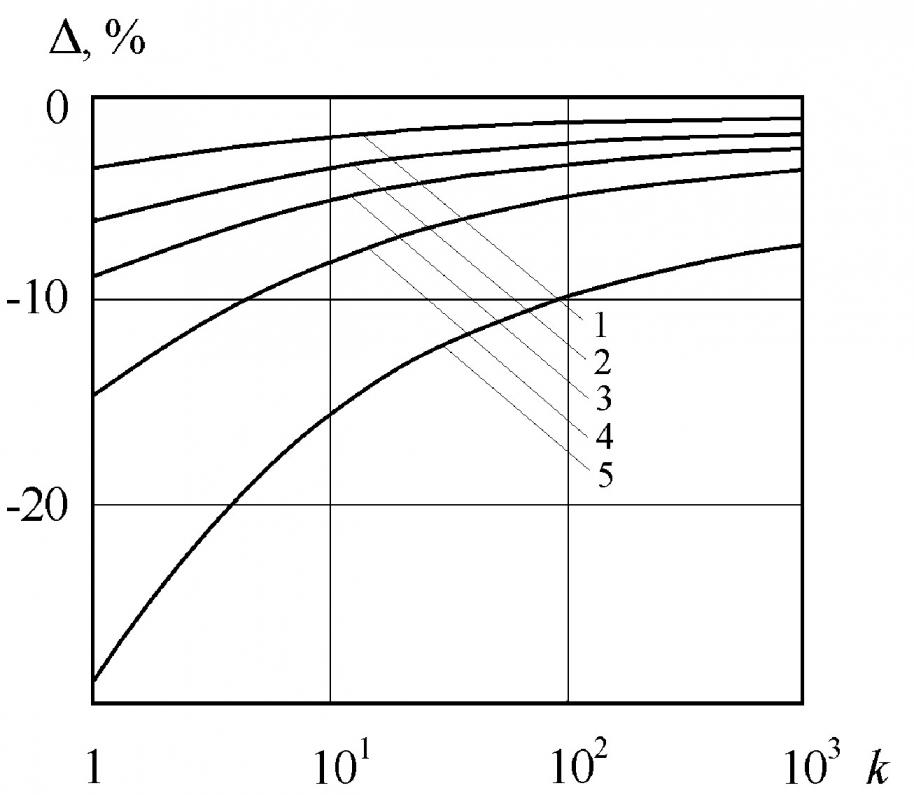
Рисунок 3
В результате исследований получены аналитические выраже-ния для количественной оценки границ, в которых меняется реактивность токоведущего прямоугольного плёночного проводника в однородной и слоистой средах при изменении распределения заряда и тока по ширине от равномерного до предельно неравномерного, в том числе при
неизвестном распределении, обусловленном суперпозицией любых факторов, формирующих это распределение; для высокоомных проводников (резисторов) найдены границы, в которых изменяется ёмкость резистора в процессе функционирования электронного модуля при предельно возможном изменении распределения заряда вдоль вектора тока, которое обусловлено изменением модуля эквивалентного сопротивления нагрузки от 0 до, а также получена формула для индуктивности проводника круглого сечения в слоистой среде:
],
где l длина проводника, r его радиус; 
коэффициенты аппрокси-мации математической модели среды для магнитостатической задачи, аппроксимация проводится в базисе функций Чебышева первого рода.
Оценка точности расчёта паразитных реактивностей проводилась двумя способами: сравнением с результатами натурного эксперимента и сравнением с результатами, полученными по известным методикам. Для повышения степени достоверности сделанных выводов результаты натурных экспериментов обрабатывались при помощи методов математической статистики.
В результате проведённых теоретических исследований, дополненных натурными и вычислительными экспериментами с использованием разработанных математических моделей, получены сле-
дующие частные научные результаты:
1. Получено аналитическое решение задачи расчёта реактивностей проводников прямоугольного сечения в слоистой среде, позволяющее проводить двухстороннюю оценку значения реактивности при известном (квадратичном или экспоненциальном) и неизвестном меняющемся распределении заряда и тока с учётом влияния конструкции модуля; получены экономичные формулы для реактивностей проводника круглого сечения в слоистой среде; указана область предпочтительного использования полученных формул. Рассмотрено вычисление матрицы емкостей низкоомных и высокоомных проводников (резисторов). Формулы для расчёта реактивностей проводников в слоистой среде, вектор тока в которых перпендикулярен плоскостям слоёв коммутации, получены впервые (по сведениям автора).
2. Установлено, что с увеличением неравномерности распределе-ния заряда/тока по сечению проводника его ёмкость растёт монотонно, а индуктивность монотонно уменьшается.
3. Доказано, что в однородном пространстве для проводника с коэффициентом формы k
1 максимально возможное увеличение ёмкости из-за неравномерности распределения заряда по ширине имеет место для квадратного проводника (при k = 1) и составляет 1/3.
5. Доказано, что в однородном пространстве для проводника с коэффициентом формы k
1 максимально возможное уменьшение индуктивности из-за неравномерности распределения тока по ширине имеет место для квадратного проводника (при k = 1) и составляет 1/4.
6. Установлено, что допущение о равномерной по ширине плот-ности тока и заряда может обеспечить умеренную погрешность расчёта реактивности лишь для проводников с большим коэффициентом формы в отсутствие полей, создаваемых соседними проводниками, и может быть принято для оценки точной нижней границы ёмкости и точной верхней границы индуктивности. для оценки точной верхней границы ёмкости и точной нижней границы индуктивности при неизвестном произвольном распределении тока и заряда должны использоваться формулы, при выводе которых распределение полагалось максимально неравномерным и описывалось функцией Дирака.
7. Доказано, что в слоистой среде, как и в однородном пространстве, реактивность проводника прямоугольной формы с предельно асимметричным распределением заряда равна реактивности с симметричным предельно неравномерным распределением.
8. Получено аналитическое решение задачи расчёта ёмкости резистора с произвольным коэффициентом формы в слоистой среде и найдены границы, в которых изменяется его ёмкость при предельно возможном изменении распределения заряда вдоль вектора тока.
9. Предложена приближённая кубатурная формула, основанная на интерпретации максвелловского метода средних геометрических расстояний и ориентированная на использование как при расчёте емкостей и индуктивностей, так и при решении аналогичных задач; исследована погрешность формулы и показано, что она обладает высокой точностью практически во всём диапазоне изменения размеров и формы токоведущих проводников за исключением, возможно, перемычек межслойной коммутации (в наиболее неблагоприятном случае куба относительная погрешность формулы составляет 7.16%).
10. Исследованы погрешность приближения бесконечно тонкого проводника и погрешность метода средних геометрических расстояний, выявлена область корректного использования каждого из названных приближений, установлены предельные значения их погрешностей.
11. Установлено, что при необходимости снизить время расчёта реактивностей целесообразно ориентироваться на совместное использование приближённых методов: приближения бесконечно тонкого эквипотенциального проводника или метода средних геометрических расстояний совместно с приближением бесконечно большой неравномерности распределения заряда/тока.
Анализ и обобщение результатов натурного и вычислительного экспериментов показывают, что предложенные приёмы расчёта паразитных емкостей и индуктивностей, формирующие в совокупности метод вычисления, значительно более экономичны по сравнению с методами, требующими пространственной дискретизации на мелкой сетке (методами конечных элементов, моментов и т.д.), практически не уступая этим методам в точности.
В качестве примера применения разработанных методов приведён расчёт комплексного сопротивления вертикального заземляющего вывода; полученные формулы имеют самостоятельное прикладное значение.
В третьей главе разработаны математические методы и модели для оценки паразитных электромагнитных связей в коммуникаторе (системе коммутационных проводников) электронного модуля. Указанные методы и модели основаны на электродинамическом подходе (а именно на решении волнового уравнения для поляризационного потенциала электромагнитного поля элементарного излучателя в слоистой среде), в то время как традиционные методы оценки через паразитные ёмкости и индуктивности учитывают только статическую составляющую поля и приводят к математическим моделям коммуникатора большой размерности, а известные методы, учитывающие все составляющие поля, требуют непомерно больших затрат машинного времени. В частности, в главе 3 предложен и разработан метод эквивалентной постоянной распространения, исследованы варианты его реализации, точностные характеристики и область корректного использования при оценке электромагнитного взаимовлияния элементов коммуникатора. Суть предлагаемого метода можно изложить на примере горизонтального канала беспроводной (паразитной) электромагнитной связи. Под горизонтальным каналом понимается такой, в котором токи источника и рецептора протекают параллельно плоским границам раздела слоёв принятой выше физической модели конструкции. Этот случай является наиболее важным, поскольку в силу конструктивно-технологичеких особенностей модулей нулевого и первого уровней большая часть токов коммуникатора протекает параллельно границам раздела слоёв модели.
Поляризационный потенциал (вектор Герца) электромагнитного поля, создаваемого в -ом слое 
горизонтальным элементом тока (элементарным диполем), имеет две компоненты, вертикальную и горизонтальную. Рассмотрим горизонтальную компоненту, которая, как известно, описывается интегралом Зоммерфельда. Этот интеграл является решением волнового уравнения для вектора Герца:
, (6)
где 
функция Бесселя первого рода нулевого порядка; функция 
математическая модель слоистой среды, определяемая на частоте из граничных условий для поляризационного потенциала; r радиус в цилиндрической системе координат; z0 и z аппликаты элементарного источника излучения и точки, где вычисляется поле, соответственно; 
амплитудный множитель; параметр разделения; 
dх0 и I длина и ток элементарного диполя; 
абсолютная диэлектрическая проницаемость -го слоя; круговая частота; =3.14159...; интегралы вида (6) традиционно именуются интегралами Зоммерфельда. Такой интеграл является практически точной макроскопической математической моделью электромагнитного поля в слоистой среде.
Поле в слоистой среде можно рассчитать, представив исходную математическую модель (6) с помощью простейшего тождественного преобразования в виде легко вычисляемой главной составляющей и части, вычисляемой приближённо:
,
где 
главная составляющая поляризационного потенциала электромагнитного поля диполя, второе слагаемое поправка;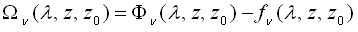 
разностная математическая модель среды; 
определяется аналогично 
для физической модели среды, которая соответствует главной составляющей.
Первое слагаемое (главная составляющая поляризационного потенциала) описывает поле у плоской границы раздела двух полупространств или другую легко вычисляемую часть поля в слоистой среде, известную из классических работ.
Сущность предлагаемого подхода использование интеграла Зоммерфельда в качестве исходной математической модели физических процессов, представление этой модели в виде суммы главной составляющей (cвободной от интегралов и поэтому легко вычисляемой) и поправки и вычисление интеграла (поправки) с помощью эквивалентной постоянной распространения kэ, которая показывает, как изменяется набег фазы в рассматриваемой слоистой среде по сравне-нию со свободным пространством. В принятых выше обозначениях локальная постоянная распространения
,
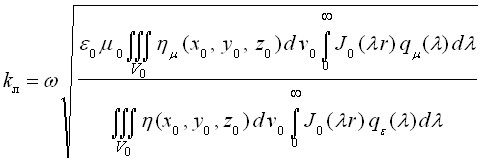где 
и q() разностные математические модели той же среды, для которой получена динамическая модель, полученные при решении электростатической и магнитостатической задач; V0 объём проводника источника помехи. Эквивалентная постоянная распространения находится усреднением локальной по длине и высоте (толщине) канала связи. При этом поле поправки описывается выражением того же вида, который используется для однородной среды, но вместо постоянной распространения однородной среды используется постоянная kэ:
.
Тогда распространение электромагнитной энергии моделируется с помощью динамической модели и лишь один параметр kэ этой модели, который учитывает влияние не прилегающих к границе раздела слоёв, рассчитывается в квазистатике. Такое приближение достаточно кор-ректно, если расстояние между границами раздела крайних слоёв, фор-мирующих учитываемую при анализе среду, много меньше длины волны, т.к. в этом случае |kR|<<1 (k постоянная распространения волны в среде, R расстояние между источником поля и точкой, где вычисляется поле) и превалирует статическая составляющая напряжён-ности поля, обратно пропорциональная кубу расстояния R. В электро-нике (особенно в микроэлектронике) вплоть до диапазона сантиметро-вых волн и субнаносекундных длительностей импульсов толщины учи-тываемых при анализе слоёв много меньше длин волн гармонических составляющих сигнала, учитываемых при анализе. Таким образом, попе-речные размеры структур электроники, как правило, удовлетворяют указанному ограничению и лежат в области корректного использования предлагаемого метода. Функции Грина для электростатической и магнитостатической задач вычисляются по изложенной в главе 1 методике, разработанной на основе решения уравнения Лапласа. При таком подходе необходимость интегрирования по переменной в комплексной области отпадает и требуемые вычисления кардинально упрощаются. В этом основная идея предлагаемого метода.
Разработана методика расчёта kэ и рассмотрена реализация метода эквивалентной постоянной распространения для горизонтального и вертикального каналов связи и для магнитного диполя (горизонтального витка бесконечно малых размеров); получены математические модели (аналитические выражения) для скалярного потенциала электромагнитного поля в горизонтальном и вертикальном каналах связи, несущие информацию о времени задержки и длительности фронта переходного процесса в канале; дан пример использования методики.
Область корректного использования метода эквивалентной постоянной распространения можно оценить с помощью сравнения результатов, полученных названным методом, с результатами, которые базируются на известных строгих аналитических решениях. Теоретически доказано, что на постоянном токе метод даёт точные значения поля; следовательно, наибольшей точностью метод обладает в области нижних (не значит низких) частот. Как показал вычислительный эксперимент, рабочие частоты метода могут составлять единицы и даже десятки гигагерц. Теоретически доказано, что для вертикального диполя в свободном полупространстве над идеально проводящей плоскостью метод даёт точные значения как векторного, так и скалярного потенциалов поля на любой частоте. Более информативен случай горизонтального диполя на плоской границе немагнитных гомогенных изотропных полупространств, для которого также известно строгое решение. Именно через поле горизонтального диполя вычисляются помехи в коммуникаторе микросхем и печатных плат. Для такой структуры проведён вычислительный эксперимент. Анализ и обобщение результатов эксперимента позволяют сделать следующие выводы. Относительные погрешности моделирования модуля и фазы вектор-потенциала отрицательны (т.е. их значения завышены). Относительная погрешность моделирования модуля от нулевого значения на постоянном токе монотонно возрастает по абсолютной величине с увеличением частоты, но погрешность моделирования-фазы почти не меняется вплоть до частоты, при которой обеспечивается набег фазы- 
.- До указанной частоты эта погрешность составляет единицы процентов и при дальнейшем увеличении частоты происходит её быстрое увеличение по абсолютной величине, поэтому по частотному диапазону рабочую область метода эквивалентной постоянной распространения целесообразно ограничить частотой, при которой ошибка моделирования модуля не превосходит уровня 8-10%, который как раз соответствует набегу фазы 
. Получена формула для оценки снизу верхней граничной частоты рабочей области метода:
,
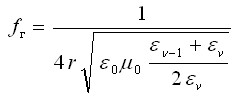Рисунок 4
и по этой формуле построены зависимости (рис.4), из которых видно, что при -1=1 рабочая область метода покрывает практически весь диапазон частот и параметров немагнитных материалов печатных плат и, тем более, микросхем и микросборок различного функционального назначения (за исключением, возможно, имеющих особую специфику СВЧ конструктивов) и включает предназначенные для вычислительной техники импульсные схемы осваиваемого ныне субнаносекундного диапазона.
Предложен способ использования компенсирующей поправки, основанный на учёте совокупного влияния (т.е. на эффекте взаимо-компенсации погрешностей) принятых при расчёте kэ аппроксимаций, который заметно повышает точность метода и расширяет его рабочую область. Как показал вычислительный эксперимент, добиваться высокой точности при вычислении kэ в данном случае нецелесообразно. Наоборот, оказалось целесообразным несколько "загрубить" вычисление kэ (например, снизив порядок формулы численного интегрирования) таким образом, чтобы выбранный способ вычислений давал стабильную ошибку до 4-6%, занижающую значение kэ. Эта ошибка, компенсируя погрешность метода, может рассматриваться как некая компенсирующая поправка, целью введения которой является не просто повышение точности расчётов, а прежде всего снижение времени счёта при одновременном повышении точности или незначительном её понижении. Как правило, зная знак погрешности и используя различные методы понижения времени счёта, указанного повышения точности удаётся добиться. Кроме того, результаты вычислительного эксперимента позволяют сделать вывод о том, что метод устойчив к технологическому разбросу значений параметров.
Предлагаемый метод эквивалентной постоянной распространения приводит к математическим моделям, которые занимают промежуточное положение среди известных: они уступают моделям, основанным на строго динамическом подходе и пространственной дискретизации, по широкополосности, значительно превосходя их по экономичности (требуемому расходу машинного времени и требуемой ёмкости оперативной памяти), а с другой стороны, они значительно превосходят модели, использующие взаимные ёмкости и индуктивности, как по экономичности, так и по широкополосности, позволяя учесть все составляющие поля, а не только статическую, и таким образом более адекватно описывают физические процессы в коммуникаторе. Однако, эти модели не всегда допускают схемотехническую интерпретацию.
В четвёртой главе разработан метод получения математических моделей нового класса, которые допускают схемотехническую интерпретацию и, в отличие от известных моделей, позволяют точно (по Элмору) смоделировать характеристики переходного процесса, обладая высокой точностью также и в частотной области. В основе метода лежит результат Элмора, который дал физическую трактовку моментам импульсной характеристики четырёхполюсника и, в частности, указал, что абсолютная величина первого момента импульсной характеристики четырёхполюсника имеет физический смысл времени задержки переходного процесса; с тех пор метод Элмора широко используется для оценки параметров переходного процесса. Метод Элмора нередко называют также и методом моментов; он был предложен для оценки параметров переходного процесса в широкополосных усилителях, которые рассматривались как четырёхполюсники с сосредоточенными параметрами; С. Я. Шац распространил метод моментов на электрически короткие объекты с распределёнными параметрами, в частности на транзисторы. Проведённые исследования позволяют распространить область корректного использования метода моментов на электрически длинные объекты, в том числе на проводники (линии с распределёнными параметрами). Предлагаемый метод даёт возможность получать универсальные (т.е. ориентированные на использование и в частотной, и во временной областях) схемотехнические модели нового класса, обладающие уникальным свойством точным воспроизведением характеристик переходного процесса, в том числе времени задержки (по Элмору), с возможностью одновременного использования известных методов непосредственной минимизации ошибки моделирования в частотной области. В то же время известные автору универсальные модели, предлагаемые другими специалистами, обычно основаны на аппроксимации характеристик моделируемого объекта в частотной области, что позволяет при синтезе модели судить о предполагаемой точности моделирования во временной области только косвенно, эвристически; убедиться же, насколько верны были эти предположения, можно лишь по получении модели на основании прямого вычислительного эксперимента.
Предлагаемый метод трансформации математических моделей, не допускающих непосредственную схемотехническую реализацию, позволяет при синтезе модели исходить прежде всего из требуемой точности моделирования во временной области; требования к точности моделирования в частотной области также учитываются.
Техника метода заключается в следующем. Для определения параметров математической модели n-го порядка (n1) и параметров соответствующего моделирующего четырёхполюсника надо получить с помощью исходной математической модели выражение для нормиро-ванного коэффициента передачи и потребовать равенства первых n+1 членов разложения коэффициента передачи моделируемого объекта в ряд Маклорена по степеням частоты соответствующим членам разложения коэффициента передачи моделирующего четырёхполюсника (при этом для получения указанных первых n+1 членов ряда для коэффициента передачи нередко оказывается необходимым учитывать большее число членов ряда Маклорена для поля). При необходимости повысить точность моделирования в частотной области при получении моделей n-го порядка (n>1) дополнительно накладывается условие равенства коэффициентов передачи на какой-либо частоте или условие минимизации ошибки на интервале. Полученные уравнения решаются относительно значений па-раметров эквивалентной схемы, обеспечивающих указанные равенства. Эти значения позволяют точно (по Элмору) смоделировать характерис-тики переходного процесса, в том числе время задержки в канале электромагнитной связи, с учётом всех составлющих поля, включая поле излучения, с точностью, определяемой принятой степенью квазистацио-нарного приближения. Метод прост, приводит к простым эквивалентным схемам и имеет широкую область применения. В диссертации метод использован для получения математи-ческих моделей и соответствующих им эквивалентных схем проводного и беспроводного каналов связи.
Беспроводной канал, как верти-кальный, так и горизонтальный, образо-ванный прямолинейными проводниками в непроводящей слоистой среде, модели-руется с помощью пары П-образных четырёхполюсников (рис. 5), подключаемых между концами проводников. Проводной канал связи моделируется с помощью П-образного четырёхполюсника, (рис. 6).
Получены формулы для расчёта параметров схемных элементов для каждого случая. Эти значения параметров позволяют точно (по Элмору) смоделировать время задержки переходного процесса в канале электромагнитной связи. Так для проводного канала значения коэффи-циентов пересчёта физических характеристик линии (полных распределённых активного сопротивления R, активной проводимости утечки G, ёмкости C и индуктивности L) в параметры её эквива-лентной схемы (рис. 6) рассчитываются по следующим формулам:
Рисунок 6
Для часто встречающегося на практике случая |G(p) | << | pC |, когда можно пренебречь активной проводимостью утечки, аналитические выражения для коэффициентов пересчёта упрощаются:
a=1; 
e=0.5; 
n=1 + 1/(6Q2); 
m=0.5.
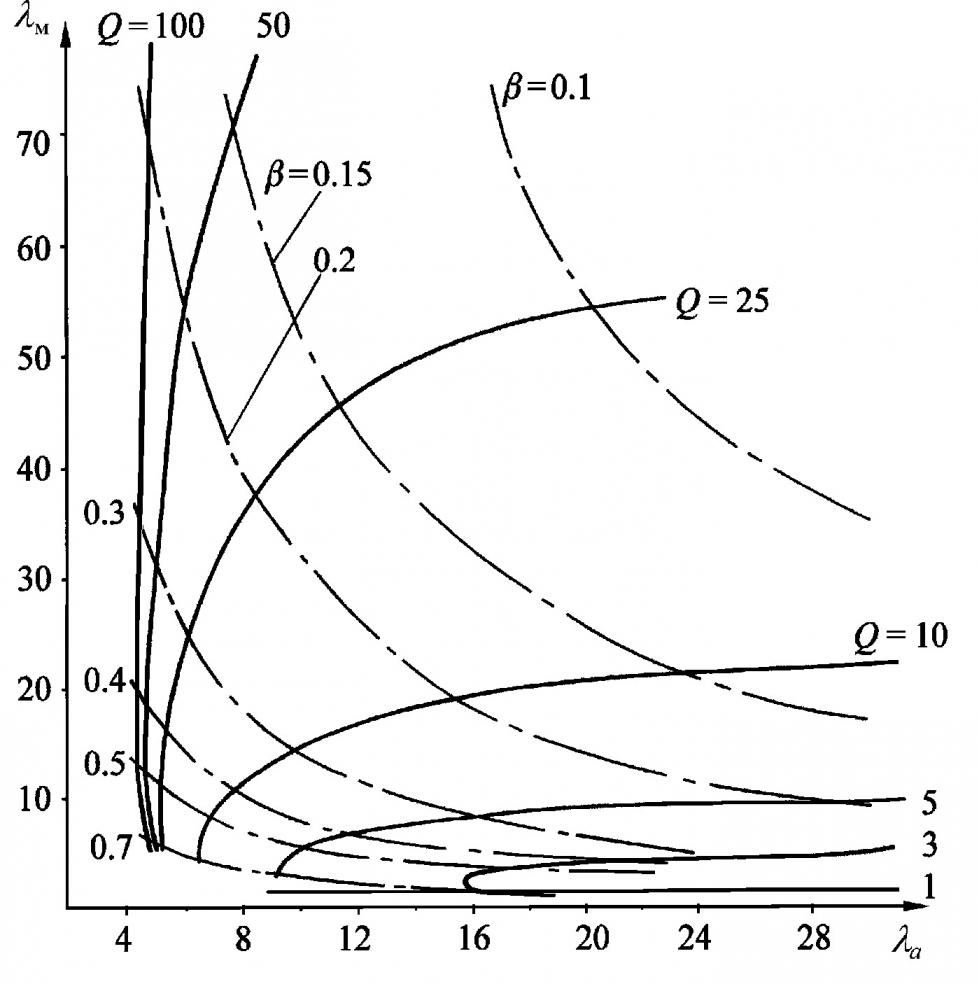
На примере схемы проводного канала (рис.6) показано, что метод приводит к получению математических моделей, в значительной степени отвечающих противоречивым требованиям высокой точности и малой размерности как в частотной области, так и во временной. Результаты сравнительного исследования П-образной схемы (рис. 6) и широко принятой цепочечной схемы из
Рисунок 7
одинаковых Г-образных звеньев для случая согласованной нагрузки (Zн=Z) и G=0 приведены на рисунке 7. Здесь по оси абсцисс отложено эквивалентное количество звеньев а, из которых должна состоять цепочечная схема, обеспечивающая такое же, как у П-образной схемы, расхождение с результатами моделирования аргумента на основе уравнения Гельмгольца, по оси ординат эквивалентное количество звеньев м для модуля входного сопротивления. Значения а и м получены численным методом с абсолютной погрешностью не хуже 0.05. Следует, однако, учитывать, что физический смысл имеют лишь целочисленные значения а и м. Сплошные линии – линии фиксированной добротности Q; штрих-пунктирные линии – линии фиксированного коэффициента фазы 
.
Полученные эквивалентные схемы проводного и беспроводного каналов связи в широком диапазоне частот обеспечивают выигрыш не менее чем на десятичный порядок по количеству элементов в сравнении с известными цепочечными схемами при точном воспроизведении времени задержки переходного процесса (чего цепочечные схемы не обеспечивают) и высокой точности моделирования длительности фронта, причём нередко длительность фронта также воспроизводится точно.
Для снижения размерности математической модели модуля в целом предлагается метод её редукции за счёт отказа от учёта второстепенных ПЭМЭ. Разбраковка ПЭМЭ на существенные и несущественные должна производиться автоматически с учётом особенностей моделируемого устройства, что влечёт за собой необходимость использования формализованных критериев отбраковки. Редукция математической модели обычно является двухступенчатой. Предварительная редукция проводится на основании ранжирования цепей схемы. Для цепей первой группы (первого ранга) необходимо учитывать все паразитные параметры, для цепей второй группы только собственные индуктивности, ёмкости и активные сопротивления; в третью группу выделяются цепи, где паразитные электромагнитные эффекты не учитываются. Определить ранги цепей можно, например, следующим образом. К первой группе можно условно отнести наиболее ответственные сигнальные цепи, ко второй остальные сигнальные цепи и цепи подачи напряжения питания постоянного тока, проволочные перемычки и выводы навесных элементов с учётом сопротивлений контактов, к третьей группе все прочие цепи (цепи термокомпенсации, цепи ручной регулировки усиления и др.). Система ранжирования должна быть гибкой с тем, чтобы ранжирование можно было проводить, исходя из размерности решаемой задачи и возможностей используемого технического обеспечения, поэтому при необходимости можно разбить цепи на большее или меньшее число групп.
Дальнейшая отбраковка паразитных параметров проводников должна производиться по их радиусу зоны электромагнитного влияния (РЗЭВ). Для получения значения РЗЭВ необходимо приравнять полученное в работе (и соответствующее моделируемой конструкции) выражение для коэффициента передачи канала паразитной связи его допустимому значению и решить одним из известных численных методов полученное трансцендентное уравнение на верхней граничной частоте спектра полезного сигнала; решением уравнения будет искомый РЗЭВ. Для сигналов с неограниченным спектром находится эффективная граничная частота, как это принято в радиотехнике. Решение проводится для трёх значений длины проводников, имеющихся на плате, и по ним определяются коэффициенты степенного многочлена второй степени, аппроксимирующего зависимость РЗЭВ от длины проводника; с помощью этого многочлена результат решения корректируется для каждого проводника конкретной длины. Допустимый коэффициент передачи является величиной, обратной требуемому коэффициенту переходного затухания помехи, значение которого разработчик схемы может назначать обоснованно и квалифицированно, учитывая особенности функционирования разрабатываемого устройства. Описанная двухступенчатая отбраковка во многих случаях позволяет значительно понизить размерность математической модели (разумеется, в ущерб её точности); однако, эта размерность может всё ещё оставаться слишком большой.
После описанной редукциии нередко требуется адаптация мате-
матической модели устройства к возможностям технического обеспечения (к ресурсам машинного времени и оперативной памяти). Адаптация проводится за счёт отбраковки дополнительных элементов схемы, отражающих влияние тех ПЭМЭ, которые, как правило, наименее существенно влияют на нормируемые выходные электрические характеристики (отказ от учёта наименьших задержек и наиболее слабых паразитных связей), поэтому очевидно, что указанная адаптация проводится в ущерб точности моделирования. Строго говоря, критическими могут оказаться любые пути сигналов, длинные и короткие, а также как сильные, так и слабые связи. Тем не менее, основанием для проведения адаптации может явиться тот факт, что разработчик часто оказывается перед выбором: использовать упрощённую математическую модель, сознательно не учитывая часть информации о проектируемом устройстве, либо, в лучшем случае, решить лишь часть задачи, получив промежуточные результаты, состав и ценность которых будут определяться отведёнными ресурсами времени.
Оценить время счёта, рассчитав число необходимых вычислитель-ных операций (пример такого расчёта имеется), можно не всегда и не для всех методов интегрирования системы дифференциальных уравнений, описывающих состояние схемы, и тогда предпочтительно использовать регрессионную модель, параметры которой определяются по результатам предыдущих сеансов моделирования схем данного класса. Параметрами такой модели могут быть число узлов, суммарное количество элементов, количество реактивностей, средняя связность, число обусловленности системы дифференциальных уравнений, описывающих состояние схемы, и т.д.
Предлагаемые решения в значительной степени отвечают противоречивым требованиям по размерности моделей, их точности и универсальности. Как показывает вычислительный эксперимент, предлагаемые математические модели и методы обеспечивают приблизительно ту же точность моделирования фронта и амплитуды помехи, что основанные на строго динамическом подходе и требующие пространственной дискретизации на мелкой сетке (например, основанные на методе FDTD), но значительно (на 2-3 десятичных порядка) превосходят их по быстродействию, хотя и уступают им по точности моделирования второстепенных параметров переходного процесса, в частности по точности моделирования мелких осцилляций.
Апробация работы. Материалы диссертации докладывались, обсуждались и были одобрены на научно-технических конференциях, симпозиумах и семинарах, основные из которых следующие:
63-я научно-техническая конференция научно-технического общества радиотехники, электроники и связи им. А. С. Попова (Санкт-Петербург, апрель 2008 г.); научная сессия Государственного университета аэрокосмического приборостроения (Санкт-Петербург, 10-14 апреля 2008 г.); 7-й Международный симпозиум по электромагнитной совместимости и электромагнитной экологии (Санкт-Петербург, 26-29 июня 2007 г.); третья международная научно-практическая конференция "Исследование, разработка и применение высоких технологий в промышленности". (Санкт-Петербург, 14-17 марта 2007); 62-я научно-техническая конференция научно-технического общества радиотехники, электроники и связи им. А. С. Попова (Санкт-Петербург, апрель 2007 г.); научная сессия Государственного университета аэрокосмического приборостроения (Санкт-Петербург, 9-13 апреля 2007 г.); межвузовская конференция по научному программному обеспечению “Практика применения научного программного обеспечения в образовании и исследованиях” (Санкт-Петербург, 5-7 февраля 2007 г.); XXXVI научная и учебно-методическая конференция профессорско-преподавательского и научного состава Университета информационных технологий, механики и оптики (С.-Петербург, 30 января - 2 февраля 2007 г.); девятая Российская научно-техническая конференция по электромагнитной совместимости технических средств и электромагнитной безопасности (Санкт-Петербург, 20-22 сентября 2006 г.); Х Международная научная конференция “Решетневские чтения” (Красноярск, 8-10 ноября 2006 г.); научная сессия Государственного университета аэрокосмического приборостроения (Санкт-Петербург, 10-14 апреля 2006 г.); семинар “Прогрессивные методы конструирования и гибкое автоматизированное производство микроэлектронной аппаратуры” в Московском доме научно-технической пропаганды (Москва, 1986 г.); семинар “Автомати-зация проектирования электронной аппаратуры” в Республиканском доме экономической и научно-технической пропаганды (Севастополь, 28-30 октября 1980 г.); конференция ”Автоматизация конструкторского проектирования РЭА и ЭВА” в Пензенском доме научно-технической пропаганды (Пенза, 26-28 сентября 1979 г.); VII научно-техническая конференция “Технология и машинное проектирование изделий электронной техники” (Москва, 23-24 мая 1979 г.); 33-я научно-техническая конференция профессорско-преподавательского состава Ленинградского института авиационного приборостроения (Ленинград, 2-4 января 1979 г.); семинар “Машинные методы проектирования электронно-вычислительной аппаратуры” в Ленинградском доме научно-технической пропаганды (Ленинград, 1979 г.); XXXIX научно-техническая конференция по узловым проблемам радиотехники, электроники и связи научно-технического общества радиотехники, электроники и связи им. Попова (Ленинград, 8-12 апреля 1974 г.) и др.
Публикации. Выносимые на публичную защиту научные результаты опубликованы в 75 печатных работах (из них 4 в соав-торстве), 28 из которых (1 в соавторстве) опубликованы в изданиях, которые входят в перечень, рекомендованный ВАК РФ для докторских диссертаций по исследуемой проблеме (пп. 1 - 28 следующего перечня):
1. Конников, И. А. Схемотехническое моделирование линии с распределёнными параметрами // И.А. Конников / Электричество. 2009. №3. С. 50-53.
2. Конников, И. А. Плёночный проводник как источник электромагнит-ного излучения // И. А. Конников / Вестник МЭИ. 2009. №1. С. 163-170.
3. Конников, И. А. Метод расчёта поля излучателя в слоистой среде // И. А. Конников / Радиотехника и электроника. 2008. №1. C. 70 - 72.
4. Конников, И. А. Вычисление поля вертикального источника в слоистой среде // И. А. Конников / Инженерная физика. 2008. №2. C.11 - 14.
5. Конников, И. А. Расчёт взаимных помех выводов микросхемы // И. А. Конников / Вопросы радиоэлектроники. Cер. ОТ. 2008. Bып. 1. C. 58 - 73.
6. Конников, И. А. Моделирование электромагнитных наводок в САПР электронных модулей // И. А. Конников / Вестник МГТУ им.Н.Э.Баумана. Cер.Приборостроение. 2007. №4(69). C. 3 - 20.
7. Конников, И. А. Вычислениe параметров переходного процесса в канале электромагнитной связи // И. А. Конников / Электромагнитные волны и электронные системы. 2007. № 11. C. 52 - 60.
8. Конников, И. А. Вычисление квазистационарного поля в слоистой среде // И. А. Конников / Журнал технической физики. 2007. № 4. C. 138 - 140.
9. Конников, И. А. Ёмкость прямоугольной плёнки в слоистой среде // И. А. Конников / Судостроение. 2007. № 4. C. 57 - 59.
10. Конников, И. А. Использование САПР для математического моделирования электромагнитного поля // И. А. Конников / Известия вузов. Cep. Приборостроение. 2007. № 7. C. 57 - 62.
11. Конников, И. А. Моделирование паразитных электромагнитных эффектов при автоматизированном проектировании электронных модулей // И. А. Конников / Информационные технологии. 2007. № 5. C. 9 - 17.
12. Конников, И. А. Вычисление функции Грина для уравнения Лапласа // И. А. Конников / Журнал технической физики. 2007. № 1. C. 15 - 20.
13. Конников, И. А. Использование метода Элмора для расчёта электромагнитных полей в радиолокации и микроэлектронике // И. А. Конников / Судостроение. 2007. № 2. C. 40 - 43.
14. Конников, И. А. Влияние плотности распределения заряда на ёмкость прямоугольной плёнки в слоистой среде // И. А. Конников / Электричество. 2007. №3. C. 37 - 41.
15. Конников, И. А. Математическая модель конструкции микросхемы // И. А. Конников / Математическое моделирование. 2007. T. 19. № 4. C. 37-44.
16. Конников, И. А. Два способа вычисления функции Грина для уравне-ния Лапласа // И. А. Конников / Прикладная физика. 2007. № 2. C. 17 - 24.
17. Конников, И. А. Расчет сопротивления заземляющего вывода // И. А.
Конников / Технологии электромагнитной совместимости. 2007. №1(20). C. 11-16.
18. Конников, И. А. Моделирование электромагнитных наводок в САПР электронных модулей / И. А. Конников // Авиакосмическое приборостро- ение. 2007. № 10. C. 2 - 9.
19. Конников, И. А. Метод вычисления функции Грина для слоистой среды / И. А. Конников // Известия вузов. Сер. Физика. 2007. № 7. С.70- 76.
20. Конников, И. А. Моделирование распределённых RLC-структур // И. А. Конников / Известия вузов. Cep. Приборостроение. 2006. №12. C. 38 - 44.
21. Конников, И. А. Ёмкость тонкого проводника прямоугольного сечения // И. А. Конников / Авиакосмическое приборостроение. 2006. № 11. C. 19 - 25.
22. Конников, И. А. Оценка точности вычисления функции Грина в слоистой среде // И. А. Конников / Вычислительные технологии. 2006. № 5. C. 55 - 62.
23. Конников, И. А. Помехи элементарного источника электромаг-нитного поля в радиоэлектронном модуле // И. А. Конников / Технологии электромагнитной совместимости. 2006. №4. C. 18 - 26.
24. Конников, И. А. Расчёт индуктивности прямоугольного печатного проводника // И. А. Конников / Известия вузов. Cep. Приборостроение. 2006. № 7. C. 52 - 56.
25. Конников, И. А. Расчёт индуктивности плёночного элемента коммуникатора // И. А. Конников / Судостроение, 2005. № 6. C. 35 - 37.
26. Конников, И. А. Ранжирование электромагнитных связей в коммуникаторах микросборок судовой РЭА // И. А. Конников, С. А. Соколов, Е. С. Янчук / Судостроение. 1986. № 10. C. 32 - 34.
27. Конников, И. А. Индуктивность плёночных проводников в слоистых средах // И. А. Конников / Судостроение. 1981. № 11. C.27-28.
28. Конников, И. А. Расчёт емкостей прямоугольных плёночных проводников с произвольным коэффициентом формы // И. А. Конников / Судостроение. 1980. № 8. C. 32 - 33.
29. Конников, И. А. К расчёту ёмкости плёночных элементов микро-сборок / И. А. Конников // Вопросы радиоэлектроники. Сер. ТПО. 1984. Bып. 1. C. 24 - 29.
30. Конников, И. А. Квазистационарные математические модели проводников, резисторов и катушек индуктивности / И. А. Конников // Вопросы радиоэлектроники. Сер. ТПО. 1984. Bып. 1. С. 47 - 55.
31. Конников, И. А. Принципы организации подсистемы учёта конструктивно-технологических факторов при автоматизированном проектировании микросборок / И. А. Конников // Вопросы радиоэлектроники. Сер. ТПО. 1982. Bып. 3. С. 8 - 12.
32. Конников, И. А. Исследование собственных электрических парамет-
ров проводников перспективных коммутационных плат / И. А. Конников
// Вопросы радиоэлектроники. Сер. ТПО. 1982. Bып.1. C. 3 - 9.
33. Конников И. А. Универсальные математические модели плёночных
элементов микросборок / И. А. Конников // Вопросы радиоэлектроники.
Сер. ТПО. 1981. Bып. 2. C. 28 - 32.
34. Апушкинский, Е. Г. К расчёту параметров полосковых линий / Е. Г.
Апушкинский, Э. К. Вилькс, И. А. Конников, О. A. Нестеров // Вопросы
радиоэлектроники. Сер. ТПО. 1980. Bып. 3. C. 11 - 14.
35. Конников, И. А. О влиянии конструкции микросборки на её выход-
ные электрические характеристики / И. А. Конников // Вопросы радио-
электроники. Сер. ТПО. 1980. Bып. 3. C. 24 - 28.
36. Конников, И. А. Расчёт паразитных реактивностей плёночных проводников при автоматизированном проектировании микросхем и микросборок / И. А. Конников // Вопросы радиоэлектроники. Сер. ТПО. 1980. Bып. 1. C. 69 - 74.
37. Конников, И. А. О принципах учёта паразитных электромагнитных эффектов при автоматизированном проектировании микросхем и микросборок / И. А. Конников // Вопросы радиоэлектроники. Сер. ТПО. 1979. Bып. 3. C. 18 - 22.
38. Конников, И. А. К расчёту индуктивностей проводников круглого сечения / И. А. Конников // Вопросы радиоэлектроники. Сер. ТПО. 1979. Bып. 3. C. 15 - 18.
39. Конников, И. А. О математическом обеспечении учёта конструктивно-технологических факторов при автоматизированном проектировании микросборок / И. А. Конников // Вопросы радиоэлектроники. Сер. ТПО. 1979. Bып. 3. C. 12 - 15.
40. Конников, И. А. Расчёт паразитных реактивностей плёночных резисторов / И. А. Конников // Вопросы радиоэлектроники. Сер. ТПО. 1979. Bып.2. C.45 - 53.
41. Конников, И. А. Интеграл Зоммерфельда в расчётах помех. Получе-
ние эквивалентной схемы / И. А. Конников // Петербургский журнал электроники. 2009. №1. C. 67 - 76.
42. Конников, И. А. Интеграл Зоммерфельда в расчётах помех. Расчёт эквивалентной постоянной распространения / И. А. Конников // Петербургский журнал электроники. 2008. №1. C. 74 - 84.
43. Конников, И. А. Интеграл Зоммерфельда в расчётах помех. Методы вычисления / И. А. Конников // Петербургский журнал электроники. 2007. №4. C. 61 - 68.
44. Конников, И. А. Схемотехническое моделирование проводников микросхем / И. А. Конников // Петербургский журнал электроники. 2007. № 3. C. 93 - 97.
45. Конников, И. А. Расчёт электромагнитного поля в электронных моду-лях с использованием интеграла Зоммерфельда / И. А. Конников // Тех-нология и конструирование в электронной аппаратуре. 2007. № 5. C.22-28.
46 Конников, И. А. Моделирование распределённых RLCG-структур в САПР / И. А. Конников // Сборник докладов “Научная сессия ГУАП. Технические науки”. Ч.2. ГУАП: СПб, 2007. С. 124 - 127.
47. Конников, И. А. Метод моделирования электромагнитного поля в микроэлектронике / И. А. Конников // 62-я научно-техническая конференция, посвящённая дню радио. Апрель 2007. Tруды конференции / СПб.: СПб ГТУ “ЛЭТИ”, 2007. С. 17 - 18.
48. Конников, И. А. Специфика использования методов радиотехники при решении задач микроэлектроники / И. А. Конников // 62-я научно-техническая конференция, посвящённая дню радио. Апрель 2007. Tруды конференции / СПб.: СПб ГТУ “ЛЭТИ”, 2007. С. 18 - 19.
49. Конников, И. А. Метод вычисления параметров математической модели конструкции электронного модуля / И. А. Конников // 62-я научно-техническая конференция, посвящённая дню радио. Апрель 2007. Tруды конференции / СПб.: СПб ГТУ “ЛЭТИ”, 2007. С. 14 - 15.
50. Конников, И. А. Моделирование линий с распределёнными параметрами / И. А. Конников // 62-я научно-техническая конференция, посвящённая дню радио. Апрель 2007. Tруды конференции / СПб.: СПб ГТУ “ЛЭТИ”, 2007. С. 15-17.
51. Конников, И. А. Моделирование поля при оценке внутренней электро-магнитной совместимости электронных модулей / И. А. Конников // 7-й международный симпозиум по электромагнитной совместимости и электромагнитной экологии 26-29 июня 2007. Tруды симпозиума. СПб., 2007. С. 304 - 305.
52. Конников, И. А. Проектирование электронных модулей с учётом пара-зитных электромагнитных эффектов / И. А. Конников // Высокие технологии, фундаментальные и прикладные исследования, образование. Т. 9. Сборник трудов Третьей международной научно-практической конференции "Исследование, разработка и применение высоких технологий в промышленности". 14-17 марта 2007. / СПб.: Издательство Политехнического университета, 2007. C. 117 - 118.
53. Конников, И. А. Паразитные ёмкости элементов коммуникатора / И. А. Конников // Петербургский журнал электроники. 2007. № 2. С.90-96.
54. Конников, И. А. Программный продукт для моделирования паразитных электроманитных эффектов в электронных модулях / И. А. Конников // Труды межвузовской конференции по научному програм-мному обеспечению "Практика применения научного программного обеспечения в образовании и исследованиях". 5-7 февраля 2007 г. / СПб.: Издательство Политехнического университета, 2007. С. 97 - 98.
55. Конников, И. А. Взаимовлияние объектов малых размеров в микросхеме / И. А. Конников // Технология и конструирование в электронной аппаратуре. 2006. № 6. С. 9 - 14.
56. Конников, И. А. О расчёте поля излучателя в слоистой среде в квазистационарном приближении / И. А. Конников // Материалы Х Международной научной конференции "Решетневские чтения". 8 - 10 ноября 2006 г. / Мин. образования и науки РФ; Федеральное космическое агенство. Красноярск. 2006. С. 91 - 92.
57. Конников, И. А. Характеристический размер конструкции микросхемы / И. А. Конников // Сб. докладов девятой Российской научно-технической конференции по электромагнитной совместимости технических средств и электромагнитной безопасности. 20-22 сентября 2006 г. / РАН; ЛЭТИ; ВИТУ. Спб. 2006. С. 268 - 271.
58. Конников, И. А. Математическая модель конструкции микросхем и
печатных плат / И. А. Конников // Сб. докладов девятой Российской научно-технической конференции по электромагнитной совместимости технических средств и электромагнитной безопасности. 20-22 сентября
2006 г. / РАН; ЛЭТИ; ВИТУ. Спб. 2006. С. 266 - 268.
59. Конников, И. А. Расчёт матрицы емкостей элементов коммуникатора / И. А. Конников // Сб. докладов девятой Российской научно-технической конференции по электромагнитной совместимости технических средств и электромагнитной безопасности. 20-22 сентября 2006 г. / РАН; ЛЭТИ; ВИТУ. Спб. 2006. С. 263 - 265.
60. Конников, И. А. Поле элементарного источника в слоистой среде / И. А. Конников // Сб. докладов девятой Российской научно-технической конференции по электромагнитной совместимости технических средств и электромагнитной безопасности. 20-22 сентября 2006 г. / РАН; ЛЭТИ; ВИТУ. Спб. 2006. С. 524 - 529.
61. Конников, И. А. Математическая модель конструкции микро-электронного модуля / И. А. Конников // Сборник докладов “Научная сессия ГУАП. Технические науки”. Ч.2. ГУАП: СПб, 2006. С. 111 - 115.
62. Конников, И. А. Ёмкость тонкого проводника прямоугольного сечения в микросхеме / И. А. Конников // Технология и конструирование в электронной аппаратуре. 2006. №4. C. 18 - 23.
63. Конников, И. А. Экономичный расчёт ёмкости прямоугольного плёночного проводника / И. А. Конников // Петербургский журнал электроники. 2005. №3. C. 102 - 107.
64. Конников, И. А. Емкостные наводки полупроводниковых микросхем / Петербургский журнал электроники. 2005. № 4. С. 73 - 76.
65. Конников, И. А. О проблеме учёта конструктивно-технологических факторов при разработке микроэлектронной аппаратуры / И. А. Конников // Прогрессивные методы конструирования и гибкое автоматизированное производство микроэлектронной аппаратуры. Материалы семинара / М.: МДНТП, 1986. C. 41 - 45.
66. Конников, И. А. Некоторые вопросы математического обеспечения учёта паразитных электромагнитных эффектов / И. А. Конников // Технология и машинное проектирование изделий электронной техники. Тезисы докладов и рекомендации научно-технических конференций / Сер. 3 "Микроэлектроника". 1980. Bып. 1 (145). М.: ЦНИИ "Электроника", 1980. C.45 - 47.
67. Конников, И. А. Расчёт ёмкости плёночных проводников в микросхе-мах и многослойных печатных платах / И. А. Конников, В. И. Чернявский // Обмен опытом в радиопромышленности. 1980. Bып. 10. C. 16 - 20.
68. Конников, И. А. Исследование алгоритмов вычисления паразитной ёмкости плёночных резисторов / И. А. Конников, Ю. С. Мишин, А. С. Сё-мин // Физика полупроводников и микроэлектроника: Межвуз. сб. науч. тр.
/ Рязанский радиотехнический институт. 1979. Bып. 6. C. 92 - 94.
69. Конников, И. А. Математическая модель плёночных элементов микросборок / И. А. Конников; под ред. Г. А. Петухова // Машинные методы проектирования ЭВА. Материалы краткосрочного семинара 5 - 6 июля / Л.: ЛДНТП, 1979. С. 68 - 72.
70. Конников, И. А. Метод эквивалентной постоянной распространения для моделирования электромагнитного поля в микроэлектронике / И. А. Конников // Научная сессия ГУАП. Сб. докл.: В 3 ч. Ч. II. Технические науки. / СПб ГУАП: СПб., 2008. С. 109 - 110.
71. Конников, И. А. Область корректного использования метода эквива-лентной постоянной распространения / И. А. Конников // Научная сессия ГУАП. Сб. докл.: В 3 ч. Ч. II. Технические науки. / СПб ГУАП: СПб., 2008. С. 111 - 115.
72. Конников, И. А. Метод эквивалентной постоянной распространения для моделирования электромагнитного поля в слоистых средах / И. А. Конников // 63-я научно-техническая конференция, посвящённая дню радио. Апрель 2008. Труды конференции / СПб.: СПб ГТУ “ЛЭТИ”, 2008. С. 25 - 27.
73. Конников, И. А. Использование методов радиотехники при решении задач микроэлектроники / И. А. Конников // 63-я научно-техническая конференция, посвящённая дню радио. Апрель 2008. Труды конференции / СПб.: СПб ГТУ “ЛЭТИ”, 2008. С. 23 - 25.
74. Конников, И. А. Метод получения эквивалентной схемы канала электромагнитной связи в слоистых средах / И. А. Конников // 63-я научно-техническая конференция, посвящённая дню радио. Апрель 2008. Труды конференции / СПб.: СПб ГТУ “ЛЭТИ”, 2008. С. 27 - 28.
75. Конников, И. А. Область корректного применения метода эквива-лентной постоянной распространения / И. А. Конников // 63-я научно-техническая конференция, посвящённая дню радио. Апрель 2008. Труды конференции / СПб.: СПб ГТУ “ЛЭТИ”, 2008. С. 28 - 30.
[1] В качестве наибольшего размера rmax, необходимого для прямых расчётов поля или последующего интегрирования функции Грина, может быть принята, например, длина самого длинного прямоугоьного проводника на подложке или радиус зоны электромагнитного влияния такого проводника.
