Разработка и исследование методов эффективного использования технологической информации для управления качеством продукции в металлургии
На правах рукописи
Журавлева Марина Гарриевна
Разработка И ИССЛЕДОВАНИЕ методов эффективного
использования технологической информации
для управления качеством продукции в металлургии
Специальность 05.13.06
«Автоматизация и управление технологическими
процессами и производствами (металлургия)»
АВТОРЕФЕРАТ
диссертации на соискание ученой степени
кандидата технических наук
Липецк – 2009
Работа выполнена в ГОУ ВПО «Липецкий государственный технический
университет» (ЛГТУ)
Научный руководитель доктор технических наук, профессор
Кузнецов Леонид Александрович
Официальные оппоненты: доктор технических наук, профессор
Бурковский Виктор Леонидович
кандидат физико-математических наук, доцент
Лубенец Юрий Владимирович
Ведущая организация Учреждение Российской академии наук
Институт проблем управления
им. В.А.Трапезникова РАН (ИПУ РАН), г. Москва
Защита состоится «02» июня 2009 г. в 12:00 часов на заседании диссертационного совета Д212.108.02 при ГОУ ВПО «Липецкий государственный технический университет» по адресу: 398600 г. Липецк, ул. Московская, 30, ауд. 601.
С диссертацией можно ознакомиться в библиотеке ГОУ ВПО «Липецкий государственный технический университет».
Автореферат разослан «____» 2009 г.
Ученый секретарь
диссертационного совета Ведищев В.В.
ВВЕДЕНИЕ
Актуальность. Для обеспечения задаваемого потребителями уровня качества продукции на металлургических предприятиях внедряются системы качества, ориентированные на управление качеством на основе статистических методов обработки производственных данных в соответствии с международными стандартами ИСО серии 9000. Особенно актуально использование статистических методов в управлении качеством для многоэтапных процессов металлургического производства, технологические факторы и показатели качества продукции которого содержат существенную случайную составляющую, задаются диапазонами разрешенных значений и в их пределах рассматриваются как случайные величины.
Значения факторов и показателей качества, хранящиеся в массивах технологических измерений, часто не подчиняются нормальному закону распределения, массивы могут содержать пропуски и наблюдения, резко выделяющиеся на фоне остальных. Традиционные статистические методы не позволяют исследовать взаимосвязи и осуществлять текущий контроль металлургических технологий и качества инвариантно к видам распределений контролируемых величин, восстанавливать пропущенные данные в массивах технологических измерений, выполнять кластеризацию технологий и продукции по диапазонам разрешенных значений (полей допусков) или распределениям характеристик.
Для эффективного решения задач автоматизированного контроля процессов и управления качеством в металлургическом производстве целесообразна разработка процедур, учитывающих перечисленные особенности фактической информации о технологиях и продукции. Разработка таких подходов может опираться на непараметрические и специальные методы оценки тесноты связей и проверки гипотез, итеративные стратегии восстановления пропущенных данных, бутстреп-методы построения доверительных интервалов. Их применение позволит корректно выявлять причины неслучайной вариабельности технологических процессов и повысить эффективность использования фактической технологической информации в соответствии с современными концепциями всеобщего менеджмента качества. Следовательно, разработка методов, расширяющих возможности статистического контроля и управления качеством металлургической продукции, является актуальной задачей.
Цель и задачи исследования. Целью работы является разработка и исследование комплекса методов и автоматизированных процедур, инвариантных к видам распределений контролируемых переменных и обеспечивающих эффективное решение задач контроля технологических процессов и управления качеством продукции металлургического производства. Для достижения цели поставлены и решены следующие задачи исследования:
- Разработка и исследование инструментов автоматизированного контроля технологических процессов металлургического производства инвариантно к видам распределений контролируемых технологических переменных.
- Разработка и исследование схемы и процедур анализа взаимосвязей между технологическими переменными процессов металлургического производства, инвариантных к отклонениям от нормальности в распределениях переменных.
- Исследование эффективности применения итеративной стратегии «ожидание-максимизация» (EM-алгоритма) для идентификации статистических моделей технологических процессов металлургического производства по массивам технологических измерений, содержащим пропущенные значения.
- Разработка методик, алгоритма и автоматизированных процедур кластеризации для выделения групп однородных технологий и продукции металлургического производства по диапазонам полей допусков и распределениям характеристик.
Методы исследования. В работе использованы современные методы теории вероятностей, многомерного статистического анализа, непараметрической статистики, теории проверки статистических гипотез, статистического контроля качества, системного анализа, анализа эффективности алгоритмов, объектно-ориентированного проектирования и программирования.
Достоверность основных положений и выводов. Достоверность результатов диссертационного исследования подтверждается корректным использованием современных методов теории вероятностей и математической статистики, обработки экспериментальных данных, программирования, сравнением результатов практической реализации разработанных методов и алгоритмов с экспериментальной информацией, проведенными исследованиями возможности и эффективности их применения для обработки фактических данных металлургического производства, сопоставимостью с результатами, полученными с помощью существующих подходов, использованием математического, алгоритмического и программного обеспечения в научных исследованиях и на практике.
Научная новизна работы. В работе получены и выносятся на защиту следующие результаты, характеризующиеся научной новизной:
1. Формализованные методы построения карт контроля процессов с помощью непараметрических критериев проверки гипотез об однородности двух выборок и бутстреп-метода процентных точек, отличающиеся инвариантностью к изменениям вида распределения контролируемой переменной, позволяющие обоснованно осуществлять автоматизированный текущий статистический контроль металлургического производства.
2. Алгоритм выделения групп взаимосвязанных технологических переменных на основе непараметрического коэффициента конкордации, отличающийся полиномиальной сложностью по времени, инвариантностью к видам распределений переменных, позволяющий выявлять группы тесно связанных друг с другом переменных для контроля многомерных технологий и качества продукции металлургического производства.
3. Схема комплексного анализа взаимосвязей между технологическими факторами и показателями качества продукции металлургического производства, отличающаяся инвариантностью к отклонениям от нормальности в технологических данных.
4. Коэффициент, позволяющий оценивать степень тесноты связи между двумя технологическими переменными на основе среднего значения величины условной частоты, отличающийся устойчивостью к шуму и резко выделяющимся наблюдениям в выборках переменных.
5. Схема анализа эффективности применения стратегии «ожидание-максимизация» (EM-алгоритма) для построения статистических линейных моделей технологических процессов металлургического производства по массивам измерений с пропущенными значениями, отличающаяся использованием непараметрических критериев для проверки качества прогноза по моделям.
6. Методики и алгоритм кластеризации, позволяющие выделять группы однородных металлургических технологий и продукции, отличающиеся тем, что анализируемые с их помощью технологические факторы и показатели качества продукции являются случайными величинами, задаваемыми с помощью диапазонов полей допусков или распределений.
Практическая значимость. Разработанные инструменты автоматизированного текущего контроля процессов и анализа данных могут применяться для обработки массивов технологических измерений с пропусками, значения которых не подчиняются нормальному закону, корректно учитывать многомерность металлургических технологий и качества в условиях невыполнения гипотезы о нормальности. Разработанное математическое, алгоритмическое и программное обеспечение может использоваться на предприятиях металлургического и других видов сложных производств в системах информационной поддержки управления качеством.
Реализация и внедрение результатов работы. Разработанные методы реализованы в виде двух программ, зарегистрированных в Отраслевом фонде алгоритмов и программ Федерального агентства по образованию (свидетельство об отраслевой регистрации разработки «Расширенный статистический анализ данных» №10656 от 15.05.2008), (свидетельство об отраслевой регистрации разработки «Кластеризация объектов по выборочным распределениям признаков» №10657 от 15.05.2008), на которые имеются официально зарегистрированные информационные карты. Результаты работы внедрены и используются: в труболитейном цехе и центральной заводской лаборатории ОАО "Липецкий металлургический завод «Свободный сокол»" для решения задач диагностики состояния технологических процессов производства напорных труб из высокопрочного чугуна с шаровидным графитом и кластеризации марок чугуна и видов трубной продукции, в ООО «Петроком-Липецк» для автоматизации обработки информации о качестве эмали для рулонного листового проката, в учебном процессе ЛГТУ.
Апробация результатов работы. Основные теоретические и практические результаты исследований были представлены: на международных конференциях «Современные проблемы информатизации в технике и технологиях» (Воронеж, 2001), «Современные проблемы информатизации в экономике и обеспечении безопасности» (Воронеж, 2009), «Современные сложные системы управления СССУ/HTCS» (Воронеж, 2003; Тверь, 2008), «Сложные системы управления и менеджмент качества CCSQM'2007» (Старый Оскол, 2007); на «Молодежной научно-технической конференции технических вузов центральной России» (Брянск, 2000); на Всероссийской конференции «Новые технологии в научных исследованиях, проектировании, управлении, производстве» (Воронеж, 2008); на Российской конференции с международным участием «Технические и программные средства систем управления, контроля и измерения УКИ’08» (Москва, 2008).
Публикации. По теме диссертационного исследования опубликовано 14 работ, в том числе: три статьи в журналах из перечня периодических журналов, рекомендованных ВАК для публикации основных результатов диссертации. В работах, опубликованных в соавторстве, автором осуществлено применение и анализ эффективности EM-алгоритма для идентификации моделей процессов металлургического производства по данным с пропусками [1, 14]; разработан непараметрический алгоритм выявления групп взаимосвязанных технологических переменных, показаны его преимущества на примере анализа данных процесса выплавки стали [2]; разработаны формализованные методы построения карт контроля процессов на основе ранговых критериев Вилкоксона-Манна-Уитни, Ансари-Брэдли, бутстреп-метода процентных точек, проведен анализ их эффективности на примерах обработки данных о выплавке стали [3, 12, 13]; разработаны методики, алгоритм и автоматизированные процедуры кластеризации объектов по диапазонам и распределениям характеристик [810]; разработаны и исследованы коэффициент для оценки тесноты парной связи на основе условной частоты [5, 6] и комплексный подход к анализу взаимосвязей между переменными процессов металлургического производства [7].
Структура и объем диссертации. Диссертация состоит из введения, пяти глав, заключения, списка литературы, включающего 133 наименования, шести приложений. Каждая из глав, за исключением первой, соответствует решению одной из поставленных задач: в начале главы описаны разработанные методы и (или) алгоритмы решения задачи, затем – примеры их реализации и анализ эффективности. Основная часть работы изложена на 127 страницах текста, работа содержит 37 рисунков и 25 таблиц.
содержание работы
Во введении обоснована актуальность темы диссертационного исследования, сформулированы цели и задачи исследования, показаны новизна и практическая значимость работы, выделены основные защищаемые положения.
В первой главе проведен анализ особенностей управления качеством продукции металлургического производства с позиций современного менеджмента качества, выявлены недостатки существующих статистических инструментов контроля и моделирования технологических процессов, показана целесообразность использования нетрадиционных статистических технологий в качестве основы для эффективного управления качеством продукции металлургического и других видов сложных производств.
Необходимость выявления причин разброса процессов, принятия решений на базе фактической информации, способствующих непрерывному улучшению качества процессов и продукции, определяет использование статистических методов в основе управления качеством металлургической продукции. При этом решаются задачи текущего контроля технологических процессов и получения существенной для принятия управленческих решений информации из массивов технологических измерений.
Анализ литературных источников по теме диссертации показал, что существующие статистические инструменты обработки фактической информации не учитывают ряд особенностей металлургического производства: невыполнение требования нормальности распределений, в том числе в случае многомерных технологий и качества, взаимосвязи между технологическими факторами и показателями качества продукции, распределения которых содержат отклонения от нормальности (шумы, резко выделяющиеся наблюдения), наличие пропусков в массивах технологической информации, неоднородность информации о технологиях и продукции. Исходя из анализа этих проблем, сформулированы цель и задачи исследования, представленные во введении.
Во второй главе разработаны формализованные методы автоматизированного текущего контроля процессов, инвариантные к видам распределений контролируемых переменных, включающие построение нестандартных карт контроля (КК).
КК представляет собой график, на который периодически наносится значение – результат проверки гипотезы о состоянии процесса. Это значение сопоставляется со значениями границ области управляемости процесса (контрольными границами). При выходе за пределы контрольных границ выдается сигнал о статистической разладке – возможном нарушении стабильности состояния. Если законы распределения контролируемых величин отличаются от нормального, контрольные границы, получаемые по известным схемам, могут приводить к ошибкам диагностики состояния. Построение корректных контрольных границ возможно на основе непараметрических критериев Вилкоксона-Манна-Уитни (U-критерия), Ансари-Брэдли в картах контроля средних значений и рассеяния. Пусть имеется базовая выборка Q объема n значений контролируемой переменной, полученная в ходе функционирования процесса в стабильном состоянии. Из информации о поступающих в некоторые моменты времени t1, t2, … партиях продукции извлекаются мгновенные выборки Q1, Q2, … равных объемов m, состоящие из значений переменной. Для построения КК средних значений U-критерия можно вычислять величину:
, 
, i = 1, 2, …, n, j = 1, 2, …, m, (1)
где qi – i-е наблюдение из базовой выборки, qrj – j-е наблюдение из r-й мгновенной выборки. Статистика U имеет математическое ожидание Е(U) = nm/2 и дисперсию 
. Контрольные границы с учетом факта приближенной нормальности ее распределения определяются по формуле:
, (2)
где 
– нижняя, 
– верхняя контрольные границы, знак «-» в символе «
» используется при вычислении нижней, «+» – верхней границы; 
– квантиль стандартного нормального распределения для вероятности ошибочной диагностики разладки. Автоматизированное построение КК средних значений U-критерия предполагает: задание m и, создание графика и нанесение на него средней линии (y = nm/2); выбор в каждый момент времени tr, r = 1, 2, … мгновенной выборки Qr, вычисление по формулам (1) и (2) значений статистики U, величин 
, 
и нанесение их на график. Карты рассеяния можно строить описанным способом на основе непараметрических критериев Ансари-Брэдли, U-критерия для дисперсии.
Для построения простых и многомерных КК металлургических технологий и качества (бутстреп-карт) с переменными границами по скалярной характеристике y можно воспользоваться бутстреп-методом процентных точек. Пусть по текущей r-й мгновенной выборке объема m получены выборочное значение yr и выборочная функция 
бутстреп-распределения yr, вычисленная по M случайным бутстреп-выборкам, извлеченным с возвращением из r-й мгновенной выборки, где M >> m; 
– значение y в i-й бутстреп-выборке; i = 1, 2, …, M. Величина yr удовлетворяет неравенствам 
,
а нижняя Кнboot и верхняя Квboot контрольные границы вычисляются по формулам: 
,
где yn – номинальное значение y, а 
, 
– значения обратной функции бутстреп-распределения для аргументов /2, 1-/2.
В многомерном случае можно строить бутстреп-карты усреднённых по тесно взаимосвязанным переменным средних значений. Для выделения групп таких переменных разработан алгоритм (рис. 1) на основе коэффициента конкордации W, инвариантного к видам распределений переменных. На его вход поступает 2p переменных: по исходным p переменным создаются дополнительные, имеющие соответствующие обратные значения. На каждом этапе по двум наиболее тесно взаимосвязанным переменным из множества еще не включенных в группы создается (если связь значима) текущая группа. Включение переменной hk в текущую группу возможно, если она не является более тесно связанной с другими переменными hk+1, hk+2, …, также не включенными в группы (см. рис. 1). Анализ показал, что алгоритм имеет полиномиальную сложность порядка O(np3), где n – объем выборки значений p переменных.
Рис. 1. Блок-схема алгоритма выделения групп: W – коэффициент конкордации
Предложенные способы построения КК реализованы в разработанной программе расширенного статистического анализа данных. Совмещенные КК средних и U-критерия для = 0,27%, n = 100, m = 15, построенные по переменной x – процентному содержанию никеля в стали, %, распределение которой отличается от нормального (табл. 1), показаны на рис. 2. КК средних позволила диагностировать статистическую разладку по 4, 5, 6, 11, 15-й выборкам, а КК Uкритерия – по 1, 2, 4, 5, 6, 7, 8, 9, 10, 11, 13, 17, 20, 21, 22, 31, 33, 37, 38, 39-й выборкам (рис. 2). Примерно в 27% случаев от общего числа проверок с помощью КК U-критерия были выявлены дополнительные моменты статистической разладки, не учтенные с помощью существующего подхода.
КК Uкритерия и бутстреп-карты используются на предприятиях ООО «Петроком-Липецк» и ОАО "Липецкий металлургический завод «Свободный сокол»".
Таблица 1. Характеристики и проверка гипотезы о нормальности
| Переменная | N | Среднее | СКО | As | As | Ek | Ek |
| x, % | 494 | 0,009 | 0,003 | 1,52 | 0,11 | 3,32 | 0,22 |
| Tкп, °С | 506 | 874 | 23,3 | 0,11 | 0,11 | -1,70 | 0,22 |
| Tсм, °С | 506 | 689 | 54,9 | 0,16 | 0,11 | -1,26 | 0,22 |
Примечания: N – число наблюдений; As, Ek – оценки показателей асимметрии и эксцесса; СКО – среднеквадратическое отклонение; As, Ek – СКО показателей асимметрии и эксцесса. Если верно одно из условий: |As| >5As, |Ek| > 5Ek, гипотеза о нормальности отклоняется.
Рис. 2. КК переменной x: U-критерия и средних значений
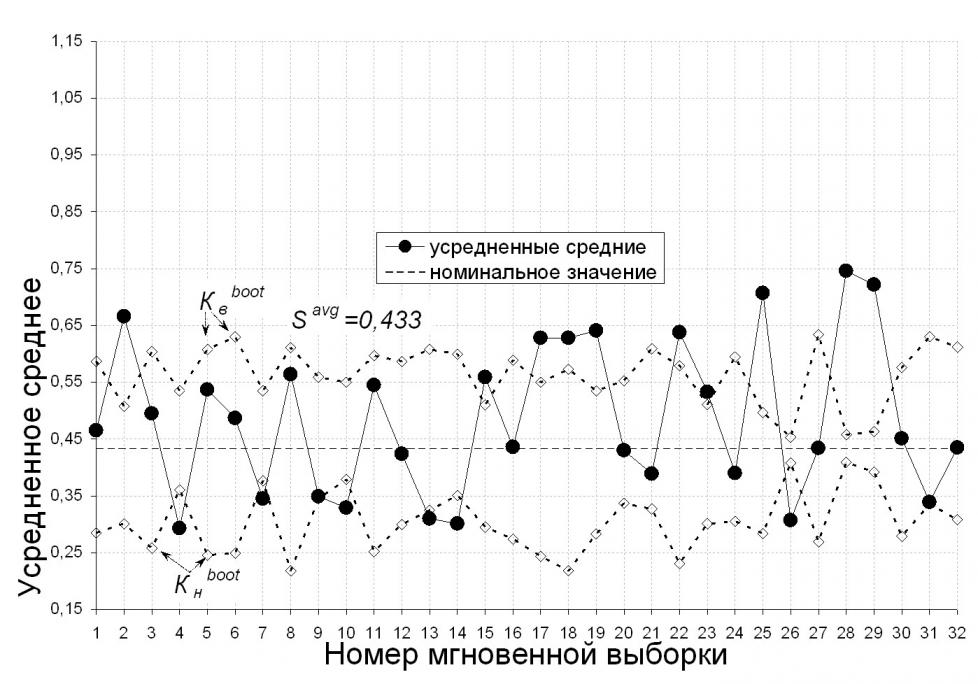
По данным, состоящим из 506-ти пронормированных совместных наблюдений тесно взаимосвязанных факторов процесса горячей прокатки, температуры конца прокатки, Tкп, °С, и температуры смотки Tсм, °С (табл. 1), строились разработанная КК усреднённых средних (рис. 3, а) и известная КК Хотеллинга (рис. 3, б). КК Хотеллинга (рис. 3, б) позволила выявить 5 моментов возможной разладки процесса: по 2, 23, 25, 28 и 29-й мгновенным выборкам. По 2, 4, 7, 9, 10, 13, 14, 15, 17, 18, 19, 22, 23, 25, 26, 28, 29, 31-й выборкам с помощью карты контроля усреднённых средних обнаружена статистическая разладка (рис. 3, а), т.е. она позволила выявить 12 дополнительных моментов возможной разладки.
Таким образом, во второй главе разработаны формализованные методы автоматизированного текущего контроля процессов и показана эффективность их применения для контроля технологических процессов металлургического производства.
а
б
Рис. 3. Многомерные КК: а – усреднённого среднего; б – Хотеллинга
В третьей главе предложена схема комплексного анализа взаимосвязей между переменными процессов металлургического производства, позволяющая обнаруживать парные связи по данным с шумами, выбросами, т.е. наблюдениями, резко выделяющимися на фоне остальных (рис. 4). Она основана на вычислении параметрических и непараметрических критериев оценки степени тесноты парной связи. В рамках схемы разработан непараметрический коэффициент, позволяющий оценивать степень тесноты связи любой формы между двумя переменными. Он вычисляется по таблице совместных и частных частот фактора и показателя качества продукции как среднее условных частот:
, где 
и 
– количество категорий фактора и частная частота, соответствующая j-й категории фактора; 
– максимальная из совместных частот в j-й категории фактора. Частотный коэффициент ' показывает усредненную степень влияния фактора на отклик. Нормированный частотный коэффициент вычисляется по формуле
,
где 
– количество категорий показателя качества. Значимость коэффициента можно проверять с помощью 2-распределения, так как получено равенство: 
, где X2 – величина, имеющая 2-распределение.
Рис. 4. Иерархия парных коэффициентов (к.) оценки тесноты связи: является частным случаем; измеряется посредством; является частью. В прямоугольниках: с закругленными краями ( ) даны обобщающие определения; обычных ( ) – названия коэффициентов, применяемых для анализа технологических взаимосвязей; со сдвоенной линией ( ) – коэффициентов, не применяемых с этой целью; со сдвоенной пунктирной линией ( ) – коэффициент
Двумерная выборка переменных x2 (присадка SiMn, т) и y2 (содержание кремния в стали, %), процесса выплавки стали многократно загрязнялась шумом, по ней вычислялись коэффициенты оценки тесноты связи между x2 и y2 (рис. 5).
Рис. 5. Средние значения коэффициентов (к.) при возрастании шума
Увеличение объемов шума с 0 до 30% привело к следующим относительным изменениям корреляционного отношения, коэффициентов Спирмена, Кендалла, Гудмена, Сомерса, Крамера, Гутмана, информационного и разработанного частотного соответственно: 67, 90, 90, 91, 91, 60, 92, 67, 34%.
Исследование влияния факторов выплавки стали на концентрацию марганца в готовой стали с помощью схемы комплексного анализа позволило добавить к полученному посредством традиционного анализа набору существенных факторов дополнительные. Это улучшило построенную модель зависимости (величина коэффициента детерминации возросла с 0,34 до 0,86).
Таким образом, в третьей главе разработана схема комплексного анализа взаимосвязей, устойчивая к наличию в данных шума и выбросов, и показано, что ее использование для обработки фактических данных позволяет получать усовершенствованные модели процессов металлургического производства.
В четвертой главе разработана схема анализа эффективности применения стратегии «ожидание-максимизация» (EM-алгоритма) для идентификации статистических моделей процессов металлургического производства по данным с пропусками. В рамках схемы по исходным данным, из которых были удалены пропуски, строилась контрольная модель, сравнивавшаяся с тремя моделями (видов А, В, С), получаемыми многократно по массиву комплектной информации, но с искусственно вводимыми пропусками. После ввода заданного количества пропусков они вновь заполнялись: безусловными средними, условными средними, с помощью EM-алгоритма. Модель вида А строилась по данным, полученным при заполнении пропусков безусловными средними, вида В – условными средними, вида C – с помощью EM-алгоритма. На каждом шаге количество пропусков увеличивалось, выполнялся поиск наилучшей модели по нормам разностей векторов оценок параметров моделей вида А, В, С и контрольной, оценивалось качество предсказания исходного отклика с помощью моделей на основе непараметрических критериев 2 и Колмогорова-Смирнова.
Таблица 2. Фрагмент статистического исследования построенных моделей
| m,% | Модель | Norma | R | F | 2 | p(2) | D | p(D) |
| - | контр. | - | 0,82 | 49,90 | - | - | - | - |
| 1 | А | 2,94 | 0,77 | 34,88 | 7,46 | 0,38 | 0,08 | 0,41 |
| В | 0,21 | 0,82 | 49,83 | 0,53 | 0,999 | 0,03 | 1,00 | |
| С | 0,20 | 0,82 | 49,83 | 0,57 | 0,999 | 0,03 | 1,00 | |
| 10 | A | 14,65 | - | - | 149,05 | 0,00 | 0,72 | 0,00 |
| B | 1,10 | 0,82 | 48,38 | 4,87 | 0,68 | 0,04 | 0,97 | |
| C | 0,83 | 0,82 | 48,91 | 1,35 | 0,99 | 0,04 | 0,99 | |
| 25 | A | 20,34 | - | - | 227,66 | 0,00 | 0,96 | 0,00 |
| B | 3,54 | 0,72 | 26,10 | 19,11 | 0,01 | 0,08 | 0,41 | |
| C | 1,92 | 0,80 | 43,45 | 9,98 | 0,19 | 0,06 | 0,77 |
Примечания: контр. – контрольная; m – число пропусков, %; Norma – норма разности векторов оценок параметров; R – коэффициент множественной корреляции; F, 2, D – величины критериев Фишера, 2, Колмогорова-Смирнова; p – доверительная вероятность. Количество групп для расчета значения 2 – 8; Fкр, 9, 244, p = 0,99 = 2,48.
По результатам построения моделей вида А, В, С (табл. 2) зависимости характеристики «глубина сферической лунки» от ряда факторов процесса производства листового проката по массиву из 254-х наблюдений можно видеть, что максимально устойчивыми к количеству пропусков оказались модели вида С. Получена результирующая модель с R = 0,83, F = 63,45 (см. табл. 2).
Таким образом, в четвертой главе показана целесообразность практического использования стратегии «ожидание-максимизация» (EMалгоритма) для получения устойчивых к колебаниям количества пропущенных данных уточнённых моделей технологических процессов металлургического производства.
В пятой главе разработаны оригинальные методики кластеризации технологий и продукции по диапазонам полей допусков и распределениям характеристик. Предложенный подход формализован без потерь общности на примере кластеризации продукции по показателям качества.
Проверку близости друг к другу значений какого-либо показателя качества двух или большего количества единиц продукции можно выполнять как проверку близости друг к другу распределений показателя в этих единицах. Пусть имеется p показателей качества
i-й анализируемой единицы продукции, g единиц продукции. Показатели заданы односторонними или двусторонними ограничениями: {
}, {
} или {
}, где 
, 
– соответственно минимальное и максимальное разрешаемые значения показателя j, j = 1, 2, …, p, характеризующего i-ю единицу продукции, i = 1, 2, …, g. В случае двусторонних границ разности верхнего и нижнего значений диапазона могут интерпретироваться как допустимый размах, составляющий для нормального закона 6 ( – СКО), а среднее является серединой поля допуска. Оценки среднего и СКО s записываются в виде
; 
i=1, 2, …, g, j {1, 2, …, p}. (3)
В случае односторонних ограничений средние значения 
задаются заранее и оценки СКО вычисляются по формулам:
или 
i=1, 2, …, g, j {1, 2, …, p}. (4)
Две единицы продукции можно считать сходными по показателю, если с заданной доверительной вероятностью 1 гипотеза о равенстве средних и дисперсий распределений показателя в этих единицах не отклоняется. Гипотезу о средних можно проверять по критерию Стьюдента (tкритерий), о дисперсиях – по критерию Фишера (F-критерий). Для l-й и k-й единиц продукции по каждому из p показателей статистика t-критерия вычисляется с использованием формул (3) и (4) по формуле 
, j = 1, 2, …, p,
объем выборки принят равным единице. Если с заданной вероятностью 1- каждая из величин tj подчиняется стандартному нормальному распределению, k-я и l-я единицы продукции считаются сходными по средним значениям показателей. Аналогично применяются F-критерий, U-критерий, критерий Ансари-Брэдли. Возможна кластеризация по площадям под кривыми плотностей распределений показателя качества в разных единицах продукции.
Разработан алгоритм кластеризации: вначале при сравнении каждой единицы продукции с остальными по всем показателям посредством проверки гипотез о среднем и рассеянии (или вычисления площадей) выделяется единица продукции, сходная с максимальным количеством других единиц, затем они помещаются в новый кластер. Процесс повторяется до тех пор, пока все единицы не окажутся в кластерах (единицы продукции, не сходные с другими, помещаются в отдельные кластеры). С помощью разработанной на основе алгоритма программы проведена кластеризация марок стали (табл. 3, 4) по данным нормативных документов на основе t- и F-критериев для двух значений.
Таблица 3. Кластеры и соответствующие им марки стали
| № кластера | Объединенные марки, 1- = 0,9999999, а |
| 1 | 08Ю, 10ЮА, 15ЮА, 20ЮА, 08пс, Ст1пс, Ст1сп, Ст2пс, Ст2сп, 15пс, 15, 20пс, 20, Ст3Гпс, Ст3сп, Ст5пс, Ст5сп, Ст3пс |
| 2 | 09Г2, 16ГС, 17ГС, 10ХНДП, 17Г1С, 10Г2С1, 12ГС |
| № кластера | Объединенные марки, 1- = 0,99999, б |
| 1 | 08Ю, 10ЮА, 15ЮА, 20ЮА, 08пс, Ст1пс, Ст1сп, Ст2сп, 15пс, 15, 20пс, 20, Ст3пс, Ст3сп, Ст2пс |
| 2 | 09Г2, 12ГС, 17ГС, 17Г1С, 10Г2С1, 16ГС |
| 3 | Ст5сп, Ст5пс |
| 4 | Ст3Гпс |
| 5 | 10ХНДП |
Таблица 4. Границы кластеров по концентрациям некоторых элементов
| № кл. | C | Si | Mn | Cr | Ni | Cu | |
| а | 1 | 0,40 | 0,37 | 0,17-1,15 | 0,30 | 0,30 | 0,30 |
| 2 | 0,22 | 0,12-1,15 | 0,20-1,9 | 0,85 | 0,65 | 0,55 | |
| № кл. | C | Si | Mn | Cr | Ni | Cu | |
| б | 1 | 0,25 | 0,37 | 0,17-0,70 | 0,30 | 0,30 | 0,30 |
| 2 | 0,22 | 0,12-1,15 | 0,70-1,9 | 0,35 | 0,35 | 0,35 | |
| 3 | 0,26-0,40 | 0,03-0,33 | 0,47-0,85 | 0,30 | 0,30 | 0,30 | |
| 4 | 0,12-0,25 | 0,13 | 0,77-1,15 | 0,30 | 0,30 | 0,30 | |
| 5 | 0,14 | 0,12-0,42 | 0,20-0,70 | 0,45-0,85 | 0,25-0,65 | 0,25-0,55 | |
Примечание: № кл. – номер кластера.
Таким образом, в пятой главе разработаны методики кластеризации продукции и технологий по диапазонам полей допусков и распределениям характеристик, позволяющие структурировать информацию о продукции и технологиях металлургического производства с требуемой степенью детализации.
ОСНОВНЫЕ ВЫВОДЫ И РЕЗУЛЬТАТЫ РАБОТЫ
В диссертации решены актуальные задачи эффективного использования технологической информации, обеспечивающие реализацию контроля и управления качеством продукции металлургического производства на современном уровне развития теории и практики управления качеством. Получены следующие основные результаты теоретических и экспериментальных исследований:
1. Разработаны методики построения карт контроля процессов на основе непараметрических критериев проверки гипотез и бутстреп-метода процентных точек, позволяющие осуществлять автоматизированный текущий контроль металлургической технологии по скалярной и векторной переменным, распределения которых могут не подчиняться требованию нормальности. Исследование на данных металлургического производства показало, что практическое применение предложенных инструментов позволяет повысить точность регистрации моментов статистической разладки технологических процессов.
2. Разработан формализованный, инвариантный к видам распределений переменных алгоритм, позволяющий получать эффективное разбиение исходного множества технологических переменных на группы для осуществления текущего контроля многомерных технологий и качества продукции металлургического производства.
3. Разработаны математические и программные инструменты инвариантного к шуму, выбросам и видам распределений переменных анализа технологических взаимосвязей в металлургическом производстве, позволяющие выявлять дополнительные факторы технологии, существенно влияющие на качество продукции, и получать уточненные статистические модели процессов металлургического производства.
4. Показана эффективность и осуществлено практическое применение стратегии EMалгоритма для идентификации работоспособных моделей технологических процессов металлургического производства по массивам технологических измерений, содержащим пропущенные значения.
5. Разработаны оригинальные, статистически обоснованные, методики и автоматизированные процедуры кластеризации технологий и продукции по диапазонам полей допусков и распределениям факторов технологии и показателей качества продукции, практическое использование которых позволяет улучшить структуризацию металлургических технологий и продукции с целью построения адекватных моделей для прогнозирования и управления, автоматизировать экспертизу металлопродукции и ведение нормативно-технической документации.
РАБОТЫ, ОПУБЛИКОВАННЫЕ ПО ТЕМЕ ДИССЕРТАЦИИ
Публикации в изданиях, рекомендованных ВАК:
1. Кузнецов Л.А., Корнеев А.М., Журавлева М.Г. Идентификация статистических моделей технологических процессов с заполнением пропусков в данных // Проблемы управления. – 2007. – № 1. – С. 46-50.
2. Кузнецов Л.А., Журавлёва М.Г. Непараметрический алгоритм группировки компонент векторного признака качества технологического процесса // Системы управления и информационные технологии. – 2008. – № 3(33). – С. 38-43.
3. Кузнецов Л.А., Журавлева М.Г. Построение карт контроля качества с помощью непараметрического критерия Вилкоксона-Манна-Уитни // Заводская лаборатория. Диагностика материалов. – 2009. – Т. 75, № 1. – С. 70-74.
Другие публикации:
4. Журавлева М.Г. Идентификация связи между случайными величинами // Молодежная научно-техническая конференция технических вузов центральной России: тезисы докладов. – Брянск: БГТУ, 2000. – С. 45-47.
5. Кузнецов Л.А., Журавлева М.Г. Дополнительные возможности статистического анализа сложных производственных систем // Современные проблемы информатизации в технике и технологиях: труды VI Международной открытой научной конференции. – Воронеж: ВЭПИ, 2001. – С.18.
6. Кузнецов Л.А., Журавлева М.Г. Исследование непараметрических критериев оценки стохастической связи // Современные сложные системы управления (СССУ/HTCS 2003): сборник трудов научно-практической конференции. – Воронеж: ВГАСУ, 2003. – С. 280-283.
7. Кузнецов Л.А., Журавлева М.Г. Многоаспектный статистический анализ производственных данных //Сложные системы управления и менеджмент качества CCSQM'2007: сборник трудов международной научной конференции. – Старый Оскол: ТНТ, 2007. – С. 71-75.
8. Кузнецов Л.А., Журавлёва М.Г. Непараметрическая кластеризация объектов по выборочным распределениям признаков // Новые технологии в научных исследованиях, проектировании, управлении, производстве: труды Всероссийской конференции. – Воронеж: ВГТУ, 2008. – С. 17.
9. Кузнецов Л.А., Журавлёва М.Г. Кластеризация объектов, характеризующихся интервальными признаками // Современные сложные системы управления: материалы VIII Международной научно-практической конференции СССУ’2008. – Тверь: ТГТУ, 2008. – Ч. 1. – С. 107-112.
10. Кластеризация объектов по выборочным распределениям признаков / Л.А. Кузнецов, М.Г. Журавлёва. – М.: ВНТИЦ, 2008. – № 50200801067 от 22.05.2008.
11. Расширенный статистический анализ данных / М.Г.Журавлёва. – М.: ВНТИЦ, 2008. – № 50200801066 от 22.05.2008.
12. Кузнецов Л.А., Журавлева М.Г., Вишняков Д.Ю. Техника построения многомерных непараметрических карт контроля качества // Электротехнические комплексы и системы управления. – 2008. – № 3. – С.50-53.
13. Кузнецов Л.А., Журавлева М.Г. Непараметрический подход к построению карт контроля технологических процессов [Электронный ресурс] // Технические и программные средства систем управления, контроля и измерения (УКИ’08): труды Российской конференции с международным участием. – Москва: ИПУ РАН, 2008. – С. 98-107. – 1 электрон. опт. диск (DVD-ROM).
14. Кузнецов Л.А., Журавлева М.Г. Исследование целесообразности построения статистических моделей процессов по неполным данным с помощью стратегии EM-алгоритма // Современные проблемы информатизации в экономике и обеспечении безопасности: сборник трудов по итогам XIV Международной открытой научной конференции. – Воронеж: «Научная книга», 2009. – Вып. 14. – С. 50-51.
Подписано в печать 24.04.2009. Формат 6084 1/16.
Бумага офсетная. Ризография. Печ. л. 1,0. Тираж 100 экз. Заказ №.
Издательство Липецкого государственного технического университета.
Полиграфическое подразделение Издательства ЛГТУ.
398600 Липецк, ул. Московская, 30.
