Математическая модель условий электродугового синтеза углеродных нанотрубок
На правах рукописи
Иванов Алексей Иванович
МАТЕМАТИЧЕСКАЯ МОДЕЛЬ УСЛОВИЙ
ЭЛЕКТРОДУГОВОГО СИНТЕЗА
УГЛЕРОДНЫХ НАНОТРУБОК
Специальность 05.13.18 –
АВТОРЕФЕРАТ
диссертации на соискание ученой степени
кандидата технических наук
Воронеж – 2006
Работа выполнена на кафедре «Управление качеством и машиностроительные технологии» ГОУВПО «Воронежской государственной технологической академии».
Научный руководитель:
Официальные оппоненты:
Ведущая организация:
Защита состоится « 9 » 11 2006 г. на заседании диссертационного совета Д 212.035.02 в ГОУВПО «Воронежской государственной технологической академии» по адресу: 394017, г. Воронеж, проспект Революции, д. 19.
Отзывы на автореферат (в двух экземплярах), заверенные гербовой печатью учреждения, просим направлять в адрес совета академии.
С диссертацией можно ознакомится в библиотеке ГОУВПО «Воронежской государственной технологической академии».
Автореферат разослан «___» __________ 2006 г.
Ученый секретарь
диссертационного совета Хаустов И. А.
Общая характеристика работы
Актуальность работы. Развитие науки и техники тесно связано с получением и исследованием новых материалов. В настоящее время большое внимание привлекают углеродные нанотрубки (УНТ), применение которых представляется перспективным в различных областях знания – электронике, химии, биологии и др. Наиболее производительным методом синтеза нанотрубок признается электродуговой.
Проблемой создания эффективной технологии является недостаточность знаний об условиях и механизмах синтеза. Решение данной задачи экспериментальными методами затруднительно. Синтез УНТ проходит в условиях разрежения, в плазме (температура более 4000 К), в окружении инертного газа. Поэтому исследование условий электродугового синтеза методами математического моделирования является эффективным инструментом.
Известные работы авторов Н. А. Поклонского А. Г. Николаева, Р. Дубровского, А. М. Попова, Г. Н. Чурилова, Л. С. Полака, T. W. Ebbesen и др. создают предпосылки для более полного описания условий синтеза, но не отвечают на целый ряд вопросов с точки зрения неоднородности условий формирования депозита.
Совокупность известных математических моделей можно классифицировать по методу моделирования на статистические и физические. Среди совокупности моделей, описывающих физику процесса, можно выделить термодинамические модели (Н. И. Алексеев), энергетические (Г. А. Дюжев, Ю.Е. Лозовик, Н. А. Поклонский), дрейфовые (T. W. Ebbesen, E. G. Gamaly) и магнитно-гидродинамические (А. С. Корнеев, В. Н. Пожелаев).
Известные модели, несмотря на свое многообразие, в полной мере не описывают условия синтеза УНТ и не объясняют неоднородность распределения нанотрубок в депозите на катоде. Исходя из этого разработка и последующее исследование математической модели условий электродугового синтеза УНТ является актуальной и перспективной задачей.
Диссертационная работа выполнены на кафедре «Управление качеством и машиностроительные технологии» Воронежской государственной технологической академии с 2003 по 2006 гг.
Работа проводится при поддержке гранта Российского фонда фундаментальных исследований № 06–08–01310 «Математическое моделирование микромеханических процессов в технологиях формирования нанопленок».
Целью работы является разработка и исследование математической модели, позволяющей выявить условия электродугового синтеза углеродных нанотрубок.
Для достижения поставленной цели в диссертационной работе сформулированы следующие задачи исследования:
- Провести анализ особенностей моделирования электродугового синтеза УНТ.
- Разработать математическую модель движения несущей фазы при электродуговом синтезе углеродных нанотрубок.
- Разработать алгоритм моделирования условий электродугового синтеза УНТ.
- Обосновать адекватность математической модели, описывающей синтез УНТ.
- Реализовать результаты математического моделирования в виде комплекса проблемно-ориентированных программ для проведения вычислительных экспериментов.
- Определить области распределения физических характеристик процесса, выявить условия в области преимущественного синтеза углеродных нанотрубок.
- Исследовать свойства математической модели в условиях варьирования входных параметров с использованием вычислительного эксперимента.
Методы исследования. Для решения поставленных задач в работе использовались методы вычислительной математики и моделирования, теории дифференциальных уравнений в частных производных, теории магнитной гидродинамики и численных методов решения.
Научная новизна.
- Предложен алгоритм математического моделирования условий электродугового синтеза углеродных нанотрубок на основе уравнений магнитной гидродинамики, отличающийся тем, что несущей фазой плазмы являются однозарядные ионы, исходные уравнения преобразуются представлением искомых функций в виде рядов с разложением по безразмерной аксиальной координате, а ряд граничных условий определяется на основе численных методов последовательного приближения.
- Получена математическая модель, отличающаяся описанием изменения однородности плазмы и депозита в зоне формирования УНТ.
- Предложен алгоритм уточнения граничных условий, основывающийся на анализе чувствительности модели к изменению массивов входных данных.
Практическая значимость. Разработан алгоритм расчета размеров областей наибольшей концентрации углеродных нанотрубок, позволяющий вырабатывать оптимальную стратегию проведения синтеза при использовании различного графитового сырья и варьировании конструкционных и технологических параметров синтеза.
По полученному алгоритму разработан пакет прикладных программ, реализующий выдачу рекомендаций для оптимального проведения синтеза. Применение пакета программ позволяет повысить выход углеродных нанотрубок.
Апробация работы. Основные положения и результаты диссертационной работы докладывались и обсуждались на: III международной научно–практической конференции «Моделирование. Теория, методы и средства» (г. Новочеркасск, 2003 г.), на XVII международной научной конференции «Математические методы в технике и технологиях» (г. Кострома, 2004 г.), на XII международном симпозиуме «Динамические и технологические проблемы механики конструкций и сплошных сред» (г. Москва, 2006 г.), на XIX международной научной конференции «Математические методы в технике и технологиях» (г. Воронеж, 2006 г.), а также на XLIII, XLIV, XLV отчетных конференциях Воронежской государственной технологической академии (2004, 2005, 2006 гг.).
Публикации. По теме диссертации опубликовано 9 печатных работ.
Структура и объем работы. Материал диссертации изложен на 138 страницах машинописного текста. Диссертация состоит из введения, пяти глав, выводов, списка литературы и приложений, содержит 79 рисунков и 6 таблиц. Библиография включает 98 наименований.
Содержание работы
Во введении обосновывается актуальность темы диссертации, формулируются цели и задачи исследования, научная новизна и практическая значимость работы.
В первой главе приведены данные, свидетельствующие об актуальности исследования свойств и применений углеродных нанотрубок и ставится задача повышения эффективности технологии их получения.
Сложность обусловлена недостатком знаний о процессах, приводящих к формированию УНТ. Анализ состава плазмы позволил установить, что в зависимости от степени участия и вида углеродной компоненты возможны три механизма образования: из нейтральных частиц углерода, заряженных углеродных частиц и смешанный механизм.
Исследование механизмов синтеза прямыми экспериментальными методами затруднено, вследствие агрессивности плазмы, что выражается в значительных температурах и быстротечности дугового разряда. С учетом этого наиболее целесообразным является исследование условий в области синтеза углеродных нанотрубок на базе известных теоретических методов изучения процессов в плазме электрической дуги. В частности, изучение траекторий движения частиц теоретическими методами позволяет установить области их концентрации и сравнением с распределением УНТ в депозите ответить на вопрос о механизмах синтеза.
Анализ методов описания плазмы и оценочные расчеты основных свойств плазмы показали, что рационально проводить исследования плазмы основываясь на теории магнитной гидродинамики.
Во второй главе построена и проверена на адекватность математическая модель магнитно–гидродинамических процессов в электрической дуге между цилиндрическими графитовыми электродами.

Особенности геометрии исследуемой области и физические особенности дугового процесса позволяют сделать ряд допущений. Течение плазмы рассматривается в цилиндрических координатах. Анализ условий протекания синтеза позволил ввести допущения осесимметричности и стационарности. Т. к. торцевые поверхности электродов плоские, вектор напряженности электрического поля принят постоянным в каждой точке и имеющим только аксиальную составляющую. Действием тангенциальных сил пренебрегали. Плазма рассматривалась как сжимаемая среда. Анализ степени ионизации плазмы показал, что преобладающей является заряженная компонента, преимущественно состоящая из однозарядных ионов углерода, что позволило рассматривать их как несущую фазу.
На оси разряда вводится в рассмотрение плазменное ядро, в котором ток, температура считаются постоянными. Радиус ядра принят равным ![]() .
.
Движение плазмы в межэлектродном зазоре происходит под действием сил (рис. 1): кулоновской ![]() , силы вязкого трения
, силы вязкого трения ![]() , давления
, давления ![]() и силы Ампера
и силы Ампера ![]() .
.
Система исходных уравнений магнитной гидродинамики в цилиндрических координатах, включающая уравнения неразрывности, движения, уравнения электродинамики, с учетом изложенных допущений примет следующий вид:

В соответствии с принятыми допущениями и расчетной схемой граничные условия могут быть записаны в виде:

Здесь: ![]() – размерные аксиальная и радиальная координаты;
– размерные аксиальная и радиальная координаты; ![]() – плотность тока в плазме;
– плотность тока в плазме; ![]() – плотность заряженной компоненты плазмы;
– плотность заряженной компоненты плазмы; ![]() – скорость заряженной компоненты плазмы;
– скорость заряженной компоненты плазмы; ![]() – напряженность электрического поля;
– напряженность электрического поля; ![]() – коэффициент, учитывающий заряд ионов в плазме;
– коэффициент, учитывающий заряд ионов в плазме; ![]() – давление плазмы;
– давление плазмы; ![]() – коэффициент динамической вязкости;
– коэффициент динамической вязкости; ![]() – индукция магнитного поля;
– индукция магнитного поля; ![]() – магнитная проницаемость среды.
– магнитная проницаемость среды.
Для решения системы (1) введем функцию ионного тока ![]() , такую что
, такую что
![]() , (3)
, (3)
где ![]() – элементарная площадка перпендикулярная вектору
– элементарная площадка перпендикулярная вектору ![]() ,
, ![]() . Функция тока имеет физический смысл распределения ионного тока в дуге, при этом по условию сохранения заряда суммарный ионный ток для любого сечения дуги постоянен и выполняется условие квазинейтральности
. Функция тока имеет физический смысл распределения ионного тока в дуге, при этом по условию сохранения заряда суммарный ионный ток для любого сечения дуги постоянен и выполняется условие квазинейтральности 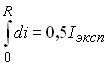 , где
, где ![]() – экспериментально измеряемый ток во внешней по отношению к плазме цепи.
– экспериментально измеряемый ток во внешней по отношению к плазме цепи.
Приближенное решение системы (1) после подстановки (3) искали в виде разложения функций тока, аксиальной компоненты скорости и давления в функциональные ряды по степеням безразмерной аксиальной координаты![]() :
:
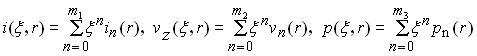 , (4)
, (4)
где ![]() ,
, ![]() ,
, ![]() – коэффициенты разложения,
– коэффициенты разложения, ![]() .
.
Проверкой сходимости выявлено, что с достаточной степенью точности можно ограничится значениями ![]() =2,
=2, ![]() =2 и
=2 и ![]() =1.
=1.
В итоге задача свелась к решению системы уравнений относительно компонент разложения (4).
Часть граничных условий находилась на основе численных экспериментов с математической моделью. При этом использовалось условие достижения заданной точности модели
![]() , (5)
, (5)
где ![]() – неизвестные константы модели,
– неизвестные константы модели, ![]() ;
; ![]() – средний ионный ток, фиксируемый по результатам эксперимента
– средний ионный ток, фиксируемый по результатам эксперимента ![]() ;
; ![]() – ионный ток, рассчитываемый по модели из зависимости
– ионный ток, рассчитываемый по модели из зависимости  ;
; ![]() – допустимая дисперсия расчетных и экспериментальных данных,
– допустимая дисперсия расчетных и экспериментальных данных, ![]() .
.

Для ускорения поиска минимального значения условия (5) использовался последовательный симплекс – метод.
Проверка адекватности математического моделирования показала, что данные по скорости ![]() хорошо совпадают с данными В. C. Мечева и др (рис. 2). Расхождение экспериментальных и теоретических данных составило не более 30 %, что является удовлетворительным при описании плазменных процессов.
хорошо совпадают с данными В. C. Мечева и др (рис. 2). Расхождение экспериментальных и теоретических данных составило не более 30 %, что является удовлетворительным при описании плазменных процессов.

Математическая модель позволила описать движение заряженной компоненты плазмы. Расчеты показали, что в условиях, типичных для синтеза УНТ происходит отклонение ионов от прямолинейного движения, что приводит к снижению концентрации ионов в центре и на краю депозита и их преимущественной концентрация в области ![]() , где
, где ![]() – диаметр электрода. Экспериментальные исследования также показали радиальную неравномерность депозита, причем визуально выделяются 3 зоны – центральная «а», середина «б» и край «в» (рис. 3). Наблюдается соответствие экспериментальных и расчетных размеров областей. По проведенным эмпирическим оценкам и опубликованным данным (например, Дж. Харрис) наибольшая концентрация нанотрубок наблюдается в области «б». Это позволяет сделать вывод об образовании углеродных нанотрубок в зонах с преобладающей концентрацией углеродных ионов. В третьей главе проведен анализ результатов математического моделирования с целью определения условий синтеза УНТ и выполнена оценка влияния точности задания основных параметров модели на точность решений.
– диаметр электрода. Экспериментальные исследования также показали радиальную неравномерность депозита, причем визуально выделяются 3 зоны – центральная «а», середина «б» и край «в» (рис. 3). Наблюдается соответствие экспериментальных и расчетных размеров областей. По проведенным эмпирическим оценкам и опубликованным данным (например, Дж. Харрис) наибольшая концентрация нанотрубок наблюдается в области «б». Это позволяет сделать вывод об образовании углеродных нанотрубок в зонах с преобладающей концентрацией углеродных ионов. В третьей главе проведен анализ результатов математического моделирования с целью определения условий синтеза УНТ и выполнена оценка влияния точности задания основных параметров модели на точность решений.

На основании анализа совпадения расчетных и экспериментальных размеров областей показано, что возможно уточнение рассчитанных по (5) констант модели для увеличения точности прогноза размеров областей (рис. 4). Проведено уточнение констант по методике численного эксперимента, в качестве условия достижения заданной точности использовались расхождение экспериментальных и расчетных относительных площадей областей депозита. Уточнение констант позволило в среднем на порядок увеличить точность прогноза, расхождение составило ![]() ,
, ![]() ,
, ![]() , где
, где ![]() , %.
, %.
Анализ распределения ионного тока (рис. 5) и других параметров электрической дуги показал, что каждая из зон характеризуется специфическими условиями. Область в диапазоне ![]() характеризуется значениями ионного тока
характеризуется значениями ионного тока ![]() А, высокими значениями скорости
А, высокими значениями скорости ![]() м/с, малыми
м/с, малыми  значениями давления
значениями давления ![]() кПа (давление гелия в камере составляет порядка 70 кПа) и значениями индукции магнитного поля
кПа (давление гелия в камере составляет порядка 70 кПа) и значениями индукции магнитного поля ![]() Тл. Для области депозита в диапазоне
Тл. Для области депозита в диапазоне ![]() характерен наибольший ионный ток
характерен наибольший ионный ток ![]() А, значения скорости ионов порядка
А, значения скорости ионов порядка ![]() м/с, давления
м/с, давления ![]() кПа,
кПа, ![]() Тл. Экспериментально показано, что эта зона является более благоприятной для формирования нанотрубок, чем центр. В области
Тл. Экспериментально показано, что эта зона является более благоприятной для формирования нанотрубок, чем центр. В области ![]() плазма состоит преимущественно из нейтральных частиц. Исследования состава депозита в этой области показали преобладание графитовых фракций – неупорядоченного графита, графитовых капсул, графитовых кластеров.
плазма состоит преимущественно из нейтральных частиц. Исследования состава депозита в этой области показали преобладание графитовых фракций – неупорядоченного графита, графитовых капсул, графитовых кластеров.
Для оценки влияния точности входных параметров на точность решения модели проведен ряд численных экспериментов. Для оценки точности использовались значения площадей областей депозита, в частности области «б», как зоны преимущественного формирования УНТ. В качестве входных параметров рассматривались: точность задания граничных условий, констант и погрешности вносимые методом моделирования.

Анализ влияния изменения температуры может быть косвенно проведен через безразмерное значение коэффициента динамической вязкости ![]() , где
, где ![]() – некоторое характерное значение коэффициента динамической вязкости. Изучение зависимости приращения относительных площадей зон депозита от изменения в широких пределах коэффициента динамической вязкости показало, что температура плазмы не оказывает значительного влияния на результаты счета относительных площадей областей по модели (рис. 6).
– некоторое характерное значение коэффициента динамической вязкости. Изучение зависимости приращения относительных площадей зон депозита от изменения в широких пределах коэффициента динамической вязкости показало, что температура плазмы не оказывает значительного влияния на результаты счета относительных площадей областей по модели (рис. 6).
Представляет интерес изменение площади областей при варьировании радиуса электродов. Сравнительный анализ расчетной и экспериментальной площади «б» депозита (рис. 7) показал достаточно хорошее совпадение, расхождение составило не более 5 %.

В работе проводились исследования зависимости площади зоны «б» от начальной скорости ионов, от среднего заряда плазмы, давления. Показано, что при увеличении скорости площадь области «б» практически не изменяется; для снижения среднего заряда ионов, т.е. уменьшении степени ионизации плазмы характерно уменьшение площади; изменение давления практически не оказывает влияния на размеры зоны (изменение площади менее 1 %).
Анализ влияния точности моделирования позволил установить, что метод решения итоговой системы обыкновенных дифференциальных уравнений и шаг интегрирования оказывает влияние на точность решения модели (рис. 8). Для оценки погрешности использовалось значение относительной площади зоны «б» в сравнении со средним экспериментальным ее значением. Установлено, что достаточным для решения является метод Рунге – Кутта 4–го порядка, с разбиением расчетной области на 100 узловых точек.
В четвертой главе изложена методика проведения экспериментов на установке электродугового синтеза углеродных нанотрубок, методы рентгеноструктурного анализа содержания нанотрубок в депозите и алгоритмы обработки экспериментальных данных, использовавшихся при формировании допущений к модели, граничных условий и при анализе математической модели.

В пятой главе на основании полученной модели и обработки данных экспериментов, разработан комплекс программ, позволяющий прогнозировать размеры площадей зон депозита и оценивать выход нанотрубок в зависимости от заданных начальных условий и выдавать рекомендации по оптимизации синтеза.
В приложениях к диссертационной работе приведены справочные данные, листинги программ управления процессом и программ, использовавшихся при расчетах, ряд промежуточных выражений, полученных при построении модели.
Основные выводы и результаты работы
- Анализ особенностей математического моделирования электродугового синтеза углеродных нанотрубок позволил выделить несущую среду плазмы – однозарядные ионы и предложить алгоритм моделирования на основе реологического подхода и уравнений магнитной гидродинамики.
- Границами применимости модели являются условия преимущественного существования однозарядных ионов как несущей фазы, т.е. температура плазмы (3,5
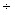 4)·103 К, давление гелия 400
4)·103 К, давление гелия 400 600 Торр и степень ионизации плазмы
600 Торр и степень ионизации плазмы 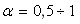 .
. - Разработана математическая модель, описывающая движение несущей фазы плазы между цилиндрическими графитовыми электродами в условиях синтеза УНТ.
- Предложен алгоритм моделирования движение несущей фазы плазы. Ввиду сложности определения граничных условий моделирование проводилось представлением искомых функций в виде рядов с разложением по безразмерным аксиальным координатам на основе численных методов последовательного приближения.
- Выполнена проверка адекватности модели теоретическим данным других авторов, расхождение составило не более 30 %. Выполнено сравнение результатов счета площади областей депозита с экспериментальными результатами, установлено, что расхождение в среднем составляет 10 %. Сравнительный анализ площади области «б» с экспериментальными результатами показал, что расхождение составляет 1–5 % при изменении радиуса в диапазоне 5–12 мм.
- Математическая модель и результаты исследований положены в основу прикладной программы САП для инженерного расчета площади области преимущественного образования углеродных нанотрубок.
- Математическое моделирование показало, что условия электродугового синтеза в депозите различны и можно выделить области: в диапазоне
 , характеризующуюся значениями ионного тока менее 1 А, скорости ионов
, характеризующуюся значениями ионного тока менее 1 А, скорости ионов 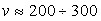 м/с, давления
м/с, давления 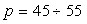 кПа, индукции магнитного поля
кПа, индукции магнитного поля  Тл; область в диапазоне
Тл; область в диапазоне 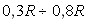 , с характерными значениями ионного тока
, с характерными значениями ионного тока  А, скорости ионов
А, скорости ионов  м/с, давления
м/с, давления 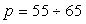 кПа,
кПа,  Тл; область
Тл; область  , в которой плазма состоит преимущественно из нейтральных частиц.
, в которой плазма состоит преимущественно из нейтральных частиц. - На основании вычислительных экспериментов с математической моделью установлены определяющие параметры процесса и область их варьирования: средний экспериментальный ток
 А, радиус электрода в диапазоне
А, радиус электрода в диапазоне 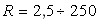 мм, размер межэлектродного зазора
мм, размер межэлектродного зазора  мм.
мм.
Основные положения работы опубликованы
в следующих работах:
- Иванов, А. И. Математическое моделирование электродугового процесса синтеза углеродных нанотрубок [Текст] / Г.В. Абрамов, С.Н. Аксенов, А.И. Иванов, Г.В. Попов // Материалы XIX международной научной конференции «Математические методы в технике и технологиях», г. Воронеж. – 2006. – С. 142–147.
- Иванов, А. И. Магнитная гидродинамика как инструмент описания механизма образования углеродных нанотрубок [Текст] / А.И. Иванов, Г.В. Попов //"Вопросы современной науки и практики. Университет им. В.И. Вернадского". – 2006. – №4. –С. 34 – 39.
- Иванов, А. И. Гидродинамическое описание синтеза углеродных нанотрубок [Текст] / А.И. Иванов, Г.В. Попов // Материалы XLIV отчетной конференции за 2005 г., Воронеж, ВГТА. – С. 105–107.
- Иванов, А. И. Технология углеродных нанотрубок. Проблемы и пути решения. [Текст] / С. Н. Аксёнов, С.В. Ершов, А. И. Иванов, Г. В. Попов // Вестник ВГТА. –2005. – № 10.– С. 162–168.
- Иванов, А. И. Математическая модель гидродинамических процессов в плазме при синтезе нанотрубок [Текст] / А. И. Иванов, Г.В. Попов, С. Н. Аксенов // Материалы XLIV отчетной конференции за 2005 г. – Воронеж: ВГТА – С. 105–107.
- Иванов, А. И. Гидродинамическое описание динамики синтеза углеродных нанотрубок [Текст] / А. И. Иванов, Г.В. Попов // Материалы XII международного симпозиума «Динамические и технологические проблемы механики конструкций и сплошных сред».– М. : МАИ. – 2006 г. – С. 163 –165.
- Иванов, А. И. Диагностика процесса получения углеродных нанотрубок [Текст] / С. Н. Аксенов, А. И. Иванов, Г.В. Попов // XVII Международная научная конференция «Математические методы в технике и технологиях». – Кострома. – 2004.– т. 10. – С. 88–90.
- Иванов, А. И. Физическое моделирование процесса получения углеродных нанотрубок [Текст] / С. Н. Аксенов, А. И. Иванов, Г.В. Попов // Материалы III Международной научно–практической конференции. – Новочеркасск : ЮРГТУ (НПИ). – 2003. – С. 36–39
- Иванов, А. И. Экспериментальные и теоретические предпосылки синтеза углеродных нанотрубок [Текст] / / С. Н. Аксенов, А. И. Иванов, Г.В. Попов // Материалы XLIII отчетной конференции за 2004 г.– Воронеж : ВГТА – С. 174 –175.
Подписано в печать Формат 60![]() 84 1/16. Бумага офсетная. Ризография. Усл. печ. л. 1,0. Тираж 100 экз. Заказ
84 1/16. Бумага офсетная. Ризография. Усл. печ. л. 1,0. Тираж 100 экз. Заказ
ГОУВПО «Воронежская государственная технологическая
академия» (ГОУВПО «ВГТА»)
Адрес академии и участка оперативной полиграфии
ГОУВПО «ВГТА»:
394017 Воронеж, пр. Революции,19

