Разработка и исследование комплексного гибридного генетического алгоритма разбиения схем
На правах рукописи
Дуккардт Александр Николаевич
РАЗРАБОТКА И ИССЛЕДОВАНИЕ КОМПЛЕКСНОГО ГИБРИДНОГО ГЕНЕТИЧЕСКОГО АЛГОРИТМА РАЗБИЕНИЯ СХЕМ
Специальность: 05.13.12 – Системы автоматизации проектирования
Автореферат
диссертации на соискание ученой степени
кандидата технических наук
Таганрог - 2007
Работа выполнена в Южном федеральном университете.
Научный руководитель: доктор технических наук, профессор
Лебедев Борис Константинович.
Официальные оппоненты: заслуженный деятель науки РФ
доктор технических наук, профессор
Чернышев Юрий Олегович (РГАСХМ,
г. Ростов-на-Дону),
кандидат технических наук, доцент
Родзин Сергей Иванович (Технологический институт Южного федерального университета в г. Таганроге).
Ведущая организация: Федеральное государственное унитарное предприятие «Таганрогский научно-исследовательский институт
связи», г. Таганрог.
Защита диссертации состоится 23 августа 2007 г. в 1420 на заседании диссертационного совета Д 212.208.22 при Южном федеральном университете по адресу: 347928, Таганрог, пер. Некрасовский, 44, ауд. Д-406.
С диссертацией можно ознакомиться в Зональной научной библиотеке Южного федерального университета по адресу: 344000, Ростов-на-Дону, ул. Пушкинская, 148.
Автореферат разослан « 20 » июня 2007 г.
Ученый секретарь
диссертационного совета Д 212.208.22,
доктор технических наук, профессор Целых А.Н.
Общая характеристика работы
Актуальность темы. Современный этап развития человеческой цивилизации, характеризующийся высокими темпами роста развития науки и техники, нелегко представить без использования изделий микроэлектронной промышленности в повседневной жизни. Использование различных достижений микроэлектроники при производстве интегральных схем (ИС), больших ИС (БИС), сверхбольших ИС (СБИС), суперкристаллов, обуславливает повышение основных характеристик электронных вычислительных средств (ЭВС) проектируемых на их основе, например, снижаются массогабаритные показатели, уменьшаются потребляемая и рассеиваемая мощности, повышаются быстродействие и надёжность. Современные ЭВС, такие как, персональные компьютеры, оборудование вычислительных и специальных пользовательских сетей, контроллеры и другие управляющие устройства и системы содержат в своём составе десятки, а иногда и сотни СБИС. Однако к характеристикам ЭВС предъявляются неоднозначные требования в зависимости от класса и назначения аппаратуры, использующей СБИС и суперкристаллы. Какая-то из характеристик или их совокупность могут быть определяющими, тогда как требования к остальным снижаются.
Применение на этапе проектирования САПР способствует повышению степени интеграции СБИС на уровне узлов, блоков и всей системы в целом. Сегодня СБИС способны выполнять сложнейшие наборы функции, а геометрические размеры транзисторов сократились до 0.18 мкм и меньше. Неуклонное повышение степени интеграции СБИС привело к тому, что в них более 60% общей временной задержки сигнала приходится на задержки в межсоединениях. Рост размера области, отводимой для межсоединений, опережает рост размера области, предназначенной для активных элементов. В чипе, содержащем 10 миллионов транзисторов и использующем 4 слоя металлизации, около 40% площади отводится под межсоединения.
Сейчас, на всех стадиях проектирования топологии СБИС интенсивно используют средства автоматизации проектирования (САПР) и многие фазы могут быть полностью или частично автоматизированы. Важнейшим этапом в цикле проектирования СБИС, является этап конструкторского проектирования, на котором решаются задачи разбиения, планирования, размещения, трассировки, упаковки, верификации.
Поскольку схема может содержать несколько миллионов транзисторов, то невозможно спроектировать топологию всей схемы целиком в связи с ограниченными возможностями вычислительных средств, поэтому схема разбивается группировкой компонентов в блоки. В результате разбиения формируется множество блоков и множество соединений между блоками.
В связи с большой сложностью и размерностью задач конструкторского проектирования, а также с возникновением новых тенденций в технологии изготовления СБИС, появляется необходимость в разработке новых направлений, методик, алгоритмов для решения данного класса задач.
В этой связи диссертационная работа посвящена решению актуальной и важной научно-технической проблемы: разработке и исследованию новых и развитию существующих алгоритмов решения задачи разбиения схемы, обеспечивающих не только достижение требуемых результатов, но и поднимающих процесс исследования на высокий уровень, не требующий от ученых-исследователей навыков в области программирования.
Данная работа является развитием результатов исследований, проводимых на кафедре САПР Таганрогского технологического института Южного федерального университета в рамках приоритетного национального проекта «Образование», а также аналитической ведомственной целевой программы «Развитие научного потенциала высшей школы» (2006 – 2008 гг.) на тему «Разработка бионических методов и принципов поиска оптимальных решений при проектировании».
Цель диссертационной работы состоит в разработке и исследовании комплекного гибридного генетического алгоритма разбиения схем с учетом числа межузловых связей и общей временной задержки. Для достижения поставленной цели в работе были решены следующие основные задачи:
- Модифицирован аддитивный критерий для оценки качества решения задачи разбиения с учетом числа внешних связей и временной задержке сигнала.
- Построена архитектура генетического поиска для решения задачи разбиения схем.
- Разработаны способы представления разбиения схем, учитывающие специфику задачи. Предложенные структуры, кодирующие альтернативные решения, реализованы с использованием гомологичных хромосом и отличаются тем, что кодирование и декодирование имеет линейную сложность, а использование генетических операторов не приводит к образованию недопустимых решений.
- Разработаны гибридные генетические процедуры, процедура локального улучшения, алгоритм адаптации множества виртуальных популяций и отдельных решений.
- Построены модифицированные генетические операторы.
В качестве методов решения поставленных задач в диссертационной работе использовались элементы теорий множеств, алгоритмов, графов, а также методы и средства эволюционного моделирования, генетического поиска, теории вычислительных систем, параллельного и объектно-ориентированного программирования.
Научная новизна работы заключается в решении задачи разбиения схем с использованием гибридных генетических процедур. В работе:
- Построена архитектура генетического поиска для решения задачи разбиения схем.
- Разработаны и теоретически обоснованы новые технологии и механизмы генетического поиска, повышающие его эффективность – распараллеливание процесса поиска на базе виртуального набора популяций, адаптация виртуального набора популяций, чередование генетических операторов и типов хромосом в процессе поиска.
- Разработаны и исследованы с учетом специфики решаемых задач, с ориентацией на большие размерности принципы кодирования решений в виде структурированных и многохромосомных представлений, отличающихся гомологичностью, простотой, линейной оценкой трудоемкости для задачи разбиения схем
- Разработаны механизмы преодоления алгоритмом «локальных ям», и увеличения скорости поиска на основе эвристических методов и метода моделирования отжига.
К числу наиболее важных научных результатов диссертации относятся:
- новая архитектура комплексного гибридного генетического алгоритма для решения задачи разбиения схем;
- принципы кодирования решений и структуры хромосом, учитывающие специфику решаемых задач с ориентацией на задачи большей размерности, отличающиеся гомологичностью, линейными оценками пространственной и временной сложности и имеющих широкую сферу применения;
- новые технологии и механизмы генетического поиска на базе адаптируемого виртуального набора популяций с альтернативными структурами хромосом и генетических операторов;
- новые технологии и средства повышения эффективности выхода из “локальных ям” и снижения общего времени поиска квазиоптимальных решений;
- новые и усовершенствованные операторы генетического поиска обеспечивающие снижение времени поиска.
Практическая ценность работы заключается в реализации программного комплекса «Partitioning», использование которого позволяет на 15-20% ускорить процесс решения задачи разбиения схем, при этом получать решения, не уступающие по качеству по сравнению с существующими аналогами, благодаря использованию новых способов представления решений в задаче разбиения, а так же модифицированной архитектуре генетического поиска. Данная среда позволяет автоматизировать процесс разбиения, сделать его доступным для специалистов различных областей науки, не обладающих навыками программирования.
Реализация и внедрение результатов работы. Основные теоретические и практические результаты диссертационной работы использованы в госбюджетных научно-исследовательских работах Технологического института Южного федерального университета «Разработка теории и принципов построения интеллектуальных систем принятия решений при проектировании на основе квантовых вычислений и бионических методов поиска» и «Разработка бионических методов и принципов поиска оптимальных решений при проектировании», а так же в рамках приоритетного национального проекта «Образование».
Материалы диссертации использованы в учебном процессе на кафедре САПР ТТИ ЮФУ при преподавании следующих дисциплин: «Методы оптимизации», «Эволюционное моделирование и генетические алгоритмы», «Автоматизация конструкторского и технологического проектирования».
Апробация основных теоретических и практических результатов работы. Результаты диссертации докладывались и обсуждались на Всероссийских и Международных научно-технических конференциях: «Интеллектуальные САПР», (г. Таганрог, 2003 - 2005 гг.); VII Всероссийская научная конференция студентов и аспирантов «Техническая кибернетика, радиоэлектроника и системы управления», (г. Таганрог, 2004г.); II Всероссийская научная конференции молодых ученых, аспирантов и студентов «Информационные технологии, системный анализ и управление», (г. Таганрог, 2004 г.); III Всероссийская научная конференции молодых ученых, аспирантов и студентов «Информационные технологии, системный анализ и управление», (г. Таганрог, 2005 г.); Международная научно-техническая конференция «Интеллектуальные САПР», (г. Таганрог, 2006 г.).
Получено свидетельство об официальной регистрации программы для ЭВМ.
Публикации. По теме диссертационной работы опубликовано 7 печатных работ, сделано 2 доклада на Всероссийских и Международных научно-технических конференциях.
Структура и объем работы. Диссертационная работа состоит из введения, четырех глав и заключения, изложенных на 139 страницах, содержит 38 рисунок, 17 таблицы, 103 наименований библиографии и приложения.
КРАТКОЕ СОДЕРЖАНИЕ РАБОТЫ
Во введении дано обоснование актуальности темы диссертационной работы, описаны цель работы и основные научные положения, выносимые на защиту, определены круг задач, объект и предмет исследования, указаны методы исследования, показаны научная новизна и практическая значимость, а так же подтверждены достоверность полученных результатов.
В первой главе рассмотрены основные проблемы и перспективы решения задач разбиения, обоснован выбор критериев оценки качества разбиения, приведена постановка задачи разбиения схем с учетом временных задержек. А так же в результате проведенного анализа аналогов выявлены недостатки существующих моделей временных задержек:
В ходе диссертационной работы разработан алгоритм разбиения схем, который минимизирует число разрезов цепи С и величину оценки суммарной временной задержки D. Однако, оптимизация величины С не обязательно приводит к оптимизации величины D и наоборот. По этой причине в настоящей работе применяется обобщенная функция оценки, отвечающая требованиям многокритериальной оптимизации.
, (1)
где p1 и p2 компоненты вектора предпочтения
Итак, решаемая в диссертационной работе дискретная задача разбиения может быть сформулирована следующим образом.
Задача разбиения схемы состоит в отыскании такого разбиения k из множества возможных разбиений K некоторого гиперграфа H, представляющего модель схемы, при котором минимизируется (либо максимизируется) некоторая величина F, являющаяся весовой функцией разбиения, и учитываются все поставленные в задаче ограничения.
Пусть Н = (Х, Е) – гиперграфовая модель схемы, где Х = {xi | i = l, 2, ..., n} – множество вершин, моделирующие элементы схемы, Е = {еj | ej X, j = l, 2, ..., m} – множество гиперрёбер, моделирующие электрические цепи. Вес вершин задается множеством = {i | i = l, 2, ..., n}, вес рёбер — = {j | j = l, 2, ..., m}.
Необходимо сформировать К – узлов, т. е. множество Х разбить на К непустых и непересекающихся подмножеств Хv:
Х = Хv, (i, j), Xi Xj = , Хv . (2)
Одним из параметров целевой функции F является количество рёбер, пересекающих разрез:
С = {ej | (v) [ej Хv ej]} (3)
Величина оценки задержки D в выражении (1) выражается комбинацией двух факторов, которые напрямую влияют на задержку схемы: задержка цепей, количество разрезов каждой цепи.
, (4)
где i – вес ребра; ei коэффициент, принимающий значение 1 или 0, в зависимости от того разрезается ребро или нет; |EK| – количество ребер в гиперграфе H; Dj – текущая задержка j-ой цепи(ребра); kj – число разрезов цепи j.
Предлагаемая оценка задержки цепи Dj содержит два компонента. Первый – это задержка вентилей. Задержка вентилей считается постоянной и в дальнейшем не учитывается. Второй компонент – это задержка проводников, которая оценивается, используя модель задержки Эльмора для ребра e (ребро соответствует проводнику) в соответствии со следующей формулой:
, (5)
где Re – общее сопротивление проводника e, Ce – общая емкость проводника e, Сi –общая емкость истоков каждой цепи. Для вычисления Re и Ce нам необходимо длина каждого ребра. Средняя длина цепи[116], соединяющая m элементов определяется по формуле:
, (6)
где ai и bi – геометрические размеры узлов между которыми распределены элементы цепи;,, –настроечные параметры, вычисленные как = 1.1, = 2.0, = 0.5. Удельное сопротивление на единицу длины проводника считаем r = 0.115, удельная емкость на единицу длины проводника с = 0.00015.
Отмечено, что при решении задач разбиения схем эффективно использовать модели и методы, учитывающие предварительные знания о решаемых задачах.
Приведены модифицированная классификация и краткий обзор существующих методов и критериев оценки качества эффективности разбиения. Указано, что перспективна разработка совместных генетических и поисковых алгоритмов, позволяющих решать проблемы предварительной сходимости и получать наборы квазиоптимальных решений.
Во второй главе выбрана стратегия поиска.
В реальных условиях вместимость узлов (блоков) разбиения намного превосходит число элементов соединяемых одной цепью. Поэтому если ребро назначается в узел целиком, оно не попадает в разрез, что соответственно приводит к уменьшению числа внешних связей. Данный подход к решению поставленной задачи наиболее точно отражает ее специфику и учитывает критерий числа межмодульных связей. Однако при данном подходе не все ребра могут быть назначены целиком. Ребра, назначаемые последними, могут быть помещены в различные узлы. И существует некоторая вероятность того, что можно улучшить полученное решение путем незначительных изменений составов узлов. Такое изменение можно сделать путем перестановок вершин между узлами.
На основе приведенных рассуждений, в работе была выбрана стратегия поиска «Эволюция – Эволюция». Обобщенная схема приведена на рисунке 1.
Рисунок 1. Обобщенная схема стратегии поиска «Эволюция – Эволюция»
Здесь под входными параметрами понимается:
- разбиваемая схема;
- ограничения;
- критерии и цели оптимизации.
ГА – генетический алгоритм с элементами альтернативного развития решений, решает задачу разбиения путем назначения гиперребер в узлы.
Миграция – производит выделение в полученной популяции лучших решений и передача их в качестве параметров на следующий шаг поиска
ГГА – гибридный генетический алгоритм, производит улучшение полученных решений на предыдущем шаге путем случайных перестановок вершин между узлами.
Данный подход к решению поставленной задачи разбиения требует разработки новых методов представления альтернативных решений. Поэтому в ходе выполнения работы были разработаны новые методы кодирования и декодирования альтернативных решений, обеспечивающие гомологичность закодированных решений, что позволяет использовать модификации генетических операторов, близких к естественным.
Поэтому для первого генетического алгоритма предложен метод кодирования при котором задается размещение гиперребер по узлам. Предлагается представлять решение поставленной задачи в виде двух векторов P1 и P2:
- P1 – последовательность назначения ребер в узлы – определяет, в какой последовательности будут назначаться ребра.
- P2 – последовательность формирования узлов – определяет, в какой последовательности будут формироваться узлы.
Эта методика кодирования учитывает специфику поставленной в работе задачи и подразумевает получение качественных (с точки зрения оценки) решений еще на стадии кодирования решения. Это можно объяснить тем, что существует большая вероятность назначить все вершины инцидентные ребру в один узел, что приведет к существенному уменьшению числа внешних связей.
Решение задачи представляется набором последовательностей, поэтому решения, закодированные в предложенном генетическом алгоритме, являются мультихромосомными.
Рассмотрим принцип кодирования последовательности назначения ребер в узлы – P1. Хромосома H1 состоит из генов, число которых на единицу меньше числа назначаемых ребер m:
H1={gt| t = 1, 2, …, (m-1)}.
Ген gt может принимать значения в интервале 
, то есть чем больше порядковый номер t, тем меньшее значение он может принять.
Для декодирования хромосомы используется опорный вектор номеров ребер 
. Процесс декодирования хромосомы H1 начинается с первого гена g1. В результате декодирования на шаге t гена gt, по вектору B1 определяется номер назначаемого на шаге t ребра. После декодирования очередного гена gt вектор B1 уменьшается путем удаления из него номера элемента, определенного при декодировании gt. Кодирование и декодирование последовательности формирования узлов P2 проводиться аналогичным способом.
ГГА производит улучшение решений путем случайных перестановок элементов(вершин) между узлами. Поэтому в данном алгоритме необходимо знать точных состав узлов. Следовательно, предложено решение представлять в виде дихотомического дерева G.
Дихотомическое разбиение вектора 
можно задать с помощью вектора di, состоящего из нулей и единиц. Размерности di и 
совпадают. Если элемент вектора di равен 0, то соответствующий элемент вектора 
принадлежит первому подмножеству; если – 1, то второму. 
. Например, {V=<1,3,7,8,9,10,2>; d=<0,1,1,0,0,1,0>}, {V1=<1,8,9,2>, V2=<3,7,10>}.
Таким образом, разбиение V на Vv можно задать с помощью набора векторов 
, число (k -1) которых равно числу вершин дерева G, подвергающихся ветвлению; k – число формируемых узлов 
. Каждый вектор di кодируется и представляется в виде хромосомы Hi. Суть кодирования заключается в том, что для каждой единицы задается ее месторасположение относительно нулей в векторе di. В качестве базы кодирования хромосом используется zi нулей, относительно которых в di размещаются единицы.
Число генов Hi равно числу единиц в соответствующем векторе di, а значения gij лежит в интервале 1<=gij<=zi+1. Восстановление di по Hi осуществляется следующим образом. Пусть Hi=<2,2,4,1>, ei=4 zi=3. Имеется база из zi=3 нулей. Номера позиций в базе с 1 по 4. Это значит, что в позициях базы, номера которых равняются значениям генов, необходимо поместить единицы. В нашем случае di=<1,0,1,1,0,0,1>.
Необходимо отметить, что в соответствии с процедурой декодирования, порядок расположения генов в хромосоме не имеет значения, важно только, какие значения имеют гены. Это приводит к избыточности пространства решений, представленного хромосомами. Пусть Pi – число перестановок генов в хромосоме Hi. Тогда одному решению задачи разбиения соответствует 
наборов хромосом.
Устранить избыточность можно путем использования модифицированной структуры хромосомы, отличающейся от основной тем, что в пределах каждой хромосомы Hi гены упорядочены по возрастанию их значения.
Используемые в работе способы представления альтернативных решений требуют разработки новых генетических операторов. Генетические операторы, такие как оператор кроссинговера и оператор мутации, были модифицированы таким образом, что бы их можно было применять для мультихромосомных представлений. В модифицированном операторе кроссинговера заложен принцип многодетной семьи, то есть от одной пары родителей может получиться до 6 потомков. Для этого введен параметр n, регулирующий число потомков. Разное количество потомков получается путем различных последовательностей применение оператора рекомбинации и оператора кроссинговера к одной и той же паре родителей. Модифицированные генетические операторы имеют сложность O(n).
В третьей главе разработана структура комплексного гибридного генетического алгоритма (ГАЭАР), которая представлена на рисунке 2. Рассмотрим более подробно блоки входящие в структуру алгоритма.
Блок генерации начальной популяции — предназначен для создания начального множества (популяции) особей. Применение рассмотренного выше способа кодирования особи позволяет уменьшить поисковое пространство и, следовательно, сокращается время решения задачи, поскольку алгоритму требуется меньшее число итераций для нахождения оптимального решения.
Так как процесс кодирования и декодирования решений основывается на опорные вектора, то в работе используется набор виртуальных популяций, что позволяет распараллелить процесс генетического поиска.
Блок модифицированных процедур ГО — набор процедур, реализующих различные генетические операторы, использующих динамические параметры и предназначенных для формирования особей-потомков, отличающихся более высоким значением целевой функции по сравнению с родительскими особями.
Блок локального улучшения решений — процедура, основанная на эвристике локальной оптимизации и методе моделирования Отжига, которая предназначена для формирования нового решения, путем анализа текущей популяции, подпопуляции, либо отдельных хромосом.
В качестве предлагаемой эвристики локального улучшения решений в разработанном алгоритме, используется эвристика, основанная на моделировании Отжига, которая генерирует за один шаг одно хорошее решение. Данная эвристика изменяет состав кусков графа случайно-направленным образом.
На каждой итерации выполняется операция преобразования начального решения. Рассмотрим операцию преобразования. Для каждого узла ki K выбирается вершина vl ki Выбор вершины vl осуществляется по нижеописанному алгоритму:
- vj ki рассчитывается величина pj и откладывается на отрезке [0; 1]
(7)
где nouter – число внешних связей вершины, ninner – число внутренних связей вершины, m – число вершин в узле. Если ninner = 0, то принимается, что ninner = 1. Величина 
определяет вероятность выбора вершины vj, при этом если вершина не имеет внешних связей, то nouter принимается равным единице. Таким образом, достигается отличная от нуля вероятность выбора вершин, не имеющих внешних связей.
- На интервале [0; 1] генерируется число p, подчиняющееся нормальному закону распределения.
- Вершина vl ki выбирается таким образом, чтобы выполнялось условие p (pl-1; pl].
То есть из каждого узла ki K выбирается строго по одной вершине, следовательно, количество выбранных вершин равно |K|. Далее происходит перераспределение выбранных вершин по узлам в соответствии со следующим алгоритмом:
- Все выбранные вершины переносятся в «Буфер» - множество B (|B| = |K|).
- Выбирается первый не заполненный узел kj K.
Рисунок 2. Структурная схема комплексного гибридного генетического алгоритма
- vi B рассчитывается количество связей с узлом kj – qij.
- vi B рассчитывается величина pij и откладывается на отрезке [0; 1].
(8)
- На интервале [0; 1] генерируется число p, подчиняющееся нормальному закону распределения.
- вершина vi назначается в узел kj если выполняется условие
p (pi-1j;pij], и удаляется из B.
- Если B то переходим на п.2, в противном случае перераспределение вершин между узлами считается завершенным.
После этого производится оценка полученного решения. После принятия или отклонения решения начинается новая итерация алгоритма.
Блок альтернативного развития особей – блок декодирования, полученных с помощью модифицированных генетических операторов, потомков альтернативными методами. Такой подход позволяет получить различные решения (фенотип), которые закодированы одним и тем же генетическим кодом.
Для имитации развития особи в различных условиях в алгоритм было введено несколько операторов декодирования генетического материала. Причем для большего соответствия естественным процессам была введена случайная величина n выбираемая из множества {1, 2}, которая определяет количество используемых операторов декодирования. На рисунке 3 приведена структурная схема, отображающая механизм альтернативного развития особи при n = 2.
Алгоритм работы блока реализующего предложенный механизм:
- На вход блока реализующего предложенный механизм подается особь, полученная после кроссинговера или мутации.
- Производится оценка величины n.
- Копирование входящей особи n раз. Эта операция названа «Клонированием».
- Для каждой копии особи вызывается свой ранее определенный оператор декодирования.
- После декодирования производится оценка полученных решений.
- Выбор одного лучшего решения.
Рисунок 3 Структурная схема, отображающая механизм альтернативного развития особи при n = 2.
В разработанном алгоритме используется два оператора декодирования:
- последовательного назначения гиперребер в узлы;
- оператор назначения гиперребер в узлы, основанный на реберной связности.
Блок Миграции – После завершения работы первого ГА производит выборку решений для создания популяции для следующего ГА.
Блок Адаптации – введен для увеличения скорости генетического поиска. На каждой итерации осуществляется анализ набора популяций и на основе результатов производится адаптация. Суть заключается в смене опорного вектора Bl, если в течение некоторого числа генераций в виртуальной популяции B = {Bl|П} не появляются индивидуальности с лучшим значением целевой функции.
В четвёртой главе описаны задачи и цели вычислительного эксперимента. Составлена программа проведения эксперимента. Приведены результаты вычислительного эксперимента при анализе разработанного алгоритма на тестовых примерах. Произведено сравнение разработанного алгоритма с существующими аналогами решения задач разбиения схем. Наиболее значимые результаты вычислительного эксперимента отражают следующие таблицы и графики.
Рисунок 4 Зависимость среднего времени поиска для стратегий поиска
Рисунок 5 Зависимость среднего значения ЦФ для стратегий поиска
На рисунках 4, 5 приведены зависимости времени поиска и качества решения от количества вершин для различных стратегий поиска. Проанализировав графики можно сделать выводы, что при использовании стратегии «Эволюция – Эволюция» требуется в среднем на 50% больше процессорного времени, но в то же время, при этом алгоритм находит в среднем на 15,5% лучшее решение, чем при использовании поиска на основе стратегии «Эволюция». Приведенные практические результаты доказывают эффективность примененной стратегии поиска и выбор представления решения задачи разбиения.
Таблица 1
Описание тестовых схем
| Circuit | PI/PO | No. of gates |
| cordic | 23/2 | 881 |
| misex3 | 14/14 | 1349 |
| X3 | 135/99 | 1369 |
| c6288 | 32/32 | 2435 |
| s15850 | 39/75 | 4321 |
| frisc | 19/16 | 4400 |
| elliptic | 130/112 | 4711 |
Таблица 2
Результаты вычислительных экспериментов
| Cordic | misex3 | X3 | c6288 | s15850 | Frisc | Elliptic | ||
| Pure hMetis | D. | 21,9 | 67,6 | 18,78 | 59,21 | 81,14 | 169,33 | 271,02 |
| Cut | 327 | 543 | 211 | 182 | 617 | 838 | 508 | |
| CPU (s) | 2 | 5 | 4 | 31 | 28 | 34 | 16 | |
| Net& Path Based | D. | 16,41 | 61,16 | 16,65 | 56,26 | 78,93 | 150,2 | 205,25 |
| Cut | 278 | 614 | 261 | 216 | 671 | 869 | 619 | |
| CPU (s) | 5 | 13 | 6 | 80 | 37 | 61 | 22 | |
| PPFF | D. | 20,6 | 64,3 | 16,04 | 59,19 | 82,1 | 165,17 | 231,33 |
| Cut | 313 | 540 | 228 | 201 | 615 | 851 | 510 | |
| CPU (s) | 6 | 14 | 8 | 79 | 43 | 66 | 25 | |
| VPR | D. | 21,5 | 64,3 | 17,04 | 60,01 | 80,73 | 167,2 | 233,02 |
| Cut | 319 | 543 | 216 | 204 | 622 | 843 | 513 | |
| CPU (s) | 10 | 18 | 13 | 85 | 47 | 71 | 27 | |
| ГАЭАР | D. | 15,93 | 60,7 | 17,05 | 56,26 | 77,01 | 153,3 | 204,97 |
| Cut | 280 | 610 | 253 | 209 | 651 | 842 | 567 | |
| CPU (s) | 4 | 14 | 6 | 73 | 31 | 49 | 17 |
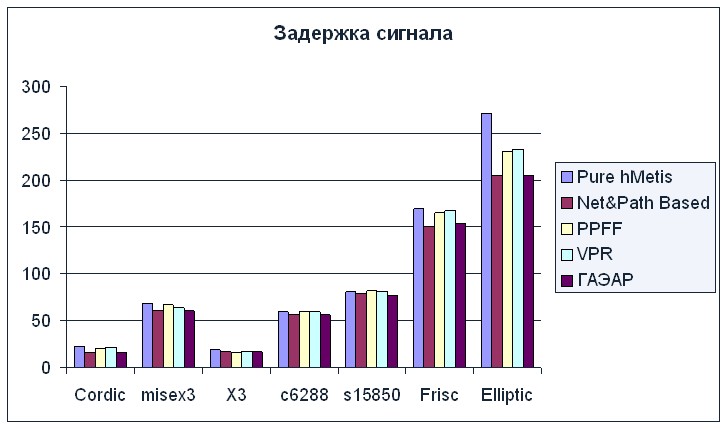
Рисунок 6 Результаты сравнений по критерию «временная задержка»
Рисунок 7 Результаты сравнений по критерию «число межмодульных соединений»
Рисунок 8 Результаты сравнений по времени выполнения
Из приведенных данных можно сделать вывод, что разработанный алгоритм позволяет находить решения не уступающие по качеству, а иногда и превосходящие результаты полученные с использованием других алгоритмов. При этом время, затраченное на поиск решения, меньше в среднем на 15%.
В заключении сформулированы основные выводы и результаты диссертационной работы.
В приложении приведены акты об использовании результатов диссертационной работы и приведено описание программного продукта
ОСНОВНЫЕ РЕЗУЛЬТАТЫ РАБОТЫ
В ходе выполнения диссертационной работы получены результаты:
- На основе анализа существующих методов разбиения обоснована актуальность разработки гибридных генетических процедур, обеспечивающих получение квазиоптимальных решений за приемлемое время поиска.
- Сформулированы стратегии и принципы поиска, построена архитектура поиска на основе методов эволюционного моделирования, позволяющих эффективно управлять поиском, повышать быстродействие системы, получать квазиоптимальные решения за приемлемое время.
- Предложены новые принципы кодирования и декодирования решений, обеспечивающие гомологичность закодированных решений, что позволяет использовать генетические операторы близкие к естественным.
- Предложены новые и модифицированные генетические операторы, обеспечивающие уменьшение времени поиска.
- Разработана и реализована эвристика локального улучшения решений на основе метода моделирования отжига, позволяющая сократить время поиска.
- Разработана и теоретически обоснована новая технология генетического поиска на базе виртуального набора популяций на одном наборе генотипов для распараллеливания генетического поиска без увеличения сложности алгоритма.
- Разработан программный модуль, позволяющий решать задачу разбиения схем, проводить сравнительный анализ предложенного алгоритма с существующими, на основе выполнения тестовых задач.
- Выполнены тестирование и обработка экспериментальных данных, что позволило уточнить теоретические оценки временной сложности разработанных алгоритмов размещения. Проведенные исследования показали, что разработанный комплекс позволяет находить решения не уступающие по качеству, а иногда и превосходящие результаты полученные с использованием других алгоритмов. При этом время, затраченное на поиск решения, меньше в среднем на 15%.
ОСНОВНЫЕ ПУБЛИКАЦИИ ПО ТЕМЕ ДИССЕРТАЦИИ
1. Дуккардт А.Н., «Методы Генетического поиска для мультихромосомных представлений», VII Всеросийская научная конференция студентов и аспирантов «Техническая кибернетика, радиоэлектроника, и системы управления», Таганрог, 2004, с. 108
2. Дуккардт А.Н., Лебедев Б.К. «Подход к решению задачи разбиения на основе квантовых алгоритмов», XI МНПК студентов и молодых ученых «Современные техника и технологии СТТ’2005» г. Томск
3. Дуккардт А.Н., Лебедев Б.К., «Разбиение на основе комбинированных генетических процедур», Известия ТРТУ. Тематический выпуск "Интеллектуальные САПР". Таганрог: Изд-во ТРТУ, 2006. №8. С. 46-51
4. Дуккардт А.Н., «Решение задачи разбиения на основе процедуры «Выбивания»», Известия ТРТУ. Тематический выпуск "Интеллектуальные САПР". Таганрог: Изд-во ТРТУ, 2006. №6. С. 63-66
5. Дуккардт А.Н., «Разбиение на основе процедуры «Выбивания»», VIII всероссийская научная конференция студентов и аспирантов «Техническая кибернетика, радиоэлектроника и системы управления» Таганрог: Изд-во ТРТУ, 2006. С. 89-90
6. Дуккардт А.Н.,, «Разбиение на основе процедур «Выбивания» и «Дублирования»», IV Всероссийская научная конференция молодых учёных, аспирантов и студентов «Информационные технологии, системный анализ и управление». Таганрог: Изд-во ТРТУ, 2006. С. 199-201
7. Дуккардт А.Н., Лебедев Б.К., «Гибридный генетический алгоритм с элементами антимонопольного развития», Известия ТРТУ. Тематический выпуск "Интеллектуальные САПР". Таганрог: Изд-во ТРТУ, 2007. №1. С. 86-91
В работах [2, 3, 7], опубликованных в соавторстве, лично автору принадлежат следующие результаты - разработка методов альтернативного развития решений, модификация аддитивного критерия оценки качества разбиения с учетом временных задержек и числа межмодульных связей.
Соискатель Дуккардт А.Н.
Подписано в печать . .2007 г. Заказ
Формат 60х84 1/16. Печать офсетная
Печ. л. 1,0. Тираж 100 экз.
Издательство Таганрогского государственного радиотехнического университета
ГСП 17А, Таганрог, 28, Некрасовский, 44
Типография Таганрогского государственного радиотехнического университета
ГСП 17А, Таганрог, 28, Некрасовский, 44
