Математическое моделирование взаимодействия пульсирующего сдавливаемого слоя жидкости с упругими трехслойными элементами гидроопор

На правах рукописи

Христофорова Алевтина Владимировна

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ВЗАИМОДЕЙСТВИЯ
пульсирующего СДАВЛИВАЕМОГО СЛОЯ ЖИДКОСТИ С УПРУГИМИ ТРЕХСЛОЙНЫМИ ЭЛЕМЕНТАМИ гидроопор

Специальность 05.13.18 – Математическое моделирование, численные методы и комплексы программ

А в т о р е ф е р а т

диссертации на соискание ученой степени

кандидата физико-математических наук

Саратов – 2009

Работа выполнена в ГОУ ВПО «Саратовский государственный технический университет»

Научный руководитель – доктор технических наук, доцент

Попов Виктор Сергеевич

Официальные оппоненты: - доктор физико-математических наук, доцент

Андрейченко Дмитрий Константинович,

- кандидат физико-математических наук

Кондратов Дмитрий Вячеславович

Ведущая организация: ГОУ ВПО «Московский авиационный институт

(государственный технический университет)»

Защита состоится « 23 » декабря 2009 г. в 13:30 часов на заседании диссертационного совета Д 212.242.08 при ГОУ ВПО «Саратовский государственный технический университет» по адресу: 410054, Саратов, ул. Политехническая, 77, Саратовский государственный технический университет, корп. 2, ауд. 212.

С диссертацией можно ознакомиться в научно-технической библиотеке ГОУ ВПО «Саратовский государственный технический университет»

С авторефератом можно ознакомиться на сайте www.sstu.ru

Автореферат разослан « 23 » ноября 2009 г.

Ученый секретарь

диссертационного совета Терентьев А.А.

ОБЩАЯ ХАРАКТЕРИСТИКА РАБОТЫ

Актуальность работы. Все более широкое использование упругих многослойных элементов конструкций в современной технике требует разработки математических моделей для исследования их статики и динамики. Вопросы деформирования трехслойных элементов конструкций при статических и динамических нагрузках достаточно хорошо изучены. Однако их поведение при взаимодействии с жидкостью исследовано крайне мало. В то же время стенки каналов, в которых находится жидкость, все чаще изготавливают из слоистых материалов, а движение жидкости в различных гидравлических системах происходит с существенными пульсациями давления, вызванными особенностями работы насосов.

Существенный вклад в развитие математических моделей упругих слоистых элементов конструкций внесли работы А.Я. Александрова, С.А. Амбарцумяна, В.В. Болотина, Л.Э. Брюккера, В.В. Васильева, К.З. Га­лимова, А.Г. Горшкова, Э.И. Григолюка, Я.М. Григоренко, В.И. Королева, Л.М. Куршина, А.П. Прусокова, Э.И. Старовойтова, С.П. Тимошенко, Н.Г. Ченцова, А.П. Чулкова, А.В. Яровой, M.P. Bieniek, A.M. Freudenthal, J.K. Ebsiogly, A.C. Eringen, J.I. Foss, J. Mayers, L.M. Habip, E.J. Plantemma, E. Reisser, J. Solvey, K.P. Soldatos, M. Stein, C.-T. Wang и др. Вопросы разработки математических моделей для исследования динамических задач гидроупругости хорошо изучены для однородных упругих элементов в работах К.П. Андрейченко, А.С. Вольмира, А.Г. Горшкова, Э.И. Григолюка, М.А. Ильгамова, Д.А. Индейцева, Л.И. Могилевича, В.И. Морозова, М.С. Натанзона, А.Т. Пономарева, В.С. Попова, И.М. Рапопорта, Ф.Н. Шклярчука, M. Amabili, R.C. Ertekin, J.W. Kim, M.P. Pandoussis, F. Pellicano и др. Однако работ, посвященных математическому моделированию динамики взаимодействия трехслойных упругих элементов с жидкостью применительно к гидроопорам, применяемым в станках, машинах и приборах, практически нет.

В связи с вышесказанным актуальной и имеющей несомненный научный и практический интерес является разработка математических моделей для исследования динамики взаимодействия трехслойных элементов (стержней и пластинок) с жидкостью, в которой поддерживается гармонически пульсирующее давление, применительно к гидроопорам.

Целью работы является разработка математических моделей гидроупругости трехслойных элементов конструкций, взаимодействующих с пульсирующим сдавливаемым слоем вязкой жидкости, построение и исследование на их основе амплитудных и фазовых частотных характеристик гидроопор.

Согласно данной цели сформулированы задачи исследования:

1. Разработка математической модели для исследования механической системы, состоящей из упругого трехслойного стержня (балки-полоски) и абсолютно твердого вибратора, взаимодействующих друг с другом через сдавливаемый слой вязкой несжимаемой жидкости, в котором поддерживается противодавление, гармонически изменяющееся во времени.

2. Разработка математической модели для исследования механической системы, состоящей из упругой трехслойной круглой пластины и абсолютно твердого вибратора, взаимодействующих друг с другом через сдавливаемый слой вязкой несжимаемой жидкости, в котором поддерживается противодавление, гармонически изменяющееся во времени.

3. Решение динамических задач гидроупругости трехслойных упругих элементов конструкций, входящих в состав гидроопор с гармонически пульсирующим противодавлением в рабочем слое жидкости и построение на их основе, амплитудных частотных и фазовых частотных характеристик (АЧХ и ФЧХ).

4. Исследование путем математического моделирования АЧХ и ФЧХ гидроопор с упругими трехслойными статорами прямоугольной и круглой формы на базе найденного решения динамических задач гидроупругости.

Научная новизна. Новые научные результаты, полученные в работе:

1. Предложена математическая модель гидроопоры, отличающаяся учетом упругих свойств круглого трехслойного статора с несжимаемым заполнителем, взаимодействующего через слой вязкой несжимаемой жидкости с гармонически изменяющимся давлением, с абсолютно жестким вибратором опоры, имеющим упругий подвес.
2. Предложены математические модели гидроопоры, в которой статор представляется упругим трехслойным стержнем (балкой-полоской) со сжимаемым или несжимаемым заполнителем, взаимодействующим через слой вязкой несжимаемой жидкости с гармонически изменяющимся давлением, с абсолютно жестким вибратором опоры, имеющим упругий подвес.
3. На основе предложенных математических моделей и полученных аналитических решений в среде Maple-12 разработан комплекс программ для исследования и построения АЧХ и ФЧХ гидроопор с трехслойными элементами конструкций.
4. Показано наличие двух резонансных частот у вибратора и статора на главной моде для режима установившихся вынужденных гармонических колебаний в опорах с трехслойным статором с несжимаемым заполнителем. При этом выявлено, что использование трехслойного статора с несжимаемым заполнителем приводит к сдвигу резонансных частот в низкочастотную область по сравнению с однородным статором.
5. Установлено, что применение в опоре трехслойного статора со сжимаемым заполнителем существенно искажает форму колебаний на главной моде вибратора и статора и приводит к удвоению числа их резонансных частот. При этом расчеты показали существенный сдвиг значений резонансных частот в высокочастотную область до 1-2 порядков и снижение амплитуд колебаний до 2-3 порядков по сравнению с однородным статором и трехслойным статором с несжимаемым заполнителем.

Достоверность полученных результатов обеспечивается корректной физической и математической постановкой задач, применением классических математических методов и методов возмущений, использованием апробированных подходов теории многослойных стержней и пластин, механики жидкости и теории упругости. Полученные результаты в частных случаях полностью совпадают с известными результатами других авторов и не противоречат имеющимся физическим представлениям.

Практическая ценность и реализация результатов. Результаты диссертации могут найти применение при математическом моделировании динамики сложных механических систем, включающих упругие трехслойные конструкции, абсолютно жесткие тела и жидкость. В частности, данные модели применимы для определения резонансных частот колебаний упругих трехслойных и однородных конструкций, взаимодействующих с жидкостью, в которой поддерживается гармонически пульсирующее противодавление.

Работа выполнена в рамках комплексной внутривузовской программы 11В.01 «Совершенствование методов гидравлического расчета водопропускных, дорожно-транспортных и коммунальных очистных сооружений» Саратовского государственного технического университета (СГТУ). Результаты работы использованы: при выполнении проектов СГТУ-181, СГТУ-196, СГТУ-236, проводимых в рамках госбюджетных научно-исследовательских работ СГТУ; при выполнении грантов РФФИ № 06-08-00043а,
№08-01-12051-офи, а также грантов Президента РФ МД-234.2007.8 и МД-551.2009.8, имеется акт о внедрении.

Апробация работы. Основные положения и результаты работы докладывались, обсуждались и были одобрены на: конференции молодых ученых СГТУ (Саратов, 2007), Международной конференции «Проблемы и перспективы прецизионной механики и управления в машиностроении» (РАН Институт проблем точной механики и управления, Саратов, 2007), XIV Международном симпозиуме «Динамические проблемы механики конструкций и сплошных сред» им. А.Г. Горшкова (Москва-Ярополец, МАИ, 2008, 2009), конференции молодых ученых СГТУ (Саратов, 2007), Второй Всероссийской научной конференции по волновой динамике машин и конструкций (Нижний Новгород, 2007).

Публикации. По теме диссертационной работы опубликовано 11 научных работ, из них 5 работ в профильных периодических научных изданиях, рекомендованных ВАК РФ для публикации основных результатов кандидатских диссертаций.

На защиту выносятся следующие положения:

1. Математические модели гидроопор, которые позволяют учитывать влияние упругого трехслойного статора, круглого или прямоугольного в плане, с несжимаемым заполнителем, совместно с учетом упругой податливости подвеса абсолютно жесткого вибратора и инерционных свойств жидкости с гармонически пульсирующим давлением на АЧХ и ФЧХ гидроопор. Данные модели позволяют осуществить переход к исследованию гидроупругих колебаний в опорах с однородными упругими статорами прямоугольной и круглой формы.

2.  Математическая модель гидроопоры, которая позволяет производить оценку влияния сжимаемости заполнителя трехслойного статора совместно с учетом упругой податливости подвеса абсолютно жесткого вибратора и инерционных свойств жидкости с гармонически пульсирующим давлением при исследовании АЧХ и ФЧХ гидроопоры.

3. Построенные амплитудные и фазовые частотные характеристики рассматриваемых опор с учетом упругой податливости трехслойных элементов их конструкций, возможности сжатия заполнителя данных элементов и инерции движения жидкости с гармонически пульсирующим давлением позволяют оценивать резонансные частоты колебаний гидроопор и их элементов, и амплитуды их колебаний при резонансе. Найденные резонансные частоты колебаний дают возможность оценивать критические частоты, при которых возможна вибрационная кавитация в жидкости.

Структура и объем работы. Диссертация состоит из введения, четырех глав, заключения, списка использованной литературы и приложений. Объем диссертации 171 страница, из них 4 страницы приложений. В работе 18 рисунков и 22 таблицы. Список литературы включает 105 наименований.

СОДЕРЖАНИЕ РАБОТЫ

Во введении дана общая характеристика работы, изложены проблемы, которым она посвящена, выполнен анализ текущего состояния исследований по проблематике диссертационного исследования.

В первом разделе приведены сведения из работ Горшкова А.Г., Старовойтова Э.И., Яровой А.В. и др. о выводе уравнений равновесия и динамики трехслойного стержня (балки-полоски) и круглой упругой трехслойной пластины на базе использования принципа возможных перемещений Лагранжа. Рассмотрен случай, когда материал заполнителя считается несжимаемым в поперечном направлении. Дан обзор по выводу уравнений равновесия и динамики трехслойного стержня (балки-полоски) со сжимаемым заполнителем.

Во втором разделе рассмотрен вопрос построения математической модели для исследования колебаний в гидроопоре с упругим трехслойным статором и абсолютно твердым вибратором, имеющим упругий подвес при пульсации давления в рабочем слое жидкости.

Схема гидроопоры представлена на рис.1. Опора включает: абсолютно жесткий вибратор I с упругой связью, упругий трехслойный статор II (балка-полоска) с несжимаемым заполнителем 3, имеющий свободное опирание на торцах, и тонкий слой вязкой несжимаемой жидкости III в зазоре между вибратором и статором, находящиеся в едином корпусе. Гидроопора работает следующим образом: в торцевые технологические полости нагнетается жидкость и ее вибратор I поднимается на высоту щелевого зазора h. В жидкости, как в щелевом зазоре, так и вне его, поддерживается давление, имеющее постоянную р0 и гармоническую по времени р1(t) составляющие. Длина b статора и вибратора значительно больше их ширины и считается бесконечно большой. Вибратор за счет пульсации давления совершает поступательные колебания вдоль оси z. Статор представляет собой совокупность несущих слоев 1, 2 толщиной h1 и h2 и несжимаемого заполнителя 3. На его торцах имеются жесткие диафрагмы, препятствующие относительному сдвигу слоев. Жидкость полностью заполняет зазор h и на торцах свободно истекает в окружающую жидкость, находящуюся в технологических полостях корпуса опоры.

Ставится задача определения АЧХ и ФЧХ статора и вибратора на базе нахождения законов их движения при заданном гармоническом законе пульсации давления жидкости в полостях корпуса опоры.

Вводится декартова система координат Oxyz, связанная со срединной поверхностью заполнителя статора, рассматривается плоская задача, для которой введены безразмерные переменные и малые параметры

, , , , , , , (1)

, , , , , ,

где – относительная толщина слоя жидкости; – относительная амплитуда колебаний вибратора; – амплитуда колебаний вибратора; – закон движения вибратора; – заданный гармонический закон пульсации давления; – средняя толщина слоя жидкости; – частота колебаний; – компоненты скорости жидкости; wm, um – амплитуды упругих перемещений трехслойного статора; – угол поворота нормали в заполнителе; – амплитуда пульсации давления; – кинематический коэффициент вязкости.

Поставленная динамическая задача гидроупругости опоры включает:

– уравнения динамики тонкого слоя жидкости (с точностью до )

(2)

– уравнения динамики трехслойного статора с несжимаемым заполнителем

, (3)

– уравнение движения вибратора

, (4)

где при ; – коэффициенты, отражающие жесткостные свойства статора; , – плотность материала k-го слоя, k = 1, 2, 3 – номер слоя; m1 – масса вибратора; n1 – коэффициент жесткости подвеса вибратора; n3 – сила, действующая на вибратор со стороны слоя жидкости при .

Записано выражение для силы n3

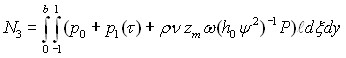. (5)

Граничные условия прилипания жидкости к вибратору и статору, свободного торцевого истечения и свободного опирания статора имеют вид

при , при ,

при при . (6)

В ходе решения задачи (2)-(6) исследуются вынужденные установившиеся колебания элементов опоры при гармонической пульсации давления в жидкости. Решение представляется в виде асимптотического разложения по относительной амплитуде колебаний вибратора :

Р = Р0 + Р1+…, U = U0 + U1 +…, U = U0 + U1 +…, W = W0 + W1 +… . (7)

Подставляя (7) в (2)-(6) и рассматривая первый член разложения, линеаризуем задачу гидроупругости. Для решения данной задачи определяется частное решение неоднородных линейных уравнений в виде гармонических функций по времени с коэффициентами, зависящими от координат

. (8)

Под Т0 понимаются Р0, U0, U0, W0 коэффициенты АТ, ВТ для Р0 и W0 зависят только от, для U0, U0 они зависят от и. Решая (2), найдено давление в жидкости

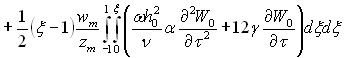, (9)

где, – частотозависимые коэффициенты.

Форма прогиба статора представлялась в виде бесконечного ряда

. (10)

Производя подстановку (9), (10) в последнее уравнение (3) и раскладывая функции от, входящие в его правую часть, в ряды по , находим постоянные и переходим к обыкновенному дифференциальному уравнению по времени относительно . Решая данное уравнение, находим функции , выраженные через искомый закон движения вибратора и заданный закон изменения давления. Осуществляя подстановку , в (9) с учетом (10), а затем в (5) и уравнение динамики вибратора (4) и решая его, находим закон движения вибратора

, (11)

и его АЧХ и ФЧХ

, . (12)

С учетом (11) прогиб трехслойного статора определен в виде

, (13)

и найдены АЧХ и ФЧХ упругого статора для k-й моды его колебаний

, . (14)

Здесь обозначены: D – коэффициент, характеризующий жесткость трехслойного статора; – заданный фазовый сдвиг в законе пульсации давления, – выражения зависящие от частоты, геометрических и физических параметров опоры, представлены в диссертации (не приведены ввиду громоздкости).

Как частный случай, рассмотрена возможность перехода к задаче гидроупругости для опоры с упругим однородным статором.

Полученные АЧХ вибратора и статора гидроопоры позволяют исследовать возможность возникновения их резонансных колебаний, найти резонансные частоты и соответствующие им коэффициенты динамичности. Проведены расчеты резонансных колебаний в опорах с трехслойным и однородными статорами на главной моде колебаний. На рис. 2-3 приведены безразмерные АЧХ и (или коэффициенты динамичности, т.е. отношение АЧХ к ее статическому значению при  = 0) для модели опоры с параметрами  = 0,1 м; h0/ = 0,04; h1/ = 0,05; h2/ = 0,07; c/ = 0,05; b/ = 10; 0 =0,3;  = 1,84103 кг/м2;  = 2,510-4  м2/с; m1 = 15 кг; n1 =9,5109 кг/c2.

Рис. 2. АЧХ вибратора Рис. 3. АЧХ статора

1 – трехслойный статор (Д16Т-фторопласт-Д16Т); 2 – трехслойный статор (латунь-фторопласт-Д16Т); 3 – однородный статор (алюминиевый сплав Д16Т)

Расчеты показали наличие двух резонансных частот у вибратора и статора. Изменение материала первого несущего слоя статора незначительно (до 10-12%) изменяет резонансную частоту и амплитуду колебаний трехслойной конструкции. Значения резонансных частот вибратора и статора практически совпадают. Выявлено, что применение трехслойного статора приводит к уменьшению (до 3-3,5) раз значений резонансных частот. Наибольший сдвиг наблюдается на низких частотах. Использование маловязких жидкостей (вода) приводит к резкому возрастанию амплитуд колебаний (до 20 раз). Для эффективного подавления амплитуд колебаний на резонансных частотах следует уменьшать рабочий зазор между статором и вибратором и использовать рабочие жидкости с высокой вязкостью. Расчеты подтвердили правомерность выбора в качестве малого параметра относительной амплитуды колебаний вибратора.

В третьем разделе рассмотрена осесимметричная задача гидроупругости применительно к опоре с круглым трехслойным статором с несжимаемым заполнителем (рис.4). При этом считается, что статор представляет собой упругую трехслойную пластину, жестко защемленную по контуру.

Введены в рассмотрение безразмерные переменные и малые параметры

, , , , , , , , , , . (15)

Здесь Vr, Vz – компоненты вектора скорости жидкости; r – расстояние от оси пластины; R – радиус пластины.

Рассматривая асимптотическое разложение по и ограничиваясь первым членом разложения, с учётом (15), сформулирована линеаризованная задача гидроупругости опоры с круглым трехслойным статором

, , , (16)

, , ,

,

граничные условия прилипания жидкости к вибратору и статору, жесткой заделки статора, а также условие свободного торцевого истечения и ограниченности давления в центре имеют вид

при , при ; (17)

при , при ; при .

Здесь , , – коэффициенты, отражающие жесткостные свойства статора.

Решение задачи (16), (17) для установившихся гармонических колебаний ищется в виде (8). В результате найдено давление в жидкости

. (18)

Представляя форму прогибов статора в виде бесконечного ряда по функциям Бесселя, найдены закон движения вибратора, прогиб статора

,

, (19)

а также АЧХ и ФЧХ вибратора, АЧХ и ФЧХ статора для k-й моды

, , , . (20)

Здесь обозначены: J0 – функция Бесселя нулевого порядка первого рода; I0 – модифицированная функция Бесселя нулевого порядка; k – корень трансцендентного уравнения (k = 0, 1, 2,…) I1(k)/I0(k) = – J1(k)/J0(k), (здесь J1(k), J0(k) – соответствующие функции Бесселя первого порядка).

Как частный случай, указана возможность перехода к задаче гидроупругости для опоры с круглым упругим однородным статором.

На рис. 5-6 приведены безразмерные АЧХ главной моды колебаний для опоры с параметрами R = 0,2 м; h0/R = 0,02; h1/R = 0,01; h2/R = 0,015; c/R = 0,03;  = 1,84103 кг/м2;  = 2,510-4 м2/с; n1 = 9,5109 кг/c2; m1 = 16,5 кг.

Рис. 5. АЧХ вибратора Рис. 6. АЧХ статора

1 – трехслойный статор (Д16Т-фторопласт-Д16Т); 2 – трехслойный статор (сталь-фторопласт-Д16Т); 3 – однородный статор (алюминиевый сплав Д16Т)

Как видно из графиков, применение трехслойного статора позволяет добиться полного подавления первой резонансной частоты опоры. Расчеты резонансных колебаний на главной моде в опорах с различными статорами показали, как и в случае опоры с трехслойным стержнем, наличие двух резонансных частот у вибратора и статора. Замена материала первого несущего слоя статора фактически не сказывается на резонансных частотах и коэффициентах динамичности как статора, так и вибратора. При замене однородного статора трехслойным с несущими слоями, выполненными из того же материала, что и однородный статор, происходит существенное (до 10 раз) смещение первых резонансных частот статора и вибратора в низкочастотную область. При этом вторая резонансная частота практически не изменяется. Показано, что использование маловязких жидкостей (воды) приводит к росту амплитуд колебаний в 20 и более раз. Резонансные частоты при этом возрастают на 30-50%, что можно объяснить увеличением плотности жидкости. Применение трехслойного статора и уменьшение толщины слоя жидкости ведет к интенсивному снижению амплитуд колебаний, вплоть до полного подавления первой резонансной частоты.

В четвертом разделе рассмотрен вопрос построения математической модели опоры, имеющей трехслойный статор со сжимаемым заполнителем. Опора состоит из: абсолютно жесткого вибратора I с упругим подвесом; трехслойного статора II (стержня), заполнитель которого сжимаем, свободно опертого на торцах; слоя вязкой несжимаемой жидкости III с пульсирующим давлением, заключенными в одном корпусе (см. рис.1).

Уравнения динамики трехслойного статора (стержня) со сжимаемым заполнителем, вывод которых рассмотрен в первом разделе, имеют вид

,

,

(21)

,

,

где F1, F2, F3, F4 – инерционные члены, qzх, qzz – напряжения, действующие на поверхность первого несущего слоя статора со стороны слоя жидкости; ai (i = 1,2,…,19) – коэффициенты, отражающие жесткостные свойства статора, u1, u2, w1, w2, – продольные перемещения и прогибы несущих слоев статора.

Используя безразмерные переменные (1), поставлена нелинейная динамическая задача гидроупругости опоры, включающая уравнения (2), (4) и (21). Граничные условия задачи аналогичны (5). Решение данной задачи проводится методом возмущений, осуществляя асимптотическое разложение вида (7) и ограничиваясь его первым членом. Исследуя режим вынужденных гармонических колебаний, решение линеаризованной задачи определялось в виде (8), форма упругих перемещений статора представлялась как

, , (22)

, .

В ходе решения определены законы распределения скоростей и давления в слое жидкости, закон движения вибратора, выражения упругих перемещений несущих слоев статора, а также АЧХ и ФЧХ вибратора и статора опоры.

Моделирование показало, что учет сжимаемости заполнителя статора приводит к существенному изменению параметров вынужденных колебаний в опоре. На рис. 7-8 приведены коэффициенты динамичности модели опоры с параметрами  = 0,1 м; h0/ = 0,04; h1/ = 0,05; h2/ = 0,07; c/ = 0,05; b/ = 10; 0 =0,3;  = 1,84103 кг/м2;  = 2,510-4  м2/с; m1 = 15 кг; n1 = 9,5109 кг/c2, на рис. 9-10 - для этой же модели с удвоенным рабочим зазором (h0/ = 0,08) для главной моды колебаний.

На главной моде колебаний наблюдаются четыре резонансные частоты, как для вибратора опоры, так и для ее статора. Значения резонансных частот статора и вибратора отличаются незначительно. Наблюдается существенный сдвиг резонансных частот в область высоких частот колебаний как по сравнению с опорой с однородным статором (резонансные частоты возрастают от 2,5 до 9,5 раз), так и с трехслойным статором с несжимаемым заполнителем (резонансные частоты возрастают от 2,5 до 33 раз). Расчеты показывают, что учет сжимаемости заполнителя статора приводит к демпфированию колебаний, что проявляется в снижении (до двух, трех порядков) значений коэффициентов динамичности и амплитуд колебаний вибратора и статора на резонансных частотах. Увеличение величины рабочего зазора приводит к росту амплитуд колебаний, как и в ранее рассмотренных случаях. Например, увеличение рабочего зазора в два раза может приводить к возрастанию амплитуд колебаний до 5-10 раз. К еще более резкому возрастанию амплитуд колебаний приводит уменьшение вязкости жидкости.

Таким образом, для эффективного подавления резонансных колебаний необходимо уменьшать рабочий зазор опоры, использовать сжимаемые заполнители трехслойного статора и жидкости с высокой вязкостью.

ОСНОВНЫЕ РЕЗУЛЬТАТЫ И ВЫВОДЫ

1. В диссертации построены и исследованы новые математические модели механических систем, включающих трехслойный стержень (балку-полоску) или круглую трехслойную пластину, взаимодействующие с абсолютно жестким телом, имеющим упругий подвес, через слой вязкой жидкости с пульсирующим давлением. Предложенные математические модели представляют собой систему уравнений динамики вязкой несжимаемой жидкости, упругой трехслойной конструкции с несжимаемым или сжимаемым заполнителем и абсолютно твердого тела, входящих в состав гидроопоры, с соответствующими граничными условиями.

2. Для исследования разномасштабных динамических процессов в рамках разработанных моделей решена проблема формирования безразмерных переменных и осуществлен выбор малых параметров рассматриваемых задач гидроупругости. Это позволило сформулировать в безразмерном виде динамические задачи гидроупругости трехслойных элементов конструкций применительно к гидроопорам и корректно линеаризовать ее.

3. Найдены решения поставленных в работе динамических задач гидроупругости трехслойных элементов конструкций при воздействии гармонической пульсации давления в жидкости и получены выражения для упругих перемещений трехслойных конструкций, гидродинамических параметров движения жидкости и закона движения абсолютно жесткого тела. Решения задач проводились методом возмущений с учетом влияния инерции движения жидкости. Рассмотрено одночленное асимптотическое разложение по относительной амплитуде колебаний абсолютно твердого тела.

4. Построены АЧХ и ФЧХ гидроопор с упругими трехслойными статорами круглой и прямоугольной формы. Проведено исследование влияния наличия в рассматриваемой механической системе упругого элемента с несжимаемым заполнителем и вязкости жидкости на гидроупругие колебания опоры. Показано, что применение трехслойной конструкции с несжимаемым заполнителем и сильновязкой жидкости приводит к сдвигу резонансных частот в низкочастотную область и может способствовать эффективному демпфированию первых резонансных частот.

5. Проведено моделирование гидроупругости опоры с учетом сжимаемости заполнителя трехслойного статора, построены АЧХ и ФЧХ вибратора и статора опоры. Установлено, что при учете сжимаемости заполнителя на главной моде наблюдаются четыре резонансные частоты и существенно изменяется форма АЧХ. Значения резонансных частот возрастают по сравнению с опорой с однородным статором до 9,5 раз по сравнению с опорой со статором с несжимаемым заполнителем до 33 раз. При этом усиливается демпфирование колебаний, что проявляется в снижении (до двух, трех порядков) значений коэффициентов динамичности и амплитуд колебаний вибратора и статора на резонансных частотах.

Результаты работы могут найти применение для исследования колебаний и расчета резонансных частот в механических системах, включающих абсолютно жесткие тела, упругие трехслойные конструкции и вязкую жидкость, а также для моделирования условий возникновения кавитации в слое жидкости, взаимодействующей с упругими, в том числе и трехслойными стенками.

Основные результаты диссертации опубликованы в работах:

Публикации в изданиях, рекомендованных ВАК РФ

1. Христофорова А.В. Математическое моделирование динамических процессов в гидродинамической опоре с трехслойным статором / В.С. Попов, А.В. Христофорова // Вестник Саратовского государственного технического университета. – 2007. – №3. – С.38-45.
2. Христофорова А.В. Гидроупругость виброопоры с трехслойной круглой пластиной с несжимаемым заполнителем при наличии противодавления / В.С. Попов, А.В. Христофорова // Вестник Саратовского государственного технического университета. – 2007. – №4. – С.18-25.
3. Христофорова А.В. Математическое моделирование взаимодействия трехслойной пластины со сжимаемым заполнителем и слоя жидкости в виброопоре при наличии противодавления / А.В. Христофорова // Вестник Саратовского госагроуниверситета им. Н.И. Вавилова /. – 2007. – №6. – С.38-45. (принята к печати 27.12.2006 г.)
4. Христофорова А.В. Математическое моделирование демпфирования колебаний в ДВС / В.С. Попов, А.А. Симдянкин, А.П. Уханов, А.В. Христофорова // Тракторы и сельскохозяйственные машины. –2007.– №8. – С.45-48. (принята к печати 25.12.2006 г.)
5. Христофорова А.В. Гидроупругость демпфера с трехслойным упругим стержнем при наличии противодавления в слое жидкости / В.С. Попов, А.В. Христофорова // НТТ - наука и техника транспорта /.– №1. – 2008. – С. 43-49. (принята к печати 22.11.2006 г.)

Публикации в других изданиях

6. Христофорова А.В. Динамическая задача гидроупругости виброопоры с трехслойным упругим стержнем при наличии противодавления /

В.С. Попов, А.В. Христофорова // Вторая Всероссийская научная конференция по волновой динамике машин и конструкций: тезисы докладов. – Нижний Новгород: ЗАО «Интек-НН», 2007. – С. 77.

7. Христофорова А.В. Моделирование динамических характеристик динамической виброопоры с трехслойным статором и противодавлением в рабочем слое жидкости / А.В. Христофорова // Молодые ученые – науке и производству: материалы конференции молодых ученых. Саратов: СГТУ, 2007. – С. 234-236.
8. Христофорова А.В. Математическая модель для исследования динамических характеристик виброопоры с упругой трехслойной пластиной при гармонической пульсации давления в рабочем слое жидкости / В.С. Попов, А.В. Христофорова // Проблемы и перспективы прецизионной механики и управления в машиностроении: материалы международной конференции. – Саратов, 2007. – С.135-141.
9. Христофорова А.В. Гидроупругость демпфера, установленного на вибрирующем основании / Л.И. Могилевич, А.А. Попова, В.С. Попов, А.В. Христофорова // Динамические и технологические проблемы механики конструкций и сплошных сред: материалы XIV международного симпозиума им. А.Г. Горшкова. – М.: Изд-во МАИ, 2008. – С. 154.
10. Христофорова А.В. Исследование динамики виброопоры с упругим трехслойным статором и твердым вибратором с упругой связью при наличии пульсирующего противодавления в рабочей жидкости / Л.И. Могилевич, А.А. Попова, В.С. Попов, А.В. Христофорова // Динамические и технологические проблемы механики конструкций и сплошных сред: материалы XIV международного симпозиума им. А.Г. Горшкова. – М.: Изд-во МАИ, 2008. – С. 153.
11. Христофорова А.В. Исследование динамики гидродинамического демпфера с трехслойной круглой пластиной / Л.И. Могилевич, В.С. Попов, А.В. Христофорова // Динамические и технологические проблемы механики конструкций и сплошных сред: материалы XV международного симпозиума им. А.Г. Горшкова. – М.: Изд-во «Типография ПАРАДИЗ», 2009. – С. 114.

Подписано в печать 19.11.09 Формат 6084 1/16

Бум. офсет Усл. печ.л. 0.93 (1,0) Уч.-изд.л. 0.9

Тираж 100 экз. Заказ 512 Бесплатно

Саратовский государственный технический университет

410054 г. Саратов, ул. Политехническая, 77

Отпечатано в издательстве СГТУ, 410054 г. Саратов, ул. Политехническая, 77