Математическое моделирование шумовых явлений в многорезонаторном магнетроне
На правах рукописи
Каминский Константин Вячеславович
МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ШУМОВЫХ ЯВЛЕНИЙ В МНОГОРЕЗОНАТОРНОМ МАГНЕТРОНЕ
Специальности 05.13.18 – Математическое моделирование,
численные методы и комплексы программ
01.04.04 – Физическая электроника
Автореферат
диссертации на соискание учёной степени
кандидата физико-математических наук
Саратов 2009
Работа выполнена в ГОУ ВПО «Саратовский государственный технический университет».
| Научный руководитель: | доктор физико-математических наук, заслуженный деятель науки РФ, профессор Байбурин Вил Бариевич |
| Официальные оппоненты: | доктор физико-математических наук, профессор Кац Альберт Маркович |
| кандидат технических наук Семёнов Владимир Константинович | |
| Ведущая организация: | ГОУ ВПО «Саратовский государственный университет им. Н.Г. Чернышевского» |
Защита состоится 14 октября 2009 г. в 13 часов на заседании диссертационного совета Д 212.242.08 при ГОУ ВПО «Саратовский государственный технический университет» по адресу: 410054, г. Саратов, ул. Политехническая, 77, Саратовский государственный технический университет, корп. 1, ауд. 319.
С диссертацией можно ознакомиться в научно-технической библиотеке ГОУ ВПО «Саратовский государственный технический университет».
Автореферат разослан « 14 » сентября 2009 г.
Учёный секретарь
диссертационного совета Терентьев А.А.
ОБЩАЯ ХАРАКТЕРИСТИКА РАБОТЫ
Актуальность работы. В последние годы методы нелинейной динамики находят все большее распространение при исследовании динамических систем самой различной природы. При этом выявляются ранее не обнаруженные хаотические режимы, позволившие объяснить ряд эффектов и особенностей систем, которые до этого не имели четкой физической трактовки.
С этой точки зрения особый интерес вызывают задачи, связанные с движением заряженных частиц в скрещенных электрических и магнитных полях в таких областях как астрофизика, физика ускорителей, СВЧ-электроника и др. Здесь необходимо отметить классические работы Г.М. Заславского, Р.З. Сагдеева, Б.В. Чирикова и др., а также работу С.В. Поршнева по движению зарядов в магнитном поле Земли. Важным классом устройств, использующих движение зарядов в скрещенных полях для целей генерации и усиления электромагнитных колебаний, являются приборы магнетронного типа.
В работах В.Б. Байбурина, А.В. Юдина, А.О. Мантурова, Н.Ю. Хороводовой, М.П. Беляева рассмотрены хаотические и регулярные траектории в скрещенных полях при различного вида неоднородностях действующих полей и их параметров, а также непосредственно в режимах магнетронного диода. Хаотические режимы в магнетронном диоде рассмотрены в теоретических и экспериментальных работах В.Г. Усыченко, Э.В. Кальянова, А.В. Смирнова, В.М. Малышева и др., в которых было экспериментально установлено, что шумовые колебания в магнетронных приборах имеют хаотическую природу.
Одним из наиболее распространенных приборов магнетронного типа является многорезонаторный магнетрон, используемый как генератор мощных электромагнитных колебаний. Существенной особенностью работы многорезонаторных магнетронов является так называемый «аномальный» шум, уровень которого значительно превышает шумы других приборов СВЧ, в частности ЛБВ. Различным аспектам этого вопроса посвящено значительное число публикаций (см., например, Ван Дузер, Д.И. Трубецков, Г.Г. Моносов, И.А. Каржавин, Г.С. Гундобин, В.И. Вислов, Par J. Arnaud, S.A. Riopoulos), однако природа аномального шума до сих пор полностью не ясна. Кроме того, можно отметить недостаточность теоретических количественных оценок уровня аномального шума, основанных на предлагаемых моделях шумовых явлений.
Таким образом, актуальной задачей является анализ различных режимов работы многорезонаторного магнетрона, основанный на расчете траекторий заряженных частиц с использованием методов нелинейной динамики и ориентированный на уточнение природы шумов, а также получение количественной оценки уровня шумов.
Целью диссертационной работы является построение математической модели движения заряженных частиц и их взаимодействия с электромагнитной волной в многорезонаторном цилиндрическом магнетроне, разработка соответствующего программного обеспечения и анализ на их основе механизма шумовых явлений.
Для достижения поставленной цели были решены следующие основные задачи:
- Создание математической модели анализа регулярных и хаотических режимов движения заряженных частиц в скрещенных полях в цилиндрической системе координат в присутствии высокочастотных полей и выбор эффективных алгоритмов и вычислительных схем численного решения уравнений движения.
- Разработка программного обеспечения для решения уравнений движения заряженных частиц в многорезонаторном магнетроне на основе полученных моделей и вычислительных схем.
- Применение разработанной математической модели и программного обеспечения при исследовании режимов температурного ограничения эмиссии и ограничения эмиссии пространственным зарядом, в частности для расчета траекторий заряженных частиц и оценки уровня шумов в различных режимах работы магнетрона.
Достоверность и обоснованность полученных результатов определяется:
- Корректностью и строгостью применяемых математических методов, предварительной оценкой допускаемых приближений и погрешностей и их физическим обоснованием.
- Соответствием основных результатов и выводов экспериментальным данным и общефизическим представлениям о характере процессов в приборах М-типа.
Научная новизна работы:
- Предложены математические модели исследования шумовых явлений в цилиндрическом многорезонаторном магнетроне в условиях режимов генерации с учетом нелинейных неоднородностей действующих постоянных полей, а также полей пространственного заряда.
- На основании предложенных моделей получены рабочие алгоритмы и вычислительные схемы с использованием метода Рунге-Кутта, позволяющие проводить анализ фазовых траекторий с учётом переменных и постоянных пространственно неоднородных магнитных и электрических полей.
- Разработано программное обеспечение, реализующее численный алгоритм расчета на основе предложенных моделей, и интерфейс пользователя, позволяющие оперативно менять параметры всех действующих полей и геометрию системы, выводить на экран траектории движения заряженных частиц, графики наведенных токов, спектр, автокорреляционную функцию, а также картину облака пространственного заряда («электронных спиц») в пространстве взаимодействия.
- С применением предложенных математических моделей и методов нелинейной динамики показано, что в режиме больших амплитуд многорезонаторного магнетрона траектории заряженных частиц являются принципиально неустойчивыми, что приводит к появлению шума. Предложен метод оценки уровня шумов в магнетроне, основанный на расчете суммарных наведенных токов большого числа зарядов и усреднения результата по всем токам. Произведена количественная оценка избыточного шума в режиме ограничения эмиссии пространственным зарядом, полученная величина согласуется с экспериментальными измерениями.
- Показано, что подбором вида изменения магнитного поля в пространстве взаимодействия можно оказывать влияние на изменение уровня шумов в магнетроне. Исходя из условий синхронизма в магнетроне предложен закон пространственного изменения магнитного поля, позволяющий, согласно расчетам, существенно уменьшить уровень шумов в выходном сигнале.
- Проведено сравнение циклоидальной траектории заряженной частицы и так называемой адиабатической траектории, соответствующей движению центра орбиты вращения частицы (ведущего центра). Показано, что циклоидальность траекторий в многорезонаторном магнетроне может вносить вклад в уровень шумов прибора, так как приводит к модуляции наведенного тока.
- Проведен анализ траекторий в магнетроне с азимутально меняющимся магнитным полем. Дано физическое обоснование механизма уменьшения уровня шумов при использовании азимутально-неоднородного магнитного поля.
- Показано, что возрастающее к аноду магнитное поле может приводить к эффекту смены направления дрейфа ведущего центра и срыву генерации в многорезонаторном магнетроне.
Основные результаты и положения, выносимые на защиту:
- Предложенные математическая модель, вычислительные схемы и разработанное на их основе программное обеспечение позволяют рассчитывать траектории заряженных частиц в пространстве взаимодействия в многорезонаторном магнетроне и проводить анализ устойчивости полученных траекторий различными методами (расчёт старшего ляпуновского показателя, спектра мощности, автокорреляционной функции), а также количественно оценивать уровень генерируемого шума.
- Неустойчивость электронных траекторий и их циклоидальность можно рассматривать как один из физически допустимых механизмов возникновения аномального шума в многорезонаторном магнетроне.
- Улучшение условий синхронизма электронов и высокочастотной волны в цилиндрическом магнетроне приводит к уменьшению времени пребывания электрона в пространстве взаимодействия, что, в свою очередь, приводит к уменьшению уровня шумов в выходном сигнале магнетрона.
- Показано, что азимутально-неоднородное магнитное поле способствует быстрому покиданию зарядом прикатодной области, уменьшению времени пролета катод-анод.
- Полученные картины распределения пространственного заряда демонстрируют срыв генерации в многорезонаторном магнетроне из-за эффекта смены направления дрейфа зарядов под воздействием экспоненциально возрастающего к аноду поля.
Практическая значимость диссертационной работы заключается в следующем:
- На основе предложенных в диссертации моделей разработано программное обеспечение, предназначенное для решения задач анализа устойчивости траекторий в многорезонаторном магнетроне, расчета наведенного тока, графического отображения распределения пространственного заряда.
- На основе анализа устойчивости электронных траекторий дано объяснение одному из допустимых механизмов возникновения аномального шума в приборах М-типа.
- Предложен метод, позволяющий количественно сравнивать уровень шума в двух режимах работы многорезонаторного магнетрона.
- Исходя из условий синхронизма, предложен закон распределения магнитной индукции в пространстве взаимодействия, позволяющий добиться существенного уменьшения уровня шумов в выходном сигнале.
- Предложена конструкция многорезонаторного магнетрона с измененной конструкцией полюсных наконечников, которая позволит достичь снижения уровня шумов в выходном сигнале.
- Даны рекомендации относительно дальнейшего усовершенствования и применения азимутально-неоднородного магнитного поля в конструкции магнитных систем магнетронов.
Апробация работы. Основные результаты работы обсуждались на Международной научной конференции XXI международной научной конференции «Математические методы в технике и технологиях» ММТТ-21 (Саратов, 2008), на международной научно-технической конференции «Актуальные проблемы электронного приборостроения» (Саратов, 2008), на заседаниях кафедры «Программное обеспечение вычислительной техники и автоматизированных систем» Саратовского государственного технического университета.
Публикации. Основные результаты диссертации изложены в 8 печатных работах (пяти статьях и трудах трёх конференций). Список публикаций приведён в конце автореферата.
КРАТКОЕ СОДЕРЖАНИЕ РАБОТЫ
Диссертация состоит из введения, четырёх глав, заключения и списка использованной литературы.
Во введении раскрывается современное состояние проблемы, обосновывается актуальность темы диссертации, формулируется цель работы.
В первой главе проведён обзор литературных источников по шумам в приборах М-типа. Представлена классификация шумов, приведено понятие аномального шума, представлены основные трактовки возникновения аномального шума.
Во второй главе предложена математическая модель движения заряженных частиц в многорезонаторном магнетроне, представлены методы нелинейной динамики, используемые при анализе траекторий частиц. Предложен метод оценки шумов в выходном сигнале магнетрона, основанный на расчете наведенных токов от большого количества частиц. Приводится описание особенностей и возможностей программного обеспечения, разработанного в рамках диссертационной работы, с помощью которого проведены исследования поведения зарядов в режимах температурного ограничения эмиссии, и ограничения эмиссии пространственным зарядом, в котором электрическое поле на катоде полностью компенсируется полем пространственного заряда.
В основе исследуемых в работе математических моделей лежит общее уравнение движения зарядов в скрещенных полях:
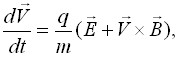(1)
где q – заряд частицы, m – масса, 
– вектор скорости, 
– векторы напряженности электрического поля и магнитной индукции соответственно, в общем случае нелинейно зависящие от координат и времени.
Уравнения движения зарядов в многорезонаторном магнетроне в двумерном случае в полярной системе координат (r, ) можно записать в виде:
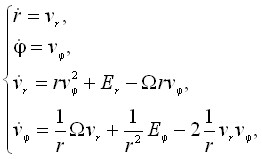(2)
где Er и E – компоненты электрического поля в радиальном и азимутальном направлении соответственно, 
– циклотронная частота, 
, B – магнитная индукция.
Как известно, строгое аналитическое решение уравнения (2) не получено, поэтому в работе уравнение (2) решается с использованием численных методов в полярной системе координат с учетом полей, действующих в пространстве взаимодействия многорезонаторного магнетрона. Уравнения движения решались методом Рунге-Кутта 4-го порядка с шагом интегрирования, соответствующим 1/500 циклотронного периода, для каждой крупной частицы. При имитационном моделировании использовались 5000 крупных частиц.
Предложен метод оценки уровня шума, основанный на расчете наведенных токов, суть которого заключается в том, что чем сильнее отличаются электронные траектории, тем значительнее изменяются связанные с ними величины наведенного тока, а значит и величины наведенной ВЧ мощности. Отношение разности ВЧ мощностей к средней величине ВЧ мощности можно рассматривать как количественную оценку шума, связанную с отдельным зарядом.
В третьей главе проведен анализ электронных траекторий в режимах температурного ограничения эмиссии и ограничения эмиссии пространственным зарядом, проведено сравнение уровня шума в указанных режимах, а также рассмотрено влияние циклоидальности траекторий на уровень шумов.
Для определенности будем рассматривать восьми резонаторный магнетрон, работающий в режиме, при котором два соседних резонатора колеблются в противофазе, то есть с фазовым сдвигом, так называемый -вид колебаний. Тогда для компонент поля можно записать следующие уравнения:
(3)
где – постоянная распространения, – частота высокочастотного поля, E0 – амплитуда высокочастотного поля, Ed и Eq – постоянное электрическое поле в магнетроне и поле пространственного заряда соответственно.
Для Ed можно записать
(4)
где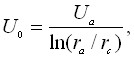 
- анодное напряжение.
При рассмотрении режима температурного ограничения эмиссии полем пространственного заряда можно пренебречь, поэтому в этом случае полагалось Eq = 0.
В режиме ограничения эмиссии пространственным зарядом, как известно, поле пространственного заряда на катоде равно постоянному электрическому полю на катоде и противоположно ему по знаку. Кроме того, как показывают многочисленные расчеты на численных моделях, основная часть пространственного заряда сосредоточена в так называемой цилиндрической «втулке» (её примерная граница показана на рис. 1).
Учитывая отмеченные обстоятельства, можно записать простые аналитические выражения для поля пространственного заряда втулки в следующем виде
(5)
где rc – радиус катода, ra – радиус анода, r0 – радиус верхней границы втулки.
В расчетах значения безразмерных параметров в уравнениях (2) – (5) были заданы соответствующим стационарным номинальным режимам работы многорезонаторного магнетрона.
На рис. 2 показано распределение по радиусу суммарного электрического поля с учетом компенсирующего поля пространственного заряда 
.
На рис. 3, 4 представлены типичные траектории зарядов для режимов температурного ограничения и ограничения пространственным зарядом соответственно.
Сплошная и пунктирная линии на этих рисунках соответствуют траекториям, выходящим из одной точки на катоде, но имеющим небольшие различия в начальных скоростях (в пределах значений начальных скоростей вылета электронов из катода, не превышающих, как известно, 0,03-0,05 от скоростей бомбардировки анода).
 |  |
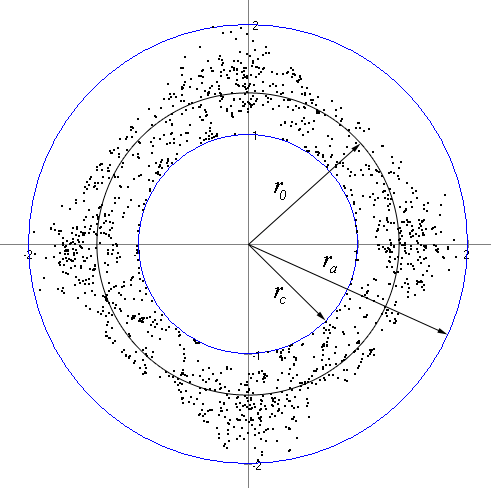| Рис. 1. Конфигурация спиц в режиме ограничения эмиссии пространственным зарядом | Рис. 2. Распределение суммарного электрического поля  по радиусу (сплошная линия),  (пунктирная линия),  (штрихпунктирная) |
 |  |
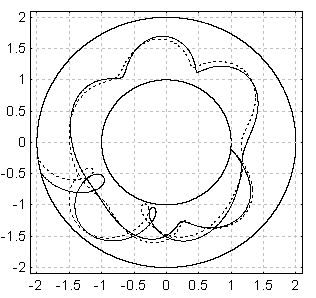| Рис. 3. Траектория заряда в режиме температурного ограничения эмиссии. Старший показатель Ляпунова равен 0,127 | Рис. 4. Траектория заряда в режиме ограничения эмиссии пространственным зарядом. Старший показатель Ляпунова равен 0,232 |
Из сравнения траекторий на рис. 3, 4 видно, что в режиме ограничения эмиссии пространственным зарядом (рис. 4) заряды значительную часть времени проводят в малоскоростной прикатодной области, расходимость траекторий, показанных сплошной и пунктирной линиями, существеннее, чем на рис. 3, соответственно больше старший показатель Ляпунова, а следовательно и уровень хаотичности.
Проведенные расчеты показали, что в режиме ограничения эмиссии пространственным зарядом мощность шума на 30-40 дБ больше мощности шума в режиме ограничения эмиссии температурой, что количественно согласуется с известными экспериментальными данными, в частности, полученными И.А. Каржавиным, Г.С. Гундобиным, В.И. Висловым.
Одной важнейших характерных особенностей электронных траекторий в приборах М-типа является их циклоидальность. Исходя из смысла теоремы Шокли-Рамо, можно ожидать, что величина тока, наведенного электронами по мере движения от катода к аноду, будет модулироваться с периодом, близким к циклотронному (из-за возвратного движения электронов по циклоиде), в то время как в случае гладкой адиабатической траектории нарастание наведенного тока в тех же условиях будет носить монотонный характер.
Известно, что для того, чтобы получить адиабатические электронные траектории, необходимо в уравнениях движения (2) исключить ускорительные члены. После чего можно получить следующую систему уравнений:
(6)
где Er, E определяются уравнением (2).
 |
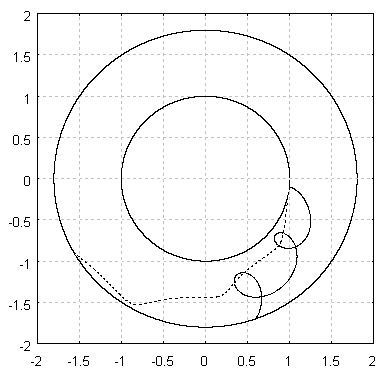| Рис. 5. Траектории заряда и ведущего центра |
На рис. 5 сплошной линией показана отдельная типичная циклоидальная траектория движения электрона в стационарном номинальном режиме работы многорезонаторного магнетрона. Адиабатическая траектория, соответствующая этому же режиму работы магнетрона, представлена на рис. 5 пунктирной линией.
Из рис. 5 видно, что адиабатическая траектория носит довольно гладкий характер, в то время как циклоидальная траектория имеет ряд участков возврата, в которых составляющие скорости меняют знак. В связи с этим естественно ожидать в соответствии с формулой Шокли-Рамо, что наведенный ток в случае циклоидальной траектории будет испытывать существенно большую модуляцию по сравнению со случаем адиабатической траектории.
 |  |
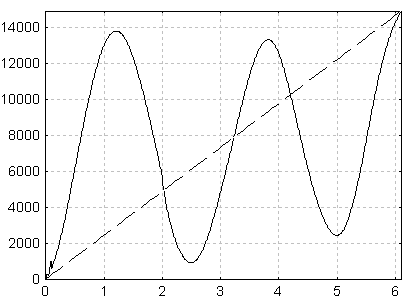| Рис. 6. Суммарный наведенный ток циклоидальных траекторий во времени | Рис. 7. Суммарный наведенный ток адиабатических траекторий во времени |
На рис. 6 и 7 представлены графики суммарного наведенного тока от 5000 крупных частиц. Из сравнения графиков на рис. 6 и 7 видно, что наведенный ток в случае адиабатических траекторий имеет существенно меньшую модуляцию.
Для оценки влияния степени модуляции для каждого графика подсчитывалась сумма квадратов отклонения от прямой, соответствующей линейному изменению наведенного тока во времени. Расчеты показали, что логарифм отношения сумм квадратов отклонений наведенного тока, соответствующего графику на рис. 6, к сумме квадратов отклонений для графика на рис. 7 составляет величину, лежащую в пределах 7-10 дБ. Эту величину, по-видимому, можно принять за оценку величины шума, возникающего за счет циклоидальности траекторий.
Таким образом, проведенный численный анализ позволяет сделать вывод о принципиальной неустойчивости траекторий зарядов в режиме больших амплитуд многорезонаторного магнетрона и возможности рассматривать эту неустойчивость как один из физически допустимых механизмов возникновения аномального шума. Полученная оценка величины избыточного шума (30-40 дБ) согласуется с экспериментальными данными. Показано, что циклоидальность траекторий также вносит свой вклад в повышенный уровень шумов.
В четвертой главе рассматриваются способы снижения шумов в выходном сигнале многорезонаторного магнетрона: за счет улучшения условий синхронизма в цилиндрическом магнетроне и с помощью азимутально меняющегося магнитного поля. Также рассматривается эффект смены направления дрейфа при использовании экспоненциально возрастающего магнитного поля.
Как известно, скорость центров орбит вращения электронов определяется отношением E/B. Как уже отмечено, в режиме ограничения эмиссии пространственным зарядом электрическое поле можно представить как сумму (4) и (5).
Следовательно, чтобы приближенно выполнить условие синхронизма вдоль радиуса, необходимо ввести изменение магнитной индукции (циклотронной частоты) аналогично закону изменения напряженности электрического поля. Соответственно, в режиме ограничения эмиссии пространственным зарядом для 
можно записать
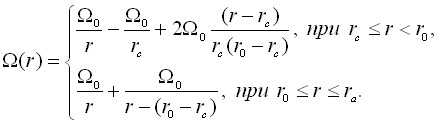(7)
На рис. 8 представлен график зависимости 
для случая ограничения эмиссии пространственным зарядом.
На рис. 9 представлены типичные траектории зарядов с учетом выражения (7) для режима ограничения эмиссии пространственным зарядом, где пунктирная и сплошная траектории соответствуют незначительно отличающимся начальным условиям.
Из сравнения рис. 4 и 9 видно, что при изменении магнитной индукции заряды быстрее достигают анода и их траектории более устойчивы.
 |  |
| Рис. 8. Распределение циклотронной частоты в пространстве взаимодействия по радиусу | Рис. 9. Траектории зарядов в режиме ограничения эмиссии пространственным зарядом с учетом изменения поля по соотношению (7) |
Расчеты, проведенные с помощью метода оценки шумов (гл. 2) показали, что в случае изменения магнитного поля согласно выражению (7) в режиме ограничения эмиссии пространственным зарядом имеет место уменьшение уровня шумов до 20 дБ по сравнению с моделью с постоянным магнитным полем.
Таким образом, подбором закона изменения магнитной индукции в пространстве взаимодействия можно влиять на уровень шумов в магнетроне.
 |
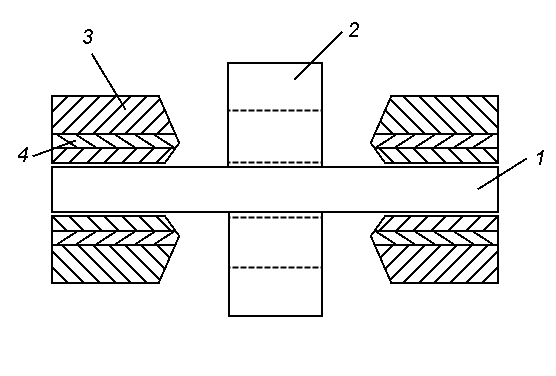| Рис. 10. Схема малошумящего магнетрона. Продольный разрез |
Была предложена конструкторская реализация изложенного механизма снижения шумов, схематически представленная на рис. 10.
Предлагается полюсные наконечники набрать из трех концентрично-расположенных кольцевых магнитных элементов с максимальной коэрцитивной силой у элемента 4. Последнее в сочетании с формой полюсных наконечников позволяет получить в пространстве взаимодействия распределение магнитной индукции, близкое к описываемому соотношением (6), что приводит к снижению уровня шума в выходном сигнале.
Известен запатентованный (US Patent 6872929, V. B. Neculaes, R. M. Gilgenbach, Y. Y. Lau.) метод уменьшения шума в выходном сигнале магнетрона, основанный на использовании азимутально меняющегося магнитного поля (за счет прикрепления дополнительных постоянных магнитов). Данный способ без физического обоснования был предложен в результате экспериментальных исследований.
Зададим закон азимутального изменения циклотронной частоты (а следовательно и магнитной индукции) следующим образом:
(8)
где 
– некоторая постоянна величина, 
– величина вариации циклотронной частоты в пространстве, k – число дополнительных возмущающих магнитов.
Патенту соответствует случай с k=2, однако представляет интерес рассмотрение увеличения числа дополнительных возмущающих магнитов (k=4).
 |  |
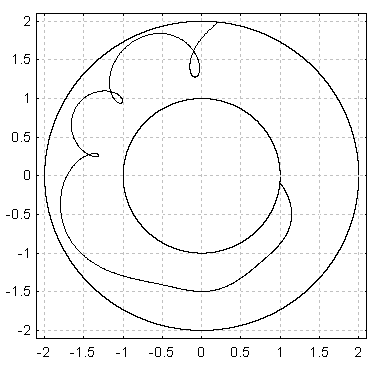| Рис. 11. Траектория заряда при азимутальном изменении магнитной индукции (k=2) | Рис. 12. Траектория заряда при азимутальном изменении магнитной индукции (k=4) |
Из сравнения рис. 11 и 12 с рис. 4 видно, что заряд в случаях азимутального изменения магнитной индукции быстро покидает малоскоростную прикатодную область. Причем для траектории на рис. 9 этот эффект выражен более ярко.
Расчеты, проведенные с помощью метода оценки шумов (гл. 2) показали, что в сравнении с режимом с постоянной магнитной индукцией режим, в котором циклотронная частота меняется по закону (8), обладает более низким уровнем шума: если в (8) k=2, то уровень шумов уменьшается на 25-28 дБ, а если k=4, то уровень шумов снижается до 27-30 дБ.
Таким образом, проведенный численный анализ объясняет, как представляется, известные экспериментальные данные и показывает, что азимутально меняющееся магнитное поле оказывает существенное влияние на изменение уровня шумов в магнетроне и приводит к их уменьшению за счет меньшего времени пребывания зарядов в прикатодной области и большей устойчивости траекторий.
В диссертации Беляева М.П. было показано, что экспоненциальное изменение магнитной индукции приводит к смене знака дрейфа в магнетронном диоде. В данной главе рассмотрена возможность появления этого эффекта в режиме генерации многорезонаторного магнетрона.
Зададим экспоненциальный закон изменения циклотронной частоты (а следовательно и магнитной индукции):
(9)
где 
– некоторая постоянная величина, – некоторая константа.
На рис. 13, а представлена типичная траектория заряда в номинальном режиме работы многорезонаторного магнетрона с магнитной индукцией, изменяющейся согласно (9). Видно, что в области, обведенной прямоугольником, изменяется направление дрейфа заряда в пространстве взаимодействия на противоположное, при этом направление вращения заряда при движении по циклоиде остается неизменным.
 |  |
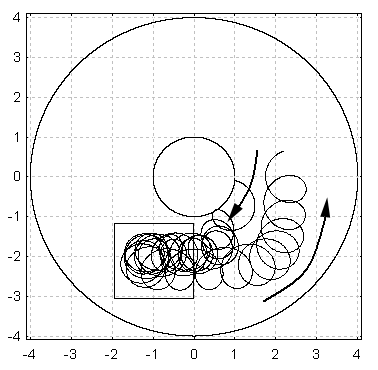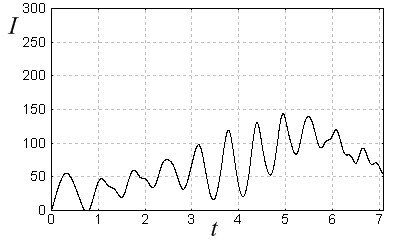| а | б |
| Рис. 13. Траектория заряда в магнетроне с магнитным полем, изменяющимся согласно (9) (a). Изменение суммарного наведенного тока во времени (б) | |
При заданном законе (9) изменения магнитной индукции вблизи катода преобладает электрический дрейф, пропорциональный, как известно, 
, но под действием тангенциальной составляющей высокочастотного поля циклоида сдвигается к аноду и попадает в область существенного изменения магнитного поля, здесь начинает преобладать магнитный дрейф (против часовой стрелки). Естественно, при этом условия синхронизма электронов с высокочастотной волной нарушаются, наведенный ток падает (рис. 13, б), соответственно лавинообразно уменьшается амплитуда высокочастотного поля на резонаторах, генерация срывается.
Чтобы приближенно учесть влияние срыва генерации на вид электронных траекторий и электронного облака, можно в расчетах с момента изменения знака дрейфа ввести уменьшенную амплитуду высокочастотного поля пропорционально уменьшению наведенного тока. На рис. 14, а приведена отдельная траектория заряда с учетом существенно уменьшенной амплитуды высокочастотного поля. Видно, что в результате уменьшения амплитуды поля заряд смещается к катоду и начинает дрейфовать, по существу, под действием только статического электрического поля (электрический дрейф), не достигая анода.
 |  |
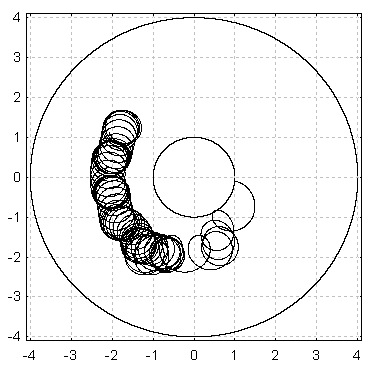| а | б |
| Рис. 14. Траектория заряда в магнетроне с учетом существенно уменьшенной амплитуды высокочастотного поля (а). Форма электронного облака при магнитном поле, изменяющемся согласно (9) (б) | |
На рис. 14, б показана форма электронного облака (5000 частиц), соответствующая изложенному механизму срыва генерации. Видно, что электроны не долетают до анода.
Описанный эффект смены знака дрейфа желательно учитывать при проектировании приборов магнетронного типа, чтобы избежать нарушения условий синхронизма. Вместе с тем указанный эффект, наряду с модуляцией анодного напряжения, может быть использован в качестве «ключа», отключающего и включающего процесс генерирования, при условии электронного управления неоднородностью магнитного поля, например, с помощью соленоида, надетого на полюсный наконечник с цилиндрическим отверстием, в котором расположен подвижный сердечник, обеспечивающий однородное магнитное поле при положении внутри наконечника и неоднородное поле при выдвинутом положении.
Таким образом, проведенный анализ показывает, что снижение уровня шумов может быть достигнуто как с помощью улучшения условий синхронизма (предполагаемое уменьшение до 20 дБ), так и с помощью использования азимутально меняющегося магнитного поля (снижение уровня шума до 30 дБ). Показано, что используемое для повышения КПД возрастающее к аноду магнитное поле может при определенных условиях приводить к срыву генерации.
В заключении подводится итог проделанной работы, формулируются результаты исследований и обосновываются перспективы использования разработанной модели для дальнейшего развития методов моделирования систем со скрещенными полями.
ОСНОВНЫЕ РЕЗУЛЬТАТЫ РАБОТЫ
- Предложены математические модели, рабочие алгоритмы и вычислительные схемы исследования хаотических и регулярных траекторий в многорезонаторном магнетроне при наличии высокочастотных и неоднородных постоянных полей.
- Предложен метод оценки уровня шумов в магнетроне, основанный на расчете суммарных наведенных токов большого числа зарядов вдоль их траекторий движения и усреднения результата по всем токам. Полученные количественные оценки согласуются с экспериментальными данными.
- Разработано программное обеспечение для моделирования и исследования траекторий в многорезонаторном магнетроне. Реализация алгоритмов выполнена на языке C++.
- Показано, что неустойчивость электронных траекторий может является одним из источников «аномального» шума в приборах М-типа.
- На основе анализа условий синхронизма в цилиндрическом магнетроне предложен закон пространственного изменения магнитной индукции, использование которого может дать существенное (до 20 дБ) уменьшение шумов. Предложена конструкция многорезонаторного магнетрона, реализующая указанный механизм уменьшения шумов.
- Показано, что циклоидальность траекторий в приборах М-типа вносит свой вклад в увеличение шумов в выходном сигнале.
- Дано физическое обоснование механизма уменьшения уровня шумов при использовании азимутально-неоднородного магнитного поля.
- Показано, что возрастающее к аноду магнитное поле может приводить к эффекту смены направления дрейфа ведущего центра и срыву генерации в многорезонаторном магнетроне.
ПУБЛИКАЦИИ ПО ТЕМЕ ДИССЕРТАЦИИ
I.Публикации в центральных изданиях, включенных в перечень
периодических изданий ВАК РФ
- Каминский К.В. Неустойчивость электронных траекторий и шумы в многорезонаторном магнетроне / В.Б. Байбурин, К.В. Каминский // Известия вузов. Прикладная нелинейная динамика. – 2007. – Т.15. №6. – С. 22-28.
- Каминский К.В. Влияние условия равенства дрейфовой скорости зарядов и фазовой скорости волны на шумы в многорезонаторном магнетроне / В.Б. Байбурин, К.В. Каминский // Известия вузов. Прикладная нелинейная динамика. – 2008. – Т.16. №5. – С. 21-25.
- Каминский К.В. Математическая модель анализа механизма шумов в многорезонаторном магнетроне / К.В. Каминский // Вестник Саратовского государственного технического университета. – 2009. – №3. – С. 108-111.
- Каминский К.В. Влияние азимутально-неоднородного магнитного поля на шумы в многорезонаторном магнетроне / В.Б. Байбурин, К.В. Каминский // Письма в ЖТФ. – 2009. – Т. 35. В. 12. – С. 90-94.
- Каминский К.В. Эффект смены знака дрейфа зарядов в многорезонаторном магнетроне / В.Б. Байбурин, К.В. Каминский, М.П. Беляев // Письма в ЖТФ. – 2009. – Т. 35. В. 19. – С. 37-43.
II. Публикации в других изданиях
- Каминский К.В. Влияние пространственно неоднородного магнитного поля на устойчивость траекторий зарядов и шумы в многорезонаторном магнетроне / В.Б. Байбурин, К.В. Каминский // Проблемы и перспективы прецизионной механики и управления в машиностроении: материалы Междунар. конф. – Саратов: ИПТМиУ РАН, 2008. – С. 298-301.
- Каминский К.В. Численный анализ влияния неоднородности магнитного поля на уровень шума в магнетроне / В.Б. Байбурин, К.В. Каминский // Математические методы в технике и технологиях: материалы Междунар. науч. конф. – Саратов: СГТУ, 2008.
- Каминский К.В. Влияние учета циклоидальности электронных траекторий на уровень шумов в многорезонаторном магнетроне / В.Б. Байбурин, К.В. Каминский // Актуальные проблемы электронного приборостроения: материалы Междунар. науч.-техн. конф. – Саратов: СГТУ, 2008. – С. 292-296.
Подписано в печать 03.09.09 Формат 6084 1/16
Бум. офсет. Усл. печ.л. 1,16 Уч.-изд.л. 1,0
Тираж 100 экз. Заказ 388 Бесплатно
Саратовский государственный технический университет
410054, Саратов, Политехническая ул., 77
Отпечатано в Издательстве СГТУ. 410054, Саратов, Политехническая ул., 77
