Оптимальное управление каталитической стадией процесса клауса
На правах рукописи
ЩЕРБАТОВ ИВАН АНАТОЛЬЕВИЧ
ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ КАТАЛИТИЧЕСКОЙ СТАДИЕЙ ПРОЦЕССА КЛАУСА
05.13.06 – Автоматизация и управление технологическими процессами и производствами (в промышленности)
АВТОРЕФЕРАТ
диссертации на соискание ученой степени
кандидата технических наук
Астрахань 2006
Работа выполнена на кафедре «Вычислительная техника и электроника» Астраханского государственного технического университета.
Научный руководитель: доктор технических наук, профессор
Проталинский Олег Мирославович
Официальные оппоненты: доктор технических наук, профессор
Львов Алексей Арленович
кандидат технических наук, доцент
Кантемиров Владимир Ильич
Ведущее предприятие: Астраханский научно-исследовательский
проектный институт газа
Защита состоится 23 ноября 2006 г. в 15 часов на заседании диссертационного совета Д 307.001.01 по присуждению ученой степени доктора технических наук в Астраханском государственном техническом университете по адресу: г. Астрахань, ул. Татищева, 16, ауд. г. 305.
Отзывы на автореферат в двух экземплярах, заверенные гербовой печатью, просим направлять по адресу: 414025, г. Астрахань, ул. Татищева, 16, АГТУ, ученому секретарю диссертационного совета Д 307.001.01.
С диссертацией можно ознакомиться в библиотеке университета.
Автореферат разослан 20 октября 2006 г.
Ученый секретарь
диссертационного совета,
профессор Г.А. Попов
ОБЩАЯ ХАРАКТЕРИСТИКА РАБОТЫ
Актуальность темы. Увеличение переработки природного газа с высоким содержанием сернистых соединений приводит к ужесточению экологических требований, предъявляемых к газоперерабатывающим предприятиям. Процесс Клауса является самым распространенным технологическим процессом получения товарной серы из сероводорода. Поэтому обеспечение экологической безопасности этого процесса позволит снизить уровень загрязнения окружающей среды вредными выбросами.
Основным направлением, которое позволит увеличить эффективность функционирования установок получения серы, является внедрение систем оптимального управления. Процесс Клауса является непрерывным и характеризуется двумя основными технико-экономическими показателями – степень конверсии сероводорода в серу и количество выбрасываемых в атмосферу вредных соединений серы. Оба эти показателя напрямую зависят от активности катализатора, засыпаемого в реакторы каталитической стадии. Поэтому необходимо обеспечить высокую активность катализатора на межремонтный интервал и исключить возможность преждевременной дезактивации катализатора.
Основные результаты исследований в области автоматического управления и математического моделирования производства серы по методу Клауса, содержатся в работах российских ученых Бродского Ю.Н., Грунвальда В.Р., Плинера В.М., Теснера П.А., Немировского В.С., Слинько М.Г., Рубинова Р.Х., а также зарубежных ученых Паскаля Х.Г. (Paskal H.G.), Сеймса Д.А. (Sames J.A.), Кларка П.Д. (Clark P.D.).
Проектная степень конверсии установок производства серы Астраханского ГПЗ равна теоретически возможной и составляет 96%, эти ограничения обусловлены термодинамическим равновесием обратимой реакции взаимодействия H2S и SO2. При нормальной эксплуатации установки, в атмосферу выбрасывается несколько тысяч тонн диоксида серы ежегодно. Но из-за функционирования установки в режиме стабилизации управляющих воздействий, фактическая степень конверсии составляет 90-95%, а ежегодные выбросы при этом возрастают в 2-3 раза.
Поэтому создание эффективной автоматизированной системы оптимального управления каталитической стадией процесса Клауса, которая позволит сохранить требуемую активность катализатора на межремонтный интервал, а также снизить выбросы вредных веществ в атмосферу, является, несомненно, актуальной научной и практической проблемой.
Целью настоящей работы является повышение эффективности управления производством серы по методу Клауса, за счет внедрения системы оптимального управления, которая позволит увеличить экологическую безопасность процесса.
Соответствующей указанной цели научной проблемой является разработка алгоритмов управления каталитической стадией процесса Клауса с использованием качественной информации.
Для достижения поставленной цели сформулированы и решены следующие задачи:
- постановка задачи оптимального управления с использованием качественной информации;
- разработка метода построения математических моделей технологических процессов со структурной неопределенностью;
- построение продукционной базы знаний для гибридной математической модели каталитической стадии процесса Клауса;
- синтез алгоритма адаптации продукционной базы знаний гибридной математической модели;
- синтез алгоритма оптимального управления каталитической стадией процесса Клауса с использованием гибридной модели;
- построение системы управления, реализующей оптимальное управление процессом.
Методы исследования. Для решения поставленных задач применялись методы математического моделирования, теория автоматического управления, методы оптимизации и математический аппарат нечетких множеств.
Научная новизна работы состоит в следующем:
- разработан метод построения математических моделей технологических процессов со структурной неопределенностью;
- впервые построена гибридная математическая модель каталитической стадии процесса Клауса;
- предложен алгоритм адаптации базы знаний интеллектуальной модели (ИМ) дезактивации катализатора;
- синтезирован алгоритм решения задачи оптимального управления, учитывающий особенности гибридной математической модели.
Практическая ценность работы состоит в следующем:
- разработано программное обеспечение, реализующего алгоритмы управления процессом с использованием гибридной математической модели;
- разработана системы оптимального управления, позволяющая повысить эффективность функционирования процесса;
- разработано программное обеспечение для моделирования процесса, позволяющее реализовать тренажерный комплекс для подготовки операторов установок Клауса.
Апробация работы. Основные положения и результаты диссертационной работы докладывались и обсуждались на следующих научно-технических конференциях: XVIII Международной научной конференции «Математические методы в технике и технологиях ММТТ-18» (г. Казань, 2005); Международных научно-технических конференций «Интеллектуальные системы» (AIS'05) и «Интеллектуальные САПР» (CAD-2005); XIX Международной научной конференции «Математические методы в технике и технологиях ММТТ-19» (г. Воронеж, 2006); Международных научно-технических конференций «Интеллектуальные системы» (AIS'06) и «Интеллектуальные САПР» (CAD-2006).
Публикации. Основные результаты диссертационной работы изложены в 11 публикациях, в том числе 3 статьи в центральных научно-технических журналах, рекомендуемых ВАК РФ, 6 в трудах международных научных конференций, 2 свидетельства об официальной регистрации программы для ЭВМ. Без соавторства опубликовано 2 работы.
Структура и объем работы. Диссертационная работа состоит из введения, 5 глав, выводов и списка литературы. Основная часть работы изложена на 189 страницах, содержит 47 рисунков, 20 таблиц, список литературы, состоящий из 150 наименований публикаций отечественных и зарубежных авторов и 4 приложения.
СОДЕРЖАНИЕ РАБОТЫ
Во введении обоснована актуальность работы, сформулированы цель и задачи исследования, научная новизна и практические результаты.
Первая глава посвящена анализу технологического процесса получения серы из сероводородсодержащих газов по методу Клауса. Приведено краткое описание технологии производства и реализация процесса на промышленной установке У-251 АГПЗ.
Проведен анализ процесса как объекта управления. В качестве управляющего воздействия выбран расход атмосферного воздуха в подогреватель технологического газа перед первым каталитическим реактором. Описано влияние управляющей переменной на выбросы вредных соединений серы.
Выделены три вида возмущающих воздействий поступающих на объект: незначительные флуктуации состава и расхода кислого газа; значительные флуктуации состава и расхода кислого газа, вызванные переходом на другой режим; изменение состава кислого газа из-за «проскока» тяжелых углеводородов с установки аминовой очистки.
Основной причиной нестационарности объекта является изменение активности катализатора из-за отложений жидкой серы, высокой температуры в реакторе и «проскока» тяжелых углеводородов с установки аминовой очистки. Присутствует значительный объем качественной информации в виде знаний операторов и технологов.
Проанализированы работы по моделированию и управлению процессом, опубликованные в отечественной и зарубежной литературе. Отмечены достоинства и недостатки перечисленных работ, ограничивающие их применение для целей управления.
Сформулирована в общем виде задача оптимального управления каталитической стадией процесса Клауса: минимизировать критерий оптимальности S при наложенных связях в виде математической модели объекта f(x1,…,xn,,u)=0 и ограничениях в виде неравенств g(x1,…,xn)0, а также ограничение на срок службы катализатора Tmin.
 | (1) |
где S(t) – выбросы в атмосферу серосодержащих соединений, [об. %], - срок службы катализатора, [мес.]; u - управляющее воздействие (расход воздуха в ТП перед КР1), [м3], 
- вектор входных координат; - вектор состояния; Tmin – межремонтный интервал функционирования установки.
Состав ограничений на вектора входных координат и состояния g(x1,…,xn)0, а также на управляющее воздействие UminuUmax определены исходя из технологического регламента.
Вторая глава посвящена разработке метода построения математических моделей объектов со структурной неопределенностью и его применение для реализации математической модели каталитической стадии процесса Клауса. Построение ММ происходит с помощью диаграммы взаимного влияния факторов (ДВВФ). Особенностью предлагаемого метода является привлечение группы экспертов в области рассматриваемого химико-технологического процесса (ХТП). Каждый эксперт строит ДВВФ, исходя из своего представления о наличии факторов и их взаимосвязях. В этом случае имеет место структурная неопределенность объекта управления.
Объединение диаграмм позволяет получить наиболее полную модель ХТП. Наличие недостоверных связей между факторами, приведет к некорректному представлению объекта с помощью ДВВФ, и как следствие - построение неадекватной ММ.
Множество элементарных физико-химических процессов, из которых состоит процесс Клауса, обозначим {Lq}. Эти процессы могут быть описаны аналитическими или регрессионными моделями, а также с использованием качественной информации. Сформулируем основную задачу метода построения математических моделей процессов со структурной неопределенностью.
На множестве {Lq} характеризуемом факторами F, построить ДВВФ D(F) рассматриваемого процесса, полученную объединением диаграмм D(F)i, i=1..Ex каждого эксперта, и обеспечивающую максимум индекса согласованности мнений экспертов :
 | (2) |
Для решения поставленной задачи необходима формализация представлений экспертов о ХТП в виде ДВВФ. Для изображения таких диаграмм предлагается использовать n-уровней – один входной (содержащий входные координаты), один выходной (содержащий выходные координаты) и n-2 промежуточных (содержащие внутрисистемные координаты).
Множество {Lq} можно представить в виде n уровней. Каждый уровень имеет конечное число объектов aRl,llmin, где lmin - величина численно равная количеству объектов из соответствующего уровня. Константа lmin определена исходя из анализа {Lq} с использованием коммуникативных и текстологических методов получения экспертных знаний.
Координаты векторов WLnLn-1=[wij] отражают степень уверенности экспертов предметной области в наличии связи между объектом n и n-1 уровней.
Для решения поставленной задачи привлекаетcя некоторое число экспертов Ex, каждый из которых включает в уровни представления {Lq} объекты, отражающие его модель, формализованную с помощью принятой системы обозначений и изображений элементов предметной области. На этом этапе использованы унарные экспертные оценки 
.
Построенные диаграммы экспертов D(F)ii=1..Ex обрабатываются с учетом полученных от экспертов сведений, которые аккумулируются для получения D(F). Объекты каждого из n уровней диаграмм экспертов, участвующих в построении D(F) объединяются в соответствии с нижеследующим выражением:
 | (3) |
В результате получаем исходную «обобщенную» модель{Lq}, где i’ - количество объектов вновь образованного m уровня. Координаты векторов WLnLn-1 для m уровня рассчитываются исходя из зависимости:
 | (4) |
где Ex - количество, участвующих экспертов; wkij - оценка k-го эксперта относительно наличия связи между объектом i уровня m и объектом j уровня m+1.
Для разрешения возникшего типа неопределенности введем итеративную процедуру порогового включения связей. Для этого введем пороги включения объекта в соответствующий уровень 
. Если wmi’j’mi’j’, то связь i’-j’ разрывается. Подобным образом рассчитываются все веса связей между объектами всех уровней.
Если по окончании процедуры порогового включения останутся «пустые» объекты, то такие вершины с ДВВФ убираются, а полученная графическая модель {Lq} принимается в качестве исходной «истинной».
Для расчета индекса согласованности мнений экспертов при составлении ДВВФ ХТП используем выражение вида:
 ,  | (5) |
где i - индекс согласованности мнений экспертов полученный для весов связей уровней i и i+1; - число связей для весов уровней ДВВФ.
Величина индекса согласованности мнений экспертов 0<1, значение =1 соответствует случаю, когда эксперты для построения ДВВФ указали наличие связей между одинаковым набором факторов для каждого из уровней.
Согласованность мнений экспертов и значение напрямую зависит от выбранных значений величин порогов включения связей. При уменьшении значений порогов включения увеличивается количество связей, включаемых в ДВВФ, и соответственно число параметров входящих в модель и вычислительная сложность самой ММ, обуславливающая ее применимость для управления быстротекущим процессом. Выбор значений порогов включения mi’j’ зависит от требуемой полноты модели и необходимой точности расчетов.
На основании предложенного алгоритма построены ДВВФ всего процесса. На рис. 1 показана диаграмма для каталитического реактора, описывающая активность катализатора.
На основании полученных ДВВФ аппаратов построена гибридная модель каталитической стадии процесса Клауса. Для описания связей, изображенных на диаграмме сплошной лини заданных аналитически использованы известные ММ технологических аппаратов, состоящие из уравнений теплового и материального балансов. Проведена параметрическая идентификация этой модели и проверена ее адекватность с применением критерия Фишера. Максимальная относительная ошибка расчетов выполняемых по этой модели не превышает величины 11,67% (рис. 2).
Рис. 1. Диаграмма каталитического реактора.
TG,PG,FGвх - температура, давление и расход кислого газа соответственно; TR - температурный режим в термическом реакторе; CH2O - содержание воды в атмосферном воздухе; df- степень конверсии каталитической стадии; 
- выход диаграммы предыдущего аппарата.
Для прогноза срока службы катализатора использована известная аналитическая модель. В качестве параметра, характеризующего активность катализатора, принята площадь активной поверхность S. Предельное значение S, при котором дальнейшее ведение процесса нецелесообразно, зависит от типа используемого катализатора и особенностей технологического оборудования. Для упрощения расчетов примем S=minS0, где коэффициент min задается в качестве параметра модели. Тогда прогноз времени работы на данном режиме установки можно выразить следующим образом:
 | (6) |
где Z –активность катализатора.
Рис. 2. Зависимость степени конверсии КР1 от соотношения концентраций H2S/SO2 при 100% нагрузке по кислому газу.
1 – экспериментальная; 2 – рассчитанная по аналитической модели.
Величина активности катализатора Z определяется с использованием интеллектуальной модели, которая описывает качественную информацию о процессе. Полученное значение Z используется в выражении (6) для расчета ограничения на срок службы катализатора, которое накладывается на оптимизируемый функционал, заданный в форме (1).
Третья глава работы посвящена синтезу базы знаний интеллектуальной модели процесса для оценки неизмеряемых координат, представляющая собой продукционную базу знаний состоящую из правил вида:
| ЕСЛИ x1 ЕСТЬ А1 И x2 ЕСТЬ В1 ТО y ЕСТЬ C1 | (7) |
Каждый элемент на ДВВФ представим продукционными правилами вида (7) как составную часть интеллектуальной модели, при этом количество ее входов равно числу входных объектов уровня m, а выходом является выходной объект уровня m+1.
Лингвистические переменные (ЛП) координат входящих в модель описаны семью термами, учитывающими отклонение параметра в положительном и отрицательном направлении.
Для этого использована интервальная шкала оценки. В качестве начала шкалы выберем ximin - минимальное значение технологического параметра, который описывает переменную в соответствии с регламентом установки. Шаг шкалы выберем исходя из величины пр, где пр - класс точности прибора, с помощью которого измеряется значение параметра, - настроечный параметр, задаваемый для достижения необходимой точности получения функции принадлежности (ФП) ЛП.
Для построения ФП использован известный метод экспертных парных сравнений. При использовании этого метода для каждой пары элементов универсального множества эксперт оценивает преимущество одного элемента над другим на основании девятибалльной шкалы Саати.
Проанализированы существующие алгоритмы нечеткого вывода, в качестве базового выбран алгоритм Мамдани.
Рис. 3. Срок эксплуатации катализатора каталитического реактора №2 при ас = 0,000135.
1 – рассчитанный по модели; 2 – экспериментальный.
Для наполнения экспертными знаниями БЗ каждый эксперт независимо продуцирует свой собственный индивидуальный набор правил (ИНП). При построении ИНП должна соблюдаться гипотеза однозначности. Для получения знаний использованы текстологические и коммуникативные методы извлечения знаний.
Полученные от экспертов знания оценены с учетом полноты описания и отсутствия в них противоречий. Значение индекса полноты для различных элементов интеллектуальной модели составляет от 0,56 до 0,97, поэтому полученные продукционные правила полно описывают неизмеряемые связи в объекте.
С целью исследования точности прогноза срока службы катализатора, рассчитываемого по выражению (6) с использованием интеллектуальной модели, проведено имитационное моделирование. Результаты показывают, что построенная модель может использоваться в составе гибридной модели, построенной для целей управления. Максимальная относительная ошибка расчетов не превышает 6,48% (рис 3).
Рис. 4. Блок-схема алгоритма адаптации интеллектуальной модели.
Синтезирован алгоритм адаптации интеллектуальной модели, для корректировки продукционных правил БЗ. В процессе функционирования установки изменяются свойства объекта, поэтому ряд правил из исходного рабочего набора могли стать неактуальными и должны быть исключены из него. Критерием недостоверности исходных правил является их соотношение с формируемым в момент времени tk текущим правилом, отражающим истинную ситуацию на объекте (рис. 4).
Особенностью алгоритма является то, что наряду с удалением и продуцированием новых правил, алгоритм корректирует антецеденты и консеквенты уже существующих правил. Консеквенты изменяются в случае если ошибка аппроксимации алгоритма адаптации не выше заданной. Антецеденты продукционных правил изменяются исходя из выражения:
 | (8) |
где xinew - вновь получаемый антецедент правила; xip - существующий антецедент правила; xiu - антецедент правила из обучающей выборки.
Описанный алгоритм реализован в виде модуля программного обеспечения для моделирования процесса и реализуемого на его базе тренажерного комплекса для операторов технологических установок Клауса.
Четвертая глава посвящена разработке алгоритмов управления каталитической стадией процесса получения серы по методу Клауса с использованием качественной информации.
Проведена декомпозиция поставленной задачи оптимизации в форме (1) и показано, что определение оптимального управления U(t) может быть сведено к поиску последовательности субоптимальных управлений Uj (где j – номер соответствующего статического режима). Задача поиска субоптимального управления является конечномерной задачей оптимизации соответствующих статических режимов функционирования процесса и определения момента tk их решения.
Основными особенностями данной задачи оптимизации являются: наличие нелинейного критерия оптимальности, заданного алгоритмом своего вычисления на некотором временном интервале; задача решается с помощью одной управляющей переменной; математическая модель объекта управления является гибридной; имеются ограничения типа неравенств наложенные на переменные вектора состояния, управления и входа объекта; объект является нестационарным, основной причиной его нестационарности является изменение активности катализатора.
Активность катализатора Z определяется с помощью интеллектуальной модели дезактивации катализатора и представляет собой нечеткую цель, достижение которой обеспечит необходимую эффективность ведения процесса.
Пусть 
- универсальное множество возможных управляющих воздействий (альтернатив). Нечеткая цель, которая обеспечивает минимум Z, описывается нечетким подмножеством, т.е. имеет место отображение ZU,[0,1]. Чем больше степень принадлежности альтернативы u нечеткому множеству Z (чем больше значение Z(u)), тем больше степень достижения указанной цели при выборе этой альтернативы.
Проведено имитационное моделирование для исследования вида функций принадлежности цели и ограничений. Анализ результатов показал, что Z(u) можно аппроксимировать с помощью типовой Гауссовой функции принадлежности. Описанная задача расчета Z, обеспечивающая минимальное значение этого параметра с учетом наложенных на него ограничений относится к классу задач нечеткого математического программирования (НМП). Это задача выполнения нечеткой цели Z, при наличии нечетких ограничений ck`(u), k=1..3, которая решена за счет пересеченя нечетких множеств цели и ограничений.
Рис. 5. Решение задачи поиска минимума Z по схеме Беллмана-Заде.
Существует три основных причины дезактивации катализатора – содержание CH4 в технологическом газе (ограничение c1`(u)); термическая деструкция из-за высокой температуры в реакторе (ограничение c2`(u)); сульфатация (ограничение c3`(u)).
В данной постановке задачи следует говорить об удовлетворении ограничениям с некоторой степенью их важности 
: 
. Влияние сульфатации на активность катализатора является наиболее сильным и как следствие, удовлетворение этому ограничению является с точки зрения эффективного решения более важным. Функция принадлежности решения, с учетом коэффициентов относительной важности k-ого ограничения, примет вид:
 | (9) |
Решена поставленная задача НМП с использованием схемы Беллмана-Заде: задаются коэффициенты относительной важности k-ого ограничения, производится аппроксимация функций принадлежности G, C1, C2. гауссовой, а C3 показательной ФП и вычисление D с помощью (9) (рис. 5).
Анализ результатов численного моделирования, показал, что целевая функция имеет несколько минимумов и непрерывна на интервале UminuUmax (т.е. при расходе воздуха 3000FA11300 м3, рис. 6).
Рис. 6. Исследование работы алгоритма поиска оптимального управляющего воздействия на входе в подогреватель.
Для решения задачи оптимального управления каталитической стадией процесса Клауса применен метод последовательного оценивания с использованием квадратичной аппроксимации (метод Пауэлла).
Задается значение начальной точки u1, которое выбирается с помощью:
 | (10) |
где k3=4.76; GBном - количество воздуха необходимое для полного окисления сероводорода до сернистого ангидрида. [м3/ч]; k1=103 - поправочный коэффициент, учитывающий размерности величин; C1, C2 - концентрации сероводорода и сернистого ангидрида после реактора, [об. доли].
Величина GBном рассчитана при фиксированном расходе кислого газа в подогреватель. Величина шага по оси FA/FG. (u) выбрана исходя из класса точности прибора, измеряющего расход воздуха в подогреватель перед первым каталитическим реактором. Использование (10) позволило выбрать точку находящуюся близко к глобальному минимуму, что значительно снизило время поиска экстремума функции, которое при заданных постоянных (табл. 1) не превышает 6с.
Синтезированный двухуровневый алгоритм (верхний уровень – задача НМП, решаемая по схеме Беллмана-Заде; нижний уровень – метод Пауэла) позволяет сделать прогноз времени Т с точность до 10 сут. (погрешность 0,56%) и достичь значения целевой функции 0,99%, что ниже допустимой нормы этого показателя в 2 раза.
Таблица 1. Результаты работы алгоритма поиска экстремума функции.
| Точка останова m | k | u* | Время работы алгоритма, сек. |
| [0,01;0,1] | [0.1;0.3;0.6] | 4,51 | до 6 |
| f*(X,u*) | Т прогнозное, сут. | Т факт., сут. | Относ. ошибка, % |
| 0,99 | 1790 | 1800 | 0,56 |
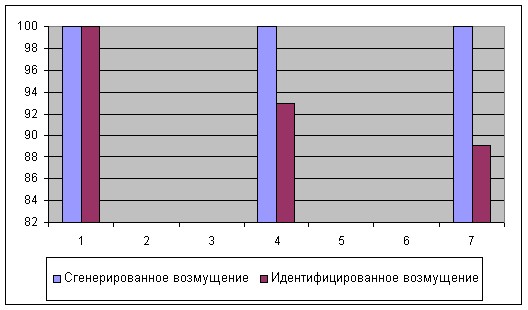
Рис. 7. Результат имитационного моделирования алгоритма определения периода квазистационарности.
Разработан алгоритм определения момента времени решения задачи оптимизации статического режима: при поступлении возмущающих воздействий (качества сырья) и изменения характеристик объекта, вследствие нестационарности (активности катализатора и состояния подогревателей). Для оценки последних показателей использованы продукционные правила.
Для проверки эффективности предложенного интеллектуального алгоритма определения периода квазистационарности проведено имитационное моделирование (рис. 7). Определение момента времени поступления возмущающего воздействия на объект происходит для 100% сгенерированных возмущений 1-го типа, 93% возмущений 2-го типа и 89% возмущений 3-го типа. Невозможность идентифицировать возмущения 2-го и 3-го типов определяется отсутствием показаний по трем из четырех приборов измеряющих показатели кислого газа (ситуации введены в имитационную модель искусственно), которые могут возникнуть из-за неисправности средства измерения или сбоя информационной подсистемы АСУ ТП.
Пятая глава посвящена исследованию и реализации системы управления каталитической стадией процесса Клауса. Для реализации синтезированных алгоритмов управления предложена двухуровневая структура построения системы управления. На первом уровне (нижнем) функционирует существующая система автоматизированного управления технологическим процессом, построенная на оборудовании американской фирмы “Foxboro”. На втором уровне предлагается надстроить автоматизированную систему управления, работающую в режиме советчика оператору, базирующуюся на разработанных алгоритмах с применением описанных методов их реализации.
Рис.8. Результаты имитационного моделирования системы оптимального управления.
В существующей АСУТП имеется контур подачи «воздуха оптимизации», добавляющий к основному потоку часть воздуха, которая позволит выйти на оптимальный режим работы, но расчет «воздуха оптимизации» не производится, система управления работает в режиме стабилизации управляющих воздействий. Поэтому предложено включить в контур управления подачей «воздуха оптимизации» высокопроизводительную ЭВМ, рассчитывающую оптимальные настройки регулятора.
Разработана функционально-алгоритмическая схема системы оптимального управления. Предложены способы взаимодействия алгоритмов оптимального управления и существующих SCADA-систем на примере TraceMode 6.0. Рассмотрен а возможная техническая реализация системы управления процессом. Разработано программное обеспечение для моделирования процесса, на его базе построен тренажерный комплекс.
Для оценки эффективности и работоспособности применения системы оптимального управления статическим режимом процесса проведено имитационное моделирование. Приведены результаты, подтверждающие работоспособность предложенных алгоритмов (рис. 8). Показано, что при субоптимальном управлении выбросы вредных веществ не выходят за границу допустимости.
Показано, что повышение эффективности функционирования процесса при оптимальном управлении по сравнению с режимом стабилизации управляющих воздействий, составляет 12%, что соответствует снижению выбросов в среднем на 0,63%.
ОСНОВНЫЕ РЕЗУЛЬТАТЫ И ВЫВОДЫ
- Проведен анализ процесса как объекта управления, позволивший выявить особенности процесса, затрудняющие его автоматизацию. Поставлена задача оптимального управления статическим режимом каталитической стадии для повышения эффективности процесса.
- Разработан метод построения математических моделей технологических процессов со структурной неопределенностью, позволяющий строить гибридные модели процессов с привлечением группы экспертов.
- Впервые синтезирована продукционная БЗ ИМ дезактивации катализатора и показано, что максимальная относительная ошибка расчетов по модели с использованием этой БЗ составляет 6,48%.
- Синтезирован алгоритм адаптации базы знаний ИМ, который позволяет в режиме реального времени корректировать не только продукционные правила, но и консеквенты и антецеденты правил.
- Предложен алгоритм субоптимального управления статическим режимом процесса, отличающийся использованием гибридной математической модели объекта управления и учетом нечетких ограничений.
- Решена задача оптимального управления процессом: разработана система оптимального управления, включая алгоритмическое и техническое обеспечение, которая позволит повысить эффективность управления процессом.
- Произведена оценка эффективности системы оптимального управления процессом. Показано, что внедрение предлагаемой системы позволит снизить выбросы серосодержащих соединений на 0,63%.
- Программный комплекс, разработанный для моделирования процесса Клауса, используется в учебном процессе в Астраханском государственном техническом университете.
- Метод построения гибридных моделей со структурной неопределенностью использован при построении математической модели энергоблока №1 Астраханской ТЭЦ-2. Использование алгоритма адаптации ИМ запланировано в составе АСУТП ТЭЦ-2.
ПУБЛИКАЦИИ ПО ТЕМЕ ДИССЕРТАЦИИ
- Щербатов И.А., Мичуров Ю.И. Интеллектуальная математическая модель дезактивации катализатора процесса Клауса // Математические методы в технике и технологиях – ММТТ-18. Сб. трудов XVIII Международ. науч. конф. В 10 т. Т. 6. Секции 6, 8 / Под общ. ред. В.С. Балакирева.- Казань: изд-во Казанского гос. технол. ун-та, 2005. С 29-30.
- Щербатов И.А., Петраченко А.А., Чернов С.В., Епимахов И.А. Моделирование процесса Клауса с использованием интеллектуальной модели дезактивации катализатора // Математические методы в технике и технологиях – ММТТ-18. Сб. трудов XVIII Международ. науч. конф. В 10 т. Т. 6. Секции 6, 8 / Под общ. ред. В.С. Балакирева.- Казань: изд-во Казанского гос. технол. ун-та, 2005. С 69-71.
- Щербатов И.А. Построение информационно-обучающей системы для студентов химико-технологических специальностей на примере процесса Клауса // Сб. материалов Международ. научно-практич. конф. «Электронный университет как условие устойчивого развития региона», Астрахань, 2005. С 267-268.
- Щербатов И.А., Проталинский О.М., Мичуров Ю.И. Гибридная модель каталитического реактора процесса Клауса // Изв. вузов. Сев.-Кавк. Регион. Техн. науки.-2005.- №2. С. 23-34.
- Щербатов И.А., Проталинский О.М. Оценка активности катализатора процесса Клауса с использованием интеллектуальной модели // Труды Международных научно-технических конференций «Интеллектуальные системы» (AIS'05) и «Интеллектуальные САПР» (CAD-2005). Научное издание в 3-х томах.- М.:ФИЗМАТЛИТ, 2005, Т.2.- С 371-374.
- Щербатов И.А., Проталинский О.М., Чернов С.В., Епимахов И.А. Математическая модель термической стадии процесса Клауса // Свидетельство об официальной регистрации программы для ЭВМ № 2005611959 от 05.08.05. Федеральная служба по интеллектуальной собственности, патентам и товарным знакам.
- Щербатов И.А., Проталинский О.М., Чернов С.В., Епимахов И.А. Математическая модель каталитической стадии процесса Клауса // Свидетельство об официальной регистрации программы для ЭВМ № 2005611958 от 05.08.05. Федеральная служба по интеллектуальной собственности, патентам и товарным знакам.
- Щербатов И.А., Проталинский О.М. Программный комплекс для обучения операторов технологического процесса получения серы // Изв. вузов. Сев.-Кавк. регион. Техн. науки.-2006.-Прил. №2.-С. 29-34.
- Щербатов И.А., Проталинский О.М. Интеллектуальная модель для прогноза срока службы катализатора установок получения серы // Математические методы в технике и технологиях – ММТТ-19. Сб. трудов XIX Международ. науч. конф. В 10-и т. Т. 6. Секции 6, 12 / под общ. ред. В.С. Балакирева.- Воронеж, Воронеж. гос. технол. акад., 2006. С 50-52.
- Щербатов И.А. Продукционная база знаний для оценки неизмеряемых параметров каталитических процессов // Математические методы в технике и технологиях – ММТТ-19. Сб. трудов XIX Международ. науч. конф. В 10-и т. Т. 6. Секции 6, 12 / под общ. ред. В.С. Балакирева.- Воронеж, Воронеж. гос. технол. акад., 2006. С 8-10.
- Щербатов И.А., Проталинский О.М., Савельев А.Н. Оптимальное управление технологическим процессом Клауса в условиях неопределенности // Изв. вузов. Сев.-Кавк. регион. Техн. науки. Спец. вып. «Математическое моделирование и компьютерные технологии».-2006.- С. 19-25.
Тип. АГТУ Зак. 760 Тир.100 от 19.10.2006г.
