Алгоритм ы повышения эффективности решения задач анализа и синтеза систем управления с использованием параллельных вычислений
На правах рукописи
СТЕПАНОВ Андрей Михайлович
алгоритмы повышения эффективности решения задач анализа и синтеза систем управления с использованием параллельных вычислений
Специальность 05.13.01 – Системный анализ, управление и обработка информации (в технической отрасли)
Автореферат
диссертации на соискание ученой степени
кандидата технических наук
Саратов - 2012
Работа выполнена в Федеральном государственном бюджетном образовательном учреждении высшего профессионального образования «Саратовский государственный технический университет имени Гагарина Ю.А.»
| Научный руководитель | доктор технических наук, профессор Большаков Александр Афанасьевич |
| Официальные оппоненты: | Абрамов Геннадий Владимирович, доктор технических наук, профессор, ФГБОУ ВПО «Воронежский государственный университет инженерных технологий», заведующий кафедрой информационных технологий, моделирования и управления |
| Петров Дмитрий Юрьевич, кандидат технических наук, доцент, Институт проблем точной механики и управления РАН (г. Саратов), старший научный сотрудник | |
| Ведущая организация: | Институт проблем управления имени В.А.Трапезникова РАН (г. Москва) |
Защита диссертации состоится «28» декабря 2012 г. в 14.00 часов на заседании диссертационного совета Д 212.242.04 при ФГБОУ ВПО «Саратовский государственный технический университет имени Гагарина Ю.А.» по адресу: 410054, г. Саратов, ул. Политехническая, 77, Саратовский государственный технический университет имени Гагарина Ю.А., главный корпус, ауд. 319.
С диссертацией можно ознакомиться в научно-технической библиотеке ФГБОУ ВПО «Саратовский государственный технический университет имени Гагарина Ю.А.».
Автореферат разослан « 27 » ноября 2012 г.
| Ученый секретарь диссертационного совета | В.В. Алешкин |
Общая характеристика работы
Актуальность работы. Расширение сфер применения автоматического управления, возрастающая сложность управляемых объектов обусловили бурное развитие теории автоматического управления. Нарастающее многообразие методов решения задач теории управления, все более сложных с вычислительной точки зрения, привело к необходимости совершенствования методов и средств информационной поддержки их применения при решении конкретных задач. Для решения задач в интерактивном режиме требуется все более высокопроизводительная вычислительная техника. Однако производительность ядра процессора компьютера достигла физического предела для текущей используемой технологии производства интегральных схем. Дальнейший рост производительности отдельного компьютера достигается в основном лишь за счет использования многоядерной организации. Для использования их возможностей необходимы специальные алгоритмы и реализующие их программы, допускающие применение параллельных вычислений. Однако их разработка пока слабо поддается автоматизации, поскольку требует учета специфики методов решения функциональных задач проблемной области, является сложной творческой работой, характеризующейся высокой трудоемкостью.
Исследованиям в области формализации знаний о методах решения задач, разработки методов и средств информационной поддержки решения задач обработки информации в процессах управления, проектирования и исследования сложных объектов, к которым относятся современные системы управления, посвящены многочисленные работы зарубежных (Н. Винер, Р.Беллман, М.Калман, К.Острем, М.Флинн, Е.Дейкстра, А.Тьюринг, Е.Валях, Г.Родригуе, Б.Мейер, Л.Льюинг, Т. Кохонен, Дж. Хопфилд, Б.Топпинг, Д.Румельхарт, Ф.Г. Энслоу и др.) и отечественных авторов (Я.З. Цыпкин, С.Н. Коровин, В.В. Солодовников, В.Н. Васильев, Б.Т.Поляк, А.Г.Александров, Е.И.Артамонов, И.П. Норенков, К.А. Пупков, В.В. Семенов, Д.А.Поспелов, В.М.Глушков, В.В.Воеводин, Вл.В. Воеводин, А.Ф.Резчиков, В.В. Топорков, А.А. Большаков, В.В.Сафронов, М.Ф. Степанов и др.).
Для повышения эффективности систем информационной поддержки разработки и исследования современных систем управления, сокращения сроков разработки, повышения качества проектируемых систем, снижения вычислительных затрат необходимы исследования возможностей применения параллельных вычислений при решении задач управления, разработка соответствующих алгоритмов, специального математического и программного обеспечения.
Это обусловливает актуальность темы диссертационного исследования, которое соответствует приоритетным направлениям развития науки, технологий и техники РФ («Информационно-телекоммуникационные системы») и критическим технологиям («Технологии распределенных вычислений и систем»).
Целью работы является повышение эффективности систем информационной поддержки разработки и исследования современных систем управления на основе комбинированных методов и моделей организации вычислительного процесса с применением параллельных вычислений.
Для достижения поставленной цели необходимо решить следующие задачи:
- Системный анализ особенностей задач теории управления для определения критериев эффективности, способов модификации алгоритмов, обеспечивающих повышение эффективности средств решения задач идентификации, оптимизации, синтеза законов управления на основе применения параллельных вычислений.
- Разработка и исследование алгоритмов, специального математического и программного обеспечения планирования действий по решению задач анализа, идентификации, оптимизации, синтеза законов управления с применением параллельных вычислений.
- Разработка и исследование алгоритмов, специального математического и программного обеспечения параметрической идентификации с применением параллельных вычислений.
- Разработка и исследование алгоритмов, специального математического и программного обеспечения решения задач анализа и синтеза законов управления с применением параллельных вычислений.
Методы исследования. Методы системного анализа для исследования задач теории управления, методов их решения для исследования возможности применения параллельных вычислений, методы теории алгоритмов, математического моделирования, теории оптимального управления, теории идентификации, теории оптимального наблюдения, теории искусственных нейронных сетей.
Объектом исследования являются системы информационной поддержки разработки и исследования современных систем, методы и алгоритмы решения задач анализа и синтеза законов управления.
Научная новизна:
- разработаны критерии целесообразности применения параллельных вычислений, отличающиеся учетом доступной априорной и апостериорной информации, что позволило разработать алгоритм оценки необходимых вычислительных ресурсов для решения задач управления в условиях ограничений на время обработки информации;
- предложен алгоритм планирования действий по решению задач анализа и синтеза законов управления, отличающийся использованием планирующей искусственной нейронной сети с применением параллельных вычислений, что позволило сократить время решения задачи планирования до приемлемых для интерактивного режима работы средств информационной поддержки разработки и исследования систем управления значений;
- создан комбинированный алгоритм планирования действий группы мобильных объектов, отличающийся использованием комплекса алгоритмов трехуровневого планирования: стратегического (лучевой алгоритм), тактического (двунаправленный нейросетевой алгоритм) и оперативного планирования, что позволило разработать соответствующее специальное математическое и программное обеспечения с использованием параллельных вычислений для поддержки управленческих решений в автоматизированных системах управления мобильных объектов;
- разработан модифицированный генетический алгоритм параметрической идентификации, отличающийся использованием средств параллельных вычислений, что позволило создать соответствующее специальное математическое и программное обеспечение параметрической идентификации с меньшими затратами времени и/или более высокой точностью оценки параметров;
- предложены способы модификации архитектуры специального математического и программного обеспечения информационной поддержки разработки и исследования систем управления, отличающиеся использованием комбинированных методов и алгоритмов планирования и выполнения действий по решению задач параметрической идентификации, анализа и синтеза законов управления с использованием параллельных вычислений, что позволило разработать компоненты интеллектуальной распределенной Интернет-системы информационной поддержки разработки и исследования систем управления.
Основные результаты исследования, выносимые на защиту:
- критерий целесообразности применения параллельных вычислений и алгоритм оценки необходимых вычислительных ресурсов для решения задач управления в условиях ограничений на время обработки информации;
- алгоритм планирования действий по решению задач анализа и синтеза законов управления, отличающийся использованием планирующей искусственной нейронной сети с применением параллельных вычислений;
- комбинированный алгоритм планирования действий группы мобильных объектов, отличающийся использованием комплекса алгоритмов трехуровневого планирования: стратегического (лучевой алгоритм), тактического (двунаправленный нейросетевой алгоритм) и оперативного планирования с использованием параллельных вычислений;
- модифицированный генетический алгоритм параметрической идентификации, отличающийся использованием средств параллельных вычислений;
- модифицированная архитектура специального математического и программного обеспечения информационной поддержки разработки и исследования систем управления, отличающиеся использованием комбинированных методов и алгоритмов планирования и выполнения действий по решению задач параметрической идентификации, анализа и синтеза законов управления с использованием параллельных вычислений.
Практическая значимость работы заключается в реализации специального математического и программного обеспечения в виде компонентов сервера планирования действий, сервера приложений распределенной системы автоматического решения задач ГАММА-3, обеспечивающих применение параллельных вычислений в процессе планирования действий и их выполнения в ходе решения задач разработки и исследования систем управления. Исследования выполнялись по гос. контракту № 02.740.11.0482 «Разработка распределенной вычислительной среды для создания систем управления жизненным циклом мобильных мехатронных комплексов». Результаты диссертации используются на проектно-производственном предприятии «ППП Дизельавтоматика» (г. Саратов), в учебном процессе СГТУ.
Достоверность и обоснованность результатов диссертационного исследования подтверждается корректным использованием математических методов, компьютерным моделированием; успешным их использованием в различных организациях; соответствием основных теоретических положений и выводов практическим результатам, полученным на основе разработанных моделей и методов.
Апробация работы. Основные результаты работы обсуждались на Международных научно-технических конференциях: Математические методы в технике и технологиях (Ярославль, 2007; Саратов, 2008, Смоленск, 2010, Саратов, 2011; Харьков, 2012); Системы проектирования, технологической подготовки производства и управления этапами жизненного цикла промышленного продукта (CAD/CAM/PDM) (Москва, 2012), Интеллектуальные системы (Вологда, 2012), Проблемы управления, обработки и передачи информации (Саратов, 2009, 2011), Логистика и экономика ресурсоэнергосбережения в промышленности (МНПК «ЛЭРЭП-5-2011») (Саратов, 2011), 5th Chaotic Modeling and Simulation International Conference CHAOS 2012 (Athens Greece 2012), International congress on information technologies-2012 (ICIT-2012).
Исследования поддержаны Государственным фондом содействия развитию малых форм предприятий в научно-технической сфере по программе «Участник молодежного научно-инновационного конкурса» (2012 - 2013 гг.).
Публикации. Основные результаты диссертационной работы опубликованы в 21 печатной работе, в т.ч. 6 статей – в журналах из списка, рекомендованного ВАК РФ.
Структура и объем диссертации. Диссертация состоит из введения, пяти разделов, заключения, списка использованной литературы и приложения. Работа изложена на 143 страницах машинописного текста, содержит 41 рисунок и 3 таблицы, список литературы включает 136 наименований.
Краткое содержание работы
Во введении обоснована актуальность темы диссертационной работы, поставлены цель и задачи исследования, определены научная новизна результатов и их практическое значение, описывается основное содержание работы.
В первой главе приведена классификация задач, решаемых в системах анализа, идентификации, оптимизации, синтеза законов управления, а также и в интеллектуальных системах автоматического управления (ИСУ). Для адаптации к изменяющимся условиям в ИСУ применяются различные подходы. Среди них выделяются методы, обеспечивающие построение закона управления наиболее точно соответствующего требованиям цели управления в текущей ситуации. Они базируются на идентификации модели объекта управления, внешней среды и последующем синтезе нового закона управления. Изменяющиеся условия (возможно и цель управления) не позволяют ограничиться одной процедурой синтеза закона управления. Поэтому ИСУ включают средства планирования действий по решению задач синтеза. Одновременное выполнение действий ИСУ по управлению заданным объектом, а также всех указанных действий с целью адаптации к изменяющимся условиям в режиме реального времени обуславливает необходимость применения параллельных вычислений. Рассмотрены виды параллелизма, приводится оценка величины ускорения при использовании параллельных вычислений, приведена классификация задач теории автоматического управления, определен критерий эффективности средств их решения (1).
 , | (1) |
 , | (2) |
где 
– оценка эффективности, 
– интегральный критерий, учитывающий вклад частных критериев (времени решения задач 
, затрат памяти 
, вычислительной сложности алгоритмов решения задач 
, финансовых затрат 
(n – количество используемых параллельных процессов) в общую оценку эффективности рассматриваемого 
подхода, использующего ресурсы 
из заданного (доступного) множества ресурсов), например, в виде аддитивного критерия (2), где 
– коэффициенты важности (
), 
– затраты времени, памяти, финансовых ресурсов, вычислительная сложность последовательного (скалярного) варианта алгоритма решения задачи соответственно.
Дана математическая формулировка цели исследования: обеспечить повышение эффективности средств информационной поддержки решения задач идентификации параметров объекта, анализа и синтеза законов управления, а также планирования действий по организации соответствующего вычислительного процесса в смысле критерия (3) за счет разработки алгоритмов с использованием параллельных вычислений.
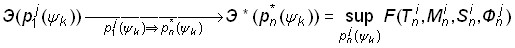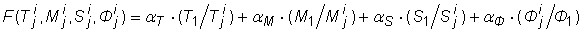 ,  . | (3) |
Выполнен обзор средств организации параллельных вычислений, обоснован выбор применяемого средства организации параллельных вычислений.
Во второй главе рассматривается методика распараллеливания вычислений.
Теорема 2.1. Критерий целесообразности применения параллельных вычислений для сокращения времени решения задачи обработки информации задается выражением
 , | (4) |
где 
– предельно возможное ускорение вычислений; 
– доля скалярных операций в алгоритме решения задачи; 
– максимальное число параллельных процессов, которые можно использовать при решении задачи; 
– накладные расходы (потери) за счет обмена данными между параллельными процессами; 
– скорость обмена данными между параллельными процессами; 
– объем передаваемых данных между параллельными процессами.
Проведено исследование возможности организации параллельных вычислений для задач синтеза и анализа систем управления. Предложены способы модификации структуры распределенной системы информационной поддержки разработки и исследования систем управления с целью повышения эффективности решения с её помощью задач анализа и синтеза систем управления за счет применения параллельных вычислений (рис. 1).
Проведены исследования эффективности систем параллельных вычислений при выполнении матричных операций. Основным критерием при распараллеливании являются затраты времени, поэтому эффективность распараллеливания измеряют затратами времени по отношению к последовательной реализации алгоритма, что и отражает коэффициент ускорения вычислений. Для систем параллельных вычислений важной характеристикой является ускорение параллельной системы, определяемое в соответствии с законом Амдала.
 |  |
Рис. 2. Зависимости значения коэффициента  закона Амдала и коэффициента ускорения вычислений от количества процессов (потоков), n – размерности задачи, a – удельного веса скалярных (нераспараллеливаемых) операций | |
Для многих задач коэффициенты сетевого закона Амдала могут быть вычислены аналитически. Однако в реальных условиях ускорение зависит от массы факторов, например общей загруженности вычислительной системы, включая накладные расходы операционной системы (в т.ч. и сетевых протоколов), объемом обрабатываемых данных, эффективностью реализации средств распараллеливания и т.д. Проведены исследования для экспериментальной оценки значения коэффициента 
закона Амдала на примере операции умножения 
матриц. Результаты исследований представлены на рис. 2. Коэффициент ускорения достигает наибольшего значения при равенстве количества процессов и узлов (процессорных ядер) вычислительной системы. Часто необходимо на имеющейся вычислительной системе с известными характеристиками (время решения на однопроцессорной системе 
) решить заданную задачу за желаемое время 
, обеспечивая ускорение вычислений 
.
Теорема 2.2. Для стационарной вычислительной сети необходимое количество узлов сети для решения заданной задачи за желаемое время определяется по формуле
 . | (5) |
Несмотря на кажущуюся простоту выражения (5), утверждение теоремы 2.2 не удается напрямую использовать для определения необходимого количества узлов вычислительной сети в целях решения рассматриваемой задачи в указанные сроки. Это обусловлено тем, что входящий в выражение (5) коэффициент 
, в свою очередь, зависит от количества используемых узлов и размерности задачи.
Для устранения обнаруженных трудностей предлагается
Алгоритм 2.1 оценки необходимых вычислительных ресурсов
1. На основе закона Амдала определить для 
-й итерации алгоритма текущее значение искомого количества узлов вычислительной сети по формуле
 . | (6) |
2. В соответствии с выражением 
определить текущее значение коэффициента сетевой деградации вычислений, соответствующего решаемой задаче. Зависимость 
определяется предварительно на основе аппроксимации данных экспериментов по исследованию вычислительной сети.
3. Определить уточненное количество узлов вычислительной сети
 , | (7) |
где 
– операция взятия ближайшего большего, чем 
, целого числа.
4. Если 
, то завершить работу алгоритма, иначе идти к п. 2.
Результаты применения алгоритма 2.1 совпадают с экспериментальными данными, полученными в результате вычислительного эксперимента по определению оценки значения коэффициента 
закона Амдала на примере задачи умножения матриц 
.
В третьей главе рассматривается возможность организации параллельных вычислений при решении задач планирования действий.
В системах решения задач, в т.ч. анализа и синтеза закона управления ИСУ, принято делить задачи на типовые и новые (непроцедурно поставленные). Для типовых задач порядок действий по их решению заранее известен. Поэтому для них необходимость планирования действий не возникает.
Процесс решения непроцедурно поставленных задач включает: 1) планирование действий на основе использования имеющихся в системе знаний; 2) выполнение построенного плана и получение результата решения задачи.
Для решения непроцедурно поставленных задач необходимо привлечение методов искусственного интеллекта. При этом наиболее перспективными для планирования действий являются системы автоматического доказательства теорем. Однако они неприменимы к задачам реального времени. Необходимое повышение быстродействия систем автоматического доказательства теорем достигается применением специального средства параллельной обработки информации – планирующих искусственных нейронных сетей (ПИНС). Параметры ПИНС (количество нейронов в слоях) определяются используемой моделью знаний о методах решения задач синтеза закона управления.
Исследован алгоритм моделирования ПИНС, определены направления повышения его эффективности – параллельные вычисления выходов нейронов каждого слоя сети. Предложен модифицированный алгоритм моделирования ПИНС, допускающий использование параллельных вычислений. Проведено исследование эффективности планирования действий с использованием параллельных вычислений на тестовой задаче при следующих параметрах ПИНС: количество нейронов решающей сети: 432, 240, 240, 55 в 0-м, 1-м, 2-м, 3-м слоях, в архивной сети: 240 и 55 в 1-м и 2-м слоях, соответственно. На рис. 3 приведены графики изменения коэффициента ускорения, критерия эффективности и потерь (накладных расходов) в зависимости от количества используемых параллельных процессов. Наибольшее значение критерия эффективности 3,14 достигается на 16 параллельных процессах, ускорение 4. Дальнейшее увеличение степени распараллеливания до 64 процессов снижает значение критерия (в два раза) в связи с ростом накладных расходов на обмен данными между параллельными процессами, хотя ускорение вычислений все еще увеличивается (на 15%).
В задачах управления подвижными объектами, например мобильными роботами, дополнительно необходимо осуществлять планирование траектории с учетом изменяющейся обстановки на местности. В системах планирования действий мобильных роботов целесообразно разбить процесс планирования на 3 этапа: стратегическое; тактическое и оперативное (детальное) планирование. На каждом этапе применяются различные методы. Многоэтапное планирование предполагает совместимость результатов работы на каждом этапе, что не каждый алгоритм планирования может обеспечить. На уровне тактического планирования траектории движения мобильного робота одним из наиболее перспективных направлений является использование нейросетевых алгоритмов. Широко распространено применение волнового алгоритма распространения сигнала в разновидности искусственной нейронной сети Хопфилда. При этом в отсутствие препятствий алгоритм затрачивает на построение траектории N шагов, где N – количество дуг между узлами сети, которые входят в искомый путь. Особенности функционирования автономного мобильного робота в условиях быстро меняющейся оперативной обстановки, поступления целеуказаний, изменения состояния самого мобильного робота требуют более оперативного решения задачи планирования траектории достижения цели. Предложен двунаправленный алгоритм планирования, использующий нейронную сеть в виде аналоговой сети Хопфилда. Исследования алгоритма осуществлялись методом математического моделирования с помощью программного средства, обеспечивающего необходимую визуализацию результатов планирования (см. рис.4). Двунаправленный алгоритм планирования естественным образом позволяет распараллелить работу в каждом направлении на два потока, что вполне выполнимо для современных роботов, обладающих более чем одним бортовым вычислителем. Достигнуто ускорение вычислений 1,7 (предельно достижимое 1,8) на двух узлах (потоках).
Ограниченные возможности отдельного мобильного робота могут существенно возрастать за счет их группового применения для решения крупномасштабных задач. Для решения одной из важных проблем человечества – поиска и диагностирования взрывных устройств предлагается использовать группу автономных мобильных роботов. Для управления такой мобильной системой предложена распределенная система управления на основе интеллектуальных самоорганизующихся систем автоматического управления и средств параллельных вычислений для разведки местности группой мобильных роботов-саперов, включая: определение минимально необходимого количества роботов; стратегическое планирование траектории для каждого робота; тактическое – на основе стратегического плана и разведывательной информации всех роботов группы; локальное (оперативное) – на основе тактического плана и сенсорной информации.
 Рис. 4. Результат решения задачи двунаправленным нейросетевым алгоритмом |   Рис. 5. Моделирование системы управления группой мобильных роботов |
Для исследования системы управления группой мобильных роботов разработана программа GroupPlanning (см. рис. 5). Данный проект успешно представлен на российском финале международного конкурса инновационных проектов Microsoft Imagine Cup 2012 (г. Москва).
В четвертой главе рассмотрены особенности решения задач параметрической идентификации динамических систем. Большое разнообразие методов параметрической идентификации свидетельствует об отсутствии универсальных алгоритмов, они оказались также неэффективны для задач большой размерности, т.к. за приемлемое время позволяют находить решение только с невысокой точностью. Для получения решения с высокой точностью требовались значительные затраты времени. Потребность решения этих трудностей привела к появлению генетических алгоритмов, сочетающих возможности как переборных, так и итерационных алгоритмов. Однако в практических задачах размерность математической модели и количество искомых параметров оказываются столь велики, что требуемые затраты вычислительных ресурсов оказываются неприемлемо большими. Выход может быть найден за счет применения параллельных вычислений при наличии достаточных вычислительных ресурсов. При этом исходный алгоритм необходимо модифицировать, выделив в нем фрагменты, которые можно выполнять параллельно.
Рассмотрено применение генетических алгоритмов для параметрической идентификации модели сложного объекта – силовой установки двигатель-генератор тепловоза 2ТЭ116, состоящей из следующих функциональных частей (рис. 6): дизельный двигатель, турбокомпрессор, впускной коллектор, выпускной коллектор, электрический генератор постоянного тока (имеет механическую и электрическую части). Уравнение механической части электрического генератора должно быть записано с учётом наличия упругой муфты между коленчатым валом двигателя и ротором генератора. В качестве исходных данных в задаче идентификации заданы экспериментальные данные: скорость вращения коленвала двигателя 
; скорость вращения вала турбокомпрессора 
; давление турбонаддува на выходе компрессора 
; напряжение на выходе генератора 
при подаче и снятии внешнего возмущения (электрической нагрузки) и управляющего воздействия 
. Исходные данные нормализованы и приведены к относительной форме в отклонениях от номинального значения.
В качестве критерия качества решения задачи идентификации использована оценка близости переходных процессов исследуемого объекта и построенной математической модели:
,
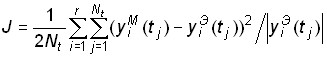где 
, 
– значения в момент времени 
i-го выхода модели и объекта, соответственно. При решении задачи идентификации с использованием генетического алгоритма обнаружены следующие недостатки: 1) оптимальное значение критерия неизменно на протяжении нескольких поколений (для ряда последовательных итераций алгоритма) и не соответствует заданным требованиям; 2) значение критерия у каждой новой особи в течение ряда поколений хуже, чем у лучшей ранее отобранной; 3) увеличение максимально допустимого количества поколений не приводит к улучшению значения критерия качества идентификации.
Это свидетельствует о недостаточной эффективности алгоритма, т.к. вычислительные затраты на построение соответствующих поколений оказались бесполезными. Предложена модификация генетического алгоритма, использующая дополнительную мутацию, если на текущем шаге улучшения критерия не произошло. Проведены исследования предложенного алгоритма, сформулированы и доказаны следующие
Теорема 4.1. Модифицированный генетический алгоритм является разрешимым.
Теорема 4.2. Вычислительная сложность модифицированного генетического алгоритма 4.1 составляет 
.
Исследования, проведенные с помощью вычислительного эксперимента, показали, что модифицированный алгоритм обеспечивает улучшение критерия качества решения задачи идентификации почти на каждом шаге, а также в целом, в среднем, на 10%. Для компенсации увеличенных затрат времени (в среднем на 20%) используем параллельные вычисления. Сравнение последовательной и параллельной реализации алгоритма приведено на рис. 7. При использовании двух потоков сокращение времени (ускорение вычислений) решения задачи идентификации составляет 1,8 раза. Разработка параллельного генетического алгоритма требует включения в программу операторов миграции (скрещивание; мутация; селекция; миграция). Проведен сравнительный анализ предложенного модифицированного и классического генетических алгоритмов идентификации с использованием параллельных вычислений. Для этого выполнен вычислительный эксперимент по решению задачи идентификации математической модели системы двигатель-генератор (28 параметров) при различных параметрах генетического алгоритма на различном количестве вычислительных узлов. В задаче идентификации определим границы интервала вариации искомых параметров: 
, где 
– номинальное значение параметра, известное на основе априорной информации. Параметры генетического алгоритма будем изменять следующим образом: максимальное количество поколений – от 8 до 120, количество «взрослых» особей – от 32 до 496, «дочерних» – от 16 до 248, «элитных» – от 2 до 31. Ген особи содержит текущие значения 28 параметров объекта и соответствующее значение критерия близости. Результаты сравнительного исследования представлены на рис. 8. Модифицированный алгоритм (параллельный вариант, так же как и последовательный) обеспечивает лучшее значение критерия идентификации по сравнению с классическим алгоритмом.
Рис. 8. Зависимости критерия идентификации от параметров алгоритма: а) классический,
б) модифицированный алгоритмы
В пятой главе приведена учитывающая сформулированные в главе 2 предложения модифицированная структура распределенной системы информационной поддержки разработки и исследования систем управления. Отличительной особенностью представленной архитектуры является наличие у серверов планирования и приложений дочерних узлов, на которых могут быть выполнены операции, допускающие использование средств параллельных вычислений для реализации мелкозернистого распараллеливания. Рассмотрены применения распределенной системы информационной поддержки разработки и исследования систем управления для решения практических задач 5.1 – 5.3 синтеза (статического и астатического законов управления) и анализа систем управления силовой установкой в условиях неполных измерений. Для решения задачи наблюдения использовался фильтр Калмана. В связи с достаточно большим разнообразием действий, используемых в процессе решения задачи синтеза (формирование матриц модели объекта, формирование параметров функционала оптимизации в задаче синтеза, решение уравнения Риккати, формирование матриц модели замкнутой системы, формирование параметров функционала оптимизации в задаче построения наблюдателя и т.д.) применить на всех этапах решения задач 5.1 – 5.3 средства параллельных вычислений совсем не просто. Требуемая для этого параллельная программа получится очень сложной, а эффект от распараллеливания будет не велик. Это обусловлено тем, что на этапах формирования матриц математических моделей, параметров функционалов оптимизации и ряда других действий доля операций, которые потенциально можно выполнять параллельно, часто меньше доли скалярных вычислений. Как следствие, накладные расходы на сетевое взаимодействие превышают собственно время выполнения вычислительных операций соответствующего алгоритма. В связи с этим акцент при разработке и реализации алгоритмов основных операций для решения задач синтеза и анализа с применением параллельных вычислений сделан на следующих операциях:
- Решение уравнения Риккати (операции care, dare языка ГАММА);
- Построение наблюдателя Калмана (операция kalman языка ГАММА);
- Анализ переходных процессов (реакция на внешнее воздействие вида: 1)
(операции step и stepYU языка ГАММА); 2) 
(операции lsim и lsimYU); 3) 
, 
(операции impulse и impulseYU) ).
Программные модули, реализующие соответствующие операции языка ГАММА для системы ГАММА-3 разработаны на языке С++ с использованием MPICH 2.1.
Исследования эффективности разработанных алгоритмов и программной реализации ряда операций синтеза (линейно-квадратическая оптимизация, построение наблюдателя Калмана) и анализа переходных процессов (моделирования) с использованием параллельных вычислений проводились при различном количестве параллельных процессов (рис. 9). В качестве объекта управления использовалась система дизель-генератор. Результаты исследований: наибольшее значение критерия эффективности 3,14 достигнуто при использовании 16 параллельных процессов; коэффициент ускорения 4. Дальнейшее увеличение степени распараллеливания до 64 процессов снижает значение критерия (в два раза) в связи с ростом накладных расходов на обмен данными между параллельными процессами, хотя ускорение вычислений все еще увеличивается (на 15%). Это совпадает с результатами, полученными при исследовании параллельных алгоритмов моделирования ПИНС, поскольку доля скалярных операций примерно одинакова (20%) и расчеты выполнялись в рамках одной вычислительной сети.
В заключении перечислены основные результаты работы, выносимые на защиту.
Приложение включает обзор средств организации параллельных вычислений, сведения об использовании результатов диссертационной работы, копии свидетельств о регистрации программ для ЭВМ.
Основные результаты работы
В диссертационной работе решена задача повышения эффективности средств информационной поддержки разработки и исследования систем управления на основе применения параллельных вычислений.
При этом получены следующие основные результаты:
- Предложен критерий оценки целесообразности применения параллельных вычислений для сокращения времени решения задачи обработки информации. Проведены исследования эффективности систем параллельных вычислений при выполнении матричных операций. Предложен алгоритм оценки необходимых вычислительных ресурсов для решения задач обработки информации с использованием параллельных вычислений.
- На основе применения принципов системного анализа проведено исследование возможности организации параллельных вычислений при решении задач синтеза и анализа систем управления. Проанализирована структура распределенной многофункциональной системы информационной поддержки разработки и исследования систем управления ГАММА-3. Выявлены компоненты системы, в которых возможно применение параллельных вычислений. Предложены способы совершенствования структуры системы и её компонентов для повышения эффективности решения задач с её помощью на основе применения параллельных вычислений.
- Предложен алгоритм планирования решений задач с помощью планирующих искусственных сетей (ПИНС) с использованием параллельных вычислений. Проведено исследование с помощью математического моделирования эффективности планирования действий с использованием параллельных вычислений.
- Предложен комплекс алгоритмов трехуровневого планирования траектории: 1) стратегическое планирование (лучевой алгоритм); 2) тактическое планирование (двунаправленный нейросетевой алгоритм); 3) оперативное (детальное) планирование. Проведено их исследование. Разработана программная реализация, допускающая проведение исследований в интерактивном режиме.
- Разработано специализированное программное обеспечение моделирования разведки местности группой мобильных роботов-саперов с использованием алгоритма трехуровневого планирования, как реализующее функции головного модуля, так и моделирующее поведение всех роботов группы с использованием многопоточной обработки, визуализации и анимации.
- Предложен модифицированный генетический алгоритм параметрической идентификации с использованием параллельных вычислений, проведено его исследование, выполнена реализация в виде команды языка ГАММА распределенной информационной системы поддержки решения задач ГАММА-3.
- Предложены способы модификации структуры распределенной системы информационной поддержки разработки и исследования систем управления, предусматривающие возможность использования средств параллельных вычислений.
- Разработаны компоненты сервера приложений, реализующие некоторые проектные операции, используемые при решении задач синтеза (care, lqr, dare, kalman) и анализа (step, stepYU, lsim, lsimYU, impulse, impulseYU) систем управления с использованием средств параллельных вычислений.
- Проведены исследования эффективности применения реализованных в системе автоматизации решения задач теории управления ГАММА-3 операций анализа и синтеза с использованием параллельных вычислений в ходе решения задач синтеза закона управления (статического и астатического) силовой установкой.
Перечень основных публикаций по теме диссертации
в ведущих научных журналах, рекомендованных ВАК РФ
- Степанов А.М. Применение параллельных вычислений в системе управления группой мобильных роботов-сапёров / А.М.Степанов // Вестник Саратовского государственного технического университета. 2012. №1 (64). Вып. 2. С. 21 – 28.
- Степанов А.М. О развитии концепции автоматического решения задач теории управления в системе ГАММА-3 / А.Г. Александров, А.М. Степанов и др. // Мехатроника, автоматизация, управление. 2011. №9. С. 14 – 19.
- Степанов А.М. Планирование траектории движения мобильного робота / А.А.Большаков, А.М.Степанов и др. // Вестник Саратовского государственного технического университета. 2010. № 4 (51). Вып. 3. С. 176 – 180.
- Степанов А.М. Интеллектуальная самоорганизующаяся система управления с вычислителем управляющего воздействия на основе автоматически конструируемой искусственной нейронной сети /А.М.Степанов, М.Ф.Степанов // Вестник Саратовского государственного технического университета. 2010. № 4 (51). Вып. 3. С. 126 – 128.
- Степанов А.М. Особенности моделирования интеллектуальных самоорганизующихся систем автоматического управления с использованием средств параллельных вычислений / А.М. Степанов, Т.М. Брагин и др. // Вестник Саратовского государственного технического университета. 2009. № 4 (43). Вып. 2. С. 134 – 137.
- Степанов А.М. Развитие концепции автоматического решения задач теории управления в системе ГАММА-3 / А.Г.Александров, А.М.Степанов и др. // Вестник Саратовского государственного технического университета. 2009. № 3 (41). Вып. 2. С. 190 – 196.
Публикации в других изданиях
- Stepanov A.M. Application of planning artificial neural networks in solver of tasks of intellectual self-organizing automatic-control systems // 5th Chaotic Modeling and Simulation International Conference CHAOS 2012. Athens, Greece, 2012. Pp. 151 – 152.
- Stepanov A.M. About architecture of parallel evaluations in an intellectual self-organizing control system // International congress on information technologies – 2012 (ICIT-2012) 6 – 9 June 2012, Saratov, Russia. Р. 118.
- Степанов А.М. Построение системы управления группой мобильных роботов на основе интеллектуальных самоорганизующихся систем управления / А.М.Степанов, М.Ф.Степанов // Интеллектуальные системы: труды Десятого Международного симпозиума. М.: РУСАКИ, 2012. С. 449 – 452.
- Степанов А.М. Об организации вычислителя интеллектуальной самоорганизующейся системы управления / А.М. Степанов // Логистика и экономика ресурсоэнергосбережения в промышленности (МНПК «ЛЭРЭП-5-2011»). Саратов: Сарат. гос. техн. ун-т, 2011. С. 59 – 62.
- Степанов А.М. Разработка пакета программ решения задач анализа систем управления в системе «ГАММА» / А.Г. Александров, А.М. Степанов и др. // Проблемы управления, обработки и передачи информации – АТМ-2011 [текст]: сб. трудов II Междунар. науч. конф. Саратов: Научная книга, 2011. С.199 – 202.
- Степанов А.М. Модифицированный нейросетевой метод планирования траектории движения мобильного робота / А.М. Степанов, М.Ф. Степанов // Математические методы в технике и технологиях – ММТТ-23: сб. трудов XXIII Междунар. науч. конф.: в 12 т. Т. 12. Секции 14, 15 / под общ. ред. В.С.Балакирева. Смоленск: РИО филиала ГОУВПО «МЭИ (ТУ)» в г. Смоленске, 2010. С. 78 – 79.
- Степанов А.М. Планирующая нейронная сеть как элемент планировщика универсального решателя задач / А.М. Степанов, М.Ф. Степанов // Математические методы в технике и технологиях – ММТТ-21: сб. трудов XX Междунар. науч. конф.: В 10 т. Т. 2. Секции 2, 6 / Под общ. ред. В.С. Балакирева. Саратов: Сарат. гос. техн. ун-т, 2008. – С. 257 – 259.
- Степанов А.М. Построение математической модели дизель-генератора по данным эксперимента / А.М. Степанов, А.М. Сычёв и др. // Математические методы в технике и технологиях – ММТТ-21: сб. трудов XX Междунар. науч. конф.: В 10 т. Т. 6. Секции 12, 13 / под общ. ред. В.С. Балакирева. Саратов: Сарат. гос. техн. ун-т, 2008. – С. 323 – 326.
Свидетельства о государственной регистрации программ
- Свидетельство о государственной регистрации программ для ЭВМ № 2012618501. Программа параметрической идентификации математической модели системы двигатель-генератор с использованием параллельных вычислений на основе MPI / А.М. Степанов.
- Свидетельство о государственной регистрации программ для ЭВМ №2012618502. Двунаправленный нейросетевой алгоритм планирования траектории / А.М. Степанов, М.Ф. Степанов.
- Свидетельство о государственной регистрации программ для ЭВМ №2012618503. Моделирование поведения группы роботов при разведке территории / А.М. Степанов, М.Ф. Степанов.
Степанов Андрей Михайлович
алгоритмы повышения эффективности решения задач анализа и синтеза систем управления с использованием параллельных вычислений
Автореферат
Корректор О.А. Панина
| Подписано в печать 26.11.12 | Формат 6084 1/16 |
| Бум. офсет. Усл. печ. л. 1,0 | Уч.-изд. л. 1,0 |
| Тираж 100 экз. Заказ 203 | Бесплатно |
| Саратовский государственный технический университет 410054, г. Саратов, ул. Политехническая, 77 | |
| Отпечатано в Издательстве СГТУ, 410054 г. Саратов, ул. Политехническая, 77 | |
| Тел.: 24-95-70; 99-87-39, е-mail: [email protected] | |
