Николаевич модели многомерного представления и обработки данных на основе алгебры кортежей в информационно-аналитической системе

На правах рукописи

       

БЕЛОВ Вадим Николаевич

МОДЕЛИ МНОГОМЕРНОГО ПРЕДСТАВЛЕНИЯ
И ОБРАБОТКИ ДАННЫХ НА ОСНОВЕ АЛГЕБРЫ КОРТЕЖЕЙ
В ИНФОРМАЦИОННО-АНАЛИТИЧЕСКОЙ СИСТЕМЕ

Специальности:

05.13.17 – Теоретические основы информатики;

05.13.01 – Системный анализ, управление и обработка
информации (приборостроение)

Автореферат

диссертации на соискание учёной степени
кандидата технических наук

ПЕНЗА 2012

Работа выполнена в ФГБОУ ВПО «Пензенский государственный университет».

Научные руководители:

доктор технических наук, профессор Макарычев Петр Петрович;

кандидат технических наук, доцент Механов Виктор Борисович.

Официальные оппоненты:

Горбаченко Владимир Иванович, доктор технических наук, доцент, зав. кафедрой информатики и вычислительных систем Пензенского государственного педагогического университета им. В. Г. Белинского
(г.  Пенза);

Федосин Сергей Алексеевич, кандидат технических наук, доцент, зав. кафедрой «Автоматизированные системы обработки информации и управления» Мордовского государственного университета им. Н. Н. Ога-рева (г. Саранск).

Ведущая организация – ОАО «Научно-производственное предприятие Рубин» (г. Пенза).

Защита состоится ___ марта 2012 г., в «______» часов, на заседании диссертационного совета Д 212.186.01 при ФГБОУ ВПО «Пензенский государственный университет» по адресу 440026, г. Пенза, ул. Красная, 40.

С диссертацией можно ознакомиться в библиотеке ФГБОУ ВПО «Пензенский государственный университет». Автореферат размещен на сайте университета.

Автореферат разослан «____» февраля 2012 г.

Ученый секретарь

диссертационного совета Гурин Евгений Иванович

ОБЩАЯ ХАРАКТЕРИСТИКА РАБОТЫ

Актуальность темы. В настоящий момент имеет место тенденция широкого использования информационных технологий для хранения, обработки и анализа данных. Данная тенденция является следствием роста объема информации, используемой для принятия управленческих решений и развития методов интеллектуального анализа данных. Разработка информационно-аналитических систем, обеспечивающих внедрение информационных технологий, является ресурсоемким процессом. Однако построение математических моделей данных и обработки данных для информационно-аналитических систем позволяет сократить количество итераций разработки и уменьшить затраты ресурсов за счет использования процедуры доказательства корректности моделей обработки данных.

Процессы обработки и анализа данных, а также методы доказательства корректности моделей обработки данных исследовались в работах А. А. Барсегяна, С. А. Васильева, Б. А. Кулика, Ф. А. Новикова, K. Ar-row, Э. Кларка (E. Clarke), R. Creeth, E. Emerson, R. Floyd, Ч. Хоара (C. Hoare), M. Lacroix, T. Pedersen, N. Pendse, A. Pirotte, Т. Саати (T. Saaty), J. Ullman и др.

Процессы обработки и анализа данных во многом зависят от модели представления данных. Выбор модели данных определяет применимые операции обработки данных и скорость проведения анализа данных. Исследованию моделей представления данных посвящены работы А. В. Вискова, Н. А. Левина, И. Д. Манделя, В. И. Мунермана, В. П. Сер-гееева, R. Agrawal, Э. Кодда (E. Codd), К. Дейта (C. Date), Б. Инмона (W. Inmon), Р. Кимбала (R. Kimball) и др.

Несмотря на успехи в этих направлениях, остаются нерешенными несколько проблем. Первая проблема связана с недостаточной развитостью подхода к формализованному описанию данных, обеспечивающих решение задач статистического, оперативного и интеллектуального анализа данных, а также анализа данных, определяемого бизнес-процессами организации. Сложность решения проблемы построения математических моделей данных обусловлена:

• отсутствием методик построения моделей данных, удовлетворяющих требованиям, выдвигаемым тестом FASMI (Fast Analysis of Shared Multidimensional Information быстрый анализ разделяемой многомерной информации);
• использованием, как правило, интуитивного подхода к разработке многомерных моделей данных и моделей вычислительных процессов.

Вторая проблема связана с недостаточной проработанностью методов проектирования с применением проверки корректности моделей обработки данных.

Третья проблема обусловлена малой исследованностью методик предварительной обработки данных, представленных в виде комплектов, при вычислении ключевых показателей эффективности с использованием номинальных и порядковых шкал. В этом случае традиционный подход к предварительной обработке данных, основанный на использовании метода анализа иерархий, не реализуем. Необходимость решения названных выше проблем определяет актуальность данного диссертационного исследования.

Целью диссертационной работы является разработка и исследование моделей представления данных, процессов обработки и анализа данных в информационно-аналитической системе с настраиваемыми метриками на основе ключевых показателей эффективности.

Для достижения поставленной цели решены следующие задачи:

• анализ процессов сбора, хранения, предварительной обработки и анализа данных в информационно-аналитических системах, реализуемых с применением настраиваемых метрик на основе ключевых показателей эффективности;
• теоретическое обоснование и исследование математических многомерных моделей данных для сбора и хранения, проведения оперативного и интеллектуального анализа средствами информационно-аналитической системы;
• теоретическое обоснование и исследование математических моделей обработки данных в процессе наполнения хранилища данных, проведения оперативного и интеллектуального анализа данных;
• разработка на основе предложенных модельных представлений данных и процессов транзакционной базы данных, многомерного хранилища данных, клиентских приложений прототипа информационно-аналитической системы и проведение экспериментов.

Предметом исследования являются математические модели и структуры многомерного представления данных, модели процессов извлечения, преобразования и загрузки данных, модели и алгоритмы обработки и анализа данных.

Объектом исследования являются процессы сбора, накопления, предварительной обработки, загрузки и анализа данных при создании информационно-аналитической системы.

Методы исследования основаны на алгебре кортежей, теории нечетких множеств, методах оперативного и интеллектуального анализа данных, теории принятия коллективных решений, теории матроидов, методах концептуального моделирования. При разработке программных средств использованы объектно ориентированный и реляционный подходы.

Научная новизна работы:

1. Предложена методика построения математической модели данных на основе настраиваемых метрик ключевых показателей эффективности, отличающаяся представлением объектов и связей в виде С-систем алгебры кортежей и обеспечивающая проверку модели данных на соответствие моделям проектируемых процессов предварительной обработки, загрузки и анализа данных аналитическими методами.
2. Доказано соответствие структуры многомерной модели данных матроидной структуре, в которой максимальные независимые подмножества функциональных взаимосвязей между мерами и измерениями являются базами, что позволяет автоматизировать эквивалентные преобразования структуры реляционных хранилищ данных.
3. Предложен жадный алгоритм поиска структуры реляционного хранилища данных, отличающейся представлением группы измерений и мер в виде матроида. Алгоритм обеспечивает выполнение требований по ограничению времени выполнения запросов в соответствии с тестом быстрого анализа разделяемой многомерной информации (FASMI).
4. Предложено формализованное описание процессов сбора, загрузки в хранилище и анализа данных  с использованием операций алгебры кортежей, что позволяет осуществить доказательство корректности моделей процессов формальными методами.
5. Разработана процедура предварительной обработки комплектов данных, отличающаяся применением рациональной и решающей функции для вычисления ключевых показателей эффективности, что позволяет уменьшить объем хранилища данных и сократить время на проведение анализа данных.

Практическая значимость исследований. Разработанные программные средства для реализации информационной технологии хранения, обработки и анализа данных при управлении организацией на основе ключевых показателей эффективности обеспечивают осуществление процессов сбора, предобработки, оперативного и интеллектуального анализа данных. Разработанный алгоритм поиска структуры реляционного хранилища данных системы оперативной аналитической обработки данных со сложностью позволяет строить хранилища данных с учетом требований скорости выполнения запросов. Разработанный подход к проектированию процессов обработки и анализа данных позволяет сократить количество итераций разработки программных средств за счет доказательства корректности моделей обработки и анализа данных на этапе проектирования.

На защиту выносятся:

1. Методика построения математических моделей данных на основе концепции многомерного пространства данных и операций алгебры кортежей.

2. Модельное представление структуры многомерных данных, отражающих совокупность ключевых показателей эффективности и используемых при принятии управленческих решений, в виде группы матроидов.

3. Алгоритм поиска структуры модели данных, удовлетворяющей требованию минимума затрат времени на выполнение запроса к многомерному реляционному хранилищу данных.

4. Модели сбора данных, преобразования и загрузки реляционного хранилища данных, оперативного и интеллектуального анализа данных в информационно-аналитической системе.

5. Процедура предварительной обработки и агрегации данных с применением рациональной и решающей функции ранжирования.

Реализация и внедрение результатов работы.

Теоретические и практические результаты диссертационного исследования внедрены:

• в Пензенском государственном университете при разработке информационно-аналитической системы оценки деятельности преподавателей, кафедр и факультетов на основе ключевых показателей эффективности;
• в ООО «Мое дело» г. Пензы для оценки деятельности сотрудников отдела «ERP» на основе ключевых показателей эффективности с применением Web-технологий.

Достоверность и обоснованность. Обоснованность и достоверность результатов определяются корректным использованием строгих и апробированных методов исследования и подтверждаются практическим применением полученных результатов при разработке программных средств, что подтверждено актом о внедрении результатов работы, а также апробацией работы на всероссийских и международных конференциях.

Апробация работы. Основные результаты работы докладывались и обсуждались на следующих конференциях: VII Всероссийской научно-практической конференции «Системы автоматизации в образовании, науке и производстве» (Новокузнецк, 2009); Международной конференции «Information Technologies in Education for All» (Киев, 2009); III Международной научно-практической конференции «Информационная среда вуза XXI века» (Петрозаводск, 2009); XII Всероссийской объединенной конференции «Интернет и современное общество» (Санкт-Пе-тербург, 2009); IX Международной научно-технической конференции «Новые информационные технологии и системы» (Пенза, 2010); XV Международной научно-методической конференции «Университетское образование» (Пенза, 2011); Международной научно-практической конференции «Молодежь и наука: модернизация и инновационное развитие страны» (Пенза, 2011); V Международной научно-практической конференции «Информационная среда вуза XXI века» (Петрозаводск, 2011).

Публикации. Основные положения диссертации опубликованы в 12 статьях и тезисах конференций. Среди них 2 статьи в журналах из перечня ВАК.

Структура и объем работы. Диссертация состоит из введения, четырех глав, заключения, списка литературы из 128 наименований и
6 приложений. Общий объем – 182 страницы. Основное содержание диссертации включает 19 рисунков и 46 таблиц.

СОДЕРЖАНИЕ ДИССЕРТАЦИИ

Во введении обоснована актуальность темы диссертации, сформулированы цель и задачи исследования, показаны научная новизна и практическая значимость результатов диссертационного исследования, приведены сведения об апробации работы и публикациях.

В первой главе дан обзор моделей представления данных в базах данных, рассмотрены современные подходы к организации сбора и обработки данных, выполнен анализ средств формализованного описания моделей данных и моделей обработки данных, определены требования к данным при проведении интеллектуального анализа данных и управлении организацией.

В диссертации рассмотрен современный подход к разработке информационно-аналитических систем, опирающийся на разделение систем оперативной обработки транзакций, с использованием которых организуется сбор данных, и систем оперативной аналитической обработки данных, с использованием которых организуется анализ данных.
В рамках такого подхода данные системы оперативной обработки транзакций загружаются в систему оперативной аналитической обработки данных посредством процессов извлечения, преобразования и загрузки данных.

Для решения проблем, сформулированных при обосновании актуальности работы, необходимо обеспечить выполнение требований теста быстрого анализа разделяемой многомерной информации. В диссертации определено, что к представлению и обработке данных относятся следующие требования:

– многомерное концептуальное представление данных с поддержкой иерархий и множественных иерархий;

– поддержка статистического, оперативного и интеллектуального анализа данных, а также анализа, определяемого бизнес-процессами организации, независимо от используемого программного приложения, визуализации результатов в доступном для конечного пользователя виде;

– одинаково высокая скорость выполнения всех запросов к системе, характеризующаяся временем выполнения большинства аналитических запросов не более 5 с.

В диссертации проведен анализ требований, предъявляемых к модели данных при реализации алгоритмов интеллектуального анализа данных и анализа данных, определяемого бизнес-процессами организации, наиболее формализованным инструментом которого являются ключевые показатели эффективности, а также анализ средств формализованного описания моделей данных и моделей обработки данных.

На основании проведенного анализа делается вывод о том, что применение алгебры кортежей (АК) предоставляет наиболее широкие возможности для моделирования структур и процессов обработки данных. При этом эквивалентные преобразования структур данных могут быть осуществлены с использованием положений теории матроидов, а для формального доказательства корректности моделей процессов возможно использование логики Хоара.

Во второй главе выполнено теоретическое обоснование модели многомерного представления данных с использованием алгебры кортежей, разработана концептуальная модель обработки и анализа данных в информационно-аналитической системе, предложено и обосновано представление структуры многомерной модели данных в виде группы матроидов, предложен алгоритм поиска структуры реляционного хранилища данных, применение которого обеспечивает выполнение требований по ограничению времени выполнения запросов, и разработаны инфологические модели транзакционной базы данных и хранилища данных.

В диссертации проведен анализ процессов сбора, обработки и анализа данных на примере информационно-аналитической системы образовательного учреждения.

В соответствии с требованиями многомерной модели описания аналитического пространства в терминах «мера» и «измерение» в диссертации выделены следующие меры: «сотрудник» (), «результат деятельности сотрудника» (), «Результат деятельности кафедры» (), результат деятельности факультета» ().

Для меры определены измерения «ученая степень» (), «должность» (), «ученое звание» (), «время» (), а также измерения «кафедра» () и «факультет» (), образующие иерархию уровней измерения. При этом существует иерархия уровней измерения «». С помощью АК измерения поставлены в соответствие мерам, при этом получены C-системы, описывающие их взаимосвязи. Для меры структура взаимосвязей мер и измерений описывается C-системой :

Для меры выделены измерения «время» (), «ключевой показатель эффективности» (), а также измерения «сотрудник» (), «кафедра» () и «факультет» (), образующие иерархию уровней измерения «». Для меры структура взаимосвязей мер и измерений описывается C-системой :

.

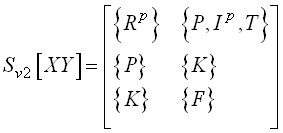Для меры определены следующие измерения: «время» (), «ключевой показатель эффективности» (), а также измерения «кафедра» () и «факультет» (), образующие иерархию уровней измерения «». Для меры структура взаимосвязей мер и измерений описывается C-системой :

.

Для меры выделены следующие измерения: «время» (), «ключевой показатель эффективности» () и «факультет» (). Для меры структура взаимосвязей мер и измерений описывается C-системой :

.

В диссертации меры и измерения с использованием АК также описываются как C-системы. Множество координат многомерного пространства описывается как декартово произведение элементов измерений. Для -мерного пространства множество координат в терминах АК задается как частный универсум отношения со схемой , где атрибут, соответствующий уровню измерения; . Таким образом, гиперкуб -мерного пространства, описывающий меры, характеризующиеся показателями, задается в виде C-сис-темы , где показатель меры; .
В случае разреженного гиперкуба данные о мерах описываются C-сис-темой , пустые ячейки описываются C-сис-темой , получаемой следующим образом:

Соответственно, разреженный гиперкуб задается следующим образом:

В диссертации показано, что операция среза в АК равнозначна заданию значения одного или нескольких атрибутов отношения. Операция вращения может быть представлена как операция перестановки атрибутов, соответствующих вращаемым измерениям, схемы отношения, задающей куб, и изменение порядка сортировки элементарных кортежей.

Операция консолидации представлена как выполнение операции соединения C-системы, задающей гиперкуб, и C-системы, задающей более высокий уровень иерархии измерения, с последующим выполнением операции элиминации атрибутов, соответствующих более низкому уровню иерархии измерения. Выполнение операции консолидации по измерению, задаваемому атрибутом гиперкуба, описываемого C-сис-темой , показано ниже:

где и C-системы, описывающие уровни измерения, образующие иерархию «»; атрибуты, позволяющие определить координаты мер в многомерном пространстве; атрибуты, имеющие информационное назначение и описывающие и . Операция детализации описана аналогичным образом, но при этом более высокий уровень иерархии заменяется более низким.

Результатом объединения C-систем, задающих структуру взаимосвязей мер и измерений, является C-система, задающая структуру многомерной модели данных. C-система , задающая структуру многомерной модели данных, отвечающей требованиям обработки данных о деятельности образовательного учреждения, имеет следующий вид:

.(1)

Соответствие требованиям проведения статистического и интеллектуального анализа данных, а также анализа данных, определяемого бизнес-процессами организации, в диссертации доказано с помощью построения соответствующих моделей обработки данных.

В общем случае, структура хранилища данных не отвечает требованиям скорости выполнения запросов быстрого анализа разделяемой многомерной информации. Для поиска соответствующей структуры хранилища данных предложена модель описания структуры многомерной модели данных в виде группы матроидов. Подготовка данных включает задание C-системы , являющейся транзитивным замыканием , множества мер и множества всех мер и измерений . С использованием АК определен критерий необходимости связи между мерой и некоторой мерой или измерением многомерной модели на основании отсутствия между ними транзитивных связей:

. (2)

Такие связи описываются C-системой .

Матроид , соответствующий части структуры многомерной модели данных, описывается конечным множеством , являющимся
C-системой, элементарные кортежи которой соответствуют связям между мерами и измерениями, и множеством независимых подмножеств .
С-система, определяющая часть структуры многомерной модели данных, задающей группу матроидов, имеет следующий вид:

, (3)

где ; мера; ; ; число мер в части структуры многомерной модели данных, описываемой C-системой (3); мера или измерение. При этом должно выполняться условие , где мера или измерение. На основании
C-системы (3) задаются матроидов в случае, если , и в случае, если , каждый из которых описывается
C-системой следующего вида:

,

где мера или измерение; ; количество мер и измерений части структуры многомерной модели данных, задающей матроид; ; .

В диссертации сформулированы следующие правила, в соответствии с которыми задается матроид :

ранг матроида , задаваемого некоторой C-системой , равняется , где множество, являющееся подмножеством объединения доменов атрибутов отношения , в котором элементы соответствуют мерам и измерениям, входящим в структуру, описываемую C-системой ;

множество является множеством элементарных кортежей, входящих в C-систему ;

множество независимых множеств включает в себя пустое множество, максимальные независимые множества (базы) и их подмножества;

максимальное независимое множество удовлетворяет условиям , и :

: ,

где меры или измерения;

: , где   меры или измерения; транзитивное замыкание ;

: ,

где множество мер и измерений части структуры многомерной модели данных, описываемой матроидом; меры или измерения.

В соответствии с условием требуется включение в максимальное независимое множество всех обязательных связей, определенных с помощью критерия (2) и входящих в конечное множество матроида. Условием задается требование отсутствия циклов. Требованием условия является наличие меры, имеющей связь со всеми остальными мерами и измерениями части структуры многомерной модели данных, описываемой матроидом.

В диссертации доказано, что является матроидом в соответствии с известными аксиомами матроидов.

удовлетворяет аксиомам независимости пустого множества и подмножеств независимого множества вследствие . Независимое множество, имеющее наибольшее число вариантов образования зависимых множеств при добавлении элементарного кортежа, задается C-сис-темой вида

,

где , , . В этом случае C-система , содержащая элементарные кортежи, в результате добавления каждого из которых в C-систему образуется зависимое множество, имеет следующий вид:

.

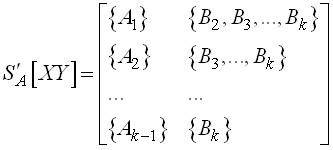Поскольку множество является независимым и выполняются условия , в C-системе содержится не более элементарных кортежей, входящих во множество . Включение любого другого элементарного кортежа в C-систему не является причиной образования зависимого множества, и поскольку , то . Следовательно, удовлетворяет аксиоме равной мощности максимальных независимых подмножеств. Таким образом, является матроидом.

Рис. 1. Алгоритм поиска структуры хранилища данных

В диссертации решена задача определения веса элемента множества .
В качестве веса предложено использование величины, обратно пропорциональной диаметру графа, задаваемого максимальным независимым множеством, которое образуется при добавлении элемента. Представление структуры многомерной модели данных в виде группы матроидов позволило использовать для уменьшения диаметра графа, соответствующего структуре реляционного хранилища данных, жадный алгоритм, имеющий сложность . Разработанный алгоритм представлен на рис. 1.

На рис. 1 используются следующие обозначения: независимое множество -го матроида; число матроидов; вес -го элемента множества -го матроида; ранг -го матроида; С-сис-тема, описывающая построенную структуру хранилища данных.

На основании полученных результатов делается вывод о том, что использование АК позволяет разрабатывать многомерную модель данных в терминах мер и измерений, при этом имеется возможность перейти к модели реляционного хранилища данных. Предложенное представление структуры многомерной модели данных в виде группы матроидов позволяет использовать для поиска структуры хранилища жадный алгоритм, имеющий сложность , применение которого обеспечивает выполнение требований по ограничению времени выполнения запросов.

Третья глава посвящена разработке моделей обработки и анализа данных. Разработаны модели выполнения запросов к транзакционной базе данных, модель процесса наполнения хранилища данных, позволяющая провести доказательство корректности моделей обработки данных, предложена процедура предварительной обработки и агрегации данных на основе рациональной и решающей функции, построена модель проведения анализа данных, определяемого бизнес-процессами организации, и модель проведения интеллектуального анализа данных методом нечеткой кластеризации.

С использованием АК проведено связывание моделей транзакционной базы данных и хранилища данных на основе построенных моделей обработки данных, преобразующих данные модели транзакционной базы данных в данные модели хранилища данных. Модели обработки данных, построенные с использованием АК, учитывают все аспекты процесса подготовки данных, включая извлечение, преобразование и загрузку данных, при этом подпроцессы представляются в виде последовательности операций АК. В диссертации показано, что корректность построенных моделей обработки данных может быть доказана с применением логики Хоара.

В диссертации предложена функция ранжирования , преобразующая линейно упорядоченных множеств, каждое из которых упорядочено в соответствии с одним из критериев решения относительно альтернатив, обозначаемых как , в линейно упорядоченное множество, упорядоченное с учетом влияния всех критериев решения:

. (4)

На основании требований, определяемых теоремой Эрроу, доказывается, что разработанная процедура обработки данных является рациональной и решающей. В результате вычислений с использованием функции (4) формируется множество , упорядоченное в соответствии с множеством критериев принятия решения:

. (5)

При этом выполняется следующее условие:

,

где степень предпочтительности альтернативы ; но-мер альтернативы; число альтернатив.

Значение вычисляется следующим образом:

, (6)

где – ранг альтернативы относительно критериев решения; – ранг альтернативы относительно критерия решения ; – количество критериев решения; – вес критерия принятия решения ; предпочтительность альтернативы относительно доминирующего критерия решения . Для весов выполняются условия ,.

Расчет значения для формулы (6) производится по следующей формуле:

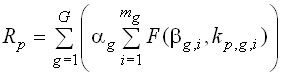, (7)

где – номер вида работы направления деятельности ; – количество видов работ направления деятельности ; – функция расчета ранга сотрудника по виду работ направления деятельности ; – вес вида работ с номером направления деятельности ; – количество работ вида направления деятельности , выполненных сотрудником . При этом следует учитывать, что , , , , .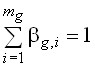

Поскольку результаты деятельности сотрудников могут быть представлены в виде комплектов, то для расчета ранга сотрудника по виду работ необходимо учитывать число экземпляров элемента комплекта. Предлагаемая функция расчета ранга сотрудника по виду работ имеет следующий вид:

, (8)

где – вес вида работ; – количество работ данного вида, выполненных сотрудником.

Доказывается, что функция, описываемая (5), (6), (7), (8) соответствует требованиям, выдвигаемым аксиомами Эрроу.

В диссертации построены модели процессов интеллектуального анализа данных и анализа данных, определяемого бизнес-процессами организации, в соответствии с требованием обеспечения возможности проведения анализа теста быстрого анализа разделяемой многомерной информации. Результаты, полученные с использованием формулы (7), представляют собой вещественные числа и соответственно мо-
гут быть использованы для проведения интеллектуального анализа методом нечеткой кластеризации. Каждый объект кластеризации представляет собой точку в -мерном пространстве , где , число объектов кластеризации. Для определения числа кластеров в диссертации применена методика оценки качества кластеризации с использованием индекса «Хие-Бени».

Результаты ранжирования позволяют задавать -мерное пространство, векторы которого задаются значениями, вычисленными с использованием метода анализа иерархий по функции (7), и -мерное пространство, векторы которого задаются значениями, вычисленными с использованием функции (8), где . В диссертации на примере данных информационно-аналитической системы образовательного учреждения получены значения и . Выигрыш в размере данных, требуемых для кластеризации, оценивается по следующей формуле:

,

где размер данных, остающихся постоянными, независимо от размерности пространства, векторы которого задают объекты кластеризации; размер данных, необходимых для задания объектов кластеризации в виде векторов 7-мерного пространства; размер данных, необходимых для задания объектов кластеризации в виде векторов
45-мерного пространства. В диссертации получены следующие значения: , , , .

По результатам кластеризации получены значения, характеризующие распределение объектов по нечетким кластерам и вычисленные по следующей формуле:

,

где номер кластера; арность пространства, в котором задаются координаты точек, характеризующие объекты кластеризации; число объектов кластеризации; степень принадлежности объекта к кластеру . Рассчитанные значения представлены в табл. 1.

Таблица 1

Распределение объектов по нечетким кластерам

Номер кластера	, %	, %
1	56,5867	57,7123
2	31,0165	33,0361
3	12,3968	9,2516

Распределение объектов по нечетким кластерам отличается незначительно, поскольку = 6,2904 %.

Разница в определении степени отношения объекта к определенному кластеру при изменении арности пространства, векторы которого описывают объект, составила 9,3274 %, медиана значения составила 0,0143.

Модели обработки и анализа данных, представляющие подпроцессы в виде последовательности операций алгебры кортежей, используют разработанные математические модели транзакционной базы данных и хранилища данных и позволяют проводить доказательство корректности моделей обработки данных с использованием логики Хоара. Применение предложенной рациональной и решающей функции ранжирования позволяет уменьшить объем хранилища данных при проведении кластерного анализа.

В четвертой главе приведено описание программных средств информационно-аналитической системы, разработанных с использованием моделей данных и моделей обработки данных, представленных в диссертации. Показаны результаты проведения анализа данных, определяемого бизнес-процессами организации, а также результаты проведения кластерного анализа, полученные на основе реальных данных.

На основе построенных моделей данных и моделей обработки данных разработаны транзакционная база данных и хранилище данных для Microsoft SQL Server 2008. Программные средства сбора данных, имеющие трехуровневую архитектуру, были реализованы с использованием платформы Java EE и фреймворка Struts. Процессы извлечения, преобразования и загрузки данных реализованы как хранимые процедуры SQL SERVER 2008. Процедуры обработки и анализа данных в соответствии с требованиями, определяемыми бизнес-процессами организации, а также процедуры кластерного и статистического анализа реализованы с использованием математического пакета Matlab. С использованием разработанных программных средств автоматизированы процессы сбора, предварительной обработки, оперативного, интеллектуального и статистического анализа данных.

При анализе результатов кластеризации в диссертации была применена дефаззификация методом выбора четкого числа, соответствующего максимуму функции.

В диссертации рассчитано среднее время проведения кластерного анализа методом нечетких c-средних с использованием подготовленных данных. Среднее время выполнения для 7-мерного пространства составило 0,14 с. Для 45-мерного пространства соответствующее значение равно 0,56 с. Таким образом, выигрыш во времени подготовки данных составил 6,40 раза. Алгоритм обработки данных, необходимых для кластерного анализа, представляющий данные в виде, соответствующем требованиям алгоритма нечетких c-средних, был реализован в качестве хранимой процедуры SQL Server 2008. Среднее время подготовки данных для проведения кластерного анализа объектов, описываемых векторами 7-мерного пространства , составило 3,12 с. Среднее время подготовки данных для проведения кластерного анализа объектов, описываемых векторами 45-мерного пространства , составило 19,96 с. Выигрыш во времени подготовки данных составил 4,00 раза. Выигрыш во времени при расчете значения для всего процесса , рассчитанный по формуле , составил 6,29 раза.

Использование 7-мерного пространства для проведения кластеризации позволило выполнить все операции, необходимые для получения результатов кластерного анализа за 3,36 с, что соответствует требованию быстрого анализа разделяемой многомерной информации.

В диссертации предложена интерпретация результатов кластерного анализа. Выполнен анализ значений атрибутов центроидов кластеров, математического ожидания значений атрибутов объектов кластеризации.
На основании максимума значения характеристической функции нечетких подмножеств определены объекты кластеризации, наиболее близкие к центрам кластеров, а также данные, характеризующие такие объекты в терминах предметной области на этапе сбора данных.

Построенные модели данных и модели обработки данных могут быть использованы при реализации информационно-аналитических систем. Применение разработанной функции обработки и агрегирования данных позволило сократить время проведения кластерного анализа в 6,29 раза. Разработанные программные средства удовлетворяют требованиям быстрого анализа разделяемой многомерной информации.

В заключении сформулированы основные результаты диссертационной работы.

В приложении А приведен словарь базовых понятий. В приложении Б приведены листинги программных средств, реализующих обработку данных для проведения кластерного анализа, статистического анализа и анализа, определяемого бизнес-процессами организации, разработанные с использованием математического пакета Matlab. В приложении В представлены листинги и результаты выполнения программных средств, реализующих метод анализа иерархий в среде Maple. В приложении Г приведены листинги хранимых процедур, реализующих извлечение, преобразование и загрузку данных в хранилище данных. В приложении Д представлены результаты моделирования процессов анализа данных в среде Matlab. В приложении Е представлены акты, подтверждающие внедрение результатов.

ОСНОВНЫЕ РЕЗУЛЬТАТЫ И ВЫВОДЫ

1. Предложена методика построения математической модели данных на основе настраиваемых метрик ключевых показателей эффективности, отличающаяся представлением объектов и связей в виде С-систем алгебры кортежей и обеспечивающая проверку модели данных на соответствие моделям проектируемых процессов предварительной обработки, загрузки и анализа данных аналитическими методами.
2. Доказано соответствие структуры многомерной модели данных матроидной структуре, в которой максимальные независимые подмножества функциональных взаимосвязей между мерами и измерениями являются базами, что позволяет автоматизировать эквивалентные преобразования структуры реляционных хранилищ данных.
3. Предложен жадный алгоритм поиска структуры реляционного хранилища данных, отличающейся представлением группы измерений и мер в виде матроида. Алгоритм обеспечивает выполнение требований по ограничению времени выполнения запросов в соответствии с тестом быстрого анализа разделяемой многомерной информации (FASMI).
4. Предложено формализованное описание процессов сбора, загрузки в хранилище и анализа данных с использованием операций алгебры кортежей, что позволяет осуществить доказательство корректности процессов формальными методами.
5. Разработана процедура предварительной обработки комплектов данных, отличающаяся применением рациональной и решающей функции для вычисления ключевых показателей эффективности, что позволяет уменьшить объем хранилища данных и сократить время на проведение анализа данных.
6. Разработана процедура кластерного анализа данных, отличающаяся применением предложенной рациональной и решающей функции, что позволило сократить время проведения кластерного анализа в
   6,29 раза.
7. Выполнена разработка и экспериментальное исследование прототипа информационной аналитической системы с функциями сбора, предварительной обработки, оперативного и интеллектуального анализа данных на основе технологии ключевых показателей эффективности.

ОСНОВНЫЕ ПУБЛИКАЦИИ ПО ТЕМЕ ДИССЕРТАЦИИ

Публикации в изданиях, рекомендованных ВАК России

1. Белов, В. Н. Исследование соответствия схемы базы данных целям OLAP средствами алгебры кортежей / В. Н. Белов, П. П. Макарычев //
   Известия высших учебных заведений. Поволжский регион. – 2011. – № 4. –
   С. 25–36.
2. Белов, В. Н. Оптимизация хранилища данных с представлением структуры в виде матроида / В. Н. Белов, П. П. Макарычев // В мире научных открытий. – 2011. – № 12. – С. 160–171.

Публикации в других изданиях

3. Белов, В. Н. Автоматизация оценки деятельности сотрудников вуза / Белов В. Н. // Системы автоматизации в образовании, науке и производстве : тр. VII Всерос. науч.-практ. конф. – Новокузнецк : СибГИУ, 2009. – С. 53–56.
4. Belov, V. ICT applications for university staff activities evaluation / V. Belov // Information Technologies in Education for All. – Kiev : IRTC,
   2009. – P. 12–18.
5. Белов, В. Н. Применение информационных технологий для оценки деятельности сотрудников вуза / В. Н. Белов // Информационная среда вуза XXI века : материалы III Междунар. науч.-практ. конф. (2125 сентября 2009 г.). – Петрозаводск, 2009. – С. 23–25.
6. Белов, В. Н. Использование ИКТ для оценки деятельности сотрудников вуза / В. Н. Белов // Новые технологии в образовании. – 2009. – № 4. – С. 78–80.
7. Белов, В. Н. Применение ИКТ для оценки деятельности сотрудников вуза / В. Н. Белов // Развитие региональной образовательной информационной среды. Сборник научных статей межрегиональной научно-практической конференции : тр. XII Всерос. объединенной конф. «Интернет и современное общество» / под ред. С. В. Агапонова, А. В. Чугунова. – СПб., 2009. – С. 11, 12.
8. Белов, В. Н. Автоматизированная информационная система оценки деятельности преподавателей / В. Н. Белов, П. П. Макарычев, В. А. Ме-щеряков // Новые информационные технологии и системы : тр. IX Междунар. науч.-техн. конф. (г. Пенза, 9–10 ноября 2010 г.) : в 2 ч. – Пенза :
   Изд-во ПГУ, 2010. – Ч. 2. – С. 125–133.
9. Белов, В. Н. Оценка деятельности сотрудников вуза на основе анализа ключевых показателей / В. Н. Белов, П. П. Макарычев // Университетское образование : сб. ст. XV Междунар. науч.-метод. конф. (г. Пенза,
   6–7 апреля 2011 г.) / под ред. В. И. Волчихина, Р. М. Печерской. – Пенза : Изд-во ПГУ, 2011. – С. 279–280.
10. Белов, В. Н. Оптимизация хранилища данных с представлением структуры в виде матроида средствами алгебры кортежей / В. Н. Белов, П. П. Макарычев // Информационная среда вуза XXI века : материалы
    V Междунар. науч.-практ. конф. (26–30 сентября 2011 г.). – Петрозаводск, 2011. – С. 29–32.
11. Белов, В. Н. Оптимизация хранилища данных с представлением структуры в виде матроида / В. Н. Белов, П. П. Макарычев // Молодежь и наука: модернизация и инновационное развитие страны : материалы междунар. науч.-практ. конф. (г. Пенза, 15–16 сентября 2011 г.) : в 3 ч. – Пенза : Изд-во ПГУ, 2011. – Ч. 1. – С. 117–119.
12. Белов, В. Н. Выбор функции для оценки деятельности сотрудников / В. Н. Белов, П. П. Макарычев // Молодежь и наука: модернизация и инновационное развитие страны : материалы междунар. науч.-практ. конф.(г. Пенза, 15–16 сентября 2011 г.) : в 3 ч. – Пенза : Изд-во ПГУ, 2011. – Ч. 1. – С. 120–122.

Научное издание

Белов Вадим Николаевич

МОДЕЛИ МНОГОМЕРНОГО ПРЕДСТАВЛЕНИЯ
И ОБРАБОТКИ ДАННЫХ НА ОСНОВЕ АЛГЕБРЫ КОРТЕЖЕЙ
В ИНФОРМАЦИОННО-АНАЛИТИЧЕСКОЙ СИСТЕМЕ

Специальности:

05.13.17 – Теоретические основы информатики;

05.13.01 – Системный анализ, управление и обработка информации
(приборостроение)

Редактор В. В. Чувашова

Технический редактор М. Б. Жучкова

Компьютерная верстка М. Б. Жучковой

Распоряжение № 7/2012 от 07.02.2012 г.

Подписано в печать 16.02.12.

Формат 60841/16. Усл. печ. л. 1,16.

Тираж 100. Заказ № 25.

Издательство ПГУ.

440026, Пенза, Красная, 40.

Тел./факс: (8412) 56-47-33; e-mail: [email protected]