Методология разработки и создания моделей бортовых вычислительных комплексов для тренажеров пилотируемых космических аппаратов

На правах рукописи

Полунина Елена Васильевна

МЕТОДОЛОГИЯ РАЗРАБОТКИ И СОЗДАНИЯ

МОДЕЛЕЙ БОРТОВЫХ ВЫЧИСЛИТЕЛЬНЫХ КОМПЛЕКСОВ ДЛЯ ТРЕНАЖЕРОВ ПИЛОТИРУЕМЫХ КОСМИЧЕСКИХ АППАРАТОВ

Специальность 05.13.11 - Математическое и программное

обеспечение вычислительных машин, комплексов и

компьютерных сетей

Автореферат

диссертации на соискание ученой степени

доктора технических наук

звездный городок 2011

Работа выполнена в Федеральном государственном бюджетном учреждении «Научно-исследовательский испытательный Центр подготовки космонавтов имени Ю. А. Гагарина»

Научный консультант:

доктор технических наук, профессор

Бурдаев Михаил Николаевич

Официальные оппоненты:

доктор физико-математических наук, профессор

Ломазова Ирина Александровна

доктор технических наук, профессор

Хачумов Вячеслав Михайлович

доктор технических наук, профессор

Зайцев Александр Владимирович

Ведущая организация:

Научно-исследовательский центр

ракетно-космических систем (4 ЦНИИ МО)

Защита состоится 23 декабря 2011 г. в 13 часов на заседании диссертационного совета ДМ002.084.01 при Учреждении Российской академии наук Институте программных систем им. А. К. Айламазяна РАН, расположенном по адресу: 152021, Ярославская область, Переславский район, с. Веськово, ул. Петра I, д. 4а.

С диссертацией можно ознакомиться в библиотеке Учреждения Российской академии наук Института программных систем им. А. К. Айламазяна РАН.

Автореферат разослан «____»____________2011 г.

Ученый секретарь

диссертационного совета, к. т. н. Пономарева С.М.

ОБЩАЯ ХАРАКТЕРИСТИКА РАБОТЫ

Актуальность. Изучение и исследование космического пространства является одной из важнейших проблем современной науки. Все более широкие масштабы приобретает в настоящее время освоение космоса с помощью пилотируемых космических аппаратов. Оно уже приносит большую пользу многим отраслям народного хозяйства.

Основная подготовка экипажей к космическим полетам проводится на тренажерах, представляющих собой сложные и дорогостоящие системы, которые являются практически единственным средством для формирования у экипажей профессиональных навыков по управлению космическим аппаратом и его системами в штатных и предполагаемых нештатных ситуациях. Эффективность и качество подготовки экипажей на тренажерах в значительной мере определяются соответствующими характеристиками моделей бортовых систем пилотируемых космических аппаратов и установленной на нем полезной нагрузки. Основу системы управления современных космических аппаратов составляют бортовые цифровые вычислительные комплексы (БЦВК), которые характеризуются большим объемом программного обеспечения, сложным взаимодействием составных частей при реализации многочисленных алгоритмов управления, разнообразием способов взаимодействия с реальной аппаратурой, возможностью наращивания вычислительных средств и замены версий штатного программного обеспечения.

В связи с этим, исследование проблемы моделирования бортовых цифровых вычислительных комплексов в тренажерах имеет актуальное самостоятельное значение.

В настоящее время существуют два способа моделирования БЦВК в тренажерах: полунатурное и функциональное. До последнего времени в основном применялось полунатурное моделирование (использование штатного БЦВК, использование эмуляторов БЦВМ, реализация штатного программного обеспечения БЦВК на наземных вычислительных средствах).

Проблемная ситуация. Полунатурное моделирование БЦВК обеспечивает высокую степень адекватности реальному изделию, приемлемые сроки разработки модели БЦВК, быструю смену версий штатного программного обеспечения, небольшие затраты на испытания тренажера. Однако его использование существенно ограничивает обучающие свойства тренажера, не позволяя осуществлять приостановку тренировки, оперативный возврат в исходное или любое предшествующее состояние, масштабирование времени; делает невозможным отработку расчетных нештатных ситуаций, связанных с отказами аппаратуры БЦВК; увеличивает время установки начальных условий тренировки и восстановления тренажера при сбоях технических средств и ошибках оператора, что существенно снижает качество тренажера и эффективность подготовки экипажей на нем. Кроме того, использование штатного программного обеспечения БЦВК в тренажере требует избыточного для задач подготовки моделирования управляемых и контролируемых БЦВК бортовых систем.

Технический прогресс в области тренажеростроения в целом направлен в сторону перехода от полунатурного моделирования БЦВК к функциональному (математическому) моделированию, свободному от недостатков полунатурного моделирования. Но без применения специальных инструментальных средств разработки функциональных моделей БЦВК требуются большие затраты на их создание и испытания на соответствие штатным изделиям, сравнимые с затратами на создание штатного программного обеспечения БЦВК. С учетом ограниченного времени создания тренажера этот способ используется при моделировании БЦВК с небольшим объемом программного обеспечения и достаточно простой организацией вычислений.

Научная проблема состоит в разработке методологии создания функциональных моделей БЦВК, под которой будем понимать совокупность принципов, метода, средств и технологии моделирования. Решение данной проблемы предполагается осуществлять на основе формализации описания процесса функционирования БЦВК и автоматизации создания программных моделей БЦВК для тренажеров.

Цель диссертационной работы - разработка математического и программного обеспечения создания функциональных моделей БЦВК для тренажеров пилотируемых космических аппаратов, использование которого позволит сократить сроки создания и модификации моделей БЦВК и повысить эффективность подготовки космонавтов.

Для достижения этой цели в работе поставлены следующие задачи:

1. Исследовать общие принципы моделирования бортовых систем пилотируемых космических аппаратов для тренажеров, методы и средства их разработки и испытания.

2. Провести анализ существующих способов моделирования БЦВК в космических тренажерах, выявить их достоинства и недостатки.

3. Провести анализ методов имитационного моделирования сложных систем с целью определения возможности и целесообразности их применения для моделирования БЦВК.

4. Разработать формализм, позволяющий адекватно описывать процесс функционирования программно-аппаратной платформы БЦВК совместно с выполнением алгоритмов рабочих программ полета.

5. Провести описание и анализ модели дискретного контура управления с применением разработанного формализма.

6. Разработать алгоритмическое и программное обеспечение системы имитации процесса функционирования БЦВК для тренажеров ПКА.

7. Разработать технологию создания модели БЦВК для тренажеров.

Методы исследования. Для решения поставленных задач в диссертационной работе использовались методы имитационного моделирования, теории множеств, теории графов, теории алгоритмов и теории сетей Петри.

Научная новизна работы определяется тем, что разработаны:

- метод моделирования БЦВК в тренажерах, в котором в качестве формального аппарата для описания БЦВК на уровне процесса функционирования программно-аппаратной платформы и выполнения алгоритмов рабочих программ полета используются модифицированные сети Петри;

- новый формализм - И-сети, разработанные на основе Е-сетей путем введения модификаций, направленных на увеличение мощности моделирования, сокращения объемов сетевых моделей и концептуальной дистанции между моделью и реальной системой, и ориентированные на имитационное моделирование сложных систем;

- набор операций на множестве И-сетей и соответствующие им преобразования структур данных И-сетей, обеспечивающие оперативное изменение И-сетевых моделей, автоматическое построение новых моделей из имеющихся моделей или их частей;

- технология создания моделей БЦВК, в рамках которой разработка модели может вестись параллельно разными группами разработчиков в двух направлениях – создание модели организации вычислительного процесса и создание программ алгоритмов управления.

Практическая значимость работы состоит в том, что в ней разработаны средства имитационного моделирования сложных систем, обеспечивающие:

- быстрое и надежное конструирование модели;

- описание моделируемой системы единым образом на всех уровнях ее рассмотрения;

- интерфейс пользователя на всех этапах проектирования, отладки и реализации модели;

- оперативное внесение изменений в модели системы и внешней среды;

- управление состоянием модели и контроль её функционирования на этапе отладки и в процессе реализации модели;

- открытость системы моделирования, возможность подключения к ней пользовательских программ анализа, как до реализации, так и в процессе реализации модели.

Основные положения, выносимые на защиту:

1. Принципы моделирования бортовых систем пилотируемых космических аппаратов для тренажеров, отвечающие назначению тренажеров и позволяющие реализовать в полной мере их обучающие свойства: адекватность штатному изделию, функционирование в реальном и ускоренном времени, управляемость, контролируемость, регистрируемость, достаточность и модульность построения.

2. Новый формализм - И-сетей, ориентированный на имитационное моделирование сложных систем, в частности, на моделирование бортовых вычислительных комплексов для тренажеров.

3. Набор операций на множестве И-сетей и соответствующие им преобразования структур данных И-сетей, обеспечивающие оперативное изменение сетевых моделей, автоматическое построение новых моделей из существующих моделей или их частей.

4. Метод моделирования БЦВК в тренажерах, в котором в качестве формального аппарата для описания процесса функционирования программно-аппаратной платформы и выполнения алгоритмов рабочих программ полета БЦВК используются И-сети.

5. Алгоритмические и программные средства системы имитационного моделирования сложных систем на основе И- сетей.

6. Технология создания функциональных моделей БЦВК для тренажеров.

Достоверность полученных результатов обеспечивается методологической обоснованностью использования выбранных методов исследования, а также адекватностью их предмету и задачам исследования, внедрением результатов диссертационной работы в практику.

Внедрение результатов. Основные результаты диссертационной работы использовались в НИИ ЦПК им. Ю.А. Гагарина, в Центре тренажеростроения при разработке тренажеров орбитального комплекса «Мир» и МКС, в ЗАО «РТСофт» при разработке модели системы управления центрифугой ЦФ 18, а также в ФГУП «НИИАО» при разработке модели бортового вычислительного комплекса транспортного пилотируемого корабля «Союз-ТМА» на комплексных тренажерах «ТДК-3» и «ТДК-4», что подтверждается соответствующими актами.

Апробация работы. Основные положения и результаты работы докладывались и обсуждались на:

- IV научном семинаре «Методы синтеза и планирования развития структур сложных систем» (Ташкент, 1986 г.);

- ХVШ Всесоюзных Гагаринских научных чтениях по космонавтике и авиации (Москва, 1988 г.);

- НТС ЦПК им. Ю.А. Гагарина в 1989, 1996. 1998. 2001-2009 гг.

- межотраслевой конференции «Тренажеры и имитаторы» (Москва 1988 г.);

- научных чтениях, посвященных разработке научного наследия и развитию идей К. Э. Циолковского (Калуга, 1993, 1994,1997, 1998, 2002, 2004, 2007 гг.);

- научно-техническом семинаре «Технические средства и технологии для построения тренажеров», (Звездный городок, 1994, 1996, 1998 гг.);

- международных научно-практических конференциях «Профессиональная деятельность космонавтов и пути повышения ее эффективности», «Информатизация подготовки и профессиональной деятельности операторов аэрокосмических систем» и «Пилотируемые полеты в космос» (Звездный городок, 1995, 2000, 2009 гг.);

- общественно-научных чтениях, посвященных памяти Ю. А. Гагарина (г. Гагарин, 1996, 1998, 2002, 2003, 2007, 2010 гг.).

Личный вклад. Выносимые на защиту результаты получены соискателем лично. В опубликованных совместных работах постановка и исследование задач осуществлялись совместными усилиями соавторов при непосредственном участии соискателя.

Публикации. Все приводимые в работе материалы основаны на обобщении результатов, содержащихся в 69 публикациях, из которых 32 печатные работы (10 опубликованы в журналах из перечня ВАК), 24 отчета по НИР, 13 программно-методических документов по разработке, испытаниям и эксплуатации тренажеров ПКА.

Структура и объем работы. Диссертация состоит из введения, пяти глав, заключения и списка литературы. Объем диссертации составляет 175 страниц машинописного текста, включая 44 рисунка, 1 таблицу, список литературы из 170 наименований.

Исследования выполнялись автором в рамках плановых НИР и ОКР, предусмотренных постановлениями Правительства по созданию и обеспечению эксплуатации орбитального комплекса «Мир» и Международной космической станции (постановление № 105-41, № 41 и №238), а также в соответствии с Концепцией Российского космического агентства и Федеральной космической программы РФ. (Раздел 4. Создание образцов космической техники научного и народнохозяйственного назначения. Раздел 7. Содержание и развитие уникальной экспериментальной базы).

КРАТКОЕ СОДЕРЖАНИЕ РАБОТЫ

Во введении проводится обоснование актуальности проблемы моделирования БЦВК в тренажерах ПКА, сформулированы цель и задачи исследования, дается общая характеристика работы, определены ее новизна и практическая значимость, а также приведены положения, выносимые на защиту.

В первой главе диссертации “Принципы и методы моделирования бортовых систем пилотируемых космических аппаратов на тренажерах” обсуждаются современные технологии создания тренажеров, сформулированы основные принципы моделирования бортовых систем пилотируемых космических аппаратов, отвечающие назначению тренажеров и позволяющие реализовать в полной мере их обучающие свойства, рассматриваются методы моделирования и испытания бортовых систем.

Показано, что к настоящему времени на основе более чем тридцатилетнего опыта построения отечественных космических тренажеров созданы технология построения тренажеров, отработаны и совершенствуются методы и средства математического моделирования логики функционирования бортовых систем и физических процессов, протекающих в них, достаточно унифицированы модели движения и модель внутренней среды пилотируемых космических аппаратов. Вместе с тем основным проблемным моментом при создании тренажеров остается моделирование бортовых цифровых вычислительных комплексов.

Рассматриваются существующие подходы к моделированию БЦВК на тренажерах.

1. Полунатурное моделирование, к которому относится: использование в тренажере штатного БЦВК; использование эмуляторов БЦВМ; использование штатного программного обеспечения БЦВК на наземных вычислительных средствах, совместимых со штатными БЦВМ.

2. Функциональное или математическое моделирование - использование математической модели БЦВК, реализованной на вычислительных средствах общего назначения.

С точки зрения выполнения требований тактико-технических заданий на соответствие работы тренажера штатному изделию полунатурное моделирование имеет преимущества перед математическим моделированием, так как в этом случае используется штатное программное обеспечение БЦВК. Однако при этом существенно ограничивается использование тренажера как обучающего средства, не позволяя осуществлять приостановку тренировки, оперативный возврат в исходное или любое предшествующее состояние, масштабирование времени.

К отмеченным выше недостаткам полунатурного моделирования, снижающим качество тренажера, добавляются следующие: невозможность ввода расчетных нештатных ситуаций, связанных с отказами аппаратуры БЦВК; большое время (от 20 до 40 минут) выставки начальных условий тренировки и восстановления тренажера при сбоях технических средств и ошибках оператора; стоимость БЦВК высока и имеет тенденцию к дальнейшему увеличению; бортовое оборудование часто модернизируется и соответствующая модернизация натурных частей в тренажерных комплексах вызывает немало затруднений; ресурсы некоторых натурных элементов не соответствуют нормам, установленным для тренажеров.

Предлагается для моделирования БЦВК применять метод функционального моделирования, который позволяет наиболее полно использовать тренажер как обучающее средство, при этом модель БЦВК органично входит в модель системы управления ПКА, все блоки которой являются программными. Но из-за больших затрат на разработку функциональной модели, и с учетом ограниченного времени создания тренажера, этот способ до настоящего время использовался только при моделировании БЦВМ с небольшим объемом программного обеспечения и простой организацией вычислений.

Проблема функционального моделирования БЦВК на тренажере состоит в самом описании объекта моделирования, учета в этом описании не только алгоритмов управления, но и особенностей организации вычислительного процесса БЦВК. Требуется найти такой подход, который на едином языке давал бы возможность адекватно описывать БЦВК (как программные, так и аппаратные части) и процесс его функционирования в системе управления ПКА. В связи с этим встает задача выбора метода и аппарата моделирования бортовых вычислительных средств в системе управления ПКА. Выбор метода должен производиться на основании таких показателей, как мощность моделирования, удобство описания объекта моделирования, наглядность построенной модели, развитые средства отладки, малые затраты на модификацию модели, контролируемость и управляемость модели в процессе реализации.

Во второй главе работы “Анализ методов и средств имитационного моделирования сложных систем” дается сравнительный анализ известных методов имитационного моделирования дискретных систем. Результаты анализа приведены в таблице 1.

Таблица 1.

Анализ средств имитационного моделирования

Средства моделирования	Достоинства	Недостатки
Языки дискретного моделирования	1.Универсальность 2.Большие алгоритмические возможности.	1. Модель слабо структурирована. 2. Слабо развиты средства контроля и управления моделью. 3. Для каждого варианта системы приходится составлять свою программу моделирования. 4.Средства имитации внешней среды, сбора и обработки статистики включены в саму модель.
Агрегатное моделирование	1.Наглядно отражается структура модели и все связи в ней. 2.Легко варьируются состав, структура и тип элементов модели. 3.От пользователя не требуется знания программирования	1. Отсутствует концепция состояния системы. 2. Высокая степень абстракции описания элементов системы, доступного лишь узкому классу специалистов.
Сети Петри	1.Наглядно отражается структура, текущее состояние и процесс функционирования модели. 2.Иерархичность. 3.Возможность модификации сетей.	1.Ограниченная мощность моделирования. 2. Каждая модификация ориентирована на определенную предметную область и выполнение определенных задач имитационного моделирования.

Целью моделирования БЦВК на тренажерах ПКА является имитация процесса функционирования моделируемой системы в реальном времени адекватно штатной - моделирование программно-аппаратной платформы одновременно с выполнением алгоритмов рабочих программ полета. И хотя существующие модификации сетей Петри не позволяют моделировать БЦВК на тренажерах, сам аппарат сетей Петри содержит большие потенциальные возможности для формализованного описания и имитационного моделирования бортовых вычислительных средств на тренажерах ПКА. Сети Петри допускают модификации, направленные на расширение задач моделирования; по самому определению им присуще свойство синхронизации процессов, с помощью которого можно обеспечить моделирование в реальном и заданном масштабах времени; благодаря концепции состояния сетевой модели легко обеспечить контроль и управление моделью в процессе имитации.

Предлагается в качестве исходного формализма для разработки аппарата формализованного описания и построения на его основе средств имитационного моделирования БЦВК на тренажерах ПКА, использовать модифицированные сети Петри – Е-сети, ориентированные на моделирование операционных систем и вычислительных процессов.

В третьей главе “Разработка имитационных сетей как средства описания процесса функционирования БЦВК” рассматриваются вопросы разработки аппарата формализованного описания процесса функционирования БЦВК на основе модифицированных сетей Петри.

Вводится новый формализм - И-сети, являющиеся дальнейшей модификацией Е-сетей и позволяющие моделировать в реальном времени не только процесс функционирования программно-аппаратной платформы, но и выполнение алгоритмов рабочих программ полета БЦВК.

И-сети (имитационные сети), предлагаемые в данной работе, включают все расширения последовательности модифицированных сетей Петри, направленных на моделирование вычислительных систем: сети Петри временные сети Петри Е-сети М-сети И-сети.

Дополнительно в И-сетях введены следующие модификации, обеспечивающие моделирование БЦВМ в тренажерах.

1) Вместо набора базовых типов переходов введен универсальный переход, условия реализации которого и правила приема меток из входных позиций могут быть любыми функциями статусов входных и выходных позиций перехода, а правила выдачи меток в выходные позиции перехода – функциями статусов входных и выходных позиций и атрибутов принятых меток. Данная модификация обусловлено тем, что БЦВМ представляет собой сложную систему из разнородных многофункциональных элементов. Моделировать все элементы системы с помощью ограниченного набора типов переходов нецелесообразно. В тех случаях, когда логика наступления некоторой активности не может быть описана каким-либо типом перехода, активность приходится моделировать несколькими связанными между собой базовыми переходами, а если это невозможно, - вводить новый тип перехода. Это приводит к увеличению размера сетевой модели и увеличивает дистанцию между сетевой моделью и реальной системой.

2) Переход может содержать процедурную часть – вычислительный алгоритм, выполняемый при срабатывании перехода. Введение в переход вычислительной части вызвано необходимостью выполнения алгоритмов рабочих программ в процессе имитации функционирования БЦВК.

3) Метка в качестве своего атрибута может содержать не только переменные, но и алгоритмы, выполнением которых управляют переходы, принявшие метку, что позволяет моделировать выполнение алгоритмов рабочих программ БЦВМ.

4) Временной параметр перехода может быть принадлежностью данного перехода, атрибутом принятой метки, а так же функцией атрибутов принятых меток и модельного времени. Во втором случае переход моделирует активность, длительность которой определяется свойствами данных, над которыми она действует.

5) Структура метки не фиксированная, как в предшествующих модифицированных сетях, а произвольная, т.е. количество атрибутов и их порядок следования в метке – произвольный в рамках одной сети. В общем случае переход может принять метку одной структуры, а сформировать и передать метку в выходную позицию другой структуры.

6) Практика сетевого моделирования показала, что в сетевой модели БЦВМ можно выделить позиции, в которых постоянно находятся метки (например, списки временных заданий, значения некоторых регистров и т.д.). Для их моделирования введены информационные позиции (графически изображаются наполовину заштрихованными кружками). При приеме метки из такой позиции ее статус не обнуляется, метка сохраняется. Статус информационной позиции обнуляется только при записи в нее нулевой информации.

7) В И-сетях из каждой позиции выходит и в каждую позицию входит не более одной дуги. Наличие у позиции нескольких входных или выходных дуг может приводить к конфликтным ситуациям (рис.1).

Рис.1. Конфликтные ситуации.

В сети A конфликт возникает, когда в позицию q1 поступает метка. Какой из переходов p1, p2 должен реализоваться и принять метку? В сети В конфликт может возникнуть при одновременном завершении переходов p1 и p2. Какая из меток m1 или m2 перейдет в позицию q3?

Если не введено ограничение на количество инцидентных позиции дуг, в определении сети должно быть предусмотрено разрешение конфликта (например, переходам могут быть присвоены приоритеты). В рамках введенного ограничения первая конфликтная ситуация может быть описана сетью А', а вторая - сетью B', где введены дополнительные позиции и переход p3, разрешающий конфликт любым заданным пользователем способом (рис. 2).

Рис. 2. Разрешение конфликтов.

Таким образом, любая сеть без ограничений может быть преобразована в сеть с ограничением путем введением дополнительных переходов, разрешающих конфликты.

Первые четыре модификации направлены на расширение имитационных возможности сетей. Следующие две модификации - 5-ая и 6-ая - введены для сокращения объема сетевых моделей и приближения модели к реальной системе. Ограничение же на количество инцидентных дуг позиции сети возлагает на пользователя разрешение возможных конфликтов в сети удобным ему способом.

Формально И-сеть определяется как набор:

N = (Q, QI, P, I, O, M), где:

Q = { qi } - конечное счетное непустое множество позиций, i=1,l;

QI Q - подмножество, быть может, пустое, информационных позиций;

P = { pi } - конечное непустое множество переходов, i=1,n;

pi = {Li, PMi, PROCi }, где:

Li - логическая функция статусов входных-выходных позиций перехода,

PMi - процедура приема меток из входных позиций переходов,

PROCi - процедура определения временного параметра перехода, преобразования входных меток, формирования выходных меток;

I Q х P {0,1} – входные дуги;

O P х Q {0,1} - выходные дуги;

При условии, что:

1) q Q, I(q)={pP I(q,p)=1}={0,pi), O(q)={pPO(p,q)=1}={0, pj};

2) I(q) O(q) ;

3) p P, {qQ I(q,p)=1} 0, {q Q O(p,q)=1} ;

М = { mq1, mq2,..., mql } - начальная разметка, где:

mqi = { aj } - конечное множество атрибутов метки.

Фаза наступления. В этой фазе принимаются метки из входных позиций перехода в соответствии с процедурой приема меток PМi. При этом статусы простых, не информационных позиций обнуляются, метки в них уничтожаются. Информационные позиции сохраняют свои метки. Выполняется процедура перехода PROCi, в которой определяется временной параметр перехода, выполняются действия над атрибутами принятых меток, формируются выходные метки. Временной параметр может быть константой или функцией атрибутов принятых меток и модельного времени.

Фаза активности. Продолжается временной промежуток равный временному параметру перехода. В этой фазе изменений в сети не происходит.

Фаза завершения. Сформированные на первой фазе при выполнении PROCi метки передаются в выходные позиции перехода, изменяются статусы выходных позиций. Статусам простых позиций, в которые передаются метки, присваиваются единичные значения, статусам информационных позиций могут присваиваться как единичные (в позицию поступает метка) так и нулевые (метка в позиции обнуляется) значения.

Обоснована и разработана структура данных И-сети, представляющая собой библиотеки программ (БП), реализующие процедуры L, РМ, и PROC переходов, и три таблицы (рис.3):

- таблицу позиций (TQ);

- таблицу переходов (ТР);

- таблицу связей (ТС).

TQ содержит информацию о позициях сети. Каждая строка содержит информацию об одной позиции: имя позиции, признак информационной позиции, статус позиции, текущую и начальную метку.

ТР содержит информацию о переходах сети. Под каждый переход отведена одна строка ТР, в которой содержится номер, имя перехода и фаза перехода. Фаза перехода равна единице, если переход находится в активной фазе и нулю в противном случае.

ТС отражает все связи в сети. На пересечении pi-cтроки и pj-столбца находятся позиции, являющиеся выходными позициями перехода pi и входными позициями перехода pj. Нулевой столбец содержит выходные периферийные позиции сети, нулевая строка - входные периферийные позиции сети. Соответственно pi-ая строка ТС содержит все выходные позиции перехода pi, pi-ый столбец - все входные позиции перехода pi.

Рис. 3. Структура данных И-сети.

Для того, чтобы с имитационными моделями можно было проводить различные манипулирования (дополнять модель, переходить с одного уровня детализации на другой, заменять отдельные части, объединять модели и т.д.) определены операции на множестве И-сетей, обеспечивающие эти манипулирования.

Пусть h(N) обозначает множество головных (входных периферийных) позиций сети N, а l(N) - множество хвостовых (выходных периферийных) позиций сети N. Позиции q h(N) l(N) назовем внутренними позициями сети.

Объединение сетей ",".

Будем рассматривать элементы сети (позиции, переходы и дуги) не как множества, а как комплекты. (Комплект является обобщением множества, в которое включены повторяющиеся элементы). Тогда, если

N1 = ( Q1, P1, I1, O1, M01 ) и N2 = ( Q2, P2, I2, O2, M02),

то N = (N1,N2) = (Q1+Q2, P1+P2, I1+I2, O1+O2, M01+M02),

т.е. операция объединения есть простое объединение комплектов исходных сетей.

Операция объединения как самостоятельная операция может применяться к сетям N1, N2 с непересекающимися множествами Р1, Р2 и Q1, Q2: P1 P2 =, Q1 Q2 =.

Пример выполнения операции объединения дан на рис. 4.

Рис. 4. Объединение сетей

Порядок формирования структуры данных сети N из структур данных исходных сетей N1, N2 следующий:

ТП, TQ и БП получаются объединением в произвольном порядке таблиц ТП1 и ТП2, TQ1 и TQ2, БП1 и БП2 соответственно.

Таблица переходов ТР получается последовательным объединением ТР1 и ТР2, при этом изменяется нумерация переходов сети N2 - i2’ = i2 + n1.

Таблица связей формируется следующим образом. Сначала ТС1 достраивается до размера (n1+n2+1)*(n1+n2+1). Затем нулевая строка ТС2 переносится в нулевую строку ТС, нулевой столбец ТС2 - в нулевой столбец ТС, остальная часть ТС2 переносится в ТС начиная с n1+1 строки и с n1+1 столбца (см. рис. 5).

Рис. 5. Преобразование ТС при выполнении операции объединения.

Слияние позиций"".

Операция слияния хвостовых позиций сети с головными позициями, задает новую сеть

N' = (N, X Y), X l(N), Y h(N),

в которой каждая пара позиций заменяется одной позицией с двойным именем zi=xi yi, разметкой М0(хi) и соответствующими позициям хi, уi инцидентными дугами. (Пример выполнения операции приведен на рис. 6).

Рис. 6. Слияние позиций.

Преобразования структуры данных сети при этой операции затрагивают только таблицы связей и позиций - ТС и TQ.

Из TQ удаляются строки, соответствующие позициям множества Y. В строках, соответствующих q X, xi заменяется на zi.

В ТС удаляются позиции q X Y из нулевых строк и столбцов и переносятся во внутренние части с двойным наименованием (см. рис. 7).

Рис 7. Преобразование ТС, TQ при слиянии позиций.

Сшивание сетей " ; ".

Операция имеет две модификации.

а) Операция без параметров - сшивает две сети N1, N2 по одноименным позициям. Заключается в объединении сетей N1,N2 c последующим слиянием одноименных позиций.

N' = ( N1; N2 ).

Если Q1 Q2 =, то эта операция тождественно равна операции объединения сетей.

Если Q1 Q2, то операция объединения N1,N2 приводит к сети N", в которой позиции представляют собой комплект.

Операция слияния одноименных позиций приводит комплект Q" к множеству Q', а сеть N' - к И-сети.

б) Операция с параметрами - N’ = ( N1; N2 )( X,Y),

X = {X1,X2 }, Y = {Y1,Y2 }, X1 l (N1),

X2 l (N2), Y h (N1), Y h (N2).

Эта операция сшивает сети N1, N2, объединяя их с последующим слиянием одноименных и указанных в операции позиций. (Пример выполнения операции дан на рис. 8).

Рис. 8. Сшивание сетей

Определим вспомогательную операцию - расщепление внутренней позиции . Эта операция создает в сети из одной внутренней позиции две периферийных позиции - головное и хвостовое (рис. 9). В структуре данных сети расщепленная позиция переносится в нулевую строку и нулевой столбец ТС (рис. 10). В TQ добавляется строка, идентичная строке, соответствующей расщепляемой позиции.

Рис.9. Расщепление внутренней позиции.

Рис. 10. Преобразование ТС, TQ при расщеплении позиции.

Введем понятие базового фрагмента сети. Базовым фрагментом Vp сети N назовем подсеть, включающую переход p, все инцидентные ему дуги и выходные и входные позиции. Если Р = {pi}, i=1,n, то все базовые фрагменты сети есть Vp1, Vp2,...Vpn, а N = ( Vp1; Vp2;...Vpn), т.е. сеть может быть получена путем сшивания всех своих базовых фрагментов. Фрагмент сети V (pi1, pi2,...pin ) есть сеть, полученная сшиванием базовых фрагментов (Vpi1,Vpi2,. Vpin ).

Выделение базового фрагмента из сети " ".

Если N = ( Q, P, I, O, M0 ), а pi P, то

N' = ( N pi ) = Vpi

Пример выполнения операции дан на рис. 11.

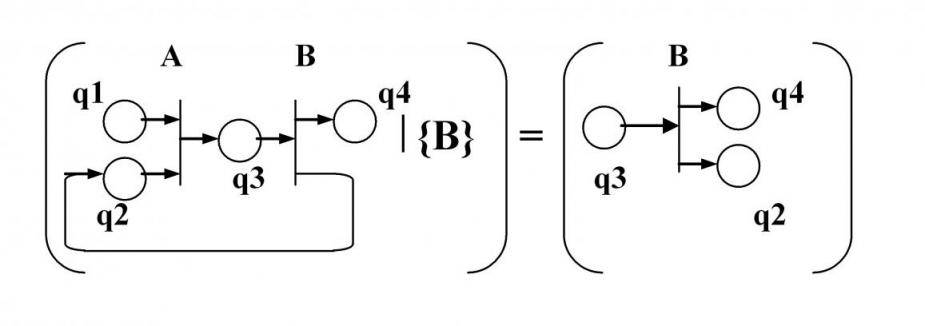
Рис. 11. Выделение базового фрагмента из сети.

Структура данных N' формируется из структуры данных N следующим образом:

ТР' - представляет собой одну строку из ТР, описывающую переход pi;

БП' - часть БП, относящуюся к переходу pi;

TQ' - совокупность строк ТQ, описывающих q I(pi) O(pi);

TC' представляет собой матрицу размером 2 х 2, дополненную следующим образом (рис. 12):

- все элементы, кроме элемента (i, i), из i-той строки ТС переносятся в элемент (1,0) ТС',

- все элементы, кроме элемента (i, i), из i-го столбца - в элемент (0,1) ТС',

- содержимое элемента (i, i) ТС переносится в элемент (1,1) ТС'.

Рис. 12. Преобразование ТС при выделении базового фрагмента.

Выделение фрагмента из сети.

Эта операция формирует новую сеть, равную фрагменту исходной сети. Операция заключается в последовательном выделении базовых фрагментов с последующим сшиванием полученных сетей по одноименным позициям.

N' = ( N { pi1,pi2,...pin}) = ((N pi1);(N pi2);...(N pin)).

Пример выполнения операции дан на рис. 13.

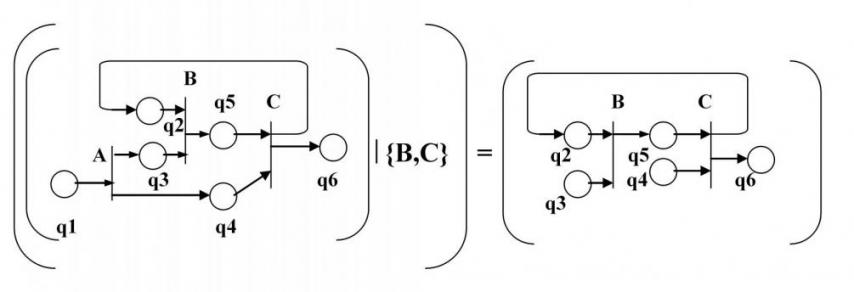
Рис.13. Выделение фрагмента.

Удаления базового фрагмента из сети.

N' = N - Vp есть сеть, получаемая из исходной в два этапа.

Сначала расщепляются все позиции общие для фрагментов Vp и V(P\{pi}).

Затем из полученного набора элементов сети удаляются все элементы, принадлежащие базовому фрагменту.

Пример выполнения операции дан на рис.14.

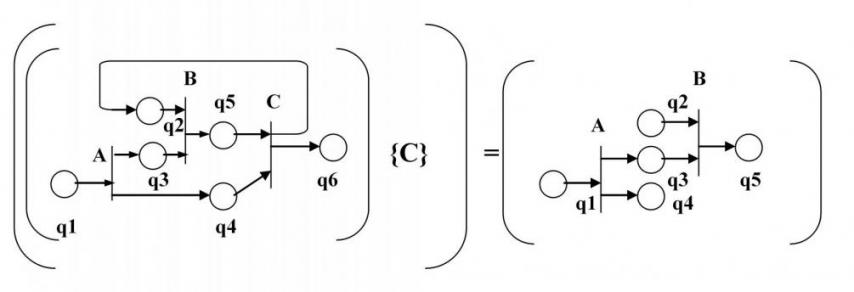
Рис. 14. Удаление базового фрагмента.

При этом структура данных сети N подвергается следующим преобразованиям (рис.15):

1) расщепленные состояния переносятся из внутренней части ТС в нулевую строку и столбец;

2) из TQ удаляются строки, соответствующие состояниям, в рi-ой строке и рi-ом столбце после расщепления;

3) из ТС удаляются рi-ая строка и рi-ый столбец;

4) из ТР удаляется строка перехода рi, из БП - программы процедур перехода рi.

Рис. 15. Преобразование ТС при удалении базового фрагмента.

Удаление фрагмента из сети.

N' = N - V (pi1,pi2,...pin) = V (P\{pi1,pi2,...pin}).

Операция удаления фрагмента из сети может быть выполнена двумя способами:

а) последовательным удалением всех базовых фрагментов, составляющих удаляемый фрагмент;

б) выделением из сети фрагмента V(P\{p,p,...p}).

N' = (N - V(pi1,pi2,...pin)) = (...((N-Vpi1)-Vpi2)-...-Vpin) = (N{pi1,pi2,...pin}).

Пример выполнения операции дан на рис.16.

Рис. 16. Удаление фрагмента.

Замена фрагмента сети на сеть " ".

Эта операция формирует сеть, в которой фрагмент сети V{pi1,pi2,...pin} заменен на сеть N1, и включает в себя две операции - удаление фрагмента из сети и сшивание оставшейся части с сетью N1 по одноименным позициям (рис.17).

N' = (N,V,N1) = ((N - V) ; N1).

Рис. 17. Замена перехода на сеть.

Замена позиции на сеть " ".

Если N = ( Q, P, I, O, M0 ) и q Q, а N1 = ( Q1, P1, I1, O1, M01 )

и xi l (N1), yi h (N1), то N' = (N, qi, N1, xi, yi )

есть сеть, полученная из сетей N, N1 следующим образом:

1) в сети N расщепляется позиция qi. В результате получаются две одноименных позиции -

qi1 l (N"), qi2 h (N"), N" = (N, qi);

2) сети N" и N сшиваются, при этом попарно сливаются позиции qi1, qi2 сети N" c позициями xi и yi сети N1: N' = (N1 ; N") ({qi1,xi},{yi,qi2}).

Пример выполнения операции дан на рис.18.

Рис. 18. Замена позиции на сеть.

Введенные операции позволяют автоматически, на уровне манипулирования структурами данных И-сетей, объединять различным образом несколько сетей в одну сеть, выделять из сети подсети, удалять из сети части сети, вставлять новые части в сеть, заменять части сети на новые, разрывать существующие и образовывать новые связи в сети.

Благодаря введенным операциям возможны параллельная разработка частей И-сетевой модели с последующим их объединением, использование при создании новой модели уже имеющихся моделей и их отдельных частей, что сокращает сроки создания И-сетевой модели БЦВК, минимизирует затраты на доработку модели при наращивании вычислительных средств БЦВК, изменении версии штатного программного обеспечения.

В четвертой главе “Применение метода И-сетей для моделирования процесса функционирования БЦВК в тренажерах” проводится разработка метода имитационного моделирования БЦВК на основе И-сетей.

При сетевом моделировании БЦВМ модули операционной системы (ОС) представляются вершинами переходами сети, данные – вершинами позициями, рабочие программы – метками. Состояние БЦВМ, под которым понимается состояние среды ОС и состояние выполнения рабочих программ, описывается разметкой сети.

Проиллюстрирована возможность применение И-сетей для формализованного описания процесса функционирования БЦВК на примере моделирования дискретного контура управления ориентацией пилотируемого космического аппарата. В данном примере рассматривается режим выполнение ориентации ПКА в системе координат, фиксируемой на момент включения режима. На рис. 19 приведены используемые базисы и функциональная схема контура управления.

Опорный инерциальный базис N является тем базисом, в котором задаются положения всех остальных базисов, используемых в алгоритме управления. В кватернионной форме положение опорного базиса соответствует единичному кватерниону (1,0,0,0). Опорный базис совмещается с базисом S, связанным с системой координат ПКА на начальный момент времени (N =S0). Выполнение ориентацией осуществляется в системе координат, задаваемой базисом P.

Рис. 19. Функциональная схема контура управления ориентацией.

Основные кинематические уравнения режима:

PN SP = SN

2SN = SN w

где: PN, SN - кватернионы, задающие положение базисов P и S в

базисе N;

SN – производная кватерниона SN;;

SP - кватернион, задающий положение базиса S в базисе Р;

w - угловая скорость движения ПКА в базисе S.

Контур управления ориентацией включает в себя систему исполнительных органов (СИО), объект управления - космический аппарат в угловом движении (КА) и кинематические соотношения углового движения (КИП), блок датчиков угловых скоростей космического аппарата (БДУС), блок формирования результирующего закона управления (БФРЗУ).

Результирующий закон управления является функцией кватерниона рассогласования SP между заданным базисом и связанным базисом S и вектора угловой скорости w: FЗУ = f (SP,w). В дискретном контуре управления ориентацией выполнение блоков КИП и БФРЗУ возлагается на БЦВМ.

Сетевая модель описанного контура управления представлена на рис. 20. Для простоты в рассматриваемом примере БЦВМ моделируется не полностью, а только в той части, которая обеспечивает выполнение данного режима. Так, рассматриваются только два источника прерывания: от таймера и от пульта оператора, с которого задается режим управления и уставочная информация. Не рассматривается механизм формирования очереди фоновых, не связанных с задачей управления программ.

М0: mq1 = mq2 = 1

mq3 = PRG(АЛГОРИТМ) Т(6) ПР (нет)

mq4 = режим (задан) л0(0,8) л1(0) л2 (0,5) л3 (0)

mqф = PRG(ФОН) Т(32) ПР (да)

mq5 = oм1(0) oм2 (0) oм3 (0)

Рис.20. И- сетевая модель дискретного контура управления ориентацией.

Подсеть, включающая переходы Р1, Р2, Р3, Р4 вместе с входными и выходными позициями, моделирует работу БЦВМ. Здесь: Р1 –таймер, Р2 –обработка прерываний, q7 – список циклически выполняемых программ, q9, q10, qф – очередь программ на выполнение, Р3 – запись программ в очередь на выполнение, Р4 – выполнение программ.

Переход Р5 моделирует систему исполнительных органов, угловое движение ПКА и датчики БДУС.

Программа, реализующая алгоритм управления, и фоновая программа представляются метками, движущимися по сети, со следующими атрибутами: Т - время выполнения программы, PROC - имя программы, ПР - признак разрешения прерывания программы во время выполнения (ПР = да для фоновых программ и ПР = нет для программы режима управления).

В реальной БЦВМ имеется два уровня программ – программы операционной системы и рабочие программы полета. Программы первого уровня управляют выполнением программ второго уровня, связь между ними осуществляется через общую область оперативной памяти. В И-сетевой модели также присутствуют два уровня программ – процедуры переходов и программы, являющиеся атрибутами меток. Процедуры переходов управляют движением меток по сети и выполнением программ, содержащихся в метках. Связь между ними также как и в реальной БЦВМ осуществляется через общую область памяти.

На данном методическом примере показано, что И-сети обладают достаточной мощностью для описания взаимодействия различных частей сложных систем, в том числе дискретной и непрерывной частей замкнутого контура управления ПКА.

Пятая глава посвящена разработке алгоритмического и программного обеспечения системы имитационного моделирования на основе использования И-сетей.

Система имитационного моделирования представляет собой совокупность программных средств, с помощью которых пользователь осуществляет создание и отладку модели сложной системы, описанной на языке И-сетей, а также наблюдает процесс функционирования модели во времени при известных воздействиях, поступающих на нее. Она включает в себя: входной язык И-сетей, транслятор с языка сетей во внутреннее представление, программу имитации функционирования И-сети во времени, программы манипулирования с моделью, программы графического отображения сети, программы анализа процесса функционирования модели.

Входной язык повторяет на естественном языке формальное описание И-сети. Собственно программируются – записываются на общеалгоритмическом языке только вычислительные части процедур переходов, если они имеются, и алгоритмы, являющиеся атрибутами меток.

Транслятор осуществляет синтаксический анализ текста и формирует структуру данных сетевой модели, повторяющую структуру данных И-сети. Информация о позициях сети помещается в таблицу позиций (TQ), о переходах - в таблицу переходов (TP), связи между вершинами сети транслируются в таблицу связей (TC). Логические функции переходов, процедуры приема меток и их преобразования переводятся сначала на алгоритмический язык среды разработки, затем после трансляции помещаются в библиотеки подпрограмм L, PM и PROC соответственно.

Имитация функционирования И-сетей во времени осуществляется по следующей схеме. Программа имитации просматривает логические функции наступления переходов и заносит в список те из них, для которых наступили условия реализации. Список упорядочивается по временным параметрам переходов tp. Для всех переходов из списка осуществляется фаза наступления. Затем выбирается из списка переход с наименьшим временным параметром tp и выполняются действия, соответствующие фазе завершения данного перехода.

Предусмотрены два режима работы программы имитации – диалоговый и автоматический. В диалоговом режиме в начале каждого цикла имитации программа выходит на диалог с пользователем. В процессе диалога может быть выведено на печать или монитор текущая разметка, граф сети, изменена разметка, закончена имитация.

Пересчет времени в процессе имитации может вестись либо "по шагам" либо "по событиям". В режиме "по шагам" после каждого цикла имитации модельное время увеличивается на единицу. В режиме "по событиям" - на временной параметр завершенного на данном цикле перехода.

Исходными данными для программы имитации являются структура данных сетевой модели и задание на моделирование, в котором задаются: время имитации, режим работы программы, режим пересчета времени, точки вывода состояния модели и подключения программ анализа. Программы анализа модели пишутся пользователем на алгоритмическом языке разработки системы имитации и подключаются к модели с помощью имеющихся в системе средств.

Блок-схема алгоритма программы имитации представлена на рис.21.

Программа имитации дополнительно к структуре данных сетевой модели в процессе имитации формирует и использует таблицу активных переходов (TPA).

Блок 1. Перед началом цикла устанавливается нулевое значение модельного времени, обнуляется таблица активных переходов.

Блок 2. Проверяется достижение заданного времени имитации. Если Т=Тк, подключаются программы анализа, которые должны работать по окончании имитации, и программа имитации заканчивает свою работу. Если время имитации еще не истекло, управление передается блоку 4.

Блок 4. Подключаются программы отображения сети и анализа, которые должны быть подключены при достижении данного модельного времени.

Блок 5. В случае диалогового режима выполняется диалог (Блок 6). после чего выполняется Блок 7. В процессе диалога пользователь может запросить данные о состоянии сети, изменить разметку и либо продолжить имитацию, либо закончить имитацию. В автоматическом режиме управление сразу передается Блоку 7.

Блок 7. Формируется таблица активных переходов - ТРА.

Для всех переходов, у которых ФАЗА=0, выполняются процедуры L. Если Li=1, т.е. наступили условия запуска перехода pi, в ТР фаза перехода pi устанавливается в единицу и в ТРА формируется строка данного перехода.

Выполняется процедура приема меток PMi, которая переписывает изображения принятых меток из TQ в ТРА в строку перехода pi.

Рис. 21. Блок-схема алгоритма имитации И-сети.

Выполняется процедура перехода PROCi. Выходные данные процедуры перехода - временной параметр p, и изображения меток, которые переход выдает в выходные позиции, вместе с именами этих позиций – также заносятся в ТРА в строку перехода pi.

Программа имитации при реализации переходов, преобразующих атрибуты принятых меток и формирующих новые метки, предварительно формирует символьную вставку, в которой используемым в процедуре атрибутам присваиваются их значения, взятые из изображений принятых меток. Затем транслирует текст процедуры со вставкой и полученный объектный модуль помещает в библиотеку PROC. После выполнения данной процедуры этот модуль из библиотеки уничтожается.

Блок 8. Подключаются программы анализа, при наступлении указанных в задании на моделировании переходов.

Блок 9. Проверка ТРА на ноль. Если ТРА не содержит ни одной строки, что означает, что при данной разметке не может наступить ни один переход, программа формирует сообщение о тупиковой ситуации (блок 10) и выходит на диалог. Пользователь может либо изменить разметку и продолжить имитацию, либо закончить имитацию. Если ТРА не пуста, управление передается блоку 11.

Блок 11. В блоке находятся все переходы из ТРА, у которых p=0, и из них формируется таблица активных переходов с нулевым временным параметром - ТРА0.

Блок 12. Проверка ТРА0 на ноль. Если ТРА0 не содержит ни одной строки, управление передается на блок 14, в противном случае выполняется блок 13.

Блок 13. Завершение переходов из ТРА0. Изображения меток из ТРА0 переписываются в TQ соответствующих строк, при этом статусы выходных позиций перехода, в которых переданы метки, устанавливаются в единичное состояние. Фазы завершенных переходов в ТР обнуляются, и управление передается на начало цикла без изменения модельного времени.

Блок 17. Завершение переходов из ТРА с минимальным временным параметром p. Блок работает аналогично блоку 13. Управление передается на блок 18.

Блок 14 анализирует порядок пересчета времени. Если "по шагам", то выполняется блок 16, в котором модельное время увеличивается на единицу, иначе выполняется блок 15, в котором модельное время увеличивается на временной параметр завершаемого на данном цикле перехода.

Блоки 18 и 19 подключают программы анализа и отображения модели по достижении меток заданных позиций и по завершении указанных в задании на моделирование переходов. Управление передается на начало цикла.

Разработанные алгоритмические и программные средства имитации соответствуют определению И-сетей и полностью реализуют их моделирующие возможности.

Разработана технология создания сетевой модели БЦВМ. На этапе содержательного описания определяется состав алгоритмов рабочих программ полета и средств ОС, участвующих в организации вычислительного процесса и подлежащих моделированию. Модель каждого алгоритма состоит из собственно алгоритма и его характеристик: приоритетность, цикличность выполнения, время выполнения, признак разрешения прерывания, признак маскирования алгоритма.

При разработке И-сетевой модели определяется структура И-сети (граф сети), структуры меток, движущихся по сети, условия наступления каждого перехода, действий, выполняемых при наступлении перехода, временные параметры переходов. При этом модули ОС представляются вершинами переходами сети, данные – вершинами позициями, рабочие программы – метками, состояние БЦВМ, под которым понимается состояние среды ОС и состояние выполнения рабочих программ, описывается разметкой сети. Далее осуществляется разработка программной модели, включающая в себя описание И-сетевой модели на входном языке и трансляцию полученного описания в структуру данных сети.

После этого проводится трансляция и редактирование полученной модели с объектными модулями рабочих программ полета, написанных на алгоритмическом языке среды разработки.

Вводится разметка сети (исходное состояние модели) и ее графическое отображение, используемое для контроля состояния модели в процессе реализации. Полученный программный продукт вместе с программой имитации включается в состав программного обеспечения тренажера.

Основные результаты работы

В результате проведенных в диссертационной работе исследований получены следующие основные результаты.

1. Сформулированы основные принципы моделирования бортовых систем ПКА, отвечающие назначению тренажера и позволяющие реализовать в полной мере их обучающие свойства: адекватность штатному изделию, функционирование в реальном и ускоренном времени, управляемость, контролируемость, регистрируемость, достаточность и модульность построения.

2. Показано, что к настоящему времени на основе более чем тридцатилетнего опыта построения отечественных космических тренажеров созданы технология построения тренажеров, отработаны и совершенствуются методы и средства математического моделирования логики функционирования бортовых систем и физических процессов, протекающих в них, а также испытания моделей в составе тренажера. Достаточно унифицированы модели движения и модель внутренней среды пилотируемых космических аппаратов. Вместе с тем основным проблемным моментом при создании тренажеров остается моделирование бортовых цифровых вычислительных комплексов.

3. На основе проведенного анализа задач, решаемых БЦВК, а также существующих способов моделирования процесса его функционирования на тренажерах, предложено использовать функциональное моделирование, которое позволяет наиболее полно реализовать обучающие свойства тренажера.

4. Установлено, что применение существующих систем имитационного моделирования для моделирования бортовых вычислительных средств на тренажерах ПКА неэффективно из-за низкой наглядности построенной модели, трудности контроля и управления моделью, а также больших затрат на программирование, отладку и модификацию модели, поэтому целесообразна разработка нового аппарата формализованного описания и создания на его основе средств моделирования БЦВК для тренажеров пилотируемых космических аппаратов.

5. Показано, что наиболее подходящим исходным формализмом для разработки аппарата формализованного описания и средств имитационного моделирования БЦВК на тренажерах, являются модифицированные сети Петри, ориентированные на моделирование операционных систем и вычислительных процессов.

6. Разработан новый формализм – И-сети, которые объединяют преимущества наглядности и удобства отображения модели, присущие сетям Петри, с гибкостью и универсальностью систем моделирования, основанных на языках программирования, и одновременно сводят к минимуму концептуальную дистанцию между моделью и реальной системой.

7. Определен набор операций на множестве И-сетей и соответствующие им преобразования структуры данных И-сети, обеспечивающие оперативное изменение И-сетевых моделей, автоматическое построение новых моделей из существующих.

8. Разработан метод создания функциональных моделей БЦВК на основе И-сетей, позволяющий единым образом адекватно описывать и имитировать процесс функционирования аппаратных и программных частей вычислительных систем совместно с выполнением рабочих программ полета.

9. Разработано алгоритмическое и программное обеспечение системы имитационного моделирования сложных систем на основе И-сетей, которое позволяет:

- осуществлять быстрое и надежное конструирование модели;

- поддерживать интерфейс пользователя на всех этапах проектирования, отладки и реализации модели;

- обеспечить расширенные возможности средств отладки и контроля, а также графическое отображение процесса функционирования модели;

- осуществлять предварительный анализ модели без ее реализации;

- подключать в процессе имитации программы сбора и анализа статистических данных.

10. Предложена технология создания сетевых моделей БЦВК, в рамках которой разработка модели может вестись аналогично разработке штатного изделия параллельно разными группами разработчиков в двух направлениях – создание модели организации вычислительного процесса и создание программ алгоритмов управления.

Разработанные метод и средства имитационного моделирования позволяют создавать модели БЦВК полностью отвечающие основным принципам моделирования бортовых систем на тренажерах ПКА. Они обеспечивают адекватное функционирование модели в реальном и другом масштабе времени, необходимую для задачи подготовки глубину моделирования, отработку всех нештатных ситуаций, в том числе связанных с отказами аппаратных частей БЦВК, минимум временных затрат на установку начальных условий тренировки, управление моделью и отображение процесса функционирования модели на пульте контроля и управления тренировкой, малые затраты на доработку модели при смене версии штатного программного обеспечения и модификации реальной системы.

Совокупность полученных в работе теоретических и практических результатов позволяет сделать вывод, что в процессе ее выполнения произведено теоретическое обобщение и решение научной проблемы, имеющей важное значение для пилотируемой космонавтики: разработана методология создания функциональных моделей БЦВК для тренажеров пилотируемых космических аппаратов, использование которой сокращает сроки создания программных моделей БЦВК и повышает эффективность подготовки космонавтов.

ПУБЛИКАЦИИ АВТОРА ПО ТЕМЕ ДИССЕРТАЦИИ

Монография

1. Полунина Е.В., Саев В.Н. Моделирование бортовых цифровых вычислительных комплексов в тренажерах пилотируемых космических аппаратов. Звездный городок, Московская область. РГНИИ ЦПК им. Ю.А. Гагарина, 2004. 98 с. (лично автором – 68 с.).

Статьи в журналах из перечня ВАК

2. Полунина Е.В. Моделирование бортовых цифровых вычислительных комплексов в тренажерах пилотируемых космических аппаратов на основе модифицированных сетей Петри // Авиакосмическое приборостроение, 2003. № 9. С. 31-37 (лично автором – 7 с.).
3. Полунина Е.В. Операции на множестве И-сетей, используемых для моделирования БЦВК в тренажерах пилотируемых космических аппаратов // Авиакосмическое приборостроение, 2005. № 4. С. 50-56 (лично автором – 7 с.).
4. Полунина Е.В. Комплексный тренажер Российского сегмента Международной космической станции // Авиакосмическое приборостроение, 2006. № 5. С. 40-45 (лично автором – 6 с.).
5. Наумов Б.А., Полунина Е.В., Саев В.Н., Синельников В.Г. Особенности разработки моделей бортовых систем для тренажеров Российского сегмента международной космической станции // Полет, 2008. № 6. С. 24-29 (лично автором – 4 с.).
6. Наумов Б.А., Полунина Е.В., Саев В.Н., Синельников В.Г. Автоматизация разработки дискретных моделей бортовых систем для тренажеров ПКА // Полет, 2009. № 5. С. 18-21 (лично автором – 2 с.).
7. Полунина Е.В. Метод И-сетей для моделирования БВК с целью подготовки космонавтов // Научно-технический сборник «Известия», №245, часть 1. Актуальные проблемы и перспективы высшего военного образования. М., Военная академия Петра Великого, 2010. С. 472-478 (лично автором - 7 с.).
8. Полунина Е.В., Саев В.Н. Система имитационного моделирования на основе И-сетей // Научно-технический сборник «Известия», № 245, часть 1. Актуальные проблемы и перспективы высшего военного образования. М., Военная академия Петра Великого, 2010. С. 478-493 (лично автором - 4 с.).
9. Полунина Е.В., Саев В.Н. Использование модифицированных сетей Петри для моделирования бортовых вычислительных комплексов в космических тренажерах. // Вестник Воронежского института МВД России, 2011. №1. С. 167-175 (лично автором - 6 с.).
10. Полунина Е.В., Саев В.Н. Средства имитационного моделирования сложных систем на основе И-сетей. // Приборы и системы. Управление, контроль, диагностика, 2011. № 6. С. 22-27 (лично автором - 4 с.).
11. Полунина Е.В. Оптимизация испытаний моделей бортовых систем в составе тренажера Российского сегмента МКС // Полет, 2011. № 9. С. 32-36 (лично автором - 5 с.).

Работы, опубликованные в других журналах и сборниках

12. Лобусов Е.С., Шахназаров В.П., Полунина Е.В. Сетевой подход к моделированию БЦВМ // IV Научный семинар «Методы синтеза и планирования развития структур сложных систем». Тезисы докладов. Ташкент, 1987. С. 84.
13. Лобусов Е.С., Полунина Е.В. Разработка средств имитационного моделирования БЦВМ на основе сетей Петри // Межотраслевая конференция «Тренажеры и имитаторы». Тезисы докладов. Москва, 1988. С. 77-78.
14. Лобусов Е.С., Полунина Е.В. Имитационное моделирование БЦВМ // Гагаринские научные чтения по космонавтике и авиации. Тезисы докладов. Москва, 1988. С. 185.
15. Муха П.А., Полунина Е.В. Метод моделирования процессов функционирования пневмогидросистемы объедененной двигательной установки орбитальной станции // Труды XXVIII чтений, посвященных разработке научного наследия и развитию идей К.Э. Циолковского (Калуга, 1993 г.). М., ИИЕТ РАН, 1994. С. 120-121 (лично автором – 1 с.).
16. Полунина Е.В. Применение модифицированных сетей Петри для моделирования дискретных систем управления в тренажных средствах // Труды XXVIII чтений, посвященных разработке научного наследия и развитию идей К.Э. Циолковского (Калуга, 1993 г.). М., ИИЕТ РАН, 1994. С. 121-123 (лично автором – 3 с.).
17. Полунина Е.В, Саев В.Н. Оценка точности метода электроаналогии для моделирования пневмогидросистемы объединенной двигательной установки в тренажерах ПКА. // II-я Международная научно-практическая конференция «Пилотируемые полеты в космос», Звездный городок, РГНИИ ЦПК им. Ю.А. Гагарина, 1995. С. 167-168 (лично автором – 1 с.).
18. Астахов А.В., Полунина Е.В. К вопросу о восстановлении процесса тренировки на тренажерах ПКА со штатными бортовыми вычислительными средствами // Материалы научно-технического семинара «Технические средства и технологии для построения тренажеров», Выпуск 2, Звездный городок, РГНИИ ЦПК им. Ю.А. Гагарина, 1996. С. 46-47 (лично автором – 1 с.).
19. Астахов А.В., Лункин К.С., Полунина Е.В., Саев В.Н. Применение новых средств восстановления и воспроизведения процесса тренировки на тренажерах ПКА // Материалы научно-технического семинара «Технические средства и технологии для построения тренажеров», Выпуск 2, Звездный городок, РГНИИ ЦПК им. Ю.А. Гагарина, 1996. С. 76-77 (лично автором – 1 с.).
20. Полунина Е.В., Саев В.Н. Управление точностью метода электроаналогии для моделирования пневмогидросистемы объединенной двигательной установки в тренажерах ПКА // ХХХII Научные чтения, посвященные разработке творческого наследия К. Э. Циолковского (Калуга, 16-19 сентября 1997 г.). Тезисы докладов. М., ИИЕТ РАН, 1997. С. 167-169 (лично автором – 2с.).
21. Наумов Б.А., Полунина Е.В. Проблемы использования штатных бортовых вычислительных средств на тренажерах ПКА // Материалы общественно-научных чтений, посвященных памяти Ю. А. Гагарина (1996-1997 гг.), Гагарин 1998. С. 234-237 (лично автором – 3 с.).
22. Полунина Е.В., Наумов Б.А. К вопросу автоматизации разработки специального программного обеспечения тренажеров пилотируемых космических аппаратов // ХХХIII научные чтения, посвященные разработке творческого наследия К. Э. Циолковского (Калуга 1998 г.). Тезисы докладов. М., ИИЕТ РАН, 1998. С. 182.
23. Полунина Е.В. К вопросу совершенствования существующих и создания перспективных тренажеров исследовательских модулей орбитальных станций // Материалы XXV общественно-научных чтений, посвященных памяти Ю. А. Гагарина, Гагарин, 1998. С. 209-213. (лично автором – 5 с.).
24. Наумов Б.А., Синельников В.Г., Шевченко Л.Е., Полунина Е.В. Основы разработки системы отображения информации пультов контроля и управления космических тренажеров. // Четвертая международная научно-практическая конференция «Пилотируемые полеты в космос», Звездный городок, РГНИИ ЦПК им. Ю.А. Гагарина, 2000. С. 214-215. (лично автором – 1 с.).
25. Наумов Б. А., Шевченко Л.Е., Полунина Е.В. Перспективы использования современных информационных технологий в системах отображения информации пультов контроля и управления космических тренажеров // Материалы XXVIII общественно-научных чтений, посвященных памяти Ю. А. Гагарина, Гагарин, 2001. Часть II. С. 81-87 (лично автором – 2 с.).
26. Полунина Е.В., Наумов Б. А., Синельников В. Г. Подготовка экипажей на комплексе тренажеров Российского сегмента Международной космической станции // Материалы XXVIII общественно-научных чтений, посвященных памяти Ю. А. Гагарина, Гагарин, 2001. Часть II. С. 67-76 (лично автором – 6 с.).
27. Полунина Е.В., Саев В.Н., Синельников В.Г. Анализ методов моделирования бортовых вычислительных средств на тренажерах ПКА // Труды XXXVII чтений, посвященных разработке научного наследия и развитию идей К. Э. Циолковского (Калуга 2002 г.). М., ИИЕТ РАН, 2002. С. 188-189 (лично автором – 1 с.).
28. Полунина Е.В., Саев В.Н., Синельников В.Г. Особенности разработки моделей бортовых систем для тренажеров российского сегмента международной космической станции // Материалы научно-технического семинара «Технические средства и технологии для построения тренажеров», Выпуск 4, Звездный городок, РГНИИ ЦПК им. Ю. А. Гагарина, 2002. С. 104-115 (лично автором – 6 с.).
29. Греченков А.В., Полунина Е.В., Саев В.Н., Синельников В. Г. Метод расчета давлений в гермоотсеках орбитальной станции с использованием конфигурационного графа // Материалы XXIX общественно-научных чтений, посвященных памяти Ю. А. Гагарина, Гагарин, 2002. С. 149-157 (лично автором – 3 с.).
30. Полунина Е.В., Саев В.Н., Синельников В.Г. Исследование и обоснование тактико-технических требований к моделям бортовых ПКА для тренажеров // Материалы XXX общественно-научных чтений, посвященных памяти Ю. А. Гагарина, Гагарин, 2003. С. 34-43 (лично автором – 6 с.).
31. Полунина Е.В., Саев В.Н. Этапы создания и перспективы развития комплексного тренажера Российского сегмента Международной космической станции // Материалы XXXIV общественно-научных чтений, посвященных памяти Ю.А. Гагарина, Гагарин, 2007. C. 67-76 (лично автором – 5 с.).
32. Полунина Е.В. К вопросу оптимизации процесса испытаний моделей бортовых систем комплексного тренажера РС МКС // VIII международная научно-практическая конференция «Пилотируемые полеты в космос», Звездный городок, РГНИИ ЦПК им. Ю. А. Гагарина, 2009. С. 195-197 (лично автором – 3 с.).