Математическая модель и численное исследование твердотельного ф а зового перехода в наноразмерном образце
На правах рукописи
УДК 539.3
ФРЕЙМАН Евгений Игоревич
Математическая модель
и численное исследование
твердотельного фазового перехода
в наноразмерном образце
Специальность 05.13.18 – математическое моделирование, численные методы и комплексы программ
АВТОРЕФЕРАТ
диссертации на соискание ученой степени
кандидата физико-математических наук
ТВЕРЬ 2011
Работа выполнена на кафедре математического анализа в ФГБОУ ВПО
«Тульский государственный университет».
Научный руководитель доктор физико-математических наук, профессор
Левин Владимир Анатольевич
Официальные оппоненты: доктор физико-математических наук,
старший научный сотрудник
Фрейдин Александр Борисович
доктор физико-математических наук, доцент
Цирулёв Александр Николаевич
Ведущая организация - Учреждение Российской академии наук «Институт химической физики им. Н.Н.Семенова РАН»
Защита состоится «23» декабря 2011 года в 12:00 часов на заседании диссертационного совета Д212.263.04 при Тверском государственном университете по адресу: 170002, г. Тверь, Садовый пер., 35, ауд. 200.
С диссертацией можно ознакомиться в научной библиотеке Тверского государственного университета по адресу: 170100, г. Тверь, ул. Володарского, 44а.
Объявление о защите диссертации опубликовано «22» ноября 2011 года на сайте ВАК и на официальном сайте Тверского государственного университета по адресу: http://university.tversu.ru/aspirants/abstaract/
Автореферат разослан «22» ноября 2011 года.
Ученый секретарь диссертационного совета, доктор физико-математических наук,
доцент С.М. Дудаков
Общая характеристика работы
Актуальность темы. Проблема описания фазовых превращений в деформируемых телах является одной из важнейших задач механики деформируемого твердого тела, а также материаловедения. Её актуальность определяется тем, что большинство материалов, используемых в современной технике, испытывают фазовые превращения либо в процессе их изготовления, либо в процессе эксплуатации, либо контактируют со средой, в которой происходят фазовые переходы. В частности, фазовые превращения ответственны за эффект памяти формы, наблюдаемый в некоторых сплавах (сплавах с памятью формы[1] ), широко используемых в современной технике. Одной из неразработанных инфраструктурных проблем наноиндустрии при проектировании, мониторинге и эксплуатации изделий является необходимость точного и быстрого проведения численного анализа поведения изделия. Часть этой проблемы - учет изменения свойств элементов наноизделия при эксплуатации в результате твердотельных фазовых переходов (в том числе и проблема "выпучивания" нано- и микропленок[2] ). Для принятия решения при мониторинге работы такого изделия требуются адекватная модель и достаточно быстрый расчет в рамках этой модели, что актуально как в России, так и за рубежом.
Одним из примеров наноструктурированного материала, в котором происходит фазовый переход, является сплав Ni65Al35[3]. Данный сплав используется изготовления конструкций с памятью формы. Под воздействием механических напряжений в сплаве Ni65Al35 происходит фазовый переход и возникают мартенситные наноструктуры, вследствие чего материал можно считать наноструктурированным. Изучая представительный объем данного сплава далее можно делать выводы об эффективных характеристиках макротел с памятью формы.
Сплавы с памятью формы используют для создания интеллектуальных материалов (материалы со специфическими функциональными характеристиками на молекулярном уровне).
Имеющиеся САЕ-системы, принятые в мировой расчетной практике (например, ведущие ANSYS, Dassault Systўmes (ABAQUS), COMSOL), не позволяют моделировать (рассчитывать) механические параметры нагруженного образца при перераспределении конечных деформаций (образования дефектов) и тем более с учетом изменения свойств материала в процессе нагружения.
Целями диссертационной работы являются:
модификация модели фазового перехода для случая конечных деформаций, учитывающая наличие собственных деформаций фаз, градиентные эффекты, поверхностное натяжение и зависимость свойств материала от фазового состояния;
разработка алгоритма решения и программного модуля, его реализующего;
проведение численных экспериментов и анализ результатов.
Методы исследования. Фазовый переход описывается на основе континуальной модели, основанной на теории Ландау - Гинзбурга и обобщенной на случай фазового превращения, вызванного механическими напряжениями с учетом конечности деформаций. Для численного решения задач в работе использовался метод конечных элементов. Программный модуль, реализующий алгоритм решения, был разработан на языке C++ c использованием математических пакетов, таких, как Boost, VTK, MKL и др.
Положения выносимые на защиту:
Усовершенствована математическая модель твердотельного фазового перехода для случая конечных деформаций, учитывающая наличие собственных деформаций фаз, градиентные эффекты, поверхностное натяжение и зависимость свойств материала от фазового состояния.
Разработан алгоритм решения связанной задачи о напряженно-деформированном и фазовом состоянии наноразмерных тел в процессе твердотельного фазового перехода, вызванного действием механических напряжений, и его программная реализация.
Проведены численные эксперименты, анализ результатов которых показал:
возможность получения установившихся наноструктур из сплава Ni65Al35, качественно согласующихся с эксперементальными данными;
существенное различие между линейным и нелинейным решением для определенных задач;
возможность образования устойчивых наноструктур, возникающих при учете поверхностного натяжения на границах наноразмерных полостей.
Научная новизна. В диссертационной работе впервые модифицирована модель фазового перехода для случая конечных деформаций, учитывающая наличие собственных деформаций фаз, градиентные эффекты, поверхностное натяжение и зависимость свойств материала от фазового состояния. Разработаны алгоритм решения и программный модуль, его реализующий. Предложен подход к моделированию поверхностного натяжения на границах нанополостей.
Достоверность и обоснованность научных результатов базируются на корректной математической постановке задачи, использовании апробированных соотношений теории многократного наложения больших деформаций и апробированных при малых деформациях моделей фазовых переходов, корректно обобщенных на случай конечных деформаций и их наложения, применении общепризнанных численных методов (таких, как метод конечных элементов). Полученные в работе результаты согласуются с решением задачи для случая однородного напряженно-деформированного и фазового состояния, которое получено в среде Maple путем численного решения системы обыкновенных дифференциальных уравнений. Результаты численных расчетов по моделированию образования стационарных наноструктур при нагружении качественно согласуются с экспериментальными данными для сплава Ni65Al35.
Практическая значимость
Автором разработан программный комплекс для расчета наноразмерных тел, в том числе и нанопленок (испытывающих конечные деформации), в которых происходят изменения свойств материалов (фазовые переходы) под действием напряжений различной природы. Данный программный комплекс является инфраструктурным продуктом для нанотехнологической отрасли.
Разработанная модель и алгоритм решения могут быть использованы как для разработки технологий получения наноструктурированных материалов с желаемыми свойствами (интеллектуальных материалов), так и для мониторинга уже существующих конструкций, сделанных из данных материалов.
Также с помощью данного программного комплекса возможно численное моделирование эффекта выпучивания нанопленок (потеря устойчивости нанопленки при фазовом переходе).
Апробация работы. Основные положения диссертационной работы докладывались и обсуждались на следующих научно-технических конференциях: «Ломоносовские чтения» в 2006, 2007, 2010 гг. (г. Москва); «Инженерные системы – 2009» (г. Москва); «Современные проблемы математики, механики, информатики» в 2005, 2007 и 2010 гг. (г. Тула), а также на IV Европейской конференции по вычислительной механике «ECCM 2010» (г. Париж) и на XVI, XVIII и XXI симпозиумах «Проблемы шин и резинокордных композитов» в 2005, 2007 и 2010 гг. (г. Москва). Результаты работы использованы при выполнении инициативных научных проектов РФФИ № 06-01-00682-а, 11-08-01284-а.
На программный модуль получено свидетельство о государственной регистрации программы для ЭВМ за № 2010611589. Для дальнейшей разработки программного комплекса создано малое предприятие «ООО «НАНОСОФТ», получившее поддержку Фонда содействия развитию малых форм предприятий в научно-технической сфере.
Публикации. Основные результаты диссертации представлены в 18 работах, 4 из которых - в изданиях, рекомендованных ВАК Минобразования РФ.
Структура и объём работы. Диссертация состоит из введения, трех глав, заключения, приложения и списка использованных источников из 117 наименований. Работа изложена на 118 страницах машинописного текста, содержит 18 рисунков.
Содержание работы
Во введении обоснована актуальность темы диссертационной работы, сформулированы цели и задачи данной работы, приведено краткое содержание диссертации.
В первой главе кратко изложены основные соотношения теории многократного наложения больших деформаций в упругих телах. Приводятся основные термины и обозначения, используемые в работе. Детально рассмотрена математическая модель твердотельного фазового перехода:
- аффинор деформаций при переходе из (n-1)-го в n-е состояние;
– аффинор собственной деформации (считается заданным для каждой фазы);
– аффинор упругой деформации;
– относительное изменение объема при переходе из m-го в n-e состояние;
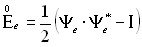– тензор упругой деформации;
– тензор обобщенных напряжений для n-ого состояния, записанный в координатах (n-1)-го состояния.
Свободная энергия записывается в виде
,
упругий потенциал – в форме потенциала Мурнагана:
,
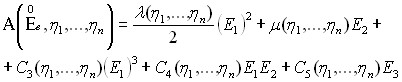где 
– инварианты тензора 
.
Определяющее соотношение, соответствующее потенциалу Мурнагана,
Постановка задачи осуществляется на основе теории многократного наложения больших деформаций и теории фазовых переходов Ландау - Гинзбурга. Механическая постановка задачи следующая. Рассмотрим произвольное упругое тело (рис. 1). Материал тела может находиться в нескольких фазовых состояниях (например, для сплава Ni65Al35 это аустенит и три мартенситных фазы). Механические свойства материала в разных фазовых состояниях различны. В процессе изотермического деформирования в теле происходит фазовый переход.
Далее приводится математическая постановка краевой задачи в координатах первого (промежуточного) состояния. Данная постановка приводится впервые, и в отличие от модели, предложенной В.И.Левитасом[4], учитывает конечность не только собственных, но и упругих деформаций фазового перехода:
уравнение движения с учетом наложения больших деформаций, записанное в координатах 
состояния
;
эволюционное уравнение для 
параметров порядка с учетом градиентных эффектов
;
;
.
Здесь P - тензор напряжений Пиолы; 
– движущие силы фазового перехода.
Граничные условия: заданные напряжения на внешней границе 
, заданные нормальные напряжения на контуре отверстий 
; в случае необходимости учета поверхностного натяжения граничные условия могут быть записаны как 
, где 
; 
– локальная кривизна деформированной поверхности, 
– коэффициент пропорциональности; нулевые производные параметров порядка по направлению нормали к контуру, как на внешней границе, так и на контурах отверстий 
.
Начальные условия: в момент 
начала фазового перехода 
в некоторой заданной области; 
– некоторое заданное значение 
; в остальной части тела в момент начала фазового перехода 
.
Рис. 1. Нелинейно – упругое тело
Во второй главе диссертации мы описываем разработанный нами алгоритм решения поставленной задачи о твердотельном фазовом переходе под действием механических напряжений с учетом конечности деформаций.
Для приближения уравнений на конечноэлементной сетке использовался метод Б.Г.Галеркина. Рассмотрим применение этого метода к нелинейному уравнению равновесия
, где 
– функции формы, которое преобразуем с помощью формулы Грина:
.
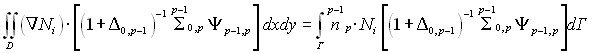В правую часть подставим граничные условия:
,
где 
– давление на границе.
При реализации МКЭ возможно использование различных типов конечных элементов. Были выбраны треугольные симплекс-элементы (рис. 2), так как для данной задачи достаточно линейного приближения перемещений, и эти элементы являются наиболее простыми с точки зрения программной реализации. 
Рис. 2. Элементы, использующиеся при расчете (слева – для уравнения равновесия, справа – для эволюционного уравнения)
Интеграл по всей области записывается, как сумма интегралов по элементам разбиения:
Нелинейная система, получающаяся при решении уравнения равновесия, решалась методом Ньютона. В качестве критерия отбора решений был выбран критерий физической достоверности: отбирались решения без самопересечения границ элементов.
Эволюционное уравнение содержит производную по времени, которая заменяется конечной разностью, этим задача разбивается на шаги по времени. Для того чтобы одновременно удовлетворить уравнениям и равновесия и эволюции на шаге по времени, использовался итерационный процесс:
1. Сохранение распределения параметров порядка.
2. Решение уравнений равновесия 
(при заданном распределении параметров порядка). Вычисление «предварительных» напряжений и деформаций.
3. Вычисление 
, k=1,...,n.
4. Решение эволюционных уравнений
, k=1,...,n. Предварительное вычисление параметров порядка 
, k=1,...,n.
5. Пересчет уравнений равновесия (при найденном предварительном распределении параметров порядка). Вычисление текущих напряжений и деформаций.
6. Вычисление 
, k=1,...,n.
7. Восстановление параметров порядка (сохраненных в п. 1).
8. Окончательное решение эволюционных уравнений
, k=1,…,n. Окончательное вычисление параметров порядка 
, k=1,...,n.
В третьей главе мы исследуем результат численного решения задачи, постановка которой приведена в первой главе, с помощью программного комплекса, реализующего алгоритм, рассмотренный во второй главе. Приводятся полученные с помощью МКЭ численные решения. Они представлены полями распределения напряжений и параметров порядка. Расчеты выполнены для сплава 
[5] для случая плоской деформации. Для тестирования программного модуля были проведены тестовые расчеты для случая однородного напряженно-деформированного и фазового состояния в среде Maple путем численного решения системы обыкновенных дифференциальных уравнений средствами пакета и сопоставлены с решением аналогичной задачи разработанным программным модулем.
В качестве экспериментального подтверждения корректности работы программы приводятся фотографии (рис. 3) мартенситных наноструктур, полученные с помощью туннельного электронного микроскопа[6]. На рис. 3 показаны полосы, соответствующие различным фазам мартенсита, которые являются чередующимися областями различной атомной структуры.
Похожие полосы из разных фаз мартенсита являются наиболее типичной структурой, которая получается при численных экспериментах с однородным образцом и случайным начальным распределением зародышей новых фаз.
Рис. 3. Мартенситные наноструктуры, возникающие в сплаве Ni65Al35
под воздействием механических напряжений
С помощью программного комплекса мы исследовали следующие задачи:
Задача 1 – образование стационарных наноструктур при однородном растяжении. Требуется показать возможность образования наноструктур в однородном теле со случайным начальным распределением параметров порядка, сравнить линейное и нелинейное решения, провести аналогию с наноструктурами, наблюдаемыми с помощью туннельного микроскопа.
Был взят образец размером L = 27 нм и приложена нагрузка py =-px = 0,7 ГПа. Начальные условия: случайное распределение параметров порядка в диапазоне от 0 до 0,1. Задача решалась в квазистатической постановке. Через некоторое время после запуска процесса фазового перехода было достигнуто стационарное напряженно-деформированное и фазовое состояние образца. Распределение параметров порядка в стационарном состоянии показано на рис. 4.
Рис. 4. Установившееся распределение параметров порядка: а – линейное решение, б – нелинейное решение; зависимость решения от времени в черной точке в центре образца для линейного (L) и нелинейного (NL) решений: в – для параметра порядка, г – для компонент напряжения
Похожие полосы описаны в статье Ph. Boullay, D. Schryvers, J.M. Ball Nano-structures at martensite macrotwin interfaces in Ni65Al35. Они же являются наиболее типичной структурой, которая возникает при расчетах в случае отсутствия отверстий.
Из результатов видно существенное отличие линейного и нелинейного решений. Из графика рис. 4, г видно, что напряжения 
различаются в 5 раз, на графике рис. 4, в показано существенное отличие распределения параметров порядка.
Задача 2 – образование стационарных наноструктур при всестороннем растяжении в теле с круговыми концентраторами напряжений. Требуется показать наноструктуры, возникающие при всестороннем нагружении тела, содержащего зародыши новых фаз в виде круговых включений, сравнить линейное и нелинейное решения.
Был взят образец размером L = 40,22 нм и приложена нагрузка – всестороннее растяжение (px = py = 1,5 ГПа). Начальные условия: в центральной окружности 1 = 0,1, 2 = 0, в двух других окружностях 1 = 0, 2 = 0,1. Диаметр включений 6,7 нм. Задача решалась в квазистатической постановке. Через некоторое время после запуска процесса фазового перехода было достигнуто стационарное напряженно-деформированное и фазовое состояние образца. Поля распределения параметров порядка в стационарном состоянии показаны на рис.5.
Рис. 5. Установившееся распределение параметров порядка; а, б – линейное решение; в, г – нелинейное решение
Из приведенных результатов видно существенное различие распределения параметров порядка при линейном и нелинейном решениях, как количественное (в нелинейном расчете ни одна область не перешла в новые фазы полностью), так и качественное (в нелинейном расчете видна «сетка» из разных фаз мартенсита, а в линейном только полосы).
Задача 3 – образование мартенситных наноструктур при изгибе пластины из материала Ni65Al35. Требуется рассмотреть подход к моделированию эффекта выпучивания нанопленок на примере изгиба пластины из материала Ni65Al35, показать значимость учета нелинейных эффектов в этой задачи.
Была взята пластина прямоугольной формы со сторонами 2х20 нм, жестко закрепленная по левой стороне, как показано на рис. 6. В правой её части было расположено включение D = 2 нм (серая окружность). Включение представляло собой “смешанный” зародыш фаз M1 и M2 (1 = 0.1, 2 = 0.1). В остальной части образца в начальный момент времени было 1 = 2 = 0. Нагрузки задавались, как показано на рис. 6: 
ГПа, 
ГПа. Задача решалась в квазистатической постановке. Собственные деформации фаз:
, 
.
Рис. 6. Схема закрепления и нагружения образца
Через некоторое время после запуска процесса фазового перехода было достигнуто стационарное напряженно-деформированное и фазовое состояние образца. Из рис. 7 и рис. 8 видно, что в случае линейного решения весь материал остался в фазе аустенита (оба параметра порядка равны нулю), а в случае нелинейного решения материал разделился на две зоны, состоящие из разных фаз мартенсита, с резким переходом между ними. Максимальные напряжения в установившемся состоянии для линейного и нелинейного решений отличались более чем в 20 раз.
Рис. 7. Нелинейное решение 1 и 2 (установившееся состояние)
Рис. 8. Линейное решение 1 и 2 (установившееся состояние)
Задача 4 – образование мартенситных наноструктур под воздействием сил поверхностного натяжения. Требуется показать, что в случае учета поверхностного натяжения в материале могут происходить фазовые превращения и образовываться стационарные наноструктуры даже без приложения внешних нагрузок.
Рассматривалось кольцо с внешним диаметром D1 = 5 нм, внутренним диаметром D2 = 2 нм. Вокруг отверстия располагалось включение в форме кругового кольца с внешним диаметром d = 2,4 нм. Включение представляло собой «смешанный» зародыш фаз M1 и M2 (1 = 0,1, 2 = 0,1). В остальной части образца в начальный момент времени 1 = 2 = 0. В качестве нагрузки было задано поверхностное натяжение на внешней и внутренней границах. Коэффициент поверхностного натяжения 
, собственные деформации фаз задавались как в предыдущей задаче.
Рис. 9. Установившееся распределение параметра порядка 1
Задача решалась в нелинейной постановке, через некоторое время после запуска процесса фазового перехода было достигнуто стационарное напряженно-деформированное и фазовое состояние образца. Установившееся распределение параметра порядка 1 показано на рис. 9, распределение 2 получается поворотом рис. 9 на 90° относительно центра образца.
Из приведенного поля распределения параметров порядка видно, что под действием поверхностного натяжения в теле образовались мартенситные наноструктуры.
В заключении приведены основные результаты и выводы диссертационной работы:
Модифицирована модель твердотельного фазового перехода для случая конечных деформаций, учитывающая наличие собственных деформаций фаз, градиентные эффекты, поверхностное натяжение и зависимость свойств материала от фазового состояния;
Разработан алгоритм решения связанной задачи о напряженно-деформированном и фазовом состоянии наноразмерных тел в процессе твердотельного фазового перехода, вызванного действием механических напряжений, и его программная реализация.
Проведены численные эксперименты, анализ результатов которых показал:
возможность получения установившихся наноструктур из сплава Ni65Al35, качественно согласующихся с экспериментальными данными.
для задачи о нагружении образца с 3 нановключениями и задачи об изгибе пластины получено качественное различие между линейным и нелинейным решениями, в задаче об изгибе пластины максимальные напряжения в установившемся состоянии отличаются более чем в 20 раз;
возможность образования устойчивых наноструктур, возникающих при учете поверхностного натяжения на границах наноразмерных полостей.
Разработанная модель и программный комплекс могут быть использованы для разработки технологий получения наноструктурированных материалов с желаемыми свойствами (интеллектуальных материалов) и мониторинга уже существующих конструкций, сделанных из данных материалов.
Публикации по теме диссертации
1. Displacive Phase Transitions at Large Strains: Phase-Field Theory and Simulations/ V.I. Levitas, V.A. Levin, K.M. Zingerman, E.I. Freiman // Physical Review Letters. 2009. 103. 025702.
2. Твердотельные фазовые переходы, вызванные действием механических напряжений в материале с наноразмерными неоднородностями: модель и вычислительный эксперимент/ В.А. Левин, В.И. Левитас, В.В. Лохин, К.М. Зингерман, Л.Ф. Саяхова, Е.И. Фрейман // Доклады академии наук, 2010, Т. 434. № 4. С. 481–485.
3. Левин В.А., Зингерман К.М., Фрейман Е.И. Вариант модели фазового перехода в теле с конечными деформациями. Численный эксперимент // Вестник Тверского государственного университета. Сер. Прикладная математика. Вып. 2(13). 2009. С. 23-30.
4. Фрейман Е.И. Вариант численного решения задачи теории многократного наложения больших деформаций для случая твердотельных фазовых переходов // Вестник Тверского государственного университета. Сер. Прикладная математика. Вып. 1(20). 2011. С. 65-77.
5. Использование пакета ABAQUS для описания развития зоны предразрушения вблизи носика повреждения в теле из упругого или вязкоупругого материала/ В.А. Левин, К.А. Ильин, Н.А. Агапов, Е.Д. Комолова, А.В. Кукушкин, Е.И. Фрейман // Проблемы шин и резинокордных композитов. материалы шестнадцатого симпозиума. М., 2005. Т. 2. С. 28 – 30.
6. К оценке микронапряжений при моделировании свойств наноматериалов в рамках механики деформируемого твердого тела при конечных деформациях/ В.А. Левин, А.В. Вершинин, Е.И. Фрейман, Е.Д. Комолова // Современные проблемы математики, механики, информатики. материалы 6-й международной конференции. Тула. 2005. C. 98 – 101.
7. Результаты решения плоских задачи задач теории многократного наложения больших деформаций с помощью программного комплекса «Наложение»/ А.В. Вершинин, В.А. Левин, Е.Д. Комолова, Е.И. Фрейман // Ломоносовские чтения. тезисы докладов научной конференции. М., 2006. С. 43 – 44.
8. Левин В.А., Фрейман Е.И. Модельная задача о развитии и торможении полости в нагруженном теле. Конечные деформации // Ломоносовские чтения. тезисы докладов научной конференции. М., 2007. С. 107.
9. Левин В.А., Фрейман Е.И. Модель вязкого роста трещины не нулевого раскрытия. Конечные деформации // Проблемы шин и резинокордовых композитов. материалы XVIII симпозиума. М., 2007. Т. 2. С. 52 – 59.
10. Левин В.А., Фрейман Е.И. К модели принудительной остановки трещины не нулевого раскрытия. Конечные деформации // Современные проблемы математики, механики, информатики. материалы 8-й международной конференции. Тула. 2007. C. 161 – 162.
11. Фрейман Е.И. Модель и её программная реализация плоской задачи о принудительной остановки трещины // III магистерская научно-техническая конференция. тезисы докладов. Тула. 2008. 136 – 138.
12. Об одном подходе к моделированию твердотельных фазовых переходов, происходящих под действием механических напряжений в наноразмерных образцах/ В.А. Левин, В.И. Левитас, К.М. Зингерман, Е.И. Фрейман, Л.Ф. Саяхова // Современные проблемы математики, механики, информатики. материалы международной конференции, посвященной 85-летию Л.А. Толоконникова. Тула, 2008. C. 245 – 249.
13. О разработке совместимого программного модуля для учета фазовых переходов под действием механических напряжений для наноразмерных образцов/ В.А. Левин, В.И. Левитас, К.М. Зингерман, Е.И. Фрейман, Л.Ф. Саяхова // Инженерные системы - 2009. материалы международной научно-практической конференции. М., 2009. Т. 1. C. 120 – 124.
14. О разработке совместимого специализированного программного комплекса "НАЛОЖЕНИЕ", предназначенного для учета изменения нагрузок, дефектов и свойств материала в процессе нагружения при больших деформациях/ В.А. Левин, А.В. Вершинин, Е.И. Фрейман, Г.Е. Пекарь // Инженерные системы - 2009. материалы международной научно-практической конференции. М., 2009. Т 1. C. 125 – 132.
15. К решению связанных задач механики деформируемого твердого тела с помощью CAE "FIDESYS" на примере задач о твердотельных фазовых переходах/ В.А. Левин, К.М. Зингерман, Е.И. Фрейман, К.А. Петровский // Проблемы шин и резинокордных композитов. материалы XXI симпозиума, М., 2010. Т. 2. С. 30 – 33.
16. Левин В.А., Фрейман Е.И., Петровский К.А. Модель, алгоритм и численная реализация твердотельных фазовых переходов в материале с наноразмерными неоднородностями // Современные проблемы математики, механики, информатики. материалы международной конференции, посвященной 80-летию Тульского государственного университета, Тула, 2010. С. 172 – 175.
17. Levin V.A., Zingerman K.M., Vershinin A.V., Freiman E.I., Kukushkin A.V., Trachenko A.V. Development and use of the CAE-system "FIDESYS" for nonlinear analysis of solids with microstructure that changed during loading [Электронный ресурс] // European Conference on Computational Mechanics, Paris: [сайт].[2010]. URL: http://www.eccm2010.org/ (дата обращения: 9.11.2011).
18. Левин В.А., Фрейман Е.И. К разработке программного модуля для решения нестационарных задач о перераспределении конечных деформаций // Ломоносовские чтения. тезисы докладов научной конференции. М., 2010. С. 126.
Технический редактор: А.В.Жильцов
Подписано в печать 17.11.2011. Формат 60x84 1 /16.
Усл. печ. л. 1,25. Тираж 100 экз. Заказ № 467.
Тверской государственный университет
Редакционно-издательское управление
Адрес: 170100, г. Тверь, ул. Желябова, 33.
Тел. РИУ: (4822) 35-60-63
[1] Уорден К. Новые интеллектуальные материалы и конструкции. Свойства и применение М.: Техносфера, 2006. 224 с.
[2] Мовчан А. А., Сильченко Л. Г. Об устойчивости пластины из сплава с памятью формы при прямом термоупругом фазовом превращении// ПММ. 2004. Т. 68. вып. 1. С. 60-72.
[3] Levitas V.I., Preston D.L. Thermomechanical lattice instability and phase field theory of martensitic phase transformations, twinning and dislocations at large strains// Physics Letters. 2005. vol. A343, p. 32-39.
[4] Levitas V.I., Preston D.L. Thermomechanical lattice instability and phase field theory of martensitic phase transformations, twinning and dislocations at large strains// Physics Letters. 2005. Vol. A343, p. 32-39.
[5] Параметры материала взяты из статьи Levitas V.I., Preston D.L. // Phys. Rev. B. 2002. V.66, 134207.
[6] Boullay Ph., Schryvers D., Ball J.M. Nano-structures at martensite macrotwin interfaces in Ni65Al35// Acta Materialia. 51 (2003) 1421–1436.
