Оптимизация проектирования перестраиваемых производственных систем на основе адаптивных методов анализа и синтеза проектных решений

На правах рукописи

БОКОВАЯ Нэлли Викторовна

ОПТИМИЗАЦИЯ ПРОЕКТИРОВАНИЯ

ПЕРЕСТРАИВАЕМЫХ ПРОИЗВОДСТВЕННЫХ СИСТЕМ

НА ОСНОВЕ АДАПТИВНЫХ МЕТОДОВ АНАЛИЗА

И СИНТЕЗА ПРОЕКТНЫХ РЕШЕНИЙ

Специальность: 05.13.12 – Системы автоматизации проектирования

(промышленность)

АВТОРЕФЕРАТ

диссертации на соискание ученой степени

доктора технических наук

Воронеж – 2010

Работа выполнена в ГОУ ВПО «Воронежский государственный технический университет»

Научный консультант доктор технических наук, доцент

Белецкая Светлана Юрьевна

Официальные оппоненты: доктор технических наук, профессор

Макаров Олег Юрьевич;

доктор технических наук, профессор

Сумин Виктор Иванович;

доктор технических наук, профессор

Хаустович Александр Владимирович

Ведущая организация ГОУ ВПО «Воронежский государственный

университет»

Защита состоится 29 октября 2010 г. в 1300 часов в конференц-зале на заседании диссертационного совета Д 212.037.03 ГОУ ВПО «Воронежский государственный технический университет» по адресу: 394026, г. Воронеж, Московский просп., 14.

С диссертацией можно ознакомиться в научно-технической библиотеке ГОУ ВПО «Воронежский государственный технический университет»

Автореферат разослан _20_ сентября 2010 г.

Ученый секретарь

диссертационного совета Родионов О.В.

ОБЩАЯ ХАРАКТЕРИСТИКА РАБОТЫ

Актуальность проблемы. В настоящее время большое внимание уделяется проблемам, связанным с проектированием сложных производственных систем. При этом значительный комплекс проектных задач связан не только с созданием новых производственных объектов, но и с необходимостью структурной и параметрической перестройки действующих систем с целью их реформирования и модернизации. Динамично изменяющиеся внешние условия требуют постоянного технического переоснащения производства, обновления номенклатуры выпускаемой продукции, совершенствования технологии ее изготовления и т.д. Это приводит к необходимости разработки математического и программного обеспечения для комплексного решения задач анализа и синтеза сложных производственных систем с учетом иерархичности и перестраиваемой структуры производства.

Процесс структурного и параметрического синтеза перестраиваемых производственных систем осложняется высокой динамичностью, нестабильностью и стохастичностью производства, что затрудняет использование аналитических моделей для принятия проектных решений. Это приводит к необходимости применения алгоритмических оптимизационных моделей, в которых отсутствуют явные аналитические формулировки критериев оптимальности и ограничений, а имеется лишь возможность определения их значений для каждого из вариантов с применением различных моделирующих процедур. Сложность оценки свойств таких моделей на априорном уровне ограничивает возможности использования стандартных оптимизационных процедур, что в конечном итоге снижает эффективность процесса оптимального проектирования. Кроме того, к особенностям задач оптимального проектирования сложных производственных систем можно отнести разнообразие постановок, высокую размерность, множественность технико-экономических требований к основным характеристикам, значительную трудоемкость этапов моделирования и анализа, наличие разнообразных корреляционных связей между параметрами, учесть которые в рамках стандартного математического обеспечения САПР становится затруднительным.

Решение указанной проблемы может быть достигнуто при использовании адаптивного подхода к проектированию производственных систем. Данный подход предполагает построение комплекса алгоритмов оптимизации, обеспечивающих совмещение процесса более полной формализации задачи с ее решением, и их объединение совместно с процедурами многовариантного моделирования в интеллектуальную адаптивную многометодную среду с возможностью ее динамической настройки на различные классы решаемых задач оптимального проектирования. При этом важным требованием к разрабатываемому математическому обеспечению является возможность эффективного решения задач, описываемых сложными алгоритмическими моделями.

Таким образом, актуальность диссертационной работы определяется необходимостью разработки теоретических основ, математического и программного обеспечения для решения задач поиска оптимальных вариантов сложных производственных систем при их реформировании и модернизации с возможностью учета динамических и стохастических аспектов производства.

Работа выполнена в соответствии с научным направлением ГОУ ВПО «Воронежский государственный технический университет» «САПР и системы автоматизации производства», а также ГБ НИР 07.04 «Оптимизация и моделирование сложных систем», ГБ НИР 10.19. «Интеллектуализация принятия решений в автоматизированных системах».

Цель и задачи исследования. Целью диссертационного исследования является разработка методологических принципов, комплекса методов, моделей и алгоритмов оптимального проектирования перестраиваемых производственных систем и создание на этой основе адаптивной среды поиска рациональных проектных решений в условиях реструктуризации и реформирования промышленного производства.

Для достижения поставленной цели необходимо решить следующие основные задачи:

провести анализ методов и средств оптимального проектирования сложных производственных систем с перестраиваемой структурой, рассмотреть особенности задач данного класса и определить принципы их алгоритмизации на основе адаптивного подхода;

разработать методику проектирования перестраиваемых производственных систем и процедуры согласования проектных решений с учетом иерархической структуры производства;

сформировать математические модели структурного и параметрического синтеза стохастических производственных систем;

построить комплекс адаптивных алгоритмов поиска оптимальных проектных вариантов с возможностью их использования для решения задач, описываемых сложными алгоритмическими моделями;

реализовать технологию имитационного моделирования производственных систем и построить схемы интегрированного взаимодействия оптимизационных и моделирующих процедур в процессе проектирования;

разработать компонентную структуру алгоритмической базы оптимального проектирования производственных систем и интеллектуальные средства компонентно-модульного синтеза адаптивных схем поиска проектных вариантов в соответствии с особенностями решаемых задач;

построить программное обеспечение поддержки принятия решений при проектировании перестраиваемых производственных систем и провести его апробацию в условиях производства.

Методы исследования. При выполнении работы использованы основные положения и методы системного анализа, теории вероятностей и математической статистики, теории графов и комбинаторики, аппарат вычислительной математики, принципы искусственного интеллекта, методы имитационного моделирования, исследования операций и принятия решений.

Научная новизна результатов исследования. В диссертации получены следующие основные результаты, характеризующиеся научной новизной:

методология и структурно-функциональные схемы оптимального проектирования сложных перестраиваемых производственных систем, основанные на интеграции моделирующих процедур и адаптивной среды рационального выбора проектных вариантов и обеспечивающие согласованное принятие решений на различных уровнях иерархии производства;

комплекс математических моделей структурного и параметрического синтеза производственных систем, отличающихся итеративным использованием имитационного моделирования в контуре принятия решений и позволяющих определять проектные варианты перестройки производства с учетом его динамического и стохастического характера;

вероятностные и детерминированные адаптивные методы параметрической оптимизации производственных систем, позволяющие на основе совмещения процесса более полной формализации задачи с ее решением учесть особенности проектируемого объекта при неполноте его априорного математического описания;

алгоритмы структурного синтеза производственных систем, основанные на сочетании рандомизированных процедур псевдобулевой оптимизации и модифицированных вариантов схемы ветвей и границ, что позволяет формировать стратегии направленного перебора проектных решений в задачах, описываемых сложными алгоритмическими моделями;

адаптивные процедуры трансформации оптимизационных моделей в процессе проектирования, обеспечивающие преобразование решаемых задач, сокращение их размерности и приведение к типовым постановкам на основе анализа априорной и текущей информации;

технология моделирования иерархических производственных систем, основанная на совместном использовании CASE-средств и имитационных процедур и позволяющая рассматривать в комплексе структуру, функции и динамику системы, а также производить ее анализ с различной степенью детализации;

методика формирования многометодной поисковой среды оптимального проектирования производственных систем, отличающаяся выделением инвариантных структурных составляющих алгоритмического обеспечения и наличием интеллектуальных средств их комплексирования, что позволяет осуществлять компонентно-модульный синтез адаптивных схем поиска проектных вариантов в соответствии с особенностями решаемых задач;

структура и программное обеспечение системы поддержки принятия проектных решений, позволяющие на основе интеграции средств функционального, имитационного моделирования и оптимального выбора решать трудноформализуемые задачи проектирования стохастических производственных систем.

Практическая значимость и результаты внедрения. В диссертации разработаны основы построения математического и программного обеспечения САПР при проектировании сложных производственных объектов с перестраиваемой структурой на основе интегрированной адаптивной среды многовариантного моделирования и поиска оптимальных проектных решений.

Реализованный при разработке алгоритмического обеспечения компонентно-модульный подход позволил сформировать библиотеку модулей оптимального проектирования производственных систем с возможностью построения на их основе процедур структурного и параметрического синтеза различного предметного назначения. При этом расширение функциональности системы обеспечивается не за счет наращивания алгоритмической базы, а на основе новых способов агрегирования и комплексирования инвариантных структурных компонентов.

Разработанные модели и алгоритмы реализованы в программном комплексе поддержки принятия решений, ориентированном на поиск оптимальных вариантов структуры и параметров производственных систем в условиях модернизации и реструктуризации производства. Программный комплекс позволяет решать задачи моделирования, анализа и структурно-параметрической оптимизации как на уровне производственных участков, так и на уровне производственной системы в целом. Использование разработанного программного обеспечения в рамках САПР позволяет улучшить технико-экономические характеристики производственных систем, уменьшить вычислительные затраты для получения оптимального варианта, сократить сроки формирования оптимальных проектных решений и повысить их качество.

Результаты работы внедрены на следующих промышленных предприятиях: ФГУП «Воронежский механический завод» – филиал ФГУП «ГКНПЦ им. М.В. Хруничева», ЗАО «УГМК – Рудгормаш» (г. Воронеж), ОАО «Рефлектор» (г. Саратов), ОАО «Прибор» ОКБ «Авиаавтоматика» (г. Курск), ОАО «Корпорация НПО РИФ» (г. Воронеж). Результаты исследования используются также в учебном процессе кафедры систем автоматизированного проектирования и информационных систем ГОУ ВПО «Воронежский государственный технический университет» и кафедры информационных систем и технологий АНОО ВПО «Воронежский институт высоких технологий» при обучении студентов специальностей 230104 «Системы автоматизированного проектирования» и 230201 «Информационные системы и технологии».

Апробация работы. Основные положения диссертационной работы докладывались и обсуждались на Всесоюзном совещании-семинаре “Разработка и оптимизация САПР и ГАП изделий электронной техники на базе высокопроизводительных мини- и микро- ЭВМ” (Воронеж, 1989); IX Всесоюзном симпозиуме “Эффективность, качество и надежность систем "Человек-техника"” (Воронеж, 1990); Международной конференции молодых ученых и специалистов “САПР-92. Новые технологии в науке, образовании и бизнесе” (Воронеж, 1992); Российском совещании-семинаре “Оптимальное проектирование технических устройств и автоматизированных систем” (Воронеж, 1992); Всероссийском совещании-семинаре “Математическое обеспечение высоких технологий в технике, образовании и медицине” (Воронеж, 1994, 1997); Всероссийском совещании-семинаре “Высокие технологии в региональной информатике” (Воронеж, 1998), Международной научно-практической конференции “Социально-экономическое развитие современного общества в условиях реформ” (Саратов, 2007); Всероссийском совещании-семинаре “Интеллектуальные информационные системы” (Воронеж, 2008-2010); Всероссийской конференции “Интеллектуализация управления в социальных и экономических системах” (Воронеж, 2008-2010); VI Международной научно-практической конференции “Исследование, разработка и применение высоких технологий в промышленности” (Санкт-Петербург, 2008); Международных конференциях “Системные проблемы надежности, качества, информационно-телекоммуникационных и электронных технологий в управлении инновационными проектами” (Москва-Воронеж-Сочи, 2008, 2009); XVI Всероссийской научно-технической конференции ”Материалы и упрочняющие технологии” (Курск, 2009); X Всероссийской научно-технической конференции “Научные исследования в области транспортных, авиационных и космических систем” (Воронеж, 2009); XXII Международной научной конференции “Математические методы в технике и технологиях: ММТТ-22” (Псков, 2009): научно-методических семинарах кафедры систем автоматизированного проектирования и информационных систем ГОУ ВПО «Воронежский государственный технический университет» (2005-2010).

Публикации. По теме диссертации опубликовано 56 научных работ, в том числе 13 – в изданиях, рекомендованных ВАК РФ и 2 монографии.

В работах, опубликованных в соавторстве и приведенных в конце автореферата, лично соискателю принадлежат: иерархические схемы оптимального проектирования производственных систем [1,2,27,29,39,41,42]; оптимизационные модели и процедуры параметрического и структурного синтеза производственных систем [4,11,14,15,18,28,31,32,36,37,40,43,44,45,47,48,54]; технология моделирования производственной системы [21,52]; библиотека модулей оптимального проектирования [12,46]; многометодные стратегии и интеллектуальные процедуры поиска проектных решений [7,9,38,51,53]; схемы интегрированного взаимодействия оптимизационных и имитационных процедур при проектировании производственных систем [6,34]; структура и программное обеспечение подсистемы оптимального проектирования [16,17,19,20,23,25,55].

Структура и объем работы. Диссертация состоит из введения, шести глав, заключения, приложений и списка литературы из 219 наименований. Основная часть работы изложена на 272 страницах и содержит 49 рисунков и 5 таблиц.

ОСНОВНОЕ СОДЕРЖАНИЕ РАБОТЫ

Во введении обоснована актуальность работы, дана ее краткая характеристика, сформулированы цель и задачи исследования, изложены основные научные положения и результаты, выносимые на защиту.

В первой главе проведен анализ направлений развития современных производственных систем и рассмотрены особенности решаемых при этом задач структурной и параметрической оптимизации.

Задачи проектирования производственных систем обобщенно формализуются в рамках стандартной математической модели:

(1)

где – вектор варьируемых переменных, определяющих структуру и параметры системы; – частные критерии оптимальности; – допустимая область, представленная системой ограничений.

Показано, что в связи с особенностями развивающихся производственных систем (динамическим характером, стохастичностью и т.д.) наиболее целесообразной является алгоритмизация их проектирования в рамках оптимизационно-имитационного подхода. При этом в оптимизационных моделях (1) ряд критериев и ограничений определяется алгоритмически с использованием моделирующих процедур. В главе рассматриваются особенности данного подхода и определяются требования к математическому и программному обеспечению интегрированных процедур имитационного моделирования и оптимизации.

Неполнота математического описания производственных систем, выраженная в отсутствии аналитических формулировок критериев и ограничений в оптимизационных моделях, осложняет оценку свойств решаемых задач на априорном уровне и снижает эффективность стандартного математического обеспечения. Наиболее целесообразным в рассматриваемой ситуации является использование адаптивного подхода к оптимальному проектированию, обеспечивающего раскрытие априорных неопределенностей в ходе оптимизационного процесса на основе динамического анализа априорной и текущей информации. При этом выделяются два основных уровня адаптации:

- внутренняя адаптация, которая предполагает построение процедур оптимального выбора, позволяющих сочетать в единой алгоритмической схеме исследование свойств оптимизационной модели с поиском наилучших вариантов;

- внешняя адаптация, предусматривающая модульную организацию алгоритмической базы с возможностью ее настройки на различные классы задач.

В работе ставится задача практической реализации адаптивного подхода на основе построения интеллектуальной поисковой среды оптимального проектирования производственных систем. При этом адаптивная поисковая среда определяется как совокупность методов и средств, обеспечивающих построение процедур параметрического и структурного синтеза производственных систем посредством комплексирования инвариантных структурных компонентов. Формируемая среда объединяет вероятностно-детерминированные алгоритмы поиска наилучших вариантов, интеллектуальные процедуры генерации алгоритмических схем и средства управления оптимизационным процессом в единую многометодную технологию принятия проектных решений.

Во второй главе рассматривается технология проектирования перестраиваемых производственных систем на основе оптимизационно-имитационного подхода и принципов декомпозиции.

Задача поиска оптимальных вариантов перестраиваемой производственной системы решается на основе двухуровневой процедуры (рис.1).

Рис. 1. Схема решения задач модернизации и перестройки производства

На верхнем уровне определяются требуемые изменения технико-экономических характеристик системы в пределах выделенных ресурсов ) для достижения общей цели предприятия. При этом осуществляется анализ рынка сбыта, проводится финансовый анализ, оцениваются возможности снабжения и т.д. Значения элементов вектора на -й итерации передаются на нижний уровень в качестве целевых установок . На нижнем уровне определяются необходимые структурно-параметрические изменения в системе с учетом данных требований.

В работе рассматривается второй уровень представленной схемы, которому соответствуют задачи структурно-параметрического синтеза производственной системы. При этом решается задача целевой оптимизации , обеспечивающая прирост технико-экономических характеристик системы в требуемом объеме с минимизацией расходуемых ресурсов . Дополнительно в соответствии со спецификой проектируемой системы определяются частные критерии оптимальности . Допустимая область определяется системой прямых и функциональных ограничений, устанавливающих требования к проектируемой системе и ее элементам. Значения и , полученные при проектировании, передаются на верхний уровень для оценки полученного результата и принятия решений об окончании или продолжении итерационного процесса.

При решении обобщенной задачи структурно-параметрического синтеза используется декомпозиционный подход. В процессе проектирования производственная система представляется в виде иерархии взаимосвязанных элементов различной степени детализации. При этом уровни детализации производственной системы связываются с соответствующими уровнями детализации изготавливаемых изделий, а блоки соответствуют производственным участкам. Каждому блоку , , ставятся в соответствие его имитационная модель и локальные оптимизационные модели структурного и параметрического синтеза. При этом оптимальный структурно-параметрический синтез каждого блока приводит к изменению его выходных характеристик и входных параметров, что, в свою очередь, требует изменения выходных характеристик связанных с ним блоков нижних уровней иерархии с целью обеспечения ритмичности производства. Обобщенная схема поиска рациональных проектных решений представлена на рис. 2.

В схеме использованы следующие обозначения: – требуемые значения выходных характеристик блока , поступающие с верхнего уровня иерархии; – выходные характеристики блока , полученные при его проектировании ; – объем внешних ресурсов, используемых при перестройке блока . Оптимальное проектирование блока заключается в определении структурно-параметрических сдвигов в данном блоке для достижения требуемых значений показателей с наименьшими затратами. В качестве характеристик , использующихся при согласовании проектных решений, будем рассматривать интенсивности и объемы выпуска соответствующих деталей и узлов, а в качестве входных параметров – интенсивности поступления на вход данного блока материалов и комплектующих . При этом .

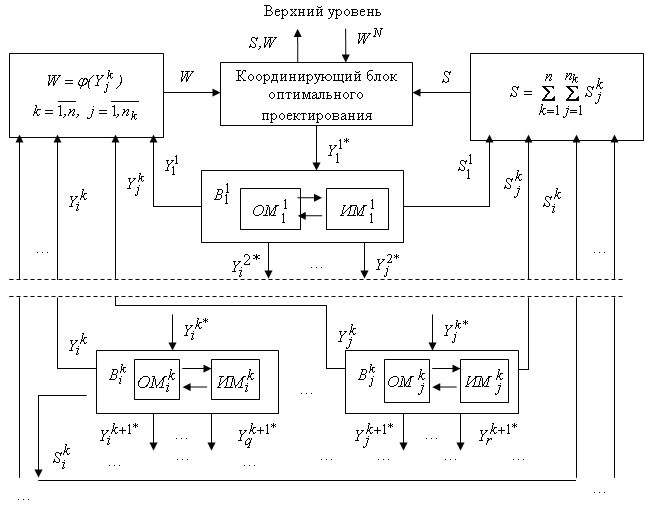
Рис. 2. Обобщенная схема поиска проектных решений

Процесс оптимального проектирования начинается с верхнего уровня иерархии (блок ). Координирующей подсистемой на основе полученных в результате планирования значений осуществляется определение требуемых значений выходных характеристик для блока , соответствующих объемам и интенсивностям выпуска системой готовой продукции. Далее осуществляется структурно-параметрический синтез блоков последующих уровней детализации относительно известной структуры и параметров блока .

Таким образом, проектирование производственной системы заключается в целенаправленном изменении ее структуры и параметров относительно первого, второго и более высоких уровней детализации. Процесс продолжается до нижнего уровня, после чего значения выходных характеристик каждого блока и затраченных ресурсов поступают в координирующий блок, обрабатываются и передаются на верхний уровень принятия решений. При этом значения технико-экономических характеристик системы связаны со значениями функциональной зависимостью .

В третьей главе рассматриваются математические модели структурного и параметрического синтеза производственных систем.

Процесс оптимального проектирования на уровне каждого блока производственной системы начинается с решения задачи структурного синтеза (в дальнейшем индекс k будем опускать).

При проектировании структуры технологического процесса важной задачей является выбор рационального варианта концентрации технологических операций и последовательности обработки изделий на используемом оборудовании с учетом его переналадок.

Пусть для изготовления j-го объекта производства необходимо выполнить совокупность технологических операций . Время, необходимое для осуществления каждой технологической операции, равно . Определено число групп технологических операций , которые однородны по своему назначению в процессе последовательного использования оборудования многоцелевого назначения для изготовления объекта производства . Варианты предшествования технологических операций для каждого объекта производства заданы последовательностями

, , , ,

где - знак предшествования, m указывает номер варианта технологического процесса изготовления данного объекта производства. Требуется распределить совокупность технологических операций между группами и определить оптимальную последовательность обработки изделий.

Для построения модели введем альтернативные переменные:

, ,

При этом значения переменных зависят от значений , так как вариант предшествования определяет распределение технологических операций между группами: . Условия предшествования технологических операций учитываются с помощью ограничений

, , , . (2)

Каждая технологическая операция при изготовлении j-го объекта производства должна относиться только к одной из групп, поэтому

, , . (3)

При изготовлении j-го объекта производства выбирается только один вариант предшествования:

, . (4)

Суммарное время выполнения i-й технологической операции в k-й группе ограничено временем работы инструмента:

, , , (5)

где - максимальное время использования i-го инструмента в одной группе.

В зависимости от типа оборудования многоцелевого назначения суммарное количество одновременно устанавливаемых инструментов в группе ограничивается следующим образом:

, , (6)

где - максимальное количество технологических операций в группе.

В модели используются следующие критерии оптимальности:

- суммарная трудоемкость изготовления объектов производства заданного ассортимента:

, (7)

где .

- суммарное время переналадок оборудования при последовательном переходе от группы изделий к группе:

(8)

где .

При этом - время, необходимое для переналадки оборудования при выполнении i-й технологической операции.

В совокупности критерии (7) – (8) и ограничения (2) – (6) представляют собой многокритериальную оптимизационную модель с альтернативными булевыми переменными. Рассмотренная математическая модель может использоваться как при проектировании новых производственных систем, так при перестройке действующих в связи с переходом на выпуск новых видов продукции.

Пусть для изготовления -го изделия известны множество возможных технологических маршрутов , стоимость его изготовления по -му маршруту. Рассмотрим задачу выбора оптимального технологического маршрута и используемого оборудования, решаемую при перестройке и модернизации производственной системы.

Исходными данными при этом являются:

- множество классов оборудования, которое входило в систему до ее перестройки, число видов оборудования в каждом классе, , а также количество оборудования каждого вида ; , ;

- множество классов оборудования и видов оборудования , , которое может быть использовано для модернизации системы.

Для обеспечения целостности технологического маршрута вводятся булевы переменные . При этом =1, если j-й класс оборудования используется для изготовления изделия i-го вида по q-му технологическому маршруту; =0 – в противном случае.

Дополнительно для каждой единицы оборудования множеств и задаются: , - стоимость обслуживания с учетом амортизации; , - занимаемая площадь; , - количество необходимых для обслуживания рабочих; стоимость продажи и демонтажа единицы оборудования множества ; стоимость приобретения единицы оборудования множества .

Варьируемыми параметрами модели являются:

- целочисленные переменные , , и , , , определяющие количество оборудования имеющихся и новых типов, которое необходимо использовать в производственной системе.

- булевы переменные , определяющие выбор технологического маршрута изготовления изделий каждого вида:

Критерии оптимальности формулируются следующим образом:

; (9)

(10)

Показатели (9) характеризуют отклонения объемов выпуска каждого вида изделий от требуемых значений , установленных подсистемой верхнего уровня. Критерий (10) определяет затраты на выпуск изделий, обслуживание и приобретение оборудования. В модели иcпользуются ограничения:

- на единственность технологического маршрута для каждого изделия:

; (11)

- на необходимость обязательного выбора оборудования, предусмотренного каждым технологическим маршрутом;

; (12)

- на используемые производственные площади , численность дополнительно нанимаемых рабочих каждой профессиональной группы и стоимость нового оборудования :

; (13)

, ; (14)

; (15)

- на предельное время простоев оборудования :

, . (16)

Задача (9) – (16) является задачей целочисленной оптимизации, в которой значения , определяются алгоритмически в результате имитационного моделирования.

В работе рассмотрены также оптимизационные модели закрепления деталей за оборудованием, распределения оборудования по участкам, закрепления деталей за оборудованием, закрепления деталей за участками.

Задача структурного синтеза решается в предположении, что все необходимые материалы и комплектующие поступают в блок с требуемой интенсивностью. После решения данной задачи осуществляется настройка входных параметров данного блока, представляющих собой значения соответствующих интенсивностей . При этом используется оптимизационная модель с алгоритмически заданными критериями и ограничениями:

, ; (17)

(18)

, (19)

.

Здесь Z, L – номенклатура деталей и комплектующих на входе и выходе блока; – стоимость деталей и комплектующих j-го вида; – интенсивность выпуска изделий производственным участком; – требуемая интенсивность, установленная подсистемой верхнего уровня; – длина очереди по -му наименованию комплектующих перед данным производственным участком; – необходимый страховой запас; – предельная длина очереди. Показатель (17) используется для согласования интенсивности выпуска изделий с требуемыми значениями . Критерий (18) характеризует стоимость материалов и деталей, находящихся в очереди перед обработкой.

После решения задачи вектор входных интенсивностей структурируется на два вектора: и . При этом вектор соответствует потоку деталей и узлов, поступающих на вход блока после обработки на предыдущих производственных участках, а вектор - потоку материалов и комплектующих, поступающих на вход блока непосредственно со складов предприятия. Далее значения вектора передаются на нижний уровень иерархической системы в качестве требуемых целевых установок.

Результаты решения задачи (17) – (19) для всех производственных участков , , используются в дальнейшем для оптимизации материальных потоков между производственной системой и внешней средой. Используемые оптимизационные модели представлены на рис. 3.

Рис. 3. Модели параметрической оптимизации производственной системы

В главе также рассматривается технология комплексного моделирования производственной системы, основанная на совместном использовании CASE-средств и имитационных процедур. На начальном этапе моделирования формируется иерархия диаграмм IDEF0 и IDEF3, отражающая структуру и функции производственной системы. Определение уровней декомпозиции осуществляется в соответствии со сформированной схемой оптимального проектирования производственной системы. На основе построенных функциональных моделей формируется комплекс имитационных моделей, соответствующих различным предметно-ориентированным участкам производственной системы. При построении имитационных моделей производственная система формализуется в виде многофазной сети массового обслуживания. Поток комплектующих и материалов представляется в виде простейшего потока заявок. Предполагается, что длительность обслуживания имеет экспоненциальную плотность распределения. При моделировании используются бесприоритетные дисциплины ожидания и обслуживания. Моделирование очереди осуществляется по принципу FIFO. С использованием аппарата массового обслуживания строятся имитационные модели для всех уровней иерархии производственной системы.

В четвертой главе рассматриваются вопросы адаптивной алгоритмизации задач оптимального проектирования производственных систем. Алгоритмическую базу предлагается формировать на основе комплексирования вероятностных и детерминированных процедур непрерывной и дискретной оптимизации.

Решение задач параметрического синтеза производственных систем связано с выделением инвариантной подзадачи скалярной безусловной минимизации алгоритмически заданной целевой функции:

. (20)

При разработке оптимизационных процедур использован известный адаптивный подход, обеспечивающий более полную формализацию задачи (2) на основе ее эквивалентной рандомизированной переформулировки:

. (21)

Итерационные процедуры поиска оптимальных вариантов формируются в множестве случайных векторов {} следующим образом:

, (22)

где - номер итерации; - направление поиска; - величина шага.

В работе рассматривается обобщенная итерационная схема, сформулированная в терминах математического ожидания:

, (23)

где площадь поверхности единичной сферы в пространстве ; случайные векторы; уровень целевой функции; неубывающая функция, удовлетворяющая условиям: ; .

Итерационная процедура (23) является обобщенной схемой нелокального поиска и предполагает построение на ее основе различных алгоритмических структур. В частности, если ограничиться одной реализацией случайного вектора , в качестве реализации вектора выбрать математическое ожидание , а функцию определить в виде , можно перейти к схеме, являющейся адаптивным расширением метода переменного многогранника Нелдера-Мида, в которой реализации случайных векторов рассматриваются как вершины многогранника, а перестраиваемое математическое ожидание – как его центр тяжести:

, где (24)

Обобщенная алгоритмическая схема представлена на рис. 4.

Рис. 4. Алгоритмическая схема адаптивных поисковых процедур

На основе различных интерпретаций итерационных процедур (23,24) рассматриваются альтернативные стратегии реализации каждого из этапов обобщенной схемы. Так, в качестве уровня целевой функции может выбираться среднее арифметическое значений функции или соответствующая медиана:

или

Вероятности для определения математического ожидания (шаг 3) могут определяться по одной из следующих схем:

или 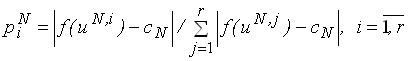. (25)

Остальные этапы также реализуются с использованием альтернативных стратегий. В результате в рамках единой обобщенной схемы формируется комплекс адаптивных алгоритмов поисковой оптимизации.

Дальнейшее повышение эффективности процедур оптимального параметрического синтеза осуществляется на основе замены переменных, обеспечивающей локальные свойства сепарабельности оптимизируемой функции:

, (26)

где - вектор новых переменных; A - матрица замены переменных, которая формируется на основе текущей информации и итерационно перестраивается при смене окрестности поиска:

. (27)

В качестве корректирующей матрицы используется оператор растяжения пространства Шора:

(28)

При соответствующем выборе параметра и направления воздействие оператора Шора (28) на текущее направление движения способствует его отталкиванию от предыдущих неперспективных направлений и ориентирует оптимизационный процесс в направлении вытянутости поверхностей уровня целевой функции, что позволяет учитывать текущую информацию, получаемую в процессе поиска. В работе рассмотрены способы последовательной корректировки оператора Представлены различные варианты модифицированных с использованием замены переменных алгоритмов нелокальной оптимизации, случайного поиска, покоординатного спуска.

При разработке алгоритмических схем решения задач структурного синтеза выделяется инвариантная задача минимизации псевдобулевой функции:

, , , (29)

где целевая функция является действительнозначной функцией булевого аргумента . Алгоритмизацию данной задачи предлагается осуществлять в 2 этапа. На первом этапе производится приближенная оценка решения с использованием рандомизированных оптимизационных процедур, а на втором – уточнение полученного решения на основе точных детерминированных методов.

С целью формирования рандомизированных стратегий поиска используется итерационная схема в множестве булевых случайных величин:

, (30)

Здесь - булева случайная величина, определяющая направление движения, - булева случайная величина, выполняющая роль шага поиска.

Построение алгоритмических схем основано на интерпретации движения (30) в вероятностных характеристиках случайных величин:

, (31)

где , , , .

В работе рассмотрены различные способы итерационной перестройки вероятностей на основе текущей информации.

При решении задач псевдобулевой оптимизации с использованием рандомизированных процедур используются два подхода:

- однократное определение вероятностей и получение начального приближения для использования последующих точных алгоритмов;

- последовательная итерационная настройка вероятностей с целью их стабилизации и фиксации соответствующих значений переменных в окончательном решении. При этом переменные , соответствующие установившимся значениям , фиксируются и участвуют в дальнейшем поиске в качестве констант.

Обобщенная алгоритмическая схема псевдобулевой оптимизации представлена на рис. 5.

Дальнейшая алгоритмизация задачи структурного синтеза осуществляется с использованием детерминированных алгоритмов, построенных в рамках модифицированной схемы ветвей и границ, отличающейся от стандартной способами вычисления верхних и нижних оценок. Для вычисления нижних оценок используются рассмотренные адаптивные процедуры непрерывной оптимизации. Определение верхних оценок основано на переходе от соответствующего непрерывного решения к дискретному с использованием различных схем дискретизации. При реализации каждого этапа обобщенной схемы структурного синтеза так же, как и при параметрическом синтезе, используются альтернативные взаимозаменяемые стратегии.

Рис. 5. Обобщенный алгоритм псевдобулевой оптимизации

Одной из основных особенностей решаемых задач оптимального проектирования является их высокая размерность и многокритериальный характер, что обусловлено множественностью технико-экономических требований к характеристикам проектируемых систем. Для решения данной проблемы в работе рассматриваются адаптивные процедуры трансформации оптимизационных моделей, обеспечивающие преобразование решаемых задач, сокращение их размерности и приведение к типовым постановкам на основе анализа априорной и текущей информации.

Агрегирование критериев оптимальности предлагается осуществлять на основе адаптивных рандомизированных процедур векторной оптимизации. На основании имеющегося набора локальных критериев неопределенность в задании обобщенного показателя отражается в рандомизации выбора отдельных целевых функций как возможного критерия оптимальности. При этом обобщенный показатель можно сформулировать в виде:

, (32)

где - случайная величина, значения которой 1,2,…,m соответствуют номерам критериев. Величины характеризуют вероятности привлечения критериев к оптимизационному процессу. При этом предпочтения ЛПР в ходе оптимального выбора связываются с перестройкой вероятностных характеристик на основе следующей итерационной схемы:

, (33)

где и - параметры, определяемые при решении задачи в диалоге с ЛПР.

Способы настройки параметров процедуры (33) представлены в таблице.

Информация ЛПР	Способы настройки параметра
Настройка параметра
1. Выделение ЛПР номера наиболее существенного критерия
2. Упорядочивание всех критериев по значимости	, , где - степень предпочтительности критериев
3. Отсутствие информации о предпочтениях ЛПР	, где , - нормирующий делитель.
Настройка параметра : , где , если на N-й и N-1-й итерациях в качестве главного показателя выбирался один и тот же критерий t и в противном случае.

При решении задач векторной оптимизации выделяются два основных этапа. Первый этап связан с адаптивной итерационной настройкой вероятностей на основании текущей информации и предпочтений ЛПР. Процесс настройки вероятностей осуществляется до достижения установившихся значений . На втором уровне производится агрегирование локальных критериев в обобщенный показатель , где - нормированные критерии, и решение соответствующей скалярной задачи. Обобщенный алгоритм векторной оптимизации представлен на рис. 6.

Рис. 6. Алгоритмическая схема векторной оптимизации

Для адаптивного учета ограничений в скалярных задачах оптимального проектирования используется релаксационный подход, основанный на последовательном введении и выведении ограничений из допустимой области. При этом на каждой -й итерации осуществляется вычисление вероятностей:

; (34)

, (35)

где , - вероятности привлечения к оптимизационному процессу ограничений-неравенств и ограничений-равенств; , - множества индексов ограничений-неравенств и ограничений-равенств, нарушенных на данном шаге; , - левые части соответствующих ограничений; , - нормирующие делители. На последующем этапе в задачу включаются ограничения, удовлетворяющие условиям: , , где и - предельные значения вероятностей, задаваемые пользователем. Ограничения, которые на данном этапе не были нарушены, временно выводятся из задачи.

Преобразование задачи с ограничениями в задачу безусловной оптимизации осуществляется с использованием аппарата штрафных функций:

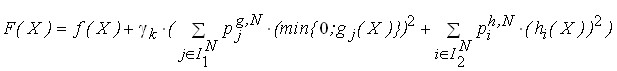, (36)

где - параметр штрафа. При этом в формировании штрафной функции участвуют только существенные ограничения, выбранные на -м шаге.

Сокращение пространства варьируемых параметров в построенной задаче безусловной оптимизации осуществляется на основе разделения переменных. При этом вектор структурируется следующим образом: , где - вектор существенных параметров, варьируемый при решении задачи; - вектор второстепенных параметров, который фиксируется на данном шаге оптимизационного процесса.

Для выделения существенных параметров оптимизационной модели использован подход, основанный на исследовании чувствительности критерия оптимальности к изменению варьируемых параметров в различных точках поиска с использованием коэффициентов чувствительности

, (37)

где .

При этом относится к группе существенных, если коэффициент превышает минимально возможное значение , задаваемое пользователем. Коэффициент может корректироваться в ходе оптимизационного процесса.

Пятая глава посвящена формированию многометодной среды оптимального проектирования производственных систем на основе компонентно-модульного подхода и интеллектуализации синтеза алгоритмических схем.

Для реализации многометодных технологий поиска проектных решений алгоритмическую базу предлагается формировать как совокупность библиотеки модулей оптимального проектирования и адаптивных процедур комплексирования модулей применительно к различным ситуациям. В состав алгоритмической базы оптимального проектирования производственных систем входят модели и процедуры, предназначенные для решения задач структурного и параметрического синтеза различных классов. При этом модели и процедуры оптимального проектирования структурно организованы в виде трех основных библиотек: библиотеки имитационных моделей; библиотеки оптимизационных моделей и библиотеки оптимизационных процедур.

Библиотека имитационных моделей содержит имитационные модели элементов проектируемой производственной системы: технологических линий, участков, цехов и т.д. В зависимости от решаемой задачи из библиотеки может быть выбрана соответствующая имитационная модель, что позволяет осуществлять процесс оптимального проектирования на различных уровнях иерархии производственной системы. При этом имитационные модели строятся для конкретной производственной системы в соответствии с ее структурой, параметрами и принципами функционирования. Проектирование новой производственной системы связано с формированием новых имитационных моделей и включением их в состав соответствующей библиотеки.

Библиотека оптимизационных моделей проектирования производственных систем включает математические модели для решения задач параметрического и структурного синтеза различных классов. Модели обобщенно формализуются в виде задач непрерывной, дискретной и непрерывно-дискретной оптимизации. При этом часть критериев и ограничений задается алгоритмически на основе имитационного моделирования. Структурный синтез производственных систем связан с проектированием технологических процессов, выбором технологических маршрутов изготовления изделий, определением состава оборудования, его компоновкой и размещением по участкам, заменой оборудования и расширением производственных мощностей, закреплением операций над деталями за оборудованием и т.д. Параметрический синтез предполагает оптимизацию материальных потоков как внутри производственной системы, так и при ее взаимодействии с внешней средой.

Основой алгоритмической базы оптимального проектирования является библиотека оптимизационных процедур (рис. 7). В состав библиотеки оптимизационных процедур включаются рассмотренные в главе 4 вероятностно-детерминированные алгоритмы параметрического и структурного синтеза производственных систем. При формировании библиотеки оптимизационных процедур используется компонентно-модульный подход, основанный на структуризации оптимизационных задач и алгоритмов их решения. В соответствии с развиваемым подходом различные алгоритмы оптимального проектирования представляют собой определенные схемы комплексирования модулей. Набор модулей выбирается таким образом, чтобы посредством их суперпозиции можно было получить решение задач оптимального проектирования производственных систем различных классов. В этой связи выделяются типовые задачи оптимального проектирования и типовые проектные ситуации с целью их покрытия формируемыми посредством комплексирования модулей алгоритмами.

Обобщенная структура библиотеки модулей оптимального проектирования может быть представлена следующим образом:

,

где – множество внешних модулей; – совокупность инвариантных модулей безусловной оптимизации; – множество схем комплексирования модулей в соответствии с графом межмодульных связей.

Внешние модули структурируются по группам в соответствии с функциональным назначением: , , где – количество групп внешних модулей, внутри каждой из которых выделяются альтернативные модули, выбираемые в зависимости от задачи: , .

Структуризация модулей безусловной оптимизации осуществляется в соответствии с классами алгоритмов, формируемых при их комплексировании: , где – количество соответствующих классов. При этом возможны пересечения модулей различных классов: .

Рассмотрим модульную организацию алгоритмов -го класса. Совокупность модулей можно разделить на две группы: , где – базовые модули, включение которых в алгоритмическую схему является обязательным; – вспомогательные модули, обеспечивающие дополнительную обработку текущей информации и подключаемые к алгоритмическим схемам по мере необходимости.

Базовые модули реализуют основные шаги обобщенной вычислительной схемы алгоритмов -го класса и структурируются следующим образом: , где – число шагов обобщенной вычислительной схемы алгоритмов -го класса; , – совокупность альтернативных взаимозаменяемых модулей , реализующих -й шаг обобщенной вычислительной схемы. При формировании алгоритмических схем из каждой группы модулей выбирается один.

Рассмотрим множество задач оптимального проектирования производственных систем . Каждой оптимизационной задаче соответствует имитационная модель проектируемой подсистемы и оптимизационная модель . При этом каждая оптимизационная модель характеризуется тройкой вида:

,

где - вектор варьируемых параметров; - допустимая область, представленная совокупностью прямых и функциональных ограничений; - частные критерии оптимальности.

Пусть - совокупность алгоритмов для решения поставленных задач. В общем случае алгоритм оптимального выбора , связывающий следующие друг за другом решения

,

имеет структуру и параметры и может быть определен в виде:

,

где - совокупность модулей, включенных в алгоритм ; - схема сборки модулей, соответствующая алгоритму .

Введем показатель эффективности решения задачи алгоритмом . Тогда выбор наилучшего алгоритма сводится к решению задачи адаптации оптимизационного процесса:

,

где - множество алгоритмов, приемлемых для решения задачи .

Задача компонентно-модульного синтеза алгоритмических схем при оптимальном проектировании может быть обобщенно сформулирована в виде:

,

где - множество формализованных постановок оптимизационных задач; - множество возможных алгоритмов их решения, представляющих собой различные схемы комплексирования модулей; - показатели эффективности решения оптимизационных задач (скорость сходимости, оценка точности результата; количество вычислений значений целевой функции для получения результата с заданной точностью и т.д.); - совокупность признаков, характеризующих оптимизационные задачи (размерность аргумента; количество критериев и ограничений; типы параметров; структурные особенности модели; качество начального приближения; требования к сходимости и т.д.); - набор критериев и условий применимости алгоритмических модулей и схем их сборки, которые формируются по результатам решения тестовых и практических задач оптимизации в зависимости от характеристик решаемых задач; - совокупность стратегий организации оптимизационного процесса.

Для решения данной задачи разработаны процедуры интеллектуальной поддержки комплексирования модулей. Обобщенная схема функционирования интеллектуальных процедур представлена на рис. 8.

Рис. 8. Схема функционирования интеллектуальных процедур

Предметная область синтеза алгоритмических схем оптимального проектирования описывается совокупностью объектов и отношений на объектах. Множество объектов, описывающих задачу, определяется в виде:

,

где - множество входных объектов, представляющих собой поименованные признаки задач оптимального проектирования; - множество выходных объектов, которые используются

при определении структуры алгоритмической базы для решения данной задачи и представляют собой названия модулей и схем их сборки.

База знаний содержит набор продукционных правил:

ЕСЛИ ТО ,

где - антецедент - й продукции, который является конъюнкцией элементарных посылок: И И … И ; - консеквент - й продукции, представляющий собой элементарное следствие , выполняемое в случае истинности антецедента и заключающееся в формировании очередного варианта синтеза; - степень истинности правила, определяемая на этапе формирования базы знаний. Элементарные посылки , и следствия являются дизъюнкцией фактов предметной области , представленных в виде “объект -значение”:

ИЛИ ИЛИ …,

где - индекс объекта, входящего в - ю элементарную посылку -й продукции; - значение данного объекта. При вводе -го факта пользователь оценивает его истинность с помощью коэффициента определенности .

Логический вывод основан на реализации прямой стратегии поиска и позволяет осуществлять управление системой продукций за счет целенаправленной (от объектов) их активизации. В процессе вывода осуществляется пересчет коэффициентов истинности заключений с использованием схемы:

, (38)

где - коэффициент определенности -й продукции, устанавливаемый при формировании базы знаний; - значение истинности -го факта, входящего в - ю элементарную посылку -й продукции; - его коэффициент определенности, вводимый пользователем. Оценка истинности фактов производится на основе сравнения значения входного объекта , введенного пользователем, и значения объекта , входящего в - ю элементарную посылку -й продукции. При этом , если значения равны, и в противном случае. Признаком выполнения продукции является выполнение условия: , где - пороговое значение.

Информация с блока логического вывода передается в генератор оптимизационных процедур, реализующий подключение соответствующих модулей, после чего производится запуск данного алгоритма оптимального проектирования. В случае неудовлетворительного результата осуществляется изменение начального приближения, настройка параметров данного алгоритма или смена алгоритмической схемы в соответствии с заложенными в систему сценариями.

Шестая глава посвящена разработке подсистемы поддержки принятия проектных решений и ее апробации в условиях производства.

Структура программного комплекса представлена на рис. 9.

Рис. 9. Структурная схема программного комплекса

Основные программные модули и интерфейсные средства реализованы в среде Delphi. Функциональное моделирование осуществляется с использованием системы BPwin, имитационное моделирование производится в инструментальной системе Arena. Для интеграции имитационных моделей с программной средой принятия решений разработаны интерфейсные средства, представляющие собой совокупность процедур для корректировки базы данных модели. Связь с базой данных модели обеспечивается средствами ADO.

Программный комплекс использован при параметрической и структурной оптимизации производственных систем изготовления нефтегазового, горнообогатительного оборудования и радиоэлектронных устройств, что позволило обеспечить уменьшение длительности производственного цикла, увеличение объема выпускаемой продукции, сокращение незавершенного производства, минимизацию простоев оборудования и его равномерную загрузку.

ОСНОВНЫЕ РЕЗУЛЬТАТЫ РАБОТЫ

1. Проведен анализ направлений повышения эффективности процессов принятия решений при проектировании сложных производственных объектов с перестраиваемой структурой. Определены принципы адаптивной алгоритмизации задач оптимального проектирования производственных систем с учетом динамического и стохастического характера производства.

2. Построены многоуровневые итеративные схемы оптимального проектирования перестраиваемых производственных систем с возможностью координации проектных решений на различных уровнях декомпозиции.

3. Сформированы математические модели оптимального выбора структуры производственной системы и ее отдельных элементов при проектировании новых производственных объектов или перестройке действующих.

4. Создан комплекс математических моделей для согласования и оптимизации материальных потоков как в пределах проектируемой производственной системы, так и при ее взаимодействии с внешней средой.

5. На основе интеграции вероятностных и детерминированных процедур непрерывной и дискретной оптимизации построен комплекс адаптивных алгоритмов оптимального проектирования производственных систем с возможностью их использования для решения задач, описываемых сложными алгоритмическими моделями.

6. Построены адаптивные процедуры агрегирования показателей качества в многокритериальных моделях принятия решений, предложены различные способы настройки весовых коэффициентов показателей и стратегии организации оптимизационного процесса в зависимости от информации ЛПР.

7. Разработаны алгоритмические схемы редукции ограничений и сокращения пространства варьируемых параметров в оптимизационных моделях структурного и параметрического синтеза с целью преобразования и типизации решаемых задач оптимального проектирования.

8. На основе совместного использования CASE- средств и имитационных процедур реализована технология моделирования производственной системы с возможностью комплексного анализа процессов производства с различной степенью детализации.

9. Построены схемы совместного комплексного использования оптимизационных и моделирующих процедур в процессе проектирования, разработаны средства их интеграции и информационного взаимодействия.

10. Предложена методика формирования адаптивной многометодной среды поиска оптимальных проектных вариантов, обеспечивающая построение процедур структурного и параметрического синтеза различных классов посредством комплексирования инвариантных структурных компонентов.

11. Разработана компонентная структура алгоритмической базы оптимального проектирования производственных систем, сформирована библиотека модулей различного функционального назначения.

12. Построены интеллектуальные процедуры компонентно-модульного синтеза алгоритмических схем оптимального проектирования на основе динамической оценки свойств решаемых задач.

13. Разработан программный комплекс поддержки принятия решений при проектировании производственных систем, ориентированный на поиск оптимальных проектных вариантов в условиях модернизации и реструктуризации производства. Программный комплекс позволяет решать задачи моделирования, анализа и структурно-параметрической оптимизации как на уровне производственных участков, так и на уровне производственной системы в целом.

14. Проведена апробация и внедрение разработанного комплекса моделей, алгоритмов и программных средств на промышленных предприятиях машиностроительного и радиоэлектронного профиля.

Основные результаты диссертации опубликованы в следующих работах:

Публикации в изданиях, рекомендованных ВАК РФ

1. Белецкая С.Ю. Технология оптимального проектирования развивающихся производственных систем / С.Ю. Белецкая, Н.В. Боковая // Системы управления и информационные технологии: научно-технический журнал. 2008. №2.2 (32). С. 223-226.

2. Белецкая С.Ю. Алгоритмическая схема решения задач модернизации и развития производства / С.Ю. Белецкая, Н.В. Боковая // Вестник Воронежского государственного технического университета. 2008. Т.4. №11. С. 144-146.

3. Боковая Н.В. Моделирование производственных систем на основе интеграции CASE-средств и имитационных процедур / Н.В. Боковая // Программные продукты и системы: научно-технический журнал. 2008. №3. С. 43-45.

4. Белецкая С.Ю. Математические модели оптимального проектирования механических цехов / С.Ю. Белецкая, Н.В. Боковая, Ю.В. Минаева // Вестник Воронежского государственного технического университета. 2008. Т.4. №12. С. 68-69.

5. Боковая Н.В. Исследование факторного влияния на развитие предприятий / Н.В. Боковая // Организатор производства: теоретический и научно-практический журнал. 2009. №1. С. 32-35.

6. Белецкая С.Ю. Взаимосвязь процедур анализа и оптимального выбора при проектировании производственных систем / С.Ю. Белецкая, Н.В. Боковая // Вестник Воронежского государственного технического университета. 2009. Т.5. № 10. С. 225-227.

7. Белецкая С.Ю. Организация современных диалоговых систем оптимального проектирования / С.Ю. Белецкая, Н.В. Боковая // Вестник Воронежского государственного технического университета. 2009. Т.5. № 10. С. 234-237.

8. Боковая Н.В. Алгоритмизация многокритериальных задач оптимального проектирования на основе вероятностного подхода / Н.В. Боковая // Системы управления и информационные технологии: научно-технический журнал. 2009. №3.2 (37). С. 217-220.

9. Белецкая С.Ю. Интеллектуализация построения алгоритмических схем оптимального проектирования сложных систем / С.Ю. Белецкая, Н.В. Боковая // Вестник Воронежского государственного технического университета. 2009. Т.5. № 12. С. 27-29.

10. Боковая Н.В. Программный комплекс поддержки принятия решений при оптимизации производственно-сбытового процесса / Н.В. Боковая // Программные продукты и системы: научно-технический журнал. 2010. №2. С. 132-134.

11. Белецкая С.Ю. Математическая модель выбора состава оборудования при проектировании производственных цехов / С.Ю. Белецкая, Н.В. Боковая, Ю.В. Минаева // Вестник Воронежского государственного технического университета. 2010. Т.6. № 1. С. 41-42.

12. Белецкая С.Ю. Компонентная организация адаптивной среды поиска оптимальных проектных решений / С.Ю. Белецкая, Н.В. Боковая // Вестник Воронежского государственного технического университета. 2010. Т.6. № 5. С. 7-10.

13. Боковая Н.В. Адаптивные схемы агрегирования критериев в задачах векторной оптимизации / Н.В. Боковая // Вестник Воронежского института МВД России. 2010. № 2. С. 200-206.

Книги

14. Белецкая С.Ю. Модели и методы оптимального проектирования развивающихся производственных систем: монография / С.Ю. Белецкая, Н.В. Боковая. Воронеж: ВГТУ, 2009. 186 с.

15. Белецкая С.Ю. Анализ и синтез стохастических технологических систем: монография / С.Ю. Белецкая, Н.В. Боковая, Д.Б. Десятов. Воронеж: Научная книга, 2010. 236 с.

16. Боковая Н.В. Информатика: учеб. пособие / Н.В. Боковая, Т.О. Толстых. Воронеж: Центрально-Черноземное книжное издательство, 2002. 200 с.

17. Базы данных: учеб. пособие / Н.В. Боковая, Ю.В. Небренчина, Т.А. Некравцева, Т.О. Толстых. Воронеж: Институт менеджмента, маркетинга и финансов, 2002. 140 с.

18. Боковая Н.В. Методы исследования социально-экономических систем и оценки рисков: учеб. пособие / Н.В. Боковая, А.У. Панин, В.А. Синюкова. Воронеж: ООО “Главреклама”, 2009. 226 с.

Статьи и материалы конференций

19. Львович Я.Е. Системное обоснование выбора структуры ГПС / Я.Е. Львович, Н.В. Гунина, Т.О. Толстых // Совершенствование организации промышленного производства в новых условиях: межвуз. сб. науч. тр. Воронеж: ВПИ, 1989. С. 32-36.

20. Гунина Н.В. Структура математического обеспечения оптимального проектирования технических систем с оборудованием многоцелевого назначения / Н.В. Гунина, Я.Е. Львович // Алгоритмы моделирования и оптимизации автоматизированных систем: межвуз. сб. науч. тр. Воронеж: ВПИ, 1990. С. 9-15.

21. Львович Я.Е. Использование E-сети для анализа функционирования гибкого автоматизированного модуля монтажа кристаллов / Я.Е. Львович, Н.В. Гунина, Т.О. Толстых // Автоматизированное проектирование в радиоэлектронике и приборостроении: сб. науч. тр. Л.: ЛЭТИ, 1991. С.44-50.

22. Гунина Н.В. Особенности информационного обеспечения формирования структуры систем с оборудованием многоцелевого назначения / Н.В. Гунина // САПР-92. Новые информационные технологии в науке, образовании и бизнесе: материалы Междунар. конф. и школы молодых ученых и специалистов. Воронеж: ВПИ, 1992. С. 213-214.

23. Гунина Н.В. Организация информационной базы данных САПР СОМН / Н.В. Гунина, Я.Е. Львович // Оптимальное проектирование технических устройств и автоматизированных систем: материалы Российского совещания-семинара. Воронеж: ВПИ, 1992. С. 63.

24. Гунина Н.В. Разработка моделей и алгоритмов систем с оборудованием многоцелевого назначения / Н.В. Гунина // Математическое моделирование: межвуз. сб. науч. тр. Воронеж: ВГТА, 1997. Вып.2. C. 89-97.

25. Боковая Н.В. Сфера функционирования системы управления производственными процессами / Н.В. Боковая, В.А. Степанцов, Т.О. Толстых // Инновационные технологии и управление в технических и социальных системах: материалы науч.-практ. конф. Воронеж: ВГТУ, 1999. С. 92-93.

26. Боковая Н.В. Особенности построения модели прогнозирования потенциала отрасли / Н.В. Боковая // Проблемы и перспективы развития регионов и предприятий в условиях ВТО: сб. науч. тр. Уфа: УИ РГТЭУ, 2007. C. 296-298.

27. Богомолова И.П. Факторы и направления адаптивного развития корпораций / И.П. Богомолова, Н.В. Боковая // Вестник РГТЭУ: научный журнал. 2008. №5(26). С. 35-44.

28. Белецкая С.Ю. Формирование математической модели оптимального технического переоснащения производства / С.Ю. Белецкая, Н.В. Боковая // Оптимизация и моделирование в автоматизированных системах: межвуз. сб. науч. тр. Воронеж: ВГТУ, 2008. С. 67-70.

29. Белецкая С.Ю. Декомпозиционные процедуры оптимального проектирования сложных производственных систем / С.Ю. Белецкая, Н.В. Боковая // Оптимизация и моделирование в автоматизированных системах: межвуз. сб. науч. тр. Воронеж: ВГТУ, 2008. С. 105-108.

30. Боковая Н.В. Задачи стратегического планирования отрасли на современном этапе / Н.В. Боковая // Социально- экономическое развитие современного общества в условиях реформ: материалы Междунар. науч.-практ. конф. Саратов: Изд-во “Научная книга”, 2008. Ч.1. С. 93-95.

31. Белецкая С.Ю. Математическая модель оптимальной компоновки оборудования производственной системы / С.Ю. Белецкая, Н.В. Боковая, Ю.В. Минаева // Прикладные задачи моделирования и оптимизации: межвуз. сб. науч. тр. Воронеж: ВГТУ, 2008. С. 20-23.

32. Боковая Н.В. Классификация моделей оптимизации производственных систем / Н.В. Боковая, С.Ю. Белецкая // Интеллектуальные информационные системы: труды Всерос. конф. Воронеж: ВГТУ, 2008. С. 212-213.

33. Боковая Н.В. Основные функции информационной системы промышленного предприятия / Н.В. Боковая // Интеллектуальные информационные системы: труды Всерос. конф. Воронеж: ВГТУ, 2008. С. 190-191.

34. Белецкая С.Ю. Проектирование развивающихся производственных систем на основе оптимизационно-имитационного подхода / С.Ю. Белецкая, Н.В. Боковая, В.Н. Кострова // Системные проблемы надежности, качества, информационно-телекоммуникационных и электронных технологий в управлении инновационными проектами (Инноватика-2008): сб. тр. Междунар. конф. М., 2008. Ч.4. С. 211-215.

35. Боковая Н.В. Интеграция процедур имитационного моделирования и оптимизации при проектировании производственных систем / Н.В. Боковая // Исследование, разработка и применение высоких технологий в промышленности: сб. трудов VI Междунар. науч.-практ. конф. Спб., 2008. С.7-9.

36. Белецкая С.Ю. Математическая модель оптимизации парка технологического оборудования / С.Ю. Белецкая, Н.В. Боковая, Ю.В. Минаева // Интеллектуализация управления в социальных и экономических системах: труды Всерос. конф. Воронеж: ВГТУ, 2009. C. 11-14.

37. Белецкая С.Ю. Формирование оптимальной производственной программы предприятия / С.Ю. Белецкая, Н.В. Боковая, Ю.В. Минаева // Интеллектуализация управления в социальных и экономических системах: труды Всерос. конф. Воронеж: ВГТУ, 2009. C. 52-53.

38. Белецкая С.Ю. Применение многометодных поисковых процедур при решении задач автоматизированного проектирования / С.Ю. Белецкая, Н.В. Боковая, Ю.В. Минаева // Оптимизация и моделирование в автоматизированных системах: межвуз. сб. науч. тр. Воронеж, 2009. С. 256-259.

39. Боковая Н.В. Принципы алгоритмизации задач оптимального проектирования сложных производственных систем / Н.В. Боковая, С.Ю. Белецкая // Оптимизация и моделирование в автоматизированных системах: межвуз. сб. науч. тр. Воронеж, 2009. С. 105-112.

40. Белецкая С.Ю. Решение задач структурного синтеза сложных систем на основе модифицированной схемы ветвей и границ / С.Ю. Белецкая, Н.В. Боковая // Прикладные задачи моделирования и оптимизации: межвуз. сб. науч. тр. Воронеж: ВГТУ, 2009. С. 16-21.

41. Белецкая С.Ю. Структурно-параметрический синтез развивающихся производственных систем / С.Ю. Белецкая, Н.В. Боковая // Прикладные задачи моделирования и оптимизации: межвуз. сб. науч. тр. Воронеж: ВГТУ, 2009. С. 389-396.

42. Боковая Н.В. Основные направления модернизации и развития производственных систем / Н.В. Боковая, С.Ю. Белецкая // Управление в социальных и экономических системах: межвуз. сб. науч. тр. Воронеж, 2009. С. 51-54.

43. Боковая Н.В. Математическая модель построения производственной программы предприятия / Н.В. Боковая, С.Ю. Белецкая // Управление в социальных и экономических системах: межвуз. сб. науч. тр. Воронеж, 2009. С. 422-425.

44. Боковая Н.В. Математическая модель оптимального выбора варианта модернизации производственной системы / Н.В. Боковая, С.Ю. Белецкая // Системные проблемы надежности, качества, информационно-телекоммуникационных и электронных технологий в управлении инновационными проектами (Инноватика-2009): сб. тр. Междунар. конф. М., 2009. Ч.4. С. 81-85.

45. Боковая Н.В. Модели проектирования производственных участков с оборудованием многоцелевого назначения / Н.В. Боковая, С.Ю. Белецкая // Прикладные задачи моделирования и оптимизации: межвуз. сб. науч. тр. - Воронеж: ВГТУ, 2009. С. 301-304.

46. Белецкая С.Ю. Организация интеллектуальной многометодной среды оптимального проектирования производственных систем / С.Ю. Белецкая, Н.В. Боковая // Оптимизация и моделирование в автоматизированных системах: межвуз. сб. науч. тр. Воронеж, 2009. С. 11-15.

47. Белецкая С.Ю. Модель оптимального производственного планирования / С.Ю. Белецкая, Н.В. Боковая, Ю.В. Минаева // Прикладные задачи моделирования и оптимизации: межвуз. сб. науч. тр. Воронеж: ВГТУ, 2009. С. 102-105.

48. Белецкая С.Ю. Преобразование оптимизационных моделей при проектировании производственных систем / С.Ю. Белецкая, Н.В. Боковая. // Материалы и упрочняющие технологии: сб. ма­териалов XVI Рос. науч.-техн. конф. с междунар. участием. Курск: Курск. гос. техн. ун-т, 2009. Ч.2. C. 109-116.

49. Боковая Н.В. Математические модели параметрической оптимизации производственных систем / Н.В. Боковая // Материалы и упрочняющие технологии: сб. ма­териалов XVI Рос. науч.-техн. конф. с междунар. участием. Курск: Курск. гос. техн. ун-т, 2009. Ч.2. C. 117-122.

50. Боковая Н.В. Повышение эффективности функционирования промышленного предприятия на базе современных ERP-систем / Н.В. Боковая // Научные исследования в области транспортных, авиационных и космических систем: труды X Всерос. науч.-техн. конф. Воронеж, 2009. С. 500-504.

51. Боковая Н.В. Интеллектуализация поиска оптимальных проектных решений на основе многометодного подхода / Н.В. Боковая, С.Ю. Белецкая // Математические методы в технике и технологиях: ММТТ-22: сб. трудов XXII Междунар. науч. конф. Псков: Изд-во Псков. гос. политех. ин-та, 2009. Т.6. С. 29-31.

52. Белецкая С.Ю. Использование элементов теории управления при моделировании экономических систем / С.Ю. Белецкая, О.Г. Яскевич, Н.В. Боковая // Моделирование систем и информационные технологии: межвуз. сб. науч. тр. Воронеж: Научная книга, 2010. С. 25-28.

53. Белецкая С.Ю. Интеллектуализация поиска оптимальных решений при проектировании производственных систем / С.Ю. Белецкая, Н.В. Боковая, О.Г. Яскевич // Моделирование систем и информационные технологии: межвуз. сб. науч. тр. Воронеж: Научная книга, 2010. С. 21-24.

54. Боковая Н.В. Построение рандомизированных процедур оптимального проектирования производственных систем / Н.В. Боковая, С.Ю. Белецкая // Интеллектуальные информационные системы: труды Всерос. конф. Воронеж: ВГТУ, 2010. С. 20-21.

55. Белецкая С.Ю. Организация программного обеспечения анализа и синтеза сложных производственных систем / С.Ю. Белецкая, Н.В. Боковая // Интеллектуализация управления в социальных и экономических системах: труды Всерос. конф. Воронеж: ВГТУ, 2010. C. 33-34.

56. Боковая Н.В. Сокращение размерности оптимизационных задач при проектировании производственных систем / Н.В. Боковая // Интеллектуальные информационные системы: труды Всерос. конф. Воронеж: ВГТУ, 2010. С. 6-7.

Подписано в печать 08.07.2010.

Формат 60x84/16. Бумага для множительных аппаратов.

Усл. печ. л. 2,0. Тираж 90 экз. Заказ № __

ГОУ ВПО «Воронежский государственный технический университет»

394026 Воронеж, Московский просп., 14