Разработка и исследование методов решения трехиндексных распределительных задач с нечеткими параметрами
На правах рукописи
Борисова Елена Александровна
РАЗРАБОТКА И ИССЛЕДОВАНИЕ МЕТОДОВ РЕШЕНИЯ ТРЕХИНДЕКСНЫХ РАСПРЕДЕЛИТЕЛЬНЫХ ЗАДАЧ С НЕЧЕТКИМИ ПАРАМЕТРАМИ
Специальность:
05.13.17 «Теоретические основы информатики»
АВТОРЕФЕРАТ
диссертации на соискание ученой степени
кандидата технических наук
Таганрог - 2008
Работа выполнена в Технологическом институте Южного федерального университета на кафедре систем автоматического управления
Научный руководитель: доктор технических наук, профессор,
Финаев Валерий Иванович
Официальные оппоненты: доктор технических наук, профессор
Ромм Яков Евсеевич,
доктор технических наук, профессор
Горелова Галина Викторовна
Ведущая организация: Южно-Российский государственный университет экономики и сервиса (ЮРГУЭС) (г. Шахты)
Защита состоится « » 2008 г. в часов на заседании диссертационного совета Д 212.208.21 при Технологическом институте Южного федерального университета по адресу: пер. Некрасовский, 44, ауд. Д-406 ГСП-17А, г.Таганрог, Ростовская область, 347928.
С диссертацией можно ознакомиться в Зональной научной библиотеке Южного федерального университета по адресу: ул. Пушкинская, 148, г.Ростов-на-Дону, 3444000.
Автореферат разослан « » 2008 г.
Ученый секретарь
диссертационного совета Д 212.208.21
доктор технических наук, профессор Н.И. Чернов
ОБЩАЯ ХАРАКТЕРИСТИКА РАБОТЫ
Актуальность темы. Решение задач транспортного типа необходимо при составлении оптимального плана перевозки груза от производителей непосредственно или поставщиков к потребителям, общее число которых может быть достаточно большим, порядка нескольких сотен. От успешного решения распределительных задач зависит эффективность производства, а повышение эффективности управления производством зависит от применения математических знаний, применения новых математических методов, включая методы искусственного интеллекта. При решении практических задач всегда невозможно гарантированно четко указать, какие численные значения будут иметь параметры распределительной задачи. Причинами подобного представления являются непредсказуемые изменения в структуре производителей, поставщиков и потребителей, неучитываемые воздействия во внешней среде, что влечет за собой невозможность точного установления начальных параметров. В диссертационной работе ставится задача развития известных методов решения распределительных (транспортных) задач при условии задания параметров задач в виде нечетких интервалов. Данный подход позволяет получать достоверные результаты в том случае, когда существует неопределенность при задании параметров, существуют ограничения допусков на изменения параметров задачи.
Диссертационная работа посвящена разработке моделей и методов решения трипланарных и триаксиальных распределительных задач при нечетком задании параметров в виде нечетких интервалов, что позволяет определять оптимальный план решения задачи также в виде нечетких интервалов. Это определяет и подтверждает актуальность диссертационной работы.
Цель диссертационной работы состоит в развитии методов системного анализа, в частности, раздела исследования операций, связанного с решением распределительных задач, нечеткого ситуационного управления применительно к транспортным задачам.
Объект исследования. Объектом исследования в диссертационной работе являются математические модели трипланарных и триаксиальных распределительных задач, методы разработки моделей принятия решений, а также информационно-управляющая система для решения транспортных задач.
Основные задачи исследования. Для достижения поставленной цели решены следующие основные задачи:
- разработка системного подхода к решению трехиндексных распределительных задач, включающего формализацию и решение распределительной задачи как системы с определенными закономерностями, применением для моделирования, как аналитических, так и неформальных подходов;
- разработка модели, метода формализации трипланарной транспортной задачи с нечеткими параметрами;
- формулировка задачи и определение условий решения двойственной нечеткой трипланарной транспортной задачи, условий оптимальности плана нечеткой трипланарной транспортной задачи;
- разработка метода и алгоритмов построения начального опорного плана в виде нечетких интервалов или чисел нечеткой трипланарной транспортной задачи;
- разработка метода и алгоритмов решения нечеткой трипланарной транспортной задачи;
- разработка модели, метода формализации триаксиальной транспортной задачи с нечеткими параметрами;
- определение необходимых и достаточных условий разрешимости нечеткой триаксиальной транспортной задачи, условий существования невырожденного плана решения задачи;
- разработка метода и алгоритмов построения начального опорного плана, а также метод потенциалов для решения нечеткой триаксиальной транспортной задачи и выполнена его алгоритмизация;
- разработка программных модулей для решения трипланарной и триаксиальной транспортной задачи с нечеткими параметрами.
Основные научные результаты:
- системный подход к решению трехиндексных распределительных задач, отличающийся тем, что для решения распределительных задач применяется последовательность методов системного анализа, для разработки математических моделей применяются аналитические и неформальные подходы, а в условиях априорной неопределенности для формализации параметров задач применяются нечеткие интервалы, лингвистические и нечеткие переменные, задаются функции принадлежности нечетких переменных, а также правила принятия решений;
- метод формализации и решения трипланарной транспортной задачи, отличающийся заданием параметров задачи в виде нечетких интервалов, заданием целевой функции, как нечеткой функции, определяющей величину транспортных издержек, формализацией условий разрешимости задачи, позволяющих определить оптимальный план транспортной задачи, содержащий параметры в виде нечетких интервалов;
- метод формализации и решения триаксиальной транспортной задачи, отличие которого состоит в формализации параметров в виде нечетких интервалов, нечеткой целевой функции, определении необходимых и достаточных условий разрешимости задачи, позволяющих определить невырожденный план задачи в виде нечетких интервалов.
Практическая ценность результатов исследований определена их применением на предприятиях в структуре информационно-управляющих систем, в задачах управления подготовкой производством, технико-экономического планирования, оперативного управления. Задание параметров задач в виде нечетких интервалов повышает степень информированности лиц, принимающих решения.
Методы проведения исследования. В диссертационной работе использованы методы исследования операций, методы функционального анализа, теория нечетких множеств, теория систем. В экспериментальных исследованиях применялось моделирование на ЭВМ.
Достоверность получаемых в диссертации результатов подтверждается логическими выводами, программными приложениями, публикациями на международных и региональных научно-технических конференциях.
Реализация и внедрение результатов работы. Результаты работы внедрены в ООО НПП «ДортрансНИИ-Инжиниринг» (г. Ростов-на-Дону), в Ростовском филиале ВНИИАС МПС России, при выполнении научно-исследовательской работы, а также в учебном процессе на кафедре системного анализа и телекоммуникаций Технологического института Южного федерального университета.
Апробация результатов работы. Научные и практические результаты, полученные в диссертации, изложены в монографии, использованы при постановке лабораторных работ на кафедре системного анализа и телекоммуникаций Технологического института Южного федерального университета.
Основные результаты докладывались и обсуждались на международной научной конференции «Статистические методы в естественных, гуманитарных и технических науках (СМ-2006)» (Таганрог, 2006), VIII Всероссийской научной конференции студентов и аспирантов «Техническая кибернетика, радиоэлектроника и системы управления» (Таганрог, 2006), международной научной конференции «Информационные технологии в современном мире» (Таганрог, 2006), международной научно-технической конференции «Интеллектуальные системы. Интеллектуальные САПР» (Москва, 2006), международной научной конференции «Проблемы развития естественных, технических и социальных систем» (Таганрог, 2007), международной научной конференции «Проектирование новой реальности» (ПНР-2007) (Таганрог, 2007).
Публикация. По теме диссертационной работы опубликована монография, четыре статьи и тезисы шести докладов.
Структура и объем работы. Диссертационная работа содержит 186 страниц машинописного текста, включая введение, четыре раздела, заключение, приложение, список литературы из 110 наименований, 49 рисунка, 12 таблиц.
КРАТКОЕ СОДЕРЖАНИЕ ДИССЕРТАЦИИ
Во введении обоснована актуальность темы, сформулированы цель исследования, научная новизна, практическая ценность, основные положения, выносимые на защиту, достоверность и обоснованность научных положений диссертации, апробация работы. Кратко рассмотрено содержание разделов диссертации.
В первом разделе разработан системный подход к решению трехиндексных распределительных задач, рассмотрена формализация и решение распределительной задачи как системы.
Сложное взаимодействие распределительной задачи, как системы с ее окружением, отражено в определении: S<A, QA, R, QR, C, CU, T, N, LN>, где A={ai}, iI={1,2,…,n} – множество элементов распределительной задачи, QA – множество свойств элементов распределительной задачи, определяющих условия (выбор методов) решения, R={rj}, jJ={1,2,…,m} – множество информационных и других видов связей между элементами, QR – множество свойств связей элементов, C – цель решения распределительной задачи, формулирующая критериальную функцию и условия достижение экстремальных значений этой функции, U – условия целеобразования, T – интервал времени, в течение которого будет существовать оптимальное решение распределительной задачи, N – лица (наблюдатели), принимающие решения относительно оптимального решения распределительной задачи, LN – язык общения наблюдателей.
Введенное определение распределительной задачи как системы, позволяет выделить из окружающей среды по ряду признаков обособленный объект - распределительную задачу и рассматривать этот объект и как совокупность взаимосвязанных элементов, и как элемент более общей системы предприятия или объектов для которых решается распределительная задача.
Распределительным задачам свойственны закономерности систем: закономерность взаимодействия части и целого; закономерность физической аддитивности; закономерность коммуникативности; закономерность историчности; закономерность эквифинальности; закономерности потенциальной эффективности. Изучение закономерностей позволяет уточнить представление об объекте, разрабатывать рекомендации по совершенствованию организационных систем, применять методы системного анализа.
Исследование опыта системного подхода позволяет предложить для решения распределительных задач последовательность методов системного анализа, приведенную на рис. 1.
При анализе методов моделирования отмечено, что в математических моделях далеко не всегда могут найти отражение особенности всех факторов, от которых зависит решение задач, поэтому при разработке моделей применяют неформальные подходы.
При решении задач исследования операций формализуют параметры задачи и определяют критериальную функцию, связывающую цель решения задачи со средствами ее достижения. Критериальная функция (целевая функция) и ограничения определяют аналитическую модель распределительной задачи, которая в общем случае задается следующим образом. Осуществляется поиск максимума (минимума) целевой функции E=f(X,Y)
max (min) E=f(X,Y), (1)
при заданных ограничениях gi(X,Y)bi, 
, где: X вектор управляемых переменных; Y вектор неуправляемых переменных; gi функция потребления i–го ресурса: bi величина i–го ресурса. Для нахождения оптимального решения задачи (1) применяются методы математического программирования.
Рис. 1
Рассмотрены аналитические модели распределительных задач, модели достаточно часто встречающихся на практике трипланарных и триаксиальных транспортных задач. Произведен анализ алгоритмов решения распределительных задач.
В диссертационной работе ставится задача развития известных методов решения распределительных (транспортных) задач при условии задания параметров задач в виде нечетких интервалов. Данный подход позволяет получать достоверные результаты в том случае, когда невозможно гарантированно четко указать, сколько транспортных средств будет участвовать в перевозках, какое количество продукции находится в распоряжении i-ro предприятия, чему равна стоимость перевозки единицы объема продукта и прочее.
Задание параметров трипланарной и триаксиальной транспортной задачи в виде нечетких интервалов является более общим способом формализации этих параметров, позволяющим учитывать существующую априорную неопределенность. Результат решения распределительной задачи будет представлять собой множество – нечеткий план или нечеткий оптимальный план, который будет представлять собой множество нечетких интервалов.
Рассмотрено применение новых информационных технологий для решения распределительных задач.
Целями проектирования информационно-управляющих систем для решения распределительных задач являются: создание баз данных производителей и потребителей продукции; создание базы данных продукции; создание базы данных стоимостей перевозок; создание базы знаний; проектирование программных модулей для решения распределительных задач.
Исходя из поставленных целей, предложена структура информационно-управляющей системы в виде, показанном на рис. 2.
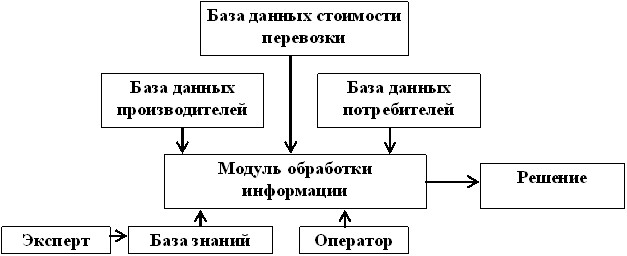
Рис. 2
Во втором разделе разработан метод формализации и решения трипланарной транспортной задачи с нечеткими параметрами. Определены следующие нечеткие интервалы:
- 
iI - нечеткое множество, определяющее нечеткое количество продукции, находящейся в распоряжении i-ro предприятия;
- 
, jJ – нечеткое множество, определяющее нечеткое количество продукции, необходимое j–му потребителю;
- 
, kK – нечеткое множество, определяющее нечеткое количество продукции, которое может быть перевезено единицами транспорта k–го типа;
- 
, iI, jJ, kK - нечеткое множество, определяющее нечеткую стоимость транспортировки единицы продукта от i-ro предприятия к j–му потребителю транспортным средством k–го типа;
- {
}, iI, jJ, kK – множество представляющее собой трехмерную матрицу (нечеткий план перевозки) нечетких интервалов 
, каждый из которых определяет нечеткое количество продукции, планируемое для перевозки от i-ro предприятия к j–му потребителю транспортным средством k–го типа.
Нечеткий план транспортировки при решении задачи с нечеткими параметрами должен удовлетворять условиям:
- верхнее модальное значение нечеткого количества продукции плюс правый коэффициент нечеткости, планируемое для вывоза из каждого предприятия, не должно превышать соответствующий нечеткий запас;
- верхнее модальное значение нечеткого количества продукции плюс правый коэффициент нечеткости, планируемое для ввоза каждому потребителю, должно быть не меньше его нечеткой потребности;
- общее нечеткое количество продукции плюс правый коэффициент нечеткости, планируемое для перевозки транспортным средством k-то типа, не должно превышать возможности данных средств.
При нечетком определении параметров трипланарной транспортной задачи формализация выше приведенных условий имеет вид:
, 
, 
где 
- нечеткое неравенство.
Вводя нечеткое равенство 
в приведенные выше условия, получим:
, 
,
. xijk
0, iI, jJ, kK. (2)
Целевая функция, определяющая величину транспортных издержек, также представлена, как нечеткая функция и определится уравнением:
(3)
Множество нечетких интервалов {
} называют нечетким планом задачи. Каждому нечеткому плану соответствует определенное значение нечеткой целевой функции (3). Если существует нечеткий план, обеспечивающий минимальное нечеткое значение целевой функции на множестве всех допустимых нечетких планов, то данный нечеткий план назовем оптимальным нечетким планом задачи. Задача линейного программирования будет нечетко разрешима, если существует оптимальный нечеткий план, который назовем нечетким решением задачи.
Рассмотрено условие разрешимости нечеткой трипланарной транспортной задачи. Для разрешимости нечеткой трипланарной транспортной задачи необходимо и достаточно выполнения условия нечеткого баланса
, (4)
где 
- нечеткий интервал.
Приведено доказательство необходимости и достаточности условия (4). Если условие нечеткого баланса (4) системы нечетких ограничений (2) выполняется, то транспортную задачу будем назвать нечетко сбалансированной. В нечетко сбалансированной трипланарной транспортной задаче общее количество продукции, заданное в виде нечеткого интервала, вывозимое из предприятий, нечетко равно общему спросу потребителей, и с общей грузоподъемностью выделенных разнотипных транспортных средств, также заданными в виде нечетких интервалов.
Сформулирована задача и определены условия решения двойственной нечеткой трипланарной транспортной задачи, условия оптимальности плана нечеткой трипланарной транспортной задачи. Для решения двойственной задачи необходимо найти вектор нечетких переменных 
максимизирующий функцию
(5)
и удовлетворяющий ограничениям
. (6)
Величины 
назовем нечеткими потенциалами задачи.
Для оптимальности плана X нечеткой трипланарной транспортной задачи необходимо и достаточно существования нечетких интервалов 
, таких, что
, (7)
причем 
.
Нечеткая трипланарная транспортная задача имеет единственный нечеткий оптимальный план X={
} тогда и только тогда, когда удовлетворяются условия
;
.
В противном случае нечеткая трипланарная транспортная задача может содержать множество нечетких оптимальных решений, которым соответствует одно и то же значение целевой функции.
Разработан метод и алгоритмы построения начального опорного плана в виде нечетких интервалов или чисел нечеткой трипланарной транспортной задачи, который соответствует методу последовательного распределения. Разработан метод потенциалов для решения нечеткой трипланарной транспортной задачи, который является обобщением известного метода потенциалов для решения трипланарной транспортной задачи с четко заданными параметрами.
Процесс решения задачи, который состоит из конечного числа однотипных итераций, составляющих основной этап алгоритм решения. Каждая итерация основного этапа состоит из двух шагов. На первом шаге проверяется оптимальность полученного в предыдущей итерации (или на предварительном этапе) опорного плана. При этом используется критерий нечеткой оптимальности. Если найденный план нечетко оптимален, то процесс решения оканчивается. Иначе выполняется второй шаг итерации, на котором получают новый опорный план, более близкий к оптимальному (с меньшим значением нечеткой целевой функции нечеткой трипланарной транспортной задачи).
На рис. 3 приведен обобщенный алгоритм решения нечеткой трипланарной транспортной задачи описанным выше методом.
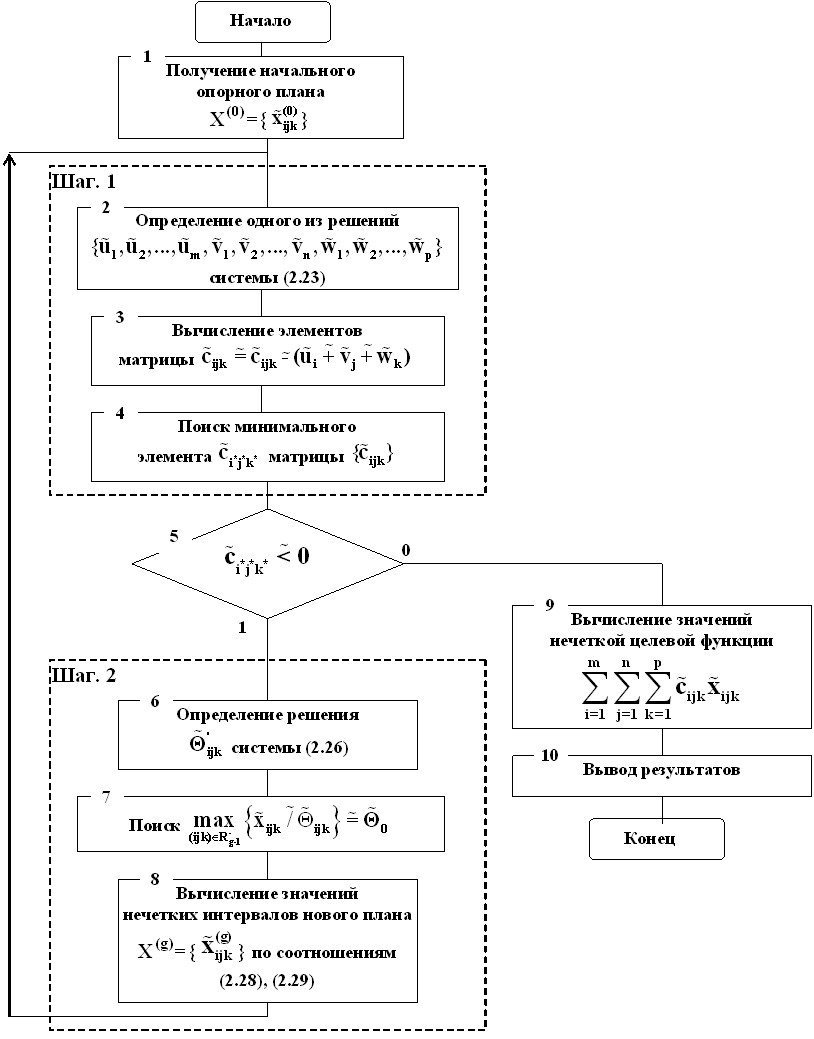
Рис. 3
Разработан алгоритм поиска начального опорного плана. Компоненты исходного плана заданы в виде нечетких интервалов, поэтому согласно правилу задания нечетких интервалов, исходный план представим в виде композиции четырех исходных планов, компоненты которого соответствуют: - нижним граничным значениям нечетких интервалов; 
- нижним модальным значениям нечетких интервалов; 
- верхним модальным значениям нечетких интервалов; - верхним граничным значениям нечетких интервалов. Алгоритм построения начального опорного плана рассматривается отдельно для каждого из четырех исходный планов.
Разработан алгоритм метода потенциалов.
В третьем разделе диссертационной работы разработан метод формализации и алгоритмы решения триаксиальной транспортной задачи при задании параметров модели в виде нечетких интервалов. Определим следующие нечеткие интервалы:
- 
- нечеткое множество, определяющее нечеткое количество продукции, поставляемой i-м производителем j-му потребителю;
- 
– нечеткое множество, определяющее нечеткое количество продукта k, необходимое потребителю j;
- 
– нечеткое множество, определяющее нечеткое количество продукта k, выпускаемого производителем i;
- 
, iI, jJ, kK - нечеткое множество, определяющее нечеткую стоимость транспортировки единицы продукта от i-ro предприятия к j–му потребителю транспортным средством k–го типа;
- {
}, iI, jJ, kK – трехмерная матрица (нечеткий план перевозки).
Решение триаксиальной транспортной задачи с нечеткими параметрами направлено на получение такого нечеткого плана перевозки, который минимизирует транспортные расходы, т.е. необходимо определить множество 
, состоящее из нечетких интервалов 
и минимизирующее нечеткую целевую функцию
(8)
и удовлетворяющий ограничениям:
, 
,
, xijk
0, iI, jJ, kK. (9)
Для разрешимости нечеткой триаксиальной транспортной задачи необходимо выполнение следующих условий:
, 
,
, 
. (10)
Условия (10) представляют собой условия нечеткого баланса нечеткой триаксиальной транспортной задачи.
Нечетко сбалансированная триаксиальная транспортная задача с параметрами, заданными в виде нечетких интервалов разрешима, если
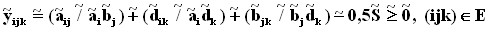, (11)
где 
, 
, 
, 
, E=IJK.
Неразрешимость нечеткой триаксиальной транспортной задачи говорит о том, что не существует плана перевозок, компоненты которого нечетко положительны, т.е. плана, не содержащего обратных перевозок и удовлетворяющего условиям задачи.
Осуществлено исследование свойств нечеткой триаксиальной транспортной задачи. Разработан метод и алгоритм построения начального опорного плана, а также метод потенциалов для решения нечеткой триаксиальной транспортной задачи и выполнена его алгоритмизация.
Общий алгоритм построения опорного плана нечеткой триаксиальной транспортной задачи разделен на два этапа.
На первом этапе алгоритма используется метод последовательного распределения, учитывающий наряду с аксиальными нечеткими ограничениями верхние и нижние границы нечеткого интервала 
. Метод позволяет построить набор нечетко неотрицательных переменных {
}, удовлетворяющий условиям
, 
,
, (12)
Если условия (12) выполняются как нечеткие равенства, то множество нечетких интервалов {
} представляет собой опорный план нечеткой триаксиальной транспортной задачи. В противном случае осуществляется переход ко второму этапу, на котором формулируется расширенная нечеткая Триаксиальная транспортная задача размера (m+1)(n+1)(p+1), эквивалентная исходной, и для нее строится опорный план.
На втором этапе осуществляется поиск множества нечетких интервалов
, i{1,2,…,m+1}=I’, j{1,2,…,n+1}=J’, k{1,2,…,p+1}=K’.
минимизирующего функцию
(13)
и удовлетворяющего ограничениям
, 
,
, 
(14)
где
(15)
M - достаточно большое число;
,
, 
,
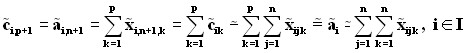. (16)
Найденное оптимальное решение в виде множества нечетких интервалов 
задачи (13) - (16) содержит в себе оптимальное решение 
исходной нечеткой триаксиальной транспортной задачи, причем 
, а множество нечетких интервалов
есть опорный план задачи.
Разработан метод потенциалов и алгоритмы для решения нечеткой триаксиальной транспортной задачи
На первом шаге алгоритма с помощью критерия оптимальности проверяется нечеткая оптимальность опорного плана, полученного в предыдущей итерации или на предварительном этапе. Если план нечетко оптимален, то процесс решения считается завершенным. В противном случае выполняется второй шаг итерации, на котором формируется новый опорный план с меньшим значением нечеткой целевой функции задачи.
Разработан алгоритм проверки условий разрешимости нечеткой трипланарной транспортной задачи, который работает до тех пор, пока не будет получен опорный план с ненулевыми значениями для всех нижних граничных значений нечетких интервалов, нижних модальных значений нечетких интервалов, верхних модальных значений нечетких интервалов, верхних граничных значений нечетких интервалов нечеткого опорного плана.
В четвертом разделе разработаны проблемно-ориентированные программные приложений, предназначенных для решения распределительных задач с нечеткими параметрами. Определено назначение распределительных задач в структуре информационно-управляющих систем, а также применение решения распределительных задач и их практическая значимость в других задачах управления производством. Иллюстративно практическая значимость методов решения распределительных задач показана на рис. 4.
Разработаны структура и программные приложения для решения трипланарной и триаксиальной транспортной задачи с нечеткими параметрами. Рассмотрены примеры решения задач, которые демонстрируют возможность проведения исследования.
Итогом решения является определение оптимального нечеткого плана транспортной задачи, а также возможность эвристического поиска параметров задачи, удовлетворяющих условию минимизации целевой функции.
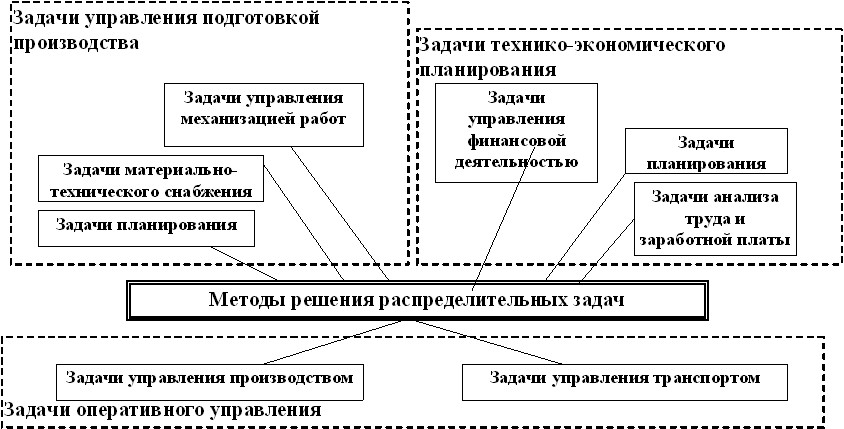
Рис. 4
Расширенный интерфейс предоставляет пользователю возможность ввести значения нечеткого количества продукции, находящегося в распоряжении i-ro центра производства, нечеткого количества продукции, необходимого j–му центру производства, нечеткого количества продукции, которое может быть перевезено всеми единицами транспорта k–го типа. Полученные решения показывают возможности разработанного метода решения трипланарной транспортной задачи с нечеткими параметрами. В итоге можно получить оптимальный план транспортной задачи, позволяющий варьировать, как производством, так и потреблением продукции при сохранении условия минимизации нечеткой целевой функции.
Заключение содержит выводы о работе.
ОСНОВНЫЕ РЕЗУЛЬТАТЫ
1. Разработана концепция системного подхода к решению трехиндексных распределительных задач, отличающаяся тем, что для решения распределительных задач применяется последовательность методов системного анализа, для разработки математических моделей применять аналитические и неформальные методы моделирования, а в условиях априорной неопределенности для формализации параметров задач применять нечеткие интервалы, лингвистические и нечеткие переменные, задать функции принадлежности нечетких переменных, а также правила принятия решений.
2. Разработан метод формализации и решения трипланарной транспортной задачи, отличающийся заданием параметров задачи в виде нечетких интервалов, заданием целевой функции как нечеткой функции, определяющей величину транспортных издержек, формализацией условий разрешимости задачи, позволяющих определить оптимальный план транспортной задачи, содержащий параметры в виде нечетких интервалов.
3. Разработан метод формализации и решения триаксиальной транспортной задачи, отличие которого состоит в формализации параметров в виде нечетких интервалов, нечеткой целевой функции, определением необходимых и достаточных условий разрешимости задачи, позволяющих определить невырожденный план задачи в виде нечетких интервалов.
4. Разработаны алгоритмы построения начального опорного плана и алгоритмы решения нечеткой трипланарной и триаксиальной транспортной задачи.
5.Разработаны программные приложения для решения трипланарной и триаксиальной транспортной задачи с нечеткими параметрами.
6. Получены результаты, свидетельствующие об эффективности предложенных моделей.
ОСНОВНЫЕ ПУБЛИКАЦИИ ПО ТЕМЕ
1. Финаев В.И., Борисова Е.А. Нечеткие интервальные оценки в распределительных задачах. Межвузовский сборник научных трудов «Математическое и программное обеспечение вычислительных систем». – Рязань: РГРУ, изд-во «Горячая линия – Телеком г.Москва», 2006.
2. Борисова Е.А., Финаев В.И. Триаксиальная распределительная задача с нечеткими параметрами//Материалы международной научно-технической конференции «Интеллектуальные системы, «Интеллектуальные САПР». – М.: Физматлит, 2006. С. 219-225.
3. Борисова Е.И., Немченко С.В. Оптимальное решение транспортной задачи при нечетком задании параметров. Материалы VIII Всероссийской научной конференции студентов и аспирантов «Техническая кибернетика, радиоэлектроника и системы управления». – Таганрог: ТРТУ, 2006.
4. Борисова Е.А., Финаев В.И. Триаксиальная распределительная задача с нечеткими параметрами// Известия ТРТУ. Тематический выпуск «Интеллектуальные САПР». – Таганрог: Изд-во ТРТУ, 2006, №8(63). – С. 17-21.
5. Борисова Е.А., Финаев В.И. Вероятностный прогноз в распределительных задачах// Материалы международной научной конференции «Статистические методы в естественных, гуманитарных и технических науках (СМ-2006)» Часть 2 – Таганрог: ТРТУ, 2006.
6. Борисова Е.А. Вероятностный прогноз в распределительных задачах//Материалы международной научной конференции «Информационные технологии в современном мире». Часть 2. – Таганрог: ТРТУ, 2006.
7. Борисова Е.И. Поиск оптимального решения многомерной распределительной задачи с нечеткими параметрами//Межвузовский сборник научных работ «Системный анализ, обработка информации и управление». Вып. 1. Ростов-Дон: Изд-во ДГТУ, 2007.
8. Борисова Е.А., Финаев В.И. Разрешимость триаксиальной задачи с нечеткими параметрами//Известия ТРТУ. Тематический выпуск «Интеллектуальные САПР». – Таганрог: Изд-во ТРТУ, 2007, №1(73). – 294 с., С.. 5-8.
9. Борисова Е.А., Финаев В.И. Применение информационных технологий при решении распределительных задач. Сб. тезисов докладов международной научной конференции «Проблемы развития естественных, технических и социальных систем». Ч.4 - Таганрог: Изд-во «Антон», ТТИ ЮФУ, 2007
10. Борисова Е.А., Заргарян Е.В. Системный подход к решению распределительных задач//Материалы Международной научной конференции «Проектирование новой реальности» (ПНР-2007). Ч. 1. - Таганрог: Изд-во ТТИ ЮФУ, 2007.
11. Борисова Е.А., Финаев В.И. Трехиндексные распределительные задачи с нечеткими параметрами/Монография. – Таганрог: Изд-во ТТИ ЮФУ, 2007. - 190с.
Лично автором в работах [1] предложено применение нечетких интервальных оценок для решения распределительных задач; в работах [2,4] осуществлена постановка триаксиальной распределительной задачи с нечеткими параметрами задачи; в работе [3] сформулированы требования к оптимальному решению транспортной задачи при нечетком задании параметров; в работе [5] предложены статистические оценки для определения начальных значений параметров распределительных задач; в работе [80] сформулированы условия разрешимости триаксиальной задачи с нечеткими параметрами; в работе [5] предложены концепции применения новых информационных технологий для решения распределительных задач; в работе [10] разработан и изложен системный подход к решению распределительных задач; в работе [11] самостоятельно написаны второй и третий разделы, посвященные формализации и поиску решений трипланарных и триаксиальных транспортных задач, в разделе 1 изложена концепция системного пдхода, в четвертом разделе разработана структура проблемно-ориентированных программных приложений и приведены результаты экспериментов.
Соискатель Е.А.Борисова
_______________________________________________________________________Отпечатано на лазерном принтере. Тираж 100 экз. 2008 г.
