Физико-химические свойства жидких d 2 o и h 2 o с позиций модели обратимых переходов квантовый газ - конденсат
На правах рукописи
БАРЫШЕВ АЛЕКСАНДР НИКОЛАЕВИЧ
ФИЗИКО-ХИМИЧЕСКИЕ СВОЙСТВА ЖИДКИХ D2O И H2O С ПОЗИЦИЙ МОДЕЛИ ОБРАТИМЫХ ПЕРЕХОДОВ КВАНТОВЫЙ ГАЗ - КОНДЕНСАТ
Специальность 02.00.04 – физическая химия
Автореферат диссертации
на соискание ученой степени
кандидата химических наук
САНКТ-ПЕТЕРБУРГ
2011
Работа выполнена на кафедре неорганической химии и биофизики ФГОУ ВПО «Санкт-Петербургская государственная академия ветеринарной медицины»
| Научный руководитель: | доктор химических наук, профессор Саргаев Павел Маркелович |
| Официальные оппоненты: | доктор химических наук, профессор Зарембо Виктор Иосифович доктор химических наук, профессор Слободов Александр Арсеньевич |
| Ведущая организация: | ОАО “Головной институт “ВНИПИЭТ” |
Защита состоится «20» апреля 2011 года в 15 час. в ауд. А-233 на заседании диссертационного совета Д 212.231.02 при Санкт-Петербургском технологическом университете растительных полимеров (СПбГТУРП) по адресу 198095, г. Санкт-Петербург, ул. Ивана Черных, 4.
С диссертацией можно ознакомиться в библиотеке СПбГТУРП.
Автореферат разослан «25» февраля 2011 г.
Ученый секретарь совета, к.х.н. А.Н. Евдокимов
ОБЩАЯ ХАРАКТЕРИСТИКА ДИССЕРТАЦИИ
Актуальность работы
Несмотря на кажущуюся всесторонность изучения структуры и свойств H2O (протиевой, легкой воды) она всё еще является полным загадок и невероятных свойств веществом и ставит перед исследователем ряд нерешенных вопросов и тонкостей, требующих разработки и применения самых совершенных методов исследований. Результатом развития технологий в атомной промышленности является крупнотоннажное производство и потребление D2O (дейтериевой, тяжелой воды). Физико-химические свойства последней незначительно отличаются от H2O-воды. Несмотря на это концентрированные растворы D2O являются, в отличие от H2O, токсичными. Близость свойств D2O и H2O не позволяет также однозначно решить проблемы с различным биологическим действием этих жидкостей исключительно экспериментальным путём.
Из-за трудностей экспериментальных исследований D2O-воды возрастает значимость развития и использования методов моделирования её физико-химических свойств. Сложности моделирования теплоемкости переохлажденной D2O связаны, главным образом, с отсутствием концепции конфигурационной составляющей.
Более успешно продвигается описание свойств переохлажденной H2O-воды: Так, широко используемое уравнение (Murphy, Koop, 2005) для расчета изобарной теплоемкости Ср при температурах от 167K до 231K дает максимум Ср (127 J / (mole K)) при 225 K. Однако из анализа расчетных значений следует, что в области температур ниже 200 K значения Ср не вполне адекватны имеющейся информации. При оценках энтальпии и энтропии по приведенным данным не обнаруживается скачкообразное изменение теплоемкости при переходе из жидкого в стеклообразное состояние, которое убедительно обосновано.
Теоретическое обоснование формы кривой температурной зависимости конфигурационной составляющей, а также изохорной и изобарной теплоемкости воды H2O с максимумом при температурах 220-240K и скачкообразным изменением в области температуры фазового перехода второго рода предложено на основании модели «структурных единиц жидкости» и теории перколяции (Саргаев П.М.). В процессе дальнейшего моделирования теплоемкости и особенностей структуры воды в жидком состоянии в рамках модели структурных единиц жидкости получены уравнения для оценки составляющих теплоемкости тяжелой воды в температурном интервале от 0 K до критической.
Далее дано обоснование принципиальных различий теплоемкости D2O- и H2O-жидкостей (в рамках теории одноатомного квантового газа по Эйнштейну); порога перколяции по узлам (а не по связям) тетраэдрической решетки; обоснована необходимость использования векторных представлений для описания структуры воды; обнаружена изотопная инвариантность структуры дейтериевой и протиевой воды, подтверждающая факт связи различий теплоемкости с фундаментальным различием природы изотопов водорода, а не особенностей структуры D2O- и H2O-жидкостей.
Все это, вместе взятое, может служить обоснованием для использования формализма модели «структурных единиц жидкости» и модели «обратимых переходов квантовый газ – конденсат» для дальнейшего сравнительного исследования физико-химических свойств протиевой и дейтериевой воды, что и предопределило основные направления данной работы.
Цель исследования: Изучение строения и физико-химических свойств D2O и H2O путём моделирования составляющих теплоёмкости и мольного объёма на линии насыщения в интервале температур от переохлаждённого (метастабильного) состояния жидкости до критической области.
Задачи исследования:
1. Построение модели, пригодной для количественного описания составляющих теплоёмкости протиевой и дейтериевой вод в жидком состоянии.
2. Получение модельных зависимостей термодинамических характеристик протиевой и дейтериевой жидкой вод, в широком диапазоне температур.
3. Сравнение модельных зависимостей термодинамических характеристик протиевой и дейтериевой воды с экспериментальными данными.
4. Проведение сравнительного анализа строения жидких D2O и H2O в области температур от состояния переохлаждённой жидкости до критических температур.
5. Прогнозирование возможного проявления обнаруженных закономерностей и особенностей в свойствах и строении дейтериевой и протиевой воды в случае других жидких систем и сред.
Научная новизна работы
1. Конфигурационная составляющая теплоёмкости воды классифицирована (дифференцирована) на две составляющие, одна из которых (теплоёмкость различимых частиц) – одинакова для D2O и H2O, а другая (теплоёмкость тождественных частиц) – различна для D2O и H2O.
2. Различия теплоёмкости тождественных частиц D2O и H2O объяснены в рамках предложенной модели равновесных переходов квантовый газ - конденсат.
3. Обнаружены бозонные пики теплоёмкости в области переохлаждённого состояния и в области комнатных температур, которые в D2O связаны с катионами D+. Пики теплоёмкости H2O объяснены проявлением протонных пар как бозонов.
4. Резкое повышение теплоёмкостей с температурой при околокритических температурах объяснено проявлением бозонов.
5. Обнаружено, что при температурах 300 - 310K частоты конфигурационных колебаний частиц D+ в D2O (и протонной пары в H2O) находятся в области дна либрационных частот и располагаются выше конфигурационных частот частиц H+ в H2O, которые находятся в области потолка трансляционных частот воды.
6. В рамках принятой модели «структурных единиц жидкости» получены формулы для оценки значений суммы показателей уравнения Ми, содержащие параметры модели, сжимаемость и константу равновесия двух типов молекул D2O-воды.
Практическая значимость работы
Обнаруженное явление образования протонной пары, особенности проявления бозонов и фермионов в свойствах воды, разработанные соотношения и результаты термодинамических расчётов могут быть использованы как в учебном процессе, так и при объяснении различного биологического действия протиевой и дейтериевой воды.
Положения, выносимые на защиту:
1. Дифференциация конфигурационной теплоёмкости воды на теплоёмкости различимых и тождественных частиц.
2. Обоснование различия теплоёмкости тождественных частиц D2O и H2O в рамках предложенной модели равновесных переходов квантовый газ - конденсат.
3. Обнаружение и обоснование бозонной природы пиков теплоёмкости тождественных частиц, как проявление катионов D+ в D2O и протонных пар как бозонов в H2O при температурах переохлаждённого состояния жидкости и в области комнатных температур.
4. Обоснование связи различий теплоёмкостей D2O и H2O при околокритических температурах с проявлением бозонов и фермионов.
5. Оценка и сравнение частот конфигурационных колебаний частиц D+ в D2O, протонной пары и частиц H+ в H2O с областью либрационных и трансляционных частот воды.
6. Разработка и апробация формул, связывающих параметры модели «структурных единиц жидкости» с параметрами уравнения Ми.
Апробация материалов диссертации. Основные результаты и положения диссертационного исследования докладывались и обсуждались на следующих международных научных конференциях:
- Юбилейная международная научная конференция, посвященная 200-летию высшего ветеринарного образования в России и 200-летию СПбГАВМ, 2008.
- XVII International Conference on Chemical Thermodynamics in Russia. Kazan, Russian Federation. June 29-July 3, 2009.
Публикации. По материалам диссертации опубликовано 8 работ, в том числе 4 статьи в журналах из Перечня ВАК РФ, а также 4 тезиса докладов на международных конференциях.
Объем и структура диссертации. Работа состоит из введения, трех глав, выводов и списка цитированной литературы (включающего 200 наименований). Она изложена на 137 страницах, содержит 23 рисунка и 5 таблиц.
Личный вклад автора в диссертационную работу состоит в получении и апробации расчетных зависимостей, соотношений и уравнений (в рамках принятых моделей структуры и межчастичных взаимодействий) для определения искомых физико-химических характеристик изотопных разновидностей воды, выполнении соответствующих расчетов, выявлении общих закономерностей и характерных особенностей исследуемых свойств, анализе, интерпретации и обобщении полученных результатов.
СОДЕРЖАНИЕ ДИССЕРТАЦИИ
Во Введении обоснована актуальность проблемы, определены цели и задачи работы, изложены научная новизна и практическая значимость.
Глава 1 (Литературный обзор) посвящена обзору научных работ по физико-химическим свойствам и структуре жидких H2O и D2O. Рассмотрены уникальные физико-химические свойства воды. Отдельный параграф посвящен обзору физико-химических свойств дейтериевой воды. Приведены геометрические и энергетические характеристики молекулы Н2О в различных фазовых состояниях. Показана история развития представлений о воде с развитием методов исследования. Рассмотрены и проанализированы имеющиеся представления о структуре воды, сформулированы соответствующие критерии. Рассмотрены и проанализированы классическое определение и количественные характеристики звуковых волн в контексте их воздействия на структурные единицы жидкой воды. Как результат, определены основные направления работы в изучении структурных и физико-химических характеристик D2O и H2O.
Глава 2 посвящена анализу и выбору методов исследования различий свойств D2O – H2O, которые проявляются в виде различной биологической активности разбавленных и концентрированных растворов D2O. Описаны методики моделирования и основные соотношения, которые используются в данной работе.
В этой части диссертации отмечается, что модель структурных единиц жидкости предложена и развита Саргаевым П.М. с соавторами. В названии модели использована терминология, предложенная Кирквудом. В основу этой модели структурных единиц жидкости положено полученное Каневским И.М. и Швецовым О.К. уравнение для идеальных дисперсных систем. Сфера применения уравнения модели расширена в область гомогенных систем с более низкими значениями числа молекул g в дисперсной частице (кластере, структурной единице) за счёт более полного и строгого учёта статистических факторов:
V/(rg1/3) + РгV = wRT,
где w = {1 - [ln(2g)] / (2g) + 1/(2g) - 1/(6g2) + 1/(90g4) -...}; =(V/Vл)2/3(Rл / Rж)2; Vл и Rл, V и Rж - объём и межмолекулярное расстояние льда (при температуре плавления) и жидкости (при температуре Т).
В рамках этой модели структурных единиц жидкости и теории перколяции её авторами теоретически получена формула для оценки конфигурационной теплоёмкости H2O (уравнение (1), см. ниже).
В диссертации обоснована возможность использования модели обратимых переходов квантовый газ – конденсат по Эйнштейну для компьютерного моделирования различия квантовых свойств частиц. Необходимость учитывать различие квантовых свойств частиц возникла при сравнительном моделировании термодинамических свойств D2O и H2O. В главе 2 приводятся примеры успешного применения модели обратимых переходов квантовый газ- конденсат. Предложены пути совершенствования модели.
Глава 3 состоит из трёх разделов, в которых излагаются методики и результаты моделирования термодинамических свойств H2O и D2O в области температур от переохлажденной жидкости до критического состояния.
В первом разделе данной главы представлены методики и результаты моделирования составляющих конфигурационной теплоёмкости воды в рамках модели структурных единиц жидкости. Основное усилие направлено как на выделение конфигурационной теплоёмкости D2O-воды из имеющихся экспериментальных данных изобарной и изохорной теплоёмкости в области температур от 235K до критической температуры, так и на оценку значений изобарной теплоёмкости и её составляющих в области температур от температуры фазового перехода второго рода (Tg) до 235K. В работе обоснована необходимость моделирования колебательной теплоёмкости (Cvib) для получения надёжных значений конфигурационной теплоёмкости (Cc) в интервале температур от температуры фазового перехода второго рода до критической температуры. Излагаются методики оценки сдвига частот межмолекулярных и внутримолекулярных колебаний, методика стандартизации и оценки значений колебательной теплоёмкости по Эйнштейну:
Cvib = i=19R{(hi / (kT))2 exp(hi / (kT)) [exp(hi / (kT)) – 1]-2},
где i – частота моды i, (при температурах 15-30K и от 30K до критической температуры). Особенности расчётов по Дебаю (при температурах от 0K до 15K). В последнем случае Cvib = aT3, постоянную a определяли по значению теплоемкости Cvib, найденной по Эйнштейну.
Из-за отсутствия экпериментальных данных при температурах от 0K до 235K расчёты теплоёмкости сопровождались оценкой температуры фазового перехода второго рода (Tg 138.5K), объёма, энтропии и энтальпии жидкости и корректировались методом последовательных приближений. Частоты мод при температуре тройной точки D2O-воды взяты по Путинцеву Н.М.. Полученные в диссертации значения диффренциальных и интегральных значений коэффициента сдвига частот (рис. 1) и частоты межмолекулярных колебаний (рис. 4-5, см. ниже) представлены в графическом виде в сравнении с другими величинами в диапазоне температур от 0K до критической температуры.
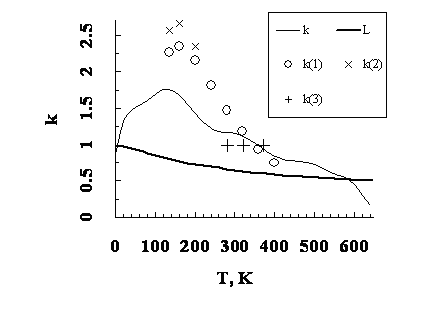
Рисунок 1 – Коэффициент сдвига частот либрационных и трансляционных колебаний дифференциальный (k) и интегральный (L) по нашим данным (k, L), по Скитсу и Райсу (k(1); k(2)) и Путинцеву Н.М. (k(3)) для D2O-воды при температурах Т (K) от 0 K до критической температуры.
Отмечается, что по мере повышения температуры от 0K до критической температуры частоты межмолекулярных колебаний уменьшаются в два раза. Результаты оценок колебательной и изобарной теплоёмкости представлены в сравнении с другими сотавляющими теплоёмкости D2O-воды на рисунке 2, а также в полиномиальном виде зависимости от температуры: Значения колебательной теплоемкости (Cvib, J /(mole K)) в интервале температур от 15 K до 30 K описываются уравнением 5-й степени по температуре (T, K) с коэффициентами (в порядке возрастания степени): – 0.928, 0.3852, – 0.054583, 3.3012·10-3; – 8.126·10-5, 7.272·10-7. В интервале температур от 30 K до критической температуры значения колебательной теплоемкости (Cvib, J /(mole K)) D2O-жидкости описываются уравнением 9-й степени температуры (T, K): – 3.278, 0.22846, – 1.94851·10-3, 3.050089·10-5, – 2.2387733·10-7, 8.8148232·10-10, – 2.03045354·10-12, 2.7535875·10-15, – 2.04120406·10-18, 6.388549·10-22. В интервале температур 138,5K – 235K значения изобарной теплоемкости (Cp, J /(mole K)) описываются уравнением 10-й степени температуры (T, K). Коэффициенты уравнения имеют значения: – 3954786.717, 265037.07262, – 7923.4323622, 139.1450968994, – 1.589521127257, 1.234154028705·10-2, – 6.59572025023·10-5, 2.395774636657·10-7, – 5.66040310787·10-10, 7.8552513276·10-13, – 4.8624376932·10-16.
Моделирование изобарной теплоёмкости и её составляющих при температурах переохлаждённого соостояния невозможно без оценки конфигурационной теплоёмкости (Cc). Использовали соотношение (Cc) = Cc1 + Cc2, в котором значения Cc1 находили по формуле используемой теории:
Сc1 = RGln (gf0 p), (1)
где f0 - число активных центров молекулы; G, p – гель-фракция и доля занятых активных центров молекулы (рассчитываются по теории перколяции); R – универсальная газовая постоянная. В случае H2O и D2O воды f0 = 4.
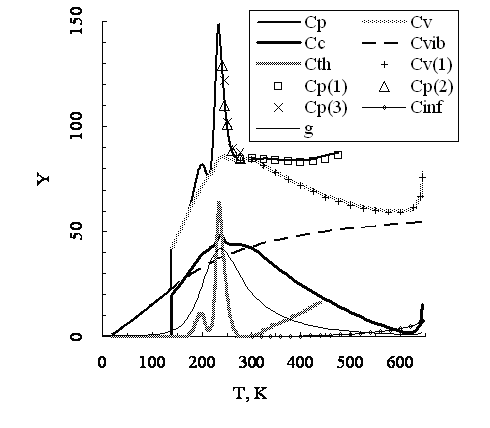
Рисунок 2 – Характеристики D2O-жидкости (Y) при температурах (T, K) от 0 K до критической температуры: Число молекул в структурной единице (g) и теплоемкость (C, J/(mole K)) изобарная (Cp), изохорная (Cv), конфигурационная (Cc), колебательная (Cvib), термическая (Cth) и инфинитная (Cinf) по нашим данным и литературным (Cp(1); Cv(1); Cp(2); Cp(3)).
Для величины Cc2 моделированием получили выражение, дающее основной вклад в теплоёмкость при тепературах от температур переохлаждённого состояния D2O-воды до 620-630K:
Сс2 = RGxpk3ln (4g3/2) - 0,65p4 (0,5 RGxpln (f1f2)), (2)
где k3 2 ((g/42)g + (4f1f2)2g 0,65 p4) + 0,5 exp(- ((1 - g /25)2)0,4).
В отличие от аналогичных формул для протиевой воды, все слагаемые уравнения (2) дают положительный вклад в теплоемкость. При расчётах изохорной теплоемкости в зависимости от температуры с использованием (2) в области температур 288-289 K проявляется максимум, который, в отличие от H2O, имеется в случае D2O воды.
Наряду с моделированием значения составляющей Сс2 определяли по «остаточному принципу» путём вычитания из изобарной (Cp) и изохорной (Cv) теплоёмкости значений других составляющих теплоёмкости. Полученные по такой методике значения для H2O и D2O представлены на рис. 3.

Рисунок 3 – Составляющая конфигурационной теплоемкости (Cс2, J/(mole K)) тождественных частиц тяжелой (D2O) и протиевой (H2O) воды на линии насыщения жидкости при температурах (T, K).
В диссертации приведено подробное описание особенностей температурного хода составляющих изобарной теплоёмкости D2O воды (рис.2) и значений Cс2 тяжелой (D2O) и протиевой (H2O) воды на линии насыщения жидкости (рис. 3). Отмечается, что в области пика изобарной теплоёмкости D2O воды при температурах переохлаждённой жидкости все составляющие теплоёмкости проходят через максимум в зависимости от температуры. Составляющая конфигурационной теплоёмкости Cс2 D2O воды при всех температурах существования жидкости имеет только положительные значения. В неравномерном температурном ходе значений Cс2 D2O воды чётко определяются два пика, один из которых расположен в области температур переохлаждённой жидкости, а другой – при температурах около 300 K. В последнем случае достигается значение Cc2 = 6.6 J/(mole K). Третий пик находится выше температуры 640 K. Более сложный вид имеет характер температурной зависимости величины Cc2 в случае H2O-жидкости: При температурах выше 350 K имеется обширная область отрицательных значений рассматриваемой составляющей конфигурационной теплоёмкости. В области температур от 0K до 350K величина Cc2 имеет положительные значения, которые практически при всех температурах находятся ниже таковых для D2O-жидкости. Первый, низкотемпературный, максимум явно выражен, тогда как высокотемпературный отмечается лишь понижением температурного наклона кривой. Третий пик находится при температурах более высоких, чем в случае D2O-жидкости.
Непосредственно из характера температурной зависимости рассматриваемой составляющей конфигурационной теплоёмкости не следует определённость о природе частиц, формирующих столь сложный вид температурной зависимости Cc2. Единственно, что можно утверждать, значения величины Cc2 связаны с вкладом «неоднородных» с позиций теории перколяции частиц и эти вклады контрастно проявляются в свойствах сравниваемых жидкостей. Различия значений Cc2 в области температур стабильного состояния D2O и H2O воды надежно установлены. Менее обоснованы результаты сравнения в области температур переохлажденного состояния жидкости, поскольку в этом случае различие значений сравниваемых величин не превышает 3 J/(moleK), что находится в пределах погрешностей оценки значений теплоемкости.
Во втором разделе данной главы представлены методика и результаты моделирования составляющих конфигурационной теплоёмкости воды в рамках модели обратимых переходов квантовый газ - конденсат. Предложенная в диссертации методика модели обратимых переходов квантовый газ – конденсат, преназначенная для идентификации частиц жидкости, участвующих в конфигурационных колебаниях, базируется на сравнении частот конфигурационных колебаний (fc) частиц жидкости и частот колебаний частиц равновесного квантового газа (fE). Сравнивая значения частот (fc) и fE при одних и тех же температурах можно оценить область температур возможного равновесного перехода квантовый газ - конденсат и массу частиц, участвующих в этом переходе. Сопоставление особенностей кривых температурной зависимости конфигурационной теплоемкости Сс2 и частот fc и fE может нести информацию, необходимую для дифференциации вкладов в величину Сс2 по типу тождественных частиц и связи конфигурационной теплоемкости тождественных частиц с возможностью равновесного перехода квантовый газ - конденсат.
В формализме модели предполагается, что в случае идеального одноатомного квантового газа по Эйнштейну скорость движения частиц (v) совпадает со скоростью звука
v = ((Cp/Cv) RT / M)1/2, (3)
где Cp/Cv – показатель адиабаты; Cp и Cv - изобарная и изохорная теплоемкость газа; M – молярная масса частицы; T - температура.
В таком случае особенностью частот колебаний частиц идеального квантового газа (FE) является то, что они определяются температурой и показателем адиабаты, но не зависят от массы частицы:
= Nh /(Mv). (4)
FE= v/ = Cp/Cv)RT /(Nh). (5)
Или, в единицах cм-1
fE = (Cp/Cv)RT /(cNh), (6)
где c – скорость света в cm/s; h – постоянная Планка; N - число Авогадро; - длина волны по де Бройлю.
В отличие от частот колебаний идеального газа, частоты конфигурационных колебаний частиц жидкости (fc), найденные по изложенной выше методике, зависят от массы частицы и скорости звука в жидкости (Cs)
fc = C2sM / (cNh), (7)
что открывает возможность определения массы (M) и, соответственно, идентификации частиц жидкости, участвующих в конфигурационных колебаниях.
В диссертации для квантового газа используется четырёхуровневая градация частот, которые представлены лучами (f1, f2, f3, f4) на рис. 4, 5, 6. Частицам квантового газа с критической адиабатой Cp/Cv = 1 соответствует луч (f1). Частицам с «тепловой длиной волны» (Cp/Cv = 2) соответствует луч (f4). Насыщенному идеальному одноатомному квантовому газу по Эйнштейну (Cp/Cv = 3/2) соответствует луч (f2). Область частот между лучами (f2) и (f3) соответствует ненасыщенному идеальному одноатомному квантовому газу по Эйнштейну, показатель адиабаты которого изменяется от 5/3 до 3/2.
На рис. 4, 5, (6) частоты конфигурационных колебаний частиц жидкости (fc) и частоты f1 – f4 идеального газа представлены в сравнении с частотами мод либрационных (fL1, fL2, fL3) и трансляционных (fT1, fT2, fT3) межмолекулярных колебаний в зависимости от температуры (T, K). Частоты конфигурационных колебаний (fc, см. рис.4 - рис. 6) рассчитывали по формуле (7), используя молярные массы молекул (D2O, H2O) и изотопов водорода (D+, H+). При расчетах приведенной массы () протонной пары (2H+) учитывали массу атома кислорода (MO) и удвоенную массу протона (M2H+) по формуле
1/ = 1/MO + 1/M2H+. (8)
Линии тренда трансляционных и либрационных частот, представленных на рисунках 4 и 5, выпуклы к оси температур. При температуре (310 K) в области первых из них располагаются частоты конфигурационных колебаний частиц с массой H+ (рис. 5), а в области вторых – частоты частиц с массой D+ (рис. 4). Частоты колебаний идеального квантового газа с различными значениями показателя адиабаты (f1, f2, f3, f4) равны нулю при температуре 0 K и под разными углами лучами расходятся по мере повышения температуры. Частоты конфигурационных колебаний молекул жидкости (fcD2O и fcH2O) расположены в области околокритических температур. Кривые температурной зависимости конфигурационных частот фрагментов молекул с массой D+, H+ и протонной пары (2H+) с повышением температуры круто падают вниз в области 200-240 K, проходят через минимум при 240-250 K и максимум при 350 K.
В диссертации отмечается, что при представлении конфигурационной теплоемкости (Cc) в виде двух слагаемых Cc1 и Cc2 первое (Cc1) оказывается практически одинаково для H2O и D2O и может классифицироваться как конфигурационная теплоемкость различимых частиц. Различие свойств D+ и H+ проявляется в слагаемом (Cc2). Вклады конфигурационных колебаний изотопов водорода входят во второе слагаемое (Cc2), которое, в отличие от (Cc1), в диссертации предложено называть конфигурационной теплоемкостью тождественных частиц.

Рисунок 4 – Частоты колебаний (f, cm-1) частиц с массой катиона дейтерия (D+) и молекул (D2O) конфигурационных (fcD+, fcD2O) в жидком состоянии D2O-жидкости в ортобарных условиях, а также в идеальном одноатомном квантовом газе ненасыщенном (f3) и насыщенном (f2) по Эйнштейну, с адиабатой 2 (f4) и критической (f1) в сравнении с частотами мод либрационных (fL1, fL2, fL3) и трансляционных (fT1, fT2, fT3) межмолекулярных колебаний в зависимости от температуры (T, K).
В диссертации сравниваются кривые Cc2(T) (рис.3) и функция fcD+(T) (Рис.4) в области температур переохлаждённого состояния и 300K функция fcD+(T) попадает в область частот квантового газа по Эйнштейну (между лучами f2 и f3). На основании этого оба низкотемпературных пика D2O воды характеризуются как бозонные. Из сравнения Cc2(T) (рис.3) и функции fc2H+(T), соответствующей протонной паре, (Рис.5) делается вывод о проявлении протонных пар как бозонов в конфигурационных колебаниях, соответственно низкотемпературные пики H2O воды классифицируются как бозонные пики. Температурное понижение теплоёмкости Cc2(T) (рис.3) воды и переход в область отрицательных значений в случае H2O (рис. 5) связывается с уменьшением содержания бозонов и конверсией протонных пар в состояние фермионов.
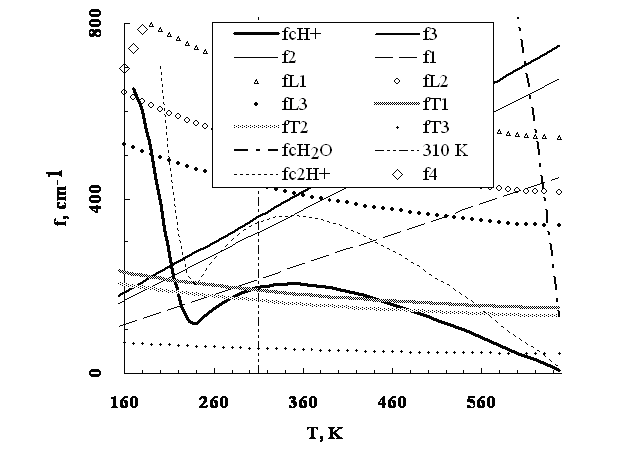
Рисунок 5 – Частоты колебаний (f, cm-1) частиц с массой молекул (H2O), протона (H+) и протонной пары (2H+) конфигурационных (fcH2O, fcH+, fc2H+) в H2O на линии насыщения жидкости, а также в ненасыщенном (f3) и насыщенном (f2) квантовом газе по Эйнштейну, с адиабатой 2 (f4) и критической (f1), в сравнении с частотами мод либрационных (fL1, fL2, fL3) и трансляционных (fT1, fT2, fT3) межмолекулярных колебаний при температурах (T, K).
Частоты (f4), соответствующие «тепловой длине волны частиц», используются в теории бозе-эйнштейновской конденсации ультрахолодных газов. В случае воды при температуре максимума произведения давления и объема насыщенного пара (около 505 K), частоты f4 перекрываются с частотами конфигурационных колебаний молекул fcD2O и fcH2O (см. рис. 6), а при более высоких температурах – с частотами надмолекулярных соединений. Пересечение кривых fcD+ и fcH+ с лучом (f4) при 210-220 K находится в области левой (низкотемпературной) границы бозонных пиков теплоемкости переохлажденных D2O и H2O жидкостей
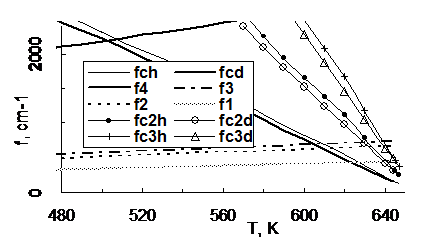
Рисунок 6 – Частоты (f, cm-1) конфигурационных колебаний частиц (мономеров (fc), димеров (fc2), тримеров (fc3)) жидких D2O (fcd, fc2d, fc3d) и H2O (fch, fc2h, fc3h), а также колебаний частиц идеального квантового газа (f1, f2, f3, f4) при температурах (T, K): f2, f3 - насыщенный (f2) и ненасыщенный (f3) квантовый газ по Эйнштейну; f1 - газ с критической адиабатой; f4 – газ с адиабатой 2.
Термодинамические свойства воды в области околокритических температур отличаются от таковых при температурах, прилегающих к тройной точке. В этом случае в величину изохорной (Cv) теплоемкости, наряду с колебательной (Cvib) и конфигурационной (Cc) теплоемкостью, заметный вклад вносит инфинитная (Cinf) составляющая. При сравнении расчетных и экспериментальных значений Cv, соответствующих области околокритических температур, обнаруживается необходимость учета дополнительного слагаемого (Cc3) в составе конфигурационной теплоемкости. Последнее слагаемое учитывает принципиально новый механизм конфигурационных колебаний, который не обнаруживается при температурах, прилегающих к тройной точке воды. Необходимость дальнейшего моделирования околокритических составляющих теплоемкости воды различного изотопного состава обусловлена сложностью задачи оценки и классификации вкладов по типу частиц.
В случае теплоемкости воды в области околокритических температур, в отличие от температур гомеостаза и переохлажденного состояния жидкости, в первом приближении отсутствует различие конфигурационной теплоемкости D2O и H2O. В диссертации расчётами показано, что в области околокритических температур, входящая в состав Cc2 составляющая Cc3, соответствующая конфигурационным колебаниям структурных единиц как целого, различна для D2O и H2O и описывается формулой
Cc3 = k1 RG(sg) 4 ln (4g), (9)
где k1 коэффициент.
В диссертационной работе проведено тщательное сопоставление расчетных и экспериментальных значений изохорной теплоемкости D2O и H2O при условиях, соответствующих непосредственной близости к критическим температурам. На основании такого сопоставления установлено, что коэффициент k1 в случае H2O близок к значению 1, тогда как в случае D2O жидкости этот коэффициент оказался в два раза больше. Установленный факт может свидетельствовать о проявлении в конфигурационной теплоемкости тяжелых тождественных частиц различий бозонов и фермионов, а температурный ход составляющей Cc3 характеризовать как бозонный пик. В случае H2O пониженным оказывается не только коэффициент k1 в расчетной формуле (9), но и расчетные значения теплоемкости Cc3, относительно таковых для D2O. Так, например, при температуре 643.89 K, которая практически соответствует критической температуре D2O, Cc3 = 12 J/(mole K). При близких условиях (644 K) в случае протиевой воды Cc3 = 10 J/(mole K). Разность значений Cc3 для сравниваемых жидкостей (2 J/(mole K)) хорошо согласуется с низкотемпературными оценками. В данном случае полученное значение находится на уровне величины Cc1, которая при рассматриваемых условиях соответствует 3 J/(mole K) для D2O и H2O. Различие значений теплоемкости Cc3 D2O и H2O отражается и в относительных величинах: Величина Сс3 D2O воды составляет 16.0 % от изохорной теплоемкости, тогда как в случае H2O - 14.3 %.
При околокритических температурах воды, аммиака (и некоторых других жидкостей) обнаружено проявление надмолекулярных соединений в обратимых переходах квантовый газ - конденсат по Эйнштейну и конфигурационных колебаниях тождественных частиц. Подъем значений конфигурационной теплоемкости тождественных частиц (бозонный пик, Cc3), связанный с такими частицами, вносит основной вклад в конфигурационную теплоемкость и температурную зависимость изохорной теплоемкости воды. Различие Cc3 D2O и H2O связано с влиянием фермионов, которое преобладает в H2O жидкости.
В третьем разделе этой главы моделируется равновесие двух типов молекул воды в рамках модели структурных единиц жидкости. В теоретическом введении путём преобразования общеизвестных соотношений для скорости звука получены формулы, связывающие изменение объёма и концентрации частиц в процессах сжатия системы с параметрами модели структурных единиц жидкости. Частная производная T = - (1/V)(dV/dP)T представлена в конечных разностях изменения объема (V) и давления (P). В качестве величины (P) используется модельная величина - давление Pg = /(rg1/3), где в - поверхностное натяжение; r – эффективный радиус молекул; g – число молекул в структурной единице жидкости. Давление (Pg) возникает в жидкости в процессе образования структурных единиц, является характеристикой жидкости в условиях равновесия с насыщенным паром. Под действием давления (Pg) объем уменьшается, концентрация (n) молекул жидкости возрастает, изменение логарифма концентрации (ln(n)) имеет положительный знак. Обратное значение изменения логарифма концентрации K = 1/(ln(n)) является интегральной величиной. Для выяснения физического смысла величины K выбраны условия интегрирования: d(1/T)/dP = C - линейная зависимость величины (1/ T) от давления P и значение (1/T) = 0 для несжатого состояния жидкости. Таким условиям соответствуют формулы для оценки величины K
K1 = kl.p. Kf (1 / (T Pc)); (10)
K2 = kl.p. Kf (C2s Cv / (Cp Pc)). (11)
где kl.p., Kf – коэффициенты; Cv, Cp, – изохорная и изобарная теплоемкости и плотность жидкости; Pc Pg – сжимающее давление.
Выбранные условия интегрирования совпадают с таковыми для определения суммы показателей степеней (m+n) в уравнении Ми для энергии взаимодействия (E) пары молекул на расстоянии a (E = Aa-n - Ba-m, где A и B - постоянные). В связи с этим в работе сравниваются результаты расчётов значений K1 и K2, полученные для величины K в рамках модели структурных единиц жидкости, с результатами расчётов суммы показателей (m+n) уравнения Ми по известной формуле
m+n = 3 (C -2), (12)
где C = d(1/T)/dP – постоянная величина, которую находили по литературным данным для зависимости объёма жидкости от давления.
В диссертации приведены результаты расчётов значений K1 и K2 для H2O и D2O (при значении коэффициентов kl.p. = 1, Kf = 1, см. таблицу ниже) в сравнении с имеющимся в литературе значением (m+n = 15,8 ± 2,9) для H2O в диапазоне температур от температуры плавления до 358 K.
Таблица
| T | K(4) (H2O) | K(5) (H2O) | K(4) D2O | K(5) D2O |
| 273 | 15,2 | 15,4 | 14,8 | 15,2 |
| 293 | 16,0 | 16,6 | 16,0 | 15,9 |
| 298 | 16,1 | 16,6 | 16,1 | 15,9 |
| 308 | 16,3 | 16,3 | 16,2 | 15,9 |
| 313 | 16,4 | 16,1 | 16,2 | 15,8 |
| 358 | 14,8 | 14,2 | 14,5 | 14,4 |
Оказалось, что средние значения величин K1 и K2 для H2O в рассматриваемом диапазоне температур совпадают с литературным значением величины (m+n), а в случае D2O (см. таблицу) практически совпадают с данными для протиевой воды (H2O).
Отличие значений коэффициента (Kf) от 1 (при kl.p. = 1) проявляется при сравнении K1 и K2 со значениями величины (m+n) в интервале температур от тройной токи до критической температуры, которое было проведено для D2O на линии насыщения жидкости (см. рис. 7, рис. 8).
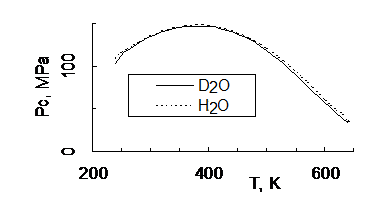
Рисунок 7 – Значения давления (Pc, MPa) для D2O и H2O в зависимости от температуры (T, K).

Рисунок 8 – Значения K1, K2 и (m+n) (Y) по формулам (10) - (12) для D2O (kd, d1, d) и H2O (kh) на линии насыщения жидкости в зависимости от температуры (T, K): kd, kh – (K1, K2) при Kf =1; d1 - при Kf = f2 / f1; d – значения (m+n) по (12).
Моделированием установлено, что при каждой температуре значение коэффициента Kf, найденное из сравнения величины K1 (или K2) с (m+n), совпадает со значением константы равновесия двух типов молекул D2O-воды. Константа равновесия Kf = f2 / f1 содержит фракции (доли) молекул (f1 – для типа 1 (в решетке) и f2 – для типа 2 (вне решетки)). Из обнаруженного факта следуют формулы для расчёта значений величины (m+n) уравнения Ми, которые содержат параметр модели структурных единиц жидкости (Pg) и константу равновесия двух типов молекул (Kf):
m+n Kf / (TPg), (13)
m+n Kf (C2s Cv / (Cp Pg)). (14)
Значения константы равновесия Kf в области температур тройной точки воды меньше 1, при температурах 320-330 K соответствуют значению 1, а при 610-620 K проходят через максимум (3.2).
ВЫВОДЫ
1. В рамках модели структурных единиц жидкости рассчитаны значения изобарной теплоёмкости и её составляющих и представлены в виде полиноминальных уравнений температурной зависимости для D2O-жидкости в области температур ниже 235 K (в которой отсутствуют данные по теплоёмкости из-за трудностей экспериментальных исследований, обусловленных неустойчивостью переохлаждённой жидкости).
2. Конфигурационная теплоемкость протиевой и дейтериевой воды дифференцирована на аддитивные составляющие различимых и тождественных частиц. Первая - одинакова у H2O и D2O. Вторая – в области температур переохлажденного состояния жидкости 300-310 K зависит от содержания бозонов и фермионов, образует два бозонных пика, которые обусловлены участием катионов D+ и протонных пар в обратимых переходах квантовый газ - конденсат по Эйнштейну. При повышении температуры до 350 K из-за распада протонных пар конфигурационная теплоемкость тождественных частиц протиевой воды уменьшается до отрицательных значений.
3. Модель обратимых переходов квантовый газ – конденсат дополнена условием: равенство частот конфигурационных колебаний частиц жидкости частотам колебаний частиц равновесного квантового газа. Обнаружено, что при температурах 300-310 K частоты конфигурационных колебаний протонов лежат в области трансляционных частот, а катионов D+ и протонных пар – в области нижней границы частот либрационных колебаний воды.
4. В рамках модели обратимых переходов квантовый газ – конденсат при частотах квантового газа с тепловой длиной волны обнаруживается проявление конфигурационных колебаний молекул D2O и H2O при температурах, соответствующих максимуму произведения давления и объёма равновесного насыщенного пара.
5. Обнаружено различие теплоёмкости тождественных частиц D2O и H2O в области бозонного пика при околокритических температурах, связанное с влиянием фермионов, которое преобладает в H2O-жидкости.
6. Получены (и апробированы в случае D2O на линии насыщения жидкости при температурах от тройной точки до критической температуры) формулы для расчёта значений величины (m+n) уравнения Ми, которые содержат константу равновесия двух типов молекул, изотермическую сжимаемость и параметр модели структурных единиц жидкости.
Основное содержание диссертации изложено в следующих публикациях:
1. Саргаева Н.П., Барышев А.Н., Саргаев П.М. Бозоно-фермионные контрасты синергетики структурных единиц жидких D2O и H2O. // Известия РГПУ им. А.И. Герцена: Естественные и точные науки. 2009. № 95. C. 120-133.
2. Саргаева Н.П., Барышев А.Н., Пучков Л.В., Саргаев П.М. Бозонный пик воды при околокритических температурах. // Вестник Казанского технологического университета. 2010. N. 2. С. 225-228.
3. Саргаева Н.П., Барышев А.Н., Пучков Л.В., Саргаев П.М. Бозон-фермионные контрасты теплоемкости H2O и D2O воды. // Вестник Казанского технологического университета. 2010. N. 1. С. 84-86.
4. Саргаева Н.П., Барышев А.Н., Пучков Л.В., Саргаев П.М. Скорость звука и структурные единицы воды. // Вестник Казанского технологического университета. 2010. N. 2. С. 238-241.
5. Саргаева Н.П., Наймушин А.Б., Барышев А.Н., Саргаев П.М., Критерии взаимодействия акустических полей с компонентами внутренней среды // Материалы юбилейной международной научной конференции, посвященной 200-летию высшего ветеринарного образования в России и 200-летию СПбГАВМ. – СПб.: СПбГАВМ, 2008. С. 81-82
6. Sargaeva N.P., Baryshev A.N., Puchkov L.V., Sargaev P.M. The speed of sound and water structural units // XVII International Conference on Chemical Thermodynamics in Russia. Abstracts. Vol. 1. Kazan, Russian Federation. June 29-July 3, 2009. P. 210.
7. Sargaeva N.P., Baryshev A.N., Puchkov L.V., Sargaev P.M. Liquid water boson peak at near-critical temperature // XVII International Conference on Chemical Thermodynamics in Russia. Abstracts. Vol. 1. Kazan, Russian Federation. June 29-July 3, 2009. P. 232.
8. Sargaeva N.P., Baryshev A.N., Puchkov L.V., Sargaev P.M. Heat capacity bose-fermi contrasts of D2O and H2O liquids // XVII International Conference on Chemical Thermodynamics in Russia. Abstracts. Vol. 1. Kazan, Russian Federation. June 29-July 3, 2009. P. 309.

