Особенности стереоспецифических сверхтонких взаимодействий в -радикалах, содержащих фторалкильные заместители
На правах рукописи
Смекалкин Даниил Михайлович
Особенности стереоспецифических сверхтонких взаимодействий в -радикалах,
содержащих фторалкильные заместители
Специальность: 02.00.04 – Физическая химия
АВТОРЕФЕРАТ
диссертации на соискание учёной степени
кандидата физико-математических наук
Москва – 2008
Работа выполнена на кафедре физической химии Московской
государственной академии тонкой химической технологии
(МИТХТ) им. М.В. Ломоносова
Научный руководитель: доктор химических наук, профессор
Поленов Евгений Александрович
Официальные оппоненты: доктор химических наук, профессор
Абронин Игорь Александрович
кандидат физико-математических наук,
ведущий научный сотрудник
Тарасов Юрий Игоревич
Ведущая организация: Новосибирский институт органической химии им. Н.Н. Ворожцова Сибирского
отделения Российской Академии Наук
Защита состоится 27 февраля 2008 г. в 12.00 на заседании диссертационного Совета Д 212.120.05 при Московской государственной академии тонкой химической технологии (МИТХТ) им. М.В. Ломоносова по адресу:
119571, Москва, проспект Вернадского 86, аудитория М-119.
С диссертацией можно ознакомиться в библиотеке Московской государственной академии тонкой химической технологии им. М.В. Ломоносова по адресу: 119571, Москва, проспект Вернадского 86. С авторефератом диссертации можно ознакомиться на сайте www.mitht.ru.
Автореферат диссертации разослан « » января 2008 г.
Учёный секретарь
Диссертационного Совета Д 212.120.05,
кандидат химических наук Ю.А. Ефимова
ВВЕДЕНИЕ
Фторорганические соединения являются синтетическими объектами. У них нет природных аналогов, и их свойства с точки зрения химии углеводородов часто необычны. Круг их применений в настоящее время широк, и они представлены во всех современных областях науки и техники, включая ключевые космические и оборонные технологии. Особо интересны фторорганические и фторуглеродные структуры для современных фундаментальных исследований в теоретической химии, квантовой химии и спектроскопии.
Валентные особенности атома фтора ярко выражены в химии фторорганических свободных радикалов. В их строении удаётся найти освещение ряда проблем структурной химии, которые не всегда поддаются однозначному описанию в рядах углеводородных систем из-за достаточно лабильных электронных свойств атома водорода.
К фундаментальным методологическим проблемам прикладной квантовой химии и спектроскопии ЭПР относится теория констант стереоспецифичных сверхтонких взаимодействий (СТВ) в -радикалах, содержащих алкильные и фторалкильные заместители, которые несут важнейшую экспериментальную информацию об электронном строении радикала. Они зависят от контактных спиновых плотностей на ядрах, обладающих магнитным моментом, и дают возможность прямого измерения части функции электронной плотности. От них зависит количественная интерпретация кинетической информации при динамических флуктуациях радикальных структур, вызывающих модуляцию сверхтонкой структуры температурно-зависимых спектров ЭПР. Их можно моделировать методами теории открытых оболочек, но их теоретическая интерпретация ограничена разрозненными задачами и не выходит за пределы эмпирических схем.
Их орбитальной анализ является актуальной задачей.
Из свойств граничной ОЗМО ранее были выведены торсионные угловые функции Ферми - контактного СТВ с ядрами 19F в группах при плоском радикальном центре. В рядах нейтральных фторэтильных радикалов •H2C-CFnH3-n и анион-радикалов паразамещённых нитробензолов •O2N-C6H4-CFnH3-n (n03) предсказанные эффекты нашли количественное подтверждение, но важные многоэлектронные особенности параметров не были теоретически изучены, и этот пробел частично восполняется в настоящем исследовании.
Актуальность темы.
Настоящая работа посвящена стереоспецифическим Ферми-контактным сверхтонким взаимодействиям (СТВ) с ядрами 19F в -радикалах. Теория торсионных угловых функций СТВ для фторалкильных групп дополнена описанием их двух новых свойств, имеющих многоэлектронное происхождение.
Первое состоит в их полной или частичной инвариантности к изоэлектронной замене атома фтора в группах RF = CFnH3-n группами –OR, где R=H, RF и 0n3. Оно названо эффектом изоэлектронных аналогий фторного СТВ (ЭИА-F). Второе заключается в сильной зависимости их параметров от заряда -радикала. Оно названо релейным зарядовым эффектом фторного СТВ (РЗЭ-F).
Оба эффекта (ЭИА-F и РЗЭ-F) проявляются в спектрах ЭПР. Проводя расчёты разного уровня, для них удаётся построить квантово-химические модели, выявляющие закономерности и объясняющие наблюдаемые «аномалии».
Обе задачи относятся к фундаментальным проблемам теории спектроскопии ЭПР, и их решение определяет актуальность темы диссертации.
Цель работы:
1) Развитие орбитальной теории торсионных функций СТВ с ядрами 19F во фторалкильных заместителях в -радикалах.
2) Аналитическое описание и квантово-химическое моделирование двух эффектов, наблюдаемых в спектрах ЭПР фторалкилированных свободных -радикалов, важных для интерпретации стереохимических и динамических закономерностей СТВ с ядрами 19F и 1H.
Объекты исследования (системы и эффекты):
I. Модельные ряды -радикалов-гомологов с топологией линейных и ароматических систем, содержащих фторалкильные заместители и их изоэлектронные аналоги, в дублетных состояниях: анион-радикалы (АР), нейтральные радикалы (НР), катион-радикалы (КР).
II. Впервые были изучены:
А) изоэлектронная инвариантность стереоспецифических констант фторного ИСТВ в рядах фторэтильных НР •>C-CFnH3-n (1 n 3) и •>C-CFn-1H3-nOR, где R=H, CH3, CF3, и АР-НР-КР паразамещённых аренов 4-X-C6H4-RF, 4-X-C6F4-RF,
Б) релейный (скачковый) зарядовый эффект параметров фторного ИСТВ в сериях АР-НР-КР линейных полиенов и перфторполиенов RR’C(CH)2k+1CRR’•, RR’C(CH)2kCRR’• (R,R’=CF3;CH3); RR’C(CH)2kCRR’•+; (CF3)2C(CF)2k+1C(CF3)2• (R,R’=CF3;CH3); (CF3)2C(CF)2kC(CF3)2• и (CF3)2C(CF)2kC(CF3)2•+ и паразамещённых фениленов и перфторфениленов:
4-X-C6H4-RF•-; 4-X-C6H4-RF•; 4-X-C6H4-RF•+; 4-X-C6F4-RF•.
Методы исследования
Были выполнены квантово-химические расчёты открытых оболочек в базисе 6-31G неэмпирическими методами МО ЛКАО ССП, как-то: неограниченным методом Хартри-Фока (НХФ) - (UHF), ограниченным методом Хартри-Фока-Рутаана для открытых оболочек (ОХФО) - (ROHF), а также гибридным методом UB3LYP теории функционала плотности (DFT). Для проверки общности установленных физических эффектов методом INDO была изучена серия изомеров в рядах АР-НР CF3-замещённых полиенов. Всего в работе было исследовано более 3000 стереохимических конфигураций радикалов, образующих эти серии.
Научная новизна.
Впервые во фторалкилзамещённых -радикалах изучены: 1) эффект изоэлектронной инвариантности (ЭИИ-F) - изоэлектронных аналогий (ЭИА-F) и
2) релейный зарядовый эффект (РЗЭ-F) Ферми-контактного СТВ с ядрами 19F.
Оба эффекта проявляются экспериментально, воспроизводятся квантово-химическими расчётами различного уровня и важны для моделирования и количественной интерпретации стереохимических закономерностей и динамических эффектов СТС в спектрах ЭПР алкил- и фторалкилзамещённых -радикалов.
Практическая значимость.
Результаты работы дополняют теорию сверхтонких взаимодействий и расширяют методологическую основу спектроскопии ЭПР. Они имеют фундаментальный характер и важны для структурно-аналитических и физико-химических исследований, выполняемых методами радиоспектроскопии в институтах РАН, в вузах РФ, СНГ и других стран.
Личный вклад.
В разных разделах личное участие автора составляет от 100 до 75%.
На защиту выносятся:
- 1) дополнение орбитальной теории торсионных угловых функций контактного СТВ с ядрами атомов в –положениях алкильных групп.
- 2) графическое представление торсионных угловых функций СТВ при замещении атома F изоэлектронными группировками OR, где R=H,CF3H3-n.
- 3) система изоэлектронных аналогий и релейный эффект в теории угловых функций СТВ с ядрами 19F в -радикалах с различными зарядами.
- 4) обоснование, подтверждение и анализ общности двух эффектов квантово-химическими расчётами разного уровня.
Публикации и апробация работы. (стр. 28 настоящего реферата)
Материалы диссертации опубликованы в виде двух журнальных статей. Результаты работы были представлены в двух докладах на V-й Всероссийской конференции «Молекулярное моделирование» (ГЕОХИ, апрель 2007) и XVIII-м Менделеевском съезде по общей и прикладной химии (сентябрь 2007) их тезисы были опубликованы в сборниках.
Структура диссертации.
Диссертация состоит из введения (4 стр.), пяти глав (154 стр.), выводов и списка литературы (19 стр.). Текст представлен на 185 страницах, и включает титул, оглавление, перечни рисунков и таблиц (8 стр.); в 20 таблицах (27 стр.) и на 13 рисунках (13 стр.) содержатся собственные численные и графические данные, выводы (1 стр.), список литературы из 170 источников (18 стр.). Собственные материалы работы изложены в 2-х статьях и тезисах 2-х докладов.
ОСНОВНОЕ СОДЕРЖАНИЕ РАБОТЫ
ГЛАВА 1. Литературный обзор. Свободные радикалы и их строение в современных исследованиях.
На 50 страницах текста диссертации содержится краткий обзор теории изотропного СТВ, в том числе данные теории и эксперимента, касающиеся особенностей строения, динамики и превращений фторсодержащих радикалов.
ГЛАВА 2. Теория торсионных угловых функций контактного СТВ в алкил-замещённых -радикалах.
На 33 страницах изложена орбитальная теория стереоспецифического изотропного Ферми-контактного сверхтонкого взаимодействия в свободных –радикалах, концепция метода НХФ о распределении нечётного числа электронов на независимых спин-ОЗМО. Анализ не ограничен граничной ОЗМО, а впервые затрагивает многоэлектронную оболочку радикала в виде подмножества -МО.
В работах [1, 2] были рассмотрены структурные фрагменты •C-CA3 и •C-CA2B. У входящего в систему –сопряжения радикального центра •C- геометрия его тригональная, и у группы -CA3 или -CA2B тетраэдрическая. Их локальная симметрия описывается группами C2V; C3V; CS.
Симметризованные орбитали (СО) из S-АО атомов A1,2,3 и A1,2 имеют вид:
-у группы CA3 : [X; Y; Z] = [(S1-S2)/21/2; (S1+S2)/21/2; (S1+S2 -2S3)/61/2]
-у группы CA2B: [X; Y] = [(S1-S2)/21/2; (S1+S2)/21/2]
Сверхсопряжение обеспечивается с участием СО [X; Y]. У группы CA3 они образуют базис дважды-вырожденного неприводимого представления точечной группы C3V (или даже C3) и полностью эквивалентны по симметрии, но понижение симметрии у группы CA2B переводит их в базисы различных неприводимых представлений, и потому они заведомо неэквивалентны.
Система декартовых координат фиксирована на заместителе. Одна ось (Z) направлена вдоль связи CC, вторая (Y) располагается в его локальной плоскости симметрии ССA’” или ССB, ей перпендикулярна третья ось (X). Радикальный центр вместе с его 2p-АО вращается относительно осей X,Y, и угол между осью 2p-АО и осью Y равен. Положения атомов A1,2,3 или A1,2, B заданы индивидуальными угловыми координатами (1; 2; 3) = (+2/3; -2/3; ).
Базисная p(C) -АО разложена на две взаимно-ортогональные компоненты, преобразуемые подобно базисным СО [X; Y]: [PX; PY] = [Psin; Pcos]. (1)
Сверхсопряжение между системой и заместителем обеспечивается слиянием базисных орбиталей во фрагменты МО вида:
[X; Y] = [PX+UXX; PY+U YY]=[Psin+UXX; Pcos+U YY]. (2)
Через фрагменты [X; Y] в состав МО угол вводится в явном виде, и возникает возможность аналитического описания торсионно зависимых электронных свойств радикала, включая Ферми -контактное СТВ с ядрами -атомов. В -МО они входят в виде скалярного произведения
=([X; Y]:[sin; cos])= X sin + Y cos = P+UXsinX+U YcosY. (3)
Роль параметров смешения [UX; U Y] центральная. Можно их назвать парциальными параметрами сверхсопряжения в ОЗМО. Во фрагменте •C-CA3 они равны из-за симметрии заместителя, но во фрагменте •C-CA2B различны.
В ОЗМО фрагмент представлен с коэффициентом CP при P-АО:
=CP+…=CP(P+UXsinX+UYcosY)+… =CP(P+1S1+2S2+3S3)+… (4)
Парциальные функции ki(i) = Cki/CkP в -ОЗМО k зависят от угловых координат атомов (1; 2; 3) и от параметров сверхсопряжения [UX; UY] (табл.1).
ТАБЛИЦА 1. Орбитальные параметры сверхсопряжения и угловые функции со
става -ОЗМО для различного числа эквивалентных атомов в заместителе.
Величина ki2(i)=(Cki/CkP)2=rk(i) является относительным парциальным вкладом в торсионную угловую функцию в k-й -ОЗМО (внутренней, граничной или виртуальной), она составлена из парциальных заселённостей S-АО (Cki2=kSi) и P-АО (CkP2=k) и выражает прямо пропорциональную связь между ними:
kSi = rk(i)k. (5)
Сумма парциальных заселённостей по всему спектру -ОЗМО равна спиновой заселённости S-АО: Si =kkSi =k[rk(i)k]. (6)
Парциальный вклад в контактную спиновую плотность на ядре -атома прямо пропорционален парциальной спиновой (одноэлектронной) заселённости базисной S-АО, и получить его можно калибровкой.
Связь между спиновыми заселённостями Si и имеет вид линейной комбинации парциальных откликов и может быть прямо пропорциональной в отдельных случаях при соблюдении специальных условий. Покажем это. Выделим из суммы слагаемое, отвечающее граничной ОЗМО с её нечётным максимальным номером k=N+1, в которой граничный электрон создаёт делокализационную одноэлектронную компоненту спинового распределения. Среди всех -МО доминанта граничной ОЗМО проявляется в положениях вблизи её пучностей, но во внутренних ОЗМО с k<N+1 формируются спин - поляризационные парциальные части спиновой плотности, и их роль может быть важной вблизи узлов ОЗМО:
Si = r N+1(i)N+1 + k<N+1rk(i)k. (7)
Первое слагаемое r N+1= r SD вызвано спин - делокализацией. Если подобным образом приближённо представить и второе слагаемое, то получим:
(krk(i)k)k<N+1= r SP(i)N+1,
Si = [r SD(i)+r SP(i)](N+1 + N+1). (8)
Калибровка приведёт к контактной спиновой плотности и к константе Ферми - контактного СТВ: ai = ASi, и R(i)= Ak2ki (i), (9)
В разных ОЗМО формируются независимые вклады и в, и в Si, и характеристики парциальных торсионных функций R (i) от -ОЗМО отличаются лишь параметрами, которые можно уточнять по необходимости.
Формула (8) эквивалентна общему выражению константы СТВ:
ai = [R SD(i)+R SP(i)](N+1 + N+1), (10)
а для ядер в группах, находящихся около пучностей граничной ОЗМО, применимо приближение прямо пропорциональной формы:
ai = R (i). (11)
Общее выражение торсионной угловой функции выводится в виде
R()=B0+ B2 cos 2+Q sin2, (12)
где параметры парциальных (в ОЗМО) торсионных угловых функций Ферми-контактного СТВ для групп СAB2; СA2B; СA3 удобно представить таблицей 2. Учёт многоэлектронных эффектов состоит в суммировании каждого парциального параметра в таблице 2 по всему -подмножеству (по Малликену). Учёт -ОЗМО дополнительно выявляет малые вклады в постоянное слагаемое B0.
В двух случаях Q =0, и торсионная угловая зависимость констант СТВ превращается в частный случай – в функцию Хеллера – Мак Коннелла: 1) для одиночного ядро атома A в группе СAB2 (U’kX =0), и 2) для ядер трёх эквивалентных атомов A группы СA3 (UX”’=UY”’). У CA2B-группы симметрия понижена от C3V до CS, и Q 0, и в торсионной функции возникает нечётная гармоника. Параметр Q оказывается фактором асимметрии заместителя.
ТАБЛИЦА 2. Выражения парциальных параметров* торсионных угловых функций СТВ для различного числа эквивалентных атомов A в замещён- ной алкильной группе через орбитальные параметры сверхсопряжения
* Полные параметры получаются суммированием по всему спектру - ОЗМО
** При учёте -ОЗМО дополнительно возникают малые вклады в B0 0
При быстром вращении CA3-группы (CF3-, CH3-) все три ядра динамически эквивалентны, и торсионный угловой множитель R() усреднён по всем поворотным ориентациям заместителя до постоянного значения, равного:
R()=[R()+R(+2/3)+ R(+4/3)]/3=B0+ B2/2= R(/4). (13)
Формула (13) удобна для определения средних значений R() на основании расчётов МО ЛКАО в сериях -радикальных CF3-замещённых гомологов и их изомеров. У CF3-группы конформационное среднее обозначим RF() R.
Графическое представление угловых функций Ферми-контактного СТВ.
Очень удобные графики торсионных угловых функций ИСТВ, возникают при замене углового аргумента квадратом косинуса: cos2=. Нечётная гармоника равна sin2=2[(1-)]. Интервалы изменения и аргумента, и функции ограничены сверху значениями (max; Rmax)=(1; B0+B2). Перенос начала координат в точку (0; R0)=(; B0+B2) превращает переменные в (X; R)=(-0; R-R0), и формула (11) описывает линейно- деформированный эллипс:
R(X)= Rlin(X)+Rell(X), (14)
Rlin(X)= B2X; Rell(X)=Q[1-4X2], (15)
R2ell/Q2+4X2 =1. (16)
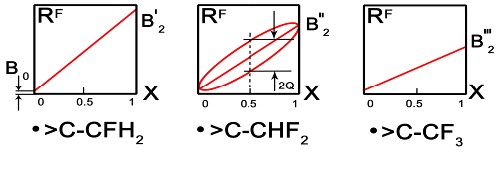
Графики торсионных угловых функций Ферми-контактного СТВ представлены на рис.1.
Параметр асимметрии Q передаётся соответствующей полуосью эллипса. В ряду CFH2-, CF2H-, CF3 – групп параметры B2F образуют пропорцию 1: () : (2/3).
Эти зависимости далее играют важную роль в анализе изоэлектронных аналогий при замещении атома F (Рис. 3).
Релейный зарядовый эффект в триаде АР-НР-КР.
Во второй главе обсуждаются теоретические основы эффекта фторного Ферми-контактного СТВ – релейного зарядового эффекта в триаде АР-НР-КР.
Релейный скачок параметров торсионной угловой функции фторного СТВ при перезарядке радикала в триаде АР-НР-КР вызван тем, что контактная спиновая плотность на ядре 19F чувствительна к изменениям на периферии оболочки. Вблизи ядра формируется электронный заряд экранирования ядра, выражаемый функцией экранирования (r), и эффективный заряд ядра в его окрестностях это разность вида (r)=Z-(r).
Контактная спиновая плотность есть линейная комбинация вкладов со стороны различных базисных АО, и для простоты можно ограничиться просто валентным слоем АО в виде вклада 2SF(0)=|2s(0)|2. При перезарядке радикала в триаде АР-НР-КР разумно искать связь между 2SF(0), F(r) и N - одноэлектронным избытком или дефицитом в оболочке частицы, возникающем при переходе от НР к АР или КР. Естественно связать электронную перезарядку с граничной ОЗМО, и в достаточно сложной ситуации проще всего проследить взаимосвязи через функционал энергии, в котором содержится вся квантово-механическая информация о системе.
Признаки одноэлектронных состояний наиболее близки к водородоподобным АО (ВАО) вблизи ядра - там, где и возникает Ферми-контактное СТВ. Отклонения от ВАО значительны при удалении от ядра - на периферии - там, где формируются валентные взаимодействия с соседними атомами.
Для явной имитации околоядерных эффектов за счёт валентной 2s(F)-АО в качестве базиса используем орбитальные уровни ВАО, вводя их с помощью модифицированной формулы Бора (5), в которой эффективный заряд ядра учитывает экранирование в непосредственной близости от него:
n= -2/2n2; (2.64)
и где все величины обретают содержание, существенно изменённое по сравнению с исходным энергетическим спектром водородоподобного иона. О правомочности такого подхода говорит существование ридберговских уровней, которые удовлетворительно описываются методом квантового дефекта в твёрдом теле и в молекуле. Физический смысл величин в такой аппроксимации может существенно отклоняться от принятой за основу формулы, за исключением мировых констант. Она превращается в «буферное» выражение с прямым назначением поддержать контролируемую количественную связь между величиною измеряемой и теоретически моделируемой в идеальной ситуации.
Прибегая к схеме «сигнал-отклик», можно избрать какую-то разумную последовательность для описания отклика заряда экранирования на возмущения в валенном слое, устанавливая порядок физически важных характеристик, следующих из функционала энергии, скажем в виде:
S(F) E N,
где следуют плотность, эффективный заряд ядра, уровень базисной ВАО, основной терм оболочки, парциальная (или полная) электронная плотность на атоме F, число электронов. Прибегая к конечным разностям [=(/q)q], представим адиабатические последствия перезарядки НР в АР или в КР цепью взаимосвязей.
Фторное СТВ. Экранирование ядер 19F и функционал энергии.
Свяжем приращение эффективного заряда ядра 19F с зарядом радикала через адиабатические изменения характеристик электронных оболочки и ОЗМО в виде последовательности производных:
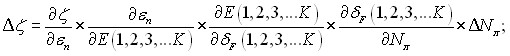(2.70)
Свяжем эффективный заряд ядра с энергией ВАО и находим производную ’. Её знак отрицателен: sign ’ = -1:
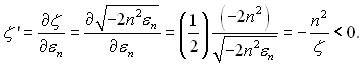(2.71)
Производная (2) 
отражает изменение орбитального уровня базисной ВАО при сдвиге электронной энергии радикала. И числитель, и знаменатель изменяются, вероятно, симбатно, и производная 
положительна, т.е. sign(n’) = +1. Производная (3) 
связана с изменением орбитальной энергии электрона при сдвиге энергии коллектива при смещении заряда внутри структуры радикала. Величина 
может быть лишь отрицательной: sign(E’) = -1. Производная (4) 
отражает сдвиг парциальной электронной плотности на атоме F при изменении заряда радикала и может быть только положительной: signF’= +1.
Наконец, последняя величина 
представляет собою главную причину
всех изменений - электронный избыток либо дефицит в радикале, т.е. N = +1; 0; -1 соответственно у АР, НР, КР.
Триада АР-НР-КР. Знаки приращений факторов R().
Перемножая знаки всех производных, получаем искомый знак приращения эффективного заряда на ядре 19F для зарядовых форм радикала АР-НР-КР:
{sign[(19F)]}АР,НР,КР = [sign ’ sign(n’)sign(E’)signF’]NАР,НР,КР =
= (-1)(+1)(-1)(+1) NАР,НР,КР = +1; 0; -1. (2.72)
О сдвигах контактной плотности в триаде АР-НР-КР.
Радиальная компонента нормированной 2s-ВАО создаёт контактную спиновую плотность на ядре 19F, равную
|2s(0)|2 =|R2s(r=0)|2 = (Z/a0)3/2 (/a0)3/2, (2.73)
где a0 – боровский радиус. С помощью сдвига эффективного заряда ядра получаем и сдвиги контактной плотности между формами АР-НР-КР в виде
|2s(0)|2 = (3/2)a0-32. (2.74)
Согласно полученной модели, константа СТВ с ядром 19F по сравнению с НР увеличена в АР и уменьшена в КР. Это и составляет суть РЗЭ-F. И его знак, и его величина отличают его от зарядовой зависимости СТВ с протонами в плоских ароматических АР и КР. Этот простой результат вовсе не очевиден.
Свяжем его со сверхсопряжением.
Избыточный заряд в оболочке АР мог бы непосредственно увеличить электронное экранирование ядра, уменьшая эффективный заряд ядра, и, как следствие, - внутреннюю долю контактной плотности, но, в согласии с опытом, получилось в точности обратное - эффективный заряд, а с ним и контактная плотность на ядре 19F в АР увеличились.
ГЛАВА 3. Модельные ряды радикалов и методы расчётов.
На 22 страницах текста описаны использованные в работе расчётные методы квантовой химии открытых оболочек.
В главе 3 очень кратко выделены методические основы четырёх необходимых приближений квантовой химии. Выполнена классификация возможностей каждого из них, в соответствии с которыми они применялись:
1) Метод НХФ, исходит из идеи независимых спин-МО (спин-ОЗМО), и в нём наиболее легко достигается многоэлектронное обобщение торсионных угловых функций для алкильного (фторалкильного) СТВ.
Одноэлектронный подход к сверхсопряжению в граничной -ОЗМО справедлив для всего -подмножества, и несовершенства однодетерминатной схемы НХФ известны. Они проявляются в гипертрофии высших мультиплетов при увеличении размеров радикала.
2) Метод B3LYP для открытых оболочек - вариант теории функции плотности (DFT) не вносит принципиальных изменений в исследуемые свойства торсионных функций фторного СТВ по сравнению с МО ЛКАО НХФ.
3) Основная роль в формировании сверхсопряжения принадлежит граничной ОЗМО, обеспечивающей спин-делокализацию, и поэтому для фторалкильных групп хорошие результаты достижимы в рамках спин-ограниченного метода Хартри-Фока-Рутаана (ОХФО-ROHF). Внутренние электроны в нём разделены на спин – спаренные и спин-распаренные слои. Для СТВ с ядрами 19F во фторалкильных группах роль спин-поляризации второстепенная, и этим методом достигаются очень корректные результаты.
4) Полуэмпирический метод Попла INDO прекрасно зарекомендовал себя в расчётах электронного строения радикалов. В диссертации он использован для проверки и иллюстрации физической общности изученных эффектов.
В данной главе наиболее важная расчётная информация получена посредством модельных расчётов методом МО ЛКАО ССП НХФ для ряда фторэтильных радикалов и их изоэлектронных аналогов.
Она представлена в табл. 3 и на рис. 3. В них демонстрируются изоэлект-ронные аналогии в теории торсионных угловых функций СТВ. Зарядовая диада в виде ион-радикальных фрагментов ±•>C-CF3 вполне может реализоваться у АР и КР с общей топологией, но дополнить её нейтральным состоянием НР, расширив до триады АР-НР-КР и сохранить при этом структуру невозможно.
1) Чтобы проследить единые закономерности <R> и параметров (BF0; BF2; QF) в зарядовой триаде АР-НР-КР, были изучены гомологи в рядах симметричных ди- и тетразамещённых линейных полиенов и перфторполиенов: НР RR’C(CH)2k+1CRR’• и АР-КР RR’C(CH)2kCRR’•±, где (R,R’=CF3,H), (R, R’= CF3, CH3), (R,R’=CH3,H); (CF3)2C(CF)2k+1C(CF3)2• и (CF3)2C(CF)2kC(CF3)2•±, где 0k9.
2) Эта же задача была рассмотрена в рядах паразамещённых фениленов, где наиболее корректно приближение (11), и формирование различающихся зарядом АР-НР-КР устойчивых радикальных центров обеспечивают заместители X, как-то: 4-X-C6H4-RF•-; 4-X-C6H4-RF•; 4-X-C6H4-RF•+, где RF= CFnH3-n
(0n3); CFn-1H3-nOR (1n3), R=H,RF (0n3); X= -NO2•, -CN•, -O•, -CH2•, -C(CF3)2•, -NH2•+, -N(CH3)2•+, в числе которых представлены АР нитробензолов 4-RF-C6H4-NO2•, цианбензолов 4-RF-C6H4-CN•, НР феноксилов 4-RF-C6H4-O•, бензилов 4-RF-C6H4-CH2•, перфторкумилов 4-RF-C6F4-C(CF3)2•, КР анилинов
4-RF-C6H4-NH2•+ и диметиланилинов 4-RF-C6H4-N(CH3)2•+.
В главе 3 рассмотрены корреляции между константами фторного, протонного и азотного СТВ в АР и НР большой серии фторорганических радикалов с оптимизированной геометрией. Для них есть литературные данные об экспериментальных спектрах ЭПР. Квантово-химические расчёты были выполнены по методу B3LYP(6-31G). Калибровочные корреляции создают представление о диапазонах точности, достижимых в независимых расчётах.
ГЛАВА 4. Эксперимент и теория. «Аномалии» и закономерности СТВ со 19F.
На 11 страницах текста обсуждаются калибровочная корреляция строго линейного вида для констант фторного СТВ в АР фторалкилированных нитробензолов 4-CF3-C6H4-NO2• (A); 3,4-O(F2C)2-C6H3-NO2• (B); 4-HF2C-C6H4-NO2• (C); 3-CF3-C6H4-NO2• (D). Линейная регрессия характеризуется очень высоким коэффициентом корреляции (r2=0.999). Абсолютные значения рассчитан-ных констант фторного ИСТВ вдвое больше измеренных (рис.2). Удивляет, что изменение фторных и азотных констант СТВ антибатное: aF(A)<aF(B)<aF(C), но при этом aN(B)<aN(A)<aN(C). Судя по азотным константам ИСТВ, -спиновая плотность в АР B смещена от NO2-группы в кольцо, но к ожидаемого увеличения контактной спиновой плотности на ядрах 19F в параположении не наблюдается. Напротив, по сравнению с АР C она уменьшена. Из этого следует, что сам фрагмент -CF2-O- по своим свойствам занимает положение промежуточное между CF3- и CF2H-группами.
Качественно эта кажущаяся аномалия объяснима, если в группе CF3 заместить один атом F фрагментом -O-R- (в цикле -CF2-O-CF2-), и если одну из неподелённых электронных пар атома -F: уподобить валентной паре атома -O-.
Известны АР, содержащие -CF2-O-CF2-фрагмент в тетрафторфурановом 5-членном и тетрафторпирановом 6-членном циклах в АР замещённых аренов. Интерпретация их спектров ЭПР сопряжена с подобными эффектами, и потому требуется развить теорию проявления изоэлектронных аналогий ядер 19F в стереохимических зависимостях констант СТВ. Формально они возникают в цепи замещений: CH3 NH2 OH F, в которой для нас важно первое звено, с появлением кислородного мостика. Из него возникает «стандартная» серия аналогов атома F, как-то: OСF3 OСH3 OH F, где замена H на СH3 подобна известной алкоксильной защите, практикуемой в лабораторном синтезе сахаров.
Можно ожидать, что, как и изотопное, изоэлектронное замещение сравнительно мало изменит характеристики торсионных угловых функций фторного ИСТВ, а искажение симметрии заместителя в сравнении с близостью потенциальных энергий притяжения к ядрам играет второстепенную роль и существенно не повлияет на графики исследуемых функций.
В первой цепи замещения CFH2 C(OH)H2 C(OCH3)H2 C(OF3)H2, можно ожидать, что сохранится вид угловой функции -протонного СТВ, и у R(cos2H) это линейно искажённый эллипс.
Во второй цепи замещения CF2H CF(OH)H CF(OCH3)H CF(OF3)H R(cos2H) имеет линейный, но R(cos2F) у -фторного СТВ – вид деформированного эллипса, вопреки тому, что один атом F из двух замещён.
В третьей цепи замещения CF3 CF2(OH) CF2(OCH3) CF2(OF3) -протонов нет, и инвариантность касается торсионной функции фторного СТВ R(cos2F). Его графическая основа – от группы CF3 – прямая линия. Искажение неизбежно, и график, конечно, примет вид скошенного эллипса, но можно полагать, что искажение будет минимальным.
Именно так и обстоит дело в ряду фторэтильных НР •>C-CFn-1H3-nOR, где R=OH, OСH3, OСF3.Хорошо соблюдается ожидаемая пропорция параметров B’2F: B”2F: B’”2F =1:(3/4):(2/3). Значения, вычисленные методом НХФ (6-31G), приведены в табл. 3. Их усреднение в рядах аналогов даёт {<B’2F>;<B”2F>; <B’”2F>} = {88.6; 66.8; 59.1} и пропорцию 1: 0.754: 0.667.
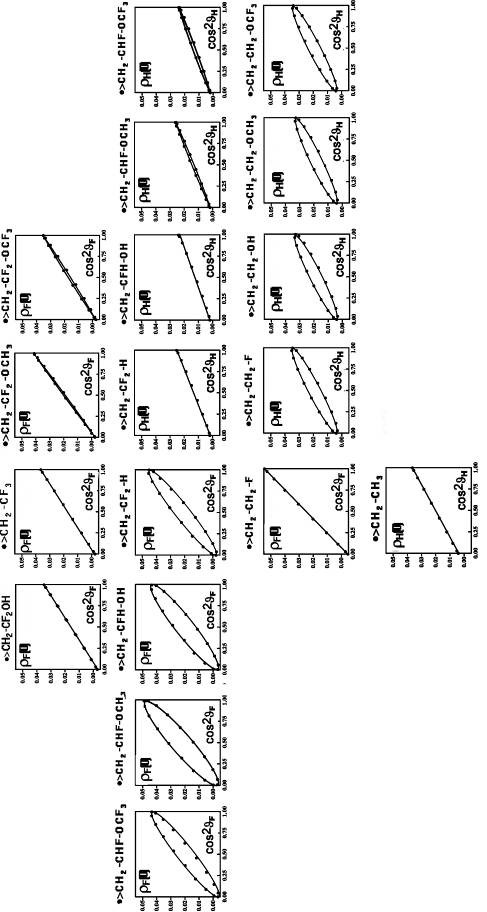
Изоэлектронные аналогии в системе торсионных функций СТВ для ядер 19F и 1H прекрасно иллюстрируют графики, представленные на рис. 3.
ТАБЛИЦА 3. Параметры торсионных угловых функций ИСТВ с ядрами 19F и 1H в рядах фторэтильных радикалов •>C-CF nH3-n по данным неэмпирических расчётов МО ЛКАО НХФ ССП (6-31G), B0F]=[B2F]=[QF]=[B0H]=[B2H]=[QH]=Гс.
| Радикал | B0F | B2F | QF | B0H | B2H | QH |
| •H2C-CF3 | -3.797 | 58.179 | – | – | – | – |
| •H2C-CF2OH | -4.680 | 56.540 | 0.109 | – | – | – |
| •H2C-CF2OCH3 | -3.908 | 65.512 | 0.093 | – | – | – |
| •H2C-CF2OCF3 | -3.758 | 56.019 | 2.314 | – | – | – |
| •H2C-CHF2 | -3.457 | 67.481 | 7.297 | 2.879 | 37.246 | – |
| •H2C-CHFOH | -5.029 | 64.861 | 7.536 | 1.961 | 35.183 | -0.015 |
| •H2C-CHFOCH3 | -4.864 | 69.693 | 5.231 | 2.760 | 38.406 | -0.009 |
| •H2C-CHFOCF3 | -5.329 | 65.056 | 8.779 | 2.910 | 34.795 | -0.012 |
| •H2C-CH2F | -6.905 | 88.613 | – | 6.030 | 54.717 | -3.420 |
| •H2C-CH2OH | – | – | – | 6.221 | 52.330 | -1.599 |
| •H2C-CH2OCH3 | – | – | – | 6.109 | 51.821 | -4.932 |
| •H2C-CH2OCF3 | – | – | – | 6.330 | 54.128 | -4.622 |
| •H2C-CH3 | – | – | – | 6.437 | 51.452 | – |
Протонное СТВ каких-то особенных «магических» соотношений въявь не обнаруживает - поведение атомов H и F принципиально разное. Слишком лабильно электронное строение простейшего атома Периодической Системы. Для него не действенны простые орбитальные правила поведения параметров сверхсопряжения, свойственные атому F. Далее встаёт задача об аналогичных закономерностях и в простейшем ряду радикалов, и в радикалах более сложных, с иными системами сопряжения.
Она решается в следующей главе диссертации.
ГЛАВА 5. Параметры торсионных угловых функций контактного СТВ с ядрами 19F в зарядовых триадах АР-НР-КР.
На 38 страницах графически иллюстрированного текста приводятся и обсуждаются результаты квантово-химических расчётов методами UHF, B3LYP, ROHF, INDO ион - радикалов и нейтральных радикалов в нескольких модельных рядах гомологов с линейными и ароматическими структурами.
Подтверждается модель «клякса-губка». У АР электрон заселяет гранич-ную ОЗМО, природа её разрыхляющая, и электронная плотность «размывается», как «клякса», и растёт эффективный заряд ядра атома F. Электронный дефицит на граничной ОЗМО в КР создаёт дырку - «губку», стягивающую электронную плотность. Эффективный заряд ядра атома F уменьшается, а с ним и <RF>.
По расчётам НХФ у АР-НР-КР диалкил- и тетраалкилзамещённых полиенов и перфторполиенов усреднённые значения <R> экспоненциально зависят от длины цепи (рис. 4). Линии для разных зарядовых состояний строго дистанцированы друг от друга. Эффект имеет настолько общий характер, что зависимости в разных сериях даже графически предельно похожи. Угловые факторы <R(CF3)> мало меняются от соседства с другим заместителем у того же плоского центра, но величины <R(CH3)> от соседнего заместителя зависят заметно.
Константы -протонного СТВ существенно лабильнее, но их абсолютные значения меньше меняются в зависимости от длины цепи в одном и том же ряду. Интервал значений RH, заметно более узкий, чем RF.
На рисунке 5 в графическом виде представлены результаты расчётов по методу ОХФО АР-НР-КР серии полиенов, содержащих на краях цепей и CF3- и CH3-группы, т.е. (CF3)(CH3)C(CH)nC(CF3)(CH3).
Всюду каждая CF3-группа находится в цис-положении к ближайшему -атому F в плоскости цепи, и возникают цис-конфигурации у нечётных гомологов (рис. 5.1.A) и транс-конфигурации у чётных гомологов (рис. 5.1.B, C), и CF3-группы всюду максимально возможно удалены друг от друга.
Качественно данные расчётов ОХФО и НХФ согласуются между собой, но количественно они отличаются. Важнейшие итоги следующие.
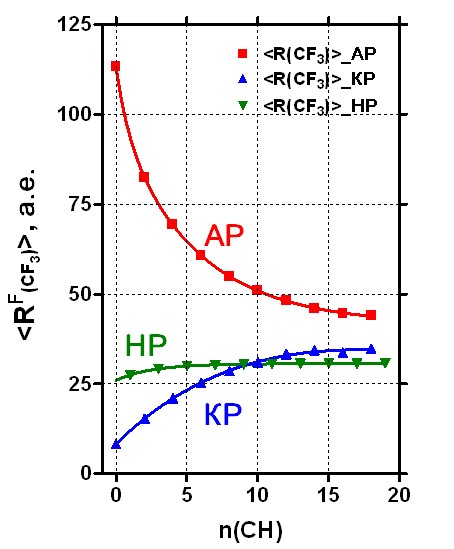
РИС.4a. Ряды (F3C)(H3C)C(CH)nC(CF3)(CH3) и (F3C)HC(CH)nC(CF3)H.
Релейный зарядовый эффект (РЗЭ-F) в цепях разной длины.
РИС. 4б. Факторы <R(CH3)> и <R(CF3)> в рядах АР-НР-КР
(F3C)(H3C)C(CH)nC(CF3)(CH3) и (H3C)HC(CH)nC(CH3)H с разной длиной цепи.
1) Релейный эффект (РЗЭ-F) фторного СТВ выражается неравенствами: [<R(CF3)>(• -)]>> [<R(CF3)>(•)]>[<R(CF3)>(• +)] и он ярко выражен. (рис. 5.3).
2) Для СТВ с 1H в расчётах ОХФО выявляется также и РЗЭ-H, но в ином порядке: [<R(CH3)>(• -)]>>[<R(CH3)>(•)]>[<R(CH3)>(• +)] (рис. 5.4).
3) В отличие от РЗЭ-F (НХФ) при РЗЭ-F (ОХФО) с увеличением числа звеньев цепи в диапазоне 1<n(CH)<18 среднее значение <R(CF3)> у анион-радикалов меняется в узком диапазоне значений от 95 и лишь до 85 Гс (рис. 5.3). Это имеет место и в перфторированном ряду (CF3)2C(CF)2kC(CF3)2•± и (CF3)2C(CF)2k+1C(CF3)2•, где 0k9 (рис. 5.2). Это свидетельствует о корректности прямо пропорциональной связи между константой -фторного СТВ и -спиновой заселённостью aF()/= RF(), т.е. в пользу выводов, приведённых в тексте диссертации в разделах (21.19 - 21.21 ), определяющих условия такой взаимосвязи.
4) Из данных расчётов ОХФО следует вывод об основной роли делокализации – сверхсопряжения для механизма фторного СТВ, но об этом трудно судить в случае протонного СТВ.
5) Уровни граничных ОЗМО с ростом длины цепи понижаются по экспоненте в близком согласии с одноэлектронной моделью квазиодномерного «ящика» (рис. 5.2).
ТАБЛИЦА 4. Изоэлектронные аналогии в АР-НР-КР паразамещённых
фениленов Параметры торсионных угловых функций (Гс) с ядрами 19F для CF3-
и CF2OH-групп в АР-НР-КР 4-X-Ar-CFn-1(OR)H3-n, вычисленные методом B3LYP(6-31G).
| Арены | RF | CF3 | CF2OH | ||||
| X- | -Ar- | B0F, | B2F | B0F | B2F | QF | |
| АР | •O2N- | -C6H4- | 0.98 | 183.00 | 0.75 | 180.77 | 10.24 |
| •NC- | -C6H4- | 6.65 | 312.50 | 6.04 | 300.73 | 24.45 | |
| НР | •(CF3)2C- | -C6F4- | -0.76 | 52.23 | -1.65 | 49.59 | 3.88 |
| •CH2C- | -C6H4- | -1.45 | 73.21 | -1.66 | 73.49 | 5.19 | |
| КР | +•H2N- | -C6H4- | -1.87 | 33.12 | -2.68 | 31.25 | 3.93 |
| +•(CH3)2N- | -C6H4- | -1.95 | 37.46 | -2.33 | 36.23 | 3.62 | |
КРАТКИЕ ИТОГИ
Следуя литературной традиции, изученные в настоящей работе системы мы называем -радикалами, содержащими фторалкильные заместители, при всей неточности такого определения из-за утраты ими должной симметрии.
Но даже приближённая локальная симметрия молекулярных фрагментов остаётся мощным инструментом теоретического прогноза свойств, кажущихся для аналитических представлений без неё почти безнадёжными.
Именно из такого положения удаётся вывести теорию торсионных угловых функций Ферми - контактного СТВ с ядрами 19F в замещённых алкильных группах при плоском радикальном центре.
ВЫВОДЫ.
- Впервые торсионные угловые функции Ферми - контактных сверхтонких взаимодействий с ядрами алкильных и фторалкильных групп в -радикалах изучены методом понижения симметрии. Введён способ их графического анализа и теоретически показана линейная связь контактной спиновой плотности на ядре атома в -положении с парциальными -спиновыми заселённостями радикального центра в спектре -ОЗМО (НХФ).
- Исследованы угловые функции Ферми - контактного СТВ с ядрами 19F и 1H в гомологическом ряду фторалкилированных -радикалов при замещении атома F кислородсодержащими группами. Установлены признаки и закономерности эффекта изоэлектронной инвариантности, согласующиеся с экспериментом (ЭИИ-F).
- Впервые описан и теоретически изучен релейный эффект во фторалкильных группах, наблюдаемый в спектрах ЭПР в виде зависимости от заряда радикала параметров угловой функции константы фторного СТВ (РЗЭ-F).
- Модельные квантово-химические расчёты торсионных угловых функций фторного и протонного СТВ в рядах линейных и ароматических -радикалов с воспроизводят релейное изменение контактных спиновых плотностей на ядре 19F при смене заряда радикала.
- Показано, что релейный эффект фторного СТВ у радикалов с разными зарядами вызван перераспределением плотности в граничной ОЗМО. Предложен механизм влияния электронного избытка и дефицита в оболочке на контактную спиновую плотность через эффективный заряд ядра в базисной s-АО.
- Выводы работы основаны на результатах модельных неэмпирических и полуэмпирических квантово-химических расчётов для 500 оптимизированных фторалкилированных радикальных структур, выделенных из 3000 пробных структурных точек. Результаты теоретических расчётов согласуются с экспериментальными спектрами ЭПР.
ПУБЛИКАЦИИ материалов диссертации:
Статьи
- Е.А. Поленов, К.В. Боженко, Л.А. Шундрин, Д.М. Смекалкин. «Орбитальная модель сверхсопряжения. Элементарная теория угловых функций стереоспецифических констант ИСТВ и их изоэлектронная инвариантность в галогеналкилзамещённых -радикалах». «Изв. РАН. Сер. физ.». 2004, т. 68, № 7, с. 1066-1069.
- Д.М. Смекалкин, Б.К. Новосадов, Е.А. Поленов. Ферми-контактные взаимодействия во фторалкилзамещённых –радикалах. Релейный зарядовый эффект граничных МО и его квантово-химическое моделирование методом INDO. М. Вестник МИТХТ. 2007, т.2,№5, с. 21-27.
Тезисы докладов
- Б.К. Новосадов, Е.А. Поленов, Д.М. Смекалкин. К вопросу о зарядовой зависимости констант СТВ в спектрах ЭПР органических -радикалов. 5-я Всероссийская конференция «Молекулярное моделирование», РАН. ГЕОХИ. МГУ. 18-20.04.2007. с. 79.
- Д.М. Смекалкин, Б.К. Новосадов, Е.А. Поленов. Моделирование релейного эффекта фторных контактных спиновых плотностей во фторметилированных свободных радикалах с разными зарядами. XVIII Менделеевский съезд по общей и прикладной химии. Москва. 23-28 сентября 2007 года. Тезисы докладов в 5 томах., т.1., с.433. 2007.
