Физические свойств а композиционных материалов на основе полипропилена
На правах рукописи
Аминева Елена Хрисанфовна
физические свойства
композиционных материалов
на основе полипропилена
Специальность 02.00.06 «Высокомолекулярные соединения»
АВТОРЕФЕРАТ
диссертации на соискание ученой степени
кандидата физико-математических наук
Нальчик – 2009
Работа выполнена в Кабардино-Балкарском государственном университете имени Х.М. Бербекова.
Научный руководитель: доктор технических наук, профессор
Данилова-Волковская Галина Михайловна
Официальные оппоненты: доктор физико-математических наук,
профессор Никитин Лев Николаевич
доктор технических наук, профессор
Морозов Юрий Львович
Ведущая организация: Институт биохимической физики
им. Н.М. Эммануэля РАН
Защита состоится «23» октября 2009 г., в 15.00 часов на заседании диссертационного совета Д 212.076.09 в Кабардино-Балкарском государственном университете им. Х. М. Бербекова по адресу: г. Нальчик, ул. Чернышевского, 173, КБГУ, диссертационный зал.
С диссертацией можно ознакомиться в библиотеке КБГУ им. Х. М. Бербекова
Автореферат разослан « » сентября 2009 г.
Ученый секретарь
диссертационного совета Борукаев Т.А.
Актуальность работы. Многообразие процессов и явлений, протекающих при получении и переработке композиционных материалов, значительное количество факторов, влияние которых должно быть учтено – энергоемкость, высокая стоимость сырья и оборудования, вызывают затруднения в проведении полного набора необходимых экспериментов для оптимизации их состава и свойств.
Актуальным и наиболее перспективным является разработка методов автоматизированного расчета и прогнозирования показателей свойств полимерных композиционных материалов (ПКМ), сочетающих способы физического и математического моделирования.
Метод автоматизированного прогнозирования позволит рассчитывать реальные величины показателей конкретных композиционных материалов, чтобы аргументировано корректировать состав и технологические режимы формования изделий из них.
Основная цель работы: разработка научно обоснованного метода прогнозирования комплекса свойств полимерных электропроводящих композитов на основе полипропилена для производства изделий специального назначения.
Поставленная цель определила необходимость решения следующих задач:
- исследование влияния составов композитов на реологические и теплофизические характеристики их расплавов;
- разработка теоретических основ определения и прогнозирования реологических, теплофизических и электромагнитных свойств полимерных электропроводящих композиционных материалов на основе полипропилена;
- обобщение и описание количественными зависимостями полученных теоретических и экспериментальных данных с целью прогнозирования
их свойств; - промышленная апробация метода прогнозирования свойств композитов, разработанных рецептур и технологических рекомендаций.
Научная новизна. Разработан метод расчета и прогнозирования свойств полимерных электропроводящих композиционных материалов, сочетающий приемы физического и математического моделирования. В рамках исследований проведен комплексный анализ и математическое описание влияния состава и концентрации компонентов на физические характеристики ПКМ и
изделий из них.
Метод позволяет расчетным путем прогнозировать влияние наполнителей и термомеханических воздействий на свойства ПКМ, получать исходные данные для оптимизации процессов его переработки в изделия с заданным комплексом свойств.
Практическое значение работы. Разработан метод прогнозирования свойств полимерных композитов с учетом взаимодействия компонентов и формирования упрочненного граничного слоя на примере электропроводящих композитов.
- Разработана методика расчета показателей реологических свойств полимеров по экспериментальным данным и определения оптимальной концентрации наполнителя в композиционных материалах, с учетом условия технологичности.
- Создана методика расчета и прогнозирования реологических, теплофизических и электромагнитных свойств на примере электропроводящих композиций.
3. Получен блок математических моделей, разработаны алгоритмы численного решения и программное обеспечение для расчетного определения оптимального состава композиционного материала с заданными свойствами или прогнозирования свойств существующих композитов.
Разработанные методики внедрены в учебный процесс подготовки инженеров по специальностям 121000 «Конструирование и производство изделий из полимерных композиционных материалов» и 170506 «Технология переработки пластмасс и эластомеров», в объеме дисциплин «Теоретические основы технологии переработки полимерных материалов», «Методы оптимизации композитных конструкций» и в промышленное производство на предприятиях Юга России.
Реализация результатов работы. Проведенные исследования послужили основой для работ по оптимизации технологии производства крупногабаритных литьевых, и профильных экструзионных изделий из ПКМ на предприятиях: ООО «Олеум» - г. Ростов на Дону, ООО «Элиар ком» - г. Москва, ООО «ВиВа» - г. Новороссийск.
Алгоритм расчета исходных данных для моделирования процессов литья под давлением изделий из ПКМ реализован в программный продукт в интегрированной среде Turbo Pascal 7.0 и Delphi 7 объектно-ориентированного программирования продукции фирмы Borland с технологией визуального и событийного программирования. Комплекс программ, для прогнозирования свойств полимерных композиционных материалов на основе полипропилена включен в состав современной автоматизированной системы проектирования и оптимизации технологических процессов литья под давлением.
Публикации. По материалам диссертации опубликовано 11 статей, одна из которых в журнале, рекомендуемом ВАК, представлены доклады на II и III Всероссийских научно-практических конференциях «Новые полимерные композиционные материалы» г. Нальчик, 2005 г., 2007 г., 4-й и 5-й региональных научно-технических конференциях г. Новороссийск. 2005 г., 2007 г.
Структура и объем работы. Диссертация включает в себя введение, литературный обзор, экспериментальную часть, выводы, список использованной литературы и приложения.
Работа изложена на 142 страницах машинописного текста, содержит 25 рисунков, 11 таблиц и список литературы, включающий 82 наименования.
Содержание работы
Во введении дается обоснование целесообразности и актуальности темы исследований, представленных в диссертационной работе.
Первая глава посвящена анализу состояния проблем и научных достижений в области прогнозирования и расчета показателей свойств полимерных и композиционных материалов, моделирования процессов их переработки. Сформулированы цель и задачи исследования, научная новизна, практическая значимость работы и основные положения, выносимые на защиту.
Во второй главе приводятся результаты исследований влияния различных видов электропроводящих наполнителей на реологические свойства полимерных композиционных материалов. Полученные данные использовались для разработки научно обоснованных методик расчетов показателей свойств и конструирования состава ПКМ с использованием математического моделирования.
На первом этапе с помощью вискозиметров постоянных давлений изучено влияние дисперсных электропроводящих наполнителей: графита элементного, порошков металлов на реологические свойства ПКМ. Применяемые наполнители вводились в идентичных условиях и обладали одинаковой дисперсностью частиц (от 7 до 15 мкм). Для расчета значений эффективной вязкости, функции релаксации и релаксационного спектра проведено исследование поведения расплавов ПКМ в условиях интенсивного сдвигового воздействия на ротационном вискозиметре. С целью обобщения экспериментальных данных разработан способ обсчета исследуемых показателей.
Предложен способ математического описания вязкостных свойств композиционных материалов по вискозиметрическим данным экспериментальных исследований. По данным экспериментальных исследований композиционных материалов на основе полипропилена проведен анализ и описание зависимостей эффективной вязкости от концентрации наполнителя математическими моделями в виде полиномов второго порядка.
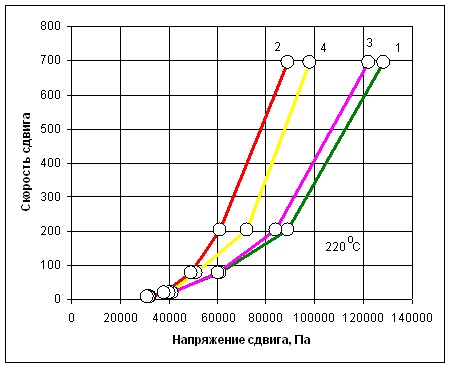
Построены графические зависимости, отражающие влияние различных наполнителей на вязкость расплавов композитов при температуре переработки композита в изделие (рис. 1).
С помощью разработанной методики экспериментальные зависимости вязкости композиционных материалов от содержания электропроводящих наполнителей: графита, порошков меди, никеля и железа обобщены регрессионными математическими моделями.
Эффективная вязкость ПП с дисперсными электропроводящими наполнителями достаточно точно описывается выражением Ландела-Мозера-Баумана:
,
где 
, и – эмпирические коэффициенты, зависящие от вида и дисперсности наполнителя, 0 – объемная доля наполнителя, g. – массовая доля наполнителя, max – максимальная объемная доля наполнителя, рассчитываемая как отношение насыпной плотности наполнителя к истинной.
Зависимость вязкости от объемной доли наполнителя () для ПП, наполненного дисперсным графитом, адекватно моделируется выражением:
;
для ПП, наполненного медным порошком:
.
В рамках предложенного метода разработан способ расчета максимально возможной концентрации наполнителя с учетом условия технологичности, позволяющий определять количество наполнителя, которое позволит переработать композит в качественные изделия без значительного изменения технологического режима и протекания интенсивных деструктивных процессов в полимерном связующем.
Способ состоит в определении приращения вязкости полимера матрицы при понижении температуры переработки от максимальной до минимально возможной, и расчете соответствующей объемной доли наполнителя увеличивающей вязкость ПКМ на эквивалентную величину (табл.1).
Таблица 1
Влияние температуры на эффективную вязкость ПП
| Температура расплава, С | 190 | 195 | 200 | 205 | 210 | 215 | 220 | 225 | 230 | 240 | 245 |
| Значение эффективной вязкости ПП, 104 Па. с | 14,2 | 10,7 | 8,1 | 6,2 | 4,6 | 3,6 | 2,2 | 2,0 | 1,7 | 1,3 | 0,9 |
Зависимость вязкости полимера в связующем от температуры адекватно описывает выражение:
,
где 0 – наибольшая ньютоновская вязкость полимера связующего, определяемая экспериментально,
Е – энергия активации вязкого течения,
Тmin, Тmax – нижний и верхний предел температур переработки.
Рассчитаны показатели реологических и теплофизических свойств электропроводящих композиционных материалов на основе ПП с металлическими и углеродными наполнителями и определены оптимальные режимы получения профильных изделий из них (табл. 1).
Таблица 2
Значения эффективной вязкости ПКМ на основе ПП с углеродным наполнителем
| Объемная доля наполнителя | 0,01 | 0,05 | 0,10 | 0,15 | 0,20 | 0,25 | 0,30 | 0,35 | 0,40 | 0,45 | 0,50 |
| Значение эффективной вязкости расплава композита, 105Па. с | 1,16 | 1,34 | 1,57 | 1,82 | 2,31 | 2,94 | 3,91 | 5,53 | 8,61 | 15,6 | 39,0 |
При этом оптимальную объемную долю наполнителя предлагается определять графически или рассчитывать из выражения:
,
где 0 – наибольшая ньютоновская вязкость;
Тк – максимальная температура переработки полимера матрицы.
Предлагаемую методику использовали для разработки алгоритма автоматизированного расчета показателей реологических свойств ПКМ.
Влияние электропроводящего наполнителя на механические свойства композиционного материала исследовалось в стандартных условиях по соответствующим ГОСТам.
Комплекс механических характеристик был выбран исходя из условий эксплуатации
изделий из полимерных электропроводящих композитов. Предположительно низкотемпературные нагреватели испытывают растягивающие напряжения, нагревание, ударные воздействия и изгибающие
деформации.
Исследовалось влияние наполнителя на модуль упругости (рис.2). Наилучшими показателями обладали композиции с углеродными наполнителями, очевидно, за счет изменения надмолекулярной структуры полимера матрицы и большего ограничения подвижности молекулярных и надмолекулярных образований. Определялось разрушающее напряжение при растяжении, относи
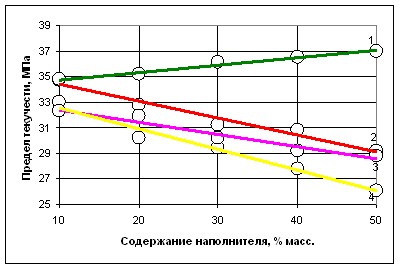
тельное удлинение, предел текучести при растяжении
(рис. 3), удельная работа ударной вязкости по Шарпи с надрезом, без надреза, деформационная теплоустойчивость по Мартенсу.
По результатам исследований выбраны наполнители для дальнейшего изучения теплофизических свойств ПКМ.
Изучены зависимости показателя теплофизических свойств композитов на основе ПП и электропроводящих наполнителей – графита, элементных порошков меди
и железа.
Удельную теплоемкость определяли методом дифференциально-сканирующей калориметрии (рис.4).
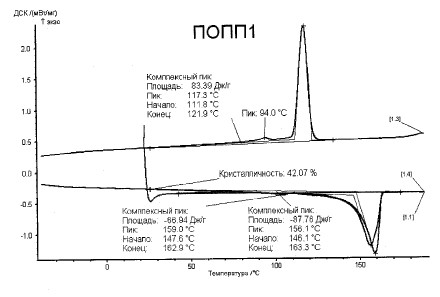
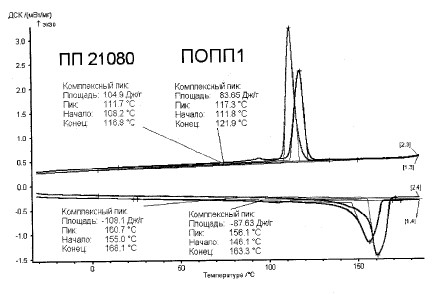
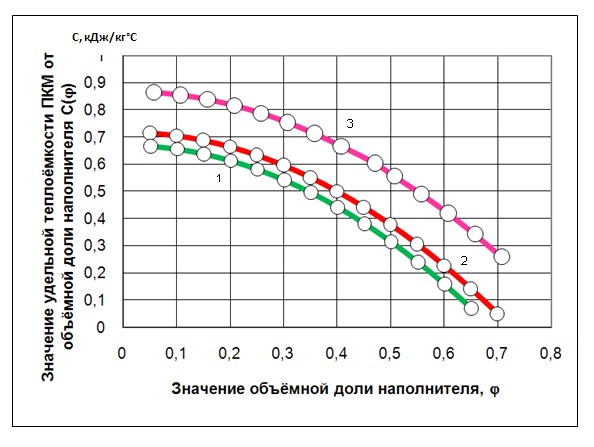
Расчетные значения удельной теплоемкости приведены на рис. 5.
Изучали влияние отдельных наполнителей на коэффициент теплопроводности, который зависит от размера и формы частиц наполнителя, их распределения в матрице полимера. На основании полученных данных предложено решение задачи о термомеханическом поведении расплава ПКМ в узлах перерабатывающего оборудования. Объем материала моделировался полым цилиндром, т.к. в большей части перерабатывающего ПКМ оборудования, процессы пластификации, смешения и дозирования протекают в шнеко-цилиндровой паре. Поэтому решение температурной задачи проводилось в цилиндрической системе координат.
Для расчета оптимальных технологических параметров переработки ПКМ в изделия предложено решение задачи о термомеханическом поведении расплава ПКМ в узлах перерабатывающего оборудования с учетом влияния наполнителя на его реологические и теплофизические показатели.
Для решения поставленной задачи использовалось уравнение, описывающее распределение температуры T в расплаве ПКМ в цилиндрической координатной системе: 
.
здесь t – время, – коэффициент температуропроводности, считающийся постоянным, r, z – цилиндрические координаты.
При стационарном температурном поле уравнение теплопроводности для осесимметричной задачи в цилиндрических координатах с учетом зависимости 
Функция температуры Т(t) определялась из решения квазилинейного уравнения теплопроводности:
.
Здесь 
– коэффициент теплопроводности материала, зависящий от температуры, 
– заданная функция внешних источников тепла.
Граничные условия приняты в виде:
;
;
;
.
Здесь 
,
,
– температуры, 
,
,
– коэффициенты теплоотдачи на всех поверхностях. Последнее граничное условие первого рода – температура известная функция 
.
К решению поставленной задачи был применен вариационно-разностный метод.
Дифференциальный оператор системы уравнений самосопряжен и положительно определен. В силу этого разностная схема была построена методом аппроксимации функционала, сохраняющим данное свойство и для сеточной задачи. Согласно методу аппроксимации функционала интегралы вычислялись по формулам численного интегрирования, а входящие в него производные заменялись разностными отношениями. Система разностных уравнений относительно неизвестных в узлах сетки получена из условия минимума аппроксимирующего функционала.
Разностная схема является консервативной, исходя из условия соблюдения вариационного принципа Лагранжа, и обладает вторым порядком точности.
Зависимость 
аппроксимировалась полиномом типа:
.
Выражение позволяет получить достаточную точность при невысокой степени полинома (
). Примененные стандартные подпрограммы для определения коэффициентов аппроксимирующего полинома 
позволяет легко автоматизировать данную процедуру.
Решение температурной задачи вариационно-разностным методом удобно с точки зрения получения сеточной функции 
и ее градиента, которые использовались в дальнейшем для решения задачи движения расплава в узлах перерабатывающего оборудования тем же методом и на той же сетке с постоянным шагом.
Для расчета коэффициента теплопроводности наполненных полимеров предложено использовать следующие выражения.
При регулярном распределении частиц наполнителя в среде полимера и невысоком их содержании (5 – 15 %) справедливо уравнение:
,
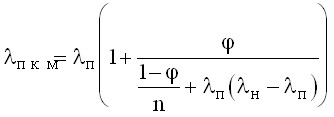где п – коэффициент теплопроводности полимера;
н – коэффициент теплопроводности наполнителя;
n – коэффициент, характеризующий форму частиц (n = 3 для шарообразных частиц, n >3 для частиц любой другой формы).
При средних значениях содержания наполнителя (15 - 70 %) показана целесообразность использование модели вида:
.
Для автоматизированного расчёта показателей удельной теплоемкости, коэффициентов теплопроводности и температуропроводности разработаны алгоритмы, использующие различные математические модели, реализованные в программный продукт объектно-ориентированного программирования (рис. 6).
Рис. 6. Блок-схема расчета показателей теплофизических свойств ПКМ,
зависящих от концентрации наполнителя
В третьей главе исследовался механизм проводимости тока в композиционных материалах на основе ПП с электропроводящими наполнителями. Получены выражения для расчетов показателей электрических и магнитных свойств.
Под действием внешнего поля 
носители заряда приходят в упорядоченное движение и приращение импульса носителя за промежуток времени (t) между двумя последовательными соударениями его с рассевающими центрами (атомами) среды (ПП) равно:
,
где m – масса носителя заряда;
u – напряжение электрического поля;
q – величина заряда;
E – напряженность электрического поля;
t – время протекания заряда.
Получено выражение для расчета проводимости через микроскопические и кинетические параметры носителей заряда:
,
где n = g0t0 – концентрация носителей заряда за характеристическое время.
При этом выражение для расчета нестационарной проводимости будет иметь вид:
,
где Г() – гамма-функция Эйлера, введенная для удобства преобразований.
Экспериментальные данные показывают, что тонкие образцы ПП (толщиной нескольких мкм) обладают более высокой проводимостью, чем толстые. Это свидетельствует об эффективном увеличении промежутка времени (t) между двумя последовательными соударениями с рассевающими носителя заряда в тонких пленках.
Согласно теории перколяции в наполненных композитах, электропроводность Qпкм может быть рассчитана теоретически при учёте поверхностного натяжения между полимерной матрицей и наполнителем:
,
где Qп - проводимость полипропилена;
Qн - проводимость графита элементного;
Q – проводимость ПКМ.
С учетом разработанных подходов для расчета значения электрической проводимости ПКМ на основе ПП предложено следующее выражение:
.
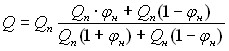Показана эффективность применения выражения для расчета проводимости, в случае если показатели проводимости компонентов ПКМ различаются не больше чем в 4-5 раз:
.
При большом различии показателей проводимости и высоком содержании наполнителя рациональнее использовать уравнение вида:
.
Подставляя вместо Q показатели соответствующих свойств, можно рассчитать показатели электромагнитных свойств ПКМ.
Диэлектрическая проницаемость рассчитывается из выражения:
.
Тангенс угла диэлектрических потерь рассчитаем из выражения:
.
Удельное объемное электрическое сопротивление можно определить из уравнения: Rпкм = Rнн Rп(1-п)
Все разработанные алгоритмы расчетов показателей свойств объединены в единый метод расчета и реализованы в пакет прикладных программ прогнозирования показателей физических свойств полимерных электропроводящих композиционных материалов.
Программный продукт позволяет адекватно прогнозировать:
- концентрацию наполнителя, позволяющую применять оптимальный технологический режим переработки ПКМ в изделия без интенсификации деструктивных процессов в связующем;
- влияние наполнителя на вязкость расплава ПКМ;
- удельную теплоемкость, коэффициенты теплопроводности и температуропроводности с учетом концентрации наполнителя, необходимые для оптимизации режимов переработки композита в изделия методом литья под давлением;
- плотность расплава ПКМ и изделий из него;
- коэффициенты линейного и объемного термического расширения, необходимые для проектирования технологической оснастки;
- деформационно-прочностные показатели (продольную и поперечную прочность, модуль упругости, относительное удлинение при растяжении и сжатии), без которых невозможно прогнозировать эксплуатационные свойства изделий из предлагаемых композиционных материалов;
- показатели электромагнитных свойств (диэлектрическую проницаемость, удельное объемное электрическое сопротивление), необходимые для проектирования изделий.
С помощью разработанного пакета прикладных программ проведено прогнозирование показателей физических свойств композиционных материалов с различными концентрациями электропроводных наполнителей для применения в качестве низкотемпературных нагревателей. Полученные расчетным путем рецептуры материалов с улучшенным комплексом механических показателей реализованы в композиционные материалы, предназначенные для производства литьевых и профильных изделий. Проведены испытания свойств полученных композитов, на базе сертифицированной исследовательской лаборатории Ростовского строительного университета. Композиционные материалы внедрены в производство альтернативных источников тепла для внутреннего обогрева помещений.
Получен акт внедрения разработанных композитов в производство низкотемпературных нагревателей. Указанные рецептуры по условиям договора
о разработке принадлежат заказчику работ.
Четвёртая глава содержит описание объектов и методов исследований, используемых в работе.
В выводах сформулированы основные результаты диссертационной работы.
ВЫВОДЫ
- Изучено влияние металлических и углеродных наполнителей на реологические, теплофизические и электрические свойства композиционных материалов на основе ПП. Выбран наполнитель, обеспечивающий максимальный уровень физико-механических показателей и оптимизировано его содержание.
- Разработан способ определения, расчета и прогнозирования показателей реологических свойств композитов по данным вискозиметрических испытаний, изучено влияние электропроводящих дисперсных наполнителей на вязкостные свойства расплавов композитов.
- Проведено количественное описание полученных зависимостей в виде математических моделей, предложен способ их численного решения.
- Предложена методика определения концентрации наполнителя в композиционных материалах с заданными свойствами, с учетом условия технологичности.
- На основании решения задачи о теплопроводности расплавов дисперснонаполненных композиционных материалов разработан метод автоматизированного расчета и прогнозирования влияния концентрации наполнителя на теплофизические показатели и технологические параметры их переработки
в изделия. - Разработана методика и алгоритм расчета деформационно-прочностных и электромагнитных показателей ПКМ с учетом параметров адгезионного взаимодействия компонентов.
- Получены оптимальные рецептуры электропроводящих композиционных материалов с заданными прочностными и улучшенными технологическими свойствами, внедренные в производство изделий электротехнического назначения
Список работ, опубликованных по теме диссертации
- Аминева, Е.Х. Математическое моделирование и методы планирования оптимального эксперимента в образовательных технологиях и научных исследованиях /Г.М. Данилова-Волковская // Материалы четвертой региональной научно-технической конференции.– Новороссийск, 2005.– С. 227–228.
- Аминева, Е.Х. Решение систем линейных алгебраических уравнений в параметрическом моделировании // Материалы четвертой региональной научно-технической конференции.– Новороссийск, 2005.– С. 229–230.
- Аминева, Е.Х. Влияние модификаторов на свойства полипропилена и композиционных материалов на его основе / Г.М. Данилова-Волковская // Новые полимерные композиционные материалы. Материалы II-й Всероссийской научно-практической конференции.– Нальчик, 2005.– С. 95–99.
- Аминева, Е.Х. Математическое моделирование процессов деструкции полипропилена при переработке. / Г.М. Данилова-Волковская, Я.Е. Гладышев// Научные труды Ростовской-на-Дону академии сельскохозяйственного машиностроения. Научное издание.– Ростов на/Д, 2006.– С. 151–153.
- Аминева, Е.Х. Метод прогнозирования и подготовки исходных данных для моделирования процессов переработки полимерных материалов /Г.М. Данилова-Волковская // Сб. трудов молодых ученых. Нальчик, 2006.– С. 297–300.
- Аминева, Е.Х. Математическое моделирование процессов деструкции полипропилена /Г.М. Данилова-Волковская, Я.Е. Гладышев //Научные труды РГАСХМ / Сб. научн. трудов. – Ростов на/Д.– 2006. – С.
- Аминева, Е.Х. Изучение адгезионного взаимодействия эпоксидной смолы и стикера в резинате / Г.М. Данилова-Волковская, С.Б. Языева. // Пластические массы – 2006.– № 11.– С.
- G.M. Danilova- and E.H. Amineva. The Electrical Conductive Compositional Material with Low Inflame on Polypropylene Basis. // Polymers, Polymer Blends, Polymer Composites and Filled Polymers: Synthesis, Properties and Application. – New York: Nova science publishers inc., 2006. – P. 171–173.
- E.H. Amineva. The Research on the Process of Thermo-Mechanical Destruction in Polypropylene // Organic and Physical Chemistry using Chemical Kinetics: Prospects and Developments– New York: Nova science publishers inc., 2007. P. 167–173.
- E.H. Amineva and B.M. Yaziev. Mathematical modeling of Thermo-Mechanical Destruction of Polypropylene // Organic and Physical Chemistry using Chemical Kinetics: Prospects and Developments– New York: Nova science publishers inc., 2007. P. 69–73.
- Аминева, Е.Х. Метод подготовки исходных данных для моделирования процессов переработки полимерных материалов / Г.М. Данилова-Волковская // Сб. трудов молодых ученых.– Нальчик, 2007.– С. 100–103.
Формат 60х84 1/16. Тираж 100. Заказ 1601.
Отпечатано в редакционно-издательском отделе
ФГОУ ВПО «Морская государственная академия имени адмирала Ф.Ф.Ушакова»
353918, г. Новороссийск, пр. Ленина, 93
