Высокоскоростное нагружение и разрушение полиметилметакрилата
На правах рукописи
Куготова Асият Мухамедовна
ВЫСОКОСКОРОСТНОЕ НАГРУЖЕНИЕ И РАЗРУШЕНИЕ ПОЛИМЕТИЛМЕТАКРИЛАТА
02.00.06 – высокомолекулярные соединения
АВТОРЕФЕРАТ
диссертации на соискание ученой степени
кандидата физико-математических наук
НАЛЬЧИК 2009
Работа выполнена в ГОУ ВПО «Кабардино-Балкарский государственный университет им. Х.М. Бербекова»
Научный руководитель: доктор физико-математических наук,
профессор Кунижев Борис Иналович
Официальные оппоненты: доктор физико-математических наук,
профессор Магомедов Гасан Мусаевич
кандидат физико-математических наук,
доцент Шетов Руслан Адибович
Ведущая организация: Таганрогский государственный
радиотехнический университет, г. Таганрог
Защита диссертации состоится «10» июня 2009 г. в 15.00 часов на заседании диссертационного совета Д 212.076.09 при Кабардино-Балкарском государственном университете им. Х.М. Бербекова по адресу: 360004, Нальчик, ул. Чернышевского, 173.
С диссертацией можно ознакомиться в библиотеке Кабардино-Балкарского государственного университета им. Х.М. Бербекова
Автореферат разослан « 7 » мая 2009 г.
Ученый секретарь
диссертационного совета Борукаев Т.А.
ОБЩАЯ ХАРАКТЕРИСТИКА РАБОТЫ
Актуальность проблемы. Свойства многих веществ, особенно металлов, подробно исследованы в высокоскоростных экспериментах, результаты которых служат основой для построения уравнений состояния веществ. Менее изучены высокомолекулярные соединения, которые представляют важный класс веществ, обладающих уникальными физическими свойствами и имеющих сложные фазовые диаграммы. К ним относится полиметилметакрилат (ПММА), являющийся одним из наиболее технологичных полимеров и, как конструкционный полимер, широко используется в нанотехнологии и при проведении взрывных испытаний. Полиметилметакрилат служит, в частности, идеальным материалом для оболочек слоистых сферических мишеней, при решении задач управляемого термоядерного синтеза, а также является промежуточной прослойкой в высокоскоростных метательных устройствах. В настоящее время достаточно полно изучены процессы высокоскоростного взаимодействия металлических ударников с металлическими и полимерными мишенями. Показано, что в этом случае форма ударного кратера приближается к затупленному по сфере цилиндру, а размеры кратера рассчитываются на основе модели пластически сжимаемой среды. При взаимодействии полиэтиленового ударника со скоростями 25 км/с на мишень из полиметилметакрилата кратер образуется по другому механизму – в результате хрупкого разрушения и лицевого откола. Поэтому методы расчета параметров кратера, разработанные для пластических материалов, не работают. В связи с этим актуальной задачей физики высокомолекулярных соединений является исследование процесса хрупкого разрушения полиметилметакрилата и зависимости геометрических размеров ударного кратера от скорости ударника, времени воздействия, физических свойств ударника и мишени. Самостоятельный научный интерес представляет проблема построения диаграмм состояния полиметилметакрилата в условиях действия высоких динамических давлений, с учетом зависимости функции Грюнайзена от температуры и плотности.
Цель работы состояла в комплексном исследовании процесса динамического нагружения полиметилметакрилата (ПММА).
В соответствии с целью в работе были поставлены и решены следующие задачи:
- исследование зависимости картины разрушения и геометрических размеров кратера от скорости ударника на баллистической стадии полета;
- построение модели откольного разрушения в полиметилметакрилате в рамках теории перколяции и фрактального анализа;
- установление аналитической связи между временем проникновения ударника в мишень, скоростью и глубиной кратера;
- исследование зависимости осевого напряжения в мишени из ПММА от времени и глубины кратера;
- исследование зависимости функции Грюнайзена ПММА от температуры и плотности по различным современным моделям;
- расчет диаграмм состояния и ударных адиабат ПММА по моделям К.Хищенко, А.Молодца и др.
Научная новизна.
1. Впервые показано, что при больших скоростях удара (0 > 3 км/с) и временах воздействия ударника на мишень (t > 20 мкс) изменяется характер неупругой деформации мишени, хрупкое разрушение переходит в хрупко-пластическое. Предложен физический механизм для объяснения этого явления.
2. Установлена аналитическая связь между временем проникновения ударника в мишень, скоростью ударника и глубиной кратера в полиметилметакрилате и предложено уравнение, связывающее глубину кратера от скорости ударника, удовлетворительно описывающее эксперименты по высокоскоростному нагружению хрупких сред.
3. Впервые получены и исследованы зависимости осевого напряжения в мишени из ПММА от времени воздействия и глубины кратера, подтверждающие предложенный механизм разрушения ПММА в экстремальных условиях.
4. Исследована зависимость функции Грюнайзена ПММА от температуры и плотности по различным современным моделям и построены диаграммы состояния ПММА в экстремальных условиях с использованием рассчитанных значений функции Грюнайзена.
5. Построены ударные адиабаты ПММА в координатах D-u, в которых наблюдается перелом и имеющих два участка, аппроксимируемых прямыми линиями, связывающиеся с проявлением структурно-фазовых переходов и деструкцией (механической и химической) макромолекул ПММА при больших скоростях удара.
Практическая значимость работы.
Результаты работы заложены в банк данных института теплофизики экстремальных состояний ОИВТ РАН г. Москва, института проблем химической физики ИПХФ РАН г. Черноголовка, КБГУ, ГУ «ВГИ» и в других научных центрах, занимающихся физикой и химией высоких плотностей энергии и используются для построения широкодиапазонных уравнений состояний различных полимерных материалов и композиций на их основе.
Результаты, полученные в работе, используются в Высокогорном геофизическом институте для изучения разрушения горных пород и льда, содержащего различные примеси.
Материалы диссертации используются при чтении лекций и проведении лабораторных занятий по дисциплине специализации «Уравнения состояния вещества» для студентов старших курсов физического факультета КБГУ.
Основные положения, выносимые на защиту:
1. Полученные теоретическим рассмотрением и экспериментальным исследованием зависимости геометрических размеров кратера в мишени из ПММА от времени и скорости удара.
2. Обнаруженные изменения характера кратерообразования и предложенный механизм разрушения хрупких материалов при больших скоростях и временах воздействия ударника.
3. Выявленные зависимости осевого напряжения в мишени из ПММА от времени и скорости воздействия ударника, подтверждающие предложенный механизм разрушения ПММА в экстремальных условиях.
4. Исследованные зависимости функции Грюнайзена ПММА от температуры и плотности.
5. Построенные диаграммы состояния ПММА в экстремальных условиях с использованием полученных значений функции Грюнайзена.
6. Ударные адиабаты ПММА построенные в координатах D-u, имеющие характерные особенности, связывающиеся с проявлением различных структурно-фазовых переходов в ПММА при высоких плотностях и давлениях.
Апробация полученных результатов. Основные результаты диссертационной работы докладывались и обсуждались на: II Всероссийской научно-практической конференции «Новые полимерные композиционные материалы» (Нальчик, 2005 г.); Малом полимерном конгрессе (Москва, 2005 г.); II Международном семинаре «Теплофизические свойства веществ» (Нальчик, 2006 г.); III Санкт-Петербургской конференции молодых ученых с международным участием «Современные проблемы науки о полимерах» (Санкт-Петербург, 2007 г.); III Всероссийской научно-практической конференции «Новые полимерные композиционные материалы» (Нальчик, 2007 г.); I Всероссийской научно-технической конференции «Наноструктуры в полимерах и полимерные нанокомпозиты» (Нальчик, 2007 г.); I Форуме молодых ученых Юга России и I Всероссийской конференции молодых ученых «Наука и устойчивое развитие» (Нальчик, 2007 г.); XXIII Международной конференции «Уравнения состояния вещества» (Эльбрус, 2008 г.); ежегодных научных конференциях молодых ученых КБГУ (Нальчик, 2005 – 2008 гг.); IV Международной научно-практической конференции «Новые полимерные композиционные материалы» (Нальчик, 2008 г.).
Структура и объем диссертации. Диссертация состоит из введения, четырех глав, выводов и списка использованной литературы из 96 наименований. Содержит 134 страниц текста, в том числе 38 рисунков и 20 таблиц.
Публикации. По материалам диссертации опубликовано 17 работ, изданных в центральной, республиканской печати, в том числе 1 работа в рекомендованных ВАК изданиях.
ОСНОВНОЕ СОДЕРЖАНИЕ РАБОТЫ
Во введении обосновывается актуальность темы диссертации, сформулированы цели и задачи исследования, раскрываются научная новизна и практическая значимость исследований, определены положения, выносимые на защиту.
В первой главе проведен литературный обзор современных моделей расчета функции Грюнайзена и уравнений состояния твердых тел и высокомолекулярных соединений. Показано, что при расчете диаграмм состояния полимеров в экстремальных условиях не учитывается зависимость функции Грюнайзена высокомолекулярных веществ от температуры, плотности и доли свободного объема. Установлено, что в хрупких материалах процессы разрушения и кратерообразования при высокоскоростном нагружении имеют аномалии по сравнению с упругими и пластичными материалами. Самостоятельный интерес представляет исследование зависимости функции Грюнайзена от температуры и удельного объема различными современными моделями и построение диаграмм состояния полиметилметакрилата в экстремальных условиях с использованием рассчитанных значений (V) и (T).
Во второй главе описаны современные методы ускорения макрочастиц для получения высоких динамических давлений в мишенях из высокомолекулярных веществ. Особенное внимание уделено электродинамическому ускорителю макрочастиц или, по другому магнитоплазменному ускорителю (МПУ), так как из существующих методов разгона макрочастиц он более технологичен, удобен в эксплуатации, а при достаточном энергопитании способен развивать значительные скорости ударника. Для исследования механизма разрушения и зависимости параметров кратерообразования в них от плотностей материалов ударника и времени воздействия ударника на мишень в качества модельного полимера выбран – полиметилметакрилат.
Третья глава посвящена исследованию процесса кратерообразования и разрушения полиметилметакрилата при высокоскоростном ударе.
По фоторегистрограммам, полученным на СФР (скоростной фоторегистратор) и ВФУ (высокоскоростная фоторегистрирующая установка) и представленным на рисунке 1 и подобным им, нами экспериментально исследован процесс высокоскоростного взаимодействия ударника из ПЭ и с мишенью из ПММА при различных скоростях ударника.
По этим фоторегистрограммам можно утверждать, что процессы интенсивного динамического нагружения материала мишени – ПММА, имеют негидростатический характер и сопровождается деформацией материала, осуществляемого путем множества малых сдвигов, реализуемых механизмами скольжении дислокаций или двойникования под действием касательных напряжений. При скорости ударника до 0,8 км/с не наблюдается существенного разрушения мишени, однако материал ударника начинает растекаться по поверхности мишени со скоростью 0,3-0,6 км/с, то есть примерно со скоростью ударника. При скоростях ударника до 1,5 км/с не происходит вылета центрального осколка, но идет выброс вещества с периферии и тогда образуется кольцеобразная каверна с характерным центральным поднятием.

Рис. 1. Фоторегистрограмма процесса высокоскоростного
взаимодействия ударника из ПЭ с мишенью из ПММА
при скорости 3 км/с, полученная на ВФУ.
В диапазоне скоростей ударника на баллистической стадии от 1,5 до 2км/с в экспериментах было установлено: а) наличие крупного центрального осколка (его размеры в 2-3 раза больше размеров ударника), б) наличие большого количества более мелких осколков, образующихся на периферии кратера. Объем кратера 10 см3, осколок остается в кратере.
При скоростях выше 2,5 км/с происходит вылет центрального осколка, который назван лицевым отколом. Такой откол по ряду признаков существенно отличается от тыльного откола, возникающего в пластических мишенях, в результате отражения ударной волны от тыльной поверхности мишени.
Известно, что контур откольного осколка и поверхность откольного разрушения являются фрактальными кластерами, состоящими из микро- и мезодефектов первого и второго уровня по терминологии академика Панина В. Е. В качестве модели образования лицевого откола с центральным осколком можно предложить следующий ход развития события разрушения ПММА при высокоскоростном ударе, когда скорость ударника выше 2,0 км/с. Первая стадия – мгновенное “взрывоподобное” возникновение множества одиночных микро- и мезотрещин в мишени из ПММА. Вторая стадия – объединение микроодиночных трещин в группы (конечные кластеры). Третья стадия – соединение (смыкание) конечных кластеров в бесконечный фрактальный (перколяционный) кластер. Четвертая стадия – разрушение образца на части (рис. 1).
Выше мы отмечали, что на третьей стадии откола конечные кластеры смыкаются во фрактальный кластер, в этом случае плотность частиц (дефектов, трещин), составляющих его является функцией вида:
![]() , (1)
, (1)
где – нормирующий множитель, Н – ширина зоны откола (в нашем случае Н=В диаметру центрального осколка), D – фрактальная размерность Хаусдорфа – Безиковича, df – размер топологического пространства (df = 2).
Выражение для разрушающего напряжения р в случае лицевого откола с учетом (1) принимает вид:
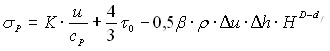 , (2)
, (2)
где u – изменение массовой скорости, h – скорость смещения берегов трещин, K – модуль объемного сжатия, 0 – сопротивление сдвига, ср – скорость продольной статистической волны.
Отсюда видно, что с увеличением фрактальной размерности откольная прочность растет по определению (D < df). Физическая интерпретация этого заключения означает, что р растет с увеличением поверхности, вовлекаемой в откольное разрушение.
На рис. 2 представлены зависимости u, u и h от скорости удара по мишени из ПММА рассчитанные по методике Савенкова Г.Г. Из анализа результатов, приведенных на рисунках 1 и 2, следует, что предложенная модель откольного разрушения не противоречит результатам хрупкого разрушения ПММА с лицевым отколом при больших скоростях удара ( > 2 км/с) и с центральным поднятием при скоростях от 0,9 км/с до 2 км/с.
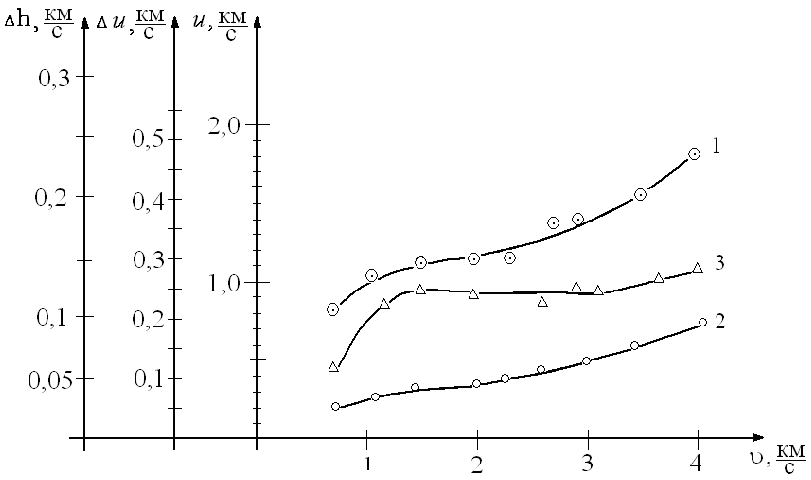
Рис. 2. Зависимость параметров u(1), u(2), h(3)
от скорости удара для ПММА.
В третьем параграфе данного раздела диссертации представлены результаты исследования зависимости геометрических размеров кратера от скорости удара, плотностей ударника и мишени, а также прочности мишени. Основываясь на теории удара Герца и сделав некоторые физические предположения о процессе внедрения ударника в мишень, получены уравнения для формы кратера, глубины внедрения и силы соударения.
Уравнение для глубины кратера h представлено в виде:
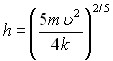 , (3)
, (3)
где – скорость ударника, m – масса ударника.
Аналитическая связь между временем проникновения ударника в мишень и скоростью ударника имеет вид:
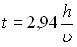 . (4)
. (4)
В литературе имеется ряд соотношений, которые описывают глубину кратера в зависимости от скорости и плотности ударника (5) и силы сопротивления, которую испытывает ударник при внедрении в мишень (7).
![]() , (5)
, (5)
где d – диаметр кратера,
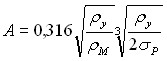 . (6)
. (6)
В уравнении (6) у – плотность ударника, м – плотность мишени, р – предел прочности мишени.
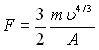 , (7)
, (7)
где А определяется по (6), m – масса ударника, – скорость ударника.
На рис. 3 представлены расчеты по уравнениям (3) (кривая 1) и (5) (кривая 2) зависимости глубины кратера в мишени из ПММА от скорости ударника. Сравнение расчетных значений h с экспериментальными данными представленными на рисунке 1 и данными Пилюгина Н.Н. показали, что уравнение (3) удовлетворительно согласуется с нашими экспериментами до скоростей удара 3,0 км/с, при более высоких скоростях ударника дает хорошее совпадение с результатами работы Пилюгина Н.Н. Здесь следует отметить, что в наших работах обнаружено изменение механизма разрушения ПММА при скоростях более 3,0 км/с. Если при меньших скоростях центральный осколок остается в кратере, то при скоростях выше 3,0 км/с, происходит выпадение центрального осколка и существенное разрушение мишени, что подтверждается данными, описанными в предыдущем разделе. Таким образом, можно утверждать, что расхождение наших экспериментальных данных по глубине кратера с данными Пилюгина Н.Н. обусловлены изменением механизма разрушения мишени из ПММА при скоростях выше 3 км/с.
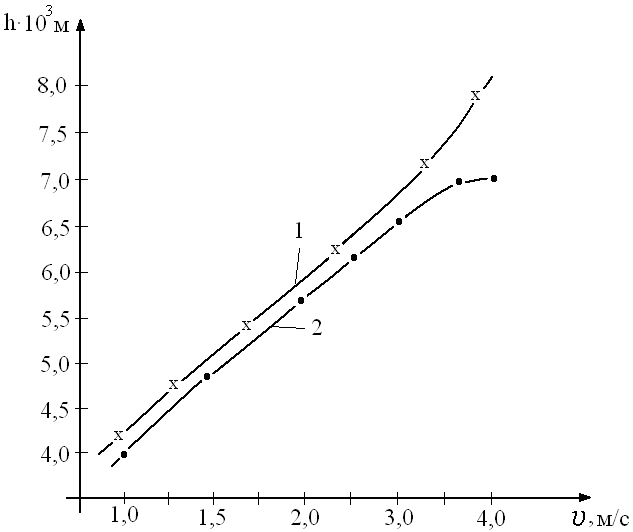
Рис. 3. Зависимость глубины кратера в мишени из ПММА,
рассчитанные по уравнениям (3) – 1 и (5) – 2.
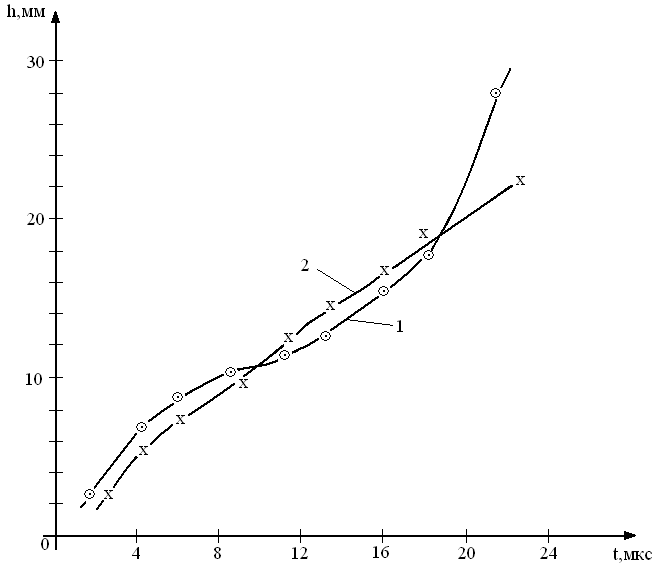
Рис. 4. Зависимость глубины кратера в ПММА от времени при скорости ударника 3,0 км/с (кривая 1 – полученная экспериментальным путем, кривая 2 – рассчитана теоретически по уравнению (4)).
Из данных рисунка 4 видно, что зависимость глубины кратера от времени воздействия ударника на мишень, полученные экспериментальным путем с точностью до 10% совпадают с данными теоретического расчета, полученными по уравнению (4) до времен 20 мкс. При больших временах t > 20 мкс наблюдается существенное расхождение (более 30%) между экспериментом и теоретическим расчетом глубины кратера. Этот факт, обнаруженный нами, можно связать с изменением характера неупругой деформации мишени в ударной волне, а именно: при больших временах удара хрупкое разрушение переходит в хрупко-пластическое. При одноосном сжатии возрастают как продольная, так и поперечная компоненты напряжений. В упругой области изменение продольного х и поперечного у напряжений происходит согласованным образом, порог разрушения быстро возрастает с увеличением поперечного напряжения сжатия и при некотором критическом значении у имеет место хрупко-пластический переход: сдвиговые напряжения становятся достаточными для активации механизмов пластического деформирования, а раскрытие трещин подавляется поперечными напряжениями.
В диссертации нами использовано выражение Н.Н. Пилюгина, связывающее радиальное напряжение сжатия х и глубину внедрения h, а также энергию ударника Е0 с формой кратера
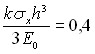 (8)
(8)
Используя данные представленные на рис. 3 при скорости ударника из ПЭ равной 3 км/с, по уравнению (8) нами рассчитана зависимость х от времени и глубины проникания, при Е0 = 7,38103 Дж. Эти данные представлены на рисунке 5 в трехмерном изображении. Если анализировать зависимость х = х (h, t), то видно, что в начальные моменты удара (t 2,4-3,0 мкс) х имеет максимальные значения в пределах 4,0-5,0 ГПа, а затем с увеличением времени ударного воздействия падает до 0,4 ГПа. С увеличением глубины проникания h ударника или глубины кратера осевые сжимающие напряжения в мишени из ПММА также вначале резко падают, а затем следует монотонное убывание х с увеличением h. Зависимости х от времени и глубины кратера хорошо согласуются с данными других авторов.
Из рисунка 5 видно, что в начальный момент ударного взаимодействия, при небольших временах t и глубины h, осевое напряжение х = х (t, h) распределено по поверхности трехугольной пирамиды, затем при средних значениях t и h происходит скручивание поверхности и, х = х (t, h) имеет минимальное значение. При предельных значениях t и h поверхность, по которой распределено напряжение х (t, h) резко возрастает и принимает форму неправильной усеченной четырехугольной пирамиды. Такое изменение х при различных значениях t и h, по-видимому, можно связать с изменением механизма хрупкого разрушения ПММА, при высоких скоростях нагружения, на хрупко-пластический.
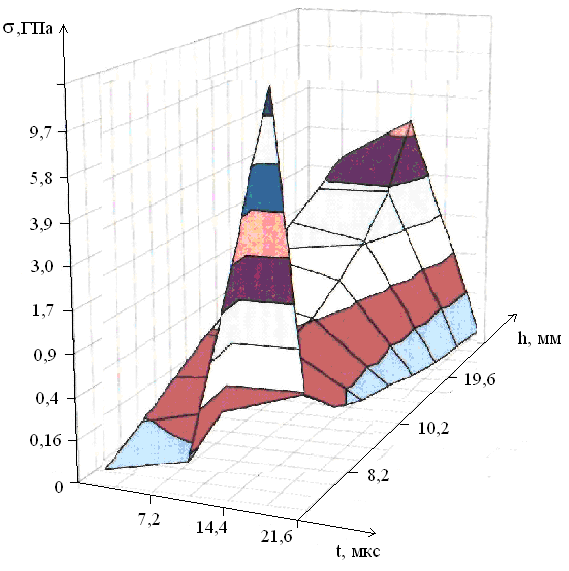
Рис. 5. Зависимость напряжения от времени и глубины кратера.
В работах Каннеля Г.И. неоднократно обсуждались экспериментальные данные, об изменении механизма разрушения хрупких материалов мишеней при высоких скоростях ударника (выше 3 км/с). Данные представленные на рис. 5 и их анализ подтвердил, что при высоких скоростях нагружения мишени в начале идет процесс хрупкого разрушения с образованием лицевого откола, затем происходит повышение температуры в мишени, хрупкое разрушение мишени переходит в хрупко-пластическое. Мы считаем, что при построении диаграмм и уравнений состояния ПММА в экстремальных условиях необходимо учесть этот факт, и исследовать влияние температуры и провести теоретический расчет зависимости функции Грюнайзена от температуры, плотности и доли свободного объема материала мишени.
Наиболее часто для расчета диаметров ударных кратеров применяют формулу Нордайка
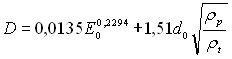 (9)
(9)
или формулу Гоулта
![]() ; А = 0,015 (10)
; А = 0,015 (10)
Недостатками этих уравнений является, то, что они не учитывают прочностные свойства материала мишени. Нами предлагается следующая безразмерная зависимость для диаметра кратера в ПММА
 . (11)
. (11)
Для пары полиэтилен и ПММА для диапазона скоростей от 1,2 до 4 км/с нами рассчитаны константы, они оказались равны А = 0,02, = 1,3.
На рис. 6 представлены рассчитанные по уравнению (11) зависимости диаметра кратера от времени воздействия ударника на мишень при скорости 3 км/с.
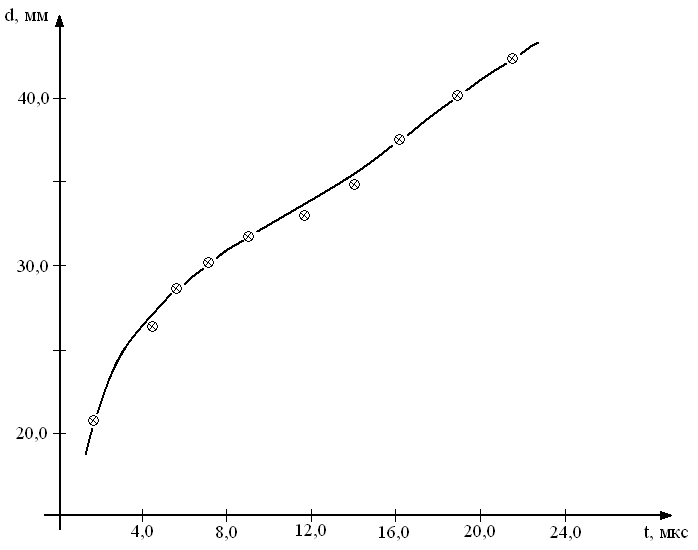
Рис. 6. Зависимость диаметра кратера в ПММА от времени
при скорости ударника 3,0 км/с.
Как видно из рисунка 6 при скорости ударника 3,0 км/с наблюдается быстрый рост диаметра кратера со временем по экспоненте до 8 мкс, затем диаметр кратера увеличивается со временем по линейному закону.
В первом параграфе 4 главы представлены результаты исследования функции Грюнайзена ПММА.
Структура уравнения Ми - Грюнайзена такова, что правая часть состоит из двух слагаемых: ![]() (12)
(12)
Первое из них соответствует потенциальному давлению и зависит только от объема, второе обусловлено колебаниями кристаллической решетки и пропорционально энергии этих колебаний Ек.
При низких температурах вклад второго слагаемого в полное давление мал, и уравнение состояния в основном определяется потенциальным членом PП (V), с ростом температуры роль теплового давления возрастает. Оно может сравняться по величине с потенциальным давлением и даже превзойти его. В этих условиях существенное значение имеет зависимость давления от объема.
Считается, что при невысоких температурах является функцией только объема V, т.е. ![]() . Установлению этого вида функции посвящен ряд работ. Молодцом А.М. предложен аналитический вид для
. Установлению этого вида функции посвящен ряд работ. Молодцом А.М. предложен аналитический вид для
![]() (13)
(13)
где ![]() - относительный объем, а параметр a определяется из (14)
- относительный объем, а параметр a определяется из (14)
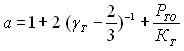 (14)
(14)
Здесь: 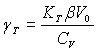 (15)
(15)
где – коэффициент теплового расширения, KT – изотермический модуль объемного сжатия, CV – теплоемкость при постоянном объеме, PTO – тепловое давление. Все величины, входящие в выражение для a, вычисляются при постоянном удельном объеме ![]() и начальной температуре T0. При этом Молодец А.М. показал, что вычисления по уравнению (13) хорошо согласуется с общепризнанными результатами для металлов до значений
и начальной температуре T0. При этом Молодец А.М. показал, что вычисления по уравнению (13) хорошо согласуется с общепризнанными результатами для металлов до значений ![]() .
.
Однако функция Грюнайзена зависит не только от объема, но и температуры. Это необходимо принимать во внимание при анализе сжатия твердых тел сильными волнами. В соответствии с этим, взяв за основу (13) и опираясь на соответствующие экспериментальные данные, сконструирована функция Грюнайзена =(V,T) для двух термодинамических переменных – объема ![]() и температуры T, в виде (16):
и температуры T, в виде (16):
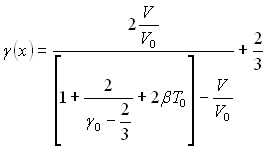 (16)
(16)
Формула (16) качественно верно передает температурную зависимость функции Грюнайзена, и с увеличением температуры, она приводит к тому, что при одних и тех же объемах функция Грюнайзена будет ближе к своему значению 2/3.
Помимо уравнения (16) в работе нами использованы уравнения (17) и (18) для расчета функции Грюнайзена:
 (17)
(17)
![]() ,
, 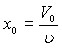 , где V0, – подгоночные параметры.
, где V0, – подгоночные параметры.
 , (18) где
, (18) где 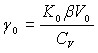 ;
; ![]() - коэффициент теплового расширения; К0- адиабатический модуль объемного сжатия; CV - теплоемкость при постоянном объеме.
- коэффициент теплового расширения; К0- адиабатический модуль объемного сжатия; CV - теплоемкость при постоянном объеме.
Недостатком формул (17) и (18) является то, что они не позволяет найти температурную зависимость (T), как в модели Молодца.
Все эти модели были созданы при исследовании ударного нагружения различных твердых тел. Для исследования полимеров мы использовали (16), (17), (18) вводя величину доли свободного объема, которая определяется по формуле: 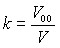 , (19)
, (19)
где V00 – удельный объем, учитывающий возможные внутренние пустоты, волокнистость тела и т.д. Все пористые тела характеризуются наличием более или менее крупных частиц или участков сплошного вещества с плотностью ![]() .
.
Таким образом, для учета доли свободного объема в ПММА в уравнениях (16), (17), (18) величину  мы заменили на
мы заменили на 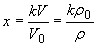 .
.
 (20)
(20)
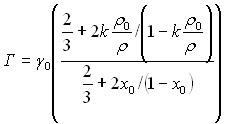 (21)
(21)
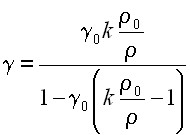 (22)
(22)
Во втором разделе четвертой главы диссертации представлены результаты исследования зависимости функции Грюнайзена от температуры.
Из выше предложенных моделей для этих целей применима модель Молодца и зависимость (V,T) имеет вид (20).
В качестве экспериментальной основы использованы данные по термодинамическим свойствам веществ в экстремальных условиях (таблица 1).
Таблица 1. Экспериментальные данные по ударному сжатию полиметилметакрилата
| U (км/с) | D (км/с) | P (ГПа) | / 0 | (г/см3) | E (106 |
| 0,2 | 2,8 | 0,672 | 0,93 | 1,292 | 0,02 |
| 0,4 | 3,1 | 1,488 | 0,87 | 1,377 | 0,08 |
| 0,6 | 3,4 | 2,448 | 0,82 | 1,457 | 0,18 |
| 0,8 | 3,8 | 3,648 | 0,79 | 1,520 | 0,32 |
| 1,0 | 4,0 | 4,800 | 0,75 | 1,600 | 0,50 |
| 1,4 | 4,5 | 7,560 | 0,69 | 1,742 | 0,98 |
Для получения ![]() необходимо зафиксировать плотность: мы выбрали минимальную плотность – 1 = 1,292 г/см3 и максимальную плотность 2 = 1,742 г/см3 из эксперимента, шаг по температуре составляет 50 К, рассчитывали
необходимо зафиксировать плотность: мы выбрали минимальную плотность – 1 = 1,292 г/см3 и максимальную плотность 2 = 1,742 г/см3 из эксперимента, шаг по температуре составляет 50 К, рассчитывали ![]() от 50 К до 500 К. Результаты расчетов приведены на рисунке 7.
от 50 К до 500 К. Результаты расчетов приведены на рисунке 7.
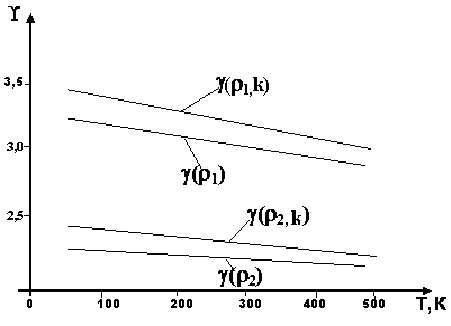
Рис. 7. Температурная зависимость функции Грюнайзена ПММА.
Как видно из рисунка 7 температурная зависимость функции Грюнайзена достаточно слабая. При небольших температурах для одной плотности учет доли свободного объема приводит к значительной разности между () – без учета доли свободного объема и с ее учетом (,k). Но с повышением температуры (,k) приближается к значения ![]() при тех же температурах. Чем большая плотность достигнута в эксперименте, тем меньше зависимость от температуры Т.
при тех же температурах. Чем большая плотность достигнута в эксперименте, тем меньше зависимость от температуры Т.
С повышением температуры влияние пористости k уменьшается, по-видимому, из – за увеличения подвижности сегментов и других структурных элементов полимера, которые заполняют пустоты, уменьшая эффективную пористость полимера, приближая ее плотность к нормальной 0.
В третьем параграфе 4 главы представлены результаты исследования зависимости функции Грюнайзена от плотности и доли свободного объема.
Уравнения (16), (17), (18) и (20), (21), (22) позволяют рассчитать зависимость функции Грюнайзена от плотности без учета доли свободного объема и с ее учетом. В наших расчетах для полиметилметакрилата коэффициент k = 1,02.
Таблица 2. Зависимость функции Грюнайзена от плотности полиметилметакрилата при Т=293 К и доли свободного объема k =1,02
| Уравнение (17) () | Уравнение (21) (,k) | |
| 1,292 | 3,70 | 3,8 |
| 1,377 | 3,30 | 3,4 |
| 1,457 | 3,10 | 3,2 |
| 1,520 | 3,03 | 3,09 |
| 1,600 | 2,80 | 2,9 |
| 1,742 | 2,59 | 2,7 |
Из таблицы 2 видно, что учет свободного объема для полиметилметакрилата не влияет на функции Грюнайзена, зависящей от плотности.
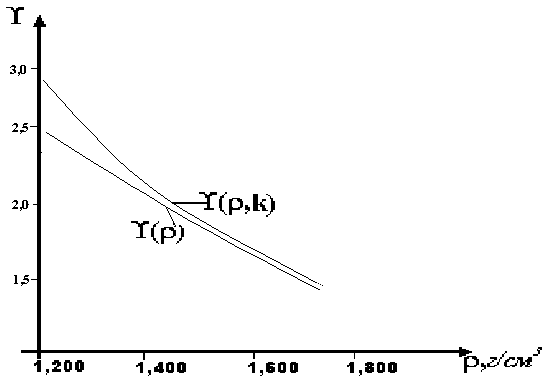
Рис. 8. Зависимость функции Грюнайзена от плотности ПММА по модели Молодца.
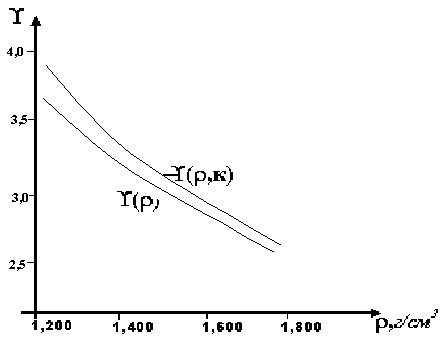
Рис. 9. Зависимость функции Грюнайзена от плотности полиметилметакрилата по модели Райса.
Как видно из рисунков 8 и 9 учет доли свободного объема для полиметилметакрилата существенно не сказывается на функции Грюнайзена. При увеличении плотности функция Грюнайзена с учетом k приближается к ![]() без ее учета, это может быть связано с тем, что при увеличении плотности, а, соответственно, и давления P, пустоты, присутствующие в ПММА, схлопываются быстрее, осуществляется сжатие участков с начальной плотностью 0.
без ее учета, это может быть связано с тем, что при увеличении плотности, а, соответственно, и давления P, пустоты, присутствующие в ПММА, схлопываются быстрее, осуществляется сжатие участков с начальной плотностью 0.
В четвертом разделе 4 главы представлены результаты расчета диаграмм состояния полиметилметакрилата в широкой области фазовой диаграммы с использованием современных моделей.
Исследования полимеров при их динамическом нагружении необходимы для построения таких уравнений состояний, которые могли бы работать в широкой области фазовой диаграммы. В связи с этим продолжаются попытки построения таких уравнений состояния, которые отображали бы либо строгие (теоретические и экспериментальные) методы расчета термодинамических свойств полимеров, либо же достаточно гладкое описание этих полимеров в конденсированной и газовой фазах с помощью полуэмпирических соотношений.
Исследования К.В.Хищенко и др. в области ударного нагружения различных веществ, привели к созданию обобщенного уравнения состояния в виде
 ,
,  . (23)
. (23)
В дальнейшем, при изучении свойств полимеров в ударно – сжатом состоянии, встал вопрос о применимости уравнения (23) для описания свойств полимерных материалов в условиях динамического нагружения, либо о построении такого уравнения состояния, которое позволило бы эффективно описать их термодинамические характеристики в широком диапазоне давлений и температур.
Применимость уравнения (23) к описанию свойств полимеров вытекает из представления последних, как пористых материалов. Уравнение состояния (23) при этом принимает вид:
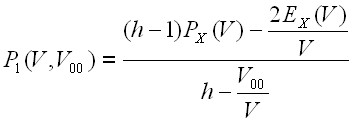 , (24)
, (24)
где V00 – удельный объем пористого полимера.
При V0 = V00, т.е. при k = 1 уравнение (24) переходит в уравнение (23) и представляет собой ударную адиабату сплошного вещества.
С учетом зависимости ![]() , полученной нами для полиметилметакрилата разными моделями и предполагая:
, полученной нами для полиметилметакрилата разными моделями и предполагая:
![]() (25)
(25)
Формула (24) примет вид: 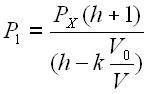 (26)
(26)
Но для исследования ударной адиабаты необходимо знать ![]() - упругую составляющую давления. Для нахождения
- упругую составляющую давления. Для нахождения ![]() воспользуемся уравнением состояния (11) и представим энергию как сумму упругой энергий
воспользуемся уравнением состояния (11) и представим энергию как сумму упругой энергий ![]() и тепловой
и тепловой ![]() , т.е.
, т.е.
![]() =
= ![]() +
+![]() (27)
(27)
Совместно решая уравнения (25), (12), и (27) относительно ![]() находим:
находим: 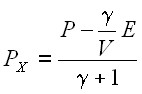 (28)
(28)
где Р и Е – полное давление и энергия, которые мы берём как экспериментальную основу для полиметилметакрилата. Расчет по формуле (28) ![]() - упругой составляющей давления и по (26)
- упругой составляющей давления и по (26) ![]() - полного давления, где функции Грюнайзена были найдены по модели Райса и Молодца для полиметилметакрилата приведен в таблице 3 и на рисунке 10.
- полного давления, где функции Грюнайзена были найдены по модели Райса и Молодца для полиметилметакрилата приведен в таблице 3 и на рисунке 10.
Таблица 3. Ударная адиабата P1 и упругое давление PX пористого и сплошного полиметилметакрилата рассчитали по модели Райса
| (г/см3) | Р(ГПа) | Е(кДж/кг) | Рх(ГПа) | Рх(k)(ГПа) | Р1(ГПа) | Р1(k)(ГПа) |
| 1,29 | 0,67 | 0,02 | 0,15 | 0,15 | 0,68 | 0,67 |
| 1,38 | 1,49 | 0,08 | 0,37 | 0,36 | 1,50 | 1,48 |
| 1,46 | 2,49 | 0,18 | 0,66 | 0,65 | 2,48 | 2,45 |
| 1,52 | 3,65 | 0,32 | 1,02 | 0,99 | 3,67 | 3,56 |
| 1,60 | 4,80 | 0,50 | 1,44 | 1,35 | 4,89 | 4,57 |
| 1,74 | 7,56 | 0,98 | 2,50 | 2,30 | 7,75 | 7,41 |
На рисунке 10 ![]() и
и ![]() - упругие составляющие давления сплошного и пористого полиметилметакрилата, P – наши экспериментальные данные.
- упругие составляющие давления сплошного и пористого полиметилметакрилата, P – наши экспериментальные данные. ![]() и
и ![]() - расчетные ударные адиабаты сплошного и пористого полиметилметакрилата с учетом доли свободного объема и без ее учета.
- расчетные ударные адиабаты сплошного и пористого полиметилметакрилата с учетом доли свободного объема и без ее учета.
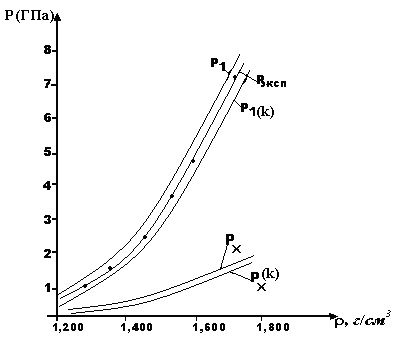
Рис. 10. Диаграммы состояния полиметилметакрилата по модели Молодца.
Как видно из таблицы 3 и рисунка 10 для полиметилметакрилата использование уравнения Хищенко (26) для ![]() и уравнения (28) для
и уравнения (28) для ![]() приводит к хорошему согласию с нашими экспериментальными данными. Причем наблюдается хорошее согласие с экспериментом как
приводит к хорошему согласию с нашими экспериментальными данными. Причем наблюдается хорошее согласие с экспериментом как ![]() – для сплошного полиметилметакрилата, так и для
– для сплошного полиметилметакрилата, так и для ![]() . Это связано с тем, что доля свободного объема полиметилметакрилата равна k = 1,02, которая не сильно отличается от коэффициента k = 1 для сплошного полиметилметакрилата.
. Это связано с тем, что доля свободного объема полиметилметакрилата равна k = 1,02, которая не сильно отличается от коэффициента k = 1 для сплошного полиметилметакрилата.
При плотности ![]() = 1,292 г/см3 отклонение
= 1,292 г/см3 отклонение ![]() от эксперимента
от эксперимента ![]() составляет по модели Райса 0,04 ГПа (или 1,6 %), а по модели Молодца 0,08 ГПа (или 2,8 %).
составляет по модели Райса 0,04 ГПа (или 1,6 %), а по модели Молодца 0,08 ГПа (или 2,8 %).
ВЫВОДЫ
- Впервые получена аналитическая связь между временем внедрения ударника в мишень, скоростью ударника и глубиной кратера, также предложено уравнение, связывающее глубину кратера со скоростью ударника.
- Установлены зависимости глубины кратера от времени воздействия ударника на мишень. При скорости ударника 0 3 км/с, полученные из эксперимента данные, хорошо совпадают с данными теоретического расчета до времен 20 мкс, при больших временах наблюдается существенное расхождение (более 30 %), что связывается с изменением характера неупругой деформации мишени, а именно при больших временах хрупкое разрушение переходит в хрупко-пластическое. Предложен физический механизм для объяснения этого явления.
- Используя предложенный механизм хрупко-пластического разрушения построены и исследованы зависимости осевого напряжения (t, h) в мишени от времени и глубины кратера в трехмерном изображении.
- Исследована зависимость функции Грюнайзена от плотности полиметилметакрилата по различным современным моделям. По полученным значениям () и (, k) построены диаграммы состояния ПММА в экстремальных условиях по моделям А. Молодца, Р. Райса и К. Хищенко. Показано, что наблюдается хорошее соответствие наших расчетных диаграмм состояния с подобными данными Р. Мачала и С. Марша.
- Построены и проанализированы ударные адиабаты ПММА в координатах массовая скорость – скорость ударной волны, имеющие переломы и аппроксимируемые прямыми линиями, описываемыми различными уравнениями. Изломы на ударных адиабатах связываются с проявлением и возможной механической и химической деструкции макромолекул ПММА при больших скоростях ударного воздействия.
ПУБЛИКАЦИИ ПО ТЕМЕ ДИССЕРТАЦИИ
- Куготова, А. М. Диаграммы состояния полиметилметакрилата и функция Грюнайзена [Текст] / А. М. Куготова, Б. И. Кунижев, Р. Х. Афаунова // Пластические массы – 2008. – № 8. – С. 35-38.
- Куготова, А. М. Исследование процесса разрушения полиуретанопласта при высокоскоростном нагружении [Текст] / А. М. Куготова, Б. И. Кунижев // Материалы I форума молодых ученых Юга России и I Всероссийской конференции молодых ученых. «Наука и устойчивое развитие». – Нальчик, 2007. – С. 200-202.
- Куготова, А. М. Процесс разрушения полиуретанопласта при динамическом нагружении [Текст] / А. М. Куготова, Б. И. Кунижев, З. Х. Гайтукиева, А. Х. Цечоева // Материалы I Всерос. науч.-техн. конф. – Нальчик, 2007. – С. 165-168.
- Куготова, А. М. Исследование процесса кратерообразования в хрупких средах при высокоскоростном нагружении [Текст] / А. М. Куготова, Б. И. Кунижев, Р. Х. Афаунова // Третья Санкт-Петербургская конференция молодых ученых с международным участием. – Санкт-Петербург, 2007. – С. 253.
- Куготова, А. М. Фрактальный анализ откольных явлений в полиметилметакрилате (ПММА) [Текст] / Б. И. Кунижев, А. С. Ахриев, А. М. Куготова // Новые полимерные композиционные материалы: Материалы IV Межд. науч.-практ. конф. – Нальчик, 2008. – С. 186-191.
- Куготова, А. М. Формы кратера и разрушение полиметилметакрилата при высокоскоростном ударе [Текст] / А. М. Куготова // Перспектива–2007: Материалы Межд. конгресса студентов, аспирантов и молодых ученых. – Т. II. – Нальчик, 2007. – С. 127-129.
- Куготова, А. М. Исследование напряжения сжатия и формы кратера в ПММА при высокоскоростном ударе [Текст] / А. М. Куготова, Б. И. Кунижев, З. С. Торшхоева, А. С. Ахриев // Новые полимерные композиционные материалы: Материалы IV Межд. науч.-практ. конф. – Нальчик, 2008. – С. 168-175.
- Куготова, А. М. Процесс кратерообразования в хрупких средах при динамическом нагружении [Текст] / А. М. Куготова, Б. И. Кунижев // Малый полимерный конгресс. – М., 2005. – С. 80.
- Куготова, А. М. Кратерообразование в полиметилметакрилате, модель откольного разрушения [Текст] / А. М. Куготова, Б. И. Кунижев, Р. Б. Тхакахов // Материалы IV Межд. науч.-практ. конф. Новые полимерные композиционные материалы. – Нальчик, 2008. – С. 175-181.
- Куготова, А. М. Разрушение полиметилметакрилата при мощных импульсных воздействиях [Текст] / А. М. Куготова, Б. И. Кунижев, А. С. Ахриев, З. С. Торшхоева, Р. Б. Тхакахов, А. К. Микитаев // Избранные труды «Поликонденсационные реакции и полимеры». – Нальчик, 2008. – С. 86-108.
- Куготова, А. М. Процесс кратерообразования в хрупких средах при высокоскоростном нагружении [Текст] / А. М. Куготова // Перспектива–2006: Материалы Всерос. науч. конф. студентов, аспирантов и молодых ученых. – Т. III. – Нальчик, 2006. – С. 236-238.
- Куготова, А. М. Кратерообразование в мишени из полиметилметакрилата при высокоскоростном ударе [Текст] / А. С. Ахриев, А. В. Балкарова, З. Х. Гайтукиева, А. М. Куготова, Б. И. Кунижев // Новые полимерные композиционные материалы: Материалы II-й Всерос. науч.-практ. конф. – Нальчик, 2005. – С. 312-314.
- Куготова, А. М. Диаграммы состояния некоторых полимеров [Текст] / А. М. Куготова, З. Х. Гайтукиева, Б. И. Кунижев // Новые полимерные композиционные материалы: Материалы II-й Всерос. науч.-практ. конф. – Нальчик, 2005. – С. 294-297.
- Куготова, А. М. Диаграммы состояния и процесс разрушения полимеров при высокоскоростном ударе [Текст] / Б. И. Кунижев, А. С. Ахриев, А. М. Куготова, А. Х. Цечоева // Теплофизические свойства веществ (жидкие металлы и сплавы, наносистемы). – Нальчик, 2006. – С. 185-188.
- Куготова, А. М. Диаграммы состояния и функция Грюнайзена полиметилметакрилата [Текст] / Б. И. Кунижев, А. М. Куготова, Р. Б. Тхакахов, Б. С. Карамурзов // Тезисы XXIII Межд. конф. – Нальчик, 2008. – С. 65.
- Куготова, А. М. Диаграммы состояния полиметилметакрилата и полиэтилена в экстремальных условиях [Текст] / Р. Х. Афаунова, А. М. Куготова, Б. И. Кунижев, Р. Б. Тхакахов // Новые полимерные композиционные материалы: Материалы IV Межд. науч.-практ. конф. – Нальчик, 2008. – С. 30-34.
- Куготова, А. М. Расчет параметров состояния твердых тел в экстремальных условиях [Текст] / А. Х. Цечоева, З. Х. Гайтукиева, З. С. Торшхоева, А. М. Куготова, А. С. Ахриев, Б. И. Кунижев // Новые полимерные композиционные материалы: Материалы IV Межд. науч.-практ. конф. – Нальчик, 2008. – С. 314-321.

