Моделирование температурного поля и напряженно-деформированного состояния алмазосодержащих инструментальных композитов на полимерной ма т рице

На правах рукописи

ЯХУТЛОВА Марианна Разиуановна

Моделирование температурного поля

и напряженно-деформированного состояния

алмазосодержащих инструментальных

композитов на полимерной матрице

Специальность: 02.00.06 – Высокомолекулярные соединения

АВТОРЕФЕРАТ

диссертации на соискание ученой степени

кандидата физико-математических наук

Нальчик

2011

Работа выполнена в Кабардино-Балкарском государственном университете имени Х.М. Бербекова.

Научный руководитель: доктор химических наук,

профессор Лигидов Мухамед Хусенович

Официальные оппоненты: доктор физико-математических наук,

профессор Никитин Лев Николаевич

доктор технических наук,

профессор Языев Батыр Меретович

Ведущая организация: Российский химико-технологический

университет имени Д.И. Менделеева

Защита состоится « 3 » ноября 2011 г. в 13.00 часов на заседании диссертационного совета Д 212.076.09 в Кабардино-Балкарском государственном университете им. Х.М. Бербекова по адресу: 360004, г. Нальчик, ул. Чернышевского, 173, КБГУ, ауд. 203.

С диссертацией можно ознакомиться в библиотеке Кабардино-Балкарского государственного университета им. Х.М. Бербекова

Автореферат разослан «____» сентября 2011 г.

Учёный секретарь

диссертационного совета Борукаев Т.А.

ОБЩАЯ ХАРАКТЕРИСТИКА РАБОТЫ

Актуальность работы. Алмазно-абразивные режущие инструменты на полимерных матрицах составляют более половины от общего потребления алмазного инструмента при обработке различных материалов, в основном металлов и сплавов, используемых в машиностроении. Алмазоносный слой этих инструментов – это инструментальный алмазосодержащий композит, представляющий собой матричную систему, в которой связующее является непрерывной фазой, а зерна алмазов распределены в ней в виде включений. Исследования и опыт эксплуатации алмазно-абразивных инструментов показывают, что уникальные свойства алмаза как инструментального материала, используются крайне неэффективно, так как большая часть алмазов выпадает из матрицы, не достигая значительного износа. Для алмазосодержащих инструментальных композитов на полимерной матрице проблема осложняется ещё и низкой теплостойкостью полимера, так как прочность алмазоудержания в значительной мере определяется его термовязкоупругими свойствами.

Исходя из изложенного, в структуре инструментальных алмазосодержащих композитов можно выделить систему алмаз – переходный слой – матрица, процессы в которой в значительной степени определяют эксплуатационные свойства этих материалов. Выделение переходного слоя на границе алмаза и матрицы, формирующегося в процессе изготовления инструмента, как отдельного элемента, связано с его существенным влиянием на алмазоудержание. Раскрытие явлений в системе алмаз – переходный слой – матрица при действии силовых и температурных факторов позволяет определить эффективные пути повышения работоспособности алмазно-абразивных инструментов.

Основная цель работы – разработка математического и программно-алгоритмического обеспечения и численное моделирование температурного поля и напряженно-деформированного состояния алмазосодержащих инструментальных композитов на полимерной матрице.

Поставленная цель определила необходимость решения следующих задач:

• разработка математической модели и программно-алгоритмического обеспечения для конечноэлементного моделирования нестационарного температурного поля системы алмаз – переходный слой – матрица;
• разработка математической модели и программно-алгоритмического обеспечения для конечноэлементного моделирования напряженно-деформи­рован­ного состояния системы алмаз – переходный слой – матрица при силовых и тепловых возмущениях;
• численное моделирование температурного поля системы алмаз – переходный слой – полимерная матрица;
• численное моделирование напряженно-деформированного состояния системы алмаз – переходный слой – полимерная матрица при силовых и тепловых возмущениях;
• численное моделирование нестационарного теплового процесса в системе алмаз – переходный слой – полимерная матрица.

Научная новизна полученных результатов заключается в:

• разработанной нелинейной математической модели температурного поля и напряженно-деформированного состояния в системе алмазное зерно – переходный слой – полимерная матрица;
• установлении влияния теплопроводности матрицы, переходного слоя и его толщины на температурное поле в системе алмазное зерно – переходный слой – полимерная матрица;
• теоретическом анализе напряженно-деформированного состояния в системе алмазное зерно – переходный слой – полимерная матрица при тепловых возмущениях и установлении зависимости напряжений от материала покрытия, теплопроводности матрицы и коэффициентов теплового расширения матрицы и переходного слоя;
• результатах моделирования напряженно-деформированного состояния в системе алмазное зерно – переходный слой – полимерная матрица при действии силовых и температурных возмущений.
• теоретическом анализе нестационарного теплового процесса в системе алмазное зерно – переходный слой – полимерная матрица и установлении влияния на него наиболее существенных факторов – теплофизических свойств матрицы и теплоотдачи во внешнюю среду.

Практическая значимость работы заключается в:

• программно-алгоритмическом обеспечении расчётов температурного поля и напряженно-деформированного состояния в системе алмазное зерно – переходный слой – полимерная матрица при силовых и тепловых возмущениях;
• рекомендациях по выбору физических свойств матрицы и переходного слоя, обеспечивающих снижение температур, напряжений и деформаций в инструментальных алмазосодержащих композитах;
• установленных закономерностях перехода нестационарного температурного поля в стационарный, позволяющих оптимизировать режимы эксплуатации алмазных инструментов на полимерной матрице.
• Апробация работы. Материалы диссертации доложены:
• на Международных научно-технических конференциях: «Наука, техника и технология XXI века» (Нальчик, 2007 г.); «Компьютерное моделирование 2008» (Санкт-Петербург, 2008 г.); «Новые полимерные композиционные материалы» (Нальчик, 2010, 2011 годы);
• на Всероссийских научно-технических конференциях: «Наука, техника и технология нового века» (Нальчик, 2003, 2005 годы); «Новые полимерные композиционные материалы» (Нальчик, 2005 г.).

Публикации. Основные результаты исследований изложены в 10 научных работах, из которых одна – в рецензируемом журнале.

Структура и объем работы. Диссертация состоит из введения и четырёх глав, выводов и списка использованной литературы. Работа изложена на 135 страницах машинописного текста, содержит 54 рисунка, 18 таблиц и список литературы, включающий 90 наименований.

Автор выражает глубокую благодарность доктору физико-матема­ти­ческих наук, профессору, заведующему кафедрой вычислительной математики КБГУ Шханукову-Лафишеву Мухамеду Хабаловичу за помощь и научную консультацию при выполнении диссертационной работы.

ОСНОВНОЕ СОДЕРЖАНИЕ РАБОТЫ

В первой главе провёден анализ состояния вопроса и поставлены цель и задачи работы. Показано, что одной из наиболее важных и сложных задач при создании алмазно-абразивного инструмента является обеспечение надёжного закрепления зерна в матрице, что связано, в первую очередь, с малыми размерами и неправильной геометрической формой технических алмазов, а также c низкой прочностью адгезионной связи на границе раздела алмаза и связующего.

Наиболее широкое применение для изготовления алмазных инструментов нашли новолачный фенолформальдегидный олигомер СФ-012, фенольное связующее СФП-012А, резольная безаммиачная анилинфенолформальдегидная смола СФ-342А. В связи с появлением новых областей применения алмазного инструмента и повышением требований к его функциональным характеристикам постоянно расширяется круг используемых полимерных связующих. Основные направления развития полимерных связующих связаны с обеспечением большей теплостойкости, механической прочности, хороших антифрикционных свойств, а также с повышением адгезии к поверхности алмаза и наполнителей.

Отмечается лучшее смачивание и более высокая работа адгезии полимера к алмазу, чем к другим материалам, что связывают с наличием на поверхности алмаза гидроксильных, карбонильных, карбоксильных и эфирных групп, с которыми реакционноспособные группы полимеров могут образовывать физические и химические связи. Зависимость краевого угла смачивания от температуры носит экстремальный характер. Температуры, при которых наблюдается наибольшее смачивание, для распространённых полимерных связующих находятся в диапазоне порядка 50–150 оС. Ухудшение смачиваемости при более высоких температурах объясняют интенсивной адсорбцией низкомолекулярных фракций и продуктов термоокисления молекулярных цепей, формированием при этом монослоя с низким поверхностным натяжением.

Анализ литературных данных по формированию структуры и свойств алмазосодержащих инструментальных композитов на полимерной матрице показал, что наиболее ответственными являются операции прессования и термической обработки. Исследования показывают, что в результате взаимодействия и конформационных ограничений, накладываемых поверхностью алмаза, наблюдается уменьшение молекулярной подвижности полимерных цепей в граничном с зерном слое. Это замедляет релаксационный процесс при отверждении наполненных связующих и способствует образованию менее равновесной структуры. Кроме того, изменяется распределение плотности сшивки макромолекул смолы вблизи дисперсных частиц алмаза, а также на разном удалении от них. Таким образом, вокруг зёрен образуется дефектный граничный слой полимера с меньшей полнотой химической сшивки молекул, чем полнота сшивки связующего в объеме, находящегося вне сферы влияния границы раздела.

Прочность алмазоудержания в значительной мере определяется термовязкоупругими свойствами связующего. По мере повышения температуры прочность удержания зерен уменьшается, особенно резко при температуре механического стеклования полимера. Выше этой температуры проявляется подвижность сегментов полимерных цепей, ослабляются связи между макромолекулами фенольного связующего и поверхностью алмаза. Дальнейший нагрев вследствие флуктуаций тепловой энергии способствует развитию высокоэластической деформации и разрушению связей, обеспечивающих прочность фиксации зерен.

Особенности системы зерно – матрица определяют расчётное моделирование как наиболее целесообразный метод его исследования. Для инструментов на полимерной матрице тепловой режим работы и напряженно-деформиро­ванное состояние системы алмаз-матрица исследованы мало и преимущественно для конкретных условий, а комплексные исследования при действии силовых и тепловых возмущений к настоящему времени не проводились.

Вторая глава посвящена разработке математической модели температурного поля и напряженно-деформированного состояния системы алмазное зерно – переходный слой – матрица.

Существующие мощные и универсальные программные средства, основанные на применении метода конечных элементов, не эффективны при решении данной задачи по двум причинам. Во-первых, исследуемая система отличается существенной нелинейностью теплофизических свойств элементов, особенно алмаза, во-вторых, работа с этими универсальными программными средствами связана с подготовкой огромных массивов исходных данных. В связи с этим целесообразно создание специализированного программного комплекса, ориентированного на решение данной задачи.

Для расчётов температурного поля и напряжённо-деформированного состояния решается двухмерная задача теории упругости с использованием метода конечных элементов. В качестве расчетной схемы принято единичное зерно эллипсоидной формы, помещённое в матрицу (рис. 1), так как даже в инструментах с высокой концентрацией алмазов поля напряжений около зерен перекрываются незначительно. Эллипсоид вращения является наиболее приближенной к реальной форме зерна. Вариацией размеров полуосей a и b зерна и параметра bk можно моделировать различные его пропорции и разное погружение в матрицу.

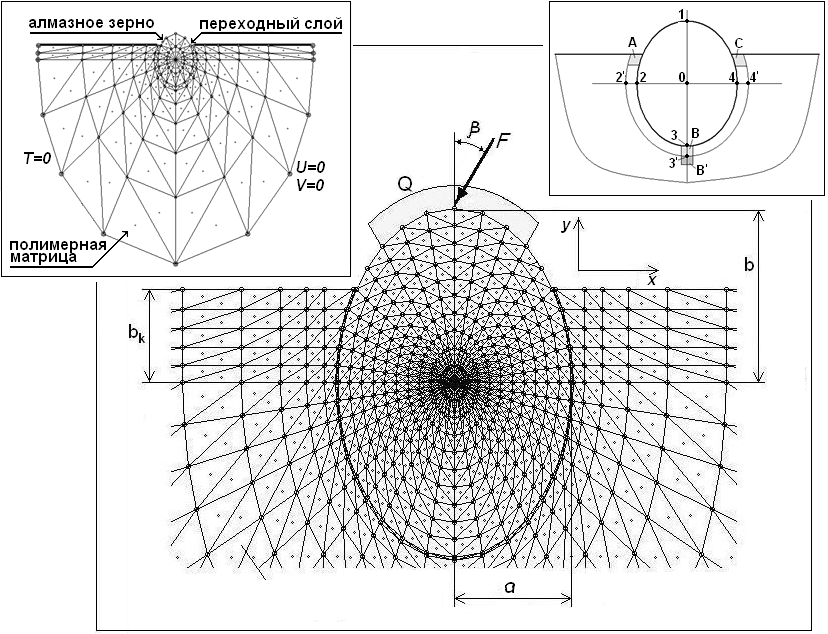
Рис. 1. Расчётная схема

С целью моделирования различных покрытий на алмазные зёрна, широко применяемых в этих инструментах, а также дефектного граничного слоя полимера, в расчётной схеме выделен переходный слой между алмазом и матрицей.

Таким образом, расчётная схема (рис. 1) представляется в виде плоской пластины, состоящей из алмазного зерна, переходного слоя и матрицы. Ниже в обозначениях физических свойств этих элементов приняты индексы 1, 2 и 3 соответственно.

Конструкция может находиться под действием возмущений от процесса резания – статической сосредоточенной нагрузки F, приложенной под углом к вертикальной оси алмазного зерна, и удельного теплового потока Q, приложенного к свободному контуру зерна, непосредственно контактирующему с обрабатываемым материалом. Учитываются конвективные потери тепла в окружающую среду на свободной от теплового потока части контура зерна и прямолинейном контуре матрицы с соответствующими коэффициентами теплоотдачи ha и hm.

Расчет поля температур в конструкции вёлся на основе решения нелинейного уравнения нестационарной теплопроводности в плоской изотропной среде

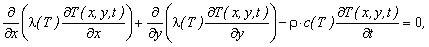
где – температура; – коэффициент теплопроводности; – плотность; – удельная теплоемкость; – время.

Это уравнение должно подчиняться следующим типам граничных условий на контуре пластины.

1) Если на границе задан поток тепла Q (Q считается положительным, если тепло теряется телом):

2) Если на границе происходит конвективный теплообмен, характеризуемый коэффициентом теплоотдачи h:

где – температура окружающей среды; – направляющие косинусы.

3) Если граница представляет собой теплоизолированный участок:

4) Если на некоторой части границы температура известна:

где – координаты точек границы.

Начальные условия при решении уравнений нестационарной теплопроводности имеют вид

.

Компоненты деформаций и напряжений находятся из соотношений двухмерной задачи теории упругости

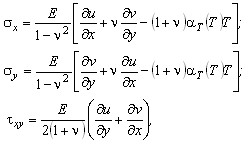
где – линейные и угловая деформации; – перемещения вдоль осей и соответственно; – нормальные и касательное напряжения; – модуль упругости и коэффициент Пуассона; – коэффициент линейного расширения.

Таким образом, задача решается с учётом зависимости удельной теплоёмкости и коэффициентов теплопроводности и теплового расширения элементов исследуемой системы от температуры.

Разработаны конечноэлементные формулировки и алгоритмы решения задач стационарной и нестационарной термоупругости.

Алгоритм решения задачи стационарной термоупругости состоит из двух этапов. На первом этапе решается задача теплопроводности и определяется поле температур в конструкции для текущего значения теплового потока. На втором этапе решается задача об определении напряжённо-деформи­ро­ванного состояния конструкции для сосредоточенной силы и установившейся температуры при текущем значении теплового потока.

Алгоритм решения задачи нестационарной термоупругости также состоит из двух этапов. На первом этапе решается задача теплопроводности для текущего значения времени и определяется поле температур в конструкции. На втором этапе решается задача об определении напряжённо-деформи­рованного состояния конструкции для сосредоточенной силы и вычисленной температуры при текущем значении времени.

Третья глава посвящена разработке программного обеспечения моделирования и обоснованию достоверности и точности получаемых результатов расчёта.

Алгоритмы решения задач стационарной и нестационарной термоупругости и определения возникающих при этом температурного поля и напряжённо-деформированного состояния реализованы в виде программ на алгоритмическом языке Turbo-C. Эти программы составляют основу разработанной системы автоматизированных расчётов, состоящей из подсистем: формирования расчётной схемы (препроцессор); расчёта температур и напряжённо-деформированного состояния (процессор); выпуска результатов расчёта (постпроцессор). Система обеспечивает также ряд сервисных возможностей – автоматизацию формирования и визуализацию геометрической модели конструкции и модели внешних воздействий на неё, визуализацию реакции конструкции на внешние воздействия, подготовку и выпуск расчётной документации, получение оперативной справочной информации об исходных данных и результатах расчета.

Препроцессор обеспечивает: формирование и визуализацию геометрической модели конструкции и модели внешних воздействий; формирование методических параметров задачи; ввод и диагностику файлов исходных данных; подготовку и выпуск расчётной (табличной и графической) информации; преобразование исходных данных из внешнего представления во внутреннее.

Работа с системой начинается с разработки базы данных материалов и формирования соответствующего файла, затем формируются файлы конструкции, нагрузок и методических параметров задачи.

При формировании базы данных материалов задаются следующие характеристики: Е[Н/м2] – модуль упругости; – коэффициент Пуассона; [кг/м3] – плотность; [Н/м2] – допускаемое напряжение; – число узлов на графике(рис. 2), где [град–1] – коэффициент линейного расширения; – пары координат узлов на графике . Аналогично задаются и зависимости и .

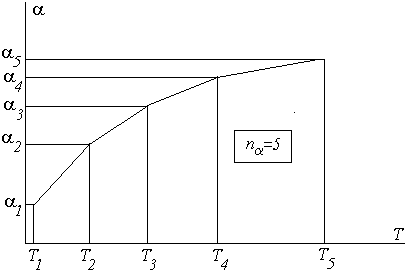
Рис. 2. График для задания зависимости

Для формирования файла расчетной схемы конструкции необходимо задать следующие характеристики (см. рис. 1): – толщина конструкции; – полуоси алмазного зерна; – число эллипсов (слоев), на которое разбивается зерно; – число секторов, на которое разбивается четверть зерна; – толщина переходного слоя; – глубина погружения зерна в матрицу; – число эллипсов (слоев), на которое разбивается матрица; – коэффициент разрежения сетки матрицы (); при = 1 толщина слоев будет одинакова, при = 2 толщина каждого следующего слоя будет увеличиваться в два раза.

Задаются параметры, определяющие нагрузку на систему: сила , угол , номер узла, к которому приложена сила ; удельный тепловой поток Q[Bm/м2] и число граней свободного контура зерна, к которым он приложен симметрично (на рис. 1 = 3). Также задаются коэффициенты теплоотдачи на свободном от теплового потока криволинейном контуре зерна и на прямолинейном контуре матрицы.

Файл методических параметров формируется в зависимости от решаемой задачи. При решении задачи стационарной термоупругости задаются начальное и конечное значения потока тепла, а также шаг по потоку тепла. При решении задачи нестационарной термоупругости дополнительно задаются конечное значение времени и шаг интегрирования по времени.

Проведены исследования и обоснование достоверности и точности получаемых результатов, а также разработаны рекомендации по выбору методических параметров расчета.

Главная погрешность решения задач определяется методом конечных элементов, точность которого напрямую зависит от степени дискретизации рассматриваемой конструкции, т.е. от размеров конечных элементов. Поэтому на первом этапе испытаний разработанного программного комплекса исследована сходимость метода конечных элементов по температуре, перемещениям и напряжениям в зависимости от числа конечных элементов. Рассматривались следующие расчётные схемы, соответствующие различным характеристикам разбиения конструкции на конечные элементы: n1 = n2 = n3 = 6 (488 элементов); n1 = n2 = n3 = 8 (840 элементов); n1 = n2 = n3 = 10 (1332 элемента);
n1 = n2 = n3 = 12 (1936 элементов).

Численные эксперименты показали удовлетворительное совпадение результатов по всем четырем расчётным схемам, в том числе для зоны концентрации напряжений, каковыми являются области сопряжения защемленной поверхности зерна с его свободной поверхностью. При этом с уменьшением числа конечных элементов большее увеличение погрешности расчётов имеет место при определении напряжений. Интенсивности напряжений, рассчитанные по различным расчётным схемам, отличаются не более чем на 1,5 %, что свидетельствует о правильности в энергетическом смысле разработанного алгоритма.

Решение каждой из задач расчёта температурного поля и напряжённо-деформированного состояния конструкции сводится к некоторому специфичному для этой задачи итерационному процессу, на каждом шаге которого решается линейная задача, порождаемая соответствующим итерационным процессом. В программе решения задачи стационарной термоупругости – это итерационный процесс по определению теплофизических характеристик материала в зависимости от температуры. В программе решения задачи нестационарной термоупругости – это итерационный процесс по определению теплофизических характеристик материала в зависимости от температуры в сочетании с методом конечных разностей при интегрировании уравнений теплопроводности по времени.

Проверена сходимость указанных выше итерационных процессов. Результаты многочисленных расчётов показали, что число итераций, необходимых для достижения относительной погрешности = 10-6, заложенной в алгоритмы, не превышает 10–12.

Проведено обоснование достоверности алгоритмов, основанное на следующих косвенных доказательствах правильности получаемого решения.

1. Использование свойств симметрии рассчитываемой конструкции:

а) если внешняя сила или тепловой поток, действующие на конструкцию, симметричны относительно оси симметрии, то компоненты температуры и напряжённо-деформированного состояния должны быть симметричны относительно этой же оси;

б) если внешняя нагрузка или тепловой поток, действующие на конструкцию, антисимметричны относительно оси симметрии, тогда компоненты температуры и напряжённо-деформированного состояния должны быть антисимметричны относительно этой же оси.

Отклонения от симметрии в случае а) и от антисимметрии в случае;
б) является следствием ошибки во внутреннем построении самого алгоритма.

2. Реакции в опорах: сумма проекций на оси х и у реакций в опорах должна быть равна сумме проекций на оси х и у внешних нагрузок.

3. Перекрёстное сравнение программ решения задач стационарной и нестационарной термоупругости. Очевидно, что при заданной тепловой нагрузке на систему результаты расчётов по второй программе при достижении установившегося теплового режима должны совпадать с результатами расчётов по первой. Поскольку в этих программах используются принципиально разные методы, то перекрестное сравнение программ указывает на правильность используемых алгоритмов.

В четвёртой главе представлены результаты моделирования температурного поля и напряженно-деформированного состояния системы алмаз – переходный слой – полимерная матрица с использованием разработанного программного комплекса.

В качестве базовых исходных данных в численных экспериментах были приняты параметры системы, характерные для условий работы алмазных шлифовальных кругов на бакелитовом связующем (таблица). Силовая и тепловая нагрузки на систему задавались из условия соответствия усилия резания алмазным зерном и температур в системе известным экспериментальным данным.

Таблица

Параметры модели

Размеры, мм					Нагрузка
a	b	k	bk		F, Н
0,200	0,250	0,200	0,100	0,010	10	30	3,0х106	5х103

На первом этапе исследований решением уравнения стационарной теплопроводности проведено моделирование влияния свойств матрицы и переходного слоя на температурное поле системы.

На рис. 3 представлено распределение температуры (здесь и далее речь идёт об избыточной температуре – выше 20 оС) в сечении по вертикальной оси зерна (см. рис. 1) при различных коэффициентах теплопроводности материала матрицы 3. В этих численных экспериментах свойства покрытия принимались идентичными свойствам матрицы. Эксперименты показали, что увеличение теплопроводности матрицы приводит к существенному уменьшению температур в системе. При одинаковой тепловой нагрузке базовому варианту с (использованию бакелитового связующего) соответствует средняя температура в зерне 300 оС, – 220о, – 170о, – 130о. При этом при всех значениях 3 алмазное зерно прогревается практически равномерно. Небольшой градиент температур в зерне отмечен лишь в сечении вдоль вертикальной оси зерна. Эксперименты показали, что температура в переходном слое при заданном значении 3 меняется несущественно – имеет место её незначительное уменьшение при приближении к охлаждаемой поверхности.

Моделирование влияния теплопроводности переходного слоя на температурное поле показало, что применение наиболее распространенных покрытий – натрийборосиликатного стекла () и никеля (), а также титана (), не приводит к существенному уменьшению температуры матрицы (см. рис. 4). Также численные эксперименты показали, что толщина покрытия практически не влияет на температурное поле. Эти результаты моделирования опровергают распространённое мнение о том, что указанные покрытия служат тепловым барьером, резко уменьшающим тепловые потоки в полимерное связующее.

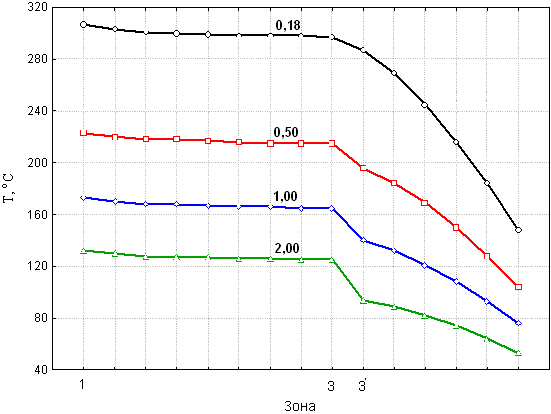
Рис. 3. Изменение температуры в сечении

по вертикальной оси зерна при различных коэффициентах

теплопроводности матрицы

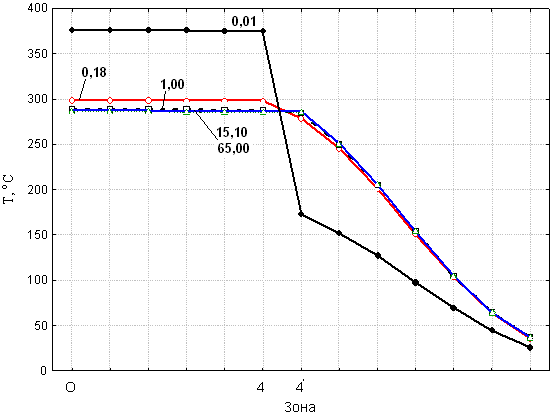
Рис. 4. Изменение температуры в сечении по горизонтальной оси

зерна при различных коэффициентах теплопроводности

материала покрытия

На втором этапе исследований проведено моделирование напряжённо-деформированного состояния системы алмаз – переходный слой – полимерная матрица при силовых и температурных возмущениях.

Исследования напряженно-деформированного состояния при силовых воздействиях показали, что левая относительно оси симметрии исследуемой системы часть является наиболее напряжённой (рис. 5). В этой области компоненты напряжений имеют преимущественно отрицательный знак, растягивающие напряжения характерны для другой части системы. При этом отмечена общая тенденция возрастания напряжений по мере приближения к границе зерно-матрица, а максимальная интенсивность напряжений i приходится на контактную область со стороны алмаза.

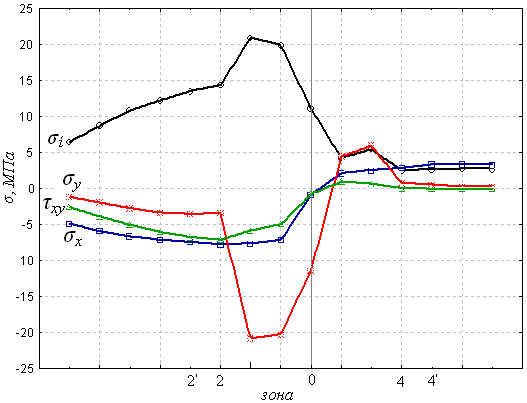
Рис. 5. Распределение напряжений в сечении

по горизонтальной оси зерна при силовом воздействии

Напряжения в контактной области со стороны матрицы увеличиваются по абсолютной величине по мере приближения к областям А и C (см. рис. 1), являющимся зонами концентрации напряжений.

При заданных исходных данных проведены также расчёты напряжённо-деформированного состояния системы при силовых возмущениях для трёхмерной модели с использованием программного комплекса COSMOS Works. Численные эксперименты показали, что расчётные напряжения, полученные на двух- и трехмерных моделях, различаются не более чем на 5–10 %.

Анализ результатов моделирования полей температурных напряжений показывает, что максимальная интенсивность напряжений приходится на переходный слой (рис. 6). При этом имеет место резкое увеличение интенсивности напряжений при переходе от поверхности зерна в покрытие. Далее, по мере удаления от контактной зоны, напряжения плавно уменьшаются.

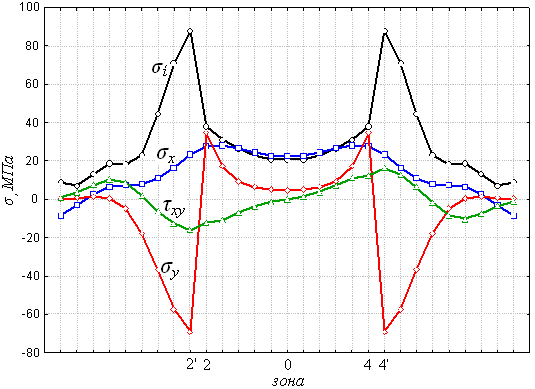
Рис. 6. Распределение температурных напряжений в сечении

по горизонтальной оси зерна

Как и в случае силового нагружения, максимальная интенсивность напряжений в системе имеет место в зонах концентрации напряжений А и С (см. рис. 1).

Исследовано влияние теплопроводности матрицы 3 на температурные напряжения в системе. Отмечена общая тенденция к повышению интенсивности температурных напряжений в конструкции с уменьшением 3. При этом зависимости носят нелинейный характер – с возрастанием градиента i при уменьшении 3, что особенно выражено при его низких значениях, характерных для полимерных матриц. Анализ результатов показывает, что уровень температурных напряжений в переходном слое существенно зависит от материала покрытия. Наименьший уровень интенсивности напряжений отмечен для покрытия из стекла. Далее следуют в порядке возрастания напряжений бакелит, свинец, медь, титан, никель (см. рис. 7).

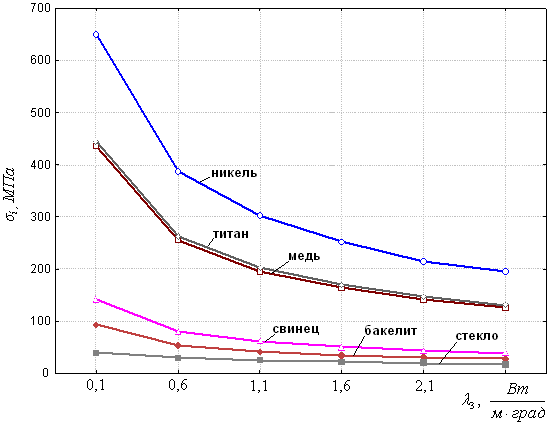
Рис. 7. Зависимость интенсивности температурных

напряжений в зоне B (см. рис. 1) от теплопроводности

матрицы 3 при различных материалах покрытия на зерно

Исследования показали, что интенсивность напряжений в переходном слое растёт с увеличением как коэффициента теплового расширения переходного слоя 2, так и матрицы 3 (рис. 8). При этом зависимость от 2 существенно более выражена. Оптимальными являются значения 2 и 3, близкие к значению коэффициента теплового расширения алмаза , т. е. случай равенства коэффициентов теплового расширения всех элементов системы. Значениям коэффициентов теплового расширения бакелитовой матрицы соответствуют оптимальные значения .

Третий этап исследований – моделирование напряжённо-деформи­рованного состояния при совместном действии силовых и температурных возмущений. Многочисленные эксперименты показали, что температурные напряжения в системе значительно превышают напряжения от силовых воздействий (см. рис. 9). Это соотношение сохраняется и при сильно заниженных режимах обработки, когда температура в системе снижается примерно на порядок.

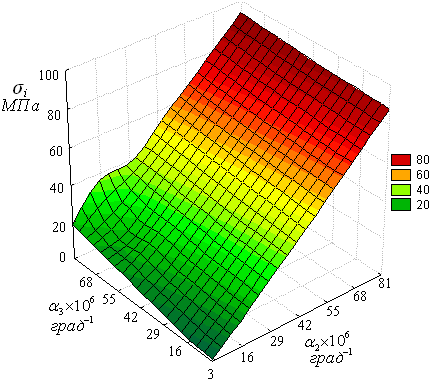
Рис. 8. Зависимость интенсивности напряжений в зоне В

(см. рис. 1) от коэффициентов теплового расширения

переходного слоя 2 и матрицы 3

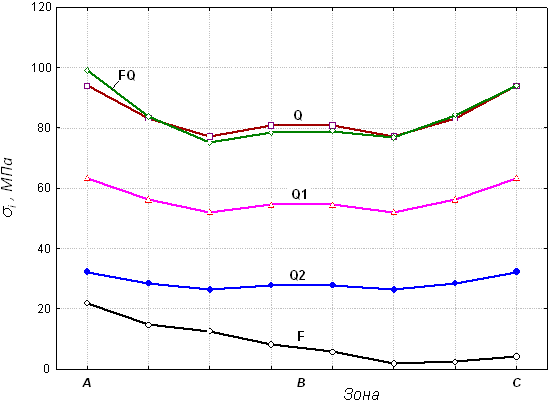
Рис. 9. Распределение интенсивности напряжений в переходном слое

при действии нагрузки: силовой (F); тепловой ;

силовой и тепловой (FQ); тепловой ; тепловой

Прерывистый характер процесса резания алмазным зерном при шлифовании приводит к соответствующему характеру тепловых воздействий на систему зерно-матрица. Поэтому представляет интерес моделирование нестационарных полей температур и напряжений в системе. Изучены переходные тепловые процессы в системе при различных значениях теплопроводности матрицы, теплоемкости матрицы и коэффициента теплоотдачи во внешнюю среду, как наиболее существенных факторов.

Как видно из рис. 10, время переходного теплового процесса практически не зависит от теплопроводности матрицы. Она определяет установившуюся температуру в системе. Для указанной зоны B’ (см. рис. 1), максимальная установившаяся температура, равная примерно 270 оС имеет место при использовании бакелитового связующего (3= 0,18 ).

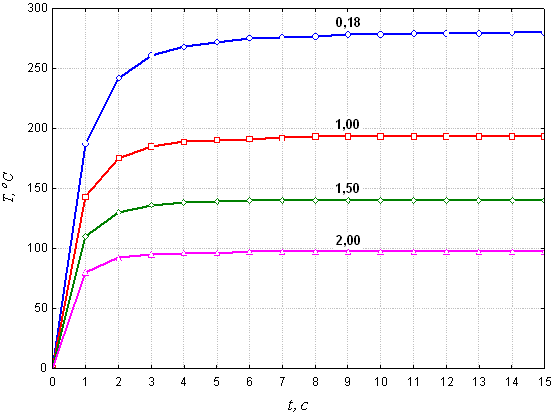
Рис. 10. Нестационарный тепловой процесс в зоне B’(см. рис. 1)

при различных коэффициентах теплопроводности матрицы 3 ()

Удельная теплоёмкость матрицы с3 не влияет на уровень установившейся температуры в системе, но влияет на время переходного теплового процесса. При заданных в численных экспериментах значениях удельной теплоёмкости матрицы c3 от 100 до 2400 стационарная температура устанавливается за время от 4 до 16 секунд. При этом для бакелитового связующего (c3=1600 ) время переходного процесса составляет 11 секунд.

Коэффициент теплоотдачи во внешнюю среду существенно влияет на переходный тепловой процесс в исследуемой системе (см. рис. 11). С его увеличением снижается уровень установившейся температуры. Время переходного процесса увеличивается с уменьшением коэффициента теплоотдачи, оно составляло в экспериментах от 5 до 104 секунд. Расчёты показали, что при базовом значении установившаяся температура 280 оС достигается за 14 секунд.

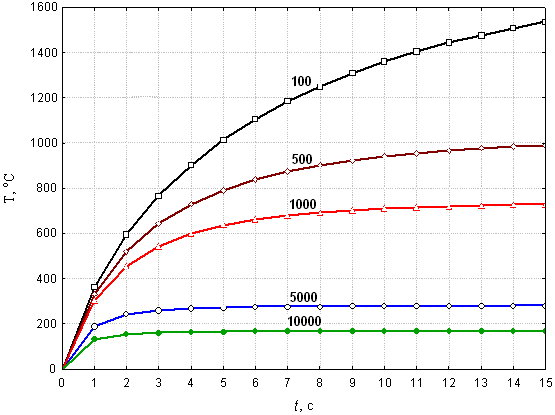
Рис. 11. Нестационарный тепловой процесс в зоне B’

(см. рис. 1) при различных коэффициентах теплоотдачи

в окружающую среду

Закономерности изменения деформаций и напряжений в переходном тепловом процессе аналогичны закономерностям изменения температур.

Результаты исследования нестационарного теплового процесса в системе могут быть использованы для оптимизации режимов эксплуатации шлифовальных кругов.

ВЫВОДЫ

1. Разработаны математические модели и алгоритмическое обеспечение расчёта температурного поля и напряжённо-деформированного состояния системы алмаз – переходный слой – полимерная матрица, основанные на решении двухмерных нелинейных задач стационарной и нестационарной термоупругости методом конечных элементов.
2. Разработана система автоматизированных расчётов, реализующая разработанные алгоритмы моделирования температурного поля и напряжённо-деформированного состояния системы алмаз – переходный слой – полимерная матрица. Проведено комплексное исследование и обоснование достоверности и точности получаемых результатов расчётов.
3. Численное моделирование стационарного температурного поля системы показало, что оно существенно зависит от теплопроводности матрицы и практически не зависит от толщины и теплопроводности переходного слоя. Отмечено, что из-за низкой теплопроводности бакелитовой матрицы алмазное зерно в процессе работы прогревается практически равномерно.
4. Моделирование напряжённо-деформированного состояния системы алмаз – переходный слой – полимерная матрица при силовых возмущениях показало, что максимальная интенсивность напряжений приходится на контактную область со стороны алмаза. При этом напряжения возрастают по мере приближения к области сопряжения свободной и защемлённой частей зерна, являющейся зоной концентрации напряжений в системе.
5. Проведено моделирование температурных напряжений в системе алмаз – переходный слой – полимерная матрица. Показано, что максимальная интенсивность напряжений имеет место в переходном слое. Исследовано влияние на напряжения в данной области теплопроводности матрицы, материала покрытия на зерно и коэффициентов теплового расширения переходного слоя и матрицы.
6. Моделирование напряжённо-деформированного состояния системы алмаз – переходный слой – полимерная матрица при действии силовых и температурных возмущений показало, что температурные напряжения в системе значительно превышают напряжения от силовых воздействий, и это соотношение сохраняется и при сильно заниженных режимах обработки, когда температура в системе снижается примерно на порядок.
7. Исследования показали, что нестационарный тепловой процесс в системе алмаз – переходный слой – полимерная матрица определяется, в основном, теплопроводностью и теплоёмкостью матрицы, а также теплоотдачей во внешнюю среду. Определены зависимости установившейся температуры и времени переходного теплового процесса от этих параметров.

Основные результаты работы изложены в следующих публикациях:

1. Карданова (Яхутлова) М.Р. Задачи стационарной и нестационарной теплопроводности для трехслойной конструкции // Матер. Всерос. научн.-техн. конф.: Наука, техника и технология нового века (НТТ-2003). – Нальчик, 2003. – С. 76–81.
2. Карданова М.Р. Решение двумерной динамической задачи теории упругости методом конечных элементов // Информационные технологии в промышленности и экономике: сборник научных трудов Института конструкторско-технологической информатики РАН. Вып. 4 / под ред. Ю.М. Соломенцева. – М., 2004. – С. 235–237.
3. Яхутлов М.М., Батыров У.Д., Карданова М.Р. Моделирование напряжённо-деформированного состояния абразивного инструмента при динамическом нагружении // Информационные технологии в промышленности и экономике: сборник научных трудов Института конструкторско-техноло­гической информатики РАН. Вып. 4 / под ред. Ю.М. Соломенцева. – М., 2004. – С. 238–241.
4. Карданова М.Р. Математическая модель абразивного инструмента на органической матрице // Матер. II Всерос. научн.-практ. конф.: Новые полимерные композиционные материалы. – Нальчик, 2005. – С. 307–311.
5. Карданова М.Р. Алгоритм решения нелинейной нестационарной задачи термоупругости для трехслойного композита // Матер. II Всерос. научн.-техн. конф.: Наука, техника и технология XXI века (НТТ-2005). – Нальчик, 2005. – С. 54–58.
6. Карданова М.Р. О физико-механических свойствах элементов алмазного инструмента на полимерной связке // Матер. III межд. научн.-техн. конф.: Наука, техника и технология XXI века (НТТ-2007). Т. 1. – Нальчик, 2007. – С. 157–159.
7. Яхутлов М.М., Батыров У.Д., Карданова М.Р. Программно-алгорит­мическое обеспечение моделирования напряжённо-деформиро­ванного сос­тояния в системе алмаз-матрица // Труды межд. научн.–техн. конф.: Компьютерное моделирование 2008. – СПб., 2008. – С. 272–275.
8. Яхутлов М.М., Карамурзов Б.С., Батыров У.Д., Ошхунов М.М., Карданова М.Р. Напряжённо-деформированное состояние системы зерно-мат­рица алмазного инструмента при силовых возмущениях // Сверхтвердые материалы. – Киев, 2009. – № 6. – С. 81–88.
9. Карданова М.Р., Лигидов М.Х., Шхануков-Лафишев М.Х., Яхутлов М.М. Тепловой режим в алмазосодержащем инструментальном композите на полимерном связующем // Матер. VI Межд. научн.-практ. конф.: Новые полимерные композиционные материалы. – Нальчик, 2010. – С. 178–185.
10. Карданова М.Р., Лигидов М.Х., Шхануков-Лафишев М.Х., Яхутлов М.М. Моделирование температурного поля в композиционном алмазосодержащем материале на органической матрице // Пласт. массы. – 2010. – № 5. – С. 34–38.

В печать 28.09.2011. Тираж 100 экз. Заказ № 6379.

Полиграфический участок ИПЦ КБГУ

360004, г. Нальчик, ул. Чернышевского, 173.