Адаптивные алгоритмы и методы формирования и решения уравнений состояния электрических цепей с изменяющимися параметрами

На правах рукописи

Савёлов Николай Семёнович

Адаптивные алгоритмы и методы формирования

и решения уравнений состояния электрических

цепей с изменяющимися параметрами

Специальность 05.09.05 – Теоретическая электротехника

Автореферат

диссертации на соискание ученой степени

доктора технических наук

Новочеркасск – 2011г.

Работа выполнена на кафедре «Автоматика и телемеханика» ГОУ ВПО

«Южно-Российский государственный технический университет (Новочеркасский политехнический институт)»

Научный консультант: доктор технических наук, профессор

Лачин Вячеслав Иванович

Официальные оппоненты: доктор технических наук, профессор

Гусев Геннадий Григорьевич

доктор технических наук, профессор

Басан Сергей Николаевич

доктор технических наук, профессор

Высоцкий Виталий Евгеньевич

Ведущая организация: Федеральное государственное автономное

образовательное учреждение высшего

профессионального образования

«Южный федеральный университет»

Защита состоится 23 июня 2011г. в 14.00 на заседании диссертационного совета Д 212.304.01 в ГОУ ВПО «Южно-Российский государственный технический университет (Новочеркасский политехнический институт)» по адресу: 346428, г. Новочеркасск Ростовской обл., ул. Просвещения, 132, ауд. 107 (главный корпус)

С диссертацией можно ознакомиться в библиотеке ЮРГТУ (НПИ) по адресу: 346428, г. Новочеркасск Ростовской обл., ул. Просвещения, 132.

Автореферат разослан _____________2011г.

Учёный секретарь диссертационного совета,

д.т.н. П.Г. Колпахчьян

ОБЩАЯ ХАРАКТЕРИСТИКА РАБОТЫ

Актуальность проблемы. Теоретическая электротехника относится к одной из наиболее быстро развивающихся наук, достижения которой существенно влияют на уровень развития техники и технологий. Это определяется важной и все более возрастающей ролью электротехники, электроэнергетики и электромеханики в современном мире. Необходимость решения сложных теоретических и практических задач в данной предметной области требует дальнейшего развития теоретических основ электротехники, методов моделирования электроэнергетических процессов и систем.

Одним из основных разделов теоретической электротехники, имеющим исключительно широкое практическое применение, является теория электрических цепей. Многие методы теории цепей успешно используются не только в электротехнике, но и в других областях науки и техники, так как имеют универсальный характер.

В теории цепей усилиями зарубежных и отечественных учёных (Анисимов Б.В., Артым А.Д., Астахов В.И., Атабеков Г.И., Басан С.Н., Баталов Б.В., Бахвалов Ю.А., Белецкий А.Ф., Бененсон З.М., Бессонов Л.А., Бутырин П.А., Влах И., Высоцкий В.Е., Глориозов Е.Л., Гусев Г.Г., Данилов Л.В., Демирчян К.С., Ильин В.Н., Калахан Д.А., Ковалёв О.Ф., Колесников Э.В., Круг К.А., Лин Пен-Мин, Лосев А.К., Матханов П.Н., Миронов В.Г., Миткевич В.В., Нагорный Л.Я., Нейман Л.Р., Некрасов С.А., Норенков И.П., Павленко А.В., Петренко А.И., Поливанов К.М., Попов В.П., Птах Г.К., Пухов Г.Е., Ракитский Ю.В., Сигорский В.П., Сингхал К., Ткачёв А.Н., Толстов Ю.Г., Филин В.А., Филиппов Е.С., Чечурин В.Л., Чуа Л.О., Шакиров М.А., Шимони К. и многие другие) достигнуты значительные теоретические и практические результаты, но в ней, как в каждой непрерывно развивающейся науке, возникают всё новые актуальные проблемы, требующие углубления исследований.

В настоящее время, как и в других областях современной науки, в теоретической электротехнике и, в частности, в теории цепей быстро возрастает роль математического моделирования. В этой связи всё более актуальными становятся следующие две фундаментальные проблемы: развитие теории и методов формирования математических моделей электрических цепей и развитие теории и методов исследования и численной реализации этих моделей с целью получения новых знаний об изучаемых объектах.

Достаточно часто объектами исследования являются рассматриваемые в диссертации цепи, компонентные уравнения которых описываются квазилинейными функциями с параметрами, изменяющимися во времени, причём между отдельными изменениями цепи анализируются как линейные. Для таких цепей математические модели должны корректироваться (переформировываться) при изменении указанных параметров.

Универсальной формой математической модели электрической цепи являются уравнения состояния, а метод переменных состояния является общепризнанным, одним из наиболее эффективных методов как теоретической электротехники, так и других наук, таких как современная теория управления. Представление математических моделей электрических цепей и других динамических объектов в виде уравнений состояния имеет ряд важных преимуществ. Они обеспечивают выполнение наиболее глубокого и всестороннего анализа динамических свойств электрической цепи. Такие уравнения имеют минимально возможную размерность. Для анализа уравнений состояния созданы высокоэффективные методы. Многие подходы к исследованию динамических объектов требуют представления математической модели именно в форме уравнений состояния. Эта форма широко используется в таких современных эффективных математических пакетах программ, как Matlab и Mathcad. Однако формирование уравнений состояния требует значительных вычислительных затрат, что особенно важно при анализе цепей с изменяющимися параметрами, уравнения состояния которых необходимо переформировывать после каждого изменения параметров их элементов. В этой связи актуальными являются проблема сокращения вычислительных затрат на повторные формирования уравнений состояния, проблема эффективного выявления таких изменений параметров, которые существенно изменяют свойства цепи, что находит проявление в изменении вида уравнений состояния, а также проблема формирования с малыми вычислительными затратами частично символьных функций, которые существенно упрощают анализ влияния параметров элементов на свойства цепи.

Так как характер переходного процесса в электрической цепи часто существенно изменяется во времени, что особенно характерно для цепей с изменяющимися параметрами, актуальной является также проблема эффективного выявления областей в пространстве состояний, отличающихся динамикой переходных процессов. Это, во-первых, позволяет выполнять более полный анализ особенностей переходных процессов в цепи, и, во-вторых, увеличивает эффективность численных методов расчёта переходных процессов.

Исследования велись в соответствии с научными направлениями Южно-Российского государственного технического университета (Новочеркасского политехнического института) «Теория и принципы построения информационно-измерительных систем и систем управления» и «Интеллектуальные электромеханические устройства, системы и комплексы».

Цель работы и задачи исследований. Целью диссертации является разработка эффективных методов формирования и решения уравнений состояния электрических цепей с изменяющимися параметрами, обеспечивающих снижение вычислительных затрат при анализе переходных и установившихся режимов в условиях локального изменения параметров цепи и рационального выбора шага интегрирования системы обыкновенных дифференциальных уравнений (ОДУ). Для достижения указанной цели решены две основные задачи и ряд подзадач.

Задача 1. Разработка новых эффективных методов формирования уравнений состояния электрических цепей.

Задача 1.1. Разработка новой алгоритмической основы методов формирования уравнений состояния в виде модификации метода исключения Гаусса для решения систем линейных алгебраических уравнений (СЛАУ).

Задача 1.2. Разработка методов анализа электрических цепей с изменяющимися параметрами в режимах постоянного и переменного тока на новой алгоритмической основе, обеспечивающих сокращение вычислительных затрат.

Задача 1.3. Разработка полной математической модели электрической цепи.

Задача 1.4. Разработка двухэтапного метода формирования уравнений состояния электрических цепей.

Задача 1.5. Разработка метода формирования частично символьных функций параметрических электрических цепей.

Задача 2. Разработка теоретических основ и новых численных методов решения уравнений состояния электрических цепей.

Задача 2.1. Разработка новых подходов к анализу переходных процессов на базе количественной оценки изменения их характера.

Задача 2.2. Разработка нового метода выявления областей в пространстве переменных состояния, отличающихся динамикой переходных процессов в электрических цепях.

Задача 2.3. Обеспечение устойчивости численных алгоритмов расчета переходных процессов в электрических цепях.

Методы исследований и достоверность полученных результатов. Методологической основой диссертационной работы являются основные положения теории электрических цепей, теории графов, линейной алгебры, теории обыкновенных дифференциальных уравнений и численных методов. Достоверность полученных результатов обеспечивается корректным применением этих положений и подтверждается результатами математического моделирования.

Научная новизна. Предложен новый подход к формированию математических моделей электрических цепей с изменяющимися параметрами в форме уравнений состояния, а также новый подход к построению численных методов решения этих уравнений. Получены следующие новые научные результаты.

1. Разработана новая алгоритмическая основа методов формирования уравнений состояния – модификация метода исключения Гаусса для решения СЛАУ, отличающаяся от известных меньшими вычислительными затратами при повторных решениях после изменений матрицы, соответствующим локальным изменениям в цепи.

2. Разработаны новые методы анализа линейных электрических цепей в режимах постоянного и переменного тока с изменяющимися параметрами элементов на основе предложенной модификации метода исключения Гаусса, отличающиеся от известных меньшими вычислительными затратами на повторный анализ цепи после изменения её параметров и на выявление параметров, приводящих к вырожденности матрицы СЛАУ.

3. Разработана новая математическая модель электрической цепи, отличающаяся тем, что она включает все исходные уравнения, необходимые для формирования уравнений состояния.

4. Разработан новый двухэтапный метод формирования уравнений состояния электрических цепей, отличающийся от известных меньшими вычислительными затратами на повторные формирования уравнений после изменения параметров элементов и на выявление параметров, существенно изменяющих свойства цепей.

5. Разработан новый метод формирования частично символьных функций параметрических электрических цепей, отличающийся от известных меньшими вычислительными затратами.

6. Разработан новый метод выявления областей в пространстве состояний с различной динамикой переходных процессов в электрических цепях, отличающийся от известных тем, что указанные области определяются непосредственно, без решения задачи Коши, что снижает вычислительные затраты.

7. Разработан новый подход, обеспечивающий устойчивость численных алгоритмов расчёта переходных процессов в электрических цепях, отличающийся от известных меньшими вычислительными затратами за счёт увеличения шага интегрирования.

Практическая ценность. Полученные результаты могут быть использованы при анализе электрических цепей с изменяющимися параметрами в режимах постоянного и переменного тока, формировании математических моделей в форме уравнений состояния для электрических цепей, при формировании частично символьных функций электрических цепей, при решении уравнений состояния электрических цепей.

Эти результаты открывают принципиально новые возможности при решении задач анализа переходных и установившихся режимов электрических цепей. Использование полученных результатов снижает вычислительные затраты.

Реализация результатов работы. Результаты диссертационной работы реализованы в следующих программах, зарегистрированных в объединённом фонде электронных ресурсов «Наука и образование», институт научной информации и мониторинга:

• «Ускоренное формирование уравнений состояния электрических цепей». Свидетельство о регистрации № 15954;
• «Эффективный анализ квазилинейных электрических цепей». Свидетельство о регистрации № 15955;
• «Ускоренное решение систем линейных алгебраических уравнений». Свидетельство о регистрации № 15979.

Полученные результаты внедрены:

• во Всероссийском научно-исследовательском и проектно-конструкторском институте электровозостроения «ОАО ВЭлНИИ» для анализа переходных процессов в тяговых двигателях, моделируемых с помощью схем замещения;
• в учебном процессе Южно-Российского государственного технического университета (Новочеркасского политехнического института), включая подготовку магистерских диссертаций;
• в Техническом университете Ильменау, Федеративная Республика Германия, для проектирования устройств мехатроники, моделируемых с помощью схем замещения в виде электрических и магнитных цепей.

Научные результаты, выносимые на защиту.

1. Используемая в качестве алгоритмической основы методов формирования уравнений состояния модификация метода исключения Гаусса для решения СЛАУ.
2. Методы анализа электрических цепей с изменяющимися параметрами в режимах постоянного и переменного тока.
3. Математическая модель электрической цепи, включающая все исходные уравнения, необходимые для формирования уравнений состояния.
4. Метод первоначального формирования уравнений состояния.
5. Метод коррекции уравнений состояния.
6. Метод формирования частично символьных функций электрических цепей.
7. Новый подход к выявлению областей в пространстве состояний, отличающихся различной динамикой переходных процессов в электрических цепях.
8. Новый метод исследования переходных процессов в электрических цепях.
9. Новый подход к обеспечению устойчивости численных методов расчёта переходных процессов в электрических цепях.

Апробация работы. Основные результаты диссертационной работы докладывались и обсуждались на следующих конференциях и семинарах: ежегодных научно-технических конференциях ЮРГТУ (НПИ); научных семинарах кафедр автоматики и телемеханики, прикладной математики и теоретической электротехники ЮРГТУ (НПИ), кафедры электрофизики Московского энергетического института, института Проблем моделирования в энергетике АН УССР, 1986г., г. Киев; I-ой Всесоюзной конференции по теоретической электротехнике, 1987г., г. Ташкент; заседании электромеханической секции научно-технического совета научно-производственного объединения «Магнетон», 1990г., г. Владимир; Третьей Всероссийской научно-технической конференции с международным участием «Теория цепей и сигналов» (ТЦ и С - 96), 1996г., г. Таганрог; Международном научно-практическом коллоквиуме «Проблемы мехатроники - 2003», 2003г., г. Новочеркасск; Международной научно-практической конференции «Микропроцессорные, аналоговые, цифровые и электромеханические устройства и системы», 2006г., г. Новочеркасск; VII-ой Международной научно-практической конференции «Компьютерные технологии в науке, производстве, социальных и экономических процессах», 2006г., г. Новочеркасск; Международном научно-практическом коллоквиуме «Проблемы мехатроники - 2006», 2006г., г. Новочеркасск; VII-ой Международной научно-практической конференции «Методы и алгоритмы прикладной математики в технике, медицине и экономике», 2007г., г. Новочеркасск; VII-ой Международной научно-практической конференции «Моделирование. Теория, методы и средства», 2007г., г. Новочеркасск; VII-ой Международной научно-практической конференции «Современные энергетические системы и комплексы и управление ими», 2007г., г. Новочеркасск; 50-ой Юбилейной научной конференции Московского физико-технического института (МФТИ) «Современные проблемы фундаментальных и прикладных наук», 2007г., г. Долгопрудный; VIII-ой Международной научно-практической конференции «Теория, методы и средства измерений, контроля и диагностики», 2007г., г. Новочеркасск; VII-ой Международной научно-практической конференции «Микропроцессорные, аналоговые и цифровые системы: проектирование и схемотехника, теория и вопросы применения», 2007г., г. Новочеркасск; VIII-ой Международной научно-практической конференции «Методы и алгоритмы прикладной математики в технике, медицине и экономике», 2008г., г. Новочеркасск; Международной конференции, посвященной 100-летию со дня рождения Л.С. Понтрягина «Дифференциальные уравнения и топология», 2008г., г. Москва, Московский государственный университет им. М.В. Ломоносова, Математический институт им. В.А. Стеклова РАН; IX-ой Международной научно-практической конференции «Теория, методы и средства измерений, контроля и диагностики», 2008г., г. Новочеркасск; Международном научно-практическом коллоквиуме «Мехатроника - 2009», 2009г., г. Новочеркасск, IX-ой Международной научно-практической конференции «Микропроцессорные, аналоговые и цифровые системы: проектирование и схемотехника, теория и вопросы применения», 2009г., г. Новочеркасск; VI Всероссийской межвузовской конференции молодых учёных, Санкт-Петербургский государственный университет информационных технологий, механики и оптики, г. Санкт-Петербург, 2009г.; 52-ой научной конференции Московского физико-технического института (МФТИ) «Современные проблемы фундаментальных и прикладных наук», 2009г., г. Долгопрудный; научном семинаре кафедры мехатроники технического университета Ильменау, 2010г., г. Ильменау, Федеративная Республика Германия; Всероссийской конференции с элементами научной школы для молодёжи «Мехатроника и робототехника. Современное состояние и тенденции развития», 2010г., г. Новочеркасск; научном семинаре кафедры теоретических основ электротехники Московского энергетического института (технического университета), 2010г., г. Москва; 53-й научной конференции Московского физико-технического института (МФТИ) «Современные проблемы фундаментальных и прикладных наук», 2010г., г. Долгопрудный.

Публикации.

По результатам диссертационной работы опубликовано 49 работ, из них 18 в журналах, рекомендованных ВАК для опубликования основных научных результатов диссертаций на соискание учёной степени доктора наук.

Структура диссертации. Диссертация состоит из введения, 7 основных разделов, заключения, списка литературы, приложений и содержит 315 страниц.

СОДЕРЖАНИЕ РАБОТЫ

Во введении выполнен анализ основных используемых методов расчёта переходных процессов в электрических цепях с изменяющимися параметрами, обоснована актуальность темы, определены цель и задачи исследования, указаны научная новизна и практическая значимость работы. Результаты анализа представлены на рис. 1.

В первом разделе выполнен анализ проблем формирования математических моделей цепей с изменяющимися параметрами в форме уравнений состояния и их решения, а также анализа линейных электрических цепей в режимах постоянного и переменного тока с изменяющимися параметрами элементов.

В общем случае для нелинейных цепей уравнения состояния записываются в следующем виде:

, (1)

, (2)

где – столбец переменных состояния, – время, – столбец выходных величин, и – векторные функции векторного переменного.

Для линейных или линеаризованных цепей уравнения состояния имеют вид:

, (3)

, (4)

где - вещественные матрицы, - целое число, - столбец независимых величин.

Уравнения (3), (4) допускают преобразование в форму с двумя первыми слагаемыми в правой части выражения (3).

Анализ показал, что при использовании известных методов в случае необходимости переформирования уравнений при изменении параметров цепи практически все вычисления (или значительная их часть) должны быть повторены, что приводит к неоправданно большим вычислительным затратам. Эти методы не обеспечивают выполнение эффективного анализа влияния изменений в цепи на ее свойства и формирование частично символьных функций.

Поэтому первой из основных задач диссертации является разработка нового подхода к формированию уравнений состояния, который бы обеспечивал достижение следующих целей:

• сокращение вычислительных затрат на переформирование уравнений;
• упрощение процедуры выявления существенных изменений в цепи, которые приводят к изменению структуры уравнений состояния;
• сокращение вычислительных затрат на формирование частично символьных функций.

С целью иллюстрации возможности приложения предложенного общего подхода к решению частной, но важной в теории цепей проблемы ставится также задача разработки эффективных алгоритмов анализа линейных электрических цепей в режимах постоянного и переменного тока с изменяющимися параметрами элементов.

В электрических цепях характеры переходных процессов, определяемых уравнениями состояния, могут существенно изменяться во времени, что существенно затрудняет анализ. Это изменение особенно характерно для электрических цепей с изменяющимися параметрами. Однако до настоящего времени фактически не была сформирована теоретическая основа для оценки изменения характера переходного процесса, так как не существовал критерий, позволяющий однозначно количественно оценивать это изменение.

В соответствии с этим второй основной задачей диссертации является разработка нового подхода к оценке изменения характера переходного процесса, который бы обеспечивал достижение следующих целей:

• возможность количественной оценки изменения характера переходного процесса;
• выявление областей в пространстве состояний, отличающихся динамикой переходных процессов;
• обеспечение устойчивости численных методов решения уравнений состояния на основе количественной оценки изменения характера переходного процесса.

Результаты выполненного анализа представлены на рис. 2.

Второй раздел посвящен разработке новой алгоритмической основы методов формирования уравнений состояния и разработке на этой основе новых методов анализа линейных электрических цепей с изменяющимися параметрами элементов.

Задача формирования и переформирования уравнений состояния на основе базовой системы уравнений, составленной, например, на основе 1-го и 2-го законов Кирхгофа, для линейной электрической цепи аналогична задаче первоначального и повторного решения СЛАУ вида

, (5)

где А – квадратная действительная невырожденная матрица; Х – матрица неизвестных; В – матрица правой части.

Обратимся к системе (5), считая для упрощения изложения, что матрица В состоит из одного столбца b и матрица Х состоит из одного столбца х. Пусть - порядок матрицы А. Обозначим i-ый столбец А через , . Будем учитывать, что, в общем случае, не все неизвестные , , системы (5) подлежат определению, что особенно характерно для задачи формирования уравнений состояния электрической цепи, т.к. переменными состояния являются не все токи и напряжения. Называем неизвестное искомым, если оно должно быть определено и неискомым в противном случае. Предложена следующая модификация метода исключения Гаусса.

Пусть F – квадратная матрица порядка n, подвергающаяся определенным ниже преобразованиям; , - i-ая строка F; , , - соответственно F и f после m-го преобразования; Е – единичная матрица порядка n. Предположим, что

, (6)

(в противном случае для продолжения вычислений достаточно выполнить перестановку

двух строк ). Для каждого фиксированного значения m выполняем указанные ниже преобразования всех строк матрицы F, а затем переходим к следующему значению m.

Модификация применительно к первоначальному решению СЛАУ описывается выражениями

;

для при , а также для при и одновременно при условии, что - неискомое;

(7)

для остальных i (то есть для при и одновременно при условии, что - искомое, а также для , при );

,

причем предполагается, что - искомое.

Назовем обработкой столбца совокупность операций по изменению F, выполняемых в соответствии с (7) при использовании ; назовем ведущей строкой для столбца строку , , которая использовалась (при ) для изменения других строк матрицы F при обращении к .

Пусть - искомое неизвестное. Назовем образующей строкой для столбца строку .

Получены выражения для оценки верхней и нижней границы вычислительных затрат, необходимых для формирования матрицы .

Минимальное число операций умножения и деления, необходимых для получения матрицы , соответствует случаю наличия одного искомого неизвестного и определяется равенством

. (8)

Максимальное число указанных операций соответствует случаю, когда все неизвестные являются искомыми и определяется равенством

. (9)

Обратимся к повторному решению СЛАУ. Доказано следующее предложение. Пусть для невырожденной матрицы в соответствии с (7) сформирована матрица (верхний индекс для упрощения обозначений не используем), и затем столбец из , такой, что - искомая величина, заменен на столбец , в результате чего матрица преобразована в матрицу . Пусть - строка матрицы , являющаяся ведущей для столбца . При этих условиях равенство имеет место тогда и только тогда, когда - вырожденная.

Пусть для сформирована матрица и затем столбец , соответствующий искомому неизвестному , заменен на столбец , в результате чего преобразована в , причем . Пусть - образующая строка для . Предполагаем, что имеется другое, кроме , искомое неизвестное и - образующая строка для . Исходя из приведенного выше предложения имеем

. (10)

Преобразуем строку в строку :

. (11)

Вычислим новое значение искомого неизвестного :

. (12)

Преобразуем строку в строку в соответствии с выражением

. (13)

Вычислим новое значение искомого неизвестного :

. (14)

Умножим (13) на столбец , получим

. (15)

Обозначим через число искомых неизвестных, а через – число операций умножения и деления, требующихся для вычисления новых значений неизвестных. Тогда при использовании выражения (12) (без непосредственного вычисления строки ) и выражения (15)

. (16)

При непосредственном использовании выражений (11) и (13) с целью преобразования строк матрицы , соответствующих искомым неизвестным, с последующим применением выражений (12) и (15)

. (17)

Пусть изменились несколько столбцов матрицы . Обозначим через число изменённых столбцов, тогда число операций умножения и деления, необходимых для преобразования строк матрицы , определяется выражением

. (18)

Из анализа выражений (16) – (18) следует вывод, что модификация обеспечивает резкое сокращение вычислительных затрат на повторное решение, причём они сокращаются прямо пропорционально числу и числу .

Показано, что при малом числе искомых неизвестных по сравнению с общим числом неизвестных предложенная модификация имеет преимущества перед формулой Шермана-Моррисона по вычислительным затратам.

Преимущества предложенной модификации по сравнению с другими методами особенно наглядно проявляются при решении задачи расчёта передаточных функций линейных электрических цепей. Пусть осуществляется расчёт частотных характеристик цепи в режиме переменного тока с многовариантным анализом (режим stepping программных систем схемотехнического моделирования) с изменением параметра одного элемента, расположенного на выходе цепи и при формировании СЛАУ непосредственно по законам Кирхгофа. После очередного изменения частоты матрица СЛАУ в общем случае радикально изменяется, что требует выполнения её первоначального решения. Затем многократно выполняется повторное решение СЛАУ. В рассматриваемом случае изменяется один столбец матрицы и , т.к. искомой является одна величина – комплекс напряжения на выходе цепи. В соответствии с выражением (16) для каждого повторного анализа требуется всего умножений. При таких многократных расчётах погрешность не накапливается. Преимущество модификации сохраняется и при расположении элемента с варьируемым параметром в любой части цепи (тогда , т.к. нужно использовать два выражения – (12) и (15)), а также при использовании метода узловых напряжений. Применение выражений (11) и (13) обеспечивает формирование частично символьных функций с очень малыми вычислительными затратами (подробнее этот вопрос рассмотрен на примере формирования уравнений состояния).

Важным преимуществом предложенной модификации является то, что она обеспечивает простое выявление таких параметров элементов цепи, которые приводят к вырождению матрицы, т.е. соответствуют цепи, в которой токи и напряжения не могут быть определены однозначно. Для этого достаточно выполнить проверку условия (10). Таким образом, для выявления принципиального изменения свойств цепи, состоящего в том, что электрический режим становится не определенным однозначно, достаточно выполнить одно скалярное умножение векторов. Вычисления особенно упрощаются при учёте разреженности матрицы . При этом может потребоваться только несколько (иногда два) умножений чисел.

Третий раздел посвящен разработке адаптивного метода формирования уравнений состояния.

Он основывается на применении описанной выше алгоритмической основы и предложенной автором системы уравнений особой формы, непосредственно используемой при формировании уравнений состояния. Эта система названа промежуточной. Такая промежуточная система формируется на основе еще одной системы уравнений, называемой базовой. В качестве базовой могут применяться различные системы, в частности система, сформированная по широко известной методике на основе 1-го и 2-го законов Кирхгофа для электрических цепей и компонентных уравнений и описываемая ниже. Предполагается, что в каждой ветви цепи расположен один элемент.

Пусть безреактивные элементы цепи описываются выражением

, (19)

где - действительная квадратная матрица порядка ; - столбец, первые элементов которого являются токами, а остальные элементов – напряжениями; - столбец, первые элементов которого являются напряжениями, а остальные элементов – токами, причем в столбцах и нет одинаковых элементов; - столбец, первые элементов которого являются независимыми токами, а остальные элементов – независимыми напряжениями.

Пусть для конденсаторов применимо выражение

, (20)

где - действительная квадратная матрица емкостей; - столбец токов конденсаторов; - столбец напряжений конденсаторов.

Пусть индуктивные элементы цепи описываются выражением:

, (21)

где - действительная квадратная матрица индуктивностей; - столбец напряжений катушек индуктивности; - столбец токов катушек индуктивности.

Пусть и - соответственно редуцированная матрица инциденций и матрица независимых контуров. Представим матрицы и в виде блочных матриц: , . Принимаем следующие условия: подматрицы и соответствуют ветвям цепи, элементы которых описаны первыми уравнениями системы (19); подматрицы и соответствуют ветвям цепи, элементы которых описаны последними уравнениями системы (19); подматрицы и соответствуют ветвям цепи, в которых расположены конденсаторы; подматрицы и соответствуют ветвям цепи, в которых расположены катушки индуктивности.

Из подматриц матриц и составим блочные матрицы:

; ; ; .

Используем обозначение: .

Составим блочные матрицы:, .

Составим столбцы , и :

; ; , .

В итоге получаем базовую систему уравнений:

. (22)

Предложен следующий метод формирования промежуточной системы. Продифференцируем систему (22) раз, получим системы

; ; … ; . (23)

Системы (22) и (23) составляют промежуточную систему уравнений

. (24)

Предложено располагать подматрицы матрицы и части столбца таким образом, чтобы обеспечить регулярную структуру, показанную на рис. 3 ().

Промежуточная система позволяет (при достаточно большом ) сформировать уравнения состояния для каждой цепи, которая может быть описана этими уравнениями, поэтому она названа полной.

Так как до завершения формирования уравнений состояния число в системе (3), (4) неизвестно вне зависимости от используемого метода формирования, предложен алгоритм формирования уравнений состояния, при котором вначале анализируется подсистема , а затем, в случае необходимости, к ней добавляется подсистема и анализируются совместно две указанные подсистемы и так далее, то есть система (24) анализируется по подсистемам, выделенным на рис. 3 скобками. Характерной особенностью матрицы является повторение в ней подматриц , и . Поэтому при любом достаточно хранить только эти подматрицы.

Изложим порядок первоначального формирования системы уравнений для переменных состояния, имеющей вид

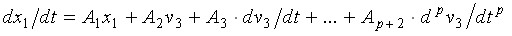, (25)

где - вещественные матрицы; - столбец переменных состояния, полученный из столбца исключением тех его элементов, которые являются зависимыми величинами.

Алгоритм формирования уравнений состояния в основной своей части состоит в преобразовании дополнительной матрицы. При практических вычислениях может потребоваться переиндексация (или перестановка) строк такой матрицы. С целью упрощения изложения предполагаем, что это не требуется.

Предполагаем, что справедливы два указанных ниже допущения. Их выполнение является необходимым и достаточным условием для того, чтобы соответствующая цепь могла быть описана уравнениями состояния.

Обратимся к подсистеме уравнений 1 (рис. 3). Начнем формирование дополнительной квадратной матрицы порядка ( - число уравнений подсистемы 1). Вначале обработаем столбцы подматрицы (входящей, в свою очередь, в подматрицу ).

Принимаем первое допущение: для каждого столбца подматрицы в матрице будет найдена ведущая строка.

После завершения обработки всех столбцов подматрицы продолжим преобразование матрицы , перейдя к обработке столбцов подматрицы матрицы . Величины, соответствующие этим столбцам, то есть элементы столбца , считаем искомыми.

Может оказаться, что для некоторого столбца подматрицы не найдена ведущая строка, то есть среди строк матрицы , не ставших ведущими для ранее обработанных столбцов подматриц и , нет строки, не ортогональной к столбцу . В таких случаях без преобразования матрицы переходим к обработке следующего столбца подматрицы . Строки матрицы , не ставшие ведущими ни для одного столбца подматриц и , назовем свободными. Если для каждого столбца подматрицы найдена ведущая строка, то преобразуем ведущие строки в образующие, а затем, умножая их на столбцы подматриц и , вычислим элементы матриц и уравнения для переменных состояния (25).

Если существуют свободные строки матрицы , то, используя их, приступим к обработке столбцов подматрицы , считая соответствующие элементы столбца искомыми величинами.

Принимаем второе допущение: для каждой свободной строки матрицы найдется столбец подматрицы , для которого строка станет ведущей.

Если для некоторого столбца подматрицы нет ведущей строки, то переходим к обработке следующего столбца подматрицы без преобразования матрицы . В соответствии со вторым допущением для каждой свободной строки соответствующий столбец будет найден.

Пусть для некоторого столбца подматрицы определена ведущая строка. Пусть столбец соответствует элементу столбца . Тогда переменная является зависимой переменной состояния.

После того, как для каждой свободной строки будет найден столбец подматрицы , для которого является ведущей, преобразования непосредственно матрицы заканчиваются.

Выделим в матрице две подматрицы: и . В подматрицу включим те строки матрицы , которые являются ведущими для столбцов подматрицы , а в подматрицу - те строки, которые являются ведущими для столбцов подматрицы , то есть свободные строки.

Назовем удлинением строки увеличение числа элементов этой строки добавлением справа нулевых элементов. Назовем сдвигом строки увеличение числа элементов этой строки добавлением слева нулевых элементов.

Используя удлинение строк подматрицы и сдвиг строк подматрицы , сформируем матрицу . Матрицу будем использовать для анализа подсистемы 2 промежуточной системы уравнений.

Обозначим матрицу подсистемы 2 через , а столбец переменных – через . Подсистема 2 задает взаимно однозначное соответствие между столбцами матрицы и элементами столбца . Учитывая это, разделим столбцы матрицы на группы. В одну группу включим столбцы матрицы , соответствующие столбцу , в другую – соответствующие столбцу и так далее. В соответствии с этим для краткости изложения будем говорить о столбцах матрицы группы , группы и так далее.

Преобразование матрицы выполняется аналогично описанному преобразованию матрицы .

В дальнейшем, при необходимости, циклы преобразований повторяются. При этом от подсистемы 2 переходим к подсистеме 3 и так далее.

Опишем формирование уравнений для переменных состояния в виде следующего алгоритма, который обозначим через .

1. Формируем единичную матрицу, порядок которой равен числу уравнений базовой системы уравнений.

2. Обрабатываем столбцы группы . Элементы столбца считаем неискомыми.

3. Обрабатываем столбцы группы . Элементы столбца считаем искомыми.

4. Проверяем наличие свободных строк. Если свободных строк нет, то переходим к п.8, иначе переходим к п.5.

5. Обрабатываем столбцы группы и выявляем зависимые переменные состояния. Элементы столбца считаем искомыми.

6. Проверяем наличие независимых переменных состояния. Если независимых переменных состояния нет, то переходим к п.9, иначе переходим к п.7.

7. Выполняем удлинение и сдвиг строк. Переходим к п.3.

8. Формируем образующие строки для столбцов группы , соответствующих производным независимых переменных состояния. Формируем матрицы уравнения для переменных состояния.

9. Конец преобразований.

Выходные уравнения формируются аналогично.

Вычислительные затраты на первоначальное формирование уравнений состояния по предложенному методу несколько превышают затраты при использовании известных методов – примерно на 30 процентов в типичных случаях. Но это многократно компенсируется резким сокращением вычислительных затрат на повторное формирование. Выигрыш возникает уже при одном переформировании.

Четвертый раздел посвящен определению критерия для анализа изменений в электрических цепях с изменяющимися параметрами и разработке метода коррекции математических моделей в форме уравнений состояния.

Предполагаем, что изменению параметра элемента электрической цепи соответствует изменение одного столбца базовой системы (22) (если изменяется большее число столбцов, то преобразования выполняем аналогично при последовательном обращении к таким столбцам).

Предложенная алгоритмическая основа обеспечивает строгое разделение различных изменений в цепи на два существенно отличающихся класса. К первому классу отнесены названные неосновательными изменения в цепи, в результате которых не изменяется столбец независимых переменных состояния , величина , а также вид по крайней мере того скалярного уравнения из уравнений состояния (3), (4), которое определяет элемент столбца или , соответствующий измененному столбцу промежуточной системы уравнений (24). При этом имеется ввиду, что некоторый коэффициент указанного скалярного уравнения останется ненулевым, если он был ненулевым до изменения в цепи, и останется нулевым, если он был таким до изменения. В этом смысле к неосновательным отнесены те изменения в цепи, которые не приводят к качественному изменению ее свойств. Ко второму классу отнесены остальные изменения в цепи, названные основательными. Хорошая приспособленность предложенного подхода к проблеме классификации изменений в цепи объясняется, во-первых, применением полной системы уравнений и, во-вторых, использованием строк дополнительной матрицы, каждая из которых неортогональна только к одному столбцу матрицы промежуточной системы уравнений из всех столбцов, соответствующих неизвестным величинам. Такая строка формируется при обработке всех указанных столбцов и поэтому содержит достаточно полную информацию об анализируемой цепи.

Пусть с использованием подсистемы промежуточной системы получена матрица , ведущие строки для соответствующих столбцов преобразованы в образующие и сформированы матрицы уравнений состояния. Обозначим через i-ый элемент столбца промежуточной системы . Пусть является элементом или столбца , входящего в столбец , или столбца .

Сделаем следующие обозначения: пусть - столбцы матрицы , соответствующие величинам , ; - строка матрицы , являющаяся образующей для столбца ; - общее число используемых образующих строк; - используемые образующие строки.

Пусть в цепи произошло изменение, в результате которого столбцы заменены на столбцы соответственно . Обозначим через матрицу после изменения столбцов. Дадим определение.

Пусть

; (26)

при , .

Изменение в цепи, удовлетворяющее условию (26), будем называть неосновательным, а другое – основательным.

Обозначим через матрицу после описываемого ниже изменения, а через , - строки матрицы .

Выполним в соответствии с (11) и (13) преобразования:

, (27)

(28)

при , .

Получаем

, (29)

(30)

при , .

Обозначим через столбец матрицы , для которого строка является образующей, . Таким образом, при и при , .

Поэтому получаем

(31)

при , .

Матрица , полученная после выполнения преобразований (27) и (28), состоит, в соответствии с (29) – (31), из образующих строк и может быть использована для повторного вычисления элементов матриц уравнений состояния.

Показано, что предложенный подход обеспечивает настолько малые вычислительные затраты на переформирование уравнений состояния, что в случае, когда число таких переформирований не особенно велико, этими затратами можно пренебречь по сравнению с затратами на первоначальное формирование.

В случае определенных основательных изменений в цепи повторное формирование уравнений состояния также может быть выполнено со значительно меньшими, в сравнении с первоначальным формированием, вычислительными затратами.

Пятый раздел посвящен разработке методов формирования уравнений состояния специального типа, а также частично символьных функций электрических цепей.

Предложено дополнять промежуточную систему уравнений подсистемами, получаемыми из базовой как её дифференцированием, так и интегрированием. Такое дополнение обеспечивает формирование уравнений, расширяющих возможности по анализу электрических цепей, в частности, при расчёте установившихся режимов.

Проинтегрируем базовую систему уравнений (22) раз, получим системы

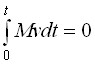, . (32)

Обозначая через значение столбца при , получаем

.

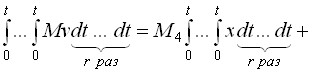
Базовая система и системы (33) составляют промежуточную систему уравнений

. (33)

Объединим эту систему с системой (24). Получим систему

. (34)

Использование системы (33) и алгоритма, аналогичного алгоритму А1, обеспечивает формирование уравнений вида

,

,

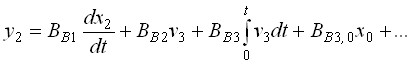
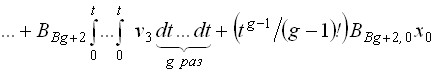где , , …, ; , …, ; , , …, ; , …, – действительные матрицы; – столбец переменных состояния, полученный из столбца х исключением зависимых переменных (здесь зависимыми называются те переменные, производные которых вошли в столбец выходных величин ). Эти уравнения могут использоваться, например, для расчета режимов при заданных производных переменных состояния. Предложены алгоритмы, основанные на использовании объединённой промежуточной системы (34).

Показано, что предложенный подход к формированию уравнений состояния эффективен при формировании частично символьных функций электрических цепей.

Для конкретизации предположим, что при формировании полной системы используется только дифференцирование базовой системы раз. Пусть необходимо получить выражения для некоторых переменных (токов, напряжений, производных переменных состояния) с символьным представлением параметра элемента цепи. В качестве примера рассмотрим сопротивление некоторого резистора. Предположим, что для конкретных численных значений параметров всех элементов, включая сопротивление , сформирована промежуточная система уравнений (24). Пусть для столбцов матрицы , соответствующих указанным переменным, включая ток рассматриваемого резистора, сформированы образующие строки , 1, 2,…,. Обозначим через образующую строку для столбца матрицы промежуточной системы, соответствующего току . Тогда .

Выполним замену столбца , имеющего численные элементы, на столбец , в котором сопротивление будет фигурировать в виде символа. Тогда столбцы , ,…, с численными элементами, соответствующие переменным , ,…, , заменяются на столбцы , ,…, с символьным представлением сопротивления .

Умножая строки , 1, 2,…, на столбец , сформируем частично символьные функции:

, 1, 2,…,.

Предполагаем, что для всех используемых значений сопротивления выполняется условие, соответствующее неосновательным изменениям:

; , 1, 2,…,, 1, 2,…,.

Основываясь на выражениях (11) и (13), сформируем строки , 1, 2,…, с символьным представлением сопротивления :

, (37)

, 1, 2,…,, . (38)

Тогда

; , , 1, 2,…,, ,

где - столбец матрицы , для которого строка является образующей.

Пусть в качестве заданных используются величины , 1, 2, …, (в качестве примера можно назвать напряжение независимого источника напряжения). Обозначим через , 1,2,…, соответствующие этим величинам столбцы матрицы . Предположим, что необходимо получить частично символьную функцию для тока указанного резистора. Тогда

. (39)

Аналогично формируются частично символьные функции для остальных переменных, соответствующих образующим строкам , 1, 2,…,, .

Использование выражений (37) – (39) для формирования частично символьных функций не требует применения дополнительных алгоритмов (основанных, например, на использовании сигнальных графов). Это обеспечивает сокращение вычислительных затрат в сравнении с известными способами формирования таких функций.

Шестой раздел посвящен разработке нового подхода к анализу переходных процессов в электрических цепях, а также нового метода выявления областей в пространстве переменных состояния, отличающихся динамикой переходных процессов, и нового метода обеспечения устойчивости численных алгоритмов расчёта переходных процессов.

В качестве основы для исследования явления изменения характера переходного процесса и разработки практически применимых алгоритмов введено понятие изменчивости частного решения системы ОДУ (и изменчивости соответствующей интегральной кривой).

Пусть электрическая цепь описывается уравнением (1) с числом переменных состояния . Пусть начальным условиям соответствует частное решение .

В наиболее общей форме изменчивость определена как отличие частного решения на следующем отрезке времени от этого же решения на предыдущем отрезке. Понятие изменчивости можно наполнить конкретным смыслом различными способами.

Рассмотрим способ количественной оценки изменчивости, основанный на сравнении столбцов х, соответствующих трем точкам интегральной кривой.

Обратимся к интегральной кривой, проходящей через некоторую точку с координатами . Пусть h – шаг по оси времени, , , - столбцы переменных состояния, соответствующие моментам времени и .

Таким образом, рассматривается некоторый участок интегральной кривой, имеющий начальную точку с координатами , среднюю точку с координатами и конечную точку с координатами . Дадим соответствующую графическую иллюстрацию для (рис. 4).

Сделаем обозначения:

, , . (40)

Столбец сс характеризует изменчивость интегральной кривой (и изменчивость соответствующего частного решения) на участке от точки с координатами до точки с координатами и назван столбцом изменчивости.

Численно изменчивость измеряется евклидовой нормой столбца сс, которая названа скаляром изменчивости и обозначена через cs. Таким образом,

. (41)

Величина cs, естественно, зависит от значения шага h, который может изменяться в очень широких пределах.

Область пространства решений, в которой изменчивость интегральных кривых изменяется медленно, названа областью стабилизации. Область стабилизации, в которой переменные состояния изменяются медленно, названа областью успокоения.

По мере развития переходного процесса, описываемого системой (1), интегральные кривые, расположенные в области стабилизации (успокоения), по истечении достаточного времени могут значительно уменьшить свою изменчивость уже по сравнению с той, которую они имели при входе в эту область стабилизации. Тогда будем говорить об области стабилизации следующего порядка: второго, третьего и так далее (рис.5). Через обозначены конкретные моменты времени, а через - точки в пространстве решений, для которых изображены проходящие через них интегральные кривые. Моменту времени соответствуют точки .

Использование понятия изменчивости позволяет целенаправленно выполнять коррекцию переменных состояния для перемещения точки в область стабилизации того или иного порядка, например, из точки в точку или в точку .

Предложено осуществлять коррекцию для выявления областей в пространстве переменных состояния, отличающихся динамикой переходных процессов, с целью всестороннего анализа динамических свойств электрических цепей. Предложено также выполнять коррекцию с целью обеспечения устойчивости численных методов расчёта переходных процессов в электрических цепях. При этом используется малая, в смысле нормы, коррекция переменных состояния, находящаяся в пределах допустимой погрешности. Перевод точки в соответствующую область стабилизации обеспечивает сохранение устойчивости метода расчёта при многократном увеличении шага интегрирования.

Оценка изменчивости интегральных кривых выполняется на основе линеаризации системы (1). Сделаем обозначения: , . Запишем линеаризованную систему в виде

Рис.5. Области стабилизации (успокоения)

, (42)

где А – матрица, элементы которой определяются следующим образом: при .

Сделаем обозначения: , , , , . В соответствие с (40) , ,

. (43)

На основе разложения матричной экспоненциальной функции и соответствующего интеграла в ряд и соотношения (43) получено выражение для столбца изменчивости (т.к. столбец сс зависит от столбца , использовано обозначение ):

, (44)

где .

Используя для скаляра изменчивости обозначение , получаем в соответствии с (41) и (44)

(45)

.

Показано, что

, (46)

где , .

Полученные результаты позволяют использовать для коррекции переменных состояния с целью уменьшения изменчивости метод наискорейшего спуска, рассматривая как целевую функцию. Пусть исходным является столбец () и выполняется минимизация по направлению . Обозначим через значение столбца , при котором достигается минимальное значение по этому направлению. Показано, что

. (47)

Таким образом, минимизация по направлению сведена к однократному использованию формулы (47). Это резко упрощает коррекцию переменных состояния с целью перехода в область стабилизации.

Показано, что количественная оценка изменчивости может производиться и при использовании производных и интегралов от столбца сс по шагу h. При этом математические выражения остаются подобными приведенным выше.

Для управления коррекцией переменных состояния с целью выявления областей стабилизации различного порядка предложено использовать смещение точек на интегральной кривой, соответствующих моментам времени , и (рис. 6).

На рис.6 изображена некоторая интегральная кривая, соответствующая элементу столбца . Точка с координатами является базовой (исходной). Остальные три точки смещаются вправо (как на рисунке) при или влево при .

При наличии смещения столбец изменчивости, зависящий от и ch, обозначаем через , причем формально определяем его так же, как и при отсутствии смещения: . Показано, что

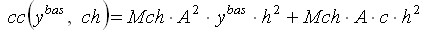, (48)

где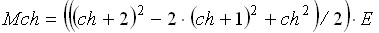

Если для вычисления матрицы Mch непосредственно применять приведенный выше матричный ряд, то малая погрешность при использовании небольшого (в единицы) числа слагаемых возможна только при малых значениях шага h. Показано, что для решения этой проблемы может быть применен известный эффективный алгоритм вычисления матричной экспоненты и интеграла от нее, основанный на последовательном удвоении отрезков времени. Показано, что при tbas=0

Mch·A2·h2= eA·ch·h – 2· e A·(ch+1)·h + e A·(ch+2)·h, (49)

Mch·A·h2·c=. (50)

На основе выражений (49) и (50) предложен алгоритм, реализующий идею удвоения при вычислении матрицы Mch·A2·h2 и столбца Mch·A·h2·c.

Предложенный подход существенно расширяет возможности по анализу переходных процессов и обеспечивает сокращение вычислительных затрат за счёт увеличения шага интегрирования.

Седьмой раздел посвящен применению предложенных методов и алгоритмов для анализа электрических цепей, моделирующих конкретные электротехнические устройства.

Для транзисторного преобразователя постоянного напряжения (рис.7), предназначенного для применения на автотранспорте, описан процесс формирования и переформирования уравнений состояния, а также выполнен расчёт переходных процессов явным методом Рунге-Кутта 4-го порядка. Показано, что несмотря на большую жёсткость уравнений состояния использование предложенного метода обеспечивает многократное увеличение шага интегрирования при сохранении устойчивости.

Выполнен анализ переходных процессов в тяговом двигателе (ТД) постоянного тока электровоза при использовании схемы замещения (рис.8).

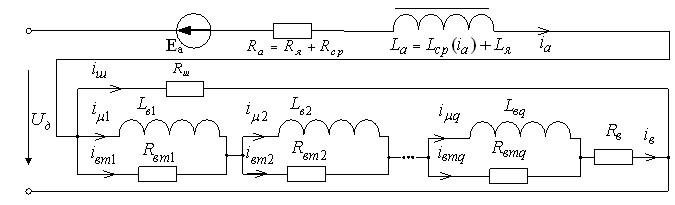
Рис. 8. Схема замещения тягового двигателя

ЭДС якоря определяется выражением

где – электромеханическая постоянная ТД,

– угловая скорость вращения якоря,

– магнитный поток системы возбуждения,

– ток первой секции обмотки возбуждения.

Переходные процессы в схеме замещения описываются следующей системой ОДУ:

…

где ,, – токи, соответственно, цепи якоря, шунтирующего резистора и цепи возбуждения; , k = 1,2…, q – токи секций обмотки возбуждения; – напряжение, приложенное к двигателю; – индуктивность слаживающего реактора; – индуктивность обмотки якоря; ,,– сопротивления, соответственно, обмоток якоря, возбуждения и слаживающего реактора; – суммарное сопротивление в цепи якоря, ; ,,..., – индуктивности секций обмотки возбуждения; , ,…, – сопротивления эквивалентных контуров вихревых токов обмотки возбуждения. Через обозначены токи контуров вихревых токов, а через обозначена суммарная индуктивность в цепи якоря, .

Магнитный поток системы возбуждения является нелинейной функцией тока .

Общая индуктивность обмотки возбуждения определяется выражением

,

где – число пар полюсов; – число витков обмотки возбуждения.

Сформированные уравнения состояния оказались жёсткими. Показано, что применение предложенного подхода позволяет многократно увеличивать шаг интегрирования явного метода после выхода из пограничного слоя, что резко сокращает вычислительные затраты. Также показано, что применение понятия изменчивости даёт возможность выявлять область стабилизации без решения задачи Коши.

Приведены результаты численных экспериментов по расчёту частотных характеристик с многовариантным анализом, а также по решению СЛАУ и систем ОДУ. Показано, что использование предложенных методов приводит к существенному сокращению вычислительных затрат.

В заключении сформулированы основные результаты и выводы из проведённых исследований.

В приложениях приведены результаты теоретических исследований, посвященных отдельным специфическим вопросам в рамках темы диссертации, а также документы о внедрении разработанных методов и алгоритмов во Всероссийском научно-исследовательском и проектно-конструкторском институте электровозостроения «ОАО ВЭлНИИ», в Южно-Российском государственном техническом университете (Новочеркасском политехническом институте), в Техническом университете Ильменау, Федеративная Республика Германия.

ОСНОВНЫЕ РЕЗУЛЬТАТЫ И ВЫВОДЫ

Разработаны новые подходы к решению актуальной проблемы формирования и коррекции математических моделей электрических цепей с изменяющимися параметрами в форме уравнений состояния, а также к решению проблемы анализа динамических режимов электрических цепей. Получены следующие основные результаты.

1. Разработана используемая в качестве алгоритмической основы модификация метода исключения Гаусса для решения СЛАУ, которая является методологической базой для построения методов анализа линейных электрических цепей с изменяющимися параметрами в режимах постоянного и переменного тока, а также формирования и коррекции уравнений состояния.

2. Предложены новые математические модели электрических цепей с изменяющимися параметрами, адаптированные к проблеме формирования и коррекции уравнений состояния.

3. Предложен новый метод первоначального формирования уравнений состояния электрических цепей, учитывающий возможное изменение параметров элементов.

4. Предложен новый метод коррекции математических моделей в форме уравнений состояния при локальных параметрических изменениях в цепи.

5. Предложен новый метод формирования частично символьных функций электрических цепей с изменяющимися параметрами.

6. Предложен новый метод выявления различных областей в пространстве состояний, отличающихся динамикой переходных процессов, протекающих в электрических цепях.

7. Предложен новый метод исследования переходных процессов в электрических цепях, отличающийся использованием количественной оценки изменения характера этих процессов.

8. Предложен новый метод обеспечения устойчивости численных методов расчёта переходных процессов в электрических цепях.

9. Разработанные теория и методы внедрены в организациях, выполняющих анализ и синтез электрических цепей: во Всероссийском научно-исследовательском и проектно-конструкторском институте электровозостроения «ОАО ВЭлНИИ», в Южно-Российском государственном техническом университете (Новочеркасском политехническом институте), в Техническом университете Ильменау, Федеративная Республика Германия.

ОСНОВНЫЕ ПОЛОЖЕНИЯ ДИССЕРТАЦИИ ОПУБЛИКОВАНЫ В

СЛЕДУЮЩИХ РАБОТАХ:

1*. Савёлов, Н.С. Расчет переходных процессов в предварительно упорядоченных электрических цепях / Савёлов Н.С. // Изв. высш. учеб. заведений. Электромеханика. – 1985. – № 4. – С. 85 – 92.

2*. Савёлов, Н.С Новый подход к формированию уравнений состояния электронных схем / Савёлов Н.С. // Изв. высш. учеб. заведений. Электромеханика. – 1986. – № 9. – С. 72 – 74.

3. Савёлов, Н.С. Формирование уравнений состояния при изменениях в электрических цепях / Савёлов Н.С. // I Всесоюзная конф. по теорет. электротехнике, 15 – 17 сентября 1987г. Секция 3. Теория цепей. Секция 4. Расчет интегральных электромагнитных параметров: Тез. докл. – Ташкент, 1987. – С. 93 – 94.

4*. Савёлов, Н.С. Формирование уравнений состояния при изменениях в электрических цепях / Савёлов Н.С. // Изв. высш. учеб. заведений. Электромеханика. – 1987. – № 12. – С. 13 – 18.

5*. Савёлов, Н.С. Усовершенствование явных методов с целью решения жестких систем дифференциальных уравнений электрических цепей / Савёлов Н.С. // Изв. высш. учеб. заведений. Электромеханика. – 1989. – № 9. – С. 14 – 20.

6. Савёлов, Н.С. Способ увеличения шага при решении жестких уравнений состояния электрических цепей явными методами. / Савёлов Н.С. // Теория цепей и сигналов (ТЦ и С – 96): Тез. докл. Третьей Всерос. науч.-техн. конф. с междунар. участием, Россия, Таганрог, 11 – 15 сент. 1996г. – Новочеркасск: / Ред. журн. «Изв. вузов. Электромеханика», 1996. – С. 81.

7*. Савёлов, Н.С. Алгоритм для повторного анализа электронных схем. / Савёлов Н.С. // Изв. вузов. Сев.-Кавк. регион. Техн. науки. – 2003. – Спецвып.: Математическое моделирование и компьютерные технологии. – С. 21 – 23.

8*. Савёлов, Н.С. Формирование уравнений состояния устройств мехатроники на основе полных исходных математических моделей. / Савёлов Н.С. // Изв. вузов. Сев.-Кавк. регион. Техн. науки. – 2003. – Спецвып.: Проблемы мехатроники – 2003: материалы междунар. науч.-практ. коллоквиума, г. Новочеркасск, 15 – 20 сент. 2003г. – С. 121 – 123.

9*. Савёлов, Н.С. Классификация изменений в эквивалентных схемах электротехнических устройств и ускоренное переформирование математических моделей. / Савёлов Н.С. // Изв. вузов. Сев.-Кавк. регион. Техн. науки. – 2003. – Спецвып.: Проблемы мехатроники – 2003: материалы Междунар науч.-практ. коллоквиума, г. Новочеркасск, 15 – 20 сент. 2003г. – С. 123 – 124.

10. Савёлов, Н.С. Коррекция переменных состояния при анализе объектов, описываемых жесткими системами дифференциальных уравнений / Савёлов Н.С. // Микропроцессорные, аналоговые, цифровые и электромеханические устройства и системы: материалы Междунар. науч-практ. конф., г. Новочеркасск, 17 окт. 2006г. / Юж.-Рос. гос. техн. ун-т (НПИ). – Новочеркасск: ООО НПО «Темп», 2006. – С. 29 – 31.

11. Савёлов, Н.С. Критерии и алгоритмы для изменения переменных состояния динамического объекта с целью выхода из пограничного слоя / Савёлов Н.С. // Компьютерные технологии в науке, производстве, социальных и экономических процессах: материалы VII Междунар. науч.-практ. конф., г.Новочеркасск, 17 нояб. 2006г.: В 3 ч. / Юж.-Рос. гос. техн. ун-т (НПИ). – Новочеркасск: ООО НПО «Темп», 2006. – Ч.1. – С. 52 – 54.

12. Савёлов, Н.С. Алгоритм вычисления скорректированных значений переменных состояния динамических объектов / Савёлов Н.С. // Моделирование. Теория, методы и средства: Материалы VII Междунар. науч.-практ. конф., г. Новочеркасск, 6 апр. 2007 г.: В 3 ч./Юж.-Рос. гос. техн. ун-т (НПИ). – Новочеркасск: ЮРГТУ, 2007. – Ч.1. – С. 22 – 24.

13. Савёлов, Н.С. Вычисление скорректированных значений переменных состояния, характеризующих динамический процесс / Савёлов Н.С. // Теория, методы и средства измерений, контроля и диагностики: Материалы VIII Междунар. науч.-практ. конф., г. Новочеркасск, 28 сент. 2007 г. / Юж.-Рос. гос. техн. ун-т (НПИ). – Новочеркасск: ЮРГТУ, 2007. – С. 79 – 80.

14. Савёлов, Н.С. Выявление соотношений переменных состояния динамического объекта, соответствующих стабилизации режима работы / Савёлов Н.С. // Методы и алгоритмы прикладной математики в технике, медицине и экономике: Материалы VII Междунар. науч.-практ. конф., г. Новочеркасск, 2 фев. 2007 г.: В 2 ч./ Юж.-Рос. гос. техн. ун-т (НПИ). – Новочеркасск: ЮРГТУ, 2007. – Ч.1. – С. 27 – 29.

15*. Савёлов, Н.С. Исследование динамических режимов на основе количественной оценки изменчивости интегральных кривых / Савёлов Н.С. // Изв. вузов. Сев.-Кавк. регион. Техн. науки. – 2007. – Спецвыпуск. ЮРГТУ(НПИ) 1907 – 2007. – С. 63-64.

16. Савёлов, Н.С., Микропроцессорная система контроля с математическим моделированием объекта / Савёлов Н.С. Ревин М.С. // Студенческая весна – 2007: сборник научных трудов аспирантов и студентов ЮРГТУ(НПИ)/ Юж.-Рос. гос. техн. ун-т. – Новочеркасск: ЮРГТУ(НПИ), 2007. – С. 79 – 80.

17. Савёлов, Н.С. Новый метод исследования динамических объектов / Савёлов Н.С. // Современные проблемы фундаментальных и прикладных наук: Тр. 50-й науч. конф. МФТИ / Моск. физ.-техн. ин-т (гос. ун-т). – Москва – Долгопрудный, 2007. Т. 2, Ч. VII.: Управление и прикладная математика. – С.138 – 140.

18*. Савёлов, Н.С. Новый метод исследования объектов, описываемых жесткими системами дифференциальных уравнений / Савёлов Н.С. // Изв. вузов. Сев.-Кавк. регион. Техн. науки. – 2007. – № 3. – С. 19 – 23.

19. Савёлов, Н.С. Обнаружение установившихся режимов электротехнических устройств на основе коррекции переменных состояния. / Савёлов Н.С. // Современные энергетические системы и комплексы и управление ими: Материалы VII Междунар. науч.-практ. конф., г. Новочеркасск, 20 апр. 2007 г.: В 2 ч./ Юж.-Рос. гос. техн. ун-т. (НПИ). – Новочеркасск: ЮРГТУ, 2007. – Ч.2. – С. 4 – 5.

20. Савёлов, Н.С. Организация вычислений скорректированных значений переменных состояния при использовании отрицательного шага / Савёлов Н.С. // Микропроцессорные, аналоговые и цифровые системы: проектирование и схемотехника, теория и вопросы применения: Материалы VII Междунар. науч.-практ. конф., г. Новочеркасск, 10 окт. 2007. / Юж.-Рос. гос. техн. ун-т. (НПИ). – Новочеркасск: ЮРГТУ, 2007. – С. 53 – 54.

21*. Савёлов, Н.С. Полные исходные системы уравнений электронных схем и формирование частично символьных функций / Савёлов Н.С. // Изв. вузов. Электромеханика. – 2007. – № 3 – С. 3 – 6.

22. Савёлов, Н.С. Программная реализация метода ускоренного анализа электрических цепей. / Савёлов Н.С., Ревин М.С. // Труды 50-й научной конференции МФТИ «Современные проблемы фундаментальных и прикладных наук»: Тр. 50-й науч. конф. МФТИ / Моск. физ.-техн. ин-т (гос. ун-т). – Москва – Долгопрудный, 2007. Т. 2, Ч. VII.: Управление и прикладная математика. – С.137 – 138.

23*. Савёлов, Н.С. Программное обеспечение для ускоренного повторного решения систем линейных алгебраических уравнений / Проскурин С.В., Савёлов Н.С. // Изв. вузов. Сев.-Кавк. регион. Техн. науки. – 2007. – Спецвыпуск.: Проблемы мехатроники – 2006: материалы междунар. науч.-практ. коллоквиума, Г. Новочеркасск, 4 – 6 сент. 2006г. – С. 83.

24*. Савёлов, Н.С. Управление коррекцией переменных состояния динамических объектов, моделируемых жесткими дифференциальными уравнениями / Савёлов Н.С. // Изв. вузов. Сев.-Кавк. регион. Техн. науки. – 2007. – № 4. – С. 23 – 24.

25. Савёлов, Н.С. Численные эксперименты с программным обеспечением для решения систем линейных алгебраических уравнений / Савёлов Н.С., Ревин М.С. // Методы и алгоритмы прикладной математики в технике, медицине и экономике: Материалы VII Междунар. науч.-практ. конф., г. Новочеркасск, 2 фев. 2007 г.: В 2 ч./Юж.-Рос. гос. техн. ун-т (НПИ). – Новочеркасск: ЮРГТУ, 2007. – Ч.1. – С. 85 – 90.

26. Савёлов, Н.С. Автоматизированный анализ электромеханических устройств с использованием модификации метода исключения Гаусса / Савёлов Н.С. Ревин М.С. // Сборник статей и сообщений по материалам 57-й научно-технической конференции профессорско-преподавательского состава, научных работников, аспирантов и студентов университета / Юж.-Рос. гос. техн. ун-т (НПИ). – Новочеркасск: ЮРГТУ (НПИ), 2008. – С. 138 – 141.

27. Савёлов, Н.С. Алгоритмы для математического моделирования устройств мехатроники, обеспечивающие сокращение вычислительных затрат / Ревин М.С., Савёлов Н.С. // Мехатроника – 2008: материалы IV Междунар. науч. – практ. коллоквиума, 18 – 20 июня 2008г. / Юж.-Рос. гос. техн. ун-т (НПИ). – Новочеркасск: ЮРГТУ (НПИ), 2008. – С. 46 – 47.

28. Савёлов, Н.С. Новое конструктивное понятие в теории обыкновенных дифференциальных уравнений = A new constructive concept in theory of ordinary differential equations / Савёлов Н.С. // Дифференциальные уравнения и топология: тез. докл. Междунар. конф., посвящ. 100-летию со дня рождения Л.С. Понтрягина (1908 - 1988), Москва, 17 – 22 июня 2008г. / Моск. гос. ун-т им. М.В. Ломоносова; Математич. ин-т им. В.А. Стеклова РАН. –М.: 000 «МАК Пресс», 2008. – С. 182 – 183.

29. Савёлов, Н.С. Сравнительный анализ формулы Шермана–Моррисона и альтернативного метода для повторного решения систем линейных алгебраических уравнений / Савёлов Н.С., Ревин М.С. //Методы и алгоритмы прикладной математики в технике, медицине и экономике: Материалы VIII Междунар. науч.-практ. конф., 25 февр. 2008г., г. Новочеркасск / Юж.-Рос. гос. техн. ун-т (НПИ). – Новочеркасск: ЮРГТУ, 2008. – С. 12 – 15.

30*. Савёлов, Н.С. Алгоритмы для математического моделирования устройств мехатроники, обеспечивающие сокращение вычислительных затрат / Ревин М.С., Савёлов Н.С. // Изв. вузов. Сев.-Кавк. регион. Техн. науки. – 2008. – Спец. вып.: Проблемы мехатроники – 2008: материалы междунар. науч.-практ. коллоквиума, г. Новочеркасск, 18 – 20 июня 2008г. – С. 113 – 114.

31. Савёлов, Н.С. К вопросу оптимизации устройств мехатроники / Ревин М.С., Савёлов Н.С. // Теория, методы и средства измерений, контроля и диагностики: Материалы IХ Междунар. науч.-практ. конф., г. Новочеркасск, 29 сент. 2008 г. / Юж.-Рос. гос. техн. ун-т (НПИ). – Новочеркасск: ЮРГТУ, 2008. – С. 32 – 34.

32*. Савёлов, Н.С. Организация автоматического выбора значений итерационного параметра при анализе устройств мехатроники / Савёлов Н.С., Ревин М.С. // Изв. вузов. Сев.-Кавк. регион. Техн. науки. – 2009. № 1. – С. 30-31.

33. Савёлов Н.С. Использование нового конструктивного понятия в теории обыкновенных дифференциальных уравнений при решении проблемы жесткости / Савёлов Н.С., Ревин М.С. // Студенческая весна – 2009: материалы Межрегиональной научно-технической конференции студентов, аспирантов и молодых ученых Южного федерального округа / Юж.-Рос. гос. техн. ун-т. – Новочеркасск: ЮРГТУ(НПИ), 2009. – С. 202 – 203.

34*. Савёлов Н.С. Решение жёстких систем обыкновенных дифференциальных уравнений классическими явными методами с использованием понятия изменчивости / Савёлов Н.С., Ревин М.С. // Изв. вузов. Сев.-Кавк. регион. Техн. науки. – 2009. – Спец.вып.: Мехатроника. Современное состояние и тенденции развития. – С. 128 – 134.

35. Савёлов, Н.С. О решении жёстких систем обыкновенных дифференциальных уравнений классическими явными методами с использованием понятия изменчивости. / Савёлов Н.С., Ревин М.С.// Труды 52-й научной конференции МФТИ «Современные проблемы фундаментальных и прикладных наук» / Моск. физ.-техн. ин-т (гос. ун-т). – Москва – Долгопрудный, 2009. Т.3. Ч. VII.: Управление и прикладная математика. – С. 70 – 72.

36. Савёлов, Н.С. Численные эксперименты с модификацией метода исключения Гаусса / Савёлов Н.С., Фам Н.К., Лыонг С.Т. // Микропроцессорные, аналоговые и цифровые системы: проектирование и схемотехника, теория и вопросы применения: Материалы IX Междунар. науч.–практ. конф., г. Новочеркасск, 26 окт. 2009. / Юж.-Рос. гос. техн. ун-т (НПИ). – Новочеркасск: ЮРГТУ, 2010. – С. 11 – 19.

37. Савёлов, Н.С. Исследование жёстких систем обыкновенных дифференциальных уравнений на основе понятия изменчивости / Савёлов Н.С., Чан Д.М. // Микропроцессорные, аналоговые и цифровые системы: проектирование и схемотехника, теория и вопросы применения: Материалы IX Междунар. науч.–практ. конф., г. Новочеркасск, 26 окт. 2009. / Юж.-Рос. гос. техн. ун-т (НПИ). – Новочеркасск: ЮРГТУ, 2010. – С. 20 – 25.

38*. Савёлов, Н.С. Алгоритм ускоренного повторного решения систем линейных алгебраических уравнений и его использование при математическом моделировании электронных устройств / Ревин М.С., Савёлов Н.С. // Науч.-техн. вестник Санкт-Петербургского государственного университета информационных технологий, механики и оптики. – 2010. – Том 66. – № 2. – С. 37 – 42.

39*. Савёлов, Н.С. Ускоренный анализ переходных процессов в тяговом двигателе постоянного тока / Савёлов Н.С., Колпахчьян П.Г., Чан Д.М. // Изв. высш. учеб. заведений. Электромеханика. – 2010. – № 4. – С. 14 – 17.

40. Савёлов, Н.С. Совершенствование и реализация методов математического моделирования мехатронных устройств и систем. /Савёлов Н.С., Ревин М.С. // Студенческая научная весна – 2010: материалы региональной научно-технической конференции студентов, аспирантов и молодых учёных вузов Ростовской области / Юж.-Рос. гос. техн. ун-т. – Новочеркасск: ЮРГТУ (НПИ), 2010. – С. 210 – 211.

41. Савёлов, Н.С. Исследование математических моделей динамических объектов для выявления областей стабилизации в пространстве переменных состояния / Савёлов Н.С., Викаренко А.А. // Студенческая научная весна – 2010: материалы региональной научно-технической конференции студентов, аспирантов и молодых учёных вузов Ростовской области / Юж.-Рос. гос. техн. ун-т. – Новочеркасск: ЮРГТУ (НПИ), 2010. – С. 75.

42. Савёлов, Н.С. Эффективные алгоритмы анализа магнитных цепей при оптимизации устройств мехатроники. / Савёлов Н.С., Ревин М.С. // Результаты исследований – 2010: материалы 59-й научно-технической конференции профессорско-преподавательского состава, научных работников, аспирантов и студентов ЮРГТУ (НПИ)/ Юж.-Рос. гос. техн. ун-т (НПИ). – Новочеркасск: ЮРГТУ (НПИ), 2010. – С. 228 – 229.

43. Савёлов, Н.С. Реализация метода ускоренного формирования уравнений состояния мехатронных устройств и систем / Савёлов Н.С., Ревин М.С. // Мехатроника и робототехника. Современное состояние и тенденция развития: сборник тезисов и статей Всероссийской конференции с элементами научной школы для молодёжи, г. Новочеркасск, 20 – 24 сентября 2010г. – Новочеркасск: ЛИК, 2010. – С. 78 – 84.

44*. Савёлов, Н.С. Эффективный метод расчёта частотных характеристик электрических цепей / Савёлов Н.С., Лыонг С.Т. // Изв. высш. учеб. заведений. Электромеханика. – 2010. – № 5. – С. 31 – 34.

45. Савёлов, Н.С. Исследование типичных жёстких систем обыкновенных дифференциальных уравнений на основе понятия изменчивости / Савёлов Н.С., Чан М.Д. // Труды 53-й научной конференции МФТИ «Современные проблемы фундаментальных и прикладных наук». Часть VII. Управление и прикладная математика. Том 3. – М.: МФТИ, 2010. – С. 49 – 50.

46. Савёлов, Н.С. Метод ускоренного расчёта частотных характеристик / Савёлов Н.С., Лыонг Т.С. // Труды 53-й научной конференции МФТИ «Современные проблемы фундаментальных и прикладных наук». Часть VII. Управление и прикладная математика. Том 3. – М.: МФТИ, 2010. – С. 51 – 52.

47. Савёлов, Н.С. Ускоренное формирование уравнений состояния электрических цепей / Савёлов Н.С., Ревин М.С. // Свид-во о регистрации электронного ресурса № 15954 / Ин-т науч. информации и мониторинга, объединенный фонд электрон. ресурсов «Наука и образование». – Зарег. 07.07.2010; выдано 19.07.2010.

48. Савёлов, Н.С. Ускоренное решение систем линейных алгебраических уравнений / Савёлов Н.С., Ревин М.С. // Свид-во о регистрации электронного ресурса № 15979 / Ин-т науч. информации и мониторинга, объединенный фонд электрон. ресурсов «Наука и образование». – Зарег. 13.07.2010; выдано 27.07.2010.

49. Савёлов, Н.С. Эффективный анализ квазилинейных электрических цепей / Савёлов Н.С., Ревин М.С. // Свид-во о регистрации электронного ресурса № 15955 / Ин-т науч. информации и мониторинга, объединенный фонд электрон. ресурсов «Наука и образование». – Зарег. 07.07.2010; выдано 19.07.2010.

Символом (*) отмечены статьи в журналах, рекомендованных ВАК для опубликования основных научных результатов диссертаций на соискание учёной степени доктора наук.

Личный вклад автора в работах, опубликованных в соавторстве: [16, 22, 25, 29, 32 – 35, 38, 47 – 49] – постановка научной задачи, разработка алгоритмов решения, систематизация полученных результатов; [23, 36, 37, 39, 41, 43 – 46] – постановка научной задачи, разработка алгоритмов решения, реализация алгоритмов, обобщение результатов численных экспериментов; [26, 27, 30, 31, 40, 42] – постановка научной задачи, разработка математических моделей и алгоритмов.