Владимировна расчет долговечности нелинейно-упругих пластинок, изгибаемых в агрессивных средах
На правах рукописи
ПЕНИНА Ольга Владимировна
РАСЧЕТ ДОЛГОВЕЧНОСТИ НЕЛИНЕЙНО-УПРУГИХ ПЛАСТИНОК, ИЗГИБАЕМЫХ В АГРЕССИВНЫХ СРЕДАХ
Специальность 01.02.04 – Механика деформируемого твердого тела
Автореферат диссертации на соискание ученой степени
кандидата технических наук
Саратов – 2009
Работа выполнена на кафедре «Механика деформируемого твердого тела» ГОУ ВПО «Саратовский государственный технический университет».
| Научный руководитель: | академик РААСН, Заслуженный деятель науки и техники, доктор технических наук, профессор Петров Владилен Васильевич |
| Официальные оппоненты: | доктор технических наук, профессор Трещев Александр Анатольевич |
| доктор физико-математических наук, профессор Землянухин Александр Исаевич | |
| Ведущая организация: | Институт проблем точной механики и управления РАН (г. Саратов) |
Защита диссертации состоится ___ марта 2009 года в ____ часов на заседании диссертационного совета Д 212.242.06 в ГОУ ВПО «Саратовский государственный технический университет» по адресу: 410054, г. Саратов, ул. Политехническая, 77, корп. 1, ауд. 319.
С диссертацией можно ознакомиться в научно-технической библиотеке ГОУ ВПО «Саратовский государственный технический университет»
Автореферат разослан ____ ______________ 2009 г.
| Ученый секретарь диссертационного совета | В.С. Попов |
ОБЩАЯ ХАРАКТЕРИСТИКА РАБОТЫ
Актуальность темы исследования. Тенденции, сформировавшиеся в промышленности, направлены на снижение материалоемкости конструкций при усилении коррозионно-силовых режимов и допущении деформаций, близких к предельному уровню. Причиной коррозии является рабочая среда, с которой контактирует материал конструкции. Под рабочими средами понимаем агрессивные эксплуатационные среды природного или техногенного характера, которые ухудшают физико-механические свойства материала в пораженной зоне конструкции и приводят к накоплению необратимых рассеянных повреждений. Это, в свою очередь, приводит к тому, что прочностные и деформационные характеристики конструкционного материала изменяются вдоль пространственных координат. Такую неоднородность называют наведенной, а время от начала эксплуатации до наступления опасного состояния – долговечностью конструкции.
Расчет напряженно-деформированного состояния конструкций в таких условиях эксплуатации является сложной задачей. Эти проблемы рассмотрены в большом количестве публикаций, но до настоящего времени общего метода расчета конструкций с учетом агрессивных воздействий рабочих сред не существует. Объясняется это малой изученностью проблемы, отсутствием специально проведенных исследований, направленных на получение тех характеристик, которые используются в расчетах.
Таким образом, на сегодняшний день интерес представляет дальнейшее развитие методов расчета пластинок, изгибаемых в агрессивных средах, а также методик определения долговечности и остаточного ресурса поврежденных пластинок. Решение этих задач является непременным условием для проектирования оптимальных и надежных инженерных конструкций.
Степень разработанности проблемы. В литературе встречаются взаимоисключающие мнения по вопросу поведения пластинок в агрессивных средах, так как теории коррозионного разрушения строятся на основе различных экспериментальных данных.
Традиционно различают два направления моделирования. В первом из них расчетная схема представляется в виде пластинки с переменной толщиной, где слой, поврежденный средой, исключается из работы. Параметр поврежденности (глубина каверны) представлен в виде различных функций. Этот подход представлен в работах Р. Aziz, Т. Champion, G. Metcalfe, A. Liddiard, Н.Д. Томашова, H. Godart, G. Drumm, Л.Я. Цикермана и многих других.
Важным достижением исследователей при построении моделей деформирования тел, контактирующих с рабочей средой, является применение методов механики сплошной среды. Это направление связано с работами авторов Palmgren, Baily, Miner и получило дальнейшее развитие в работах В.В. Новожилова, Ю.Н. Работнова, Л.М. Качанова, В.В. Москвитина, А.А. Ильюшина и др. В работах этих авторов строятся феноменологические математические модели.
Новое направление в построении моделей коррозионного процесса в виде дифференциальных уравнений, позволяющих учитывать влияние напряженно-деформированного состояния конструкции на коррозию, предложено В.М. Долинским, В.Г. Карпуниным, В.В. Петровым, И.Г. Овчинниковым, В.К. Иноземцевым, А.И. Попеско и другими авторами.
Актуальность рассматриваемой проблемы, малая степень разработанности, необходимость численного исследования и выявления факторов, влияющих на долговечность пластинок в агрессивных средах, обусловили выбор темы, постановку цели и задач работы.
Целью диссертационной работы является дальнейшее развитие методов расчета долговечности изгибаемых пластинок с учетом действия агрессивной рабочей среды. Цель исследования определяет следующие задачи:
- провести анализ и систематизацию экспериментальных данных по влиянию агрессивных рабочих сред на поведение конструкционных материалов и методов построения расчетных схем;
- провести моделирование напряженно–деформированного состояния пластинок с учетом концентрации агрессивной среды в точке материала;
- разработать методику определения долговечности изгибаемых пластинок в агрессивной среде и резерва несущей способности (остаточного ресурса) поврежденных пластинок после устранения источника агрессивной среды;
- разработать алгоритм, программное обеспечение для расчета напряженно-деформированного состояния квадратной пластинки в условиях действия агрессивных рабочих сред и выполнить численное исследование влияния факторов модели наведенной неоднородности на долговечность и остаточный ресурс (резерв несущей способности) пластинки;
- провести анализ эффектов, вызываемых в материале пластинки совместным действием поперечной нагрузки и агрессивных сред;
- результаты численных экспериментов описать аналитическими выражениями и построить графики долговечности и остаточного ресурса.
Объектом исследования являются прямоугольные в плане пластинки, изгибаемые в различных агрессивных средах. Предметом изучения являются параметры напряженно-деформированного состояния, долговечность и остаточный ресурс пластинок с учетом концентрации агрессивной среды.
В работе используются методы математического моделирования и исследования поведения объекта путем проведения численных экспериментов.
Научная новизна диссертационной работы, связана с:
- систематизацией экспериментальных данных и анализом эффектов, вызываемых в конструкционных материалах действием рабочих сред;
- построением модели деформирования изгибаемой пластинки из нелинейно-упругого материала с учетом концентрации агрессивной среды;
- разработкой методики, алгоритмов, комплекса программного обеспечения и численным исследованием поведения прямоугольной нелинейно-упругой пластинки при совместном действии нагрузки и агрессивной среды;
- результатами численных экспериментов и обширным исследованием влияния различных факторов математической модели наведенной неоднородности на долговечность, прогибы пластинок в рабочей среде и резерва несущей способности поврежденных пластинок, и их аналитическими описаниями.
Достоверность результатов работы основана на корректности математических моделей, взятых в качестве основы разработанных методик и строгости используемого математического аппарата. Это подтверждается сопоставлением результатов расчета с известными решениями, а также экспертными оценками специалистов в области механики деформируемого твердого тела, полученными при обсуждении диссертационной работы на научных конференциях, семинарах.
Положения, выносимые на защиту:
- алгоритм численного исследования задач изгиба пластинок в агрессивных средах с учетом концентрации агрессивной среды в точке напряженного материала на основе модели наведенной и развивающейся неоднородности;
- способ описания произвольной кривой деформирования материала в виде численного массива информации, заменяющий ее аналитическое описание;
- методики определения долговечности пластинок с учетом действия агрессивной среды и остаточного ресурса поврежденных пластинок после устранения источника агрессивного воздействия;
- результаты численных экспериментов и аналитические описания долговечности, относительных прогибов изгибаемых пластинок в агрессивных средах и резерва несущей способности поврежденных пластинок.
Теоретическая и практическая значимость заключается в том, что применение предложенных методик позволит повысить обоснованность инженерных решений, а методика определения долговечности и остаточного ресурса будет способствовать безопасности инженерных систем при проектировании конструкций различного назначения и предотвращению техногенных аварий.
Апробация работы прошла несколько этапов. Положения диссертационной работы обсуждались на теоретических и аспирантских семинарах кафедры «Механика деформируемого твердого тела» ГОУ ВПО «Саратовский государственный технический университет».
Положения диссертации легли в основу выступлений автора на научных конференциях:
Математическое моделирование и краевые задачи (Самара, 2006 г.);
2-м Международном форуме молодых ученых (7-я Международная конференция) (Самара, 2006 г.);
конференции молодых ученых Саратовского государственного технического университета (Саратов, 2007).
Материалы исследования нашли свое отражение в одиннадцати научных публикациях, в том числе в одном издании, рекомендуемом ВАК РФ.
Структура и объем работы. Работа состоит из введения, трех глав, заключения в виде основных результатов диссертационной работы, списка использованной литературы и приложений. Общий объем составляет 225 страниц, содержит 78 рисунков на 26 страницах, 3 таблицы, список литературы из 237 наименований на 24 страницах и 50 приложений на 66 страницах.
ОСНОВНОЕ СОДЕРЖАНИЕ РАБОТЫ
Во введении обосновывается актуальность проблемы исследования, приводится анализ состояния вопроса, определяются цель и задачи представляемой работы, положения, выносимые на защиту, а также теоретическая и практическая значимость диссертационной работы.
В первой главе проведена систематизация данных натурных и лабораторных исследований, полученных А.В. Шрейдером, Р.Н. Паркинсом, Л.А. Гликманом, М.К. Смяловски, В.И. Лихтманом, Е.Д. Щукиным, П.А. Рибиндером, В.Н. Маниным, А.Н. Громовым, А.И. Хукматовым, С.В. Ситамовым, И.В. Овчинниковым, Р.Д. Степановым, О.Ф. Шленским, В.Н. Уткиной, И.С. Шпарбером, А.М. Сухотиным, В.С. Зотиковым, А.П. Федоровым, Ю.Б. Потаповым и другими.
Анализ показывает, что действие агрессивной среды на материал конструкций приводит к ухудшению его физико-механических характеристик. При этом изменяется характер диаграммы деформирования, снижается предел прочности и модуль упругости. Концентрация агрессивной среды в точке материала является главным фактором, влияющим на деградацию свойств материала.
Считаем кривую деформирования интегральной характеристикой свойств материала. Для построения модели необходимо проведение серий специальных экспериментов для получения кривых «напряжения – деформации» образцов, различное время выдержанных в агрессивной среде, подобных рис. 1, где показано семейство кривых деформирования на сжатие материалов: а) композитного бетона в воде; б) эпоксидного бетона, выдержанного в 20% растворе едкого натра.
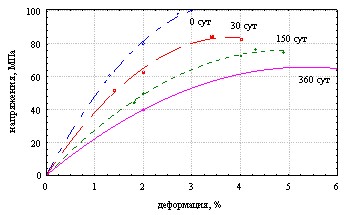
а б
Рис. 1
Математическая обработка этой информации позволила свести множество количественных и качественных факторов, описывающих взаимодействие материала конструкции с рабочей средой, к частной феноменологической модели наведенной неоднородности, развивающейся с ростом концентрации среды.
Во второй части обзора показано сегодняшнее состояние проблемы расчета элементов конструкций в агрессивных средах. Приводятся результаты, достигнутые исследователями в этой области. Рассматриваются достоинства и недостатки основных моделей, описывающих поведение пластин в условиях «коррозия под напряжением», и даются их сравнительные характеристики. Литературный анализ выполнен на основе работ авторов: Г.В. Акимова, Г.В. Карпенко, В.В. Романова, Р.Aziz, Т. Champion, A. Liddiard, B. Whitakker, Н.Д. Томашова, H. Godart, G. Drumm, Я.П. Штурмана, В.М. Долинского, В.Г. Карпунина, И.Г. Овчинникова, В.В. Петрова, В.К. Иноземцева, Ю.М. Шихова, В.В. Новожилова, Ю.Н. Работнова, Л.М. Качанова, В.В. Москвитина, А.А. Ильюшина, В.П. Селяева, А.И. Попеско и других.
Во второй главе рассматривается поэтапное построение модели наведенной и развивающейся неоднородности, расчетные алгоритмы и методики расчета долговечности и остаточного ресурса.
На рис. 2 показана расчетная схема пластинки толщиной h, нагруженной поперечной нагрузкой интенсивностью q. Источник агрессивной среды не меняет свою интенсивность в течение времени действия. На рис. 2: В(z') концентрация агрессивной среды в произвольной точке материала пластинки, z' расстояние от срединной плоскости до текущей ординаты, шаг проникновения агрессивной среды в толщу материала, h толщина пластинки, В0 – концентрация среды на поверхности материала.
а б
Рис. 2
При диффузионном переносе агрессивной жидкости в объем материала глубина пораженного слоя определяется выражением
, (1)
где – экспериментальный коэффициент, описывающий химическую активность рабочей среды и силовое сопротивление конструкционного материала.
Величина (t) мала по сравнению с толщиной пластинки, при этом наблюдается линейный или близкий к линейному закону распределения концентрации агрессивной среды по толщине материала (рис. 2, б). При таком подходе решение получено с запасом долговечности.
Реализуя идею двухшагового метода последовательного возмущения параметров (ДМВПВ)[1], нагрузку прикладываем приращениями q, а действие среды оцениваем движением фронта действия агрессивной среды в материал шагами, равными.
Приращение концентрации агрессивной среды в материале имеет вид
(2)
На основе теории малых упругопластических деформаций А.А. Илюшина в рамках механики сплошной среды записано соотношение
D=2/3Ec*D, (3)
где D – девиатор напряжений, D – девиатор деформаций, Ec*– переменный секущий модуль, учитывающий уровень концентрации агрессивной среды:
(4)
F(B) – функция деградации секущего модуля, 
секущий без влияния среды.
, (5)
i – интенсивность напряжений, i – интенсивность деформаций.
Для построения функции деградации физико-механических свойств мате-
риала F(B) определен алгоритм обработки экспериментальных данных. Для связи времени действия среды t с концентрацией агрессивной среды в точке материала B(z) определен закон проникновения агрессивной среды в материал в виде (2), где =13,05 мм/год0,5 (рис. 4).
На рис. 3 в качестве примера приведен график переменного секущего модуля, а на рис. 4 – график функции деградации F(B(z')) для частной экспериментальной пары.
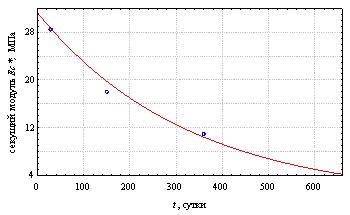
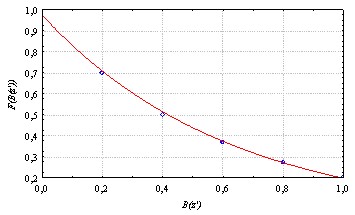
Рис. 3 Рис. 4
По результатам экспериментов композитов[2] функция деградации принята
F(B(z'))=exp(-B(z')), (6)
где – относительная скорость изменения функции деградации.
=F'(B(z'))/ F(B(z')). (7)
Запись деградационной функции в виде (6) не имеет принципиального значения и может иметь другой вид.
По аналогии с (4) переменный касательный модуль Eк* принят в виде
. (8)
Инкрементальные физические соотношения построены[3] и имеют вид
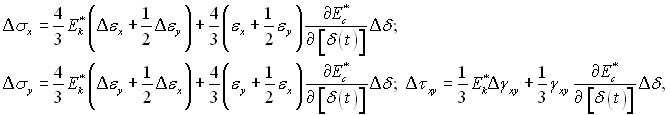(9)
где 
– приращения нормальных и касательных напряжений; 
– приращения линейных и угловых деформаций, 
– переменный касательный модуль.
Согласно технической теории, приращения деформаций имеют вид:
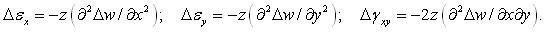(10)
Инкрементальное уравнение равновесия элемента срединной плоскости:
(11)
где 
– приращения изгибающих и крутящего моментов.
Для приращений моментов справедливы формулы:
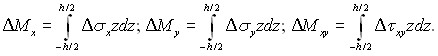(12)
После всех преобразований получено основное инкрементальное уравнение изгиба пластинки с учетом действия агрессивной среды:
(13)
где 
– «фиктивная» нагрузка, отражающая влияние агрессивной среды:
, (14)
где введены следующие обозначения переменных жесткостей:
(15)
Диапазон применимости модели – до наступления опасного состояния.
Наступление опасного состояния определяется по выражению
. (16)
Для учета нелинейности кривой i=(i) предложен способ описания ее в виде численного массива, заменяющего аналитическое описание (таблица).
| Шаг | Парам. | Формула | Краткое описание шага |
| 1 | э, э | – | Фиксируем экспериментальные данные |
| 2 | i, i | – | Сглаживаем данные при помощи метода наименьших квадратов и получаем экспериментальную кривую деформирования произвольного вида |
| 3 | n, n, nмассива | – | Формируем таблицу из численных пар значений n – n с шагом D=max/nмассива, где nмассива – количество столбцов и записываем в соответствующую ячейку таблицы |
| 4 | Ес | Ес = n / n, | Вычисляем секущий модуль |
| 5 | n | n=n+1 – n | Производим расчет приращения напряжений |
| 6 | n | n=n+1 – n | Вычисляем приращения деформаций |
| 7 | Eк | Eк=n /n | Производим расчет касательного модуля |
Для оптимизации времени поиска определен порядковый номер ячейки N:
(17)
Предложенный способ позволяет организовать численный массив информации, с помощью которого можно добиться любой степени приближения к реальной диаграмме деформирования, например путем уменьшения длины отрезков разбиения вдоль оси i. При увеличении точности аппроксимации математическая модель и расчетный алгоритм не изменяются, а коррекции подвергается соответствующий численный массив.
Основная трудность при расчете пластинки, изгибаемой в среде, заключается в вычислении ее переменных жесткостей и фиктивной нагрузки, заменяющей действие агрессивной среды. Для решения этой проблемы применялся метод конечных разностей со следующим алгоритмом действий. Пластинку разбили вдоль оси x на m, а вдоль оси y на n участков. Каждому узлу сетки срединной плоскости пластинки присвоен индекс minj.
Деформации в minj–м узле сетки определены по выражению:
, (18)
где принято следующее обозначение выражения, не содержащего переменной z'
. (19)
Выражение (19) известно для каждого из minj узлов, так как суммарный прогиб пластинки 
определен на предыдущих ступенях нагружения.
Разобьем толщину пластинки вдоль оси z на s участков. Для каждого из значений zs можно подсчитать величину 
и из таблицы определить касательный 
и секущий 
модули, соответствующие этой интенсивности деформаций. После этого можно подсчитать 
в этой же точке. Умножая полученные характеристики на 
, вычисляем подынтегральные выражения в (15). Последовательно изменяя величину zs, определим ординаты эпюры подынтегрального выражения (15). Так как этот интеграл определенный, то значение интеграла равно площади эпюры подынтегрального выражения.
При повторении вычислений для других узлов, получена эпюра изменения жесткости пластинки вдоль осей х и у. Интегральные характеристики жесткостей вида вычислены по методу Симпсона 4 порядка по 69 точкам на половине толщины пластинки h/2.
Для каждой ступени параметра q или решено уравнение типа Софи Жермен МКР. Численная реализация уравнения (13) производится в два этапа. На первом этапе производится нагружение пластинки ступенью нагрузки q:
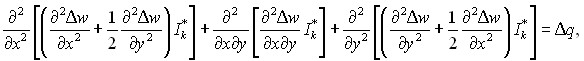(20)
На втором этапе по деформированной схеме решено уравнение
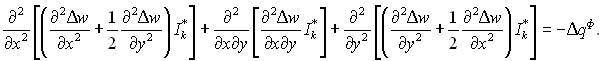(21).
В третьей главе исследована сходимость численных решений при увеличении частоты сетки вдоль стороны пластинки и возрастании числа итераций. Достоверность результатов МКР демонстрируется путем сравнения с решениями методами: Бубнова–Галеркина, Бицено-Коха, модифицированным методом Бицено–Коха. Показано, что точность решения на сетке 3232 в МКР весьма высокая. Табличный способ учета нелинейности кривой деформирования позволяет получать решения с высокой точностью на всем диапазоне деформирования.
Проведены численные эксперименты для конкретных краевых задач методом последовательного нагружения (МПН) и ДМПВП. Получаемые решения сопоставлялись с данными по методу Ньютона-Канторовича, признанного эталонным. При величине шагов нагружения в ДМПВП составляющих q=0,1qmax, точность решения достаточно высока, что дает основание отказаться от использования уточняющих итерационных процедур.
Выполнен численный анализ влияния наведенной неоднородности полиэфирного бетона в жидкой среде 20% едкого натра на примере определения долговечности прямоугольной шарнирно-опертой пластинки под действием поперечной нагрузки разного уровня интенсивности. Приращение глубины пораженного слоя пластинки задано =h/256, а глубина проникновения агрессивной среды в толщу материала – в виде (1), где = 13,05 мм/ год0,5.
Дискретизация непрерывной задачи расчета изгиба пластинки производилась путем аппроксимации области решения уравнения (13) равномерной сеткой узлов 3232 МКР. Для линеаризации нелинейного уравнения (13) применялся ДМПВП, причем нулевое приближение находилось из линейной задачи.
Проводилась пошаговая проверка наступления опасного состояния в точках сетки пластинки при возмущении каждого параметра.
Результаты одного из численных экспериментов представлены на рис. 5.
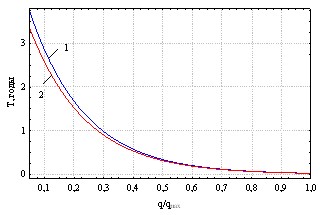
Рис. 5 Рис. 6
Восходящие кривые описывают изменение интенсивности напряжений нагруженной пластинки в среде нагрузкой, определяемой как q/qmax. Нисходящая кривая описывает изменение длительной прочности материала во времени в(t). Точки пересечения кривых характеризуют наступление опасного состояния и исчерпание несущей способности. Проекции точек пересечения кривых на ось времени определяют долговечность конструкции в среде.
Долговечность пластинки T удалось записать в виде:
– для жесткой заделки по контуру:
; (22)
– для шарнирного опирания по контуру:
. (23)
Численные коэффициенты в (22) и (23) определяются экспериментально для каждой пары «конструкционный материал – агрессивная среда».
На рис. 6 представлены графики долговечности T пластинки с условиями опирания по контуру: 1 – шарнирное, 2 – жесткая заделка.
Относительные прогибы пластинки, изгибаемой в среде, записаны в виде:
, (24)
где W(q)/h – относительный прогиб пластинки, сформированный действием поперечной нагрузки q/qmax, – экспериментальный коэффициент.
С учетом (1) выражение (24) переписано в виде
(25)
где – коэффициент, характеризующий частную пару «материал – среда».
Графики выражений (24) и (25) представлены соответственно на рис. 7 и 8.
Каждая восходящая кривая описывает развитие W/h в долях q/qmax.
Рис. 7 Рис. 8
Снижение долговечности пластинки в среде обусловлено влиянием изменяющейся концентрации агрессивной среды при фиксированном нагружении системы. Введением функций деградации и заменой аналитического описания кривой деформирования численным массивом информации ставим в соответствие произвольную точку конструкционного материала с деградационной поверхностью, которая отражает ухудшение свойств материала во времени.
На основе модели наведенной и развивающейся неоднородности проведено исследование влияние параметров математической модели на долговечность и резерв несущей способности пластинки в сложных условиях эксплуатации:
- уровня предварительного нагружения пластинки;
- концентрации агрессивной среды в произвольной точке материала и на поверхности материала;
- относительная скорость деградации секущего и касательного модулей;
- толщина пластинки.
Долговечность T пластинки, эксплуатирующейся в агрессивной среде:
, (26)
где 
. (27)
Численные коэффициенты в (26) и (27) индивидуальны для каждой экспериментальной пары.
Графические результаты экспериментов при разных значениях приведены на рис. 9 – 11. По оси ординат принята интенсивность напряжений /max.
На рис. 12 показаны кривые долговечности при разных.
Уточнено выражение (24), а именно коэффициент линейно зависит от.
Предложенная модель чувствительна к изменениям коэффициента 
. Существенное влияние этого параметра на долговечность пластинки проявляется при небольших уровнях q/qmax и практически утрачивается при нагружениях близких к максимальному уровню. Для устранения неоднозначности поведения функции деградации за пределами интервала эксперимента желательны эксперименты длительного периода.
Рис. 9 Рис. 10
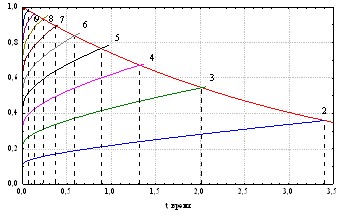
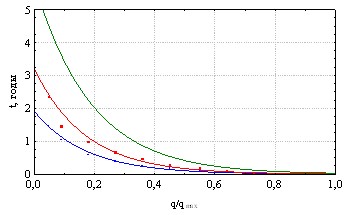
Рис. 11 Рис. 12
Следующее исследование посвящено оценке влияния параметра B0, описывающего концентрацию агрессивной среды на поверхности материала на долговечность конструкции при разных условиях закрепления. Необходимый пакет экспериментальной информации отсутствовал, поэтому предположено, что концентрация среды B0 зависит от плотности 
раствора жидкой среды. Параметр B0 варьировался в диапазоне, моделирующем практически весь спектр жидких агрессивных сред, распространенных в инженерной практике. На рис. 13–15 показаны результаты одного из численных экспериментов для разных уровней нагружения пластинки q/qmax для разных концентраций агрессивной среды.
Графики долговечности при разных B0 приведены на рис. 16.
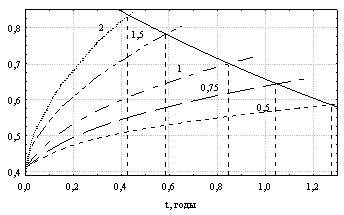
Рис. 13 (q/qmax=0,3) Рис. 14 (q/qmax=0,5)
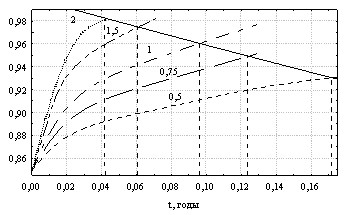
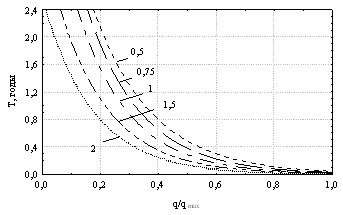
Рис. 15 (q/qmax=0,7) Рис. 16
Обработка результатов численных экспериментов показала, что долговечность пластинки T определяется выражением
(28)
; 
(29)
Получено выражение, прогнозирующее относительные прогибы:
, (30)
где 
– накопленный прогиб срединной плоскости пластинки от q;
, (31)
. (32)
или
, (33)
где 
(34)
Коэффициент 
представляет собой полином с коэффициентами:
при R2 =0,994. (35)
при R2 =0,951. (36)
На рис. 17-18 показаны семейства графиков, полученных по (30) и (33).
Численные коэффициенты в (30) – (36) определены для частной экспериментальной пары, а именно композитного бетона в 20% растворе едкого натра.
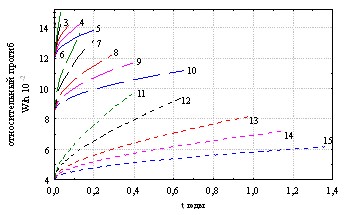
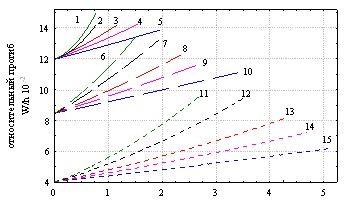
Рис. 17 Рис. 18
Отмечено, что практически полный пакет экспериментальной информации, необходимой для этого исследования, отсутствовал и был заменен на виртуальные данные. При наличии экспериментальных кривых деформирования образцов материала, выдержанных различное время в агрессивных средах разной интенсивности и проведении аналогичных вычислительных мероприятий возможно получение точных аппроксимирующих функций долговечности для любых пар «материал – среда».
Исследовано влияние толщины пластинки на долговечность при разных условиях закрепления по контуру. При варьировании толщины пластинки h получено выражение, прогнозирующее долговечность пластинки в среде:
(37)
где 
– долговечность конструкции без влияния агрессивной среды,
. (38)
Относительные прогибы срединной плоскости пластинки определены как
, (39)
где 
коэффициент, определяемый по выражению
. (40)
График 
приведен на рис. 20.
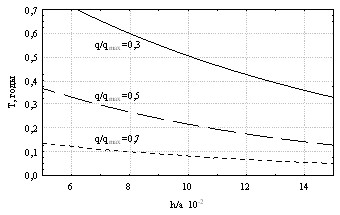
Рис. 19 Рис. 20
Установлено, что изменение толщины пластинки существенно влияет на параметры НДС. С ростом h/a возрастает нелинейность зависимости W/h, а долговечность пластинки уменьшается по экспоненциальной функции.
Резерв несущей способности Р (остаточный ресурс) пластинки поврежденной средой, после устранения источника агрессивного действия:
, (41)
текущее напряжение, 
максимальное напряжение в материале без влияния агрессивной среды.
Установлено, что развитие интенсивности напряжений поврежденной пластинки при ее дополнительном нагружении qдоп после устранения источника агрессивной среды происходит по закону:
, (42)
где 
(43)
Результаты одного из численных экспериментов приведены на рис. 21, где показаны интенсивности напряжений от дополнительной нагрузки в пластинке, выдержанной 30 суток в агрессивной среде, при предварительном нагружении q/qmax: 1 – без влияния среды; 2 – 0,059; 3 – 0,089; 4 – 0,12; 5 – 0,24; 6 – 0,472.
Семейство кривых для определения резерва несущей способности пластинки, различное время выдержанной в среде показано на рис. 22.
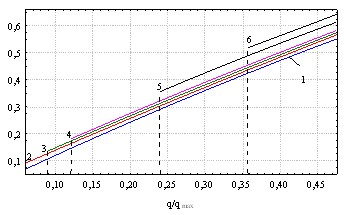
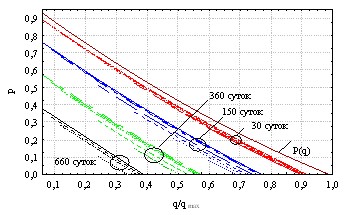
Рис. 21 Рис. 22
Установлено, что снижение остаточного ресурса несущей способности интенсивнее происходит при длительном действии среды. С ростом времени действия среды на пластинку влияние уровня предварительного нагружения пластинки оказывает влияние на остаточный ресурс конструкции.
На большом фактическом материале численных экспериментов проведено исследование оценки вклада каждого фактора в искомую величину. На базе регрессионного анализа резерв несущей способности пластинки описан в виде
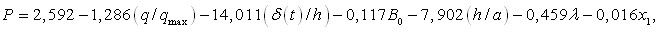(44)
где 
условия опирания: 1 – жесткая заделка, 2 – шарнирное опирание.
Статистически значимыми факторами являются уровень нагружения пластинки, глубина пораженного слоя пластинки, концентрация агрессивной среды на поверхности материала, толщина пластинки, относительная скорость деградации свойств материала и условия опирания.
Основные результаты диссертационной работы состоят в следующем:
- Анализ экспериментальных данных по влиянию агрессивных эксплуатационных сред на поведение материалов напряженных конструкций позволил выделить количественные факторы оценки деградации физико-механических свойств материала.
- На основании инкрементальных уравнений с учетом концентрации агрессивной среды в произвольной точке материала созданы численные методики для определения параметров напряженно-деформированного состояния нелинейно-упругих пластинок, изгибаемых в агрессивных средах на основе метода конечных разностей. Влияние агрессивной среды в инкрементальных уравнениях учитывается деградационной функцией F(B), входящей в секущий и касательный модули и дополнительной «фиктивной» нагрузкой.
- Разработанные методики применимы к пластинкам прямоугольной формы при разных условиях опирания. При этом обязательным является наличие результатов специально проведенных экспериментов для определения физико-механических свойств материала при действии агрессивной среды.
- Построены численные методики для определения долговечности и резерва несущей способности пластинок, изгибаемых в агрессивных средах. Методики применяются для частных пар «материал – рабочая среда» и позволяют анализировать поведение материала напряженных конструкций при разных условиях опирания, толщины и времени воздействия агрессивной среды.
- Данные методики реализованы на основе эффективного с вычислительной точки зрения способа описания кривой деформирования, позволяющего максимально приблизить табличную запись «напряжения - деформации» к экспериментальной диаграмме на всем интервале деформирования. Расчетный алгоритм при этом практически не меняется.
- На основе разработанных методик построены численные модели нелинейно-деформируемых пластинок в агрессивных средах. Создан комплекс программ для определения напряженно-деформированного состояния и долговечности пластинки. Приведены примеры решения конкретных задач. Результаты численных экспериментов показали, что эффективной является модель наведенной и развивающейся неоднородности с учетом роста концентрации агрессивной среды в точке материала. На базе этой модели проведен обширный анализ влияния уровня предварительного нагружения, относительной скорости деградации, концентрации агрессивной среды в произвольной точке материала и на поверхности материала, толщины пластинки, времени длительности среды на долговечность и резерв несущей способности нелинейно-упругих пластинок, изгибаемых в агрессивных средах.
- Получены аналитические описания функций долговечности и резерва несущей способности пластинок, изгибаемых в агрессивных средах.
По теме диссертации опубликованы следующие работы:
В изданиях, рекомендуемых ВАК РФ для публикации научных достижений
1. Пенина О.В. Определение долговечности и резерва несущей способности нелинейно-упругих пластинок при изгибе в агрессивных средах / В.В. Петров, О.В. Пенина // Вестник Саратовского государственного технического университета. 2008. №4. – С. 16 22.
В других изданиях
2. Пенина О.В. Уравнения изгиба нелинейно-упругих пластинок средней толщины с учетом деградации свойств материала во времени / В.В. Петров, И.В. Кривошеин, О.В. Пенина // Проблемы прочности элементов конструкций под действием нагрузок и рабочих сред: сб. науч. тр. Саратов: СГТУ, 2005.– С.22–30.
3. Пенина О.В. Применение метода конечных элементов в расчетах нелинейно-упругих пластин средней толщины со сложной формой в плане // Проблемы прочности элементов конструкций под действием нагрузок и рабочих сред: сб. науч. тр. Саратов: СГТУ, 2005. – С. 85–91.
4. Пенина О. В. Изгиб локально нагруженных нелинейно-упругих пластин средней толщины в агрессивной среде / О.В. Пенина // Математическое моделирование и краевые задачи: материалы III Всероссийской конференции / Самар. гос. тех. ун-т, Самара: Изд-во Самарского гос. тех. ун-та, 2006. – C. 163–166.
5. Пенина О. В. К решению задач изгиба нелинейно-упругой пластинки, работающей в агрессивной среде / О.В. Пенина // Проблемы прочности элементов конструкций под действием нагрузок и рабочих сред: сб. науч. тр. Саратов: СГТУ, 2006. С. 65–70.
6. Пенина О. В. Инкрементальные уравнения изгиба нелинейно-упругих пластин с учетом деградации свойств материала во времени / О.В. Пенина // Актуальные проблемы современной науки: тр. 2-го Междунар. форума мол. уч. (7-й Международной конференции). Самара, 2006. С. 200 – 205.
7. Пенина О.В. Применение метода конечных разностей к расчету пластинок сложной формы из нелинейно-упругого материала / И.В. Кривошеин, О.В. Пенина // Проблемы прочности элементов конструкций под действием нагрузок и рабочих сред: сб. науч. тр. Саратов: СГТУ, 2007. С.134 – 142.
8. Пенина О.В. Долговечность плит из нелинейно-деформируемого материала с учетом воздействия агрессивной эксплуатационной среды / В.В. Петров, О.В. Пенина // Проблемы прочности элементов конструкций под действием нагрузок и рабочих сред: сб. науч. тр. Саратов: СГТУ, 2007. С. 31 – 41.
9. Пенина О.В. Влияние параметров наведенной неоднородности на долговечность пластинок, изгибаемых в агрессивных средах / В.В. Петров, О.В. Пенина // Проблемы прочности элементов конструкций под действием нагрузок и рабочих сред: сб. науч. тр. Саратов: СГТУ, 2008. – С.42–48.
10. Пенина О.В. Расчет плит из нелинейно-деформируемого материала с произвольной диаграммой деформирования с учетом воздействия агрессивной эксплуатационной среды / В.В. Петров, О.В. Пенина, П.В. Селяев // Academia. 2008. №3. – С. 87–92.
11. Пенина О.В. Долговечность пластинок из нелинейно-деформируемого материала при действии поперечной нагрузки и агрессивной среды / В.В. Петров, О.В. Пенина // Георесурсы: науч.– техн. журн.– Казань: Изд-во Казан. ун-та, 2008. – №1 (24). – С. 28–32.
Подписано в печать 29.01.09 Формат 60х84 1/16
| Бум. офсет. Тираж 100 экз. | Усл. печ. л. 1,0 Заказ 20 | Уч.-изд. л. 1,0 Бесплатно |
Саратовский государственный технический университет
410054, г. Саратов, ул. Политехническая, 77
Отпечатано в РИЦ СГТУ, 410054, г. Саратов, ул. Политехническая, 77
[1] Петров В. В. Двухшаговый метод последовательного возмущения параметров и его применение к решению нелинейных задач механики твердого деформируемого тела // Проблемы прочности элементов конструкций под действием нагрузок и рабочих сред: сб. науч. тр. Саратов: Сарат. гос. техн. ун – т, 2001. С. 6 –12.
[2] Селяев П. В. Диаграммы деформирования композиционных материалов при воздействии жидких агрессивных сред // Проблемы прочности элементов конструкций под действием нагрузок и рабочих сред: сб. науч. тр. Саратов: Сарат. гос. техн. ун-т, 2006. С.46 – 52.
[3] Петров В. В. Уравнения изгиба пластинки, учитывающие влияние концентрации агрессивной среды в ее материале // Вестник РААСН. Вып. 9. Белгород, 2005. – С.315 – 320.
