Разработка методики расчета и исследования температурного состояния лопаток газовых турбин
СВЕДЕНИЯ О СОИСКАТЕЛЕ И ПРЕДСТОЯЩЕЙ ЗАЩИТЕ
| Ф.И.О. | КРАСАВИН ДЕНИС АНДРЕЕВИЧ |
| Тема диссертации: | Разработка методики расчета и исследования температурного состояния лопаток газовых турбин |
| Специальность: | 05.07.05 – Тепловые, электроракетные двигатели и энергоустановки летательных аппаратов |
| Отрасль науки: | Технические науки |
| Шифр совета: | Д212.110.02 |
| Тел. ученого секретаря диссертационного совета | 915-31-29 |
| E-mail: | [email protected] |
| Предполагаемая дата защиты диссертации: | 25 декабря 2008г. в 15-00 |
| Место защиты диссертации: | г. Москва, Берниковская наб., дом 14, каф. ИЛА, ауд. 102-5 |
Председатель
диссертационного
Совета Д212.110.02, д.т.н., профессор Соколов В.П.
Ученый секретарь
диссертационного Совета
Д 212.110.02, д.т.н., профессор Силуянова М.В.
На правах рукописи
Красавин Денис Андреевич
РАЗРАБОТКА МЕТОДИКИ РАСЧЕТА И ИССЛЕДОВАНИЯ ТЕМПЕРАТУРНОГО СОСТОЯНИЯ ЛОПАТОК ГАЗОВЫХ ТУРБИН
Специальность: 05.07.05-«Тепловые, электроракетные двигатели и
энергоустановки летательных аппаратов»
АВТОРЕФЕРАТ
диссертации на соискание ученой степени
кандидата технических наук
Москва 2008 г.
Работа выполнена на кафедре «Двигатели летательных аппаратов и теплотехника» ГОУ ВПО «МАТИ» – Российского государственного технологического университета имени К.Э. Циолковского
Научный руководитель: - доктор технических наук, профессор
Дмитренко Артур Владимирович
Официальные оппоненты: - доктор технических наук, профессор
Пелевин Федор Викторович
- доктор технических наук, старший научный сотрудник
Мякочин Александр Сергеевич
Ведущее предприятие: ФГУП ММПП «Салют»
Защита состоится « » ____________ 2009 г. в 13 час.00 мин. на заседании диссертационного Совета Д 212.110.02 ГОУ ВПО «МАТИ» Российского государственного технологического университета имени К.Э. Циолковского, по адресу: 109240, г. Москва, Берниковская наб., д.14, стр.2.
С диссертацией можно ознакомиться в библиотеке ГОУ ВПО «МАТИ» Российского государственного технологического университета имени К.Э. Циолковского.
Автореферат разослан « » __________ 200__ г.
Отзывы (в двух экземплярах, заверенных печатью учреждения) просим присылать по адресу: 121552, г. Москва, Г-552, ул. Оршанская, д.3 ГОУ ВПО «МАТИ» Российский государственный технологический университет имени К.Э. Циолковского, ученому секретарю диссертационного Совета Д 212.110.02.
Ученый секретарь диссертационного
Совета Д 212.110.02
доктор технических наук М.В. Силуянова
Общая характеристика работы
Актуальность темы
С каждым новым поколением авиационных газотурбинных двигателей (ГТД) и энергетических установок растут параметры рабочего цикла двигателя и, прежде всего, температура газа перед турбиной, которая в ближайшей перспективе должна достигать 2000К. Поэтому создание новых поколений ГТД связано с разработкой высокотемпературного газогенератора реализующего эффективный рабочий процесс двигателя. Решение этой проблемы заставляет глубоко исследовать и изучить рабочие процессы, физико-химические, газодинамические явления в двигателе, правильно определять выходные параметры двигателей и эксплуатационные характеристики его деталей, обеспечивая наибольшую информативность и достоверность, требуемую точность. В тоже время законы рынка определяют необходимость существенного сокращения сроков и стоимости создания двигателя при сохранении высоких эксплуатационных показателей, поэтому в основу современной методологии создания нового авиационного двигателя должна быть положена тщательно отработанная расчетно-аналитическая методика, построенная на разработке адекватной математической модели, что позволяет существенно сократить затраты на экспериментальную отработку изделия.
Основным элементом «горячего» тракта ГТД является охлаждаемая или неохлаждаемая ступень газовой турбины и, прежде всего, ее наиболее теплонапряженные детали сопловые и рабочие лопатки. Повышение эффективности проектирования турбины тесно связано с точностью и адекватностью результатов расчетного исследования ее температурного состояния. Принятые в настоящее время расчетные методы определения температурного состояния деталей турбины (маршевый метод, метод конечных элементов и другие.) отличаются значительной сложностью и недостаточной адекватностью получаемых результатов особенно для предельных значений температуры лопаток турбины. Получаемые при этом отличия при вполне приемлемой относительной погрешности методов (5-7%) могут достигать недопустимых отклонений от реальной температуры лопатки (до100 К). Это в значительной мере увеличивает затраты на экспериментальную отработку и сроки создания турбины. Повышение точности применяемых в практике газотурбостроения расчетных методов связано не только со значительным уменьшением масштаба разбиения расчетной области, которое значительно увеличивает трудоемкость расчетов не снимая задачи экспериментальной верификации уровня разбиения достаточного для получения требуемой точности расчетов, но и с необходимостью перехода к оптимальному (с точки зрения трудоемкости и точности полученных результатов) трехмерному моделированию температурного состояния лопаток. Поэтому исследования направленные на развитие методов моделирования и разработку расчетно-теоретической методики, обеспечивающей повышение адекватности и точности определения температурного состояния лопаток газовой турбины являются актуальной задачей современного двигателестроения.
Цель исследований
Повышение эффективности проектирования газовой турбины путем совершенствования расчетного метода и информационных средств определения температурного состояния лопаток.
Научная новизна
Новыми научными результатами, полученными в работе, являются:
1.Обобщенная трехмерная математическая модель температурного состояния лопаток газовой турбины.
2.Расчетно-теоретические методики, обеспечивающие повышение адекватности определения методом контрольного объема температурного состояния неохлаждаемых и охлаждаемых лопаток газовой турбины, за счет более полного учета факторов теплообмена в лопатке.
3.Количественные характеристики достаточности точности метода контрольного объема для описания температурных полей в лопатках при эксплуатационных условиях теплообмена.
4.Закономерности изменения температурного состояния лопаток в зависимости от принятой при расчетах точности математического описания исходных характеристик теплообмена.
Достоверность результатов
Полученные в работе теоретические и практические результаты исследований обеспечены применением адекватного математического аппарата и хорошей согласованностью расчетных характеристик, полученных на базе разработанной методики расчета температурного состояния, с экспериментальными данными, как для классических задач теплообмена, так и для лопаток ГТД и энергетических установок.
Практическая ценность работы
Применение разработанных: математической модели, расчетной методики, программного обеспечения и рекомендаций для расчета и исследования температурного состояния лопаток газовой турбины позволяют повысить эффективность аналитического проектирования деталей турбины ГТД, и тем самым сократить сроки и затраты ресурсов на ее создание. Результаты диссертации используются в учебном процессе подготовки специалистов в «МАТИ», что подтверждается «Актом о Внедрении».
Апробация работы
Результаты работы докладывались на 3 международных и всероссийских научно-технических конференциях.
Публикации
По результатам выполненных исследований и практических разработок опубликовано 7 научных работ, в том числе: 2 тезиса докладов, 5 научных статей, одна из которых опубликована в изданиях, рекомендованных ВАК РФ.
Структура и Объем работы
Диссертация состоит из введения,4-х глав, выводов, списка литературы (198 наименования). Общий объем составляет 174 страницы машинописного текста, 122 рисунка и 3 фотографии на 55 страницах, списка литературы на 15 страницах.
Содержание работы
Во ВВЕДЕНИИ обоснованы актуальность темы диссертационной работы, посвященной разработке методики расчета и исследованию тепловых параметров турбинных лопаток, необходимых для формирования конструктивно-технологических решений при создании газовой турбины авиационного двигателя или энергетической установки; определена цель работы; представлены научная новизна, практическая значимость, отражена реализация результатов.
В ПЕРВОЙ ГЛАВЕ проводится анализ современного состояния предметной области исследования, определяются проблемные вопросы и формируются задачи, способствующие их решению.
Предметной областью исследований является моделирование и расчет и температурного состояния газовой турбины на этапе её проектирования и конструкторско-технологической доводки.
Конструкция современного газотурбинного двигателя содержит целый ряд специфических деталей, среди которых необходимо выделить турбинные лопатки, определяющие техническое совершенство двигателя и в значительной мере регламентирующие сроки его создания. Теоретическим и практическим вопросам моделирования и создания газовых турбин авиационных двигателей и энергетических установок посвящены научные работы Люлька А.М., Кузецова Н.Д.,Авдуевского В.С., Уварова В.В., Жирицкого Г.С., Копелева С.З., Ковалева В.И., Леонтьева А.И., Нагоги Г.П., Галицейского Б.М., Патанкара С., Скибина В.А., Белоконя Н.И. и других ученых.
В результате анализа опубликованных материалов определены, комплекс актуальных задач теплового проектирования, экспериментальные данные которых использованы при верификации результатов расчета, и физико-математическая модель, положенная в основу, разработанной на базе метода контрольного объема, методики расчета температурного состояния лопаток. При этом отмечено, что существующие модели и методики расчета, использующие метод контрольного объема из-за чрезмерного упрощения постановки задачи дают большую погрешность (до 100К) при расчете температуры лопатки, что значительно снижает эффективность их использования при проектировании турбины. Для верификации расчетной методики как для охлаждаемых, так и для неохлаждаемых лопаток достаточно рассмотреть трехмерные течения в каналах и трубах, поэтому, тестируемая модель должна удовлетворительно описывать и процесс нестационарной трехмерной теплопроводности и конвективный теплообмен в трехмерных каналах и лопатках, для соответствующих им значений числа Маха M, интенсивности турбулентности Tu и температурного напора 0<TCT/T<2.
На основании проведенного анализа сформулирована цель работы:
Повышение эффективности проектирования газовой турбины путем совершенствования расчетного метода и информационных средств определения температурного состояния лопаток.
Для достижения поставленной цели в работе решены следующие задачи:
-разработана обобщенная трехмерная математическая модель температурного состояния лопаток газовой турбины;
-сформированы расчетные методики, обеспечивающие повышение адекватности определения методом контрольного объема температурного состояния неохлаждаемых и охлаждаемых лопаток газовой турбины, за счет более полного учета факторов теплообмена в лопатке;
-установлены количественные характеристики достаточности точности метода контрольного объема для описания температурных полей в лопатках при эксплуатационных условиях теплообмена.
-определены закономерности изменения температурного состояния лопаток в зависимости от принятой при расчетах точности математического описания
исходных характеристик теплообмена.
Во ВТОРОЙ ГЛАВЕ представлена разработка модели исследования точности численного анализа температурного состояния лопаток турбины, осуществляется постановка физико-математической задачи исследования.
Начальные условия имеют классическую запись ![]() , а граничные условия соответственно первого, второго или третьего рода. Тепловой поток
, а граничные условия соответственно первого, второго или третьего рода. Тепловой поток ![]() ,
,![]() ,
,![]() . Задается геометрическая форма тела, в котором надо определить поле температур; теплофизические свойств материала по пространству,, ; зависимость источника тепла S от искомой температуры.
. Задается геометрическая форма тела, в котором надо определить поле температур; теплофизические свойств материала по пространству,, ; зависимость источника тепла S от искомой температуры.
Рис.1 Контрольный объем
Расчётная область разбивается на непересекающиеся контрольные объёмы. На Рис.1 заштрихован типичный контрольный объём ![]() , где i–номер контрольного объёма по оси Х, j – номер контрольного объёма по оси Y. На границе области используется контрольный объём нулевой толщины. В середину каждого контрольного объёма помещается расчётная точка P(i, j). В пределах контрольного объёма параметры
, где i–номер контрольного объёма по оси Х, j – номер контрольного объёма по оси Y. На границе области используется контрольный объём нулевой толщины. В середину каждого контрольного объёма помещается расчётная точка P(i, j). В пределах контрольного объёма параметры ![]() ,
, ![]() ,
, ![]() ,
, ![]() — постоянны. Дифференциальное уравнение теплопроводности интегрируется по каждому контрольному объёму. Для вычисления интегралов используют кусочные профили, которые описывают изменение Т между узловыми точками. В результате находится дискретный аналог уравнения, в который входят значения Т в нескольких соседних узловых точках. Полученный подобным образом дискретный аналог выражает закон сохранения тепла для конечного контрольного объёма, точно так же, как дифференциальное уравнение выражает закон сохранения тепла для бесконечно малого контрольного объёма. По этой причине даже решение на грубой сетке удовлетворяет точным интег-ральным балансам тепла. Дискретный аналог для трёх измерений имеет вид:
— постоянны. Дифференциальное уравнение теплопроводности интегрируется по каждому контрольному объёму. Для вычисления интегралов используют кусочные профили, которые описывают изменение Т между узловыми точками. В результате находится дискретный аналог уравнения, в который входят значения Т в нескольких соседних узловых точках. Полученный подобным образом дискретный аналог выражает закон сохранения тепла для конечного контрольного объёма, точно так же, как дифференциальное уравнение выражает закон сохранения тепла для бесконечно малого контрольного объёма. По этой причине даже решение на грубой сетке удовлетворяет точным интег-ральным балансам тепла. Дискретный аналог для трёх измерений имеет вид:
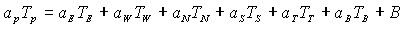 (1)
(1)
Из этого соотношения следует, что температура в контрольном объёме Р (точка Р) определяется температурой в шести соседних объёмах Е и W (по оси Х), N и S (по оси Y), T и B (по оси Z). Систему уравнений (1) решается итерационным методом, используя процедуру прогонки по осям Х Y Z. В существующих методиках расчета тепловой поток на левой границе в точке (1,j) будет равен:
![]() . (2)
. (2)
Эта формула получена в предположении линейного профиля температуры между двумя расчётными точками (1,j) и (2, j) и дает большую погрешность в оценке температурного состояния лопатки. Поэтому предлагается более точная модель теплообмена, которая получается если считать, что плотность теплового потока меняется линейно между гранями ![]() и
и ![]() приграничного контрольного объёма (2, j) :
приграничного контрольного объёма (2, j) : ![]() , где
, где ![]() ,
, ![]() .С учетом (2),после интег-рирования по координате «x»,получим:
.С учетом (2),после интег-рирования по координате «x»,получим:![]() ,при
,при ![]() :
:
![]() , (3)
, (3)
где:![]() — параметр аппроксимации удельного теплового потока на границе тела.Если
— параметр аппроксимации удельного теплового потока на границе тела.Если![]() -аппроксимация первого порядка, если
-аппроксимация первого порядка, если ![]() - аппроксимация второго порядка.
- аппроксимация второго порядка. ![]() - третьего порядка. На основании анализа этой модели получен дискретный аналог расчетной области. Полученная модель использована для тестовых расчетов нестационарной трехмерной теплопроводности тела кубической формы с постоянной теплопроводностью с наличием источника тепла постоянной мощности и без источника тепла. При этом прогоночные коэффициенты численного расчета для границ расчетной
- третьего порядка. На основании анализа этой модели получен дискретный аналог расчетной области. Полученная модель использована для тестовых расчетов нестационарной трехмерной теплопроводности тела кубической формы с постоянной теплопроводностью с наличием источника тепла постоянной мощности и без источника тепла. При этом прогоночные коэффициенты численного расчета для границ расчетной
области имеют вид:
Левая граница: Правая граница:
,,
(4)..
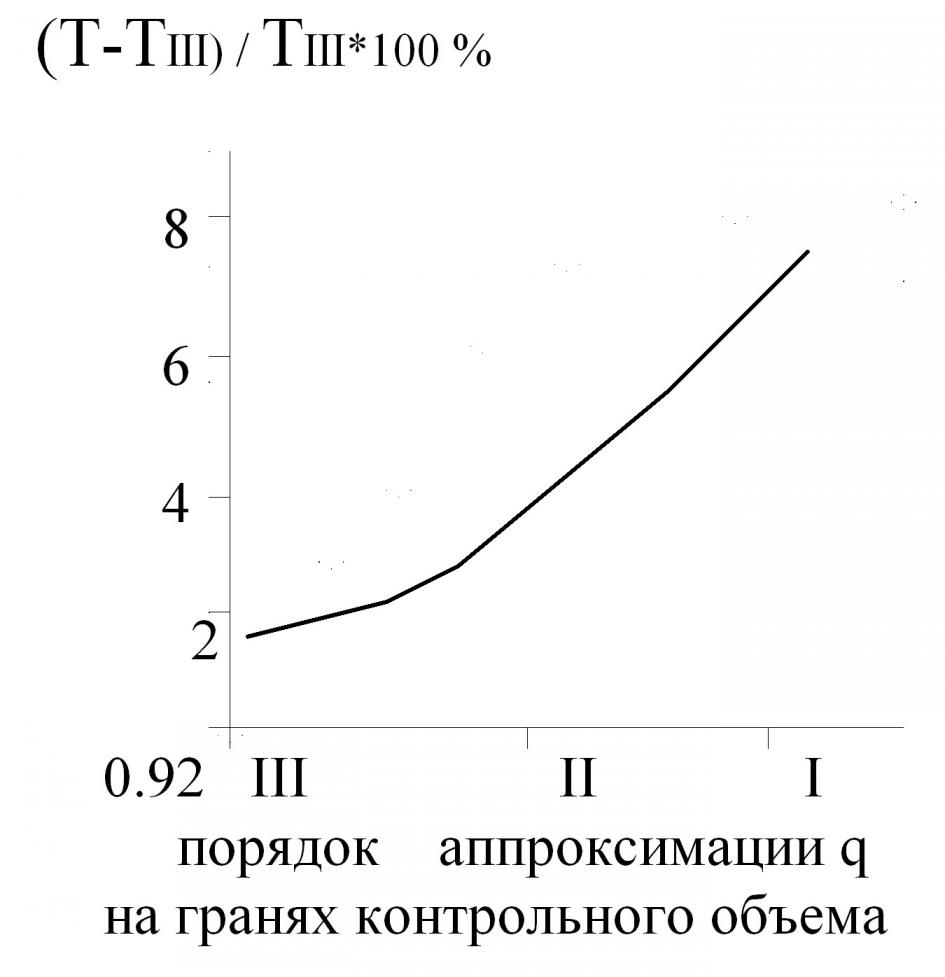
Рис.2 Точность расчета температуры в выделенном элементе при различных уровнях аппроксимации и на различных расчетных сетках
В результате в первом варианте с источником тепла при третьем порядке аппроксимации температура в центре тела при расчетной сетке ![]() =
=![]() =
=![]() =40 равна 1112К, при втором 1125К и при первом порядке аппроксимации Т=1170K.В случае
=40 равна 1112К, при втором 1125К и при первом порядке аппроксимации Т=1170K.В случае![]() =
=![]() =
=![]() =5 температура в центре тела равна Т=1117K при третьем порядке аппроксимации, при втором 1130К и при первом порядке Т=1182K соответственно. То есть третьего и второго порядка аппроксимации
=5 температура в центре тела равна Т=1117K при третьем порядке аппроксимации, при втором 1130К и при первом порядке Т=1182K соответственно. То есть третьего и второго порядка аппроксимации ![]() дает более точное распределение температуры на границе, что влечет изменение температуры в центре тела. Во втором варианте при температурных напорах Tмах/Tмин<2 на грубых сетках при решении нестационарной задачи трехмерной теплопроводности аппроксимации третьего порядка гранях контрольного объема дают результаты с точностью до 2% (погрешность составляет в абсолютных температурах 10К-12К); аппроксимации второго порядка на гранях контрольного объема дают результаты с точностью до 3-4% (погрешность составляет в абсолютных температурах 15К-25К) аппроксимации первого порядка имеют точность до 7% (погрешность составляет в абсолютных температурах 70 градусов К).
дает более точное распределение температуры на границе, что влечет изменение температуры в центре тела. Во втором варианте при температурных напорах Tмах/Tмин<2 на грубых сетках при решении нестационарной задачи трехмерной теплопроводности аппроксимации третьего порядка гранях контрольного объема дают результаты с точностью до 2% (погрешность составляет в абсолютных температурах 10К-12К); аппроксимации второго порядка на гранях контрольного объема дают результаты с точностью до 3-4% (погрешность составляет в абсолютных температурах 15К-25К) аппроксимации первого порядка имеют точность до 7% (погрешность составляет в абсолютных температурах 70 градусов К).
Анализ точности решения (рис.2) показывает, что при аппроксимациях выше третьего порядка градиент погрешности стремится к нулю, определяя тем самым приемлемое для практических расчетов усложнение расчетной модели.
В ТРЕТЬЕЙ ГЛАВЕ представлены модель и алгоритм расчета методом контрольного объема температурного поля при вынужденном конвективном теплообмене в трехмерных каналах. Описана методика решения системы дифференциальных уравнений неразрывности, движения и энергии вынужденного конвективного теплообмена при ламинарном и турбулентном режимах течения, при аппроксимации третьего, второго и первого порядка на гранях контрольного объема. Для ламинарного потока охладителя все рассчитываемые величины принимаются осредненными по времени, но детерминированными, а в случае турбулентного потока - с турбулентными компонентами ![]() ,
,![]() ,
,![]() , то есть уравнения Рейнольдса рассчитываются как производные от соответствующих корреляций второго порядка, определяемые моделью турбулентностью. Уравнение неразрывности, Навье-Стокса и энергии в тензорной записи примут вид
, то есть уравнения Рейнольдса рассчитываются как производные от соответствующих корреляций второго порядка, определяемые моделью турбулентностью. Уравнение неразрывности, Навье-Стокса и энергии в тензорной записи примут вид
![]()
![]() (5),
(5),
![]()
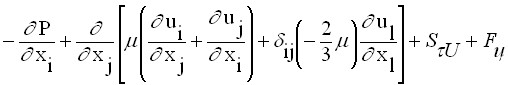 (6),
(6),
![]()
![]()
![]() (7),
(7),
Здесьi,j,l=1,2,3,Т-температура,![]() -плотность, Сp-удельная теплоёмкость,
-плотность, Сp-удельная теплоёмкость,![]() —коэффициент теплопроводности, -динамическая вязкость среды. Величины ui, uj, ul,xi, xj, xl - скорости и координаты соответствующие i, j, l. Символ Кроннекера равен ij=1 при i=j, и ij=0 при i
—коэффициент теплопроводности, -динамическая вязкость среды. Величины ui, uj, ul,xi, xj, xl - скорости и координаты соответствующие i, j, l. Символ Кроннекера равен ij=1 при i=j, и ij=0 при i![]() j. Р- давление в жидкости,
j. Р- давление в жидкости,![]() ,
,![]() -центробежная сила и работа центробежных сил. Интегрирование уравнений методом контрольного объема строится по единому алгоритму как аппроксимациями первого, так и третьего порядка на гранях контрольного объема и для ламинарного и для турбулентного течений. В трехмерном случае контрольный объем
-центробежная сила и работа центробежных сил. Интегрирование уравнений методом контрольного объема строится по единому алгоритму как аппроксимациями первого, так и третьего порядка на гранях контрольного объема и для ламинарного и для турбулентного течений. В трехмерном случае контрольный объем ![]()
![]() , где i –номер контрольного объема по оси x, j – номер контрольного объема по оси y, а k – номер контрольного объема по оси z. В середину каждого контрольного объема помещается расчетная точка P(i,j,k). Интегрируя (5) по контрольному объему можно получить дискретный аналог для переменной давления
, где i –номер контрольного объема по оси x, j – номер контрольного объема по оси y, а k – номер контрольного объема по оси z. В середину каждого контрольного объема помещается расчетная точка P(i,j,k). Интегрируя (5) по контрольному объему можно получить дискретный аналог для переменной давления ![]()
![]() а классической сетке
а классической сетке
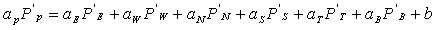 (8)
(8)
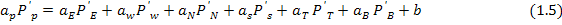 Дискретный аналог на шахматной сетке для компоненты скорости u, вдоль Х, имеет вид
Дискретный аналог на шахматной сетке для компоненты скорости u, вдоль Х, имеет вид
ae1ue1 = at1ut1+ aw1uw1+ an1un1+ as1us1+az1uz1+az2uz2 +b1+(PE-PP)dxdy (9)
Дискретный аналог на шахматной сетке для компоненты скорости v, вдоль У:
an2vn2 = ae2ve2+ aw2vw2+ at2vt2+ as2vs2+az1vz1+az2vz2 +b2+(PN-PP)dxdz (10)
Дискретный аналог на шахматной сетке для компоненты скорости w вдоль Z
an3wn3 = ae3we3+ aw3ww3+ at3wt3+ as3ws3+an1wn1+as1ws1 +b3+(PB-PP)dxdz (11)
Ниже перечислены основные операции, в порядке их выполнения. Задается поле давления ![]()
![]() , решается уравнения движения для нахождения
, решается уравнения движения для нахождения![]()
![]() ,
, ![]() решается уравнение для
решается уравнение для ![]() , рассчитывается
, рассчитывается ![]()
![]() ,
, ![]() ,
, ![]() ,
, ![]()
Представляем скорректированное давление Р как новое ![]()
![]() и возвращаемся к вычислению
и возвращаемся к вычислению ![]() .Вся процедура повторяется до тех пор, пока не будет получено сходящееся решение. В работе приводится эта известная процедура не случайно, поскольку показывается, что только корректировкой давления Р путем сопоставления расчетной массы (интегрирования по всему объему) с исходной заданной массой удается достичь сходимости решения и по полю давления и по полям скорости и температур. В этой главе дается дискретный аналог уравнения энергии.
.Вся процедура повторяется до тех пор, пока не будет получено сходящееся решение. В работе приводится эта известная процедура не случайно, поскольку показывается, что только корректировкой давления Р путем сопоставления расчетной массы (интегрирования по всему объему) с исходной заданной массой удается достичь сходимости решения и по полю давления и по полям скорости и температур. В этой главе дается дискретный аналог уравнения энергии. ![]() Для трехмерной задачи (с, представляющими верхнюю и нижнюю грани в направлении оси z, дискретный аналог имеет вид
Для трехмерной задачи (с, представляющими верхнюю и нижнюю грани в направлении оси z, дискретный аналог имеет вид
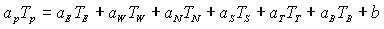 (12)
(12)
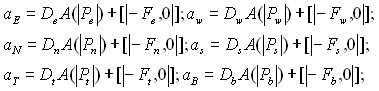 (13)
(13)
![]() (14)
(14)
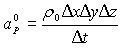 ;
;![]() ;
;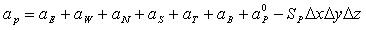
![]()
![]() , где P, E, W, N, S,T,B –узлы семиточечного шаблона, где параметр P –является числом Пекле, на гранях контрольного объема.
, где P, E, W, N, S,T,B –узлы семиточечного шаблона, где параметр P –является числом Пекле, на гранях контрольного объема.
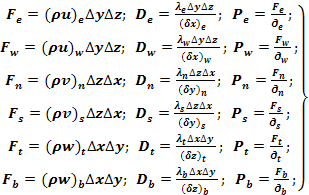 Показано, что формула более высокого порядка аппроксимации может быть применена в единой форме и для уравнения теплопроводности и для уравнения энергии в случае конвективного теплообмена. При расчете турбу-лентных течений компоненты
Показано, что формула более высокого порядка аппроксимации может быть применена в единой форме и для уравнения теплопроводности и для уравнения энергии в случае конвективного теплообмена. При расчете турбу-лентных течений компоненты ![]() ,
,![]() ,
,![]() включены в источниковый член «b» уравнений. При расчете задавались граничные условия скорости,
включены в источниковый член «b» уравнений. При расчете задавались граничные условия скорости,
давления и температуры. После вывода общего алгоритма расчета конвективного охлаждения методом контрольного объема, произведена его верификация, последующим тестированием на базе экспериментальных данных для плоских течений двухмерных потоков и трехмерных ламинарных и турбулентных течений в трубах с прямоугольным сечением. Для сравнения возможностей методики и ее программной реализации было проведено сравнение полученных данных с опубликованными экспериментальными данными. Приведены расчеты компонент скорости ламинарного потока в канале различных сечениях Рис.3-Рис.4. Результаты расчета давления вдоль оси канала для ламинарного потока рис.5. Z = [(z/Dэк)/Re]*100
Рис.3.Развитие профиля продольной скорости ламинарного потока в трубе прямоугольного сечения вдоль оси канала в сечении ZX.--,*-экперимент;__ - расчет
Рис.4 Развитие профиля скорости турбулентного потока вдоль оси
*- эксперимент; __ -расчет
Рис.5 Давления вдоль оси канала для ламинарного потока
в трубе прямоугольного сечения --,*- экперимент; __ -расчет
Результаты расчетов и сопоставление с экспериментальными данными в прямых прямоугольных каналах для теплообмена приведены для ламинарного и турбулентного потока на Рис.6 – Рис. 9.
Re
Рис.6 Теплообмен при ламинарном течении в канале на расчетной сетке
Nx, Ny, Nz =16*16*16. 1- эксперимент; Расчет:2- третий порядок; 3- второй порядок, 4-первый порядок аппроксимации плотности теплового потока.
Re
Рис.7 Теплообмен при ламинарном течении в канале на расчетной сетке
Nx, Ny, Nz =60*60*60. 1- эксперимент; Расчет:2- третий порядок; 3- второй порядок,
4-первый порядок аппроксимации плотности теплового потока.
Re
Рис.8 Теплообмен при турбулентном течении в прямоугольном канале на расчетной сетке Nx*Ny*Nz=16*16*16 1- среднее экспериментальное, Расчет:2- третий порядок 3- второй порядок, 4-первый порядок аппроксимации
плотности теплового потока.
Re
Рис.9 Теплообмен при турбулентном течении в прямоугольном канале на расчетной сетке Nx*Ny*Nz=60*60*60 1- среднее экспериментальное, Расчет:2- третий порядок 3- второй порядок, 4-первый порядок аппроксимации
плотности теплового потока
Как видно из рисунков на грубых сетках, точность расчетов по теплообмену ламинарных и турбулентных потоков с аппроксимаций первого порядка составляет до 12%, точность расчетов с аппроксимаций второго порядка на этих же сетках составляет 8%,точность расчетов с аппроксимаций второго порядка на этих же сетках составляет 6%; на частых сетках точность расчетов по теплообмену ламинарных и турбулентных потоков с аппроксимаций первого порядка составляет 6%, а точность расчетов с аппроксимациями третьего и второго порядка на этих же сетках составляет 2% и 3%.
Разработанная методика использовалась для расчетов профиля скорости, турбулентного напряжения, температуры, коэффициента трения от числа Маха и числа Стэнтона (St) от степени турбулентности с целью определения пределов применимости модели и относительной точности. Полученные сопоставительные результаты определили преимущества аппроксимации второго и третьего порядка плотности теплового потока и при расчете конвективного теплообмена Рис.10.
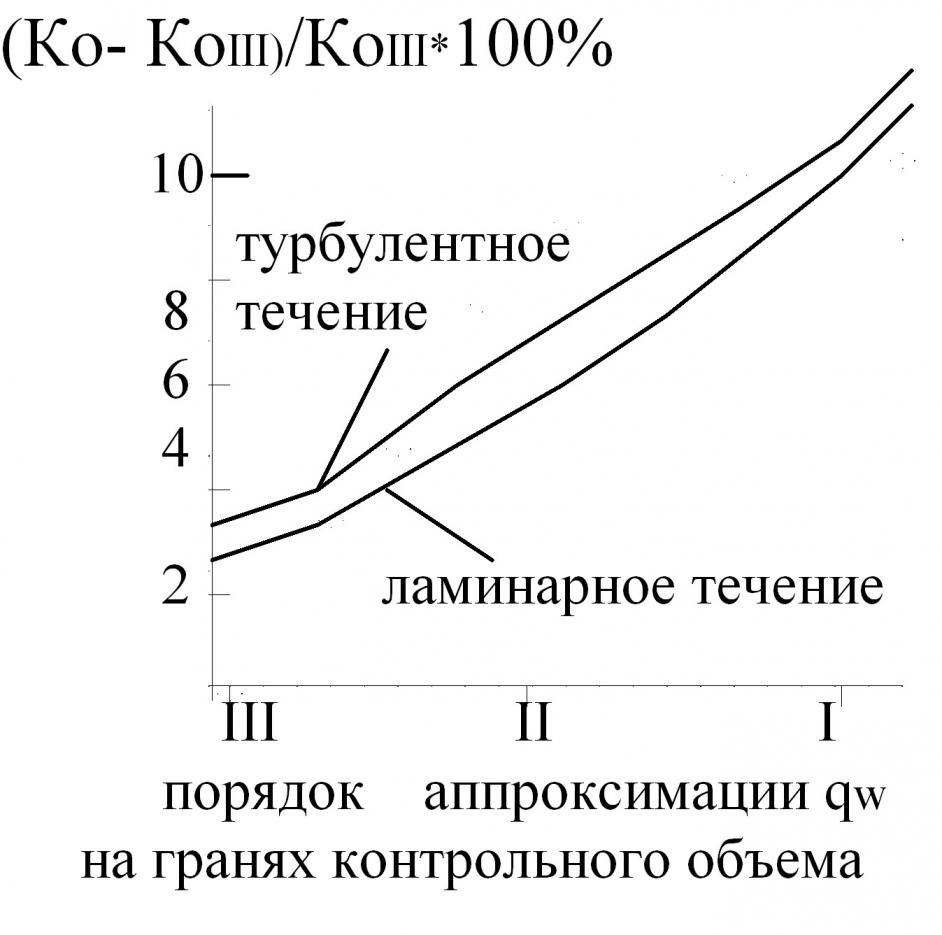
Рис10. Относительная точность расчета теплообмена Ко=Nu/ (Pr 0.43)(Pr/Prcт) 025)
В ЧЕТВЕРТОЙ ГЛАВЕ приведены результаты применения разработанной модели и методики для численного анализа температурного состояния лопаток газовой турбины. При этом решение задачи теплоотдачи «горячий газ- поверхность лопатки» реализовано в виде задания для расчета «теплопроводность в стенки лопатки» одного из типов граничных условий: первого, второго рода или третьего рода, определенных из экспериментов и полуэмпирических соотношений, полученных для неохлаждаемой или конвективно-охлаждаемой лопатки. В расчетах задавалось граничное условие третьего рода: значения температуры торможения газа на поверхности лопатки и задание локального распределения параметров теплоотдачи ![]() по профилю лопатки. Уравнение теплопроводности решается в соответствии с алгоритмом, разработанной методики. На рис. 11-12 представлены результаты расчета температуры неохлаждаемой лопатки в сопоставлении с опубликованными экспериментальными данными. Решения получены для аппроксимаций различного уровня: кривая 1-расчет с аппроксимацией третьего порядка, 2-расчет с аппроксимацией первого порядка,
по профилю лопатки. Уравнение теплопроводности решается в соответствии с алгоритмом, разработанной методики. На рис. 11-12 представлены результаты расчета температуры неохлаждаемой лопатки в сопоставлении с опубликованными экспериментальными данными. Решения получены для аппроксимаций различного уровня: кривая 1-расчет с аппроксимацией третьего порядка, 2-расчет с аппроксимацией первого порядка, ![]() - эксперимент. Результаты показали, что распределение температур на рабочей неохлаждаемой лопатке на грубой сетке с аппроксимацией первого порядка составляет 9%, второго 6%, а третьего 4%.На частых сетках результаты соответственно 6%, 4%, 3% точности соответственно.
- эксперимент. Результаты показали, что распределение температур на рабочей неохлаждаемой лопатке на грубой сетке с аппроксимацией первого порядка составляет 9%, второго 6%, а третьего 4%.На частых сетках результаты соответственно 6%, 4%, 3% точности соответственно.
Рис.11 Рис.12
Nx, Ny, Nz =20*20*20 Nx, Ny, Nz =60*60*60 Изменение относительной температуры Изменение относительной температуры
по относительной высоте пера лопатки. по относительной высоте пера лопатки.
Результаты расчета трехмерного поля неохлаждаемой лопатки даны на рис.13.
Рис.13
Температурное поле в сечениях по высоте пера рабочей неохлаждаемой лопатки при аппроксимации третьего порядка для плотности теплового потока.
Для оценки возможности применения методики для расчета температуры охлаждаемых лопаток рассматривается наиболее простой вариант конвективно-охлаждаемой сопловой лопатки без внутренних интенсификаторов теплообмена с граничными условиями третьего рода. Как и для случая неохлаждаемой лопатки была определена температура торможения горячего газа, ![]() , но с учетом охлаждения стенки лопатки отбираемым из компрессора охлаждающим воздухом с учетом распределения
, но с учетом охлаждения стенки лопатки отбираемым из компрессора охлаждающим воздухом с учетом распределения ![]() и температуры воздуха на оси канала, которая при известной температуре входа в лопатку по высоте определялась итерациями. Изменение относительной температуры среднего участка по относительной длине пера рабочей с гладким каналом лопатки представлено на рис.14 при Gв=2% в соответствии с опубликованными экспериментальными данными. Кривая 1-расчет с аппроксимацией первого порядка, 2- аппроксимация второго порядка,- эксперимент. На рис.15 представлена расчетная эффективность охлаждения среднего участка профиля лопатки с аппроксимацией второго порядка.
и температуры воздуха на оси канала, которая при известной температуре входа в лопатку по высоте определялась итерациями. Изменение относительной температуры среднего участка по относительной длине пера рабочей с гладким каналом лопатки представлено на рис.14 при Gв=2% в соответствии с опубликованными экспериментальными данными. Кривая 1-расчет с аппроксимацией первого порядка, 2- аппроксимация второго порядка,- эксперимент. На рис.15 представлена расчетная эффективность охлаждения среднего участка профиля лопатки с аппроксимацией второго порядка.
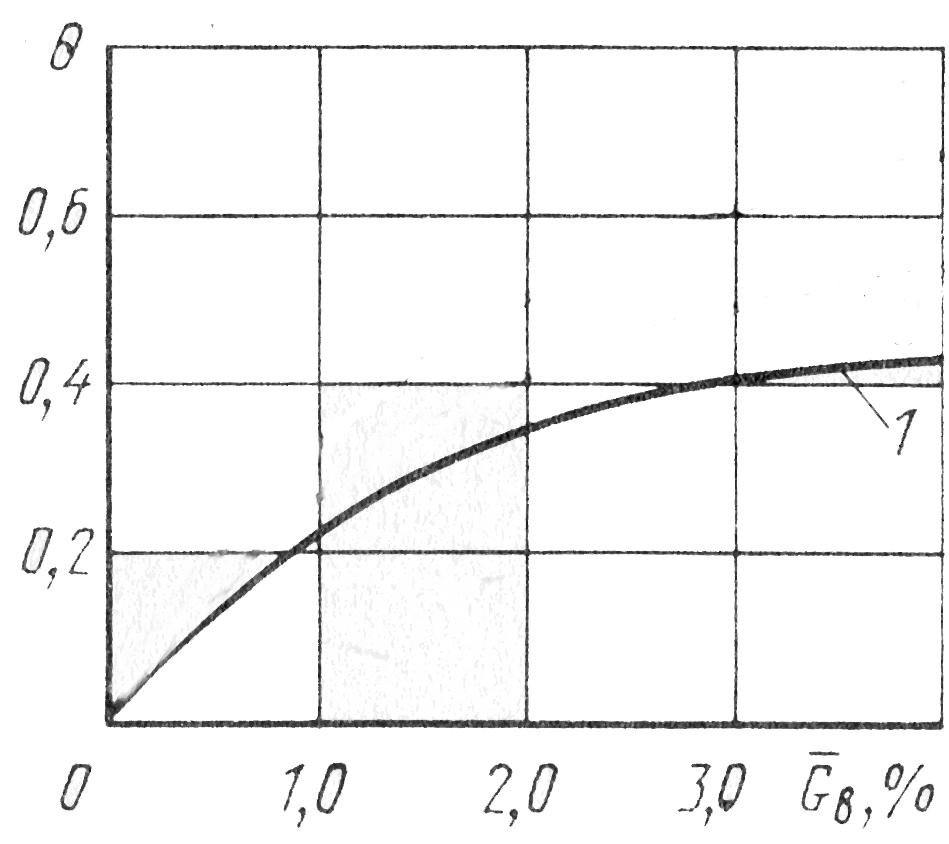
Рис.14 Изменение относительной Рис.15 Эффективность охлаждения среднего
температуры среднего участка участка профиля с аппроксимацией
по относительной длине второго порядка плотности теплового потока. пера лопатки.
Трехмерный расчет конвективно-охлаждаемой лопатки с гладкой стенкой, при задании граничного условия третьего рода со стороны горячего газа представлен на рис.16. Изменение поля температуры профиля лопатки соответствует относительному расходу воздуха Gв=2%. Расчет поля скорости и давления для сопловых лопаток с гладкой внутренней поверхностью стенки произведен на основе решения трехмерного осредненного по времени уравнения Навье-Стокса (уравнения Рейнольдса). Зависимость коэффициента гидравлического сопротивления гладких каналов срединного участка профиля лопатки от числа Рейнольдса дано на Рис.17
Рис.16. Температурное поле в сечениях по высоте пера рабочей конвективно-охлаждаемой лопатки при аппроксимации третьего порядка для плотности теплового потока.
Рис.17 Зависимость коэффициента гидравлического сопротивления гладких каналов срединного участка профиля лопатки от числа Рейнольдса:1-расчет при аппроксимации третьего порядка для плотности теплового потока; - эксперимент
На Рис. 18 представлено распределение относительной температуры стенки по относительной высоте пера сопловой лопатки.
Рис. 18 Распределение относительной температуры стенки по относительной высоте пера сопловой лопатки 1,2,3-.расчетные распределения
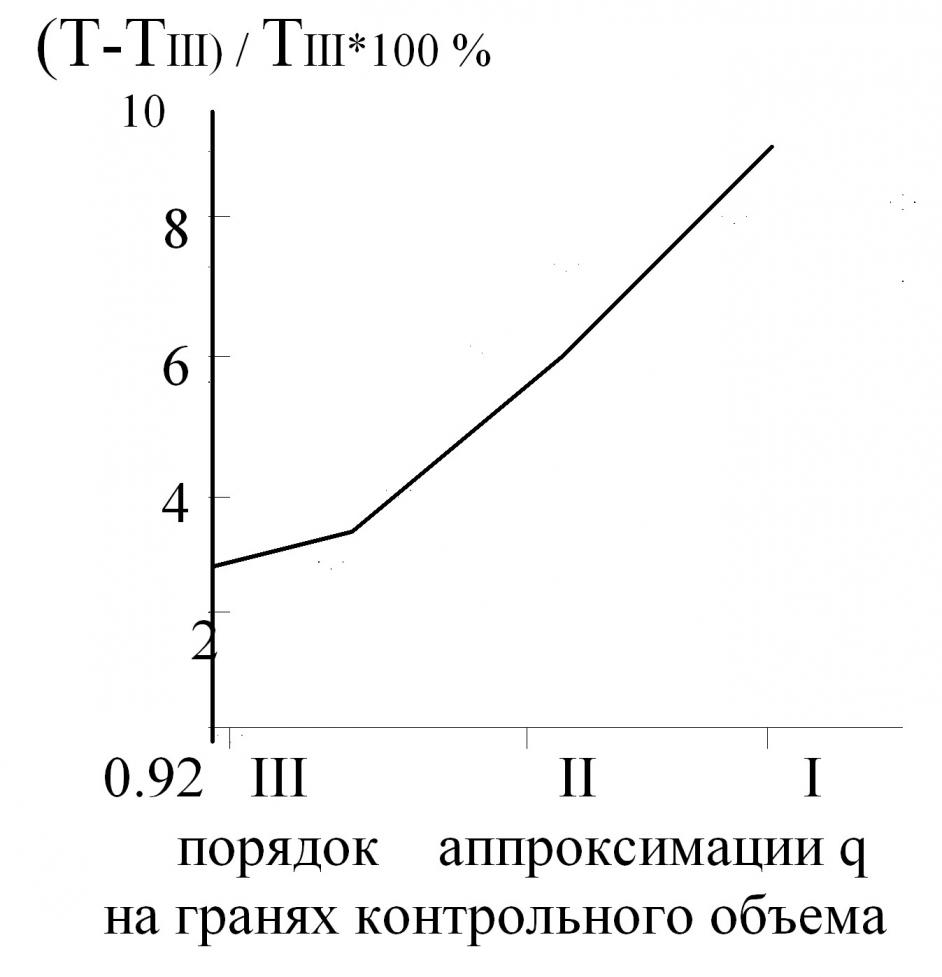
Рис. 19 Относительная точность расчета температуры стенки лопатки.
Сопоставление расчетных и экспериментальных результатов показало, что в этом случае аппроксимации величины плотности теплового потока на гранях контрольного объема третьего порядка они имеют точность до 2%-3%,второго порядка 2%-4%,первого порядка 3%-5%. Причем на грубой сетке точность расчета с аппроксимацией первого порядка составляет 9%,второго- 6% третьего-4% Рис.19, Рис20. На частых сетках точность расчетов соответственно-6%,4% 3%.
Таким образом, разработанный алгоритм расчета температурного состояния лопаток турбин с применением метода контрольного объема позволяет полу-чать приемлемую точность уже на грубых сетках, начиная с аппроксимации второго порядка для плотности теплового потока на гранях контрольного объема. Для более частых сеток точность расчетов может быть повышена.
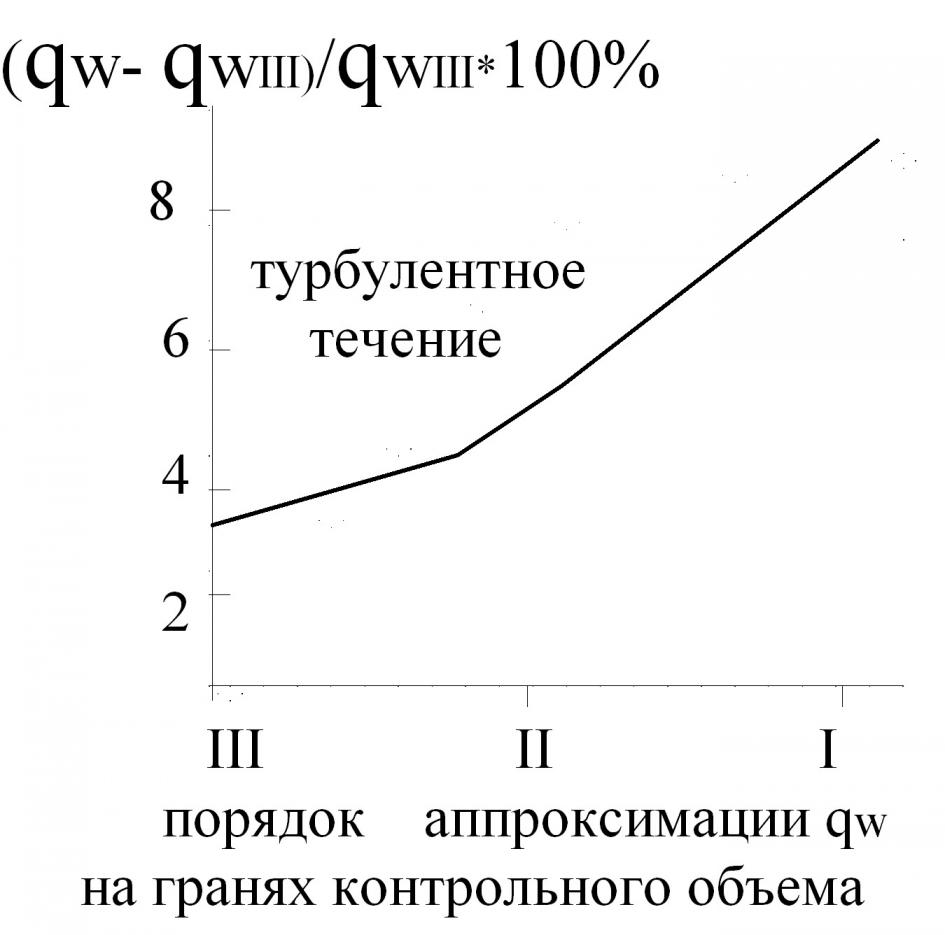
Рис20. Относительная точность расчета удельного теплового потока в стенку лопатки
ОСНОВНЫЕ РЕЗУЛЬТАТЫ И ВЫВОДЫ
1.Создание новых поколений газотурбинных двигателей при условии сокращения сроков и затрат на их проектирование определяет необходимость развития аналитических методов расчета и исследования температурного состояния лопаток газовой турбины в направлении формирования расчетных моделей, обеспечивающих повышение точности расчетов при минимизации трудоемкости их выполнения. В связи с этим для повышения эффективности создания газотурбинного двигателя целесообразно применять комплексный подход при аналитическом исследовании температурного состояния охлаждаемых и неохлаждаемых лопаток турбины, основанный на развитии метода контрольного объема.
2. Для реализации комплексного подхода к исследованию температурного состояния лопаток газовой турбины разработана обобщенная трехмерная математическая модель, учитывающая переменность теплофизических и термодинамических свойств материала лопатки и окружающей среды.
3.Сформированы расчетные методики, обеспечивающие повышение адекватности определения температурного состояния неохлаждаемых и охлаждаемых лопаток газовой турбины, за счет более полного учета факторов теплообмена в лопатке.
4.Установлены оптимальные уровни сложности математического описания теплообменных характеристик, обеспечивающие максимальную точность определения температурных полей в лопатках методом контрольного объема при эксплуатационных условиях теплообмена в турбине. При этом отмечено, что предельное насыщение точности расчетного результата метода контрольного объема, как для неохлаждаемых лопаток, так и для конвективно- охлаждаемых не превышает аппроксимаций третьего порядка величины плотности теплового потока на гранях контрольного объема.
5. Сравнение полученных расчетных закономерностей изменения температурного состояния лопаток с экспериментальными данными показало, что переход к аппроксимации третьего порядка величины плотности теплового потока на гранях контрольного объема позволяет понизить относительную погрешность определения температуры для неохлаждаемых лопаток на 5%-6%, а для каналов охлаждения лопаток на 7%-8%, что при температуре газа ~1800К и современном допустимом уровне температуры стенки лопатки 1200К~1300К составляет 60-100 градусов.
6. Разработанные модели, расчетные методики, алгоритмы и программное обеспечение позволяют повысить точность определения температурных полей лопаток без существенного увеличения времени и трудоемкости расчетов.
Основные положения диссертации отражены в следующих публикациях:
1. Красавин Д.А., Дмитренко А.В. «Температурное поле рабочей лопатки турбины, изготовленной из композиционного материала.» Всероссийская научно-техничесая конференция «Новые технологии и материалы»,НМТ- 2006,T.2, cтр58-59.
2. Красавин Д.А., Дмитренко А.В. Определение трехмерного поля температуры в телах с источником тепла. Научные труды МАТИ 2006,Т.5, стр.54
3. Красавин Д.А, Дмитренко А.В. Определение поля температуры в рабочей лопатке турбины. Тезисы докладов XXX Гагаринских чтений, «МАТИ»-РГТУ,M.,2006Т.8,с.187-188
4.Дмитренко А.В. Красавин Д.А. Расчет трехмерного поля температуры при аппроксимации второго порядка плотности теплового потока на гранях контрольного объема Третья Российская Национальная Конференция по теплообмену РНКТ4, М.,2006.,Т.3., с.200-203.
5 Красавин Д.А., Дмитренко А.В. Исследование развития ламинарного потока в прямоугольных трубах. Научные труды МАТИ.,2006.Т.2, с35-38
6. Дмитренко А.В., Красавин Д.А. Расчет трехмерного процесса теплопередачи при течении газа в лопатке рабочего колеса методом контрольного объема. ХVI Школа-семинар под руководством ак. РАН А.И.Леонтьева «Проблемы газодинамики и тепломассообмена в энергетических установках» Cанкт-Петербург, Россия, 2007,Т.2,с121-124.
7. Дмитренко А.В. Красавин Д.А. Разработка методики и алгоритма проектирования системы охлаждения лопаток турбин энергетических установок. Авиационная промышленность №3, стр.16-21, Москва, 2008г.
Подписано в печать 12.12. 2008г. Объем 1,0 п.л. Тираж 100 экз.Заказ №163_
Издательский центр “МАТИ”
109240, г. Москва, Берниковская наб., 14 стр.2

