Оценка аппроксимативных возможностей линейных операторов в связи с конечномерным представлением сигналов
На правах рукописи
Батухтина Ирина Юрьевна
оценка аппроксимативных возможностей
линейных операторов в связи с конечномерным представлением сигналов
Специальность 05.13.17 – теоретические основы информатики
АВТОРЕФЕРАТ
диссертации на соискание ученой степени
кандидата физико-математических наук
Красноярск – 2009
Работа выполнена в Читинском государственном университете (ЧитГУ)
на кафедре информатики, вычислительной техники и прикладной математики
Научный руководитель кандидат физико-математических наук, доцент
Абакумов Юрий Георгиевич
Официальные оппоненты: доктор физико-математических наук, профессор
Половинкин Владимир Ильич
доктор физико-математических наук, профессор
Попов Алексей Михайлович
Ведущая организация Тверской государственный университет
Защита состоится «07» апреля 2009 года в 14 часов на заседании диссертационного совета Д 212.099.11 при Сибирском федеральном университете по адресу: г. Красноярск, ул. Киренского, 26, ауд. УЛК 115.
С диссертацией можно ознакомиться в библиотеке Сибирского федерального университета по адресу: г. Красноярск, ул. Киренского, 26, ауд. Г274.
Автореферат разослан «___»____________ 2009 г.
| Ученый секретарь диссертационного совета кандидат технических наук, доцент |  | Л.И.Покидышева |
ОБЩАЯ ХАРАКТЕРИСТИКА РАБОТЫ
Актуальность темы. Обработка как одномерных так многомерных сигналов является основой многих направлений техники. Преобразование сигналов можно рассматривать, используя принципы теории приближения, и в частности с помощью линейных операторов 
.
Одной из характеристик приближения функции или степени достоверности представления сигнала конечной суммой, является величина отклонения представляющей суммы сигналов относительно исходного (представляемого) сигнала. В работе предложено интерпретировать эту величину в терминах аппроксимационных оценок вида 
(норма чебышевская), где 
– представляемый многомерный сигнал или приближаемая функция, 
– последовательность r-мерных представляющих сигналов или приближающая последовательность линейных операторов, для которых выполнены условия 
, 
(если не оговорено противное), 
– целое, 
.
В теории сигналов представляющие суммы, т.е. значения операторов 
, являются, как правило, частными суммами рядов Фурье по ортонормированной системе функций (одной или нескольких переменных) или частными суммами методов суммирования рядов Фурье[1]
(методы суммирования могут быть представлены как положительными операторами, так и операторами, положительными не являющимися). В диссертации система приближающих функций ортонормированной не предполагается, а рассматривается общий случай произвольной системы функций.
Получение аппроксимационных оценок 
является одной из основных задач теории приближений[2]. Величина 
зависит от характеристик 
и от тех или иных характеристик аппроксимирующих операторов. В случае положительных операторов особо выделим характеристику 
(ограничительные неравенства – оценки снизу величины 
).
Ограничительные неравенства определяют предел возможности приближения теми или иными аппроксимирующими последовательностями. Что касается теории сигналов, величина 
показывает, что возможности представления многомерного сигнала конечной суммой имеют свои ограничения, иначе говоря, 
– показатель нижней границы, лучше которой нельзя преобразовать сигнал конечной суммой по заранее выбранной системе сигналов.
Первое ограничительное неравенство было доказано В.С. Виденским для случая 
. Следуя основным идеям В.С. Виденского, Ю.Г. Абакумов разобрал случай для 
. Р.К. Васильевым было получено ограничительное неравенство для произвольного целого r>1. Хотя оценка Васильева является универсальной для линейных положительных операторов, но возможно усиление данного неравенства. Для случая неположительных операторов ограничительные неравенства, в той мере, в какой это было сделано в диссертации, ранее рассмотрены не были.
Цель работы. Целью работы являлось получение оценок снизу (или оценок ограничительного типа) для величин характеризующих аппроксимативные свойства операторов и интерпретация этих результатов в терминах конечномерного представления сигналов.
Новизна научных результатов. В работе впервые получены:
1) ограничительное неравенство на основе слоистой решетки 
для произвольного целого r;
2) оценка снизу выражений содержащих характеристики аппроксимативных свойств операторов класса 
, на основе аппроксимационных оценок для функций классов 
, 
и 
;
3) ограничительное неравенство на основе использования кубической решетки 
;
4) ограничительное неравенство на основе шахматной решетки 
для произвольного целого r;
5) оценка, не содержащая неопределенных слагаемых, для величины 
на основе гексагональной решетки 
.
Теоретическая и практическая значимость. Теоретическая значимость работы заключается в том, что для исследования вопросов теории приближений и вопроса о конечномерном представлении сигналов впервые систематически используются свойства упаковок. Практическая значимость заключается в новизне полученных оценок.
Апробация работы. Результаты диссертации докладывались:
- на Восьмом Всероссийском симпозиуме по прикладной и промышленной математике. Адлер, 2007
- в Забайкальском государственном педагогическом университете, на семинаре кафедры математического анализа;
- на научных семинарах Энергетического института ЧитГТУ, г. Чита, 2005 – 2008 г.;
- на семинарах кафедры ИВТ и ПМ Читинского государственного университета (2005-2008 гг.);
- на Второй межрегиональной научно-практической конференции: «Энергетика в современном мире» ЧитГТУ, г. Чита, 2003 г.;
- на Третьей межрегиональной научно-практической конференции «Технические науки, технологии и экономика» ЧитГТУ, г. Чита, 2003 г.;
- на Всероссийской научно-практической конференции, Чита, ЗабГПУ 2004 г;
- на IV межрегиональной научно-практической конференции «Кулагинские чтения» Чита: ЧитГУ, 2004 г.
Публикации. По теме диссертации опубликовано 14 печатных работ.
Структура и объем работы. Диссертация состоит из введения, двух глав, заключения и списка литературы. Работа изложена на 69 листах, содержит список литературы, включающий 48 наименований.
КРАТКОЕ СОДЕРЖАНИЕ РАБОТЫ
Во введении указаны актуальность темы исследования, приведен обзор литературы по теме исследования, цель, методы исследования, а также сформулированы основные результаты, полученные в диссертации.
Первая глава ставит своей задачей получение ограничительных неравенств величины 
для линейных положительных операторов, характеризующих скорость убывания нормы отклонения представляющих сигналов относительно входных. В пунктах 1.1-1.3 излагаются известные результаты, касающиеся аппроксимирующих последовательностей линейных положительных операторов, и доказана, имеющая ключевое значение лемма.
Лемма связывает задачу получения ограничительных неравенств величины 
с известной задачей нахождения наиболее плотных упаковок шаров в r-мерных пространствах[3].
Лемма 1.1. Если существует множество, состоящее из 
, попарно не пересекающихся, открытых шаров, диаметра 
и с центрами, принадлежащими 
, то выполняется неравенство
,
где 
- последовательность линейных положительных операторов.
Получение оценки величины 
сводится к задаче подбора множества из n+1 шаров, удовлетворяющих условию леммы. При этом оценка будет тем сильнее, чем больше диаметр шаров 
.
В пункте 1.4 и 1.5 на основе известных решетчатых упаковок, рассмотрены частные случаи 
и r=2.
Получены следующие ограничительные неравенства:
- Если
– линейный положительный оператор, где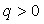 
, то оценка имеет вид
.
- В периодическом случае, если
то
.
- Для
, одна из оценок имеет вид
.
В пункте 1.6 излагается схема получения значения диаметра 
, фигурирующего в лемме 1.1, через n – размерность аппроксимирующего пространства. Это можно сделать, используя известные значения плотности какой-либо конкретной решетчатой упаковки шаров. Оценка будет тем сильнее, чем выше эта плотность.
В пункте 1.7 для 
на основе использования кубической решетки 
получена оценка
,
где 
.
На основе общей схемы (из пункта 1.6) в пп.1.8 и 1.9 получены ограничительные неравенства на основе решеток 
и 
(см. теорему 1.1).
Предварительно в пункте 1.8 приведен авторский вывод аналитического выражения плотности r-мерной упаковки шаров на основе решетки 
(образующие векторы базиса этой решетки являются ребрами правильного симплекса).
В пункте 1.9 получено аналитическое выражение плотности r-мерной упаковки на основе шахматной решетки 
(центрами шаров упаковки, являются точками с целыми координатами, в сумме дающие четное число).
В конце главы сформулирован итоговый результат.
Теорема 1.1. Пусть 
– последовательность линейных положительных операторов. Тогда для величины
выполняется оценка
.
Также выполняется асимптотически более сильная оценка
.
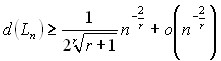Кроме того, при 
верна более сильная оценка
.
Полученная величина 
показывает, что при представлении сигналов конечной суммой с помощью положительного метода (оператора) найдется сигнал, который искажается на величину 
, где 
– мера области определения r-мерного сигнала (в одномерном случае – длина временного промежутка). Величина 
является чисто теоретической оценкой, так как сигнал, который искажается на эту величину (т.е. сигнал 
) при больших размерах области задания (или временного промежутка в одномерном случае) принимает нереально большие (с практической точки зрения) значения. Роль практического ориентира играет величина 
. Множитель к ней следует подбирать, исходя из того, какое численное значение (в соответствующих единицах) может принимать сигнал, подлежащий представлению.
Вторая глава относится к изучению аппроксимативных свойств линейных операторов 
или 
, удовлетворяющих условию 
, m>0 – целое, 
, 
, 
, 
- действительные. Это условие записывается следующим образом: при фиксированном n и х выполняется
.
Основной задачей, для неположительных операторов, остается определить теоретически возможную близость последовательностей 
к его исходному сигналу. Показателями аппроксимативных свойств последовательностей операторов являются величины
.
Оценки ограничительного типа для таких последовательностей впервые получены в диссертационной работе. При получении оценок использовалась схема В.С. Виденского с внесением в нее некоторых новых элементов.
Вторая глава содержит шесть пунктов, и 16 теорем.
В пункте 2.2 приводятся известные на настоящий момент аппроксимационные оценки. Эти оценки используются в дальнейшем для получения ограничительных неравенств.
В пункте 2.3 используются оценки для функций класса 
.
Приведем некоторые из полученных оценок ограничительного типа, и как следствие к ним некоторые теоремы.
Если аппроксимирующая последовательность 
удовлетворяет условию 
, то выполняется следующее неравенство
. (1)
На его основе получены следующие результаты:
Теорема 2.1. Для операторов 
, таких, что 
и удовлетворяющих условию 
, неверно, по крайней мере, одно из утверждений:
(1) 
,
(2) 
,
(3) 
.
Теорема 2.2. Пусть операторы 
удовлетворяют условиям теоремы 2.1 и, кроме того, 
, 
. Тогда, если 
имеет точный порядок 
, то для любого 
существует 
, такое, что для 
.
Следствие 2.1. При выполнении условий теоремы 2.2 имеет место неравенство
.
Для операторов вида
, (2)
где 
- четное положительное тригонометрическое ядро,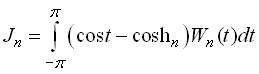 
– нормирующий множитель. В этом случае, размерность пространства, в которое 
отображает 
, не совпадает с n, и мы обозначаем ее 
. С учетом, того, что 
(так как ядро оператора 
- четное) оценка преобразуется в следующую
. (3)
На основе неравенства (3) получается ряд утверждений.
Теорема 2.4. Если операторы вида (2) удовлетворяют условиям:
(1) 
имеет точный порядок 
,
(2) 
,
то для любого 
существует 
, такое, что для 
выполняется неравенство
.
Следствие 2.2. При выполнение условий теоремы 2.4 имеет место неравенство
.
Частным видом операторов (2) являются конструкции этого вида, для которых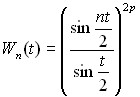 
. Хорошо известны аппроксимирующие операторы
,
которые называют обобщенными операторами Джексона. При 
получаются собственно операторы Джексона, при 
операторы Фейера. Будем обозначать (имея ввиду сокращение 
),
=
,
где 
.
Теорема 2.5. Если для 
выполнено условие 
и 
имеет точный порядок 
, то
.
Для операторов 
, удовлетворяющих условию 
, получено ограничительное неравенство
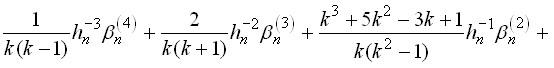
, (4)
на основе которого получена теорема.
Теорема 2.6. Если последовательность операторов 
, удовлетворяет условию 
, при этом 
если, кроме того, 
имеет точный порядок 
, 
, 
, 
, 
, то
.
В работах Е.М. Ершовой[4]
рассматривались операторы вида
, (5)
где 
- четное положительное тригонометрическое ядро, 
, 
.
Тогда неравенство (4) для операторов вида (5) примет следующую форму:
. (6)
В конкретном случае, если 
- обобщенное ядро Джексона. Тогда 
. Обозначим, операторы вида (5) через 
.
Из (6) следует, в частности, такое утверждение.
Теорема 2.7. Если для операторов 
выполняется 
, 
, 
имеет точный порядок 
, то
.
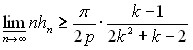В пункте 2.4 получены оценки для функций класса 
. Если 
удовлетворяет условию 
, то
,
а в периодическом случае
.
Если же ограничиться операторами свертки, то получится оценка
.
Следствия, вытекающие отсюда, слабее соответствующих утверждений, вытекающих из оценок для класса 
.
Остановимся на случае, когда 
удовлетворяют условию 
. Исходная оценка Ю.Г. Абакумова[5]
преобразуется в случае операторов 
в ограничительное неравенство
(7)
а в периодическом случае, если 
операторы свертки – в неравенство
(8)
Отсюда, в качестве заключения следуют теоремы:
Теорема 2.10. Если 
, 
удовлетворяют условию 
, где n – размерность пространства 
тогда из равенств: 
, 
, 
, 
, 
, 
хотя бы одно не верно.
Теорема 2.11. Если 
, является оператором типа свертки, при этом 
имеет точный порядок 
, и, кроме того, 
удовлетворяет условию 
, тогда из равенств: 
, 
, 
хотя бы одно не верно.
Теорема 2.12. Если последовательность операторов 
удовлетворяет условию теоремы 2.10, кроме того выполняются равенства: 
, 
, 
, 
, 
и 
имеет точный порядок 
, тогда
.
Теорема 2.13. Если последовательность операторов 
удовлетворяет условию теоремы 2.11, и если 
, 
, 
имеет точный порядок 
, то
.
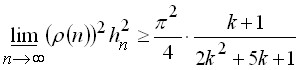Для операторов 
величина 
имеет значение 
.
Для этих операторов (7) принимает вид
.
В пункте 2.5 получены оценки для функций класса 
.
Для операторов удовлетворяющих условию 
получаем ограничительное неравенство
В качестве заключения следует теорема:
Теорема 2.14. Если 
, 
удовлетворяют условию 
, 
, тогда из равенств: 
, 
, 
, 
, 
, 
, 
хотя бы одно не верно.
В периодическом случае, если ограничиться операторами свертки, то получится оценка
. (9)
Если же операторы свертки отображают 
в 
, то (9) переходит в неравенство
. (10)
Применим (10) к операторам свертки
где 
.
Отсюда следует утверждение:
Теорема 2.16. Если для операторов 
выполнены условия: 
имеет точный порядок 
, 
, 
, то
.
Полученные в диссертационной работе неравенства для величин 
и 
, составляющих правые части аппроксимационных оценок (зависящие от характеристик входных сигналов 
и от тех или иных характеристик аппроксимирующих последовательностей операторов 
, или выходных сигналов) характеризуют скорость убывания указанной нормы или применительно к теории сигналов определяют степень достоверности представления сигнала. Причем, величина 
является характеристикой аппроксимативных свойств линейных положительных операторов, а 
для неположительных.
Итак, как можно видеть, ограничительные неравенства являются следствием аппроксимационных оценок для классов 
или 
.
Подробное изучение операторов, удовлетворяющих условиям 
и 
начато сравнительно недавно, в связи с чем пока ощущается определенный «дефицит» аппроксимационных оценок. Особенно это относится к многомерному случаю.
Таким образом, дальнейшее продвижение в получение ограничительных неравенств зависит от получения аппроксимационных оценок.
Основные результаты диссертационной работы опубликованы в работах:
- Абакумов Ю. Г., Кобысова И.Ю. Некоторые оценки снизу для величин, характеризующих аппроксимативные свойства операторов. //Вестник ЧитГУ. Выпуск 34. – Чита: ЧитГУ, 2005. - С. 153 - 155.
- Кобысова И.Ю. Об оценке снизу величины
//Вестник ЧитГТУ. Выпуск 28. – Чита: ЧитГТУ, 2003. – С. 119-122. - Кобысова И.Ю. Оценка аппроксимативных возможностей линейных положительных аппроксимативных операторов //Вторая межрегиональная научно-практическая конференция «Энергетика в современном мире» (тезисы докладов). - Чита: ЧитГУ, 2003. – С. 154-156.
- Кобысова И.Ю. Некоторые возможности предварительного анализа аппроксимативных свойств операторов. //Третья межрегиональная научно-практическая конференция «Технические науки, технологии и экономика» (материалы конференции), ч.2. – Чита: ЧитГУ, 2003. – С. 102-104.
- Кобысова И.Ю. Оценка снизу одного показателя аппроксимативных возможностей линейных положительных операторов //Вестник ЧитГУ. Выпуск 32. – Чита: ЧитГУ, 2003. – С. 148-150.
- Кобысова И.Ю. Оценка снизу величин, характеризующих аппроксимативные свойства операторов //Проблемы прикладной математики: Всероссийская научно-практическая конференция. Тезисы докладов. – Чита: Издательство ЗабГПУ, 2004. – С. 24-26.
- Кобысова И.Ю. Оценка снизу величин, характеризующих аппроксимативные свойства операторов, на основе оценок для функций класса
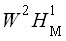//IV межрегиональная научно-практическая конференция «Кулагинские чтения» (материалы конференции). – Чита: ЧитГУ, 2004. ч. II. – 303 с. - Кобысова И.Ю. Об оценке снизу для величины
, связанных с линейными положительными операторами //Применение функционального анализа в теории прибл. – Тверь: ТвГУ, 2006. – С. 17-21. - Кобысова И.Ю., Шестакова О.Н. О связи аппроксимационных оценок и ограничительных неравенств. // Вестник ЧитГУ. Выпуск 35. – Чита: ЧитГУ, 2006. – С. 148-150.
- Батухтина И.Ю. Ограничительное неравенство для величины, характеризующей аппроксимативные свойства линейных операторов //Математический анализ и его приложение. Выпуск 6. – Чита: ЗабГГПУ, 2006. – С. 26 – 29.
- Батухтина И.Ю. Оценка снизу величин, характеризующих аппроксимативные свойства операторов для функции класса
//Математический анализ и его приложение. Выпуск 7. – Чита: ЗабГГПУ, 2007. – С. 11 – 13. - Батухтина И.Ю. Оценка снизу величин, характеризующих аппроксимативные свойства операторов для функции класса
//Математический анализ и его приложение. Выпуск 8. – Чита: ЗабГГПУ, 2008. – С. 17 – 19. - Батухтина И.Ю. Об одном ограничительном неравенстве теории приближения. – Обозрение прикл. и промышленной матем., 2008, т. 15, В.1, С. 110-111.
- Карымова Е.Ю., Кобысова И.Ю., Шерстюк Т.Ю. Тригонометрические операторы Баскакова и расчет цифровых фильтров нижних частот. – Обозрение прикл. и промышленной матем. М 2008, т. 15, В.2, С. 111.
Подписано в печать 27.02.2009 г. Формат 60х841/16
Объем 1,33 уч.-изд.л. Тираж 100 экз. Заказ №
________________________________________________________________Отпечатано в типографии
Читинского государственного университета,
672039, г. Чита, ул. Алекзаводская, 30
[1] Френкс Л.. Теория сигналов. Нью-Джерси, 1969 г. Пер. с англ., под ред. Вакмана Д.Е. М., «Сов.радио»,1974, 344 с.
[2] Н.П. Корнейчук. Точные константы в теории приближений. М.Наука. 1987
- 3 Конвей Дж. и Н.Слоэн. Упаковки шаров, решетки и группы. - М.: Мир, 1990.
[4] Ершова Е.М. Обобщенные операторы Фейера и Джексона //Применение функционального анализа в теории приближений. – Тверь: ТвГУ, 1997. – С. 69–72.
[5] Абакумов Ю.Г. О приближении некоторыми операторами класса 
функций класса 
//Вестник ЧитГУ. Выпуск 33. – Чита: ЧитГУ, 2004. – 166 с.
